Investigation of Flow and Heat Transfer Characteristics in Fractured Granite
Abstract
:1. Introduction
2. Materials and Study Methodology
2.1. Description of the Samples
2.2. Morphological Information of the Fractures
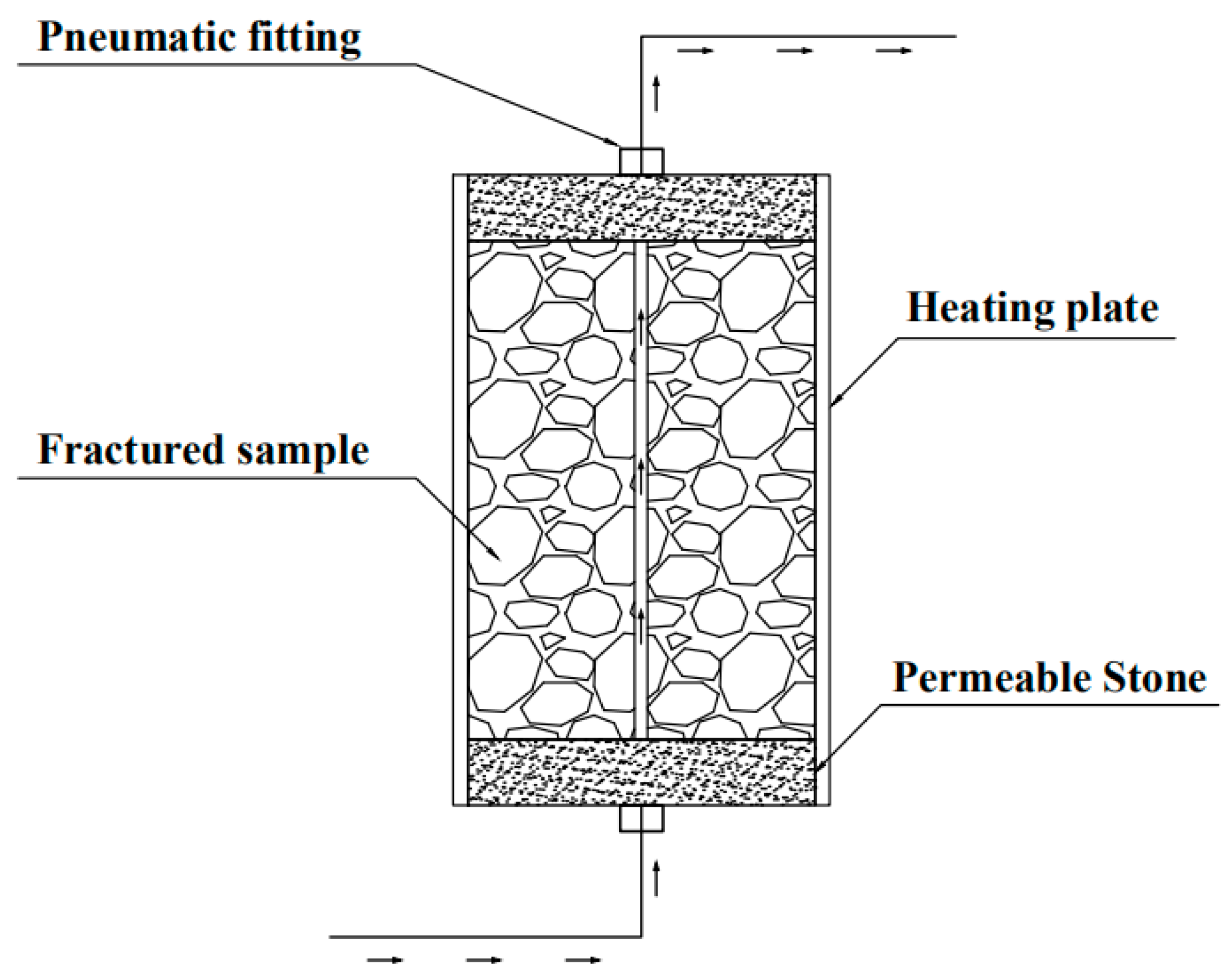
2.3. Experimental Setup
2.4. Testing Process
3. Results and Discussion
3.1. Hydraulic Properties
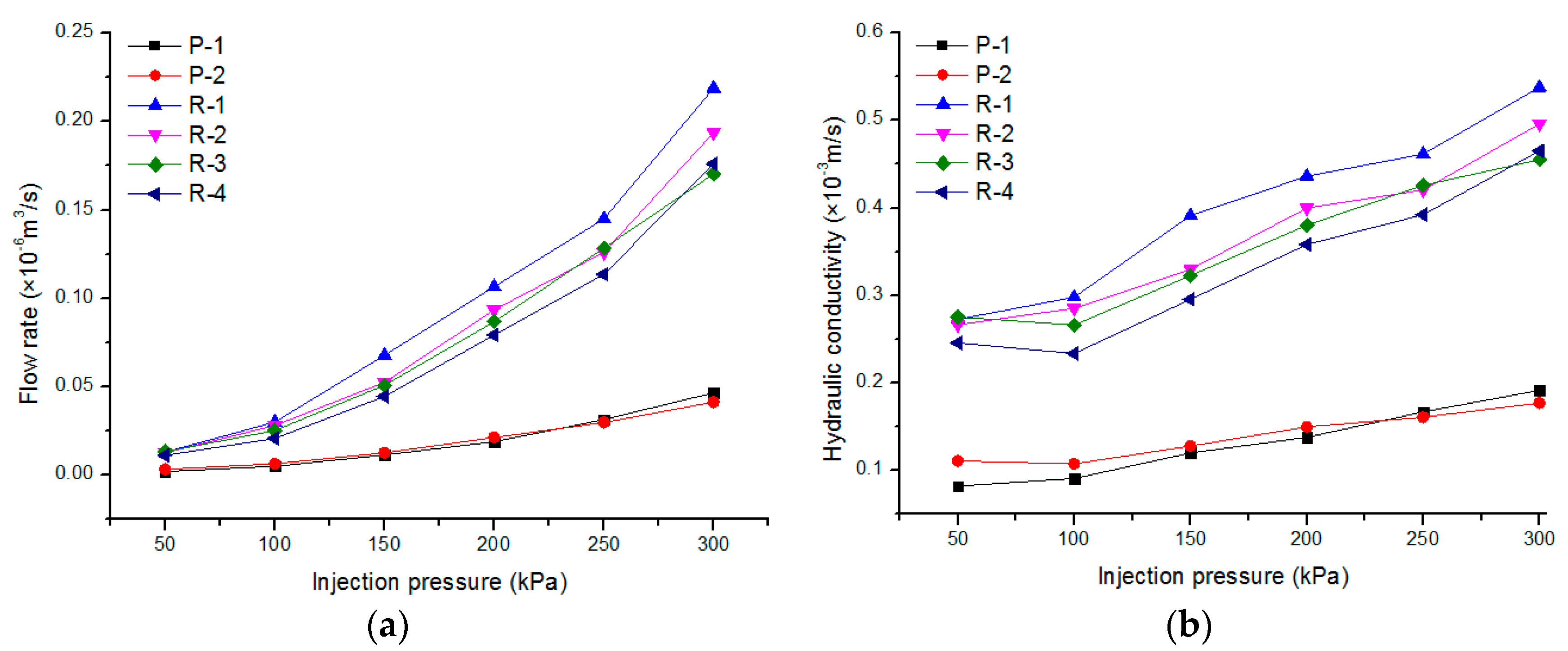
3.1.1. Effects of Injection Pressure
3.1.2. Influence of Confining Pressure
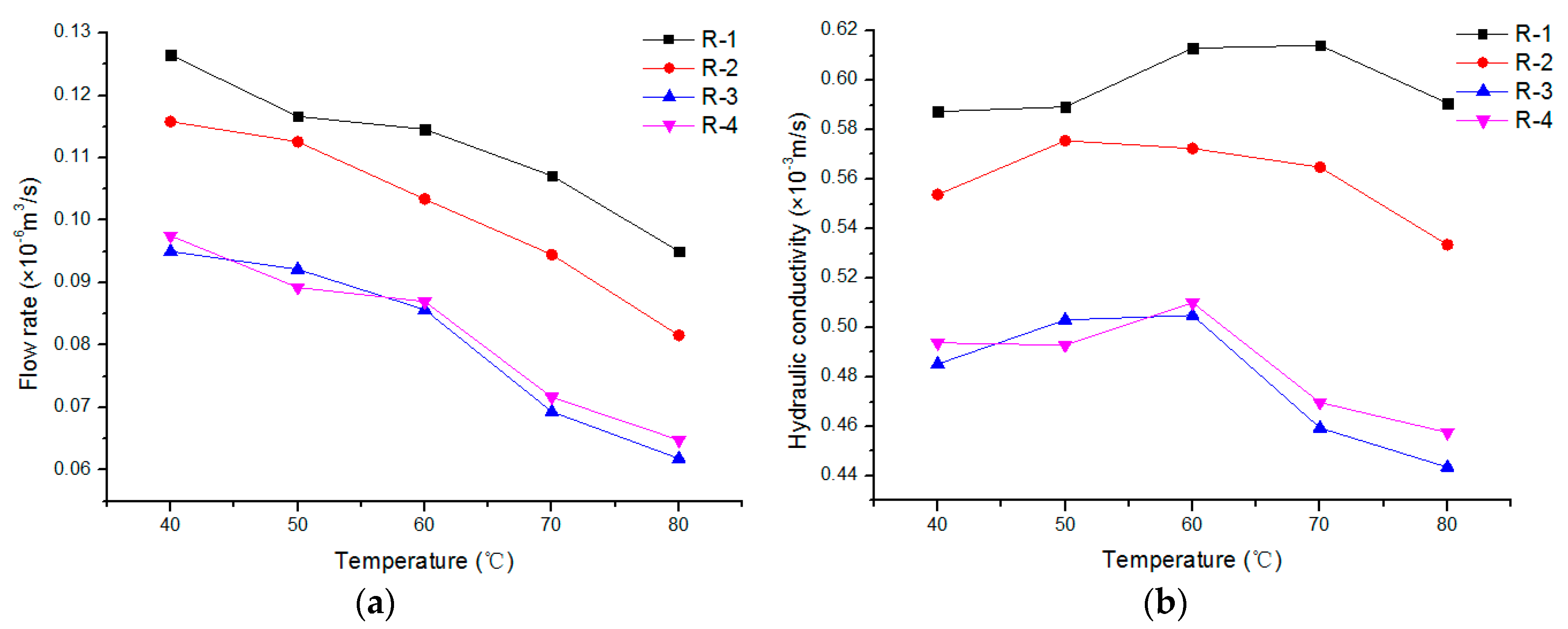
3.1.3. Influence of Temperature on Hydraulic Conductivity
3.1.4. Influence of Area Ratio
3.2. Heat Transfer Properties of the Fractured Granite
3.2.1. Analysis of Temperature Evolution
3.2.2. Heat Transport in the Rock Mass
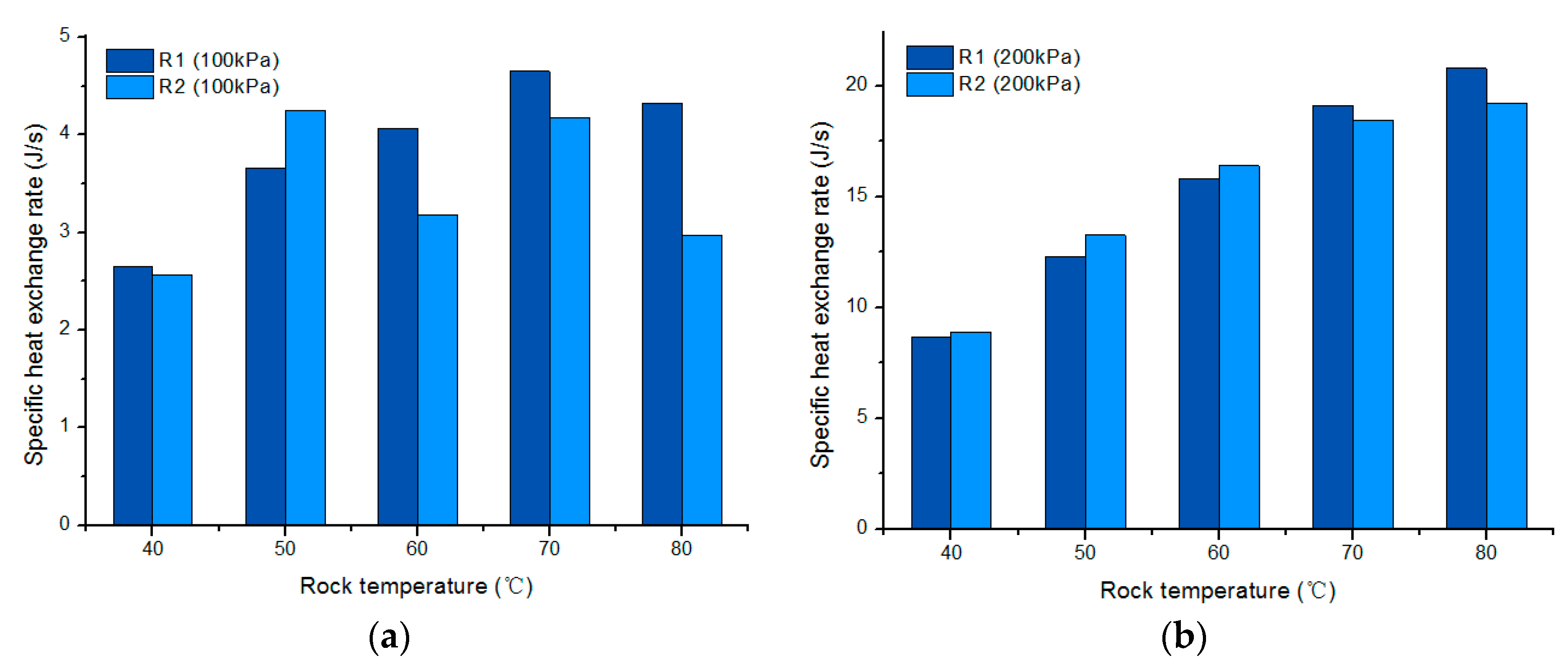
3.2.3. Specific Heat Exchange Rate
4. Conclusions
- A 3D digital model was built to analyze the morphological information of the fracture surface of the samples. The parameter of area ratio was used for the evaluation index of a fracture’s roughness. The results show that fractures with a larger value of area ratio have a higher hydraulic permeability. As revealed by the flowing tests, the hydraulic conductivity of rock mass increases with increasing injection pressure. Under constant injection pressure and temperature, the hydraulic conductivity of the rock mass decreases with the increase of confining pressure. Hydraulic conductivity increases first and then decreases with increasing rock temperature.
- Temperature distribution along the flow path: Fluid temperature keeps increasing along the flow path with an increase of rock temperature. Increase of temperature or decrease of injection pressure will raise the temperature at the same location.
- Heat transport of the rock samples: Temperature distribution at the fractured rock sample was imaged using an infrared camera. A temperature evolution process can be clearly observed during the injection of cold water into the fracture. The fluid temperature increases first along the fracture, then the rock temperature decreases from the fracture to the host rock. Therefore, the maximum temperature the fluid can reach decreases gradually with time and finally remains stable due to constant rock temperature. The findings indicate that the process of temperature evolution in a fractured rock system during the perfusion of a cold fluid can be revealed by the infrared imaging technique. Thermal gradient, thermal resistance, and even heat flux at the fracture surface can then be assessed quantitatively.
- The energy exchange rate fluctuates with time due to an unstable flow rate when the effective stress ratio is 1:4. The fluid flow rate is determined by many factors, including effective stress and temperature of the rock mass. By increasing the effective stress ratio to 1:2, the heat transfer exchange rate is positively related to the rock temperature. The specific heat transfer exchange rate of the rough fractured rock sample increases 2.16–2.40 times when the rock temperature increases from 40 to 80 °C with an injection pressure of 200 kPa under a confining pressure 400 kPa. By comparison with two different injection pressures, the specific heat transfer exchange rate increases from 3.12 to 6.46 times. Thus, both an increase of injection pressure and reaching a high temperature of rock mass can effectively improve the productivity of a geothermal plant.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Xu, T.; Zhang, Y.; Zeng, Z.; Bao, X. Technology progress in an enhanced geothermal system (Hot Dry Rock). Sci. Technol. Rev. 2012, 30, 42–45. [Google Scholar]
- Bолоцъло, И. Ф Кметодике лабораториого изучния подземных вод. Гuброzеоzuя Инэюеерная Гuолozuя 1941, 30–38. [Google Scholar]
- Lomize, G.M. Flow in Fractured Rocks; Gosemergoizdat: Moscow, Russia, 1951. [Google Scholar]
- Poмм, E.C. Flow Characteristics in Fractured Rocks; Издательстьо: Moscow, Russia, 1966. [Google Scholar]
- Louis, C.; Maini, Y.N. Determination of in-situ hydraulic parameters in jointed rock. Int. Soc. Rock Mech. Proc. 1970, 1, 235–245. [Google Scholar]
- Louis, C. A Study of Groundwater Flow in Jointed Rock and Its Influence on the Stability of Rock Masses; Imperial College: London, UK, 1969. [Google Scholar]
- Louis, C. Rock Hydraulics in Rock Mechanics; Springer: New York, NY, USA, 1974. [Google Scholar]
- Liu, Y.C.; Cai, Y.Q.; Liu, Q.S.; Wu, Y.S. Thermal-hydraulic-mechanical coupling constitutive relation of rock mass fracture interconnectivity. Chin. J. Geotech. Eng. 2001, 23, 196–200. [Google Scholar] [CrossRef]
- Zheng, S.H.; Zhao, Y.S.; Duan, K.L. An experimental study on the permeability law of natural fracture under 3-D stresses. Chin. J. Rock Mech. Eng. 1999, 18, 133–136. [Google Scholar] [CrossRef]
- Wang, Y. Coupling characteristic of stress and fluid flow within a single fracture. Chin. J. Rock Mech. Eng. 2002, 21, 83–87. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Li, B.; Wang, G.; Li, S. New advances in experimental study on seepage characteristics of rock fractures. Chin. J. Rock Mech. Eng. 2008, 27, 2377–2386. [Google Scholar] [CrossRef]
- Xiong, Y.B.; Zhang, C.H.; Wang, E.Z. A review of steady state seepage in a single fracture of rock. Chin. J. Rock Mech. Eng. 2009, 28, 1839–1847. [Google Scholar]
- Kuhlman, K.L.; Malama, B.; Heath, J.E. Multiporosity flow in fractured low-permeability rocks. Water Resour. Res. 2015, 51, 848–860. [Google Scholar] [CrossRef]
- Warren, J.E.; Root, P.J. The Behavior of Naturally Fractured Reservoirs. Soc. Petrol. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Clossman, P.J. An aquifer model for fissured reservoirs. Soc. Petrol. Eng. J. 1975, 15, 385–398. [Google Scholar] [CrossRef]
- Chen, Y.D.; Liang, W.G.; Lian, H.J.; Yang, J.F.; Nguyen, V.P. Experimental study on the effect of fracture geometric characteristics on the permeability in deformable rough-walled fractures. Int. J. Rock Mech. Min. Sci. 2017, 98, 121–140. [Google Scholar] [CrossRef]
- Zhang, W.; Dai, B.B.; Liu, Z.; Zhou, C.Y. Modeling free-surface seepage flow in complicated fractured rock mass using a coupled RPIM-FEM method. Transp. Porous Media 2017, 117, 443–463. [Google Scholar] [CrossRef]
- Zhang, Y.J. Coupled thermo-hydro-mechanical model and finite element analyses of dual-porosity fractured medium for ubiquitous-joint rock mass. Chin. J. Rock Mech. Eng. 2009, 28, 946–955. [Google Scholar] [CrossRef]
- Xiang, Y.Y.; Ren, P. A theoretical model and its calculation analysis of water flow and heat transfer in a fractured rock with local fracture wall asperity contacts. Rock Soil Mech. 2014, 35, 2845–2854. [Google Scholar]
- Dong, H.Z.; Luo, R.H.; Zhang, L. Seapage and heat transfer model of a single fracture of rock and relevant parameter sensitivity analysis. J. Hohai Univ. (Nat. Sci.) 2013, 41, 42–47. [Google Scholar] [CrossRef]
- Zhao, J. Experimental study of flow-rock heat transfer in rock fractures. Chin. J. Rock Mech. Eng. 1999, 18, 119–123. [Google Scholar] [CrossRef]
- He, Y.L.; Yang, L.Z. Mechanism of effects of temperature and effective stress on permeability of sandstone. Chin. J. Rock Mech. Eng. 2005, 24, 2420–2427. [Google Scholar] [CrossRef]
- Huang, W.B.; Cao, W.J.; Guo, J.; Jiang, F.M. An analytical method to determine the fluid-rock heat transfer rate in two-equation thermal model for EGS heat reservoir. Int. J. Heat Mass Transf. 2017, 113. [Google Scholar] [CrossRef]
- Li, Z.W.; Feng, X.T.; Zhang, Y.J.; Zhang, C.; Xu, T.F.; Wang, Y.S. Experimental research on the convection heat transfer characteristics of distilled water in manmade smooth and rough rock fractures. Energy 2017, 133, 206–218. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, Y.; Guo, Q.; Tan, L.; Zhuang, Y.; Liu, M.; Zhang, C.; Xiang, W.; Rohn, J. Experimental investigation of the hydraulic and heat-transfer properties of artificially fractured granite. Sci. Rep. 2017, 7, 39882. [Google Scholar] [CrossRef] [PubMed]
- Yasuhara, H.; Polak, A.; Mitani, Y.; Grader, A.S.; Halleck, P.M.; Elsworth, D. Evolution of fracture permeability through fluid–rock reaction under hydrothermal conditions. Earth Planet. Sci. Lett. 2006, 244, 186–200. [Google Scholar] [CrossRef]
- Schober, A.; Exner, U. 3D structural modelling of an outcrop-scale fold train using photogrammetry and GPS mapping. Aust. J. Earth Sci. 2011, 104, 73–79. [Google Scholar]
- Yanqing, W. Basic theory for rock hydraulics. Hydrogeol. Eng. Geol. 1997, 1, 24–28. [Google Scholar]
- Raven, K.G.; Gale, J.E. Water flow in a natural rock fracture as a function of stress and sample size. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 251–261. [Google Scholar] [CrossRef]









| No. | Thermal Conductivity | Volumetric Heat Capacity | Thermal Diffusivity | Density |
|---|---|---|---|---|
| (W/m·K) | (MJ/m3·K) | (m2/s) | (kg/m3) | |
| 1 | 3.05 | 2.13 | 1.43 × 10−6 | 2.71 × 103 |
| 2 | 2.99 | 2.11 | 1.42 × 10−6 | 2.58 × 103 |
| 3 | 2.87 | 1.98 | 1.45 × 10−6 | 2.65 × 103 |
| 4 | 2.98 | 2.06 | 1.45 × 10−6 | 2.67 × 103 |
| 5 | 2.96 | 2.10 | 1.41 × 10−6 | 2.64 × 103 |
| 6 | 2.99 | 2.09 | 1.43 × 10−6 | 2.66 × 103 |
| Morphological Type of Fractures | No. | Area Ratio |
|---|---|---|
| Plane | P1 | 1.013 |
| P2 | 1.022 | |
| Rough | R1 | 3.210 |
| R2 | 2.814 | |
| R3 | 2.385 | |
| R4 | 1.936 |
| No. | Injection Pressure (kPa) | Confining Pressure (kPa) | Temperature Range (°C) | Gradient (kPa/°C) |
|---|---|---|---|---|
| P1, P2, R1, R2, R3, R4 | 50–300 | 400 | 20 | 50 |
| P1, P2, R1, R2, R3, R4 | 100 | 150–400 | 20 | 50 |
| R1, R2, R3, R4 | 200 | 400 | 40–80 | 10 |
| No. | Injection Pressure (kPa) | Confining Pressure (kPa) | Temperature Range (°C) | Gradient (kPa/°C) |
|---|---|---|---|---|
| P1 | 10, 100 | 300 | 40–80 | 10 |
| R1, R2 | 100, 200 | 400 | 40–80 | 10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Qi, Y.; Zhao, Q.; Tan, L.; Xiang, W.; Rohn, J. Investigation of Flow and Heat Transfer Characteristics in Fractured Granite. Energies 2018, 11, 1228. https://doi.org/10.3390/en11051228
Luo J, Qi Y, Zhao Q, Tan L, Xiang W, Rohn J. Investigation of Flow and Heat Transfer Characteristics in Fractured Granite. Energies. 2018; 11(5):1228. https://doi.org/10.3390/en11051228
Chicago/Turabian StyleLuo, Jin, Yumeng Qi, Qiang Zhao, Long Tan, Wei Xiang, and Joachim Rohn. 2018. "Investigation of Flow and Heat Transfer Characteristics in Fractured Granite" Energies 11, no. 5: 1228. https://doi.org/10.3390/en11051228
APA StyleLuo, J., Qi, Y., Zhao, Q., Tan, L., Xiang, W., & Rohn, J. (2018). Investigation of Flow and Heat Transfer Characteristics in Fractured Granite. Energies, 11(5), 1228. https://doi.org/10.3390/en11051228





