Nonlinear Modeling and Dynamic Analyses of the Hydro–Turbine Governing System in the Load Shedding Transient Regime
Abstract
:1. Introduction
2. Mathematical Model of the Hydro–Turbine Governing System
2.1. Mathematical Model of the Francis Hydro–Turbine
2.2. Dynamic Characteristics of the Penstock System
2.3. Mathematical Model of the Generator
2.4. Mathematical Model of the Hydraulic Speed Regulation System
2.5. Nonlinear Expressions of the Hydro–Turbine Transfer Coefficients
2.6. Mathematical Model of the Hydro–Turbine Governing System
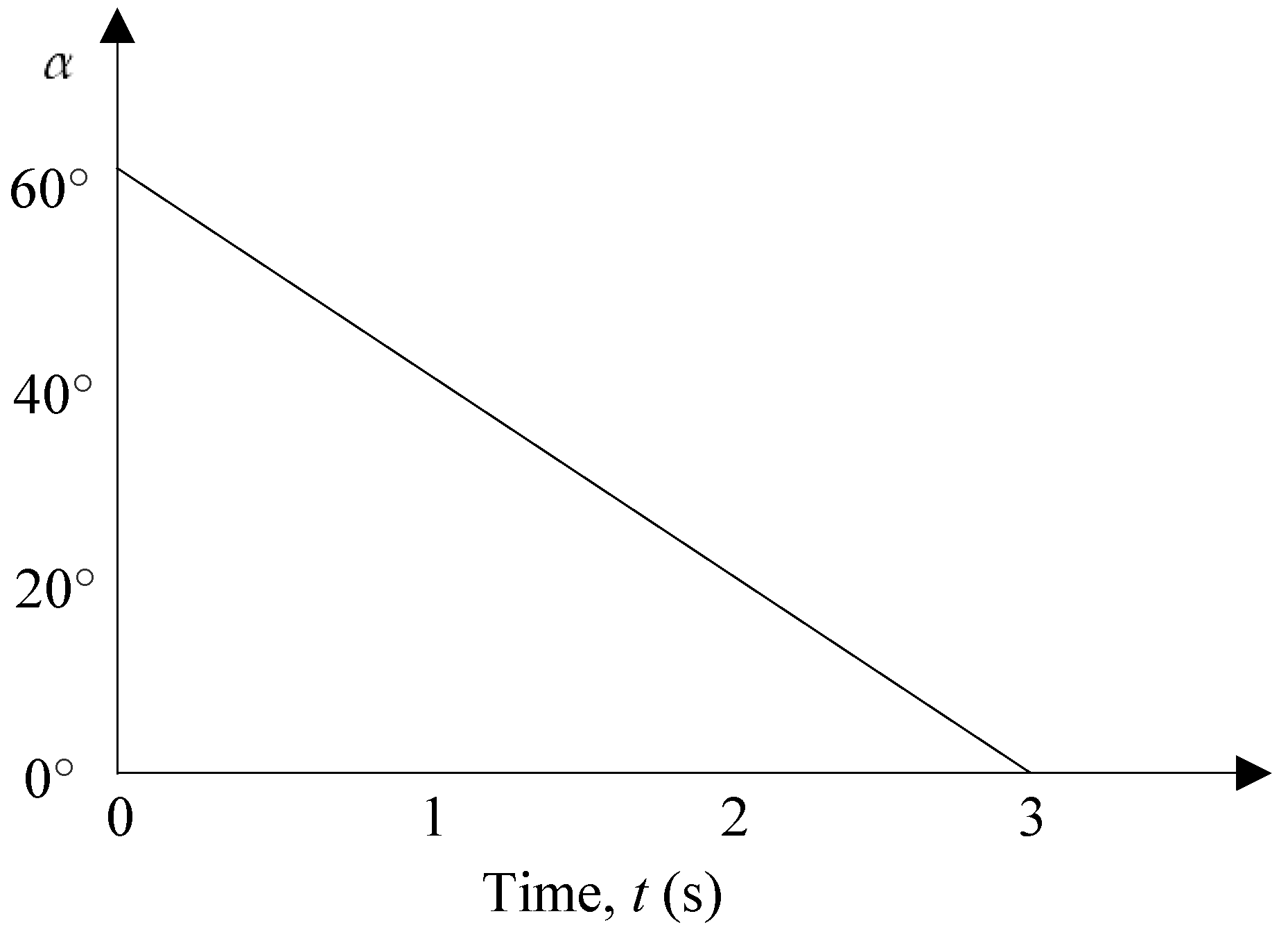
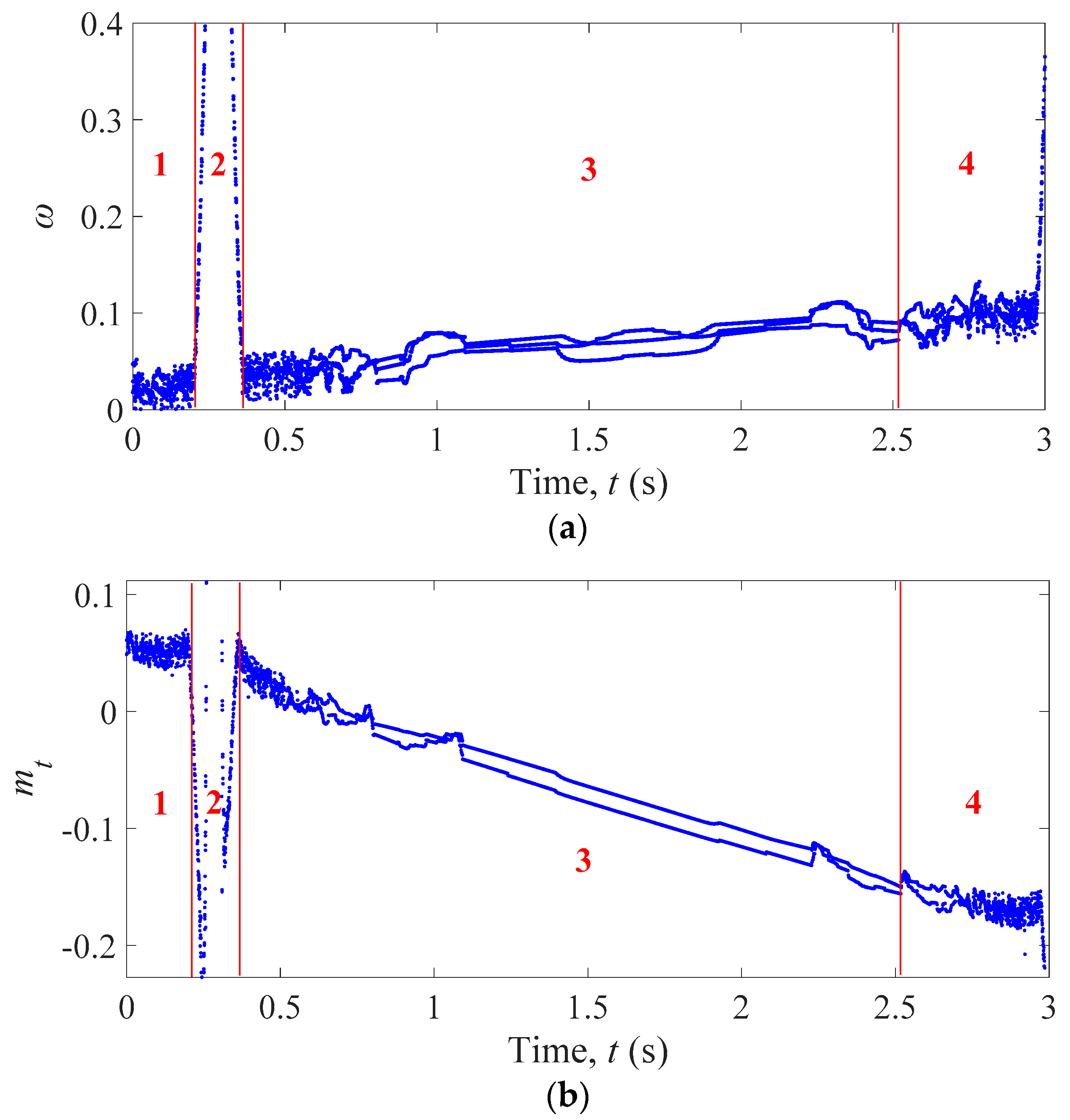
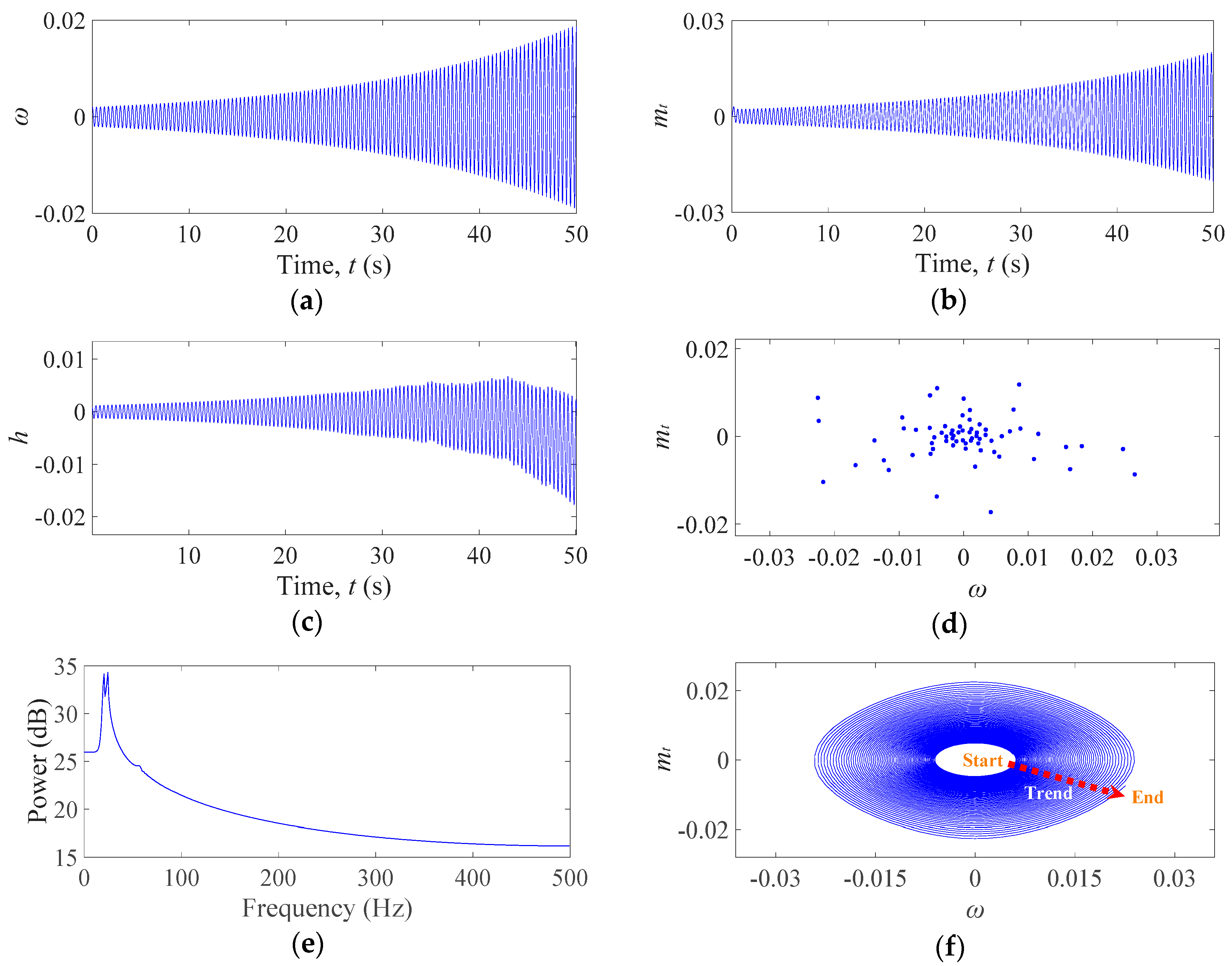
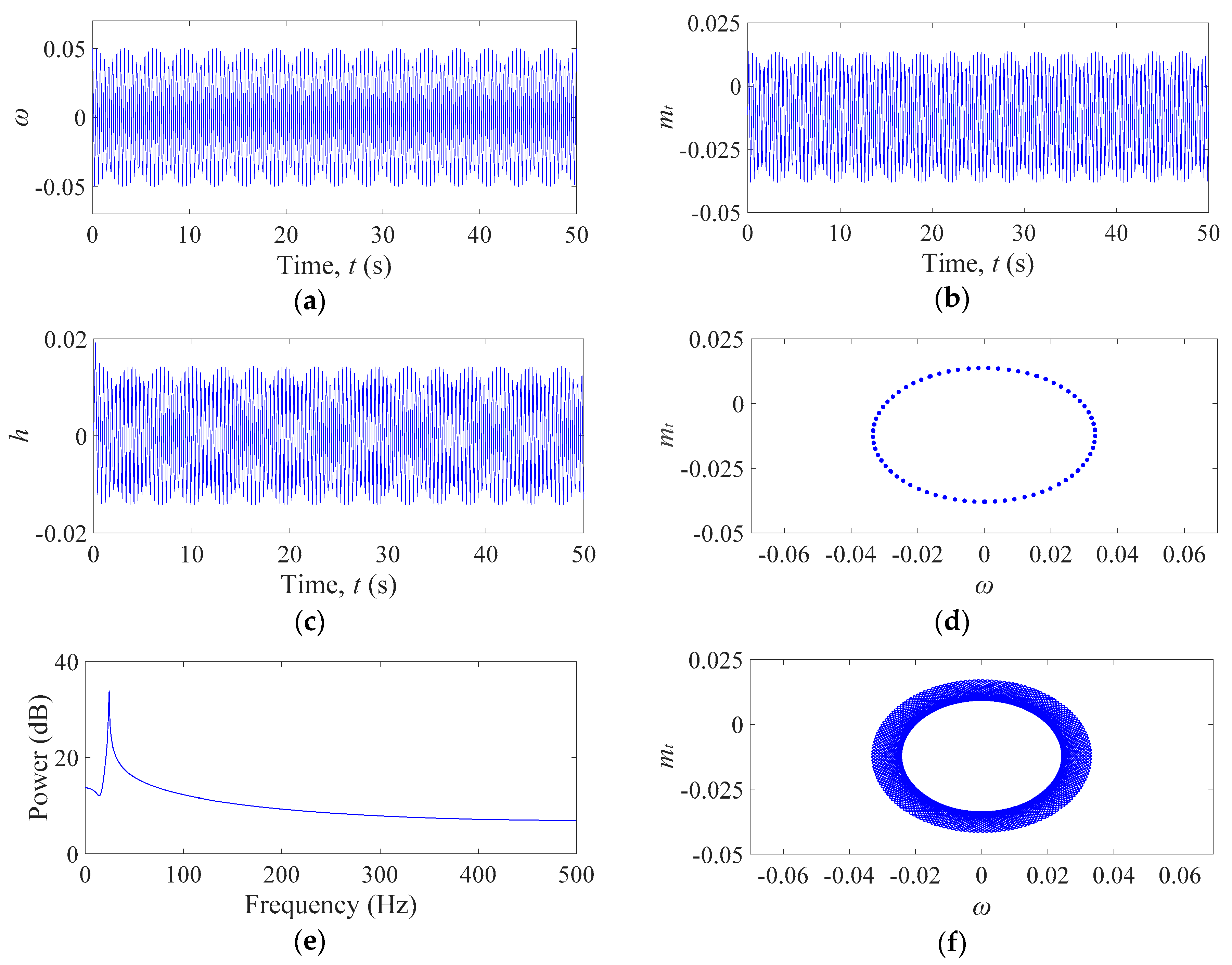
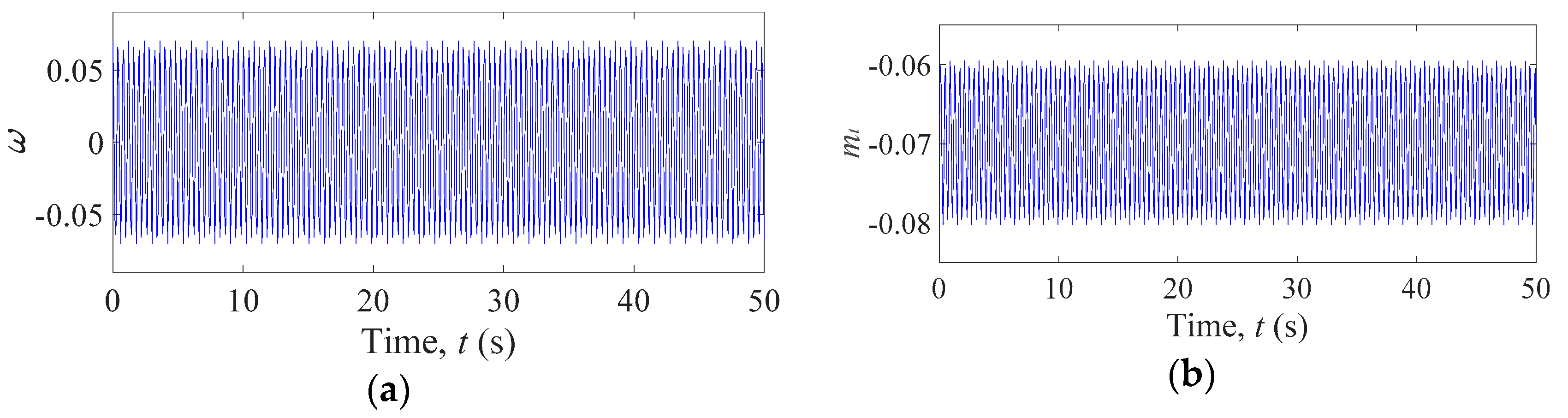
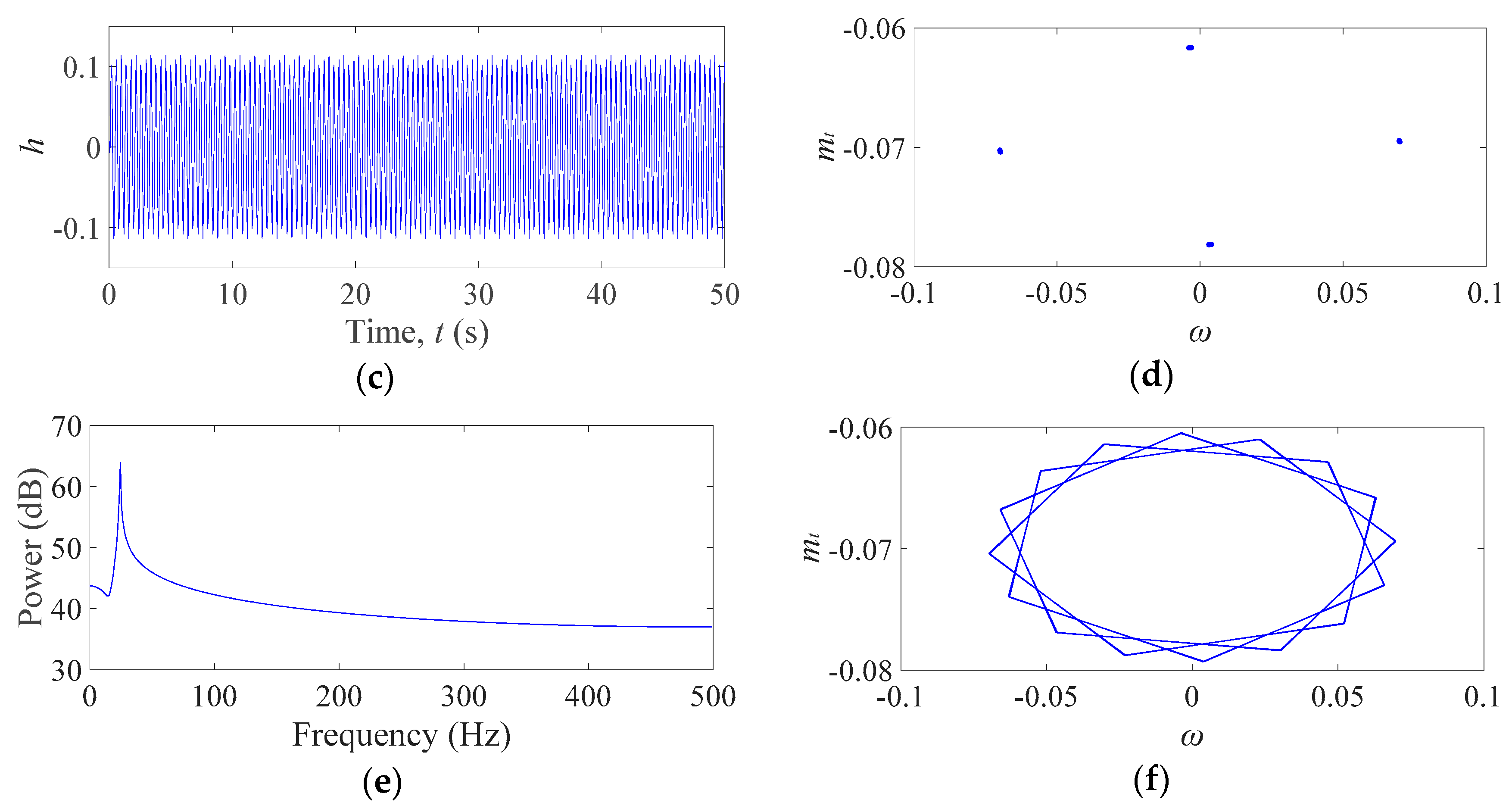
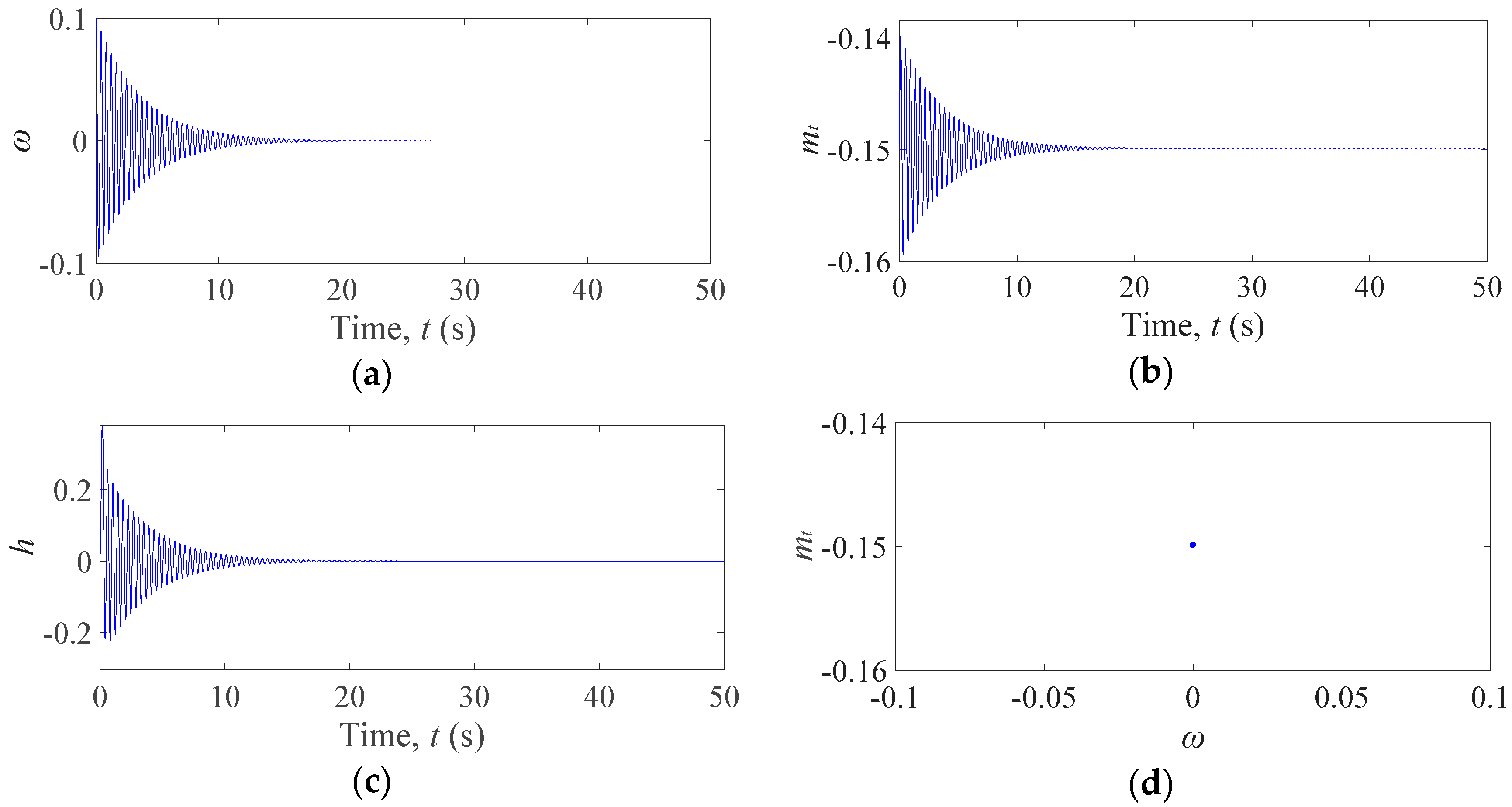
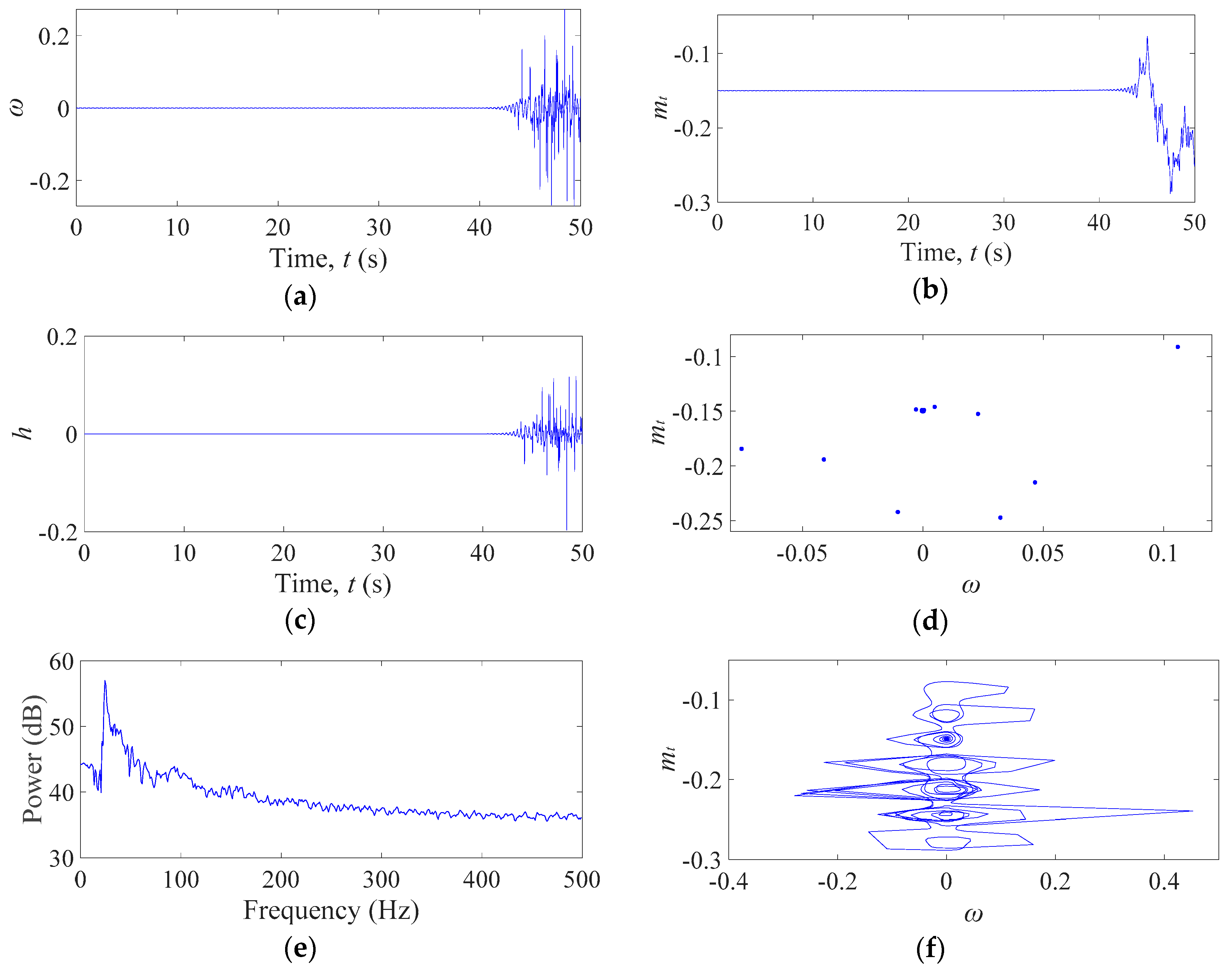
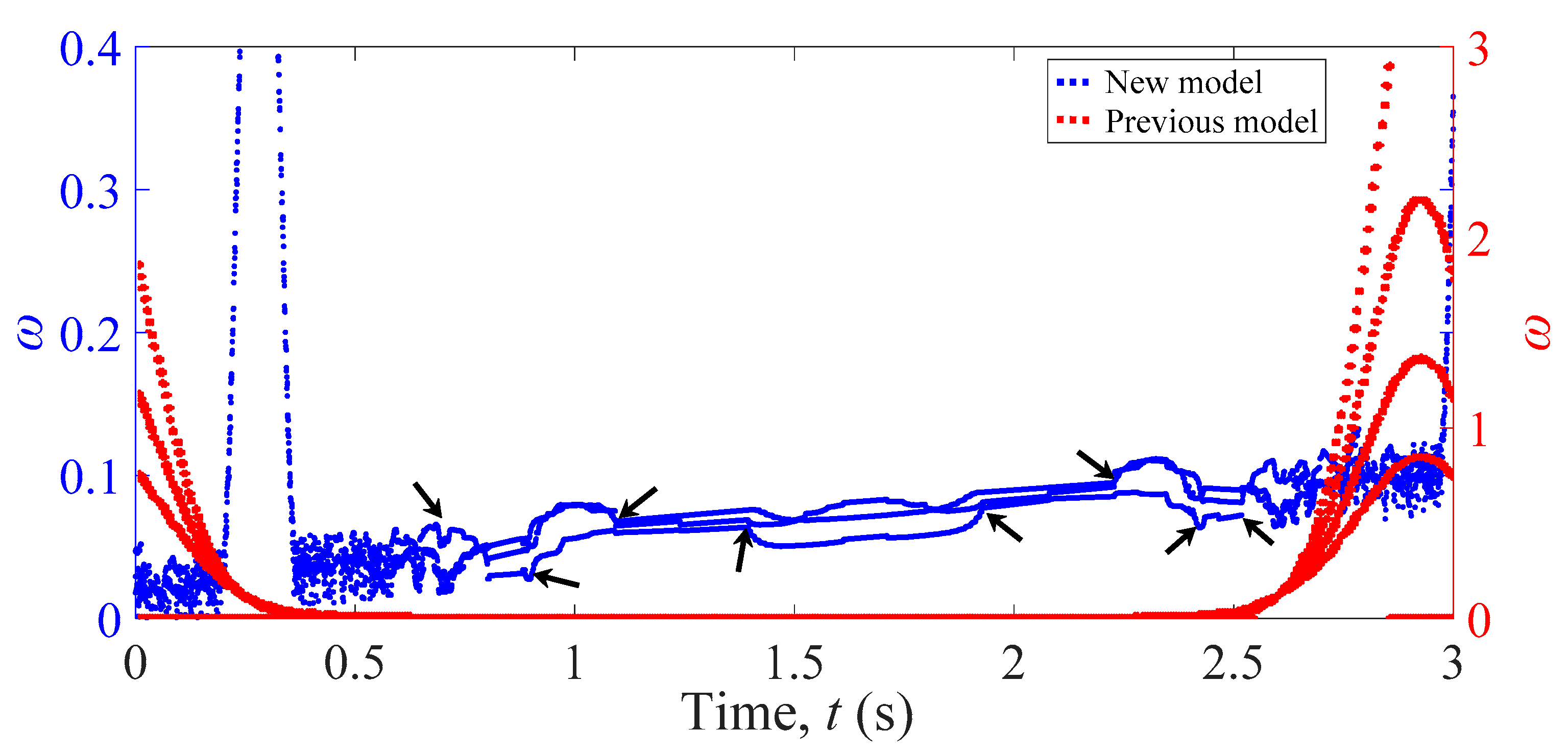
3. Nonlinear Dynamic Analyses of the Hydro–Turbine Governing System
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Li, B.; Li, T.; Xu, N.W.; Dai, F.; Chen, W.F.; Tan, Y.S. Stability assessment of the left bank slope of the Baihetan Hydropower Station, Southwest China. Int. J. Rock Mech. Min. Sci. 2018, 104, 34–44. [Google Scholar] [CrossRef]
- Giosio, D.R.; Henderson, A.D.; Walker, J.M.; Brandner, P.A. Rapid Reserve Generation from a Francis Turbine for System Frequency Control. Energies 2017, 10, 496. [Google Scholar] [CrossRef]
- Wang, W.Y.; Chen, Q.J.; Liang, X.; Dou, J.Z. A novel multidimensional frequency band energy ratio analysis method for the pressure fluctuation of Francis turbine. Math. Probl. Eng. 2018, 2018, 3494785. [Google Scholar] [CrossRef]
- Jia, J.S. A technical review of hydro–project development in China. Engineering 2016, 2, 302–312. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Gandhi, B.K. Investigation of a High Head Francis Turbine at Runaway Operating Conditions. Energies 2016, 9, 149. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Zhao, M.; McInnis, D.A.; Axworthy, D. H. A Review of Water Hammer Theory and Practice. Appl. Mech. Rev. 2005, 58, 49–76. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R.; Tijsseling, A. S. Water hammer with column separation: A historical review. J. Fluids Struct. 2006, 22, 135–171. [Google Scholar] [CrossRef]
- Tijsseling, A.S. Water hammer with fluid–structure interaction in thick–walled pipes. Comput. Struct. 2007, 85, 844–851. [Google Scholar] [CrossRef]
- Xu, B.B.; Chen, D.Y.; Tolo, S.; Patelli, E.; Jiang, Y.L. Model validation and stochastic stability of a hydro–turbine governing system under hydraulic excitations. Int. J. Electr. Power Energy Syst. 2018, 95, 156–165. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.Y.; Wu, C. Z.; Wang, X.Y. Dynamics analysis of the fast–slow hydro–turbine governing system with different time–scale coupling. Commun. Nonlinear Sci. Numer. Simul. 2018, 54, 136–147. [Google Scholar] [CrossRef]
- Zhou, W.; Lou, C.Z.; Li, Z.S.; Lu, L.; Yang, H.X. Current status of research on optimum sizing of stand–alone hybrid solar–wind power generation systems. Appl. Energy 2010, 87, 380–389. [Google Scholar] [CrossRef]
- Castronuovo, E.D.; Lopes, J.A.P. On the optimization of the daily operation of a wind–hydro power plant. IEEE Trans. Power Syst. 2004, 19, 1599–1606. [Google Scholar] [CrossRef]
- Fang, W.; Huang, Q.; Huang, S.Z.; Yang, J.; Meng, E.H.; Li, Y.Y. Optimal sizing of utility–scale photovoltaic power generation complementarily operating with hydropower: A case study of the world’s largest hydro–photovoltaic plant. Energy Conv. Manag. 2017, 136, 161–172. [Google Scholar] [CrossRef]
- Kougias, I.; Szabó, S.; Monforti–Ferrario, F.; Huld, T.; Bódis, K. A methodology for optimization of the complementarity between small–hydropower plants and solar PV systems. Renew. Energy 2016, 87, 1023–1030. [Google Scholar] [CrossRef]
- Chang, J.; Xiao, Z.; Wang, S. Neural network model predict control for the hydroturbine generator set. In Proceedings of the 2003 International Conference on Machine Learning and Cybernetics, Xi’an, China, 5 November 2003; Volume 2–5, pp. 540–543. [Google Scholar] [CrossRef]
- Eker, I. Governors for hydro–turbine speed control in power generation: A SIMO robust design approach. Energy Conv. Manag. 2003, 45, 2207–2221. [Google Scholar] [CrossRef]
- Khodabakhshian, A.; Hooshmand, R. A new PID controller design for automatic generation control of hydro power systems. Int. J. Electr. Power Energy Syst. 2010, 32, 375–382. [Google Scholar] [CrossRef]
- Ren, M.F.; Wu, D.; Zhang, J.H.; Jiang, M. Minimum entropy–based cascade control for governing hydroelectric turbines. Entropy 2014, 16, 3136–3148. [Google Scholar] [CrossRef]
- Chen, Z.H.; Yuan, X.H.; Ji, B.; Wang, P.T.; Tian, H. Design of a fractional order PID controller for hydraulic turbine regulating system using chaotic non–dominated sorting genetic algorithm II. Energy Conv. Manag. 2014, 84, 390–404. [Google Scholar] [CrossRef]
- Zhang, R.F.; Chen, D.Y.; Yao, W.; Ba, D.D.; Ma, X.Y. Non–linear fuzzy predictive control of hydroelectric system. IET Gener. Transm. Distrib. 2017, 11, 1966–1975. [Google Scholar] [CrossRef]
- Chen, D.Y.; Ding, C.; Ma, X.Y.; Yuan, P.; Ba, D.D. Nonlinear dynamical analysis of hydro–turbine governing system with a surge tank. Appl. Math. Model 2013, 37, 7611–7623. [Google Scholar] [CrossRef]
- Guo, W.C.; Yang, J.D.; Wang, M.J.; Lai, X. Nonlinear modeling and stability analysis of hydro–turbine governing system with sloping ceiling tailrace tunnel under load disturbance. Energy Conv. Manag. 2015, 106, 127–138. [Google Scholar] [CrossRef]
- Xu, B.B.; Wang, F.F.; Chen, D.Y.; Zhang, H. Hamiltonian modeling of multi–hydro–turbine governing systems with sharing common penstock and dynamic analyses under shock load. Energy Convers. Manag. 2016, 108, 478–487. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.Y.; Xu, B.B.; Wang, F.F. Nonlinear modeling and dynamic analysis of hydro–turbine governing system in the process of load rejection transient. Energy Convers. Manag. 2015, 90, 128–137. [Google Scholar] [CrossRef]
- Avdyushenko, A.Y.; Cherny, S.G.; Chirkov, D.V.; Skorospelov, V.A.; Turuk, P.A. Numerical simulation of transient processes in hydroturbines. Thermophys. Aeromech. 2013, 20, 577–593. [Google Scholar] [CrossRef]
- Yang, W.J.; Yang, J.D.; Guo, W.C.; Zeng, W.; Wang, C.; Saarinen, L.; Norrlund, P. A Mathematical Model and Its Application for Hydro Power Units under Different Operating Conditions. Energies 2015, 8, 10260–10275. [Google Scholar] [CrossRef]
- Terzija, V.V.; Akke, M. Synchronous and asynchronous generators frequency and harmonics behavior after a sudden load rejection. IEEE Trans. Power Syst. 2003, 18, 730–736. [Google Scholar] [CrossRef]
- Afshar, M.H.; Rohani, M.; Taheri, R. Simulation of transient flow in pipeline systems due to load rejection and load acceptance by hydroelectric power plants. Int. J. Mech. Sci. 2010, 52, 103–115. [Google Scholar] [CrossRef]
- Yan, D.L.; Wang, W.Y.; Chen, Q.J. Fractional–order modeling and dynamic analyses of a bending–torsional coupling generator rotor shaft system with multiple faults. Chaos Solitons Fractals 2018, 110, 1–15. [Google Scholar] [CrossRef]
- Xu, B.B.; Chen, D.Y.; Zhang, H.; Zhou, R. Dynamic analysis and modeling of a novel fractional–order hydro–turbine–generator unit. Nonlinear Dyn. 2015, 81, 1263–1274. [Google Scholar] [CrossRef]
- Lin, D.J. Bifurcation and Chaos of Hydraulic Turbine Governor; Hohai University: Nan Jing, China, 2007. (In Chinese) [Google Scholar]
- Fang, H.Q.; Chen, L.; Dlakavu, N.; Shen, Z.Y. Basic modeling and simulation tool for analysis of hydraulic transients in hydroelectric power plants. IEEE Trans. Energy. Convers. 2008, 23, 834–841. [Google Scholar] [CrossRef]
- Shou, M.H.; Zhang, X.B. Study on the dynamic model of the hydro–turbine linear control system. J. Electr. Eng. 1984, 4, 48–57. (In Chinese) [Google Scholar]
- Xu, B.B.; Yan, D.L.; Chen, D.Y.; Gao, X.; Wu, C.Z. Sensitivity analysis of a Pelton hydropower station based on a novel approach of turbine torque. Energy Convers. Manag. 2017, 148, 785–800. [Google Scholar] [CrossRef]
- Nagode, K.; Škrjanc, I. Modelling and Internal Fuzzy Model Power Control of a Francis Water Turbine. Energies 2014, 7, 874–889. [Google Scholar] [CrossRef]

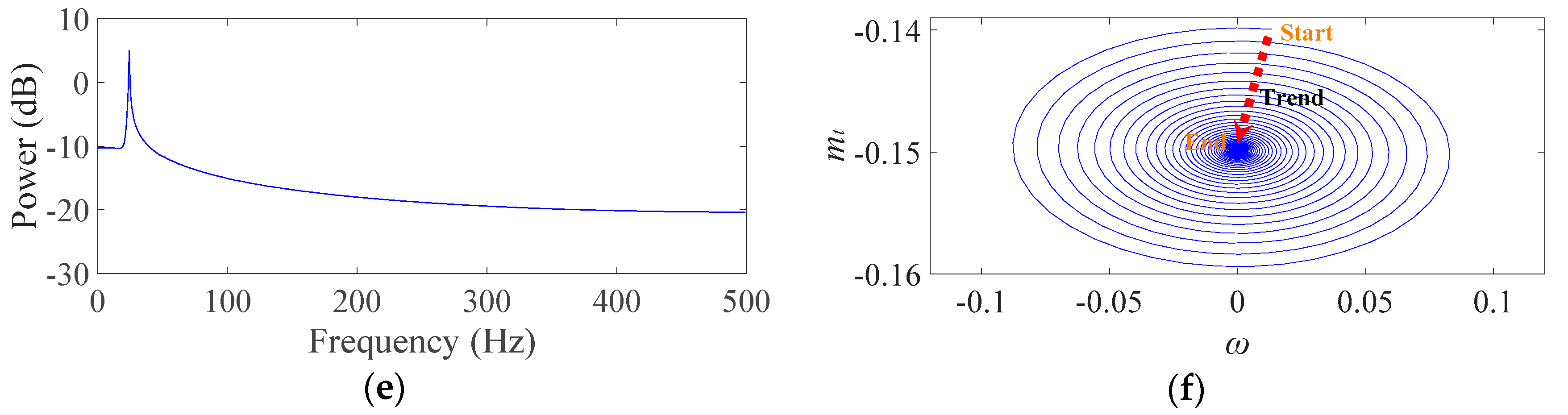
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, D.; Wang, W.; Chen, Q. Nonlinear Modeling and Dynamic Analyses of the Hydro–Turbine Governing System in the Load Shedding Transient Regime. Energies 2018, 11, 1244. https://doi.org/10.3390/en11051244
Yan D, Wang W, Chen Q. Nonlinear Modeling and Dynamic Analyses of the Hydro–Turbine Governing System in the Load Shedding Transient Regime. Energies. 2018; 11(5):1244. https://doi.org/10.3390/en11051244
Chicago/Turabian StyleYan, Donglin, Weiyu Wang, and Qijuan Chen. 2018. "Nonlinear Modeling and Dynamic Analyses of the Hydro–Turbine Governing System in the Load Shedding Transient Regime" Energies 11, no. 5: 1244. https://doi.org/10.3390/en11051244




