Calculation of Hybrid Ionized Field of AC/DC Transmission Lines by the Meshless Local Petorv–Galerkin Method
Abstract
1. Introduction
2. Principal Theory
2.1. Governing Equations
2.2. Basic Assumptions
2.3. Boundary Conditions
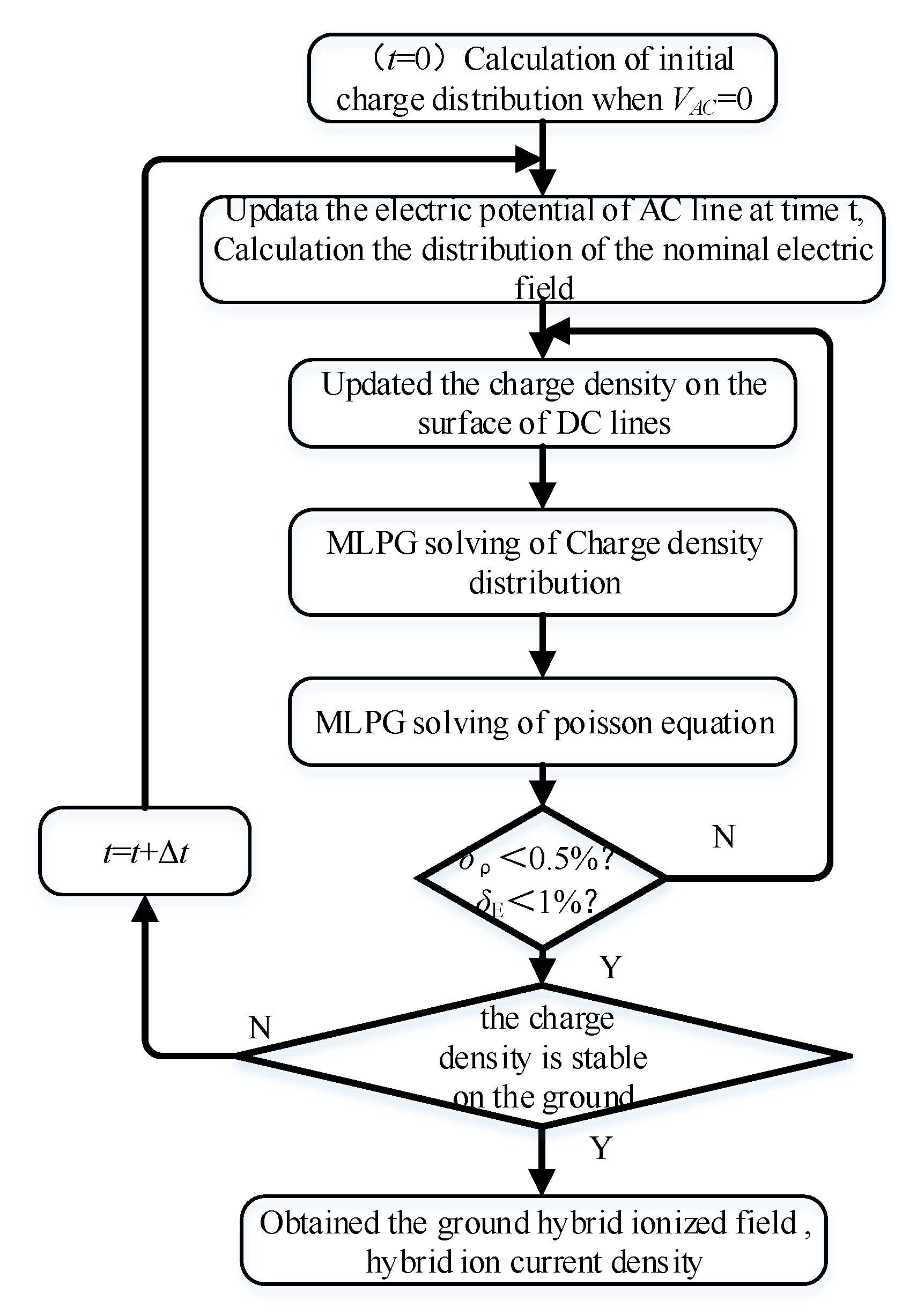
3. Calculation of Hybrid Ionized Field by the Meshless Local Petorv–Galerkin Method
3.1. Shape Function
3.2. Solving Poisson’s Equation
3.3. The Solution of the Charge Conservation Equation
3.4. Calculation Process
4. Validation Case
5. Applications
6. Conclusions
- (1)
- The MLPG method can be used to calculate the hybrid ionized field in time domain, and it can be seen from the comparison between measurement results and calculation results that the calculation method has high precision.
- (2)
- The existence of the AC line affects the space ion distribution. The shielding effect of the AC lines can reduce the hybrid ionized field near the AC side.
- (3)
- It can be seen that the calculation results related to the voltage level and parallel distance of AC lines. Appropriately reducing the parallel distance and increasing the AC voltage of the line can reduce the hybrid ionized field under the line.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Maruvada, P.; Drogi, S. Field and ion interactions of hybrid AC/DC transmission lines. IEEE Trans. Power Deliv. 1988, 3, 1165–1172. [Google Scholar] [CrossRef]
- Clairmont, B.; Johnson, G.; Zaffanella, L.; Zelingher, S. The effect of HVAC-HVDC line separation in a hybrid corridor. IEEE Trans. Power Deliv. 1989, 4, 1338–1350. [Google Scholar] [CrossRef]
- Yin, H.; He, J.; Zhang, B.; Zeng, R. Finite Volume-Based Approach for the Hybrid Ion-Flow Field of UHVAC and UHVDC Transmission Lines in Parallel. IEEE Trans. Power Deliv. 2011, 26, 2809–2820. [Google Scholar] [CrossRef]
- Zhou, X.; Cui, X.; Lu, T.; Zhen, Y.; Luo, Z. A Time-Efficient Method for the Simulation of Ion Flow Field of the AC-DC Hybrid Transmission Lines. IEEE Trans. Magn. 2012, 48, 731–734. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, J.; Lei, Y. A Calculation Method for the Hybrid Electric Field under UHVAC and UHVDC Transmission Lines in the Same Corridor. IEEE Trans. Power Deliv. 2010, 25, 1146–1153. [Google Scholar] [CrossRef]
- Li, W.; Zhang, B.; He, J.; Zeng, R. Calculation of the ion flow field of AC-DC hybrid transmission lines. IET Gener. Transm. Distrib. 2009, 3, 911–918. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, X.; Tian, W.; Zhu, Y.; Zhao, L. Study on the hybrid ion-flow field of HVDC and HVAC transmission lines by the nodal discontinuous Galerkin time-domain method. Gener. Transm. Distrib. 2017, 11, 209–217. [Google Scholar] [CrossRef]
- Guillod, T.; Pfeiffer, M.; Franck, C.M. Improved Coupled Ion-Flow Field Calculation Method for AC/DC Hybrid Overhead Power Lines. IEEE Trans. Power Deliv. 2014, 29, 2493–2501. [Google Scholar] [CrossRef]
- Straumann, U.; Franck, C.M. Ion-Flow Field Calculations of AC/DC Hybrid Transmission Lines. IEEE Trans. Power Deliv. 2013, 28, 294–302. [Google Scholar] [CrossRef]
- Ji, Q.; Zou, J.; Zhang, J.; Lu, Y.; Lee, J. Space-Time Pattern of Ion Flow Under AC/DC Hybrid Overhead Lines and Its Application. IEEE Trans. Power Deliv. 2017. [Google Scholar] [CrossRef]
- Zhou, X.; Cui, X.; Lu, T.; Liu, Y.; Li, X.; He, J.; Bai, R.; Zhen, Y. Shielding Effect of HVAC Transmission Lines on the Ion-Flow Field of HVDC Transmission Lines. IEEE Trans. Power Deliv. 2013, 28, 1094–1102. [Google Scholar] [CrossRef]
- Xiao, F.; Zhang, B.; Mo, J.; He, J. Calculation of 3-D Ion Flow Field at the Crossing of HVDC Transmission Lines by Method of Characteristics. IEEE Trans. Power Deliv. 2017. [Google Scholar] [CrossRef]
- Zhou, X. Physical Spline Finite Element (PSFEM) Solutions to One Dimensional Electromagnetic Problems. Prog. Electromagn. Res. 2003, 40, 271–294. [Google Scholar] [CrossRef]
- Li, J.; Lu, X.; Farquharson, C. A finite-element time-domain forward solver for electromagnetic methods with a complex-shape transmitting loop. SEG Tech. Program Expand. 2017, 1152–1157. [Google Scholar] [CrossRef]
- Zhang, B.; Mo, J.; He, J.; Zhuang, C. A Time-Domain Approach of Ion Flow Field around AC–DC Hybrid Transmission Lines Based on Method of Characteristics. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, X.; Tian, W. Hybrid method for calculation of ion-flow fields of HVDC transmission lines. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 2830–2839. [Google Scholar] [CrossRef]
- Benbouza, N.; Louai, F.Z.; Feliachi, M.; Zaoui, A. Electromagnetic Field Computation in Linear Electromagnetic Actuators Using the Meshless Local Petrov Galerkin Method. Acta Electrotech. Inform. 2016, 16, 27–31. [Google Scholar] [CrossRef]
- Liu, F.; Su, D.; Zhang, Y. A 3-D Unconditionally Stable Laguerre-Rpim Meshless Method for Time-Domain Electromagnetic Computations. Prog. Electromagn. Res. M 2013, 31, 279–293. [Google Scholar] [CrossRef]
- Lai, S.; Wang, B.; Duan, Y. Solving Helmholtz Equation by Meshless Radial Basis Functions Method. Prog. Electromagn. Res. B 2010, 24, 351–367. [Google Scholar] [CrossRef]
- Li, Q. Application of meshless local Petrov-Galerkin (MLPG) to problems with singularities, and material discontinuities, in 3-D elasticity. Comput. Model. Eng. Sci. 2003, 13, 571–585. [Google Scholar]
- Yuan, X.; Gu, G.; Zhao, M. Application of Meshless Local Petrov–Galerkin Method in Inhomogeneous Electromagnetic Field. In Proceedings of the International Conference on Electrical Engineering and Automation Control, Nanjing, China, 21–23 April 2017. [Google Scholar]
- Fonseca, A.; Corrêa, B.; Silva, E. Improving the mixed formulation for meshless local Petrov-Galerkin method. IEEE Trans. Magn. 2010, 46, 2907–2910. [Google Scholar] [CrossRef]
- Liu, G.; Gu, Y. An Introduction to Meshfree Methods and Their Programming; Springer: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Wang, Z.; Lu, T.; Li, X. Predictive analysis of ion flow field at the ground level under HVAC and HVDC hybrid transmission lines. In Proceedings of the 2014 IEEE Conference on Electrical Insulation and Dielectric Phenomena, Des Moines, IA, USA, 19–22 October 2014; pp. 526–529. [Google Scholar]
- Zhao, T.; Illan, J.; Cohol, J.M.; Hinton, R.D.; Sebo, S.A.; Kasten, D.G. Design, construction and utilization of a new reduced-scale model for the study of hybrid (AC and DC) line corona. In Proceedings of the IEEE Power Engineering Society, Transmission and Distribution Conference, Chicago, IL, USA, 10–15 April 1994; pp. 239–245. [Google Scholar]









| Approach Distance | Hybrid Ionized Field | Ion Current Density | ||||||
|---|---|---|---|---|---|---|---|---|
| Maxk V/m | Growth Rate | Average kV/m | Growth Rate | Max nA/m2 | Growth Rate | Average nA/m2 | Growth Rate | |
| 60 m | 17.64 | 0 | −0.185 | 0 | 13.52 | 0 | −0.205 | 0 |
| 40 m | 15.9 | −9.86% | −0.253 | −36.7% | 13.12 | −2.96% | −0.245 | −19.5% |
| AC Transmission Line Voltage | Hybrid Ionized Field | Ion Current Density | ||||||
|---|---|---|---|---|---|---|---|---|
| Max kV/m | Growth Rate | Average kV/m | Growth Rate | Max nA/m2 | Growth Rate | Average nA/m2 | Growth Rate | |
| 220 kV | 17.61 | −0.17% | −0.168 | 9.1% | 13.81 | 2.1% | −0.184 | 11.4% |
| 500 kV | 17.64 | 0 | −0.185 | 0 | 13.52 | 0 | −0.205 | 0 |
| 750 kV | 17.12 | −2.9% | −0.198 | −7.02% | 12.42 | −8.13% | −0.223 | −8.78% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Yang, H.; Yang, F.; Yao, D.; Zhang, G.; Ran, J.; Gao, B. Calculation of Hybrid Ionized Field of AC/DC Transmission Lines by the Meshless Local Petorv–Galerkin Method. Energies 2018, 11, 1521. https://doi.org/10.3390/en11061521
Li Q, Yang H, Yang F, Yao D, Zhang G, Ran J, Gao B. Calculation of Hybrid Ionized Field of AC/DC Transmission Lines by the Meshless Local Petorv–Galerkin Method. Energies. 2018; 11(6):1521. https://doi.org/10.3390/en11061521
Chicago/Turabian StyleLi, Qiang, Hao Yang, Fan Yang, Degui Yao, Guangzhou Zhang, Jia Ran, and Bing Gao. 2018. "Calculation of Hybrid Ionized Field of AC/DC Transmission Lines by the Meshless Local Petorv–Galerkin Method" Energies 11, no. 6: 1521. https://doi.org/10.3390/en11061521
APA StyleLi, Q., Yang, H., Yang, F., Yao, D., Zhang, G., Ran, J., & Gao, B. (2018). Calculation of Hybrid Ionized Field of AC/DC Transmission Lines by the Meshless Local Petorv–Galerkin Method. Energies, 11(6), 1521. https://doi.org/10.3390/en11061521




