Low-Frequency Oscillation Suppression of the Vehicle–Grid System in High-Speed Railways Based on H∞ Control
Abstract
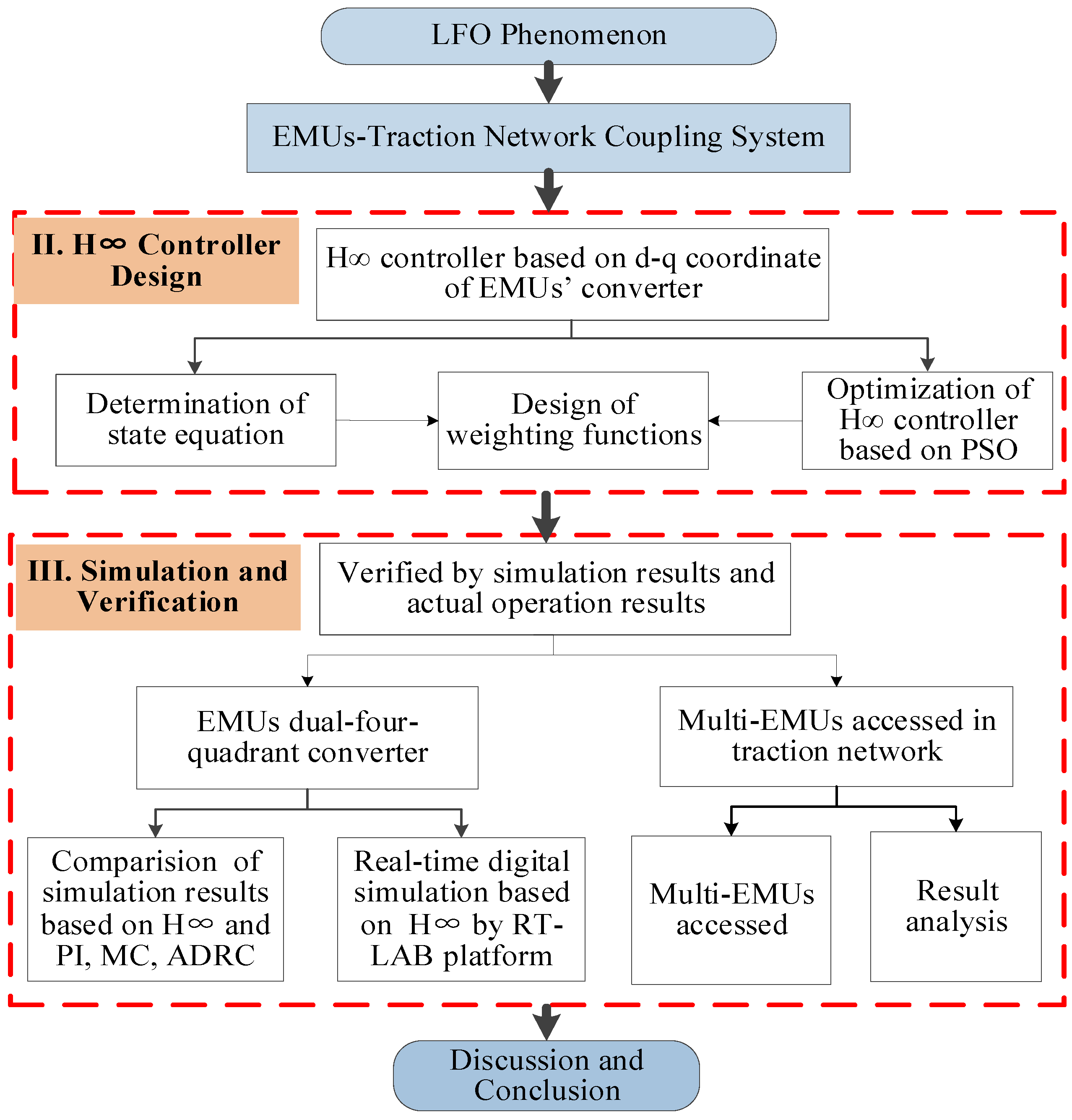
:1. Introduction
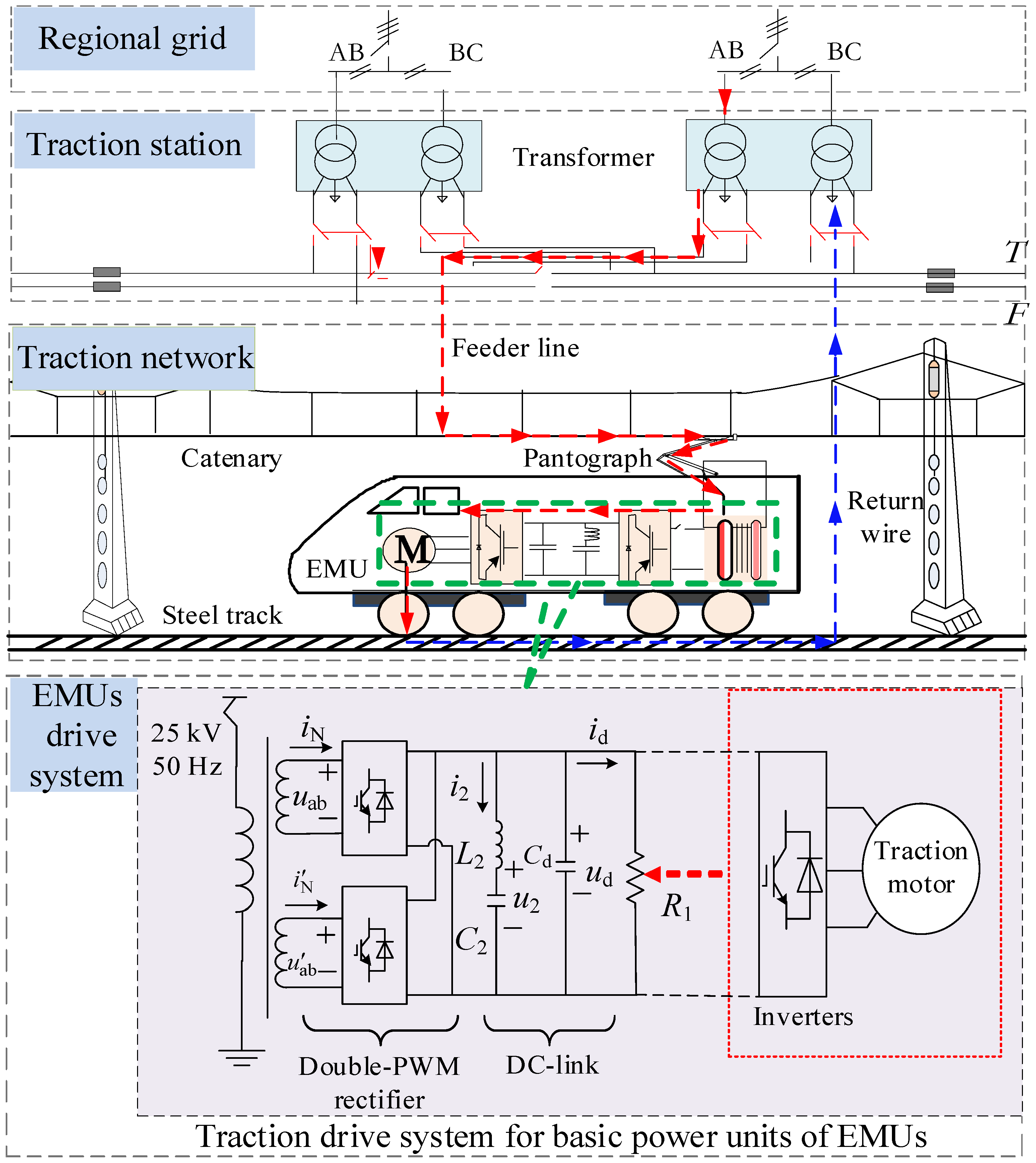
2. H∞ Controller Design of the Line-Side Converter of EMUs
2.1. Model Review of the Line-Side Converter of EMUs
2.2. H∞ Controller State Variable Problem
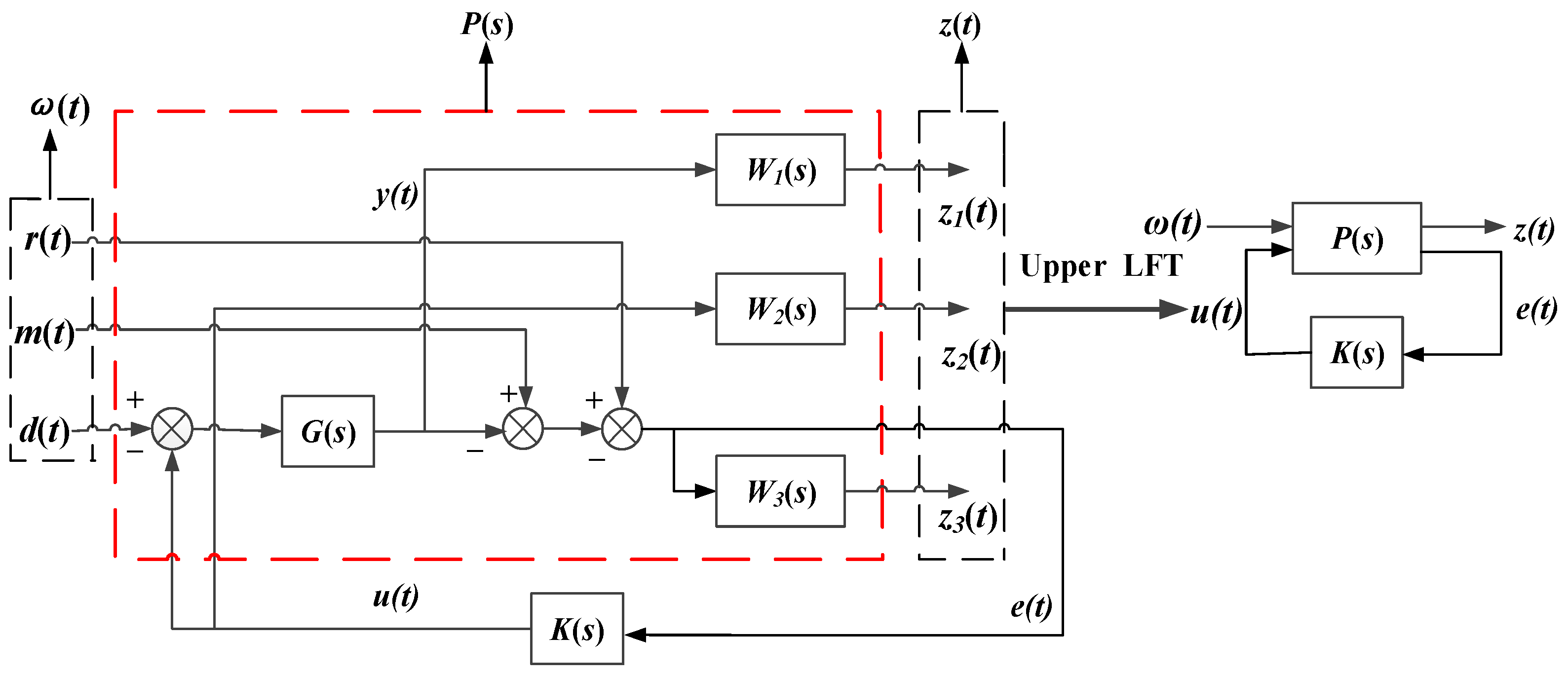
2.3. H∞ Controller Mixed Sensitivity Problem
2.4. Design of Weighting Functions
3. Simulation and Analysis for the Dual Line-Side Converter
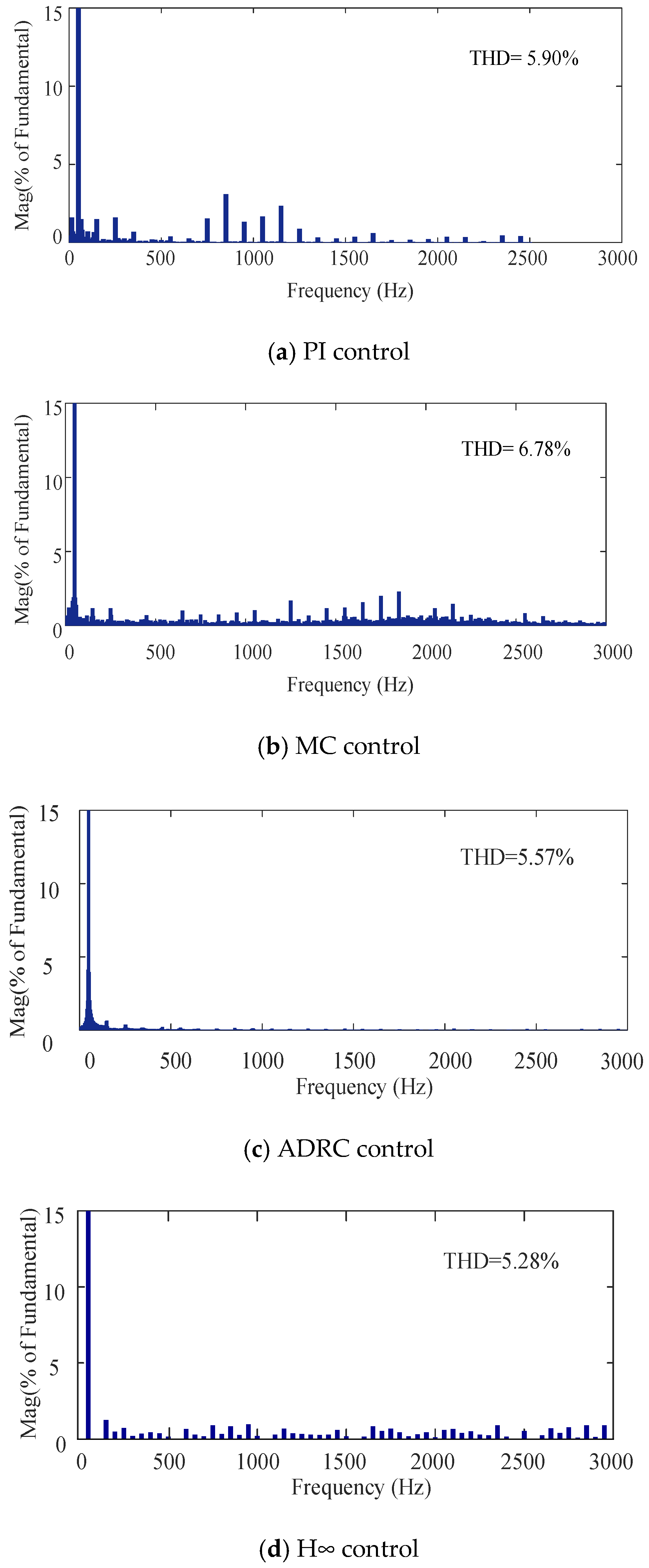
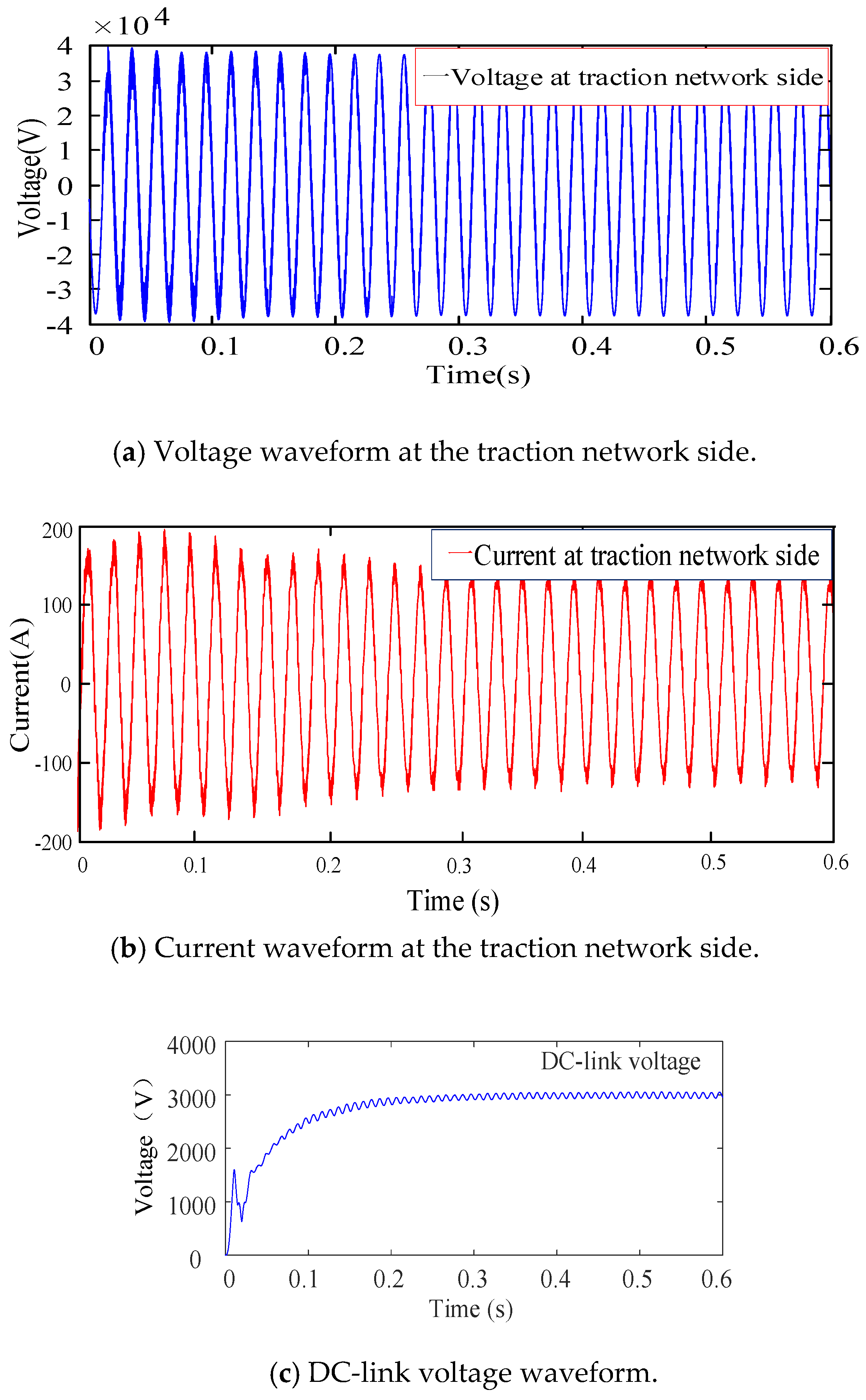
3.1. Off-Line Simulation
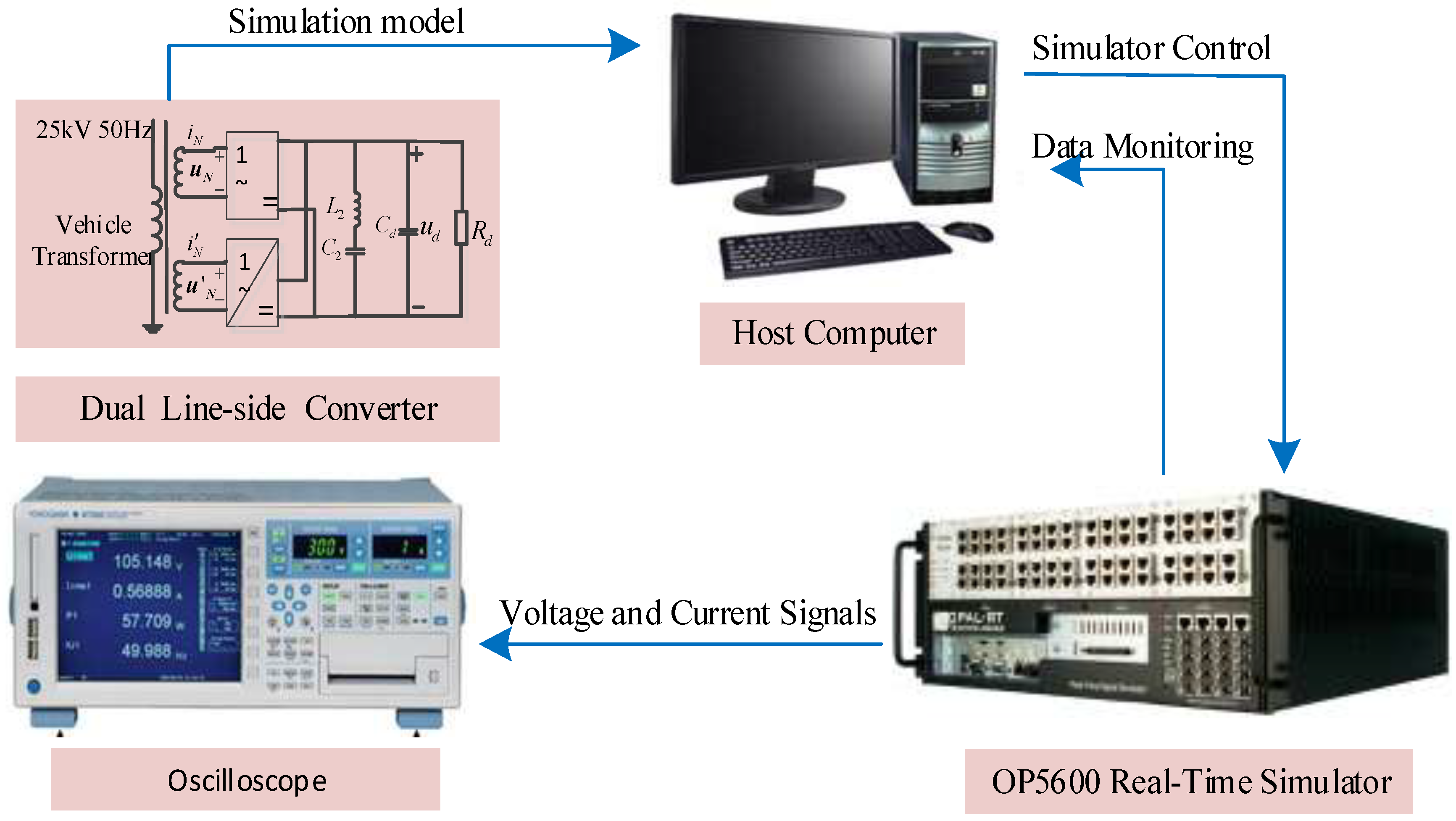
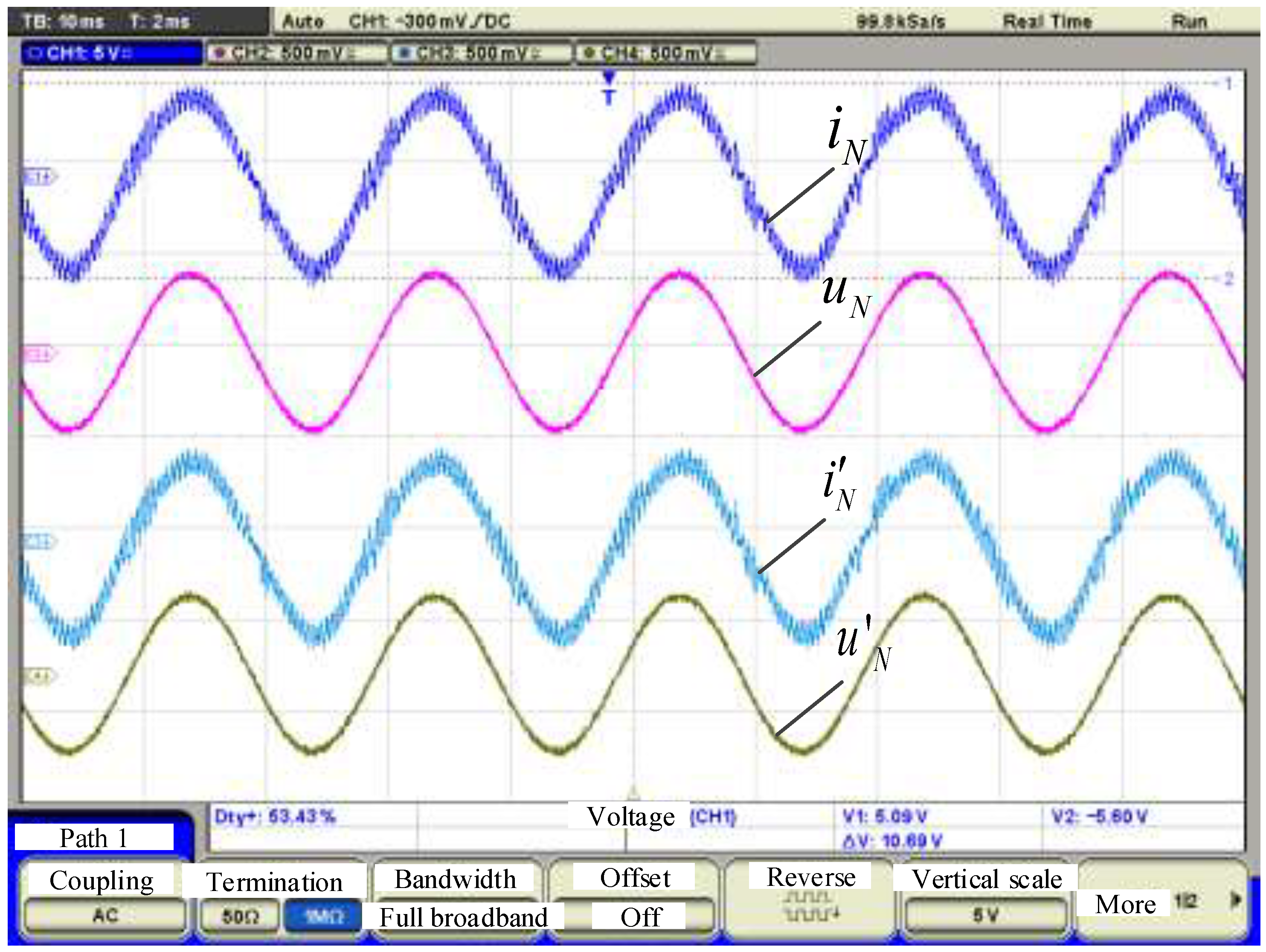
3.2. Real-Time Simulation
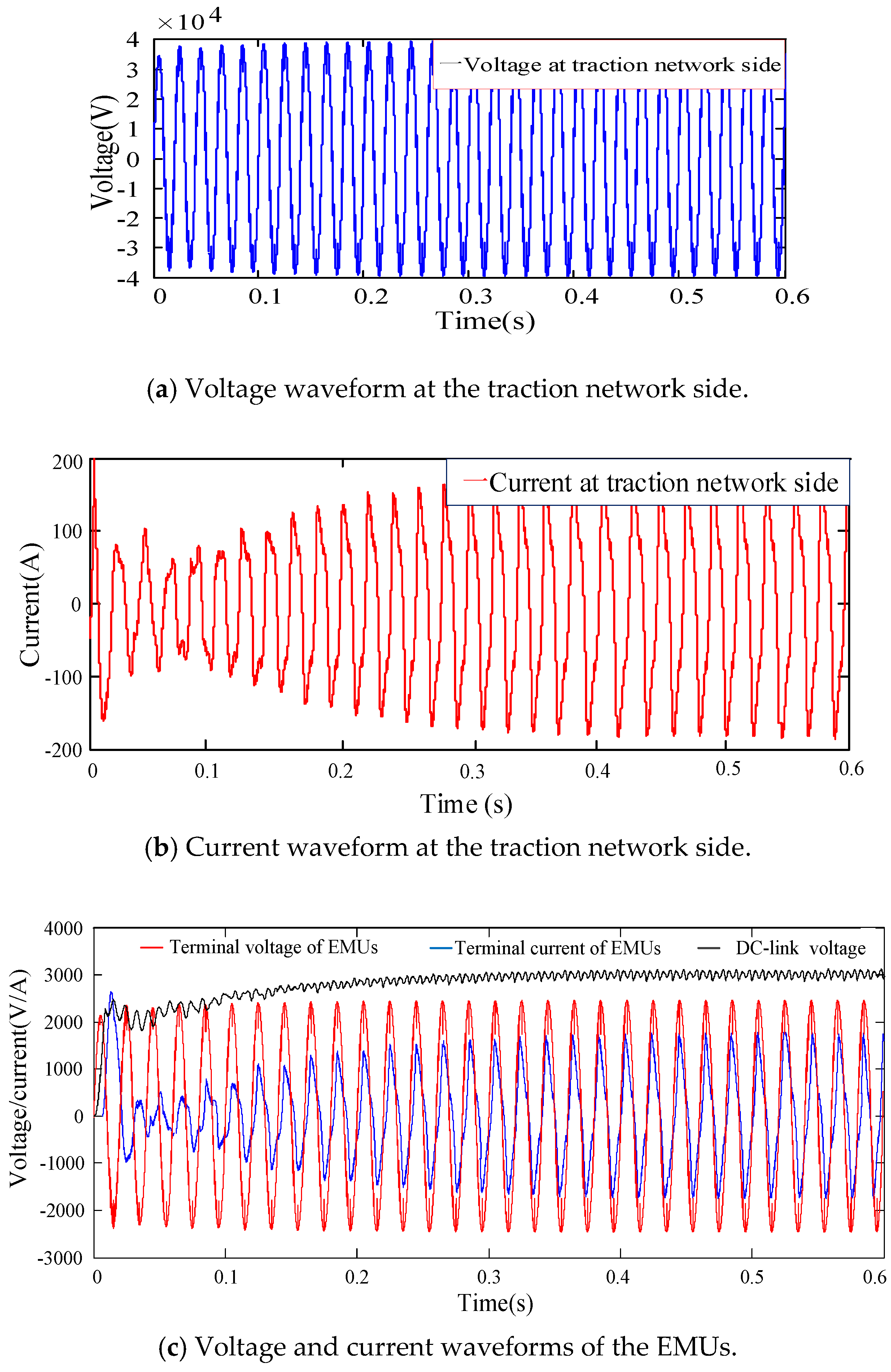
4. System Verification
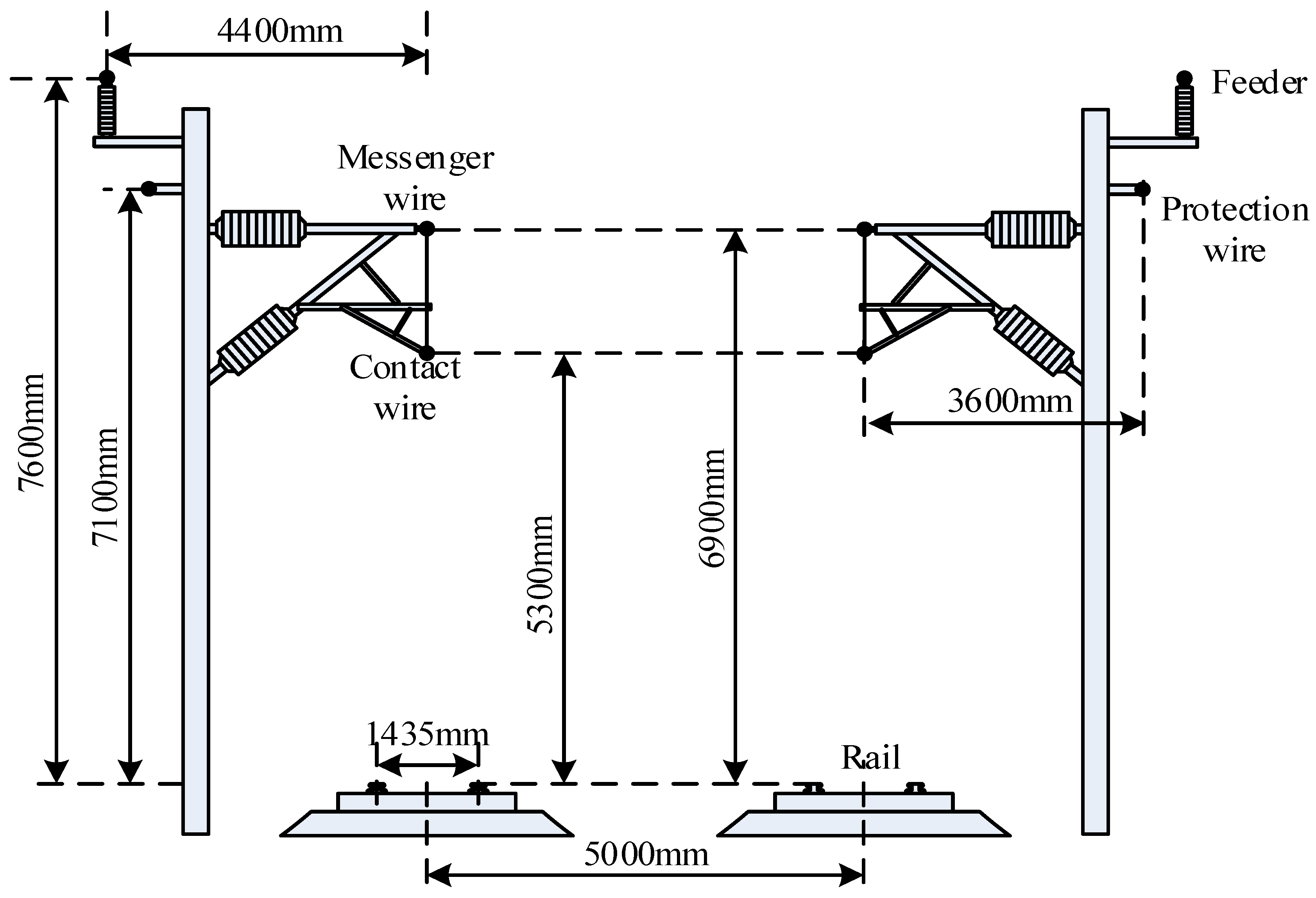
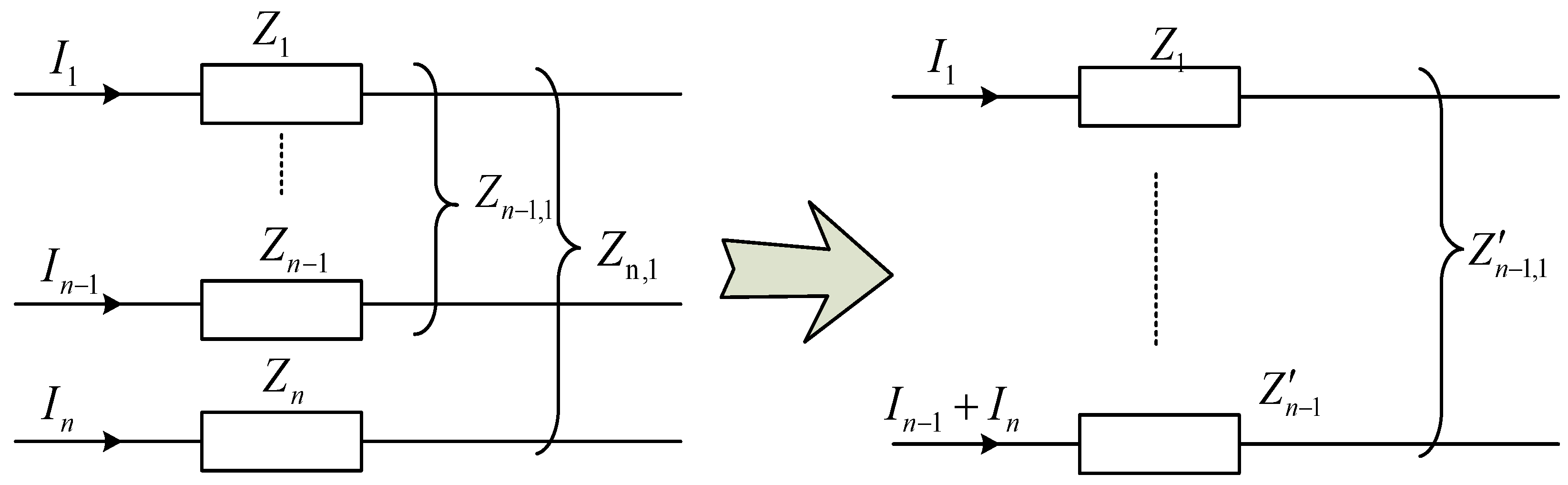
4.1. Reduced-Order Model of a Traction Network
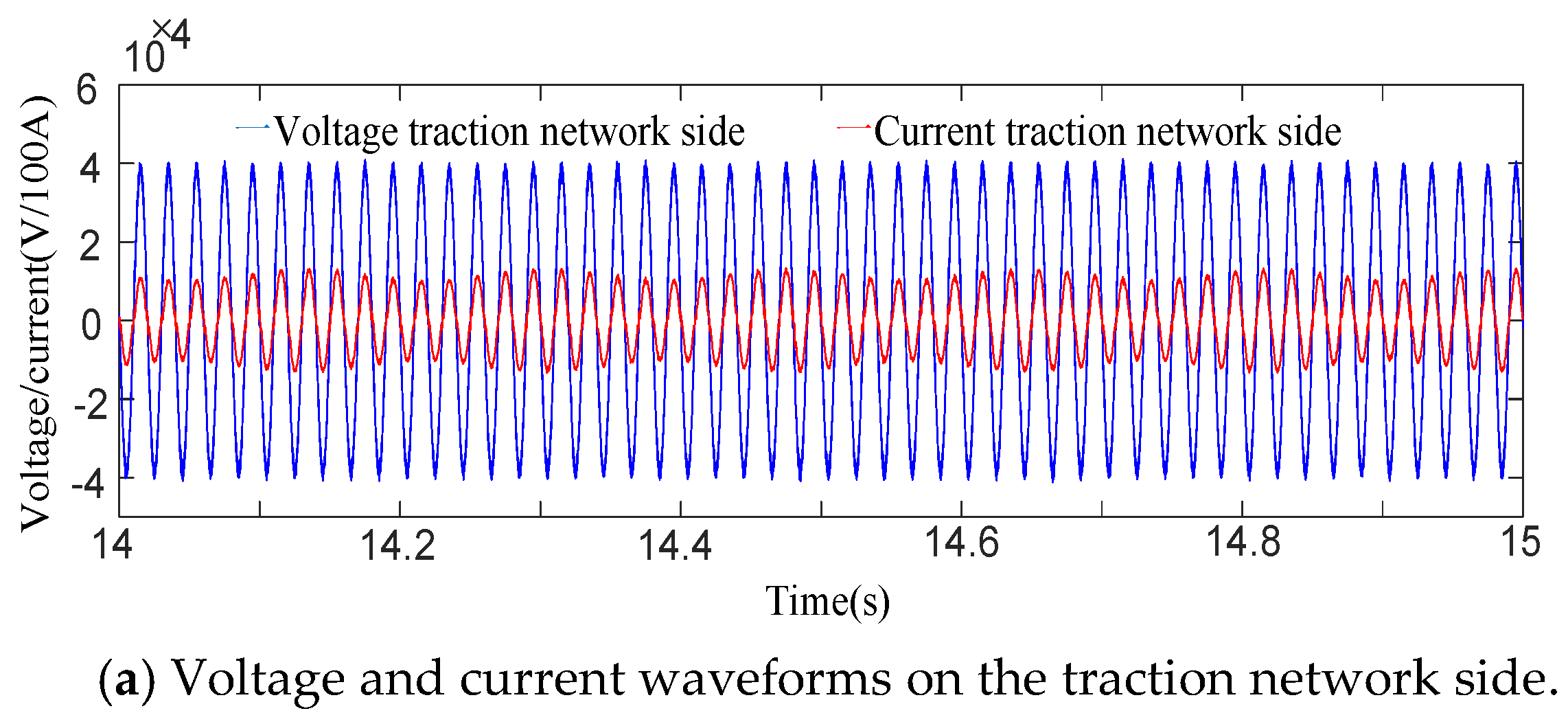
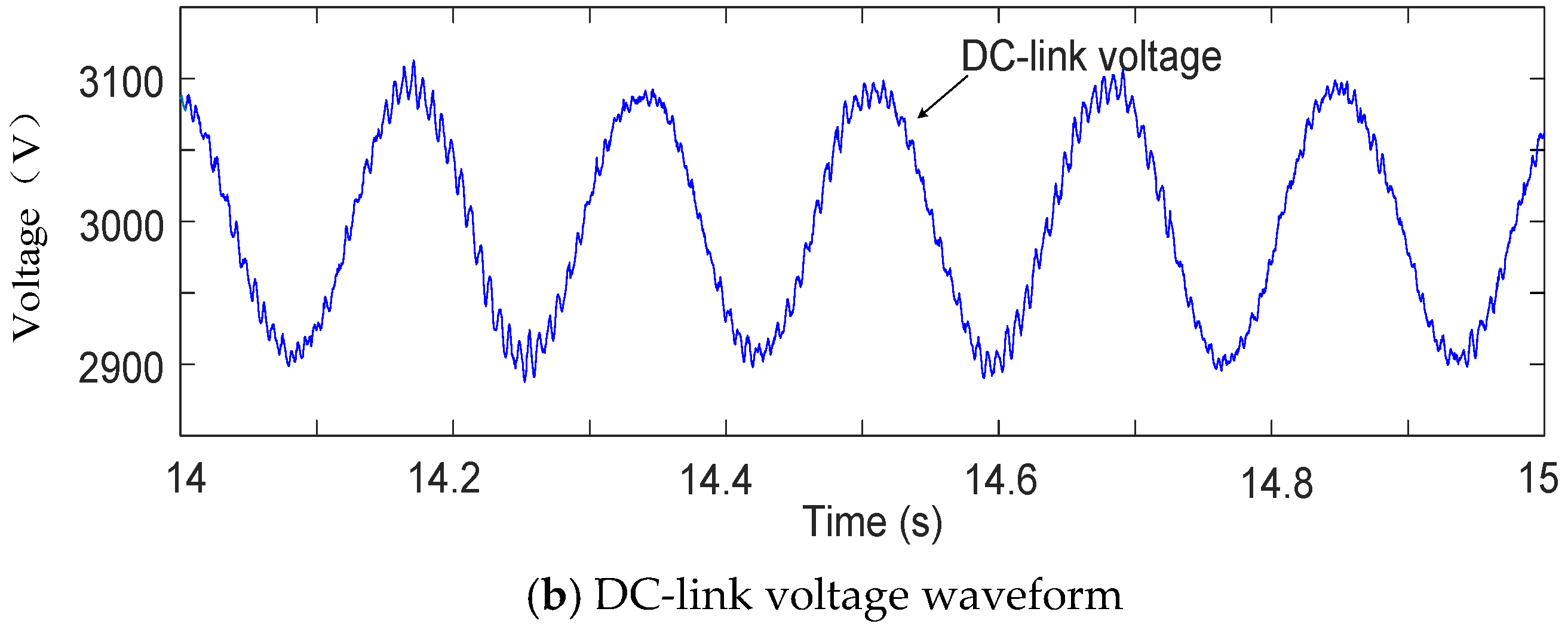
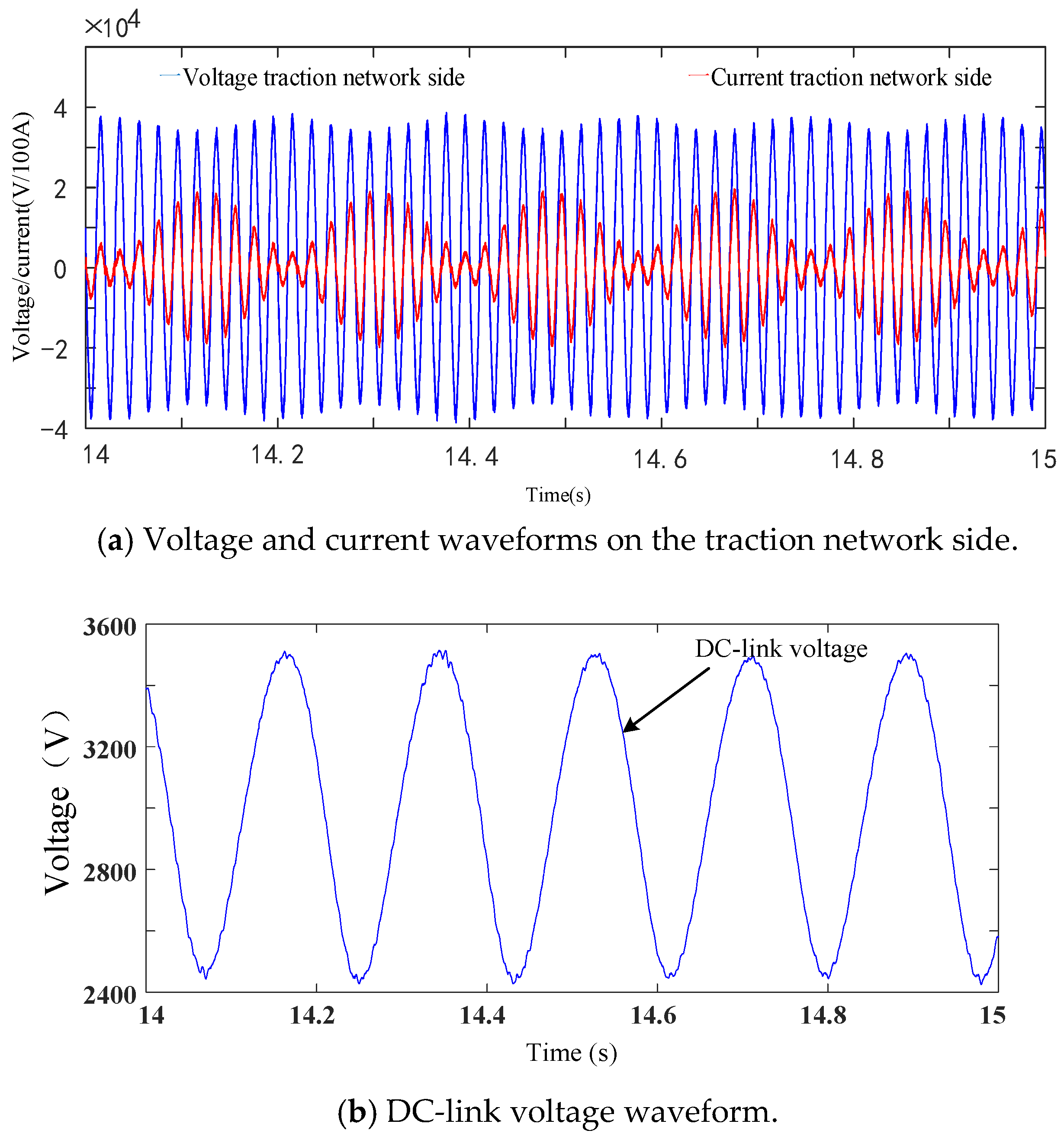
4.2. Simulation of Multi-EMUs Accessed in the Traction Network Based on PI Control
4.3. Simulation of Multi-EMUs Accessed in Traction Network Based on H∞ Control
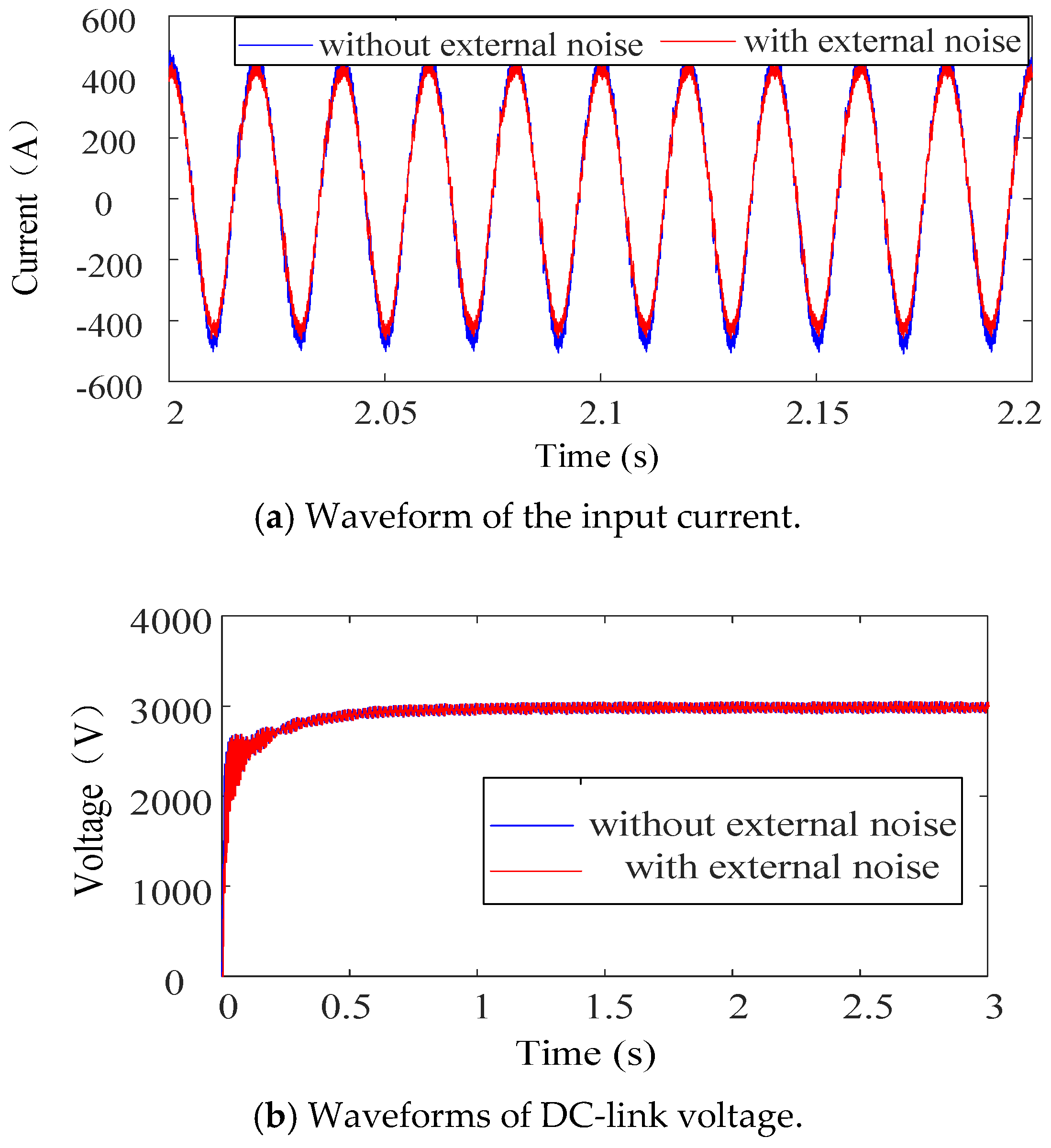
4.4. Sensitivity of H∞ Control Law Analysis
4.5. Discussion
- (1)
- Better dynamic performance, such as smaller overshoot, shorter peak time and smaller voltage fluctuation.
- (2)
- Better static performance with rated load.
- (3)
- The significant suppression capability of LFO in EMUs–traction network system.
- (1)
- In Table 4 and Table 5, the first set of data contains the original values of the model parameters. In Table 4, when the model parameter Rs decreases or Ls increases, the EMUs–traction network system becomes more unstable. LFO or a rectification failure will occur in the system based on PI control when the model parameters change, and the THD of the current will be large. In Table 5, the system is less affected when the model parameters change. Only when the model parameter Ls is expanded to 100 times will a rectification failure occur in the system based on H∞ control. Thus, H∞ control has better robustness than PI control.
- (2)
- In Table 6, the first set of data is the original value of the PI controller. When the original value of the control parameter Kp is exceeded, LFO will occur. If the control parameter Ku is reduced, LFO will also occur. In addition, it is noted that the set of parameters that exceed the original value of the control parameter Ki will cause a rectification failure. In Table 7, the first set of data contains the original values of the H∞ controller. It can be indicated that the system is stable in all cases. The control parameter K2 has a little influence on the stability of the system. However, the phenomenon that the DC-link voltage is about 12 kV will appear when the original value of the control parameter K1 is exceeded. The set of parameters that exceed the original value of the control parameter K3 can also cause this phenomenon. Actually, 12 kV DC-link voltage is not permitted in real-life operation. Thus, the problem should be studied in the future.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Traction Substation | |
| Power utility short capacity | 10 GVA |
| Rated voltages | 220 × (1 ± 2 × 2.5%)/2 × 27.5 kV |
| Rated power | 50/31.5/31.5 MVA |
| Short-circuit voltage | 10.5% |
| Short-circuit losses | 140.7 kW |
| Auto Transform in Auto Transform Station | |
| Rated voltages | 55/27.5 kV |
| Rated power | 35 MVA |
| Short-circuit voltage | 1.6% |
| Short-circuit losses | 57.271 kW |
| Earth | |
| Earth resistivity | 100 Ω/m |
| Rail to earth conductance | 2 S/km |
| Traction substation and auto transform station earth network to Earth | 4 S, 2 S |
| System Component | Value |
|---|---|
| Input voltage | us = 1550 V |
| AC-side inductance | L = 4.7 mH |
| Load resistance | Rd = 10 Ω |
| DC-link reference voltage | udc = 3000 V |
| Switching frequency | fs = 350 Hz |
| Sampling frequency | fc = 10.0 kHz |
| DC-link Capacitance | Cd = 3 mF |
References
- Wang, H.; Wu, M. Test and analysis on low frequency oscillation of traction power system voltage caused by EMUs. In Proceedings of the 27th China College Power System and Automation Annual Conference, Qinghuangdao, China, 14–18 October 2011. [Google Scholar]
- Liao, Y.C.; Liu, Z.G.; Zhang, G.N.; Xiang, C. Vehicle-grid system modeling and stability analysis with forbidden region based criterion. IEEE Trans. Power Electron. 2017, 5, 3499–3512. [Google Scholar] [CrossRef]
- Menth, S.; Meyer, M. Low frequency power oscillations in electric railway systems. Eb Elektrische Bahnen 2006, 5, 216–221. [Google Scholar]
- Heising, C.; Bartelt, R.; Oettmeier, M.; Staudt, V. Improvement of low-frequency system stability in 50-Hz railway-power grids by multivariable line-converter control in a distance-variation scenario. In Proceedings of the Electrical Systems for Aircraft, Railway and Ship Propulsion, Bologna, Italy, 19–21 October 2010. [Google Scholar]
- Zhang, G.; Liu, Z.; Yao, S. Suppression of low-frequency oscillation in traction network of high-speed railway based on auto-disturbance rejection control. Trans. Transport. Electrific. 2016, 2, 244–255. [Google Scholar] [CrossRef]
- Wang, H.; Wu, M.; Sun, J. Analysis of low-frequency oscillation in electric railways based on small-signal modeling of vehicle-grid system in dq frame. IEEE Trans. Power Electron. 2015, 9, 5318–5330. [Google Scholar] [CrossRef]
- Assefa, H.Y.; Danielsen, S.; Molinas, M. Impact of PWM switching on modeling of low frequency power oscillation in electrical rail vehicle. In Proceedings of the 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009. [Google Scholar]
- Suarez, J.; Ladoux, P.; Roux, N.; Caron, H.; Guillame, E. Measurement of locomotive input admittance to analyse low frequency instability on AC rail networks. In Proceedings of the 2014 International Symposium Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Ischia, Italy, 18–20 June 2014. [Google Scholar]
- Oettmeier, M.; Bartelt, R.; Heising, C.; Staudt, V.; Steimel, A. LQ optimized multivariable control for a single-phase 50-kW, 16.7-Hz railway traction line-side converter. In Proceedings of the 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009. [Google Scholar]
- Bartelt, R.; Oettmeier, M.; Heising, C.; Staudt, V. Improvement of low-frequency system stability in 16.7-Hz railway power grids by multivariable line-converter control in a multiple traction vehicle scenario. In Proceedings of the Electrical Systems for Aircraft, Railway and Ship Propulsion, Bologna, Italy, 19–21 October 2010. [Google Scholar]
- Wang, Y.; Wang, J.; Zeng, W. H∞ Robust Control of an LCL-Type Grid-Connected Inverter with Large-Scale Grid Impedance Perturbation. Energies 2018, 11, 57. [Google Scholar] [CrossRef]
- Tan, P.; Morrison, R.E.; Holmes, D.G. Voltage from factor control and reactive power compensation in a 25-kV Electrified railway system using a shunt active filter based on voltage detection. IEEE Trans. Ind. Appl. 2003, 2, 575–581. [Google Scholar]
- Jin, W.; Li, Y.; Sun, G. H∞ Repetitive Control Based on Active Damping with Reduced Computation Delay for LCL-Type Grid-Connected Inverters. Energies 2017, 10, 586. [Google Scholar] [CrossRef]
- Zhao, R.; Lu, S.; Tu, L. Design of decentralized controllers for parallel AC-DC system based on effective relative gain array and mixed H2/H∞ control. Power Syst. Protect. Control 2016, 24, 44–51. [Google Scholar]
- Feng, X. Electric Traction AC Drives and Control System; Higher Education Press: Beijing, China, 2009. [Google Scholar]
- Gou, B.; Ge, X.; Wang, S.; Feng, X. An open-switch fault diagnosis method for single-phase PWM rectifier using a model-based approach in high-speed railway electrical traction drive system. IEEE Trans. Power Electron. 2016, 5, 3816–3826. [Google Scholar] [CrossRef]
- Green, A.W.; Boys, J.T.; Gates, G.F. 3-phase voltage sourced reversible rectifier. IEEE Proc. B Elec. Power Appl. 1988, 6, 362–370. [Google Scholar] [CrossRef]
- Wu, G.R.; Xiao, X. Robust speed controller for a PMSM Drive. In Proceedings of the International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009. [Google Scholar]
- Li, Q.; Chen, W.; Liu, S.; Liu, X. H∞ suboptimal control for proton exchange membrane fuel cell (PEMFC) hybrid power generation system based on modified particle swarm optimization. Power Syst. Prot. Control 2010, 21, 126–131. [Google Scholar]
- Dabra, V.; Paliwal, K.K.; Sharma, P. Optimization of photovoltaic power system: A comparative study. Prot. Control Mod. Power Syst. 2017, 2, 3. [Google Scholar] [CrossRef]
- Saptarshi, D.; Pan, I. On the mixed H-2/H-infinity loop-shaping tradeoffs in fractional-order control of the AVR system. IEEE Trans. Ind. Inf. 2014, 4, 1982–1991. [Google Scholar]
- Lee, H.; Lee, C.; Jang, G.; Kwon, S.H. Harmonic analysis of the Korean high-speed railway using the eight-port representation model. IEEE Trans. Power Deliv. 2002, 2, 979–986. [Google Scholar] [CrossRef]







| Parameters | Max Value | Min Value | Optimal Value |
|---|---|---|---|
| Ka | 100 | 1 × 10−4 | 9 |
| Kb | 200 | 10 | 12 |
| Kc | 100 | 0.001 | 10 |
| Kd | 200 | 1 × 10−5 | 45 |
| Ke | 100 | 1 × 10−4 | 69 |
| Kf | 200 | 0.01 | 6 |
| Kg | 10 | 1.0 | 1 |
| 1 | 0 | 1 |
| Performance | PI Control | MC | ADRC | H∞ |
|---|---|---|---|---|
| Overshoot (%) | 16.7 | 5.5 | 0.8 | 0.3 |
| Peak time (s) | 0.0125 | 0.182 | None | None |
| Adjustment time (s) | 0.15 | 0.33 | 0.18 | 0.2 |
| Voltage fluctuation (V) | ±70 | ±30 | ±70 | ±55 |
| Conductor | Type DC | Resistance (Ω/km) | Calculation Radius (mm) |
|---|---|---|---|
| C | CuMg-150 | 0.1191 | 7.2 |
| R | UIC-60 | 0.135 | 12.79 |
| PW | LGJ-120 | 0.286 | 4.567 |
| F | 2 × LGJ-185 | 0.082 | 9.51 |
| M | THJ-120 | 0.181 | 7.0 |
| Parameter | Rs | Ls | Results | |
|---|---|---|---|---|
| Case | ||||
| 1 | 0.1 | 0.002 | Stable | |
| 2 | 0.5 | 0.002 | Stable | |
| 3 | 1 | 0.002 | Stable | |
| 4 | 10 | 0.002 | Stable, the THD of the current is large | |
| 5 | 0.02 | 0.002 | Stable | |
| 6 | 0.01 | 0.002 | Stable, the THD of the current is large | |
| 7 | 0.001 | 0.002 | Unstable | |
| 8 | 0.1 | 0.01 | Stable | |
| 9 | 0.1 | 0.02 | LFO | |
| 10 | 0.1 | 0.2 | Rectification failure | |
| 11 | 0.1 | 0.0004 | Stable | |
| 12 | 0.1 | 0.0002 | Stable, the THD of the current is large | |
| 13 | 0.1 | 0.00002 | Stable, the THD of the current is large | |
| Parameter | Rs | Ls | Results | |
|---|---|---|---|---|
| Case | ||||
| 1 | 0.1 | 0.002 | Stable | |
| 2 | 0.5 | 0.002 | Stable | |
| 3 | 1 | 0.002 | Stable | |
| 4 | 10 | 0.002 | Stable, the THD of the current is large | |
| 5 | 0.02 | 0.002 | Stable | |
| 6 | 0.01 | 0.002 | Stable | |
| 7 | 0.001 | 0.002 | Stable | |
| 8 | 0.1 | 0.01 | Stable | |
| 9 | 0.1 | 0.02 | Stable | |
| 10 | 0.1 | 0.2 | Rectification failure | |
| 11 | 0.1 | 0.0004 | Stable | |
| 12 | 0.1 | 0.0002 | Stable | |
| 13 | 0.1 | 0.00002 | Stable | |
| Parameter | Kp | Ki | Ku | Results | |
|---|---|---|---|---|---|
| Case | |||||
| 1 | 0.3 | 10 | 1 | Stable | |
| 2 | 30 | 10 | 1 | LFO | |
| 3 | 10 | 10 | 1 | LFO | |
| 4 | 3 | 10 | 1 | LFO | |
| 5 | 0.03 | 10 | 1 | Stable | |
| 6 | 0.01 | 10 | 1 | Stable | |
| 7 | 0.003 | 10 | 1 | Stable | |
| 8 | 0.3 | 1000 | 1 | Rectification failure | |
| 9 | 0.3 | 500 | 1 | Rectification failure | |
| 10 | 0.3 | 100 | 1 | Stable | |
| 11 | 0.3 | 1 | 1 | Stable | |
| 12 | 0.3 | 0.5 | 1 | Stable | |
| 13 | 0.3 | 0.1 | 1 | Stable | |
| 14 | 0.3 | 10 | 100 | Stable | |
| 15 | 0.3 | 10 | 50 | Stable | |
| 16 | 0.3 | 10 | 10 | Stable | |
| 17 | 0.3 | 10 | 0.5 | LFO | |
| 18 | 0.3 | 10 | 0.1 | LFO | |
| 19 | 0.3 | 10 | 0.01 | LFO | |
| Parameter | K1 | K2 | K3 | Results | |
|---|---|---|---|---|---|
| Case | |||||
| 1 | 0.2 | 0.6 | 0.4 | Stable | |
| 2 | 20 | 0.6 | 0.4 | Stable, DC-link voltage is about 12 kV | |
| 3 | 10 | 0.6 | 0.4 | Stable, DC-link voltage is about 12 kV | |
| 4 | 2 | 0.6 | 0.4 | Stable, DC-link voltage is about 12 kV | |
| 5 | 0.02 | 0.6 | 0.4 | Stable | |
| 6 | 0.004 | 0.6 | 0.4 | Stable | |
| 7 | 0.002 | 0.6 | 0.4 | Stable | |
| 8 | 0.2 | 60 | 0.4 | Stable | |
| 9 | 0.2 | 30 | 0.4 | Stable | |
| 10 | 0.2 | 6 | 0.4 | Stable | |
| 11 | 0.2 | 0.06 | 0.4 | Stable | |
| 12 | 0.2 | 0.012 | 0.4 | Stable | |
| 13 | 0.2 | 0.006 | 0.4 | Stable | |
| 14 | 0.2 | 0.6 | 40 | Stable, DC-link voltage is about 12 kV | |
| 15 | 0.2 | 0.6 | 20 | Stable | |
| 16 | 0.2 | 0.6 | 4 | Stable | |
| 17 | 0.2 | 0.6 | 0.04 | Stable | |
| 18 | 0.2 | 0.6 | 0.008 | Stable | |
| 19 | 0.2 | 0.6 | 0.004 | Stable | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, Z.; Liu, Z.; Hu, X.; Liu, J. Low-Frequency Oscillation Suppression of the Vehicle–Grid System in High-Speed Railways Based on H∞ Control. Energies 2018, 11, 1594. https://doi.org/10.3390/en11061594
Geng Z, Liu Z, Hu X, Liu J. Low-Frequency Oscillation Suppression of the Vehicle–Grid System in High-Speed Railways Based on H∞ Control. Energies. 2018; 11(6):1594. https://doi.org/10.3390/en11061594
Chicago/Turabian StyleGeng, Zhaozhao, Zhigang Liu, Xinxuan Hu, and Jing Liu. 2018. "Low-Frequency Oscillation Suppression of the Vehicle–Grid System in High-Speed Railways Based on H∞ Control" Energies 11, no. 6: 1594. https://doi.org/10.3390/en11061594
APA StyleGeng, Z., Liu, Z., Hu, X., & Liu, J. (2018). Low-Frequency Oscillation Suppression of the Vehicle–Grid System in High-Speed Railways Based on H∞ Control. Energies, 11(6), 1594. https://doi.org/10.3390/en11061594





