LCL Filter Design with EMI Noise Consideration for Grid-Connected Inverter

Abstract

The grid-injected current total harmonics distortion (THD) and electromagnetic interference (EMI) noise must be considered in a transformer-less grid-connected inverter for a more electric aircraft (MEA) system. This paper develops a procedure for the design of the magnetic components of the LCL filter used in harmonic control and EMI reduction of the silicon carbide (SiC) grid-connected inverter in the MEA. The LCL filter is designed with effective harmonic attenuation and a compact size. To meet the space constraint requirement, specific design attention is focused on a customized amorphous cored inductor, with a comprehensive study of the relationships of inductor winding with respect to EMI noise. Reduced THD and EMI are verified through experiments performed on a 30 kW, 230 V/400 Hz three-phase grid-connected inverter prototype with the LCL filter.

1. Introduction

The concept of more electric aircraft (MEA) is based on the increasing use of electric power to replace the non-electric subsystems (pneumatic, mechanical, and hydraulic) in the traditional aircraft. The MEA concept provides significant improvements in reliability, maintenance cost, fuel consumption, and overall weight of the aircraft [1,2,3,4]. Because of the strict weight and space constraints, an electric starter/generator (ESG) is employed that acts as a motor to start the gas turbine engine and as a generator to convert the mechanical power to electrical power used to supply the onboard loads [5]. As in Figure 1, a back-to-back power converter that contains a machine-side converter (MSC) and a network-side converter (NSC) is used as the interface between the ESG and the power grid. As the passive components of the filter dominate the total weight of the power converter, the filter design has become one of the key technologies for MEA.

The LCL filter is widely used in the grid-connected inverter because of its harmonic attenuation performance and system stability. There are two inductors used, one located at the inverter side and the other located at the grid side. Compact and efficient magnetic components design in the power inverter results in minimization of its total size and weight; thus, magnetic material plays an important role in the grid-connected high power density inverter [6,7]. Winding technology [8,9,10], switching frequency [11], and core selection [12] are three important issues in the size reduction of magnetic components in the LCL filter.

Furthermore, current harmonic distortion of the grid-connected power inverter must be considered because of the power quality requirement in the power grid. In addition to the power quality of the power grid, another important issue is the conducted electromagnetic interference (EMI), which is mainly generated by the high frequency transistor switching and parasitic components in the noise conduction path [13,14,15]. Mostly, the EMI noise in the DC side of the inverter is suppressed to meet the EMI standard [16]. In Reference [17], the reduced EMI noise in the AC side of the inverter has been observed but the parasitic components in the LCL filter are not considered. In a grid-connected inverter, the differential mode (DM) EMI is dominant compared with the common mode (CM) EMI; thus, the LCL filter can be treated as an EMI filter [18] in the high frequency range if the self-resonant frequency in the filtering inductor is high enough. The resonant frequency is relatively dependent on the parasitic components in the inductor [19]. Thus, if total harmonics distortion (THD) and EMI can be reduced at the same time with one filter, the power density would be increased pronouncedly.

To address this problem, a higher order filter with a copper foil-wound inductor is used instead. Section 2 gives the procedure to determine the output LCL filter’s parameters. Section 3 presents the magnetic components design in the LCL filter. Section 4 evaluates the performance of the copper foil and copper wire inductors in EMI noise control. Section 5 presents the experiments. Finally, Section 6 concludes the paper.

2. LCL Filter Design Procedure

2.1. Components of the LCL Filter

Figure 2 shows the LCL type grid-connected inverter system, which corresponds to the NSC shown in Figure 1. The output LCL filter is a component necessary to satisfy the harmonic limit requirement [20,21]. $L_i$ is the inverter side inductor, $C_f$ is the filtering capacitor, $L_g$ is the grid side inductor, $V_i$ is the inverter side voltage, and $V_g$ is the grid voltage.

The LCL filter is used to suppress the harmonics at the fundamental and multiples of the switching frequency $f_{sw}$. Compared with other filter topologies, the LCL topology [22] has low grid current distortion and reactive power production, good roll off of 60 dB/decade at high frequency and relatively low required switching frequency.

The bode plot of transfer function $I_g/V_i$ of the LCL filter, as given in Equation (1), exhibits 60 dB/decade attenuation above the resonant frequency, given by Equation (2). The resonant frequency should be in the range of $10f_g<f_{res}<0.5f_{sw}$ to ensure the whole system remains stable.

$${\frac{I_g(s)}{V_i(s)}|}_{V_g(s)=0}=\frac{1}{L_i{L}_g{C}_{f}s(s^2+\frac{L_i+L_g}{L_i{L}_g{C}_f})}$$

(1)

$$f_{res}=\frac{1}{2\pi }\sqrt{\frac{L_i+L_g}{L_i{L}_g{C}_f}}$$

(2)

In a two-level system, the maximum inverter side ripple current is given in Equation (3), where $V_{dc}$ is the DC input voltage, and $m$ is the modulation index.

$$\left|i_{ripple}\right|=\frac{V_A}{L_i}\cdot \frac{\frac{2}{3}{V}_{dc}-V_A}{\frac{2}{3}{V}_{dc}}\cdot T_s=\frac{2V_{dc}}{3L_i}m(1-m)T_s$$

(3)

From Equation (3), one can see that the maximum current ripple occurred with the modulation factor $m$ = 0.5 given by Equation (4).

$$\Delta i_{\max }=\frac{V_{dc}}{6f_{s}L}$$

(4)

With a rated voltage of $V_{p-p}$ (phase to phase), an operating condition of power P, and a switching frequency $f_{sw}$ in the grid-connected system, the base impedance is calculated by

$$Z_{base}=\frac{V_{p-p}^2}{P}.$$

(5)

Additionally, the base capacitance is

$$C_{base}=\frac{1}{2\pi f_g{Z}_{base}}.$$

(6)

$X$ is the percentage of absorbed reactive power under the rated condition [23]. The filtering capacitor $C_f=X{C}_{base}$. The inverter side inductor $L_i$ can be selected by the maximum ripple current requirement, as shown in Equation (4). According to Equations (7) and (8), the minimum $L_i$ is calculated with Equation (9).

$$I_{\max }=\frac{P}{3V_{ph}}\times \sqrt{2}$$

(7)

$$\Delta i_{\max }=0.1/k_{ratio}\times I_{\max }$$

(8)

$$L_{i\_\min }\ge \frac{V_{dc}}{6\times \Delta i_{\max }}\cdot T_s$$

(9)

The grid side inductor $L_g$ is chosen according to attenuation ratio $k_{ratio}$, as expressed in Equation (10). The LCL filter is expected to attenuate the grid side current in accordance with the IEEE Std 519, as shown in

Table 1. Current distortion limits for systems rated 120 V through 69 kV. (THD: total harmonics distortion.).

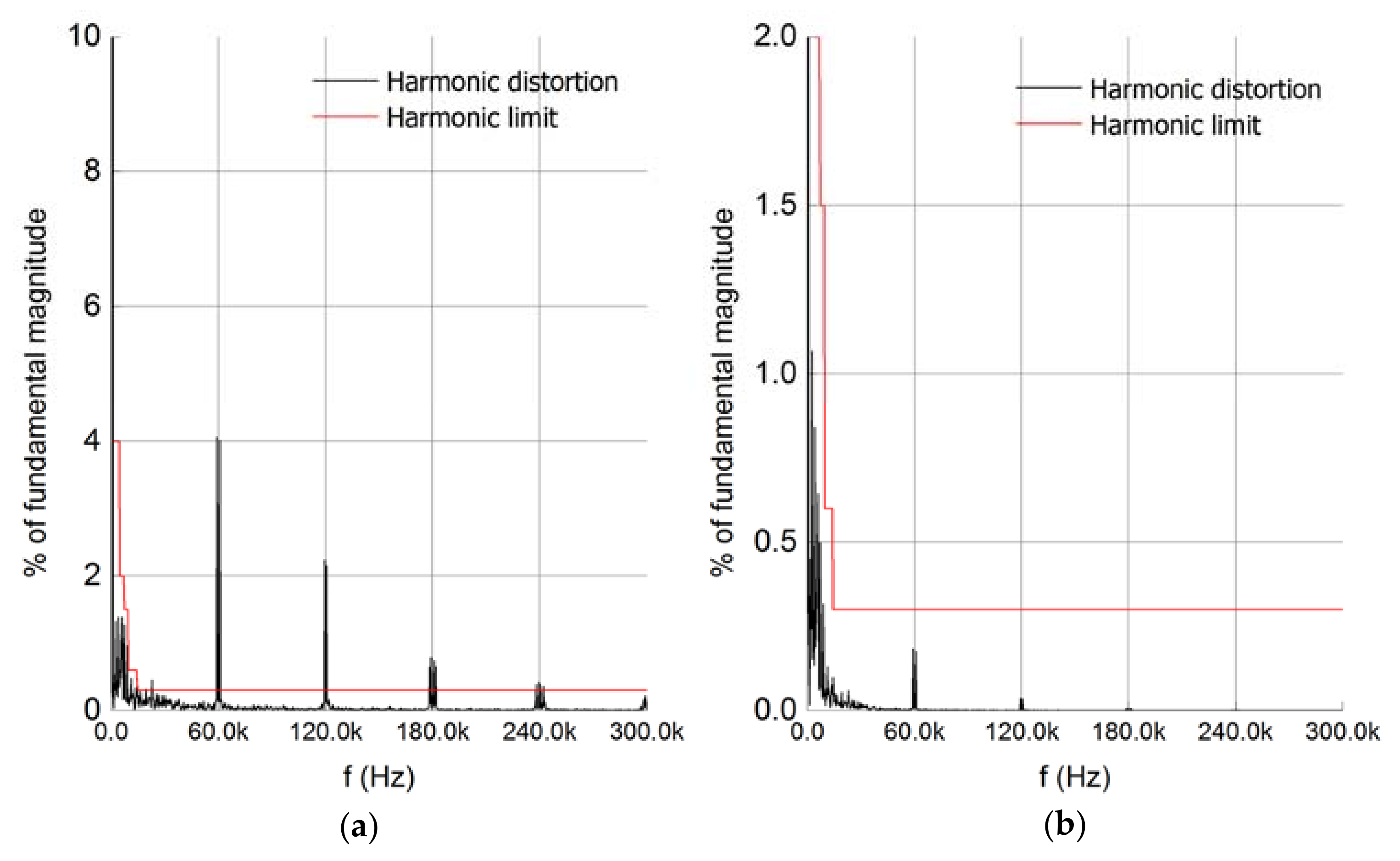
Maximum Harmonic Current Distortion in Percent of I1
$3\le h\le 11$	4.0%
$11\le h\le 17$	2.0%
$17\le h\le 23$	1.5%
$23\le h\le 35$	0.6%
$35\le h$	0.3%
THD	5%

[24]. The harmonic distortion and total demand distortion depends on the ratio of maximum short circuit current and maximum demand load current at the at the point of common coupling (PCC). In a grid-connected system, the ratio is usually smaller than 20 [25]. $L_g=r{L}_i$ is the relationship between the two inductors. To increase the power density, the silicon carbide (SiC) power module is employed in the grid-connected inverter to ensure the switching frequency can be increased to 60 kHz or higher.

$$\frac{i_g(h_{sw})}{i_i(h_{sw})}=\frac{1}{\left|1+r(1-L_{i}X{C}_{base}{w}_{sw}^2)\right|}=\frac{1}{\left|1+r(1-L_{i}X{C}_{base}{(2\pi f_{sw})}^2)\right|}=k_{ratio}$$

(10)

2.2. Simulation Results

The simulation of LCL three-phase grid-connected inverter is carried out based on Matlab/Simulink to verify the system design procedure. The grid phase voltage $V_g$ is 220 V, the DC-link voltage $V_{dc}$ is 750 V, the switching frequency $f_s$ is 60 kHz, and the rated power $P_n$ is 30 kW. Figure 3 shows the simulation currents and their THD analysis results. It reveals that the inverter side current’s total harmonic distortion is smaller than the harmonic limit. It can be found that the harmonics distortion is reduced from 6.47% to 2.26% by the LCL filter. The experimental setup can be designed according to the simulation parameters. Figure 4a shows the transient inverter side current at start time and Figure 4b shows dynamic response of grid-connected current. It can be seen that the system can be adjusted quickly and achieve stability, which shows that the system has good dynamic response performance.

3. Magnetic Material in the LCL Filter Design

3.1. Core Material Selection

To minimize the core loss and space,

Table 2. Magnetic core loss parameters.

Material	Ferrite	Power Iron	Nanocrystalline	Amorphous
$B_{max}$ (T)	0.49	0.6–1.3	1.56	1.2
$K_c$	16.9	1798	2.3	0.053
$\mathsf{\alpha }$	1.25	1.02	1.32	1.81
$\mathsf{\beta }$	2.35	1.89	2.1	1.74

shows some specifications for the different types of magnetic core materials in the power electronic converter design. $B_{max}$ is the maximum flux density, and $K_c$, $\mathsf{\alpha }$, and $\mathsf{\beta }$ are the power loss parameters related to the switching frequency and the maximum flux density variation.

$$P_{coreloss}=K_c{f}^{\mathsf{\alpha }}{B}_{max}{}^{\mathsf{\beta }}$$

(11)

The nanocrystalline core has the lowest core loss, whereas the powder iron core has the largest core loss. The low core loss, high saturation flux density, wider operation frequency, and high operation temperature of the amorphous core allow for advanced power conditioning applications with high power.

$$K_g=\frac{A_c{}^2{W}_A}{MLT}$$

(12)

The chosen amorphous EE magnetic core for the filtering inductor has an inductance L and carries a maximum current $I_{max}$ without saturating. $A_c$ is the effective cross area of the magnetic core, $W_A$ is the window area, MLT is the mean length per turn. The copper and core loss also should be considered and dissipated through the surface of the inductor winding.

In the three-phase EE core, the maximum flux density $B_{max}$ reduced to two-thirds via the increased flux density distribution. n is the number of turns, and $l_g$ is the gap length:

$$l_g=\frac{{\mu }_{0}L{I}_{\max }{}^2}{\frac{3}{2}{B}_{\max }{}^2{A}_c}$$

(13)

$$n=\frac{L{I}_{\max }}{\frac{3}{2}{B}_{\max }{A}_c}.$$

(14)

The celebrated general Steinmetz equation for core loss given in Equation (11) and the copper loss given in Equation (15) can be used to evaluate the temperature rise in the inductor.

$$P_{copperloss}=I_{rms}{}^2\times \rho \frac{n(MLT)}{A_W}$$

(15)

3.2. 3D Printing Technology for Bobbin Design

3D printing technology, as shown in Figure 5, is adopted for the bobbin fabrication to achieve the purpose of compactness. Figure 5b shows a comparison of the commercial and 3D printed bobbins; although the 3D printed bobbin is more expensive than the commercial bobbin, it can reduce the volume by up to 40%, leading to higher power density. The fabricated bobbin with a thickness of 2 mm and the acrylonitrile butadiene styrene (ABS) material is chosen for 3D printing.

4. Inductor Winding Design

4.1. Parasitic Components in the Two Types of Wound Inductors

To reduce the parasitic components at higher frequency range, the conventional copper wire for inductor winding is replaced by copper foil with an EE amorphous core, as shown in Figure 6. Copper foil winding can help to reduce the inductor’s overall material cost by 15 to 20 percent. The copper foil winding can be used in high current applications because of its size reduction benefit. The size of the copper wire for high current is large and the window area in the magnetic core is limited. Using the copper foil for the winding is a better choice in the case of limited inductor space.

Table 3. Inductor parameters.

Parameters	Li	Lg
Core type	AFEC-90a	AFEC-48a
Foil size	$0.2 \mathrm{mm}\times 80 \mathrm{mm}$	$0.4 \mathrm{mm}\times 40 \mathrm{mm}$
n	14	5
$l_g$	1 mm	0.5 mm

shows the parameters of inductors $L_i$ and $L_g$ in the LCL filter, including core type, foil size, number of turns, and air gap. All the parameters are designed according to the inverter design specification. The amorphous core with low loss and high saturation flux density is chosen for the filtering inductors’ design.

Figure 7a shows the impedance of the two types of inductors with different winding technology that is measured by a Hewlett Packard 4194A Impedance analyzer. The copper foil inductor is found to have higher resonant frequency than that of the copper wire inductor. The higher resonant frequency indicates that it has better noise attenuation for the conducted EMI noise in the range of 150 kHz to 30 MHz.

Figure 7a shows the high frequency model of the copper foil inductor, which is a second order equivalent circuit. Parasitic components of $R_1$, $R_2$, and $R_3$ can be calculated by the impedance values at $f_1$, $f_3$, and $f_5$. Figure 7b reveals that the impedance of the whole equivalent circuit can be written as Equation (16).

$$\left|Z_L\right|=\left|{\displaystyle \sum _{i=1,2,3}\frac{1}{\frac{1}{R_i}+j2\pi f{C}_i+\frac{1}{j2\pi f{L}_i}}}\right|$$

(16)

The approximate values of $L_1$, $C_1$, $L_2$, $C_2$, $L_3$, and $C_3$ can be estimated at the three frequencies $f_1$, $f_2$, and $f_3$. The difference between the simulation and the measurement can be minimized via the least squares method, as shown in Equation (17), to improve the accuracy of the inductor parasitic components derivation.

$$M_1={\displaystyle \sum _{i=1,2,3,4,5}{(Z_{si}-Z_{mi})}^2}$$

(17)

Table 4. Equivalent circuit parameters in the copper foil inductor and the copper wire inductor.

Parameters	Copper Foil		Copper Wire
	Estimated	Improved	Estimated	Improved
$L_1(\mathsf{\mu }\mathrm{H})$	90	84	90	82
$C_1(PF)$	103	110	237	260
$R_1(\Omega )$	4922	4922	3525	3525
$L_2(\mathsf{\mu }\mathrm{H})$	10.8	3.8	10.6	2
$C_2(PF)$	67.3	190	180	1000
$R_2(\Omega )$	1916	1916	626	626
$L_3(\mathsf{\mu }\mathrm{H})$	0.65	0.46	1.13	0.9
$C_3(PF)$	11.9	22	0.25	30
$R_3(\Omega )$	237	237	578	578

shows the equivalent circuit parameters in the two types of winding inductors. The value of $L_2$ in the copper foil inductor is found to be higher than that in the copper wire inductor. The larger high-frequency inductor can help to reduce the inductor of the EMI filter. More accurate circuit components in the filter can be used in the simulation model to predict the noise at low and high frequencies.

4.2. EMI Noise Model with LCL Filter Consideration

Figure 8 shows the common mode (CM) and differential mode (DM) EMI noise model with the LCL filter consideration; Equation (18) and Equation (19) are the CM and DM noise voltages, respectively. It can be found that the larger impedance of $L_i$ denotes the smaller noise voltage and reduced EMI filter requirement. Thus, the weight of the copper foil inductor is smaller than the copper wire inductor in the system requirement for the inverter. Compared to the copper wire inductor, the copper foil inductor has more efficient high-frequency noise attenuation ability and saves more space for the EMI filter design. According to the above analysis, the copper foil inductor will be designed and applied in the experiment to verify its THD and EMI noise attenuation effect.

$$V_{CM,noise}=\frac{50/3}{50/3+Z_{L_i}/3+Z_{x,CM}}{V}_{CM}$$

(18)

$$V_{DM,noise}=\frac{50}{50+Z_{L_i}+Z_{x,DM}}{V}_{DM}$$

(19)

5. Experiment Results

As shown in Figure 9, the LCL filter design was verified in a 30 kW, 750 V (DC) and 230 V/400 Hz two-level three-phase grid-connected inverter based on the early works. The SiC power module is employed to achieve a high switching frequency with the commercial product CAS100H12AM1 (1.2 kV, 100 A) from Wolfspeed. It achieves 97.9% energy conversion efficiency at an input power of 30 kW and switching frequency of 60 kHz. The filtering inductors are designed with amorphous core and are foil- or wire-wound for comparison. All the parameters in the copper foil- and copper wire-wound inductor are the same except for the winding material. The gate driver is a composite of five parts including the DC–DC converter module (G1212S-2W) which is shown in Figure 10. Integrated circuit (ACPL-P345) is chosen as the optocoupler which isolates the high working voltage and low driver voltage; the relay module which functions as a hysteresis comparator for threshold control; and the buffer is output gate current which increases the driving capability.

5.1. Copper Wire Inductor Analysis Results

Figure 11a shows the simulated flux distribution at full load by finite element analysis (FEA) software, in which the maximum flux in the core is four-fifths of the saturation flux 1.56 T. Figure 11b shows the temperature distribution in the filtering inductor after one hour full load running; the maximum temperature is 155 °C, which is lower than its Curie Temperature of 399 °C.

Figure 11c shows the experimental current in the inverter with foil-wound inductor. Figure 12a,b show a comparison of the current harmonic distortion, from which it can be found that the current distortion in the grid side is suppressed below the standard by the LCL filter. Figure 12c shows the high-frequency current spectrum, from which one can see that the spectrum is suppressed in the range of 150 kHz to 1 MHz, which is part of the EMI frequency range. The reduced EMI noise can lead to smaller EMI filter requirement.

5.2. Copper Foil Inductor Analysis Results

Figure 13a,b show the harmonic distortion of the measured current waveforms with the copper foil inductor in the LCL filter; one can see that the grid side current harmonic distortion is reduced below the standard. Figure 13c shows the reduced current spectrum in the frequency domain.

Figure 12c and Figure 13c reveal that the LCL filter is able to not only reduce the THD but also reduce the DM EMI noise at the higher frequency range. Lower resonant frequency can lead to greater noise attenuation performance, as derived from Figure 8, and Equations (18) and (19).

Figure 14 shows a comparison of the grid side current spectrum in the two types of LCL filters, one with copper wire inductor and the other with the copper foil inductor. The high-frequency current spectrum in the LCL filter with the copper foil-wound is smaller than that with the copper wire-wound. Thus, the foil-wound inductor is used in the high-power density inverter to achieve a smaller EMI filter requirement.

6. Conclusions

This paper proposed the LCL filter design in a grid-connected system using a foil-wound inductor, 3D printed components, and a SiC-based power converter. The experimental inverter and grid side currents’ spectrum were used to evaluate the noise attenuation comparison of the copper foil-wound and traditional copper wire-wound inductors in the LCL filter. Because of the higher resonant frequency, lower EMI noise, and reduced space requirement in the foil-wound inductor compared to the traditional approach, it is highly recommended for the high-power density inverter design.