A Novel Hybrid DC Traction Power Supply System Integrating PV and Reversible Converters
Abstract
:1. Introduction
2. Topology and Operating Modes of the HTPSS
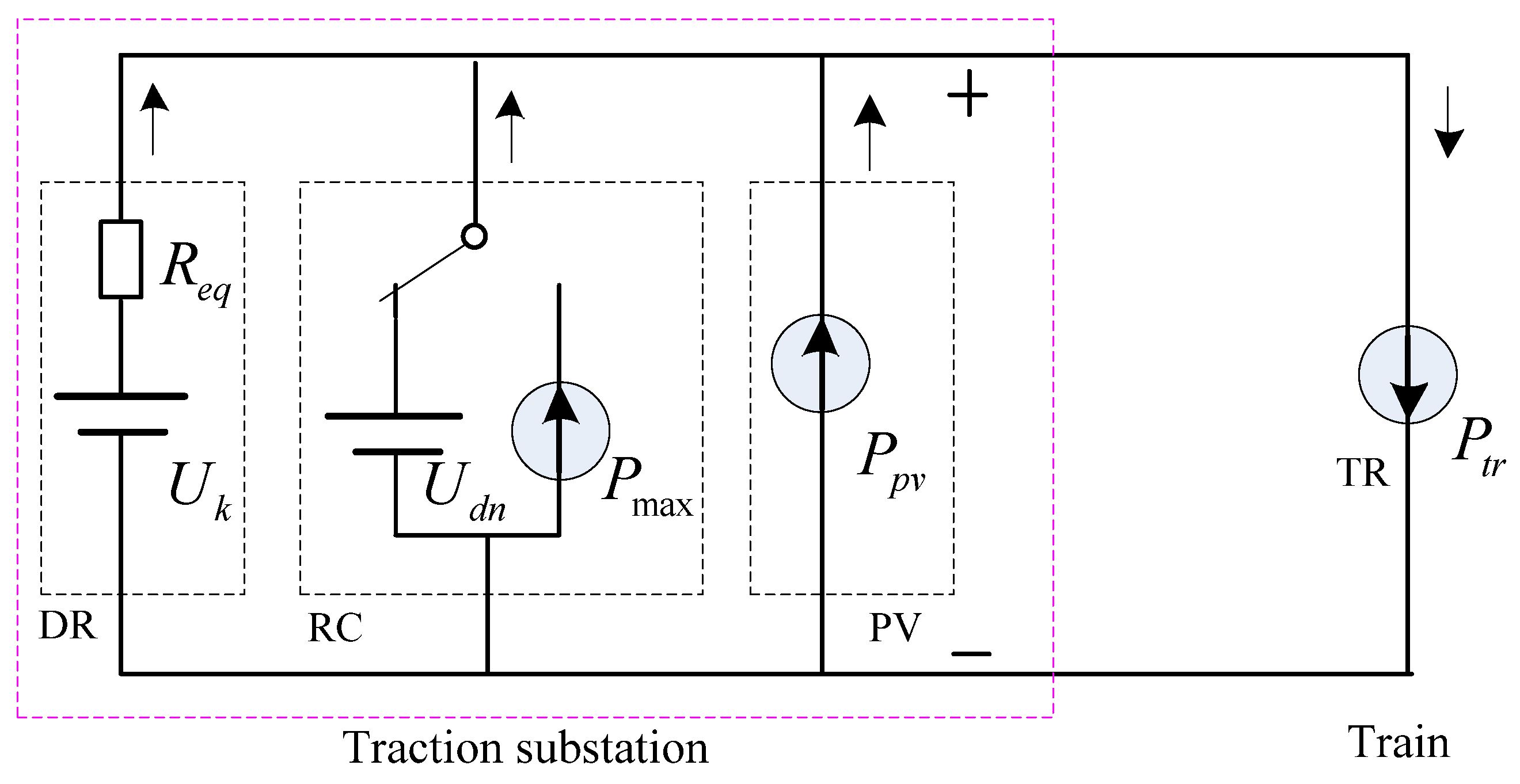
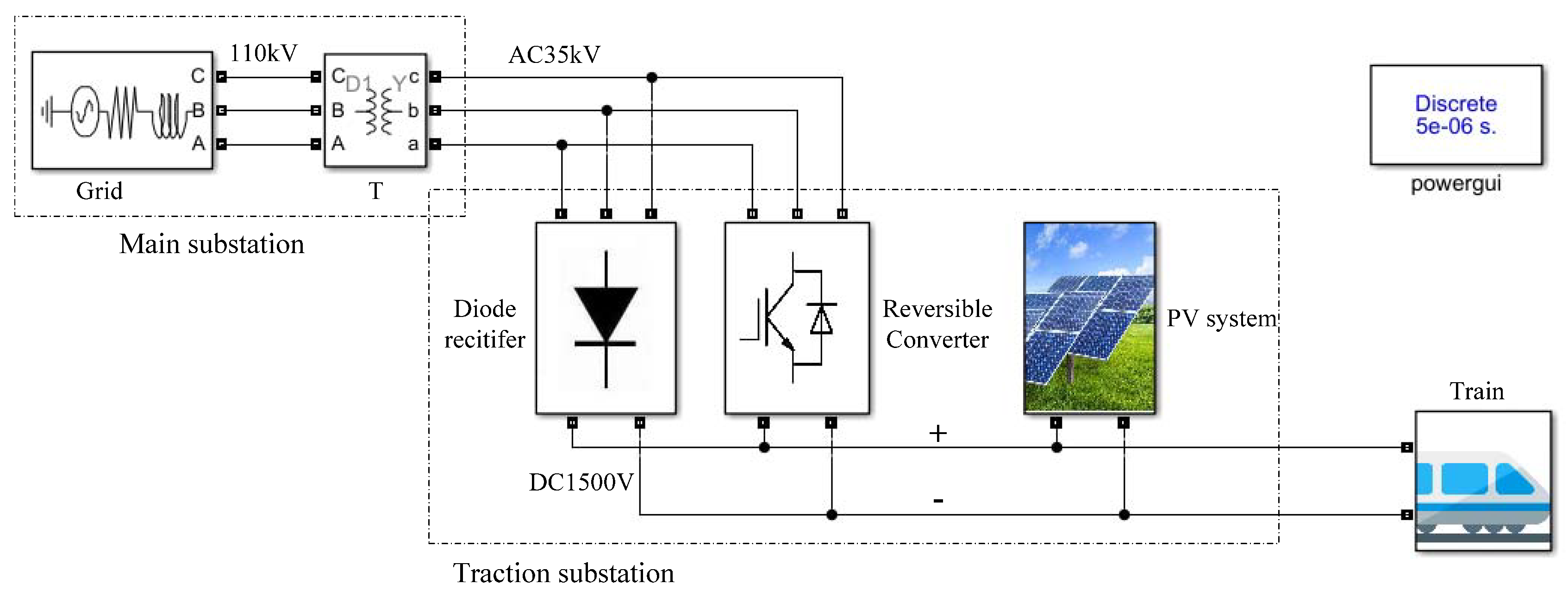
2.1. Topology of the HTPSS
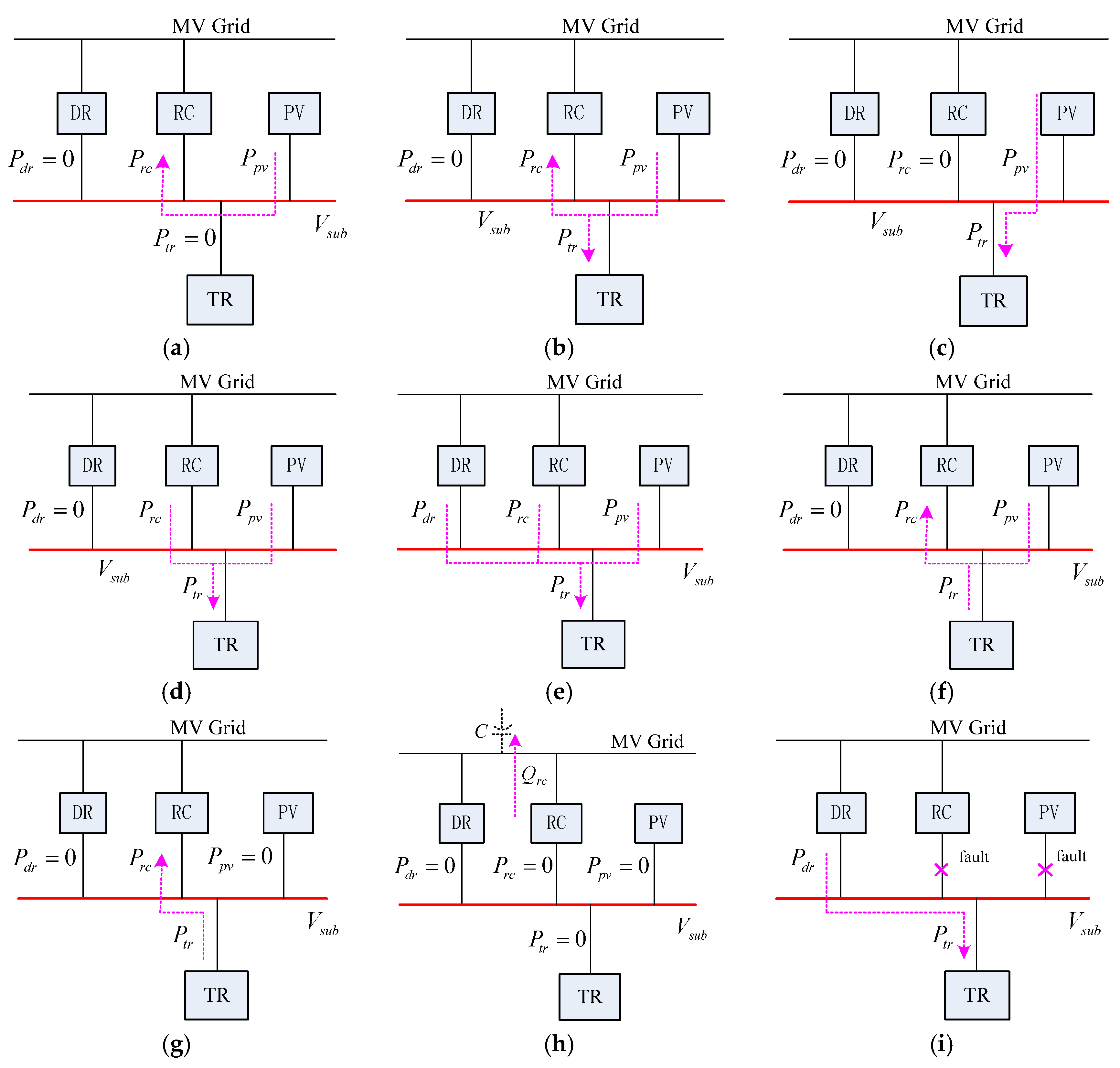
2.2. Operating Modes of the HTPSS
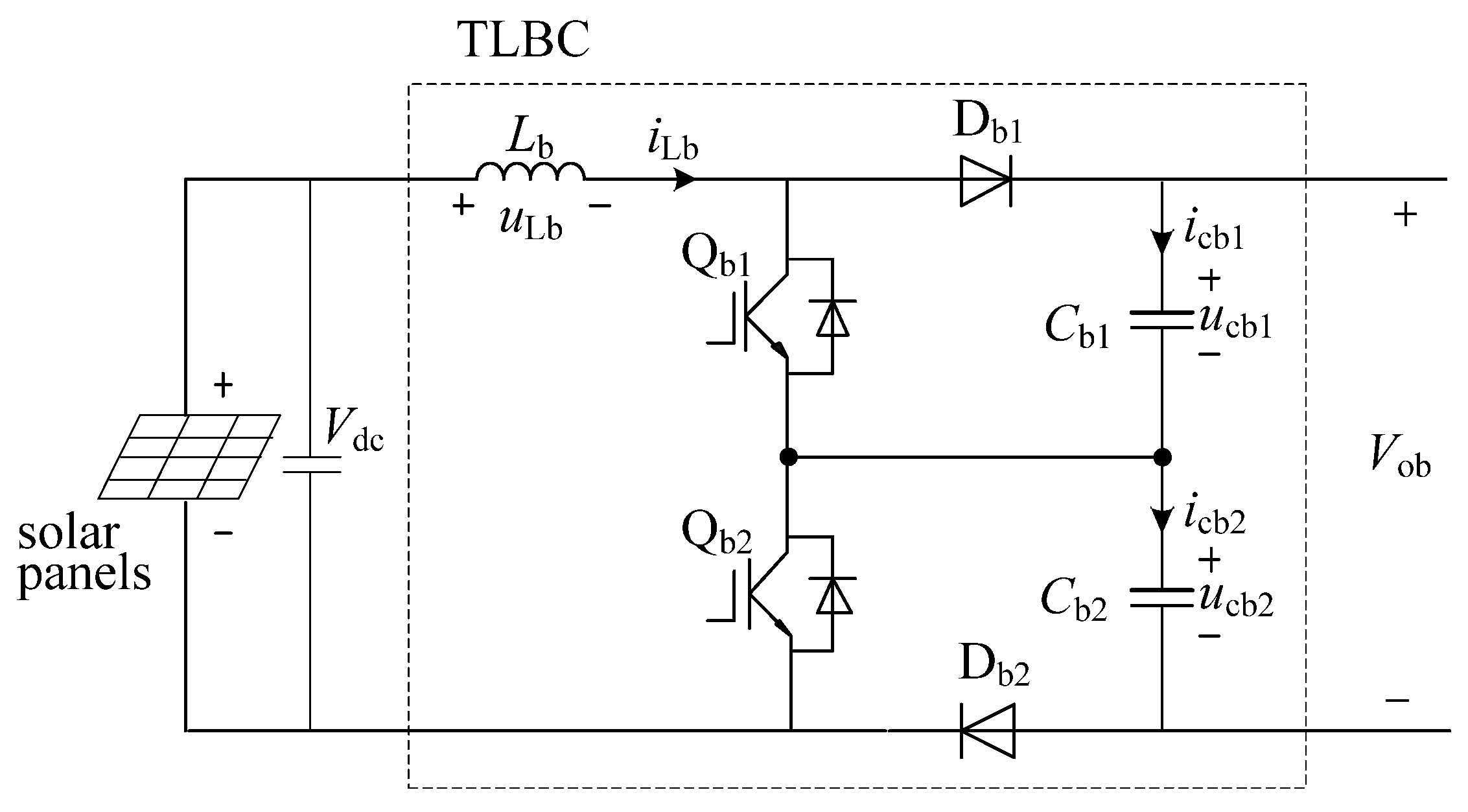
3. Three-Level Boost Converter
3.1. Main Circuit
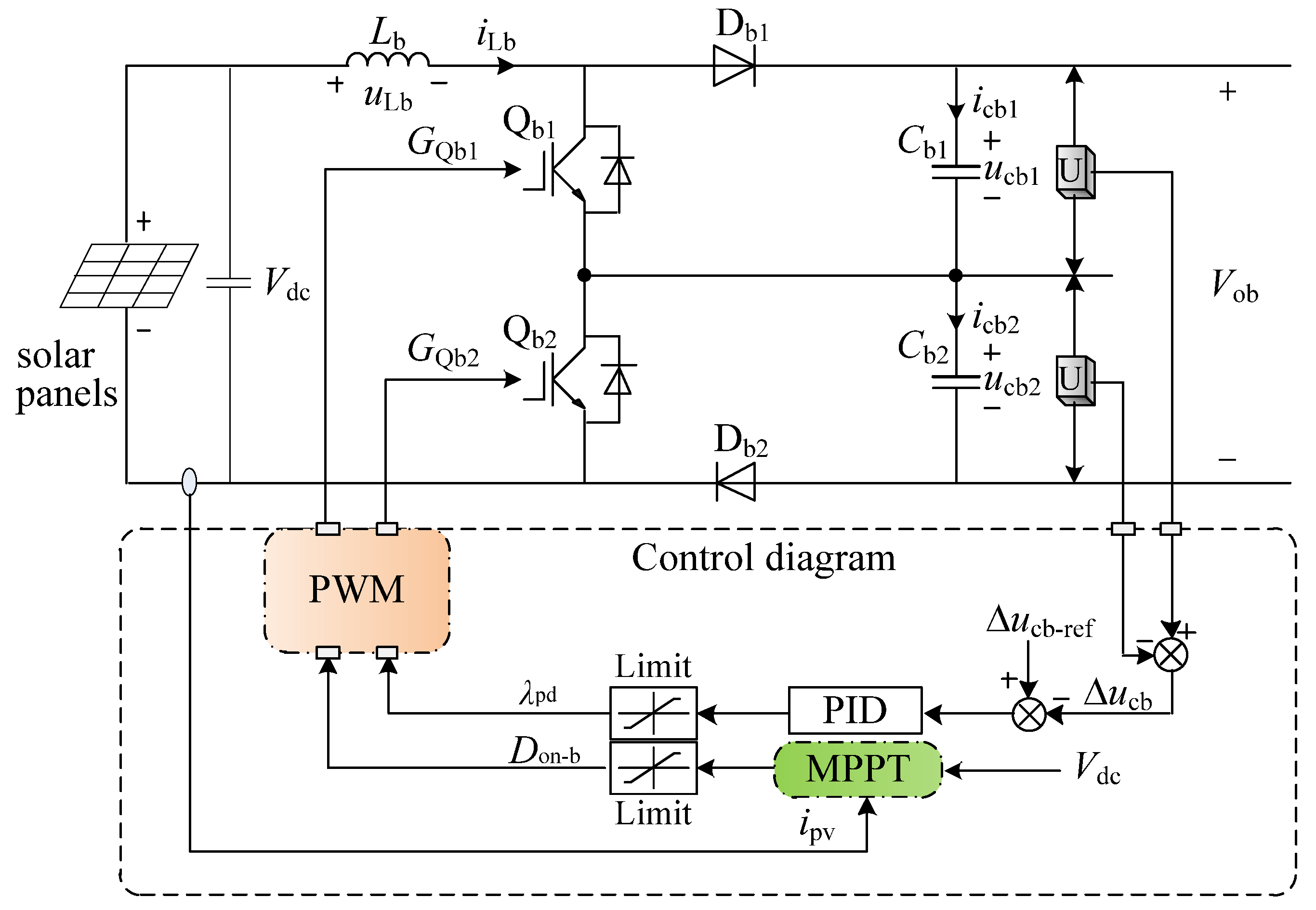
3.2. Control Scheme
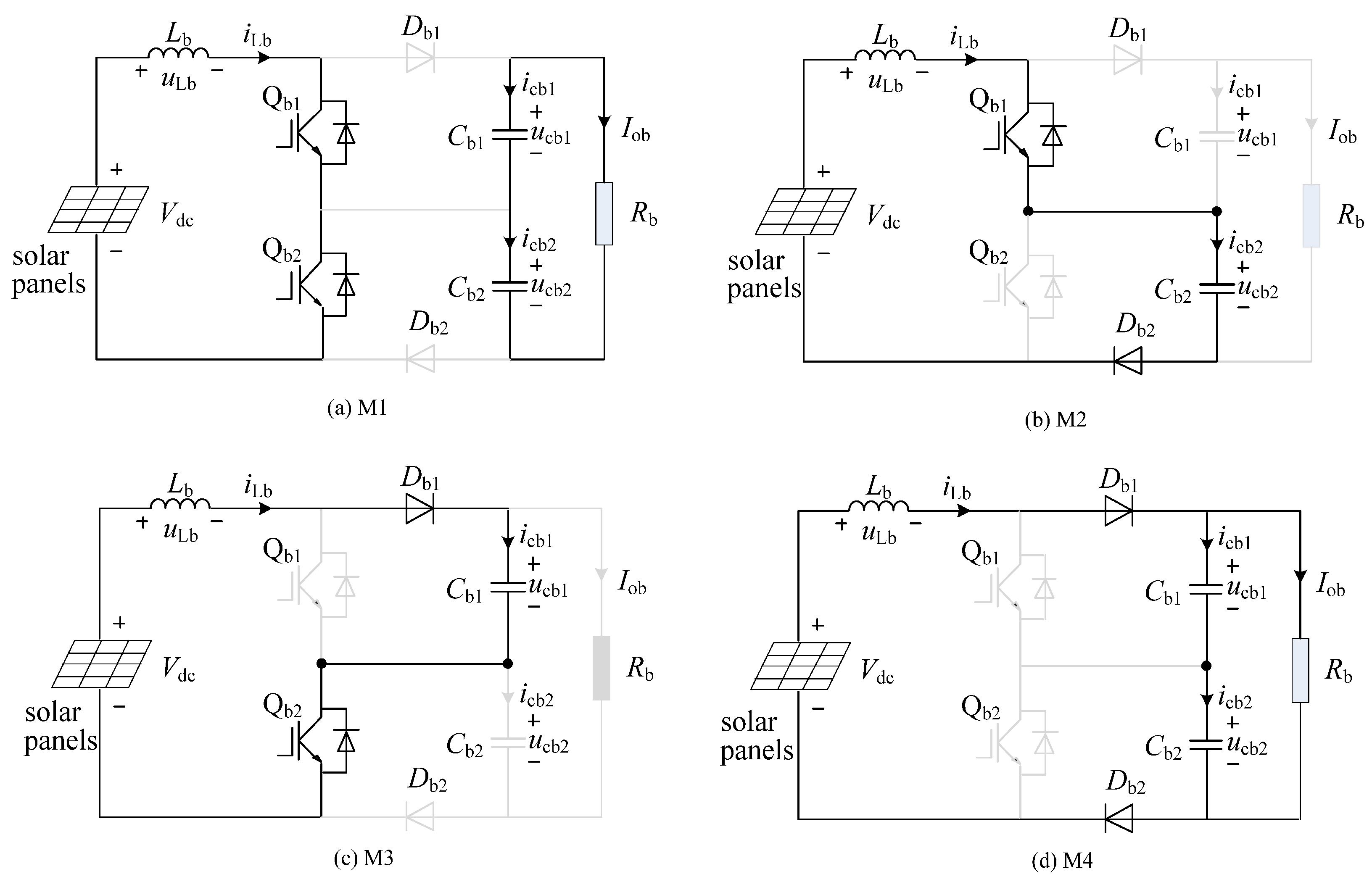
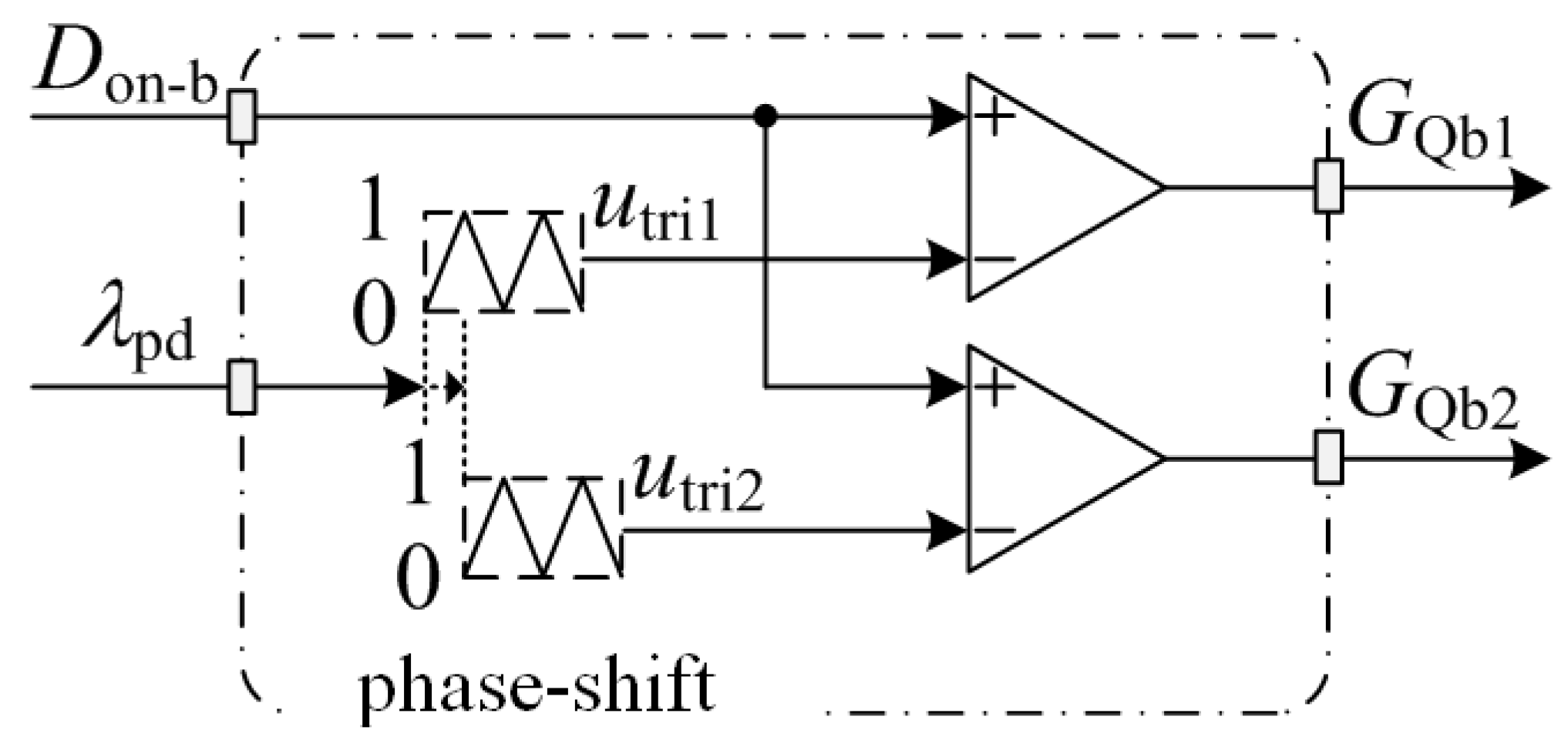
3.3. Midpoint Potential Balancing
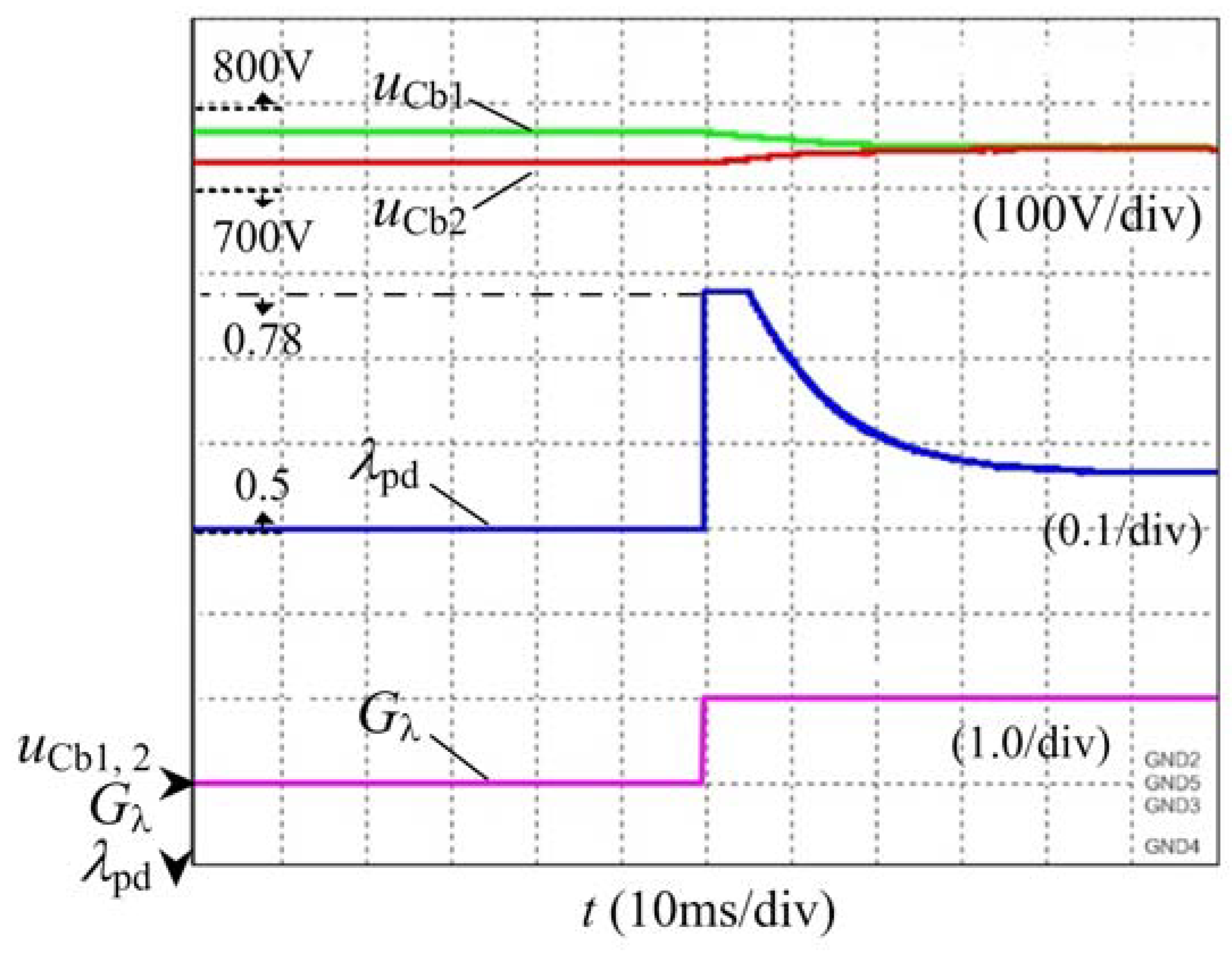
3.4. Verification of MPB Control
4. Reversible Converter
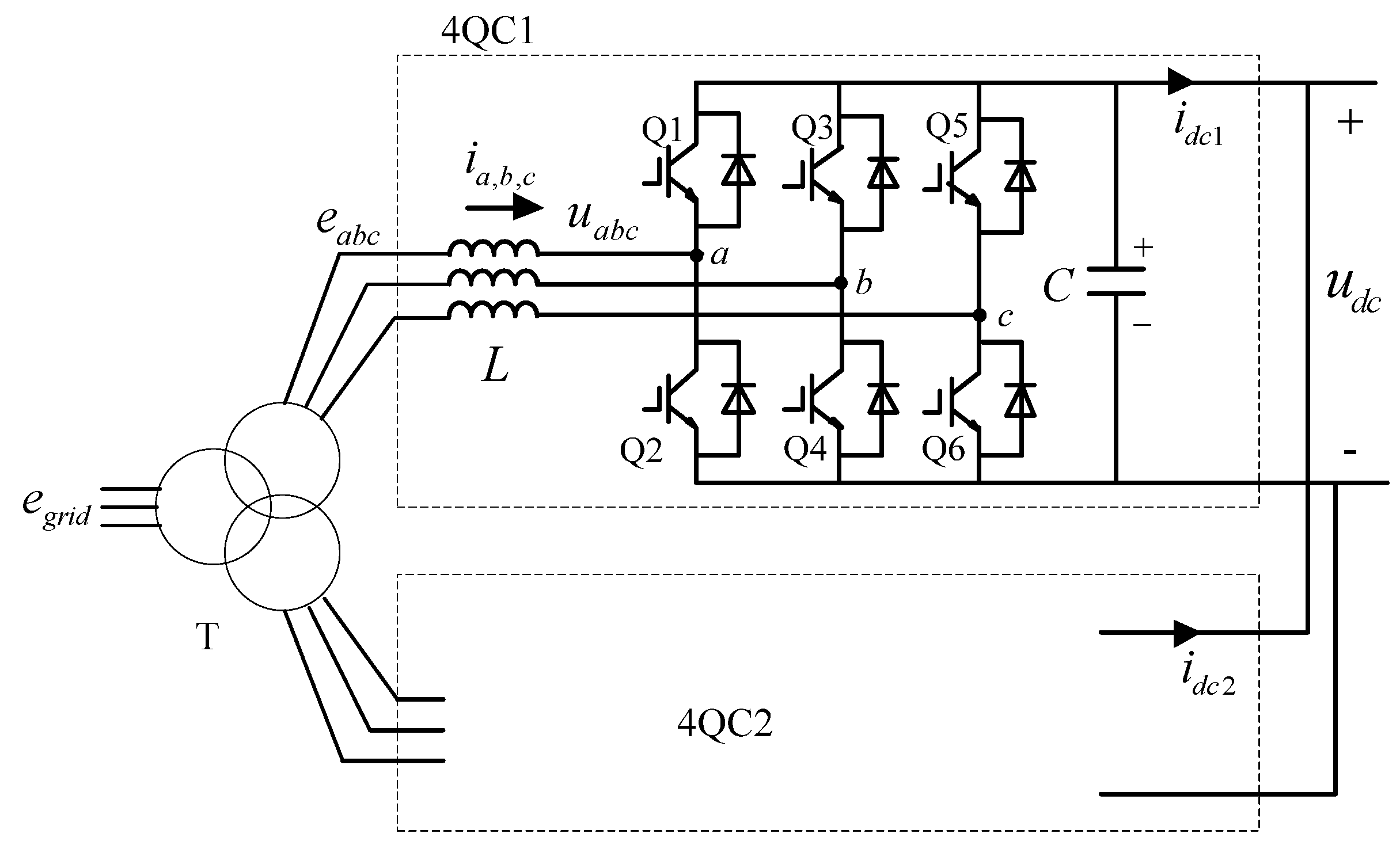
4.1. Main Circuit
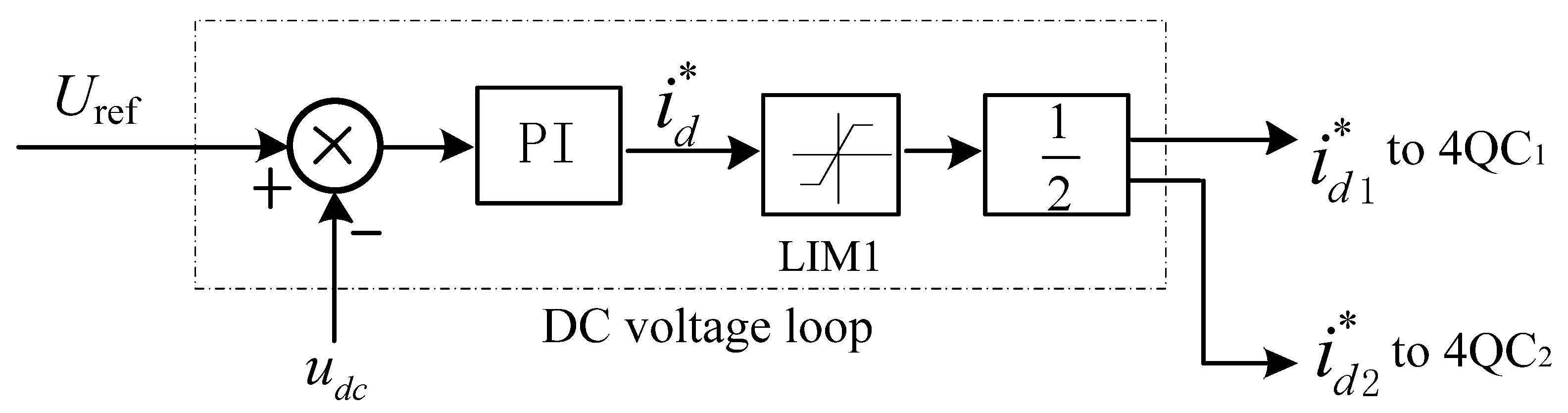
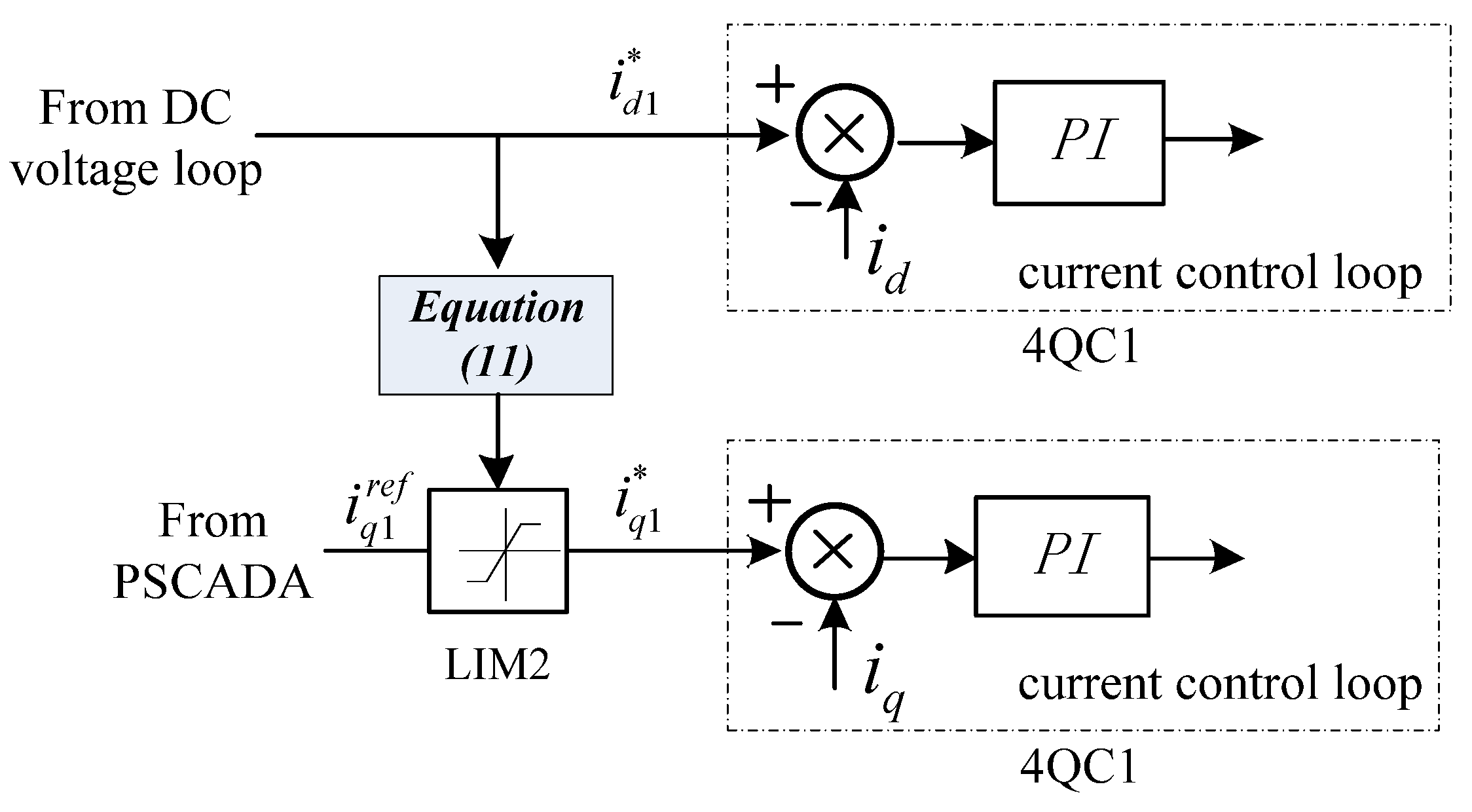
4.2. Current Decoupling Control
5. Working Characteristic and Coordinate Control
5.1. Working Characteristics
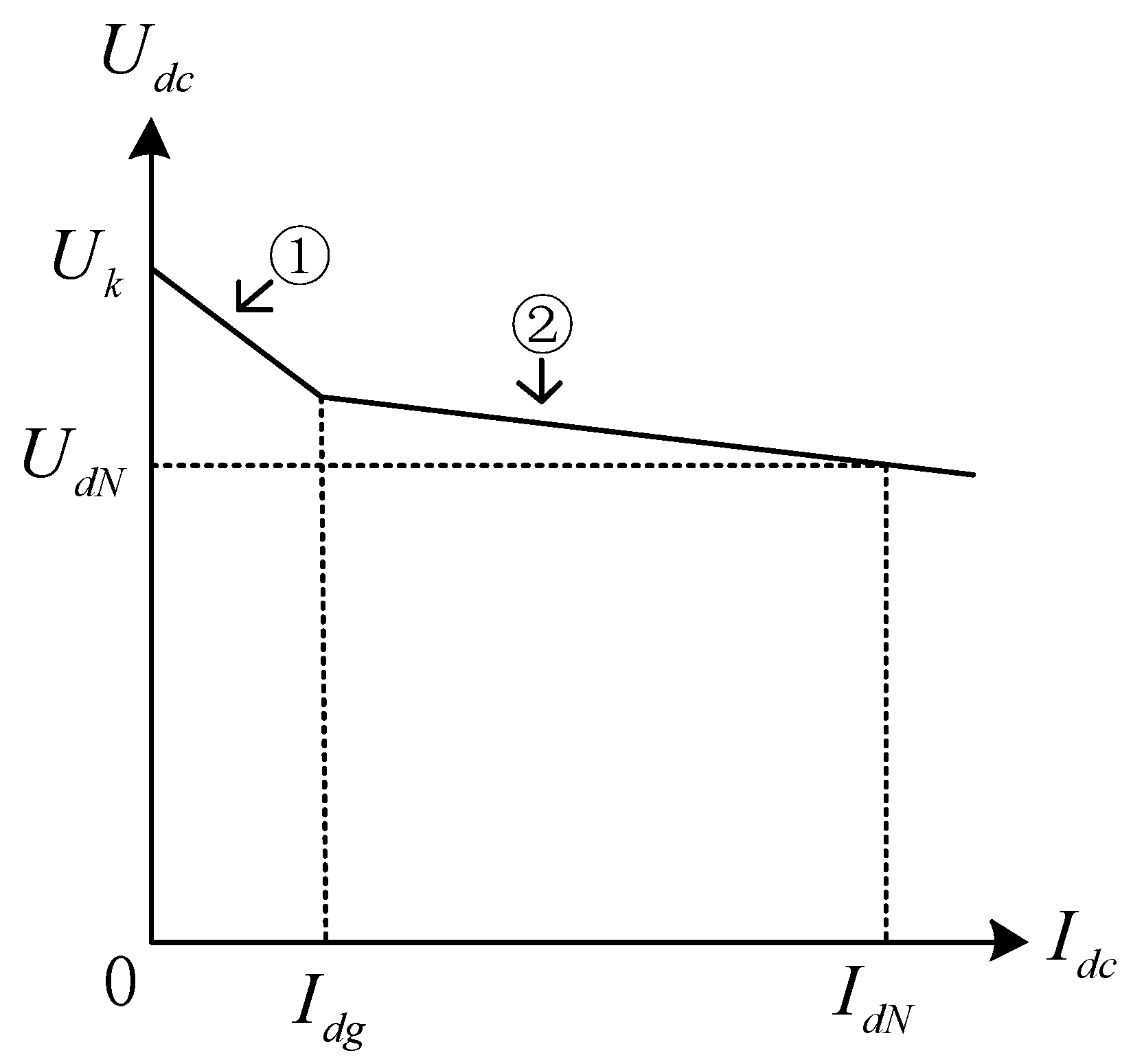
5.1.1. Twelve-Pulse Rectifier
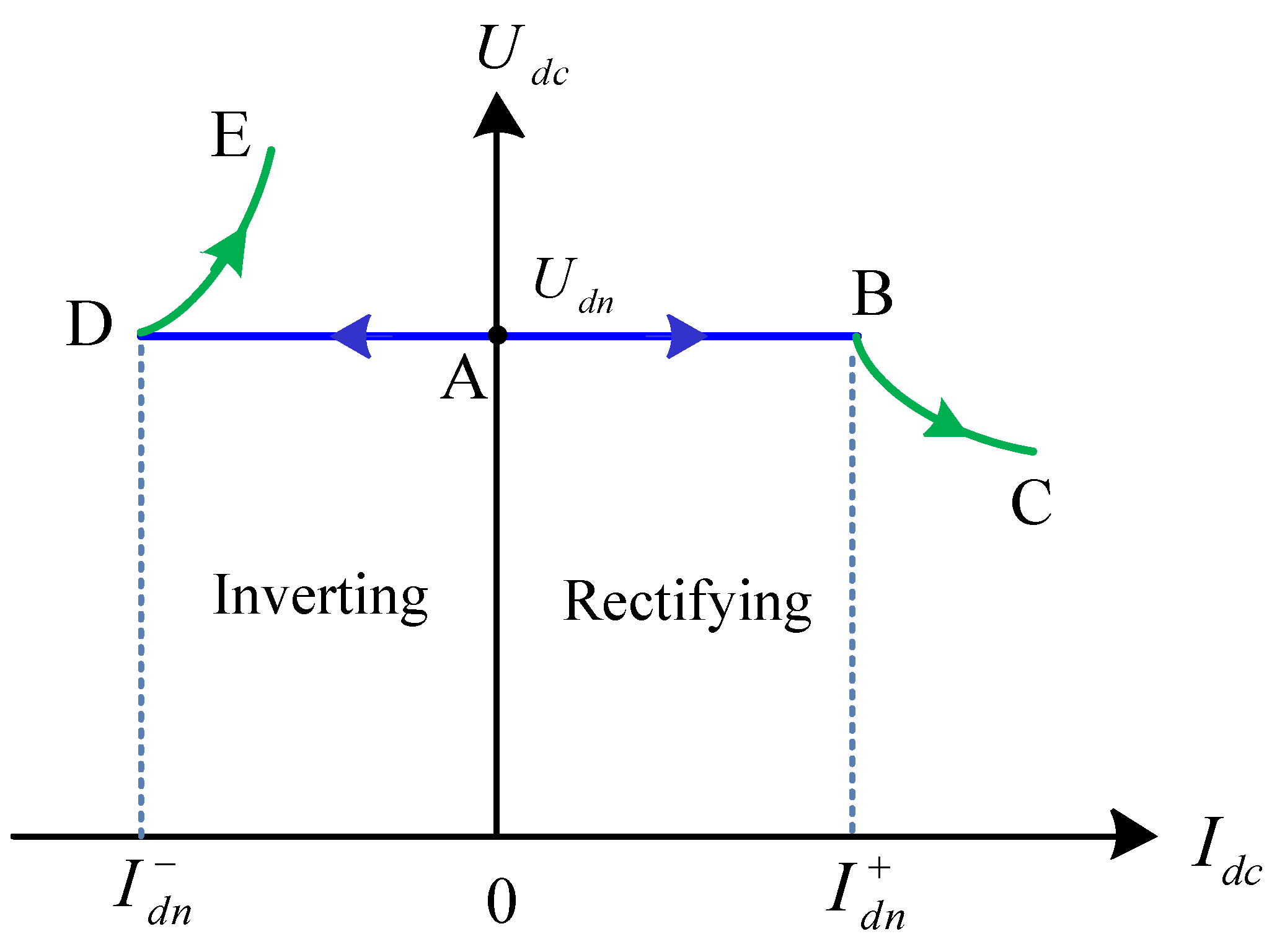
5.1.2. Reversible Converter
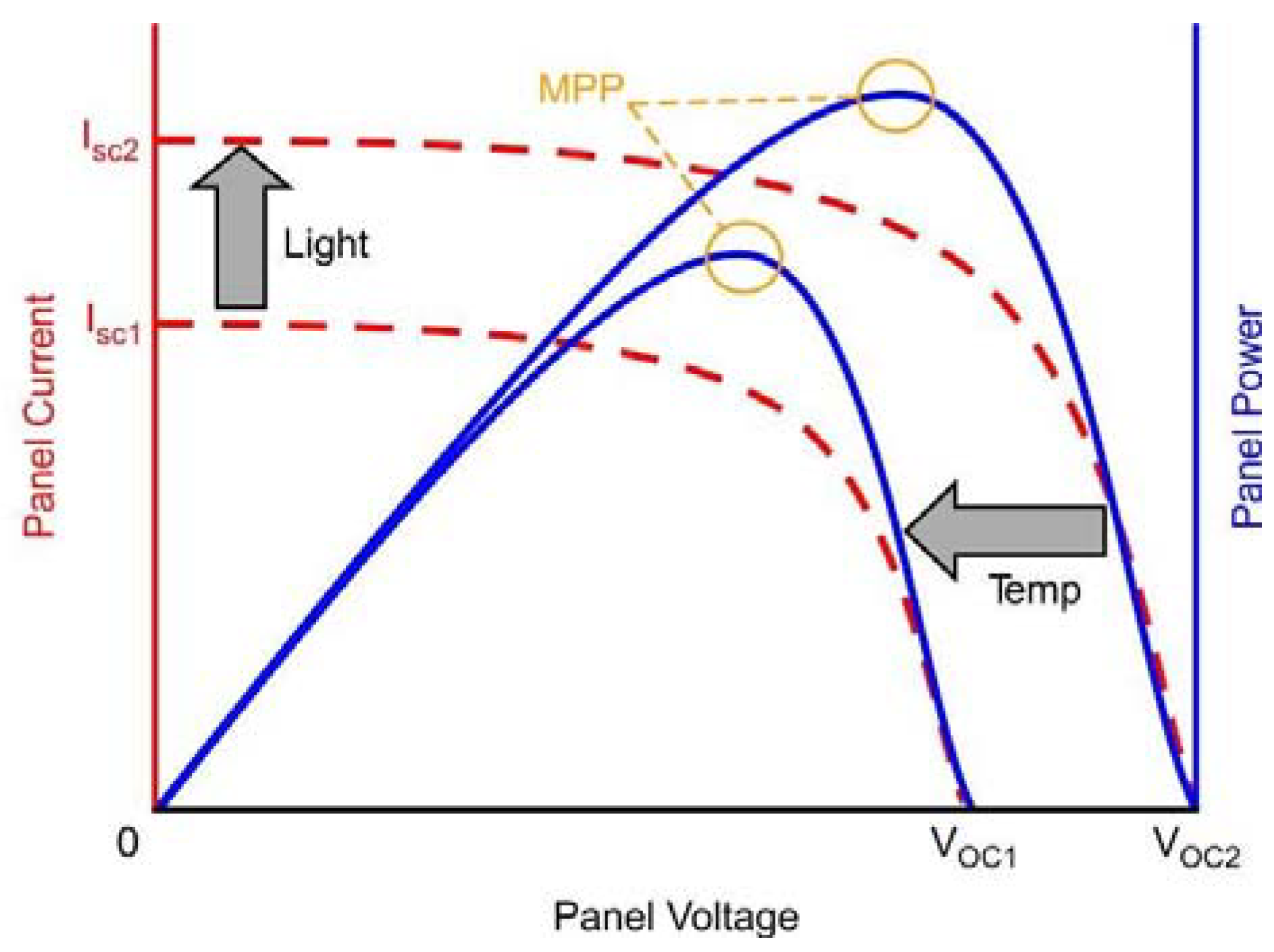
5.1.3. PV System
5.2. Coordinated Control Strategy
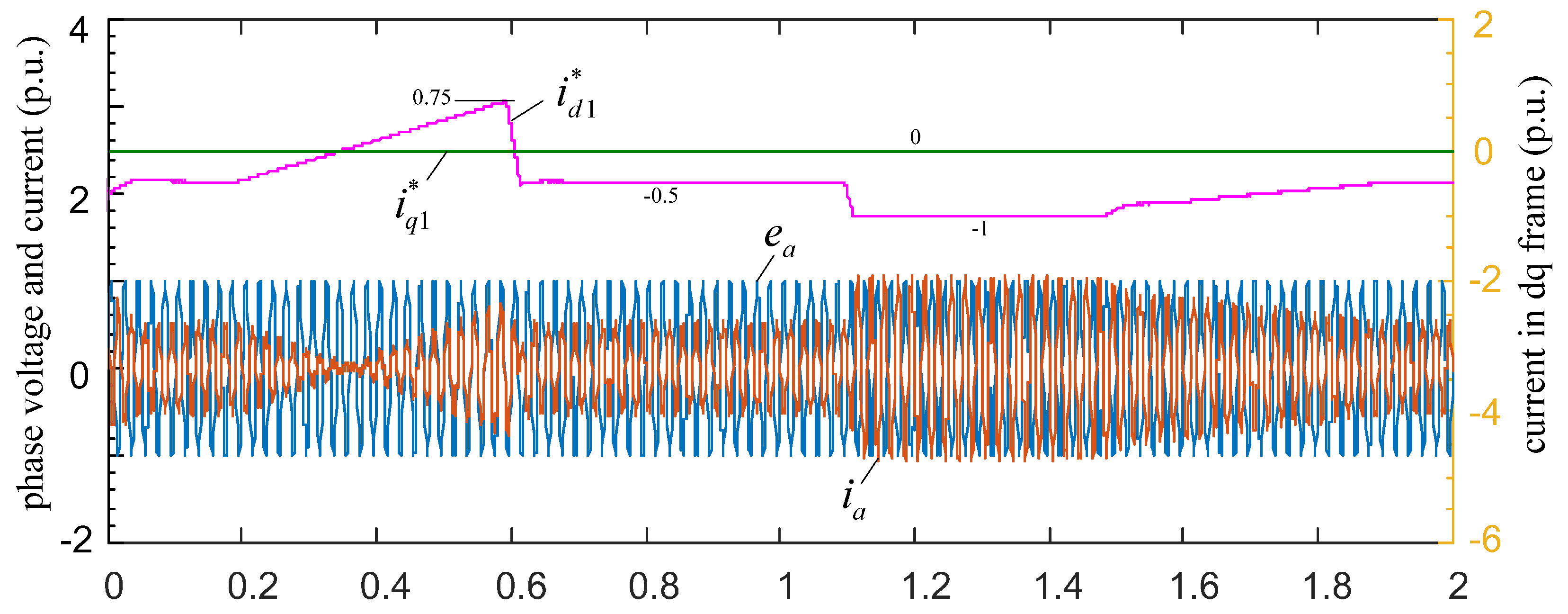
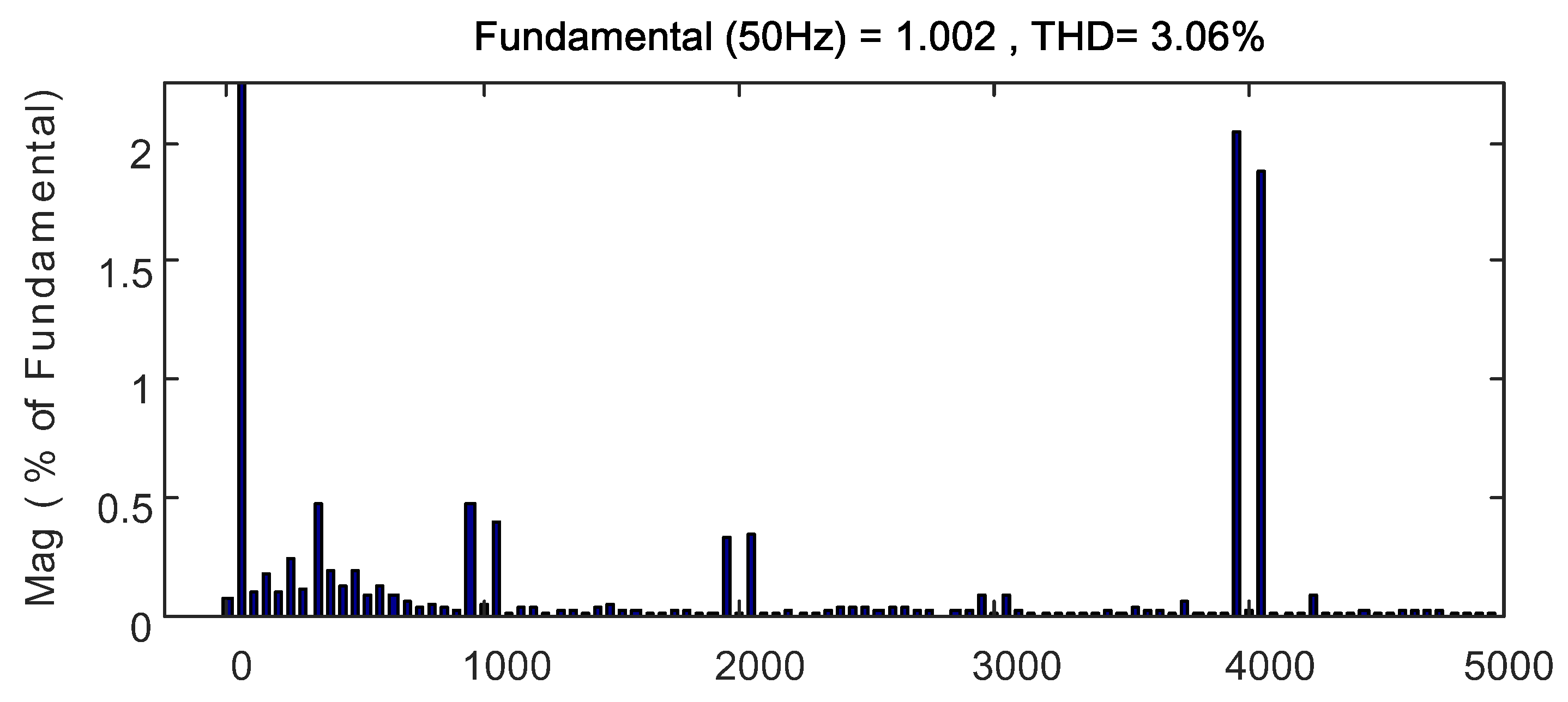
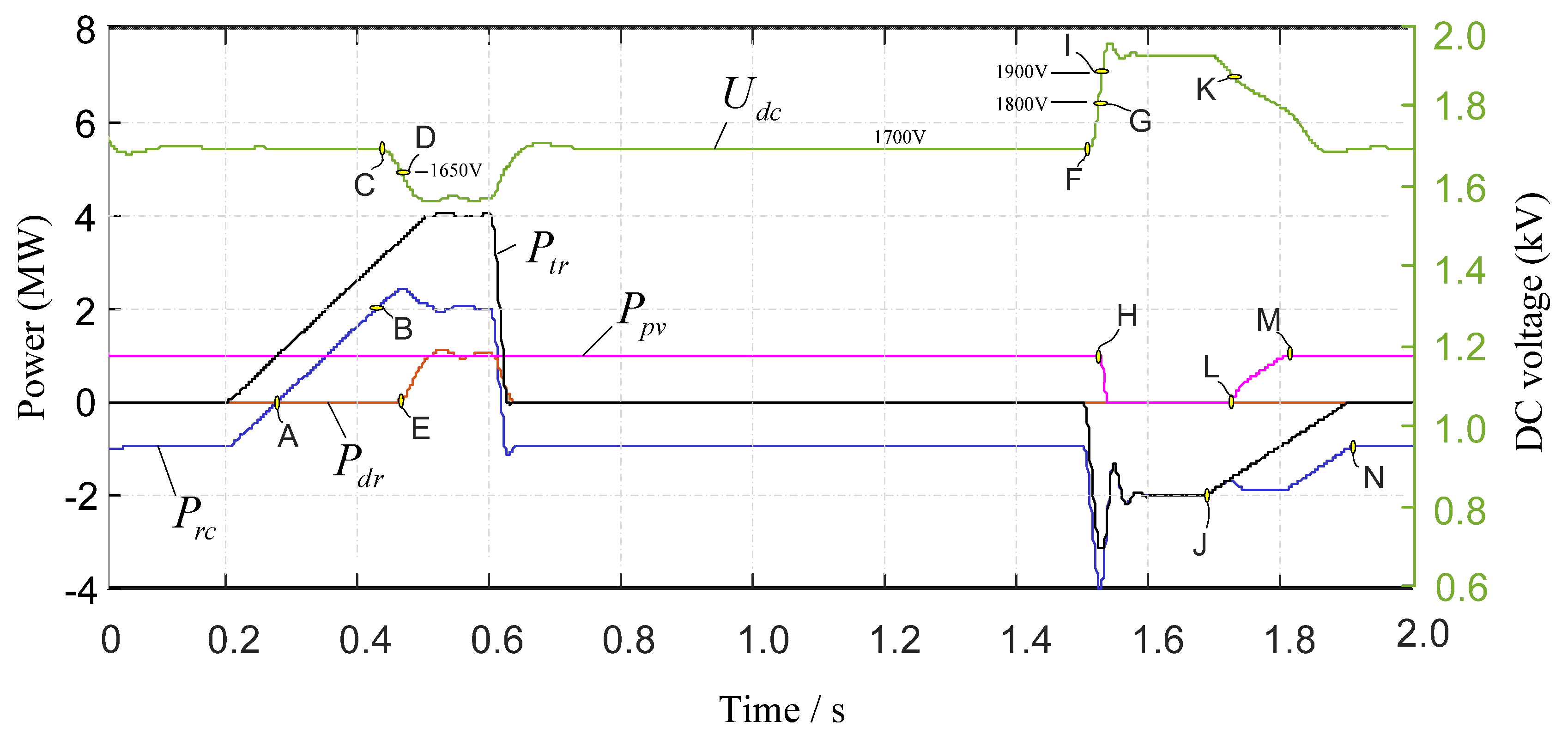
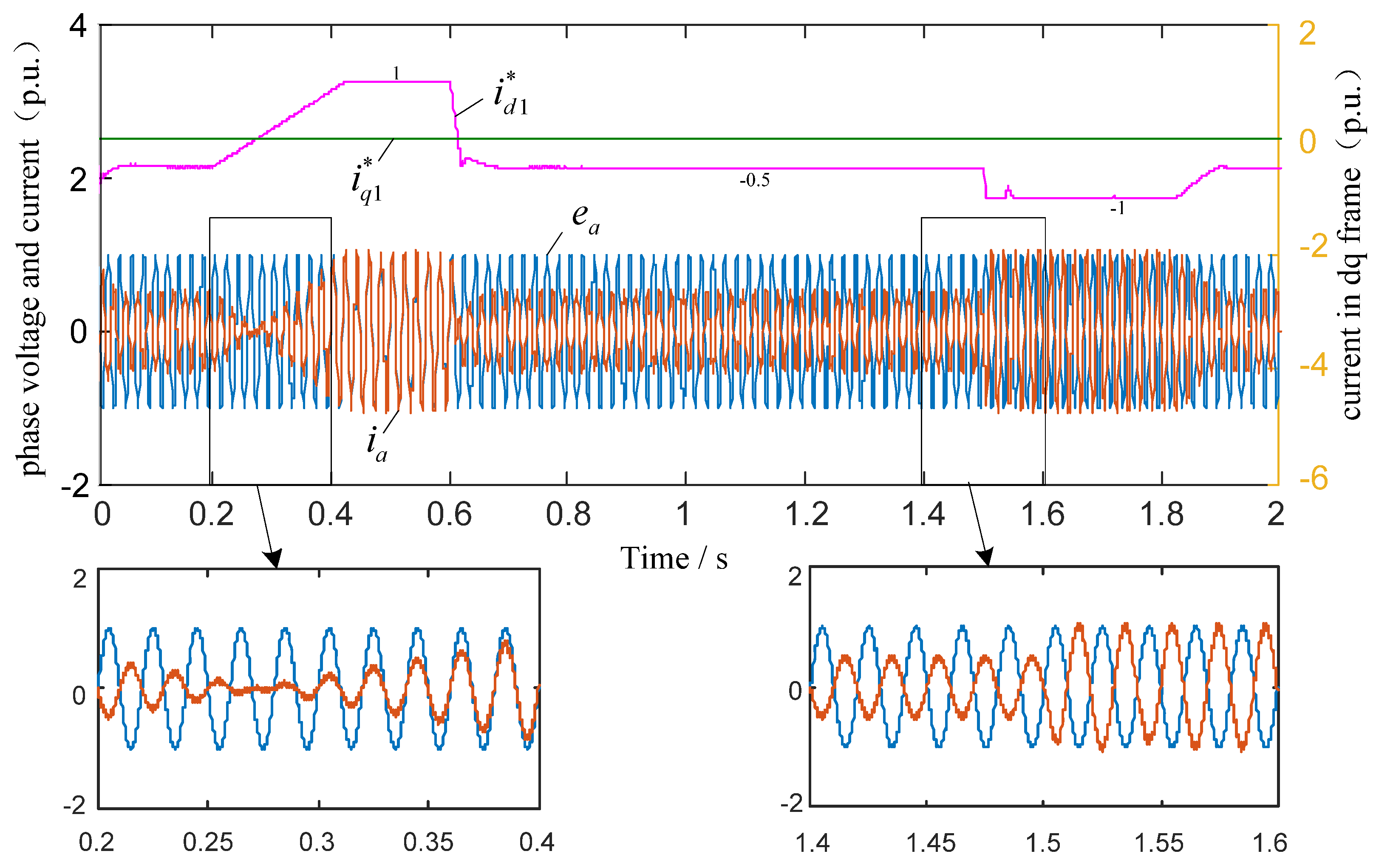
5.3. Simulation Verification
5.3.1. System Parameters
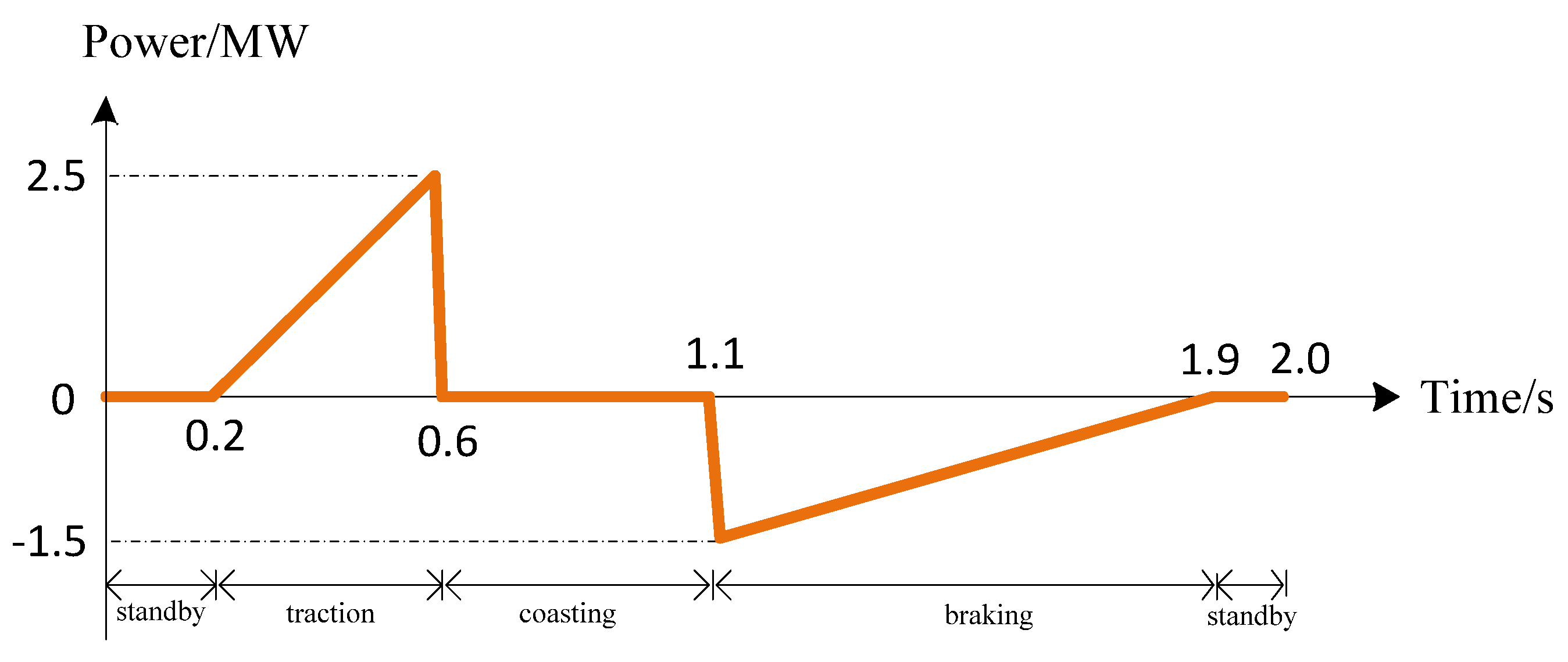
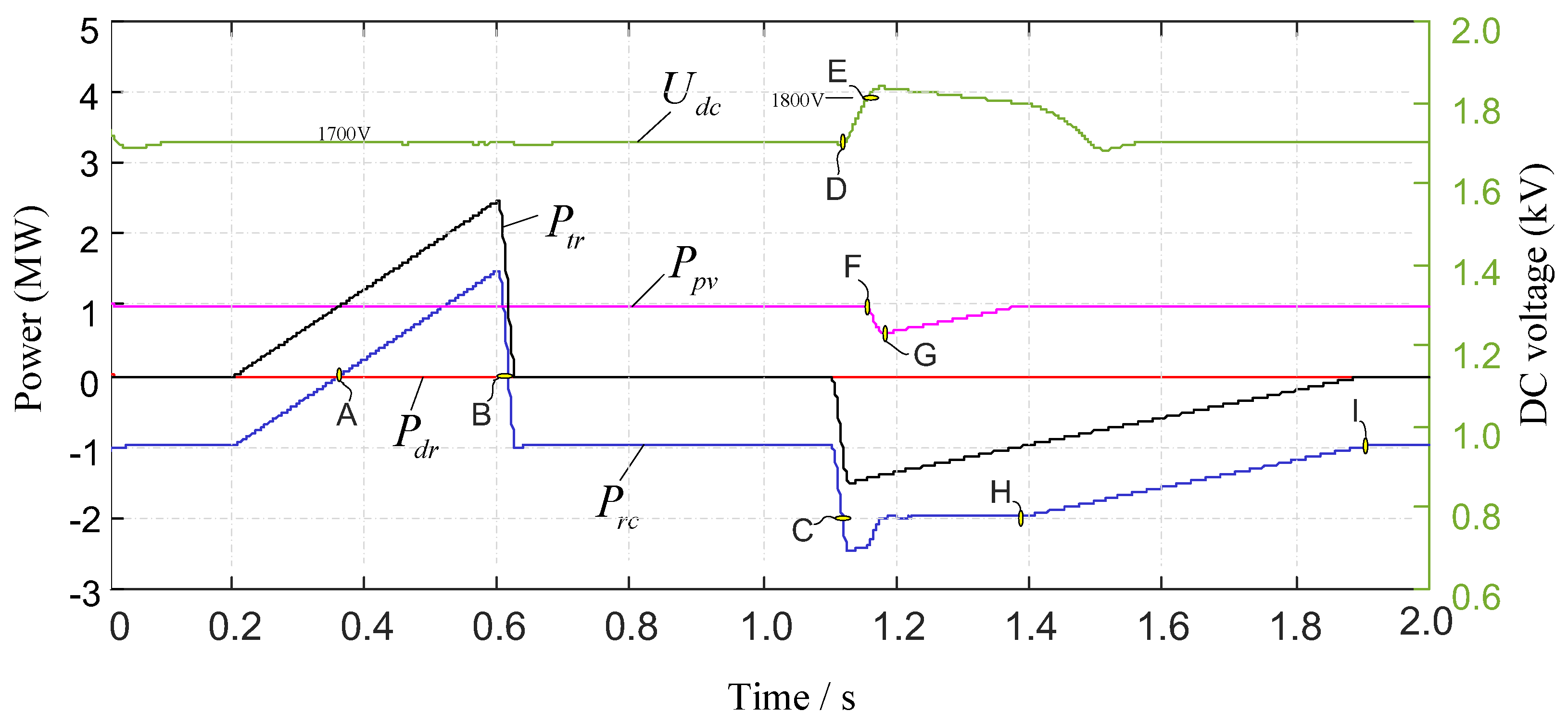
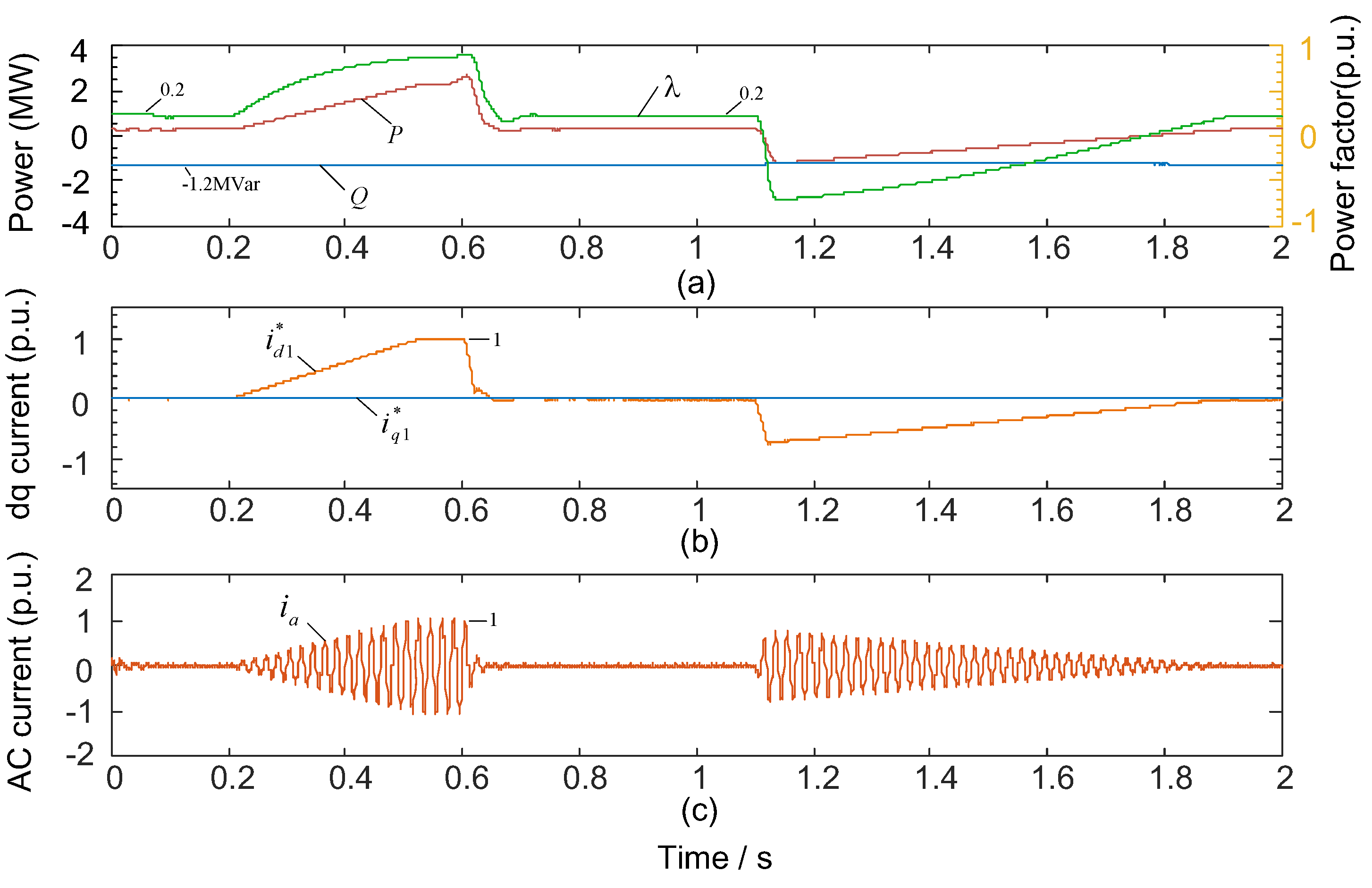
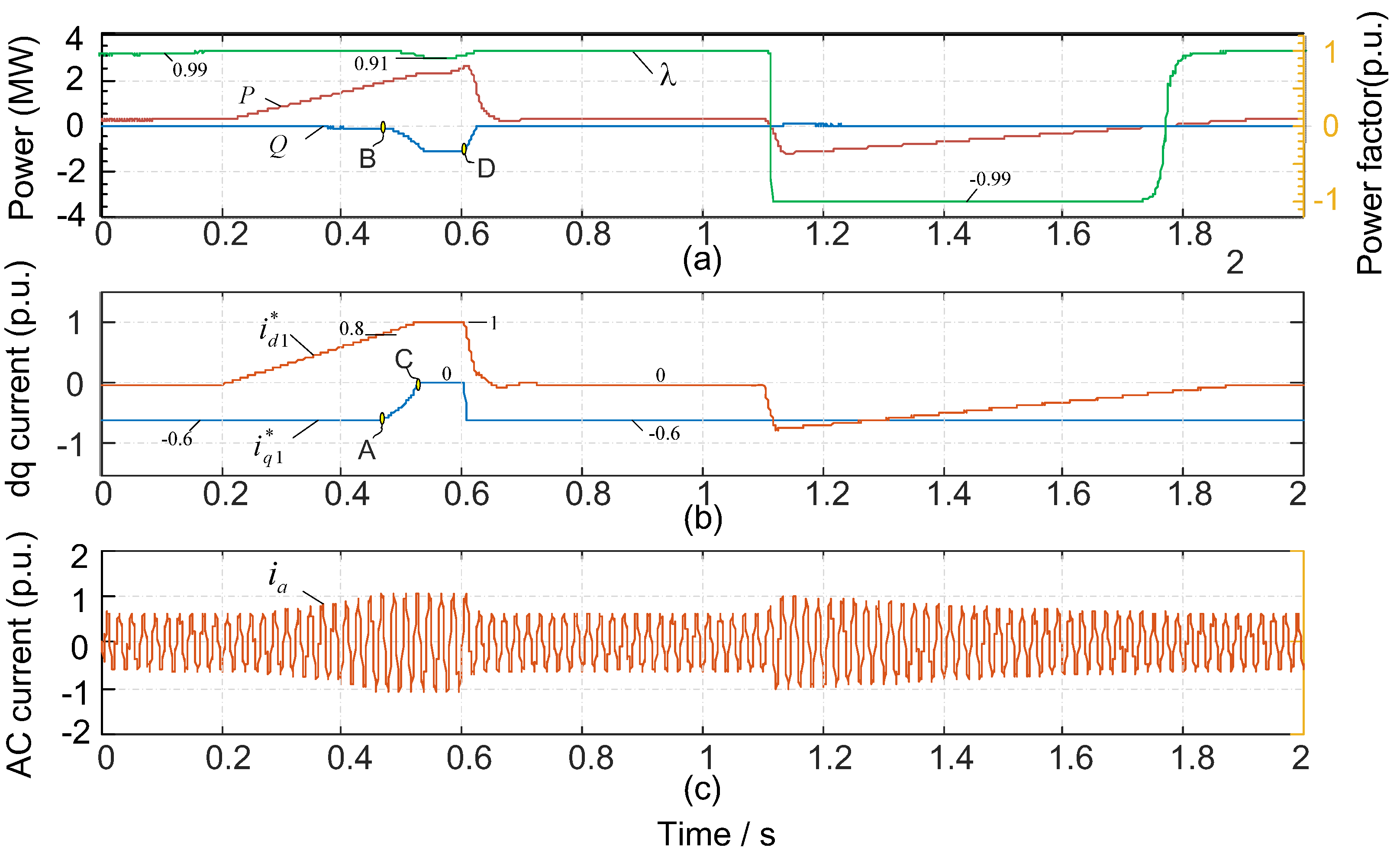
5.3.2. Case Study 1
5.3.3. Case Study 2
5.3.4. Case Study 3
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HTPSS | Hybrid Traction Power Supply System |
| TPSS | Traction Power Supply System |
| RC | Reversible Converter |
| TLBC | Three-level Boost Converter |
| MPPT | Maximum Power Point Tracking |
| MPB | Midpoint Potential Balancing |
| SVG | Static Var Generator |
| PV | Photovoltaic |
| SCADA | Supervisory Control And Data Acquisition |
| MV | Medium Voltage |
| DR | Diode Rectifier |
| P&O | Perturbation and Observation |
| DSP | Digital Signal Processor |
| FPGA | Field Programmable Gate Array |
| 4QC | Four Quadrant Converter |
| THD | Total Harmonic Distortion |
| FFT | Fast Fourier Transform |
| KVL | Kirchhoff's Voltage Law |
References
- Jabr, R.A.; Džafić, I. Solution of DC Railway Traction Power Flow Systems Including Limited Network Receptivity. IEEE Trans. Power Syst. 2018, 33, 962–969. [Google Scholar] [CrossRef]
- Tian, Z.; Hillmansen, S.; Roberts, C.; Weston, P. Energy evaluation of the power network of a DC railway system with regenerating trains. IET Electr. Syst. Transp. 2015, 6, 41–49. [Google Scholar] [CrossRef]
- Zhu, Z. Research on Reactive Power Compensation Scheme and Compensation Capacity of Subway Power Supply System. World Invert. 2014, 11, 45–47. [Google Scholar]
- Reza, S.; Azah, M.; Shareef, H. Comparative study of effectiveness of different var compensation devices in large-scale power networks. J. Cent. South Univ. 2013, 3, 715–723. [Google Scholar]
- Liu, R.; Liu, W.; Cui, H.; Zhang, J.; Liao, J. Capacity optimization design of reactive compensation device in urban rail traction power supply system. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Chicago, IL, USA, 22–24 June 2017; pp. 1–6. [Google Scholar]
- Yii, S.T.; Ruay-Nan, W.; Nanming, C. Electric network solutions of DC transit systems with inverting substations. IEEE Trans. Veh. Technol. 1998, 47, 1405–1412. [Google Scholar]
- Mellitt, B.; Mouneimne, Z.S.; Goodman, C.J. Simulation study of DC transit systems with inverting substations. Electr. Power Appl. 1984, 131, 38–50. [Google Scholar] [CrossRef]
- Suzuki, T. DC power-supply system with inverting substations for traction systems using regenerative brakes. Electr. Power Appl. 1982, 129, 18–26. [Google Scholar] [CrossRef]
- Serrano-Jiménez, D.; Abrahamsson, L.; Castaño-Solís, S.; Sanz-Feito, J. Electrical railway power supply systems: Current situation and future trends. Int. J. Electr. Power Energy Syst. 2017, 92, 181–192. [Google Scholar] [CrossRef]
- Ghaviha, N.; Campillo, J.; Bohlin, M.; Dahlquist, E. Review of Application of Energy Storage Devices in Railway Transportation. Energy Procedia 2017, 105, 4561–4568. [Google Scholar] [CrossRef]
- Jandura, P.; Richter, A.; Ferkov, Z. Flywheel energy storage system for city railway. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Anacapri, Italy, 22–24 April 2016; pp. 1155–1159. [Google Scholar]
- Douglas, H.; Roberts, C.; Hillmansen, S.; Schmid, F. An assessment of available measures to reduce traction energy use in railway networks. Energy Convers. Manag. 2015, 106, 1149–1165. [Google Scholar] [CrossRef]
- González-Gil, A.; Palacin, R.; Batty, P. Sustainable urban rail systems: Strategies and technologies for optimal management of regenerative braking energy. Energy Convers. Manag. 2013, 75, 374–388. [Google Scholar] [CrossRef]
- Gelman, V. Braking energy recuperation. IEEE Veh. Technol. Mag. 2009, 4, 82–89. [Google Scholar] [CrossRef]
- Casals, M.; Gangolells, M.; Forcada, N.; Macarulla, M.; Giretti, A. A breakdown of energy consumption in an underground station. Energy Build. 2014, 78, 89–97. [Google Scholar] [CrossRef] [Green Version]
- Kabir, E.; Kumar, P.; Kumar, S.; Adelodun, A.A.; Kim, K. Solar energy: Potential and future prospects. Renew. Sustain. Energy Rev. 2018, 82, 894–900. [Google Scholar] [CrossRef]
- Ding, M.; Xu, Z.; Wang, W.; Wang, X.; Song, Y.; Chen, D. A review on China’s large-scale PV integration: Progress, challenges and recommendations. Renew. Sustain. Energy Rev. 2016, 53, 639–652. [Google Scholar] [CrossRef]
- Kaundinya, D.P.; Balachandra, P.; Ravindranath, N.H. Grid-connected versus stand-alone energy systems for decentralized power—A review of literature. Renew. Sustain. Energy Rev. 2009, 13, 2041–2050. [Google Scholar] [CrossRef]
- Sansaniwal, S.K.; Sharma, V.; Mathur, J. Energy and energy analyses of various typical solar energy applications: A comprehensive review. Renew. Sustain. Energy Rev. 2018, 82, 1576–1601. [Google Scholar] [CrossRef]
- Hayashiya, H.; Furukawa, T.; Itagaki, H.; Kuraoka, T.; Morita, Y.; Fukasawa, Y.; Mitoma, Y.; Oikawa, T. Potentials, peculiarities and prospects of solar power generation on the railway premises. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications, Nagasaki, Japan, 11–14 November 2012. [Google Scholar]
- Hayashiya, H.; Kikuchi, S.; Matsuura, K.; Hino, M.; Tojo, M.; Kato, T.; Ando, M.; Oikawa, T.; Kamata, M.; Munakata, H. Possibility of energy saving by introducing energy conversion and energy storage technologies in traction power supply system. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–8. [Google Scholar]
- Wang, W.; Wu, M.; Li, Q.; Chen, W. Method for improving power quality of metro traction power supply system with PV integration. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 1682–1685. [Google Scholar]
- Ciccarelli, F.; Di Noia, L.; Rizzo, R. Integration of Photovoltaic Plants and Supercapacitors in Tramway Power Systems. Energies 2018, 11, 410. [Google Scholar] [CrossRef]
- Shen, X.J.; Zhang, Y.; Chen, S. Investigation of grid-connected photovoltaic generation system applied for Urban Rail Transit energy-savings. In Proceedings of the 2012 IEEE Industry Applications Society Annual Meeting, Las Vegas, NV, USA, 7–11 October 2012; pp. 1–4. [Google Scholar]
- Danandeh, M.A.; Mousavi, G.S.M. Comparative and comprehensive review of maximum power point tracking methods for PV cells. Renew. Sustain. Energy Rev. 2018, 82, 2743–2767. [Google Scholar] [CrossRef]
- Karami, N.; Moubayed, N.; Outbib, R. General review and classification of different MPPT Techniques. Renew. Sustain. Energy Rev. 2017, 68, 1–18. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel fast dynamic MPPT (maximum power point tracking) technique with the capability of very high accurate power tracking. Energy 2016, 94, 466–475. [Google Scholar] [CrossRef]
- Eull, M.; Preindl, M. Bidirectional three-level DC-DC converters: Sum-difference modeling and control. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 22–24 June 2017; pp. 573–578. [Google Scholar]
- Tan, L.; Wu, B.; Yaramasu, V.; Rivera, S.; Guo, X. Effective Voltage Balance Control for Bipolar-DC-Bus-Fed EV Charging Station With Three-Level DC-DC Fast Charger. IEEE Trans. Ind. Electron. 2016, 63, 4031–4041. [Google Scholar] [CrossRef]
- Tampubolon, M.; Lin, W.; Lin, J.; Hsieh, Y.; Chiu, H.; Yamanaka, K.; Hojo, M. A study and implementation of three-level boost converter with MPPT for PV application. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia, Kaohsiung, Taiwan, 3–7 June 2017; pp. 1143–1148. [Google Scholar]
- Kang, H.; Cha, H. A New Nonisolated High-Voltage-Gain Boost Converter with Inherent Output Voltage Balancing. IEEE Trans. Ind. Electron. 2018, 65, 2189–2198. [Google Scholar] [CrossRef]
- Lu, S.; Mu, M.; Jiao, Y.; Lee, F.C.; Zhao, Z. Coupled Inductors in Interleaved Multiphase Three-Level DC/DC Converter for High-Power Applications. IEEE Trans. Power Electron. 2016, 31, 120–134. [Google Scholar] [CrossRef]
- Zorig, A.; Belkheiri, M.; Barkat, S. Control of grid connected photovoltaic system using dual three-level stage conversion. In Proceedings of the 2015 4th International Conference on Electrical Engineering (ICEE), Boumerdes, Algeria, 13–15 December 2015; pp. 1–5. [Google Scholar]
- Dusmez, S.; Hasanzadeh, A.; Khaligh, A. Comparative Analysis of Bidirectional Three-Level DC/DC Converter for Automotive Applications. IEEE Trans. Ind. Electron. 2015, 62, 3305–3315. [Google Scholar] [CrossRef]
- Chen, H.C.; Liao, J.Y. Modified Interleaved Current Sensorless Control for Three-Level Boost PFC Converter With Considering Voltage Imbalance and Zero-Crossing Current Distortion. IEEE Trans. Ind. Electron. 2015, 62, 6896–6904. [Google Scholar] [CrossRef]
- Khaldi, H.S.; Ammari, A.C. Fractional-order control of three level boost DC/DC converter used in hybrid energy storage system for electric vehicles. In Proceedings of the Sixth International Renewable Energy Congress, Sousse, Tunisia, 24–26 March 2015; pp. 1–7. [Google Scholar]
- Vitoi, L.A.; Krishna, R.; Soman, D.E.; Leijon, M.; Kottayil, S.K. Control and implementation of three level boost converter for load voltage regulation. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 561–565. [Google Scholar]
- Xia, C.; Gu, X.; Shi, T.; Yan, Y. Neutral-Point Potential Balancing of Three-Level Inverters in Direct-Driven Wind Energy Conversion System. IEEE Trans. Energy Convers. 2011, 26, 18–29. [Google Scholar] [CrossRef]
- Krishna, R.; Soman, D.E.; Kottayil, S.K.; Leijon, M. Pulse delay control for capacitor voltage balancing in a three-level boost neutral point clamped inverter. IET Power Electron. 2015, 8, 268–277. [Google Scholar] [CrossRef]
- Zhang, G.; Qian, J.; Zhang, X. Application of a High-Power Reversible Converter in a Hybrid Traction Power Supply System. Appl. Sci. 2017, 7, 282. [Google Scholar] [CrossRef]
- Singh, J.; Dahiya, R.; Saini, L.M. Recent research on transformer based single DC source multilevel inverter: A review. Renew. Sustain. Energy Rev. 2018, 82, 3207–3224. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Elsayed, A.T.; Mohamed, A.A.; Mohammed, O.A. DC microgrids and distribution systems: An overview. Electr. Power Syst. Res. 2015, 119, 407–417. [Google Scholar] [CrossRef]
- Du, H. Output Optimization and Efficiency Improvement of High-Frequency Pulsating DC-Link Auxiliary Inverter. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2016. [Google Scholar]
- Zhang, G.; Du, H.; Chen, Y.; Liu, Z. A Midpoint Potential Balance Control Strategy Based on Pulse Phase Delays of Three-level Boost Converter. Proc. CSEE 2017, 20, 6050–6058. [Google Scholar]
- Saravanan, S.; Ramesh Babu, N. Maximum power point tracking algorithms for photovoltaic system—A review. Renew. Sustain. Energy Rev. 2016, 57, 192–204. [Google Scholar] [CrossRef]






| Abbreviation | Definition | Abbreviation | Definition |
|---|---|---|---|
| DR | 12-pulse rectifier | power of DR | |
| RC | reversible converter | power of RC | |
| PV | TLBC and PV array | power of PV | |
| TR | train | power of TR | |
| maximum power of RC | DC voltage of substation | ||
| maximum power of PV | no-load voltage of DR |
| Mode | Explanation |
|---|---|
| (a) | No power is required by the train, that is . The power produced by PV is completely fed back to MV grid. DR is in blocked state. |
| (b) | The power required by the train is less than the power produced by PV, that is . Part of PV power is fed back to MV grid. DR is blocked. DR is in blocked state. |
| (c) | The power required by the train is equal to the power produced by PV, that is . DR is in blocked state. |
| (d) | The power required by the train is more than the power produced by PV, that is . RC is activated to keep the DC voltage constant. |
| (e) | The power required by the train is more than the total power provided by PV and RC, that is . Then, , and the DR starts to work. |
| (f) | The train is in braking state. The total power generated by TR and produced by PV is equal to the power inverted by RC, that is . Then, , the DR returns to blocked state again. |
| (g) | The train is in braking state. The power generated by TR is equal to the maximum power of RC, that is . The power produced by PV is reduced to zero automatically to avoid overvoltage. |
| (h) | When the power factor becomes low in the night or long headway time, the RC can generate compensating reactive power like a SVG. |
| (i) | The DR can continue to supply the TR in case of fault of RC and PV, but the system energy consumption will increase. |
| Don-b | λpd | Charging Current | Effect on uCb1 and uCb2 |
|---|---|---|---|
| Don-b ≤ 0.5 | λpd = 0 | IuCb1 = IuCb2 | no effect |
| 0 < λpd < 0.5 | IuCb1 > IuCb2 | Increase uCb1 | |
| λpd = 0.5 | IuCb1 = IuCb2 | no effect | |
| 0.5 < λpd < 1 | IuCb1 < IuCb2 | increase uCb2 | |
| Don-b > 0.5 | λpd = 0 | IuCb1 = IuCb2 | no effect |
| 0 < λpd < 0.5 | IuCb1 > IuCb2 | increase uCb1 | |
| λpd = 0.5 | IuCb1 = IuCb2 | no effect | |
| 0.5 < λpd < 1 | IuCb1 < IuCb2 | increase uCb2 |
| Case | Working Condition | Mode Transition |
|---|---|---|
| I | λpd = 0 | M1→M4 |
| II | Don-b ≤ 0.5, 0 < λpd < Don-b or Don-b > 0.5, 0 < λpd < 1 − Don-b | M2→M1→M3→M4 |
| III | Don-b < 0.5, λpd = Don-b | M2→M3→M4 |
| IV | Don-b < 0.5, Don-b < λpd < 1 − Don-b | M2→M4→M3→M4 |
| V | Don-b < 0.5, λpd = 1 − Don-b | M2→M4→M3 |
| VI | Don-b ≤ 0.5, 1 − Don-b < λpd < 1 or Don-b > 0.5, Don-b < λpd < 1 | M1→M2→M4→M3 |
| VII | Don-b = 0.5, λpd = Don-b | M2→M3 |
| VIII | Don-b > 0.5, λpd = 1 − Don-b | M2→M1→M3 |
| IX | Don-b > 0.5, 1 − Don-b < λpd < Don-b | M1→M2→M1→M3 |
| X | Don-b > 0.5, λpd = Don-b | M1→M2→M3 |
| Item | Parameters | Value |
|---|---|---|
| 110 kV and 35 kV AC cable | Resistance per unit length (Ω/km) | 0.158 |
| Inductance per unit length (mH/km) | 0.287 | |
| Capacitance per unit length (μF/km) | 0.156 | |
| 12-pulse diode rectifier | Rated capacity (MW) | 2 |
| Input AC voltage (kV) | 35 | |
| No-load DC voltage Uk (V) | 1650 | |
| Transformer short-circuit resistance (%) | 8% | |
| TLBC | Rated capacity (MW) | 1 |
| AC filtering inductor Lb (mH) | 1 | |
| DC-Link capacitor Cb1/Cb2 (mF) | 3 | |
| Switch frequency (kHz) | 4 | |
| Threshold Ud1, Ud2 (V) | 1800, 1900 | |
| Reversible converter | AC input rated voltage (kV) | 35 |
| DC rated voltage Udn (V) | 1700 | |
| Rated capacity (MVA) | 2 × 1 | |
| AC filtering inductor L (μH) | 150 | |
| DC-Link capacitor C (mF) | 36 | |
| Switch frequency (kHz) | 2 | |
| Train | Maximum traction power (MW) | 4 |
| Maximum braking power (MW) | −3.5 | |
| Threshold Ud3, Ud4 (V) | 1900, 2000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Tian, Z.; Du, H.; Liu, Z. A Novel Hybrid DC Traction Power Supply System Integrating PV and Reversible Converters. Energies 2018, 11, 1661. https://doi.org/10.3390/en11071661
Zhang G, Tian Z, Du H, Liu Z. A Novel Hybrid DC Traction Power Supply System Integrating PV and Reversible Converters. Energies. 2018; 11(7):1661. https://doi.org/10.3390/en11071661
Chicago/Turabian StyleZhang, Gang, Zhongbei Tian, Huiqing Du, and Zhigang Liu. 2018. "A Novel Hybrid DC Traction Power Supply System Integrating PV and Reversible Converters" Energies 11, no. 7: 1661. https://doi.org/10.3390/en11071661
APA StyleZhang, G., Tian, Z., Du, H., & Liu, Z. (2018). A Novel Hybrid DC Traction Power Supply System Integrating PV and Reversible Converters. Energies, 11(7), 1661. https://doi.org/10.3390/en11071661





