Analysis, Design and Implementation of Droop-Controlled Parallel-Inverters Using Dynamic Phasor Model and SOGI-FLL in Microgrid Applications
Abstract
:1. Introduction
2. Dynamics of Power Delivery in Parallel-Inverters
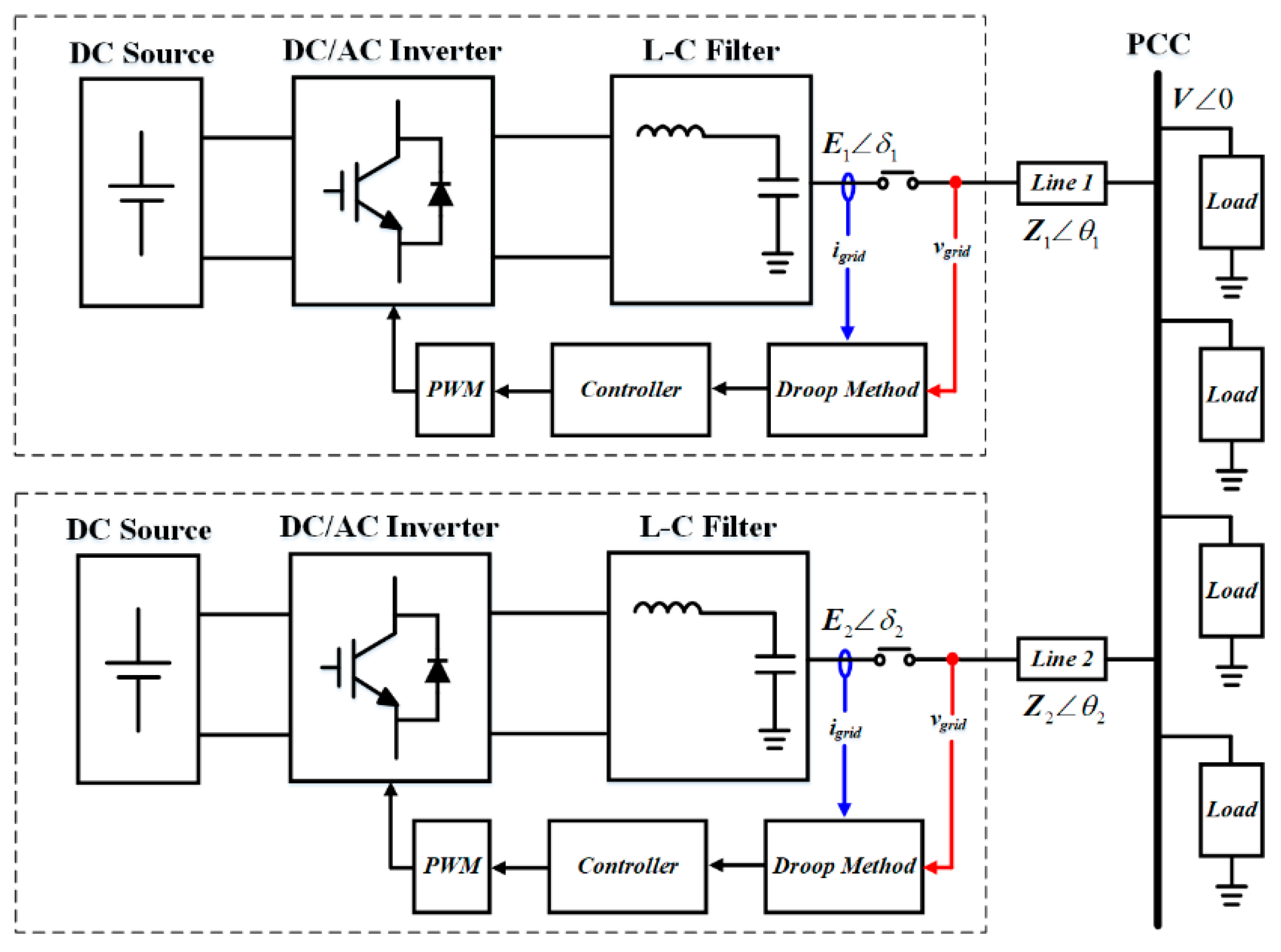
2.1. System Configuration
2.2. Dynamics of Power Delivery
2.3. Dynamics of Droop Control
3. Modeling and Analysis of Dynamic Phasor-Based Droop-Controlled Inverter
3.1. Dynamic Phasor-Based Modeling
3.2. Stability Analysis and Selection of Droop Coefficients
4. Design and Control of Droop-Controlled Inverter Using Dynamic Phasor and SOGI-FLL
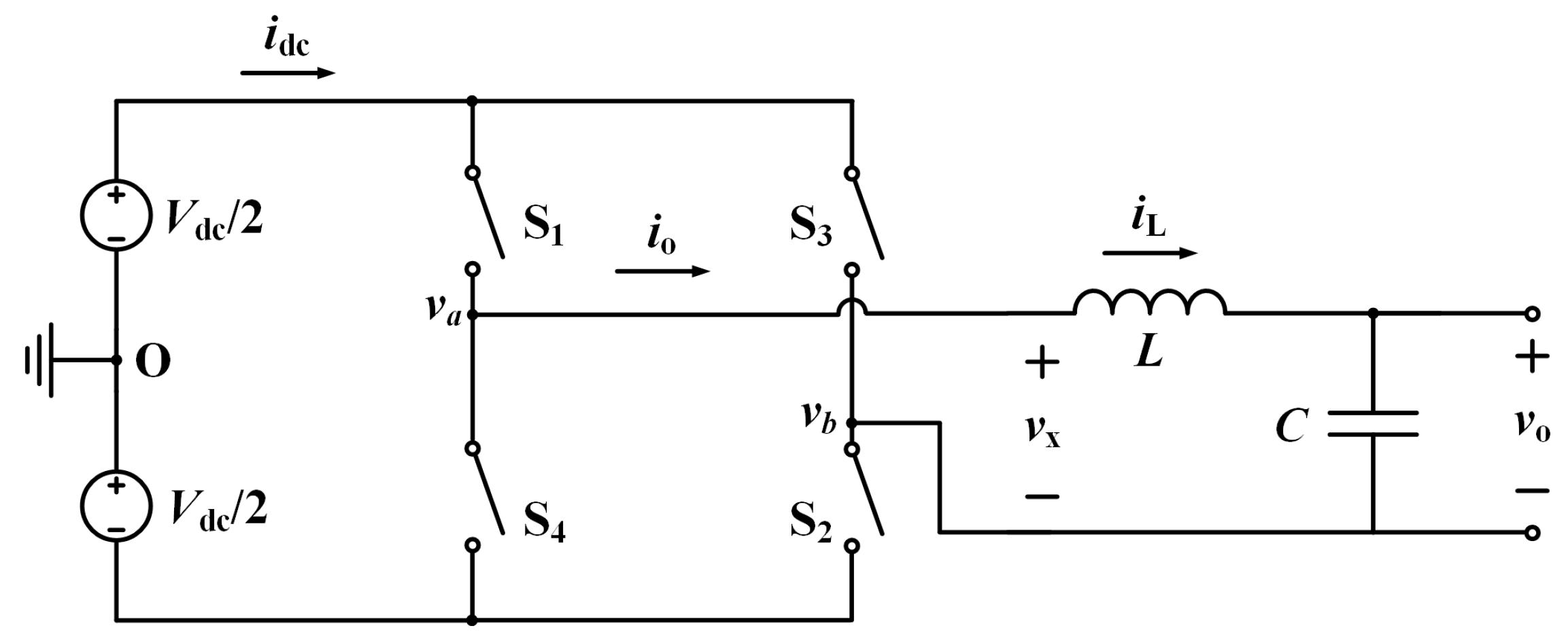
4.1. Plant Modeling Considering Unipolar Sinusoidal PWM (SPWM) in Synchronous Rotating Frame
4.2. SOGI-based QSG and FLL
4.3. The Proposed Control Block Diagram of Droop-Controlled Parallel-Inverter
5. Implementation of Droop-Controlled Parallel-Inverter
5.1. Configuration of the Experiment System
5.2. Control Sequence of Operation
6. Simulation and Experimental Results
6.1. Simulation Results
6.2. Experimental Results
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kai, Y.; Ai, Q.; Wang, S.; Ni, J.; Lv, T. Analysis and optimization of droop controller for microgrid system based on small-signal dynamic model. IEEE Trans. Smart Grid 2016, 7, 695–705. [Google Scholar]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; de Vicuna, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Dou, C.; Zhang, Z.; Yue, D.; Gao, H. An Improved Droop Control Strategy Based on Changeable Reference in Low-Voltage Microgrids. Energies 2017, 10, 1080. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Zeng, Y. Universal droop control of inverters with different types of output impedance. IEEE Access 2016, 4, 702–712. [Google Scholar] [CrossRef]
- Chaitanya, N.; Sekhar, K.C.; Anjaneyulu, K.S.R. Integrated power management strategy of parallel inverters for distributed generation system. In Proceedings of the IEEE International Conference on Advanced Communication Control and Computing Technologies (ICACCCT), Ramanathapuram, India, 25–27 May 2016. [Google Scholar]
- Han, Y.; Li, H.; Shen, P.; Coelho, E.A.A.; Guerrero, J.M. Review of active and reactive power sharing strategies in hierarchical controlled microgrids. IEEE Trans. Power Electron. 2017, 32, 2427–2451. [Google Scholar] [CrossRef]
- Zhong, Q.-C. Robust droop controller for accurate proportional load sharing among inverters operated in parallel. IEEE Trans. Ind. Electron. 2013, 60, 1281–1290. [Google Scholar] [CrossRef]
- Kim, J.-H.; Lee, Y.-S.; Kim, H.-J.; Han, B.-M. A New Reactive-Power Sharing Scheme for Two Inverter-Based Distributed Generations with Unequal Line Impedances in Islanded Microgrids. Energies 2017, 10, 1800. [Google Scholar] [CrossRef]
- Li, D.; Zhao, B.; Wu, Z.; Zhang, X.; Zhang, L. An Improved Droop Control Strategy for Low-Voltage Microgrids Based on Distributed Secondary Power Optimization Control. Energies 2017, 10, 1347. [Google Scholar] [CrossRef]
- Guerrero, J.M.; de Vicuna, L.G.; Matas, J.; Castilla, M.; Miret, J. Output impedance design of parallel-connected UPS inverters with wireless load-sharing control. IEEE Trans. Ind. Electron. 2005, 52, 1126–1135. [Google Scholar] [CrossRef]
- Matas, J.; Castilla, M.; de Vicuña, L.G.; Miret, J.; Vasquez, J.C. Virtual impedance loop for droop-controlled single-phase parallel inverters using a second-order general-integrator scheme. IEEE Trans. Power Electron. 2010, 25, 2993–3002. [Google Scholar] [CrossRef]
- Alberto, C.-M.; Pérez-Cisneros, M.A.; Domínguez-Navarro, J.A.; Osuna-Enciso, V.; Zúñiga-Grajeda, V.; Gurubel-Tuna, K.J. Dynamic phasors modeling for a single phase two stage inverter. Electr. Power Syst. Res. 2016, 140, 854–865. [Google Scholar]
- Piyasinghe, L. Dynamic Phasor Based Analysis and Control in Renewable Energy Integration; University of South Florida: Tampa, FL, USA, 2015. [Google Scholar]
- Roshan, A.; Burgos, R.; Baisden, A.C.; Wang, F.; Boroyevich, D. A DQ frame controller for a full-bridge single phase inverter used in small distributed power generation systems. In Proceedings of the APEC 2007-Twenty Second Annual IEEE Applied Power Electronics Conference, Anaheim, CA, USA, 25 February–1 March 2007. [Google Scholar]
- Turhan, D.; Andersson, G. Comparison of the efficiency of dynamic phasor models derived from ABC and DQO reference frame in power system dynamic simulations. In Proceedings of the 7th IET International Conference on Advances in Power System Control, Operation and Management (APSCOM 2006), Hong Kong, China, 30 October–2 November 2006; p. 204. [Google Scholar]
- Adarsh, N.; Ayyanar, R. Dynamic phasor model of single-phase inverters for analysis and simulation of large power distribution systems. In Proceedings of the IEEE 4th IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Rogers, AR, USA, 8–11 July 2013. [Google Scholar]
- Kulasza, M. Generalized Dynamic Phasor-Based Simulation for Power Systems. Master’s Thesis, University of Manitoba, Winnipeg, MB, Canada, 13 January 2015. [Google Scholar]
- Zhong, Q.; Shi, Q.; Wang, G.; Li, H. Short circuit analysis of PV inverter under unbalanced conditions with dynamic phasor sequence components. In Proceedings of the IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016. [Google Scholar]
- Guo, X.; Lu, Z.; Wang, B.; Sun, X.; Wang, L.; Guerrero, J.M. Dynamic phasors-based modeling and stability analysis of droop-controlled inverters for microgrid applications. IEEE Trans. Smart Grid 2014, 5, 2980–2987. [Google Scholar] [CrossRef]















| Parameter | Pure Inductive (R = 0) | Pure Resistive (X = 0) |
|---|---|---|
| 0 | ||
| 0 | ||
| 0 | ||
| 0 |
| Category | General Formula | k-th Coefficient |
|---|---|---|
| Fourier Series | ||
| Dynamic Phasor |
| Parameters | Value [Unit] | Parameters | Value [Unit] |
|---|---|---|---|
| Maximum Power Rating P | 4 kW/a module | Reference P | 1.9 kW |
| Maximum Power Rating Q | 1 kVar/a module | Reference Q | 0 |
| DC voltage | 350 Vdc | Droop coefficient KP | 0.0005 |
| AC Output voltage | 220 Vrms | Droop coefficient KQ | 0.0001 |
| AC Output frequency | 60 Hz | Line impedance R + jX | 0.14 + j1.24 |
| Filter Capacitance C | 15 μF | Cutoff frequency ωf | 10 Hz |
| Filter Inductance L | 1 mH | Damping ratio ζ | 0.707 |
| Switching frequency | 12 kHz | SOGI-FLL gain k | 1.414 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, B.-J.; Kum, H.-J.; Park, J.-M.; Won, C.-Y. Analysis, Design and Implementation of Droop-Controlled Parallel-Inverters Using Dynamic Phasor Model and SOGI-FLL in Microgrid Applications. Energies 2018, 11, 1683. https://doi.org/10.3390/en11071683
Kim B-J, Kum H-J, Park J-M, Won C-Y. Analysis, Design and Implementation of Droop-Controlled Parallel-Inverters Using Dynamic Phasor Model and SOGI-FLL in Microgrid Applications. Energies. 2018; 11(7):1683. https://doi.org/10.3390/en11071683
Chicago/Turabian StyleKim, Bum-Jun, Ho-Jung Kum, Jung-Min Park, and Chung-Yuen Won. 2018. "Analysis, Design and Implementation of Droop-Controlled Parallel-Inverters Using Dynamic Phasor Model and SOGI-FLL in Microgrid Applications" Energies 11, no. 7: 1683. https://doi.org/10.3390/en11071683
APA StyleKim, B.-J., Kum, H.-J., Park, J.-M., & Won, C.-Y. (2018). Analysis, Design and Implementation of Droop-Controlled Parallel-Inverters Using Dynamic Phasor Model and SOGI-FLL in Microgrid Applications. Energies, 11(7), 1683. https://doi.org/10.3390/en11071683




