Power System Day-Ahead Unit Commitment Based on Chance-Constrained Dependent Chance Goal Programming
Abstract
:1. Introduction
- (1)
- Wind power and load forecast error is considered to describe an accurate power balance equation to reduce the impact of wind power and load uncertainty. In order to solve the equation containing uncertain variables, the author put forward a model based on the dependent chance programming. To the authors’ knowledge, this is the first time someone has used dependent chance programming to deal the power balance equation in UC models. The novel model improves not only operation efficiency and wind power consumption, but also the level of power balance of the UC result after considering the forecast error.
- (2)
- Methodologically, we put forward the chance-constrained dependent chance goal programming and apply it to the day-ahead UC problem. According to the probability density function (PDF) of the forecast error, a reserve decision method is proposed based on chance-constrained programming (CCP) to efficiently utilize the reserve. In order to solve the multi-objective programming model rapidly, goal programming (GP) is introduced. Combined with the dependent chance programming used for solving the power balance equation containing uncertain variables, we propose chance-constrained dependent chance goal programming and apply it to the day-ahead UC problem, which introduces a novel method to deal with the uncertainties in the UC.
- (3)
- Mathematically, the stochastic problem is converted into a deterministic equivalent by mathematical derivation. Based on that, the model is transformed into a mixed integer quadratic programming (MIQP) problem, which provides an efficient solution.
2. Power Balance Equation in a Day-Ahead UC Model of a Power System
2.1. Uncertain Variables in the Power Balance Equation
2.2. Treatment of the Power Balance Equation with Uncertain Variables
3. Power System Day-Ahead UC based on Chance-Constrained Dependent Chance Goal Programming
3.1. Dependent Chance Programming
3.2. Chance-Constrained Dependent Chance Objective Programming
3.3. Power System Day-Ahead UC Model based on Chance-Constrained Dependent Chance Goal Programming
4. Model Solution
4.1. Transformation of Chance-Constrained Constraint to Deterministic Form
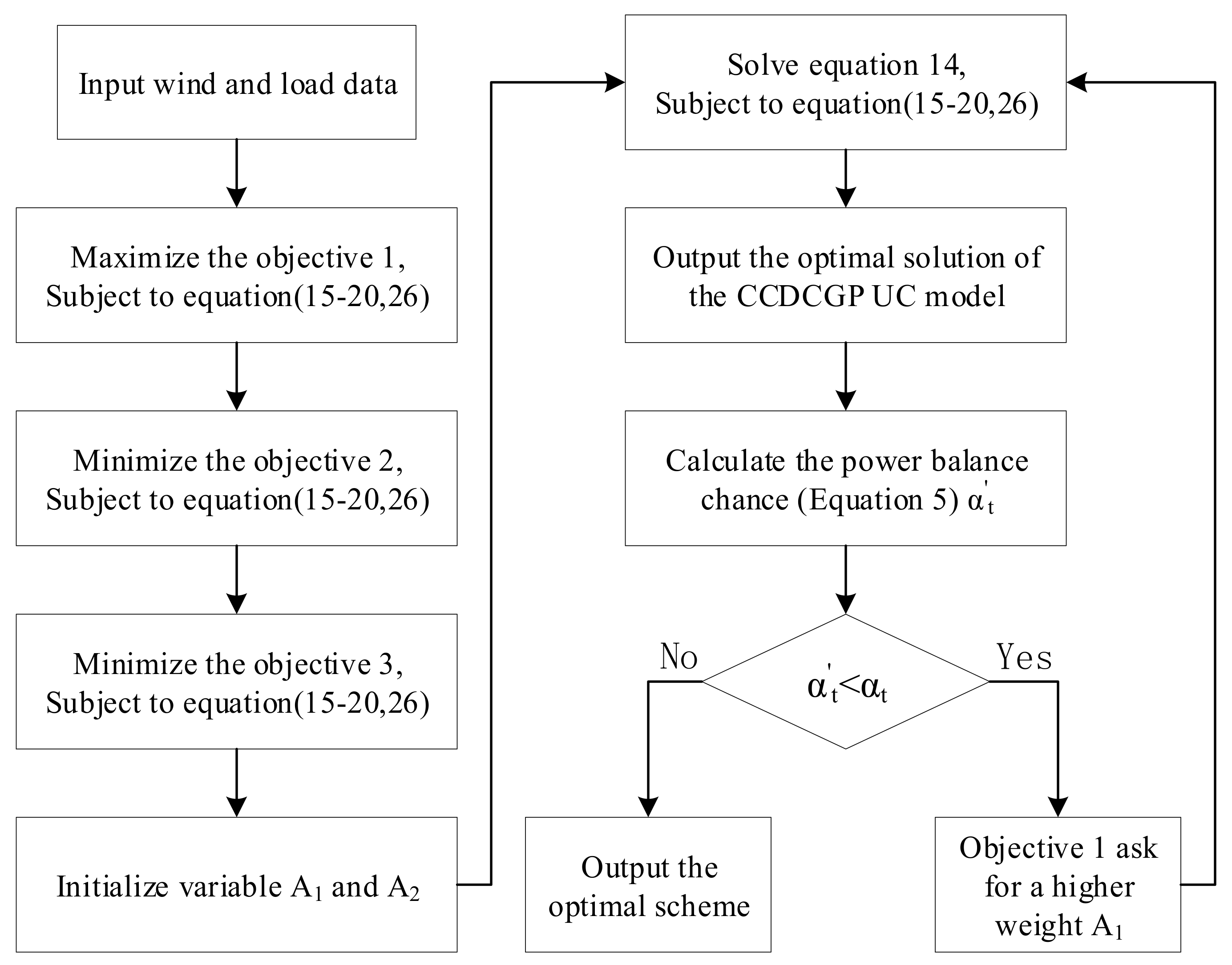
4.2. Solving Process
5. Case Study
5.1. Case Description
5.2. Analysis of Results
5.2.1. Day-Ahead UC Scheme
5.2.2. Model Validity Analysis
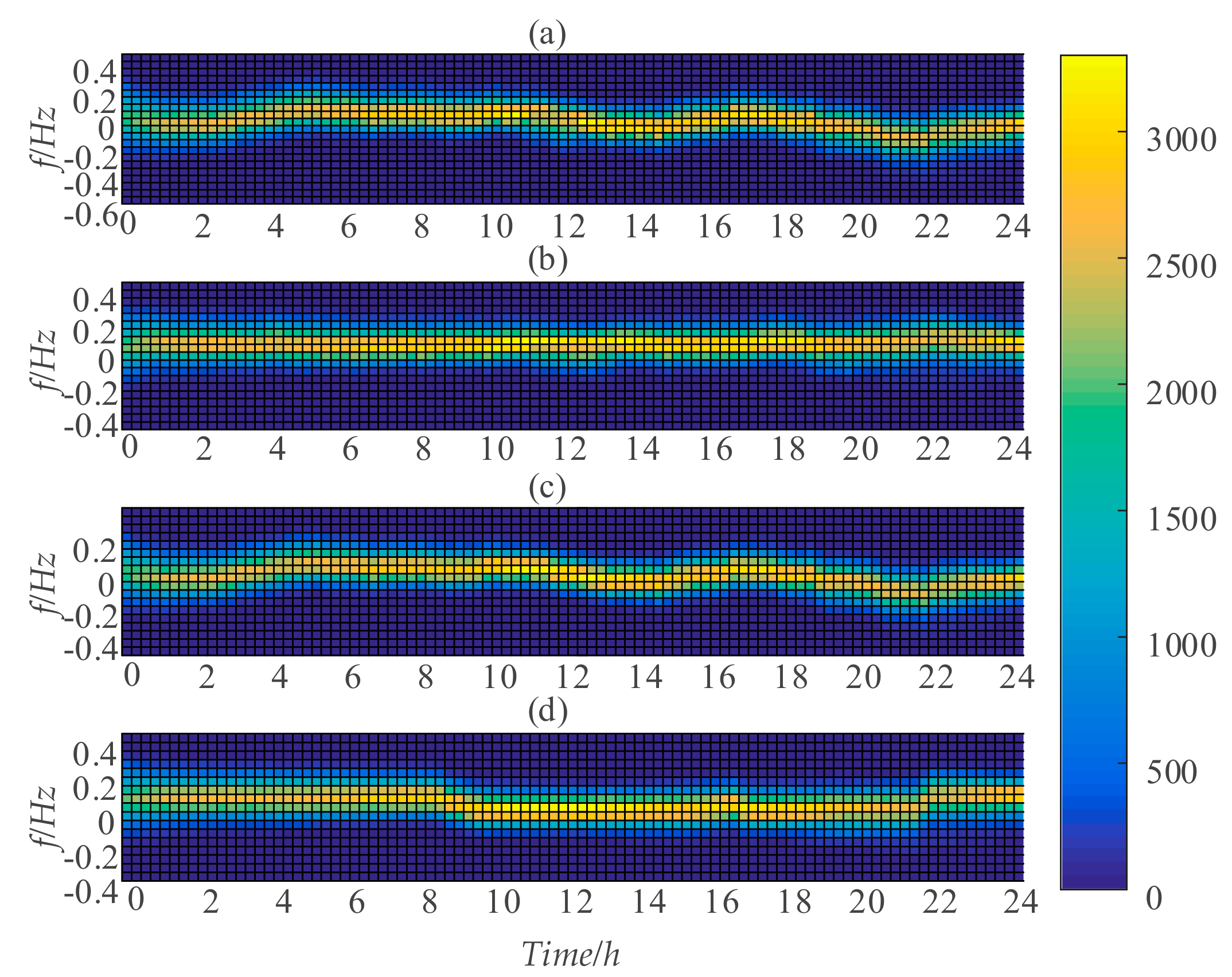
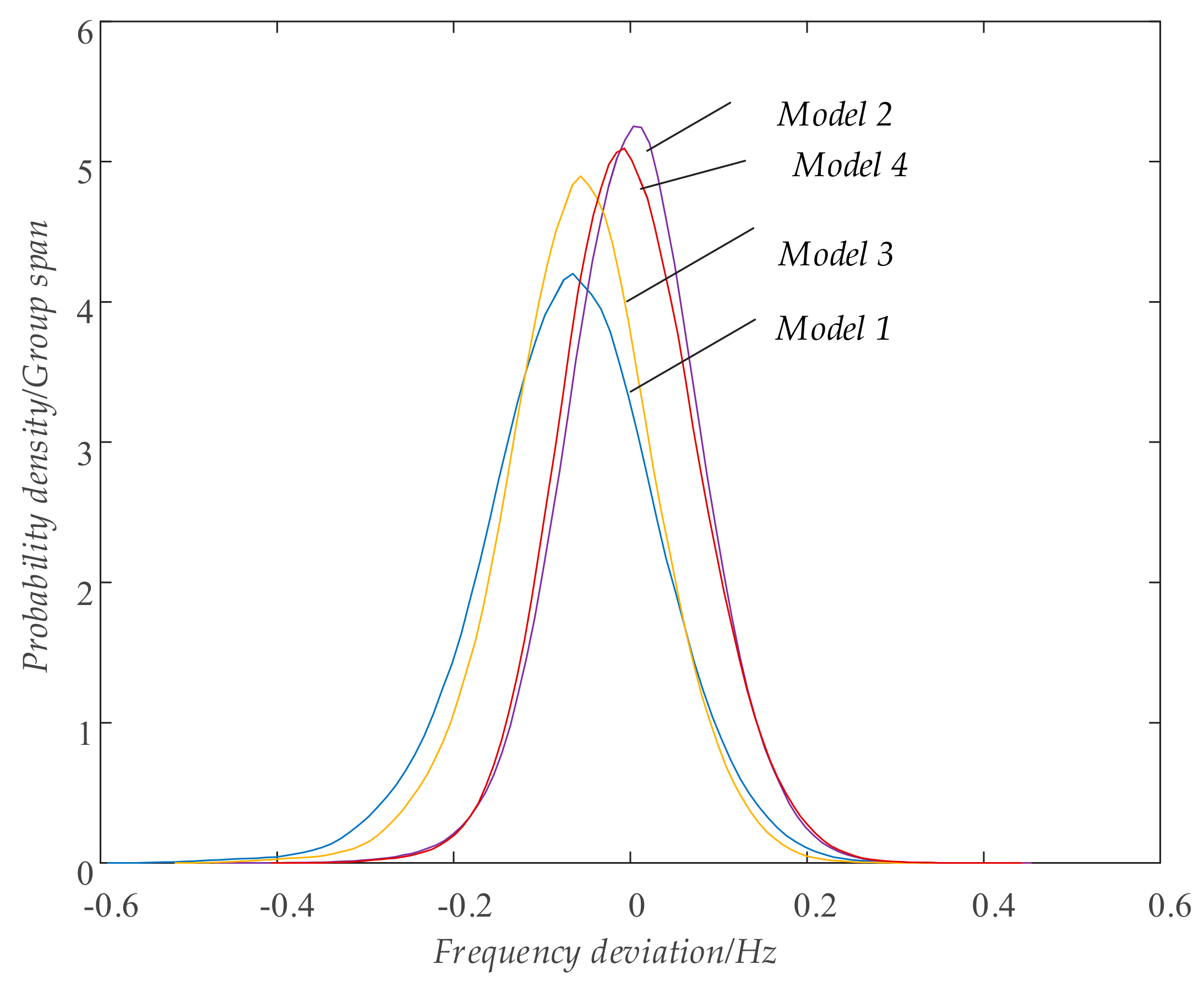
- Model 1: conventional deterministic optimisation UC model. Power balance equation uses a conventional processing model that directly ignores forecast errors. To cope with the uncertainty of wind power, the spinning reserve requirement of the system is the sum of the load reserve capacity and 30% of the predicted wind power.
- Model 2: stochastic optimisation UC model based on the scenario method. The processing approach of the power balance equation is to be balanced in each selected scenario. Adopting a Latin cube sampling strategy, dynamic scenario generation, and reduction techniques as described elsewhere [52], 10,000 initial scenarios are generated, and the 50 preserved scenarios optimised for calculation thereafter.
- Model 3: stochastic optimisation UC model based on chance-constrained programming. The power balance equation uses a conventional processing model that directly ignores forecast errors. The confidence level for the establishment of the chance constraint of system positive and negative reserve power is .
- Model 4: the proposed chance-constrained dependent chance goal programming model. The power balance equation uses the processing model where the equality constraint is loosened to an inequality constraint and is then transformed into the chance-constrained dependent chance programming model. The confidence level for the establishment of the chance constraint of system positive and negative reserve power is .
5.2.3. Sensitivity Analysis
6. Discussion
- Excluding the factor whereby the total output of the thermal units is unequal as caused by the forecast error mean value being non-zero, the proposed UC scheme is economically dominant and suffers the smallest amount of wind power curtailment.
- From the simulation results, the UC models formulated by the power balance equation that do not consider the impact of forecast errors completely have a larger deviation of power supply and load than the UC models that consider the impact of forecast errors in the power balance equation. In the UC models that consider the impact of forecast errors in the power balance equation, the proposed UC model performs better than the stochastic UC model based on scenarios. This is because the stochastic UC model based scenarios make the UC scheme based on the error distribution information obtained from the reserved scenarios, while the UC model proposed in this paper directly makes the UC scheme by using the original error distribution information, and there is no error in the expression of the forecast error distribution information caused by the scenario reduction process.
- Compared with the conventional method processing power balance equation in which the power supply predicted value is equal to load predicted value, the method proposed in this paper expands the search space of the optimization model. The obtained UC scheme can significantly improve not only operation efficiency and wind power consumption, but also the balance level of power supply and demand after considering the forecast error.
- The model proposed in this paper for processing the power balance equation with uncertain variables does not bring a power imbalance risk to the system, though the equality constraint is loosened to an inequality constraint with small imbalance errors and then solved by dependent chance programming. In contrast, considering as many realistic possible output scenarios as possible can satisfy the loosened power balance equation, therefore, the obtained solution has unique advantages in dealing with the uncertainty of wind power and load.
- When using the dependent chance programming model proposed in this paper to deal with the power balance equation containing wind power and load forecast errors, a smaller power imbalance σ is not necessarily better. Since the proposed model optimizes the objective function 1 which represents the “power balance” with the highest priority, a larger σ within a certain range does not deteriorate the imbalance of power supply and demand when the UC scheme is actually operated. On the contrary, due to the increase of σ, the feasible set under the uncertain environment is expanded, so that more wind power and load error scenarios meet the “power balance” defined by Equation (5), and the ability of the system to cope with uncertain power is improved. The negative effect is to increase the operation cost of the scheme and reduce the capacity of wind power consumption.
7. Conclusions
- The forecast errors of wind power and load in the power balance equation of the power system UC model will directly affect the formulation of the UC scheme. In particular, when the forecast error mean value is non-zero, the influence will be greater, and the effects will be greater with the increase in the scale of wind power generation.
- In power systems with large-scale, uncertain power supplies, the power balance equation in the UC model is loosened to an inequality constraint, and the chance-constrained dependent chance goal programming model proposed in this paper is used in the formulation of the solution. During practical operation of the obtained UC scheme, instead of getting larger, the power deviation will be smaller than that scheduled by the equation that only considers the predicted value.
Author Contributions
Funding
Conflicts of Interest
References
- Koltsaklis, N.E.; Dagoumas, A.S.; Georgiadis, M.C.; Papaioannou, G.; Dikaiakos, C. A mid-term market-based power systems planning model. Appl. Energy 2016, 179, 17–35. [Google Scholar] [CrossRef]
- Smith, J.C.; Milligan, M.R.; DeMeo, E.A.; Parsons, B. Utility wind integration and operating impact state of the art. IEEE Trans. Power Syst. 2007, 22, 900–908. [Google Scholar] [CrossRef]
- Sperati, S.; Alessandrini, S.; Pinson, P.; Kariniotakis, G. The “Weather Intelligence for Renewable Energies” benchmarking exercise on short-term forecasting of wind and solar power generation. Energies 2015, 8, 9594–9619. [Google Scholar] [CrossRef] [Green Version]
- Cadenas, E.; Rivera, W.; Campos-Amezcua, R.; Heard, C. Wind speed prediction using a univariate ARIMA model and a multivariate NARX model. Energies 2016, 9, 109. [Google Scholar] [CrossRef]
- Marneris, G.I.; Biskas, N.P.; Bakirtzis, G.A. Stochastic and deterministic unit commitment considering uncertainty and variability reserves for high renewable integration. Energies 2017, 10, 140. [Google Scholar] [CrossRef]
- Trombe, P.-J.; Pinson, P.; Madsen, H. A general probabilistic forecasting framework for offshore wind power fluctuations. Energies 2012, 5, 621–657. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Li, X.; Wang, Z.; Dong, X.; Liang, Z.; Liu, X.; Liang, J.; Han, X. Day-ahead unit commitment method considering time sequence feature of wind power forecast error. Int. J. Electr. Power Energy Syst. 2018, 98, 156–166. [Google Scholar] [CrossRef]
- Wang, G.; You, D.; Zhang, Z.; Dai, L.; Zou, Q.; Liu, H. Network-constrained unit commitment based on reserve models fully considering the stochastic characteristics of wind power. Energies 2018, 11, 435. [Google Scholar] [CrossRef]
- Wang, C.; Liu, F.; Wang, J.; Qiu, F.; Wei, W.; Mei, S.; Lei, S. Robust risk-constrained unit commitment with large-scale wind generation: an adjustable uncertainty set approach. IEEE Trans. Power Syst. 2017, 32, 723–733. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, J.; Watson, J.-P.; Guan, Y. Multi-stage robust unit commitment considering wind and demand response uncertainties. IEEE Trans Power Syst. 2013, 28, 2708–2717. [Google Scholar] [CrossRef]
- Kiran, B.D.H.; Kumari, M.S. Demand response and pumped hydro storage scheduling for balancing wind power uncertainties: A probabilistic unit commitment approach. Int. J. Electr. Power Energy Syst. 2016, 81, 114–122. [Google Scholar] [CrossRef]
- Zhao, J.; Wan, C.; Xu, Z.; Wong, K.P. Spinning reserve requirement optimization considering integration of plug-in electric vehicles. IEEE Trans. Smart Grid 2017, 8, 2009–2021. [Google Scholar] [CrossRef]
- Park, H.-G.; Lyu, J.-K.; Kang, Y.; Park, J.-K. Unit Commitment considering interruptible load for power system operation with wind power. Energies 2014, 7, 4281–4299. [Google Scholar] [CrossRef]
- Wang, J.; Botterud, A.; Bessa, R.; Keko, H.; Carvalho, L.; Issicaba, D.; Sumaili, J.; Miranda, V. Wind power forecasting uncertainty and unit commitment. Appl. Energy 2011, 88, 4014–4023. [Google Scholar] [CrossRef]
- Abujarad, S.Y.; Mustafa, M.W.; Jamian, J.J. Recent approaches of unit commitment in the presence of intermittent renewable energy resources: A review. Renew. Sustain. Energy Rev. 2017, 70, 215–223. [Google Scholar] [CrossRef]
- Liu, D.; Guo, J.; Huang, Y. Dynamic economic dispatch of wind integrated power systems based on wind power probabilistic forecasting and operation risk constraints. Proc. CSEE 2013, 33, 9–15. [Google Scholar]
- Zhan, Z.; Sun, Y.; Gao, D.; Lin, J.; Cheng, L. A versatile probability distribution model for wind power forecast errors and its application in economic dispatch. IEEE Trans. Power Syst. 2013, 28, 3114–3125. [Google Scholar] [CrossRef]
- Qin, N.; Bak, C.L.; Abildgaard, H.; Chen, Z. Multi-Stage optimization-based automatic voltage control systems considering wind power forecasting errors. IEEE Trans. Power Syst. 2017, 32, 1073–1088. [Google Scholar] [CrossRef]
- Bertsimas, D.; Litvinov, E.; Sun, X.A.; Zhao, J.; Zheng, T. Adaptive robust optimization for the security constrained unit commitment problem. IEEE Trans. Power Syst. 2013, 28, 52–63. [Google Scholar] [CrossRef]
- Ruiz, P.A.; Philbrick, C.R.; Zak, E.; Cheung, K.W.; Sauer, P.W. Uncertainty management in the unit commitment problem. IEEE Trans. Power Syst. 2009, 24, 642–651. [Google Scholar] [CrossRef]
- Jiang, R.; Wang, J.; Guan, Y. Robust unit commitment with wind power and pumped storage hydro. IEEE Trans. Power Syst. 2012, 27, 800–810. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, Q.; Kang, C. Unit commitment with volatile node injections by using interval optimization. IEEE Trans. Power Syst. 2011, 26, 1705–1713. [Google Scholar] [CrossRef]
- Pandzic, H.; Dvorkin, Y.; Qiu, T.; Wang, Y.; Kirschen, D.S. Toward cost-efficient and reliable unit commitment under uncertainty. IEEE Trans. Power Syst. 2015, 99, 1–13. [Google Scholar]
- Charnes, A.; Cooper, W.W. Chance-constrained programming. Manag. Sci. 1959, 6, 73–79. [Google Scholar] [CrossRef]
- Wu, H.; Shahidehpour, M.; Li, Z.; Tian, W. Chance-constrained day-ahead scheduling in stochastic power system operation. IEEE Trans. Power Syst. 2014, 29, 1583–1591. [Google Scholar] [CrossRef]
- Wang, Q.; Guan, Y.; Wang, J. A chance-constrained two-stage stochastic program for Unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 2012, 27, 206–215. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, S.; Zhou, Z.; Botterud, A.; Xu, Y.; Chen, R. Risk adjustable day-ahead unit commitment with wind power based on chance constrained goal programming. IEEE Trans. Sustain. Energy 2017, 8, 530–541. [Google Scholar] [CrossRef]
- Wu, L.; Shahidehpour, M.; Li, T. Stochastic security-constrained unit commitment. IEEE Trans. Power Syst. 2007, 22, 800–811. [Google Scholar] [CrossRef]
- Pinson, P.; Madsen, H.; Nielsen, H.; Papaefthymiou, G.; Klöckl, B. From probabilistic forecasts to statistical scenarios of short-term wind power production. Wind Energy 2009, 12, 51–62. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Shahidehpour, M.; Li, Z. Comparison of scenario-based and interval optimization approaches to stochastic SCUC. IEEE Trans. Power Syst. 2012, 27, 913–921. [Google Scholar] [CrossRef]
- Bai, W.; Lee, D.; Lee, K.Y. Stochastic dynamic AC optimal power flow based on a multivariate short-term wind power scenario forecasting model. Energies 2017, 10, 2138. [Google Scholar] [CrossRef]
- Growe-Kuska, N.; Heitsch, H.; Romisch, W. Scenario reduction and scenario tree construction for power management problems. In Proceedings of the IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003. [Google Scholar] [Green Version]
- Dupačová, J.; Gröwe-Kuska, N.; Römisch, W. Scenario reduction in stochastic programming: An approach using probability metrics. Math. Progr. 2003, 95, 493–511. [Google Scholar] [CrossRef]
- Huang, Y.; Zheng, Q.P.; Wang, J. Two-stage stochastic unit commitment model including non-generation resources with conditional value-at-risk constraints. Electr. Power Syst. Res. 2014, 116, 427–438. [Google Scholar] [CrossRef]
- Zhao, C.; Guan, Y. Unified stochastic and robust unit commitment. IEEE Trans. Power Syst. 2013, 28, 3353–3361. [Google Scholar] [CrossRef]
- Dvorkin, Y.; Pandzic, H.; Ortega-Vazquez, M.A.; Kirschen, D.S. A hybrid stochastic/interval approach to transmission-constrained unit commitment. IEEE Trans. Power Syst. 2015, 30, 621–631. [Google Scholar] [CrossRef]
- Koltsaklis, N.E.; Georgiadis, M.C. A multi-period, multi-regional generation expansion planning model incorporating unit commitment constraints. Appl. Energy 2015, 158, 310–331. [Google Scholar] [CrossRef]
- Che, L.; Liu, X.; Li, Z. An intrainterval security risk regarding regulation burden due to wind variation in high-wind-penetrated power systems. IEEE Trans. Power Syst. 2018, 33, 3213–3216. [Google Scholar] [CrossRef]
- Wang, J.; Shahidehpour, M.; Li, Z. Security-constrained unit commitment with volatile wind power generation. IEEE Trans. Power Syst. 2008, 23, 1319–1327. [Google Scholar] [CrossRef]
- Xu, Q.; He, D.; Zhang, N.; Kang, C.; Xia, Q.; Bai, J.; Huang, J. A short-term wind power forecasting approach with adjustment of numerical weather prediction input by data mining. IEEE Trans. Sustain. Energy 2015, 6, 1283–1291. [Google Scholar] [CrossRef]
- Methaprayoon, K.; Yingvivatanapong, C.; Lee, W.-J.; Liao, J.R. An Integration of ANN Wind Power Estimation into Unit Commitment Considering the Forecasting Uncertainty. IEEE Trans. Ind. Appl. 2007, 43, 1441–1448. [Google Scholar] [CrossRef]
- Shen, Z.; Wu, X.; Guerrero, J.M.; Song, Y. Model-independent approach for short-term electric load forecasting with guaranteed error convergence. IET Control Theory Appl. 2015, 10, 1365–1373. [Google Scholar] [CrossRef]
- Cai, G.; Wang, W.; Lu, J. A Novel Hybrid Short Term Load Forecasting Model Considering the Error of Numerical Weather Prediction. Energy 2016, 9, 994. [Google Scholar] [CrossRef]
- Xia, C.; Wang, J.; McMenemy, K. Short, medium and long term load forecasting model and virtual load forecaster based on radial basis function neural networks. Int. J. Electr. Power Energy Syst. 2010, 32, 743–750. [Google Scholar] [CrossRef] [Green Version]
- Ortega-Vazquez, M.A.; Kirschen, D.S. Estimating the Spinning Reserve Requirements in Systems with Significant Wind Power Generation Penetration. IEEE Trans. Power Syst. 2009, 24, 114–124. [Google Scholar] [CrossRef]
- Bouffard, F.; Galiana, F.D. Stochastic Security for Operations Planning with Significant Wind Power Generation. IEEE Trans. Power Syst. 2008, 23, 306–316. [Google Scholar] [CrossRef]
- Liu, B. Dependent-chance programming: A class of stochastic programming. Comput. Math. Anal. Appl. 1996, 199, 293–311. [Google Scholar]
- Zhou, W.; Sun, H.; Gu, H. Dynamic economic dispatch of wind integrated power systems based on risk reserve constraints. Proc. CSEE 2012, 32, 47–55. [Google Scholar]
- Li, Z.; Zhao, S.; Li, D.; Zhang, T. Fast solving of day-ahead power system scheduling chance-constrained model based on improved ε-constrained and deterministic transform by sampling. Proc. CSEE 2018, 38, 1–13. [Google Scholar]
- Unit Parameter Data. Available online: https://docs.google.Com/document/d/1jKJNnvIp5hURLiez Umr9ewiMI4vQjCqscUuvY0bgB30/pub (accessed on 18 April 2018).
- Elia. Wind-Power Generation Data & Solar-PV Power Generation Data. Available online: http://www.elia.be/en/grid-data/power-generation/wind-power (accessed on 15 July 2017).
- Ma, X. Scenario Analysis and Stochastic Programming of Wind-Integrated Power Systems. Ph.D. Thesis, Wuhan University, Wuhan, China, 2014. [Google Scholar]









| UC Model | Variable | Constraint Condition | Computing Time/s |
|---|---|---|---|
| Model 1 | 2208 | 13,708 | 36.53 |
| Model 2 | 20,448 | 212,524 | 367.27 |
| Model 3 | 2208 | 13,708 | 30.75 |
| Model 4 | 2208 | 13,612 | 24.65 |
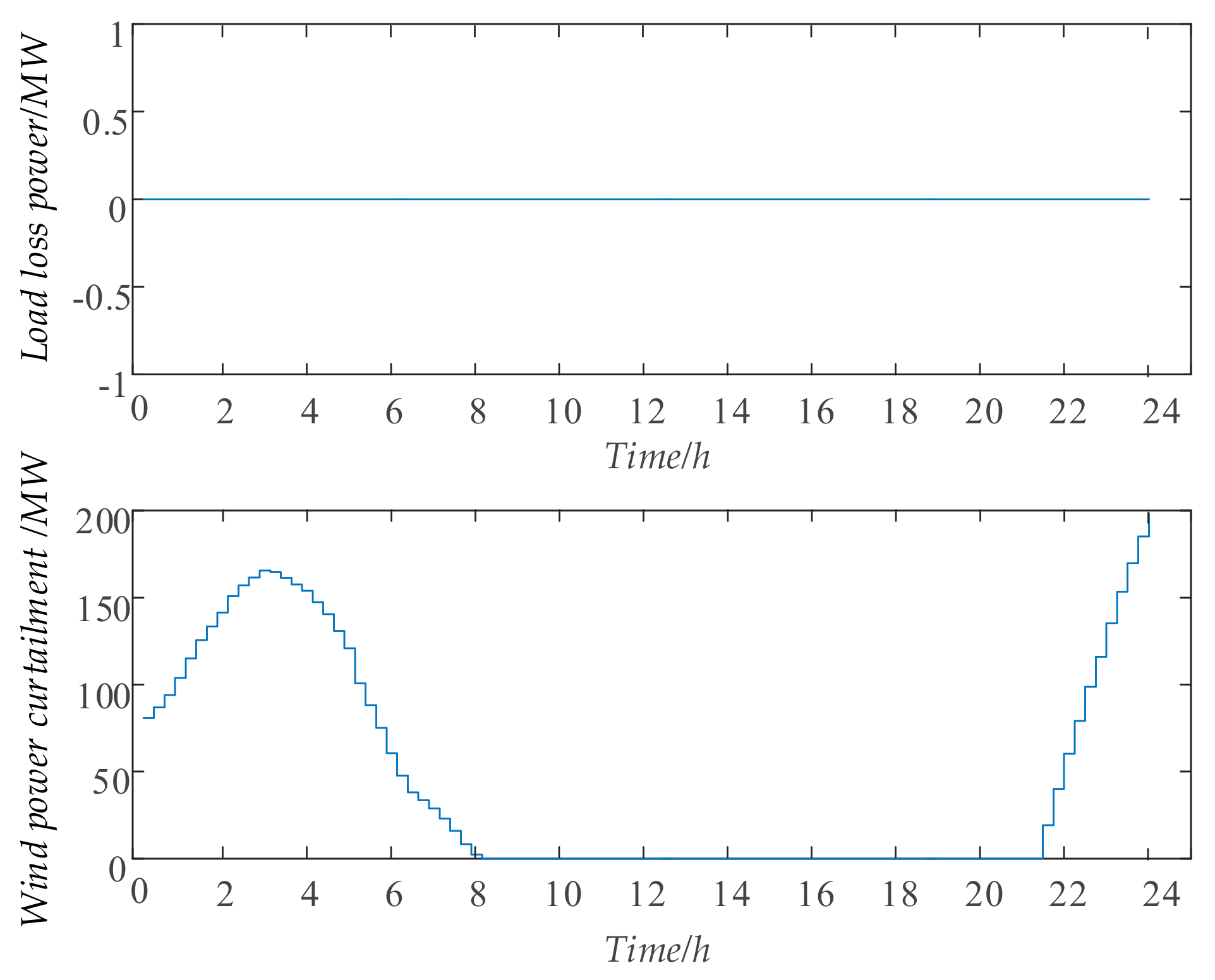
| UC Scheme | Total Cost/Dollar | Wind Power Curtailment/MW·h | Load Loss Power/MW·h |
|---|---|---|---|
| Model 1 | 259,745.75 | 2411.66 | 0 |
| Model 2 | 259,752.35 | 1743.17 | 0 |
| Model 3 | 254,609.16 | 2311.27 | 0 |
| Model 4 | 254,487.53 | 1230.59 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Jin, T.; Zhao, S.; Liu, J. Power System Day-Ahead Unit Commitment Based on Chance-Constrained Dependent Chance Goal Programming. Energies 2018, 11, 1718. https://doi.org/10.3390/en11071718
Li Z, Jin T, Zhao S, Liu J. Power System Day-Ahead Unit Commitment Based on Chance-Constrained Dependent Chance Goal Programming. Energies. 2018; 11(7):1718. https://doi.org/10.3390/en11071718
Chicago/Turabian StyleLi, Zhiwei, Tianran Jin, Shuqiang Zhao, and Jinshan Liu. 2018. "Power System Day-Ahead Unit Commitment Based on Chance-Constrained Dependent Chance Goal Programming" Energies 11, no. 7: 1718. https://doi.org/10.3390/en11071718
APA StyleLi, Z., Jin, T., Zhao, S., & Liu, J. (2018). Power System Day-Ahead Unit Commitment Based on Chance-Constrained Dependent Chance Goal Programming. Energies, 11(7), 1718. https://doi.org/10.3390/en11071718




