Analysis of Ferroresonance Phenomenon in 22 kV Distribution System with a Photovoltaic Source by PSCAD/EMTDC
Abstract
:1. Introduction
2. Preliminary and Theory
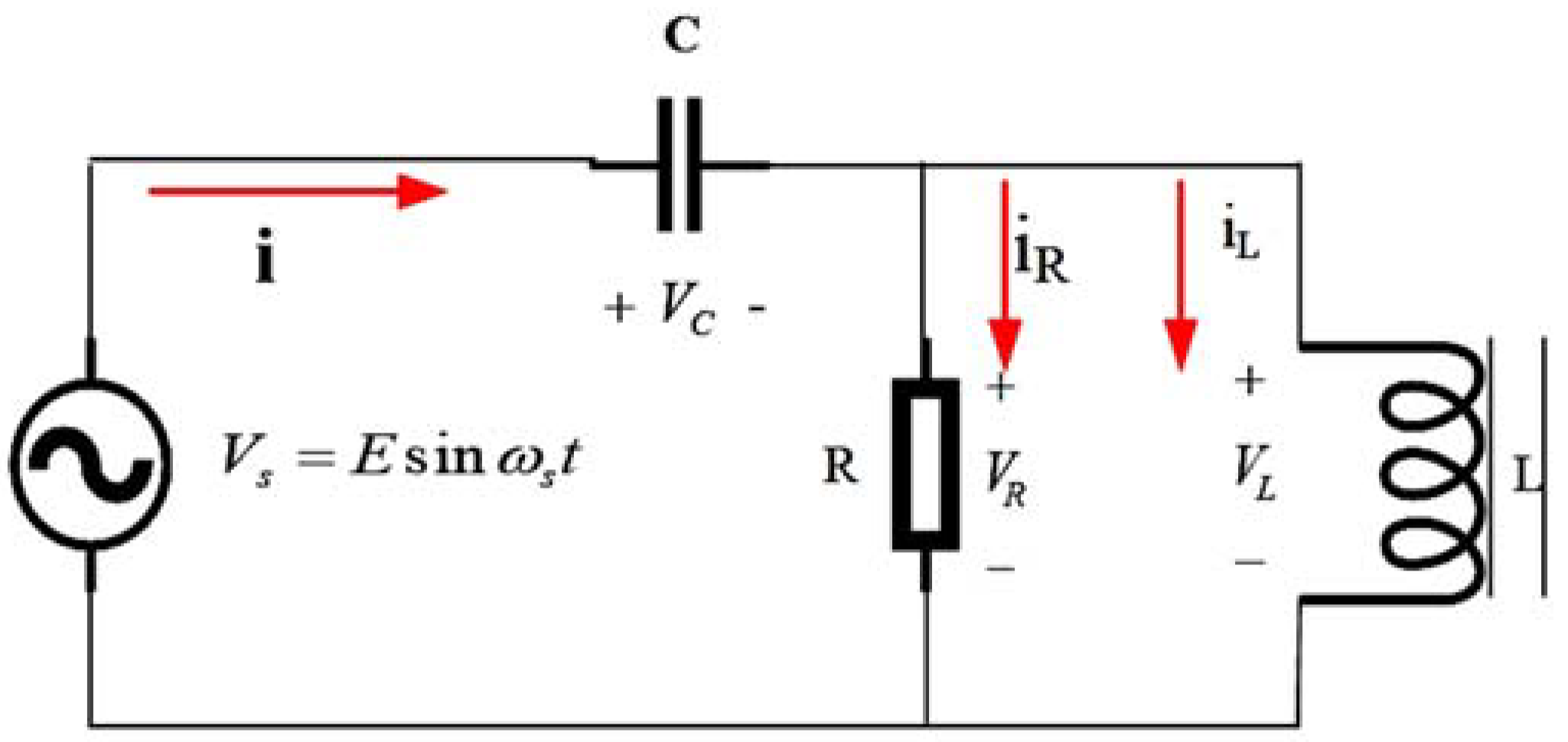
2.1. Ferroresonance in the Transformer
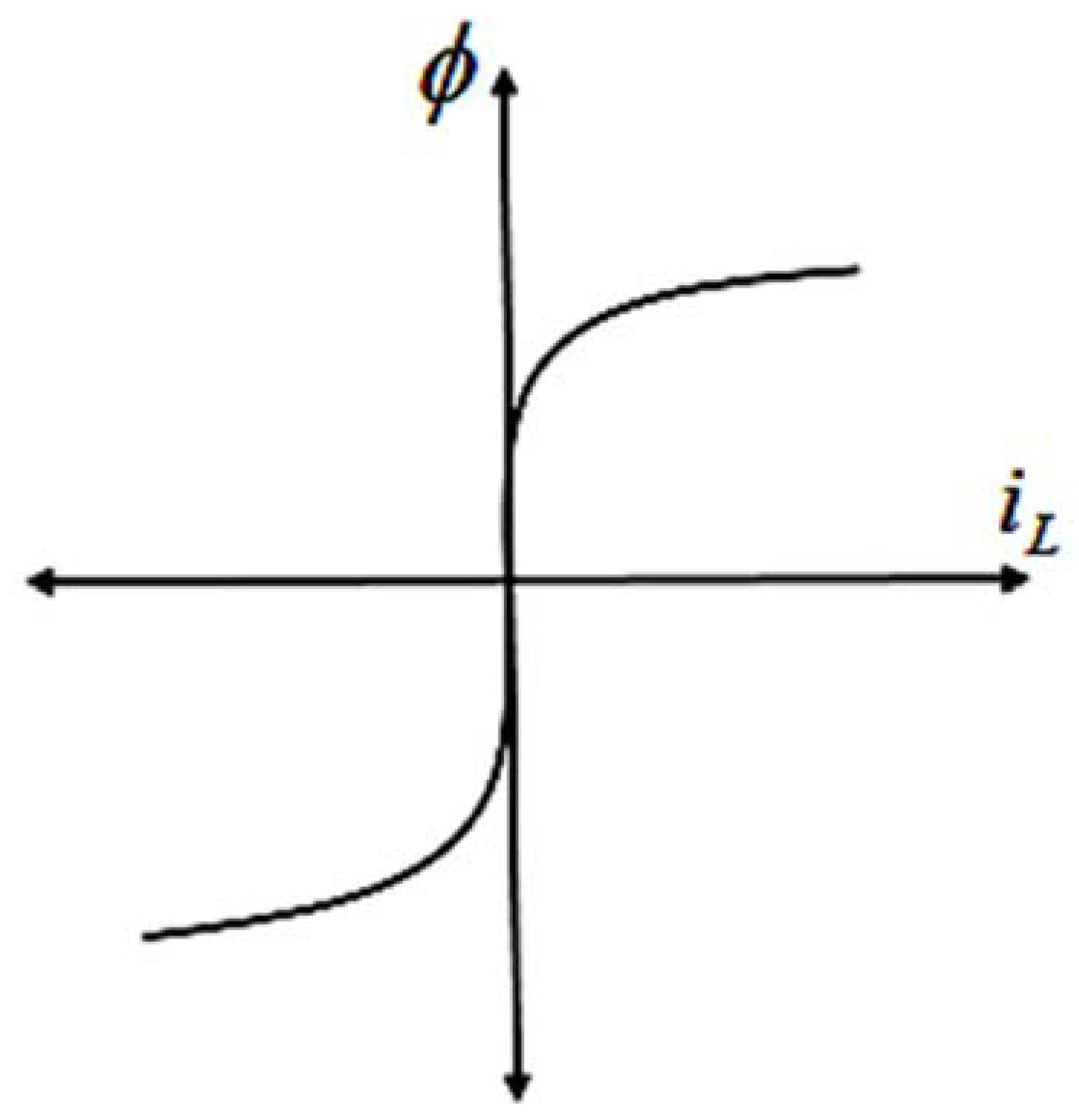
- Point 1 is a stable non-ferroresonance mode. At this point, the circuit is working with the inductive mode and remains there in the steady-state.
- Point 2 is a stable ferroresonance mode. At this point, the circuit is working with the inductive mode with both high voltage and current. This solution also remains there in the steady-state.
- Point 3 is an unstable mode and the solution will not remain there in the steady-state.
2.2. The Distribution Transformer under the Emerged or De-Energized Modes
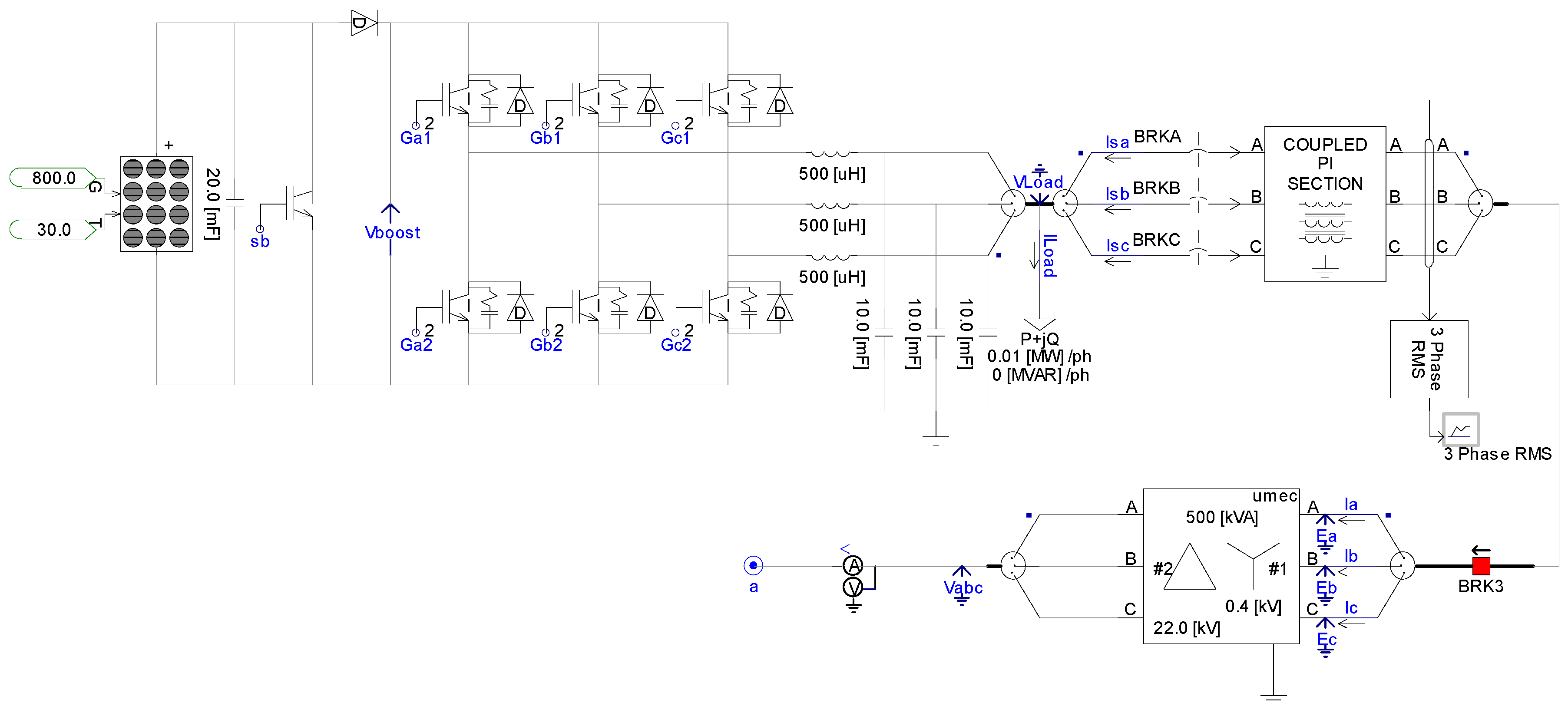
3. System Modeling for Simulation
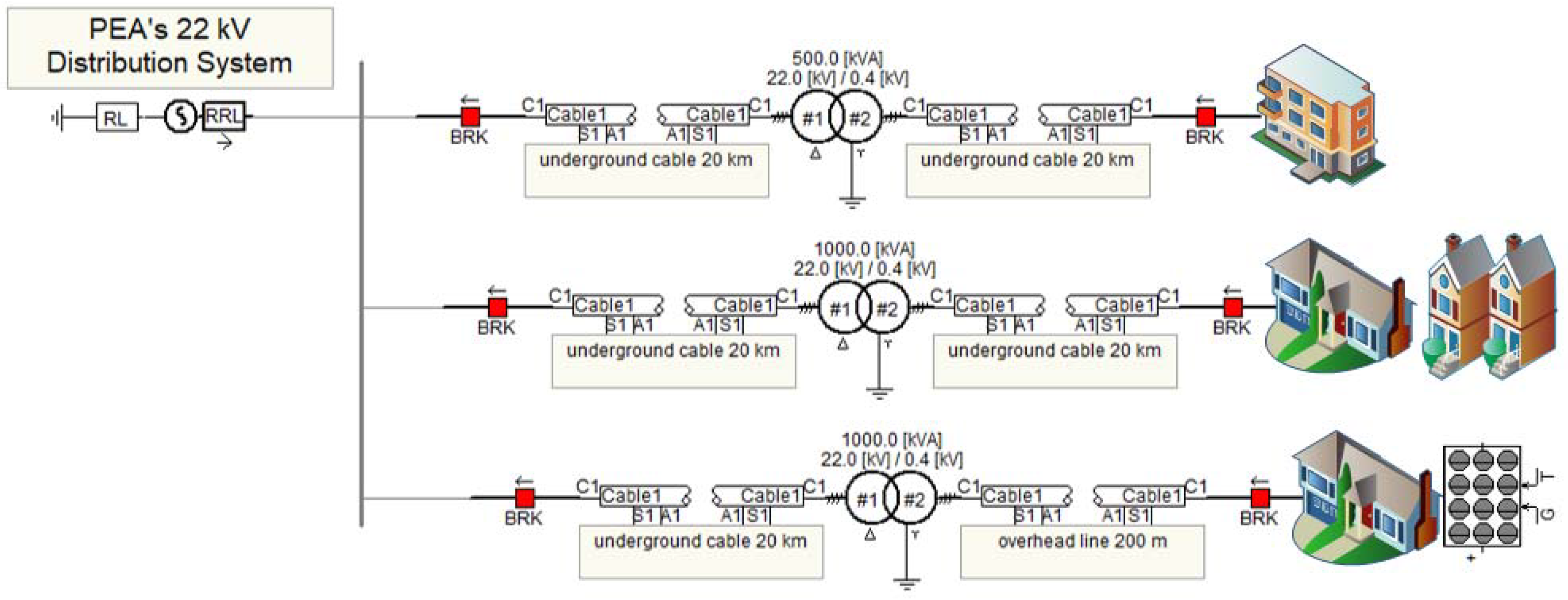
3.1. The System Under Considering
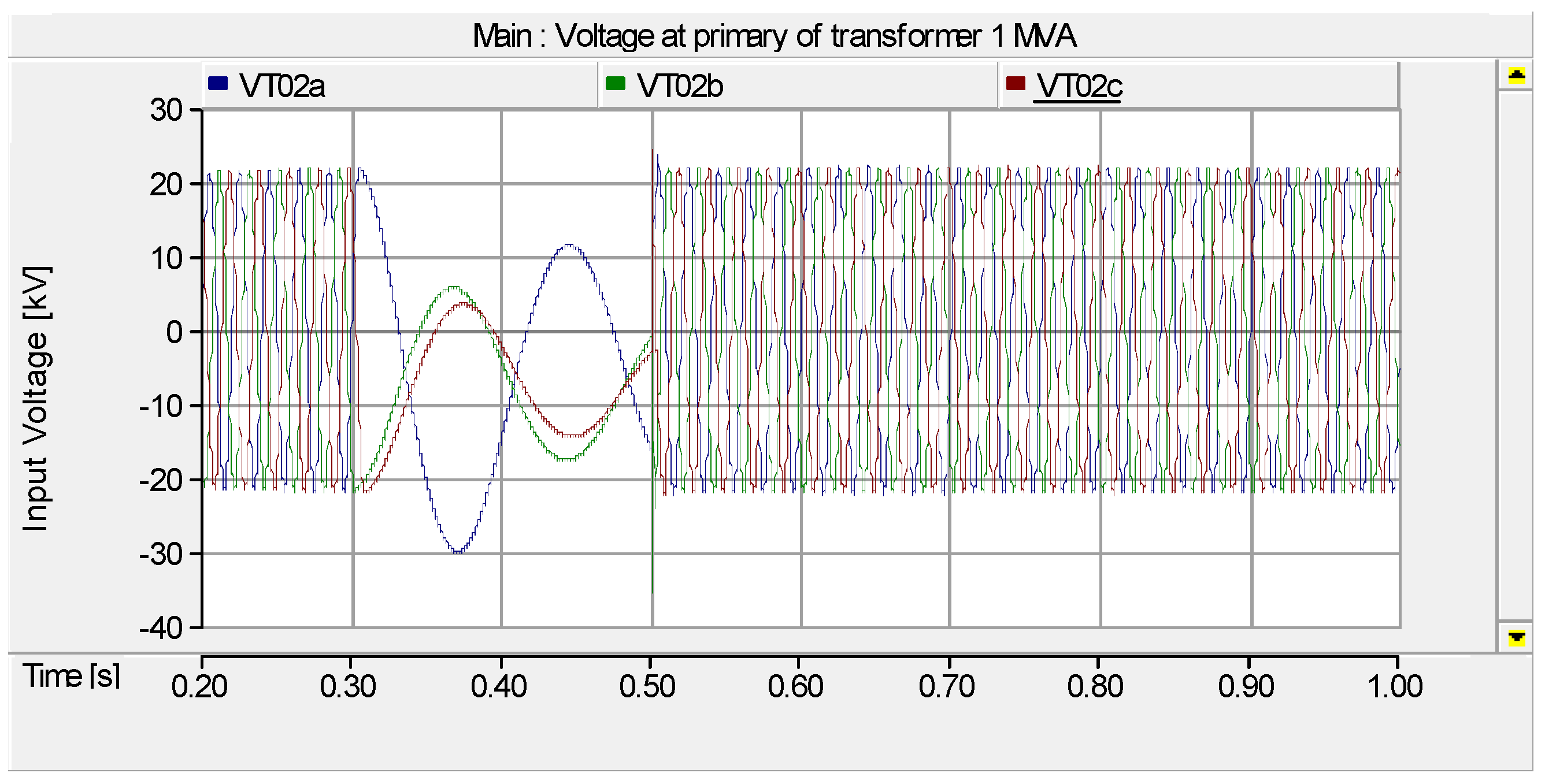
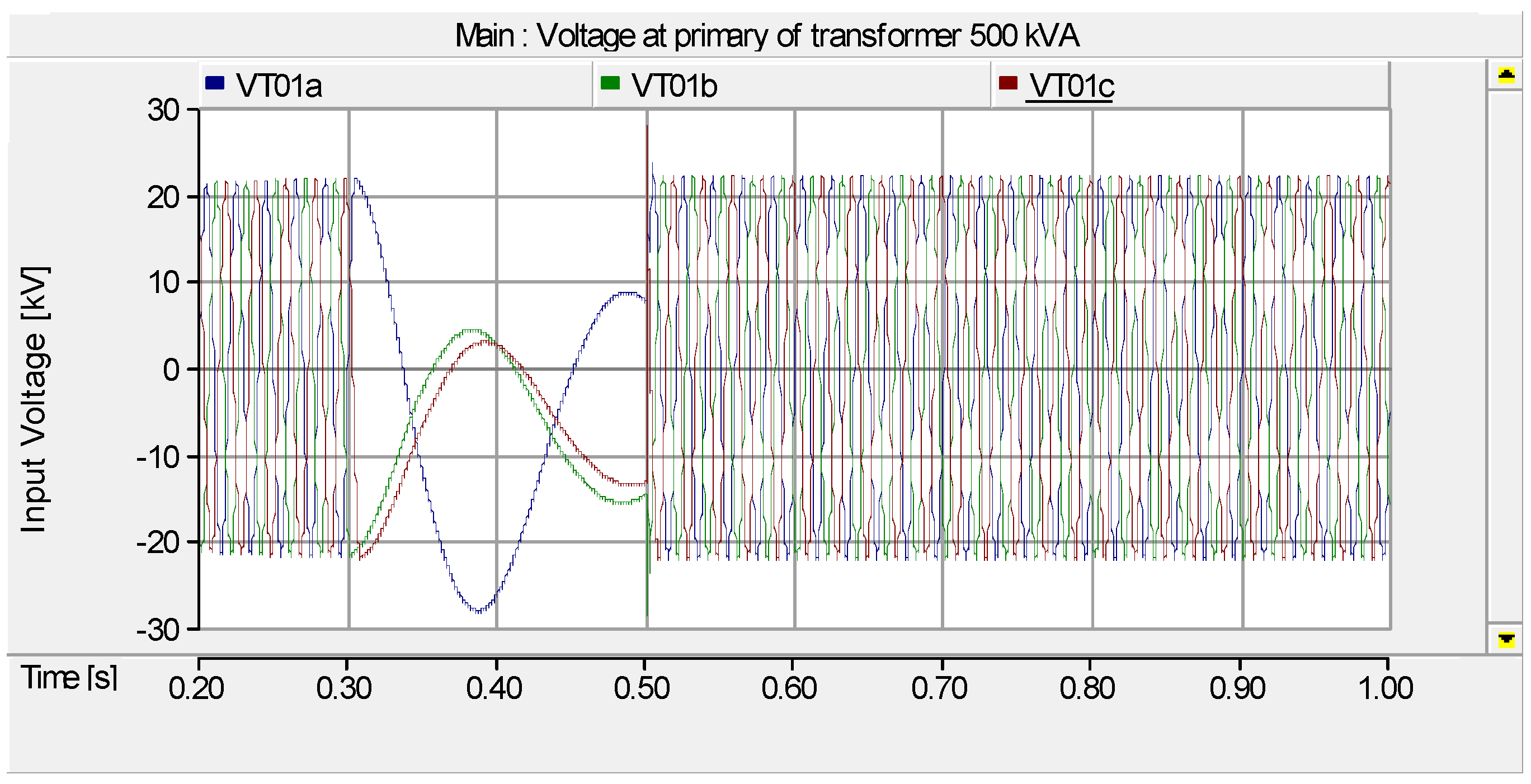
3.2. Simulation Case I: The Effect of Ferroresonance on the High Voltage (HV) Side of the Distribution Transformer
3.3. Simulation Case II and Case III: The Impact of the PV Rooftop System on the Distribution Transformer and Suburban Homes
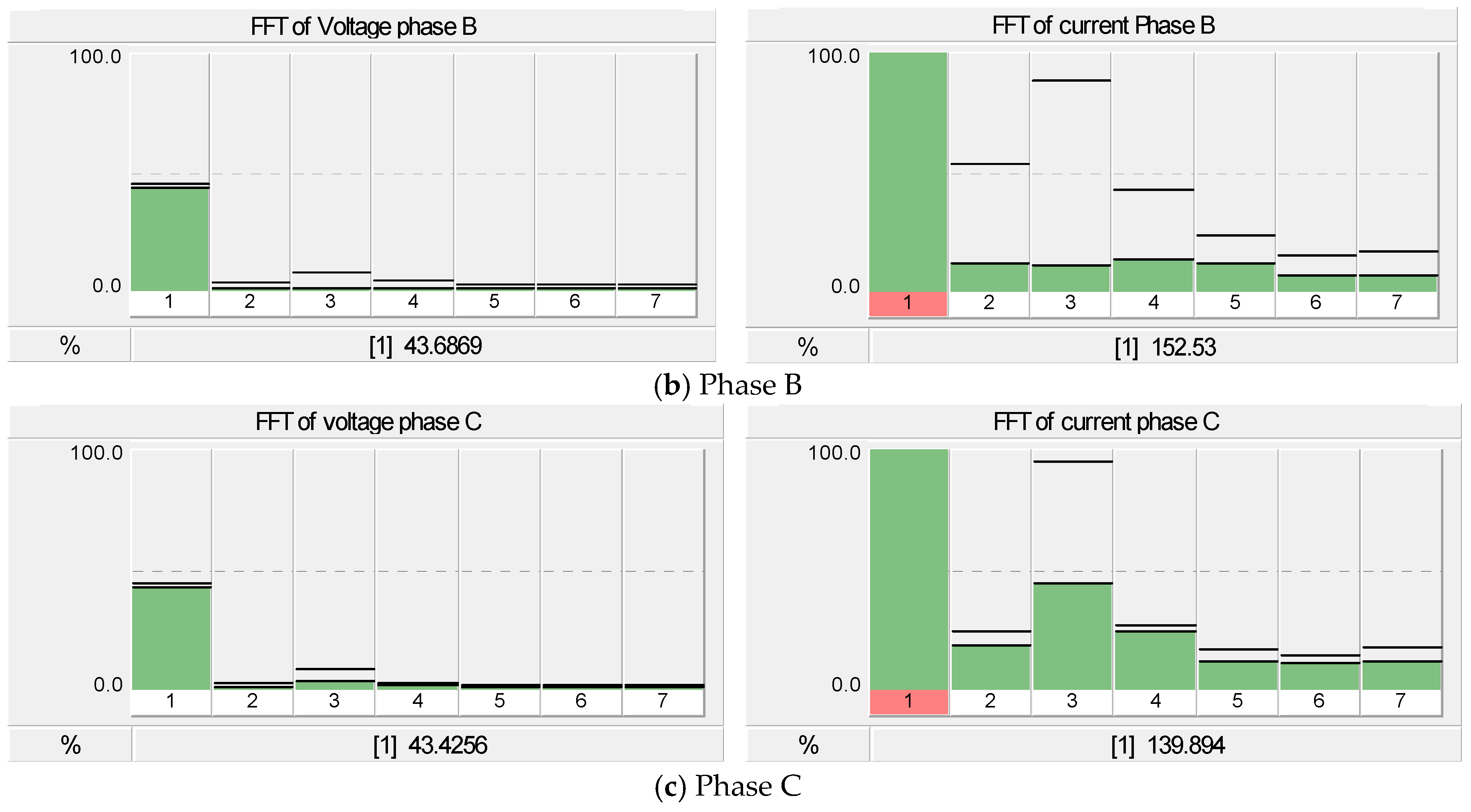
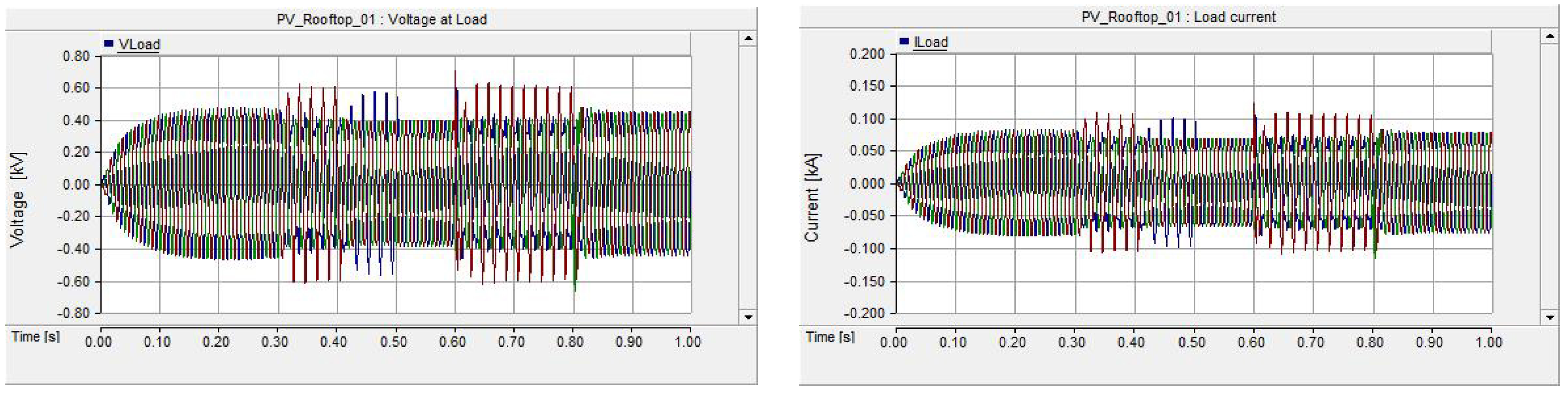
4. Simulation Results and Discussion
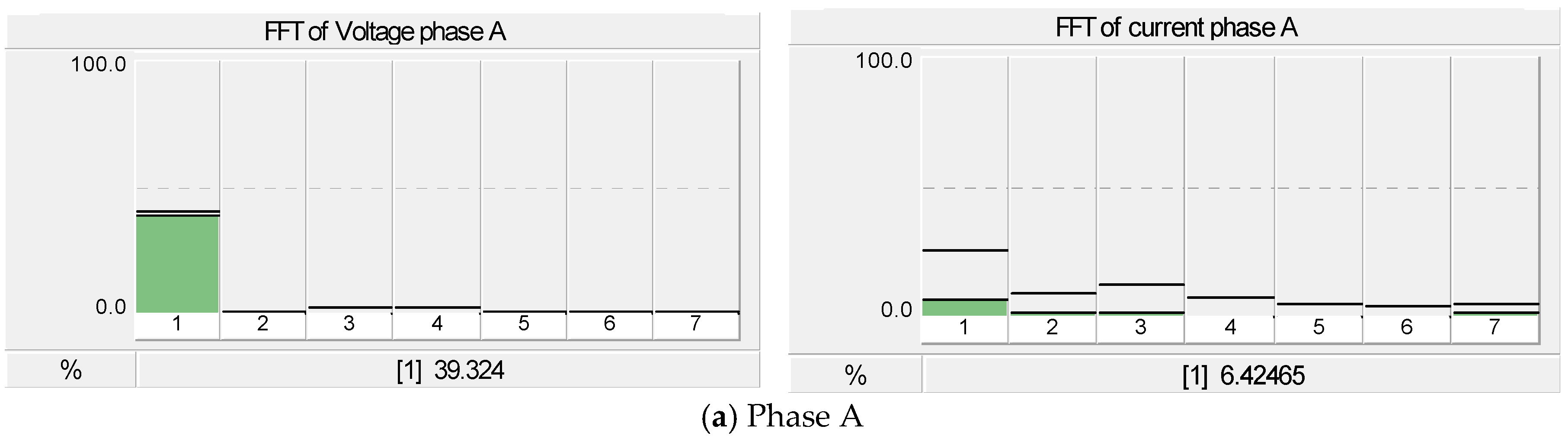
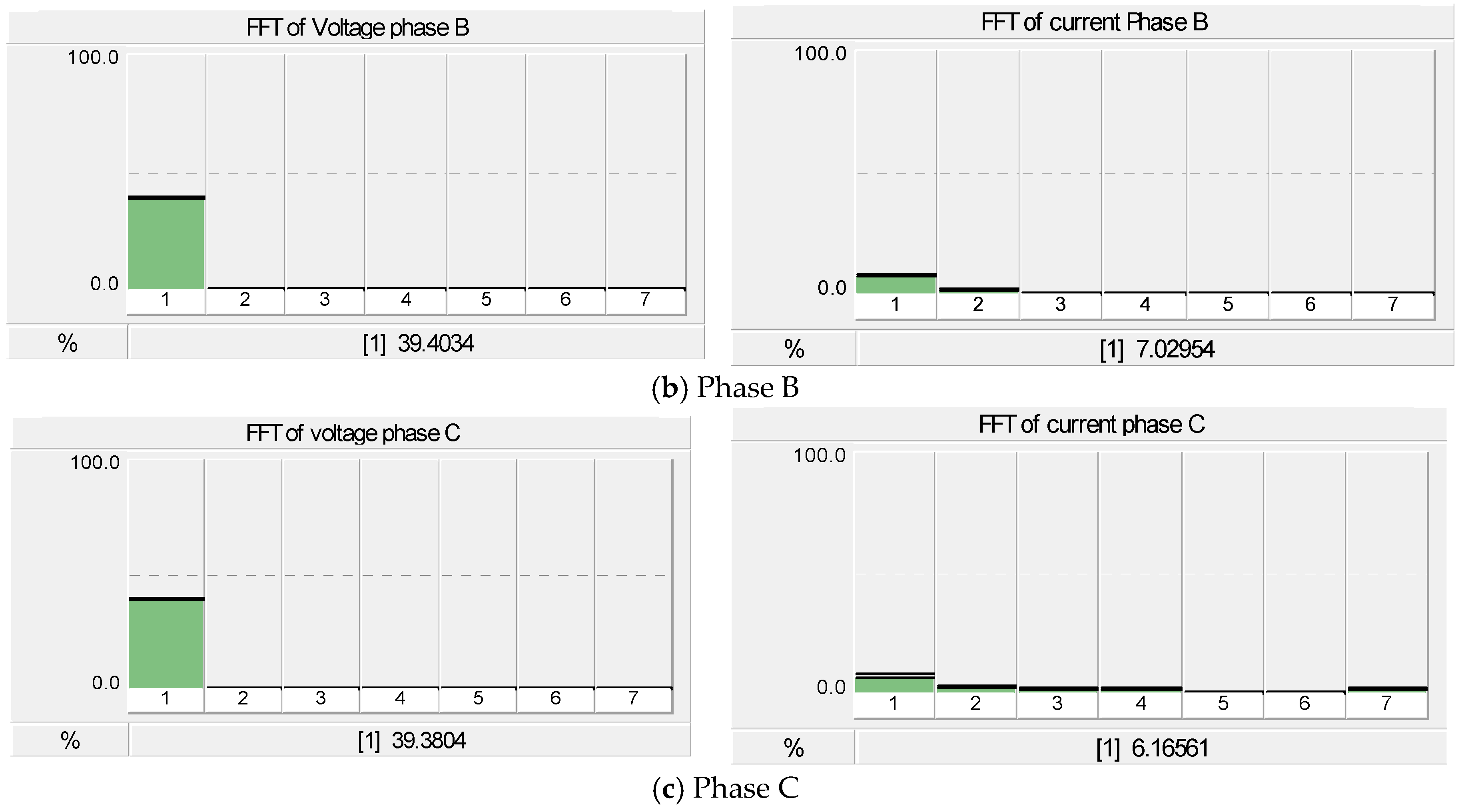
4.1. Case I: The Ferroresonance Effect on the 500 kVA and 1 MVA Transformer with Condos, Suburban and Town House Loads
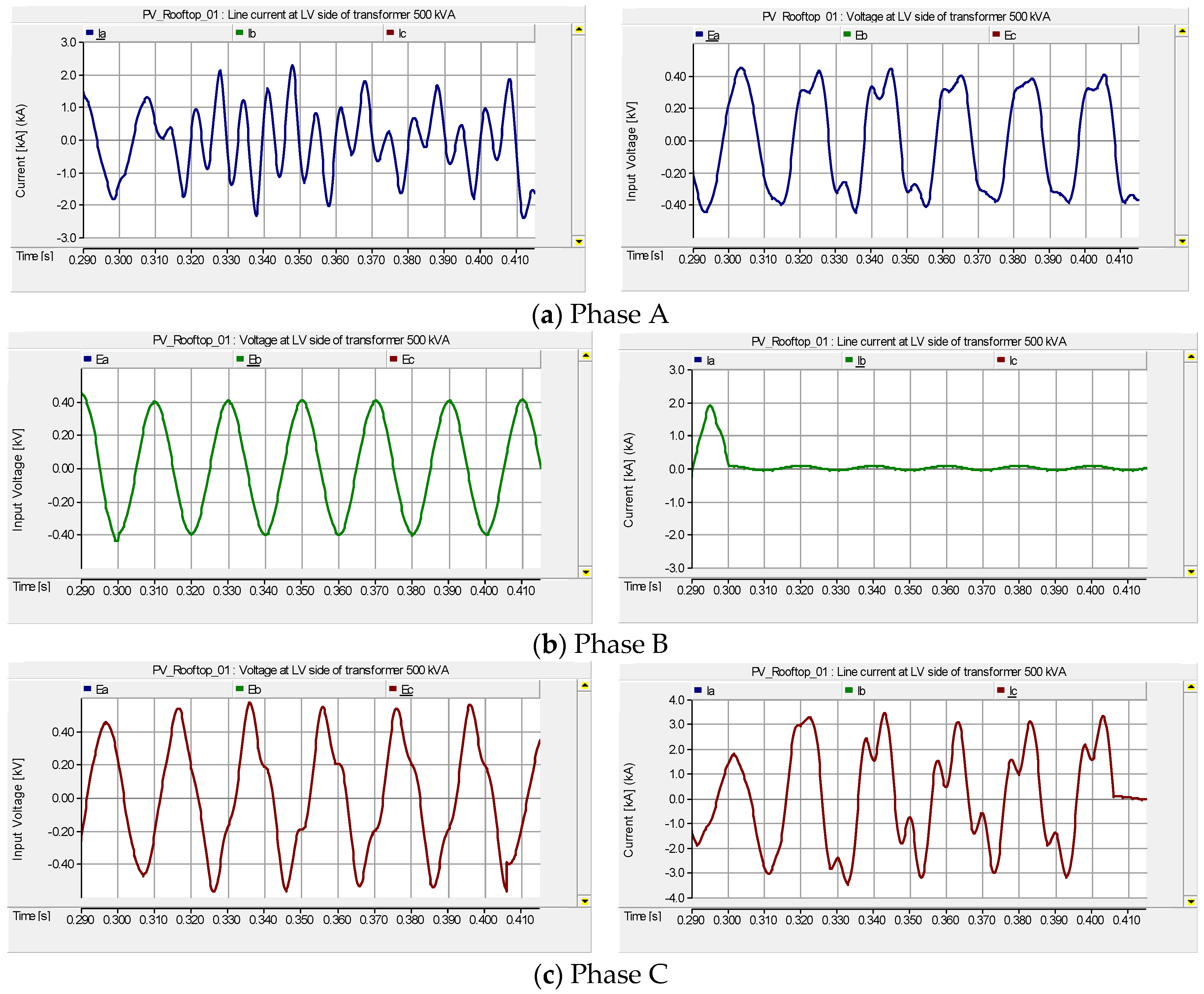
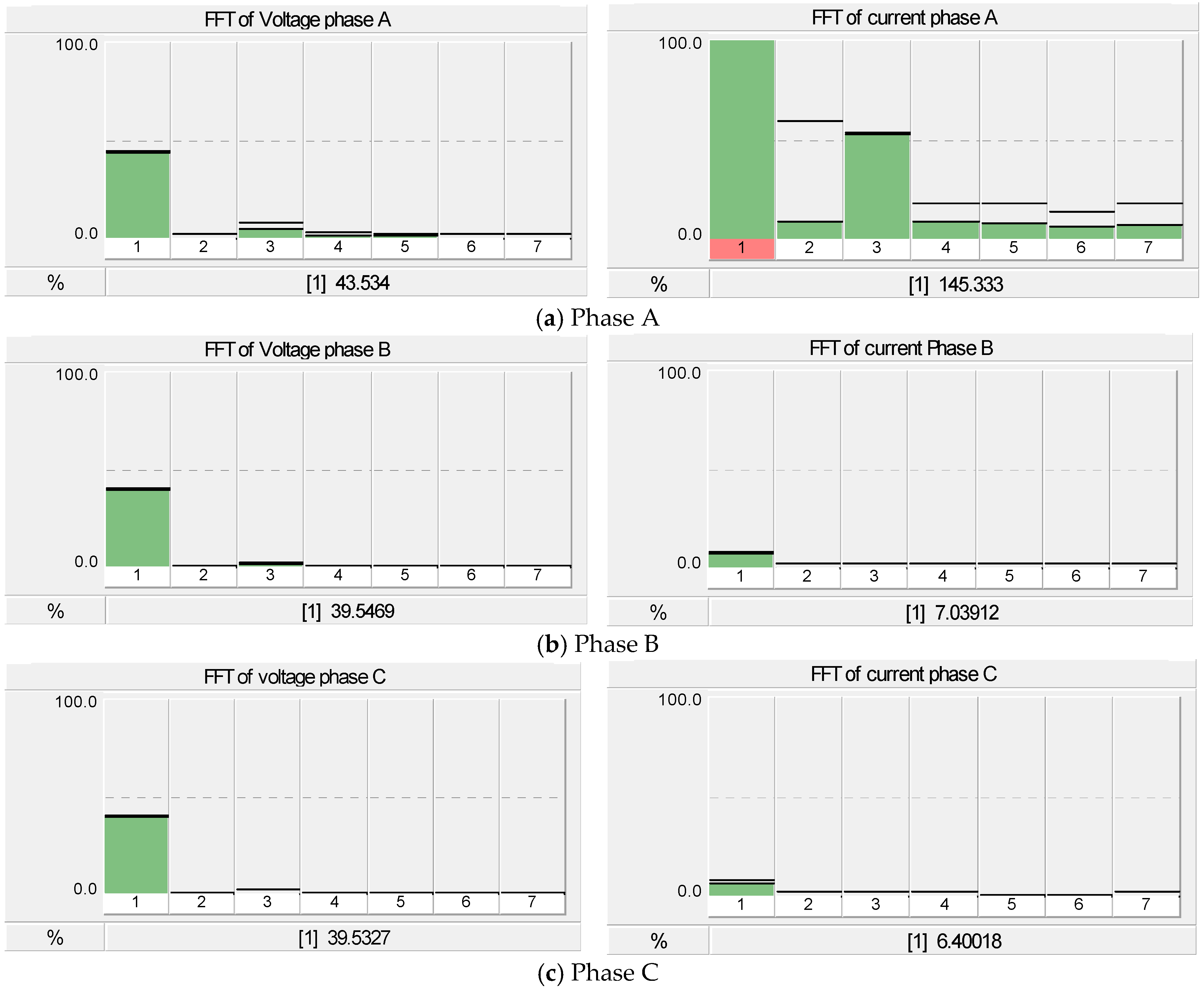
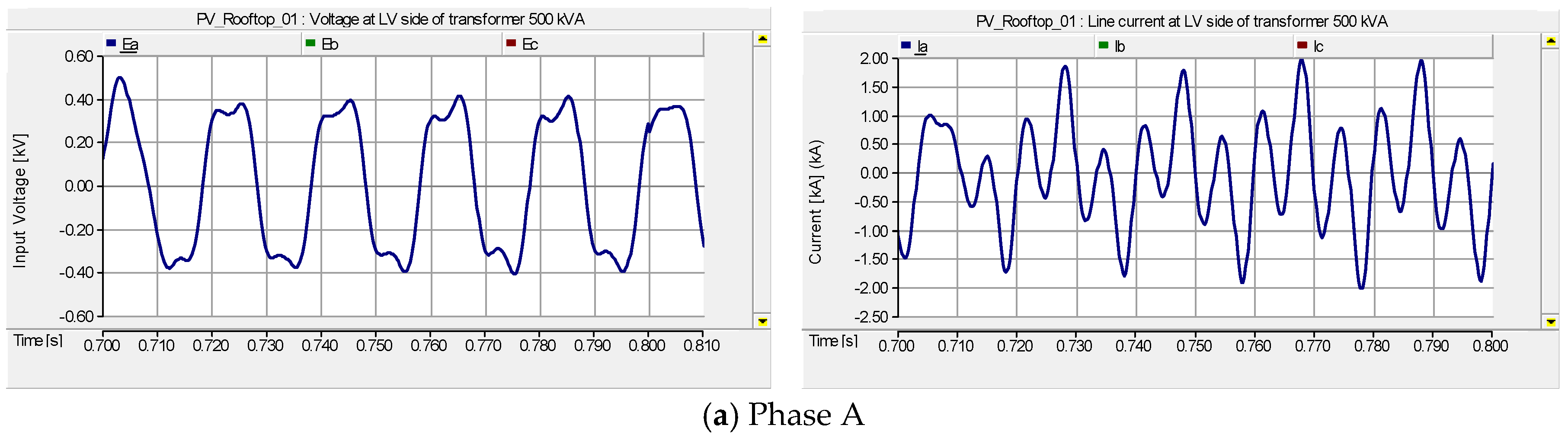
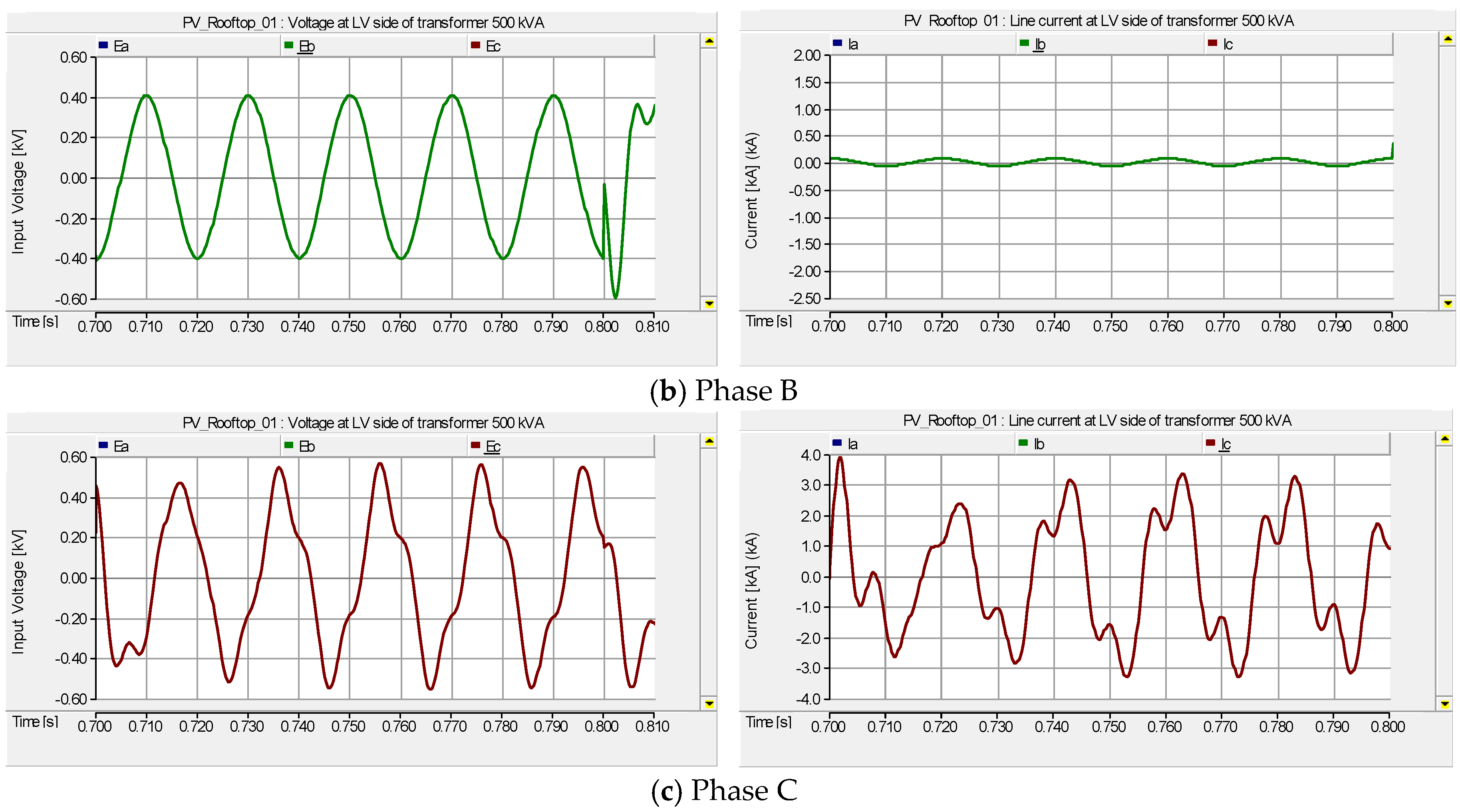
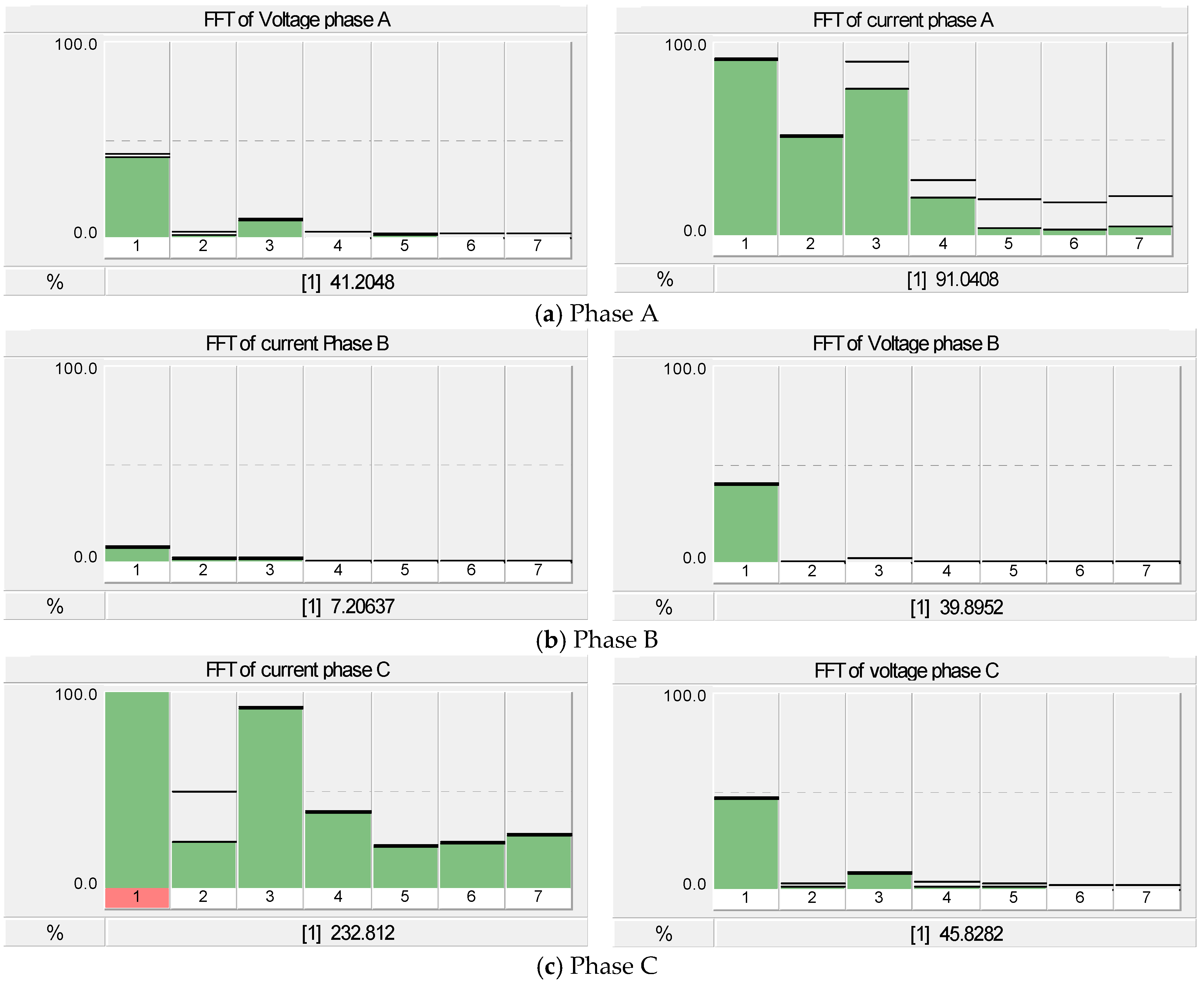
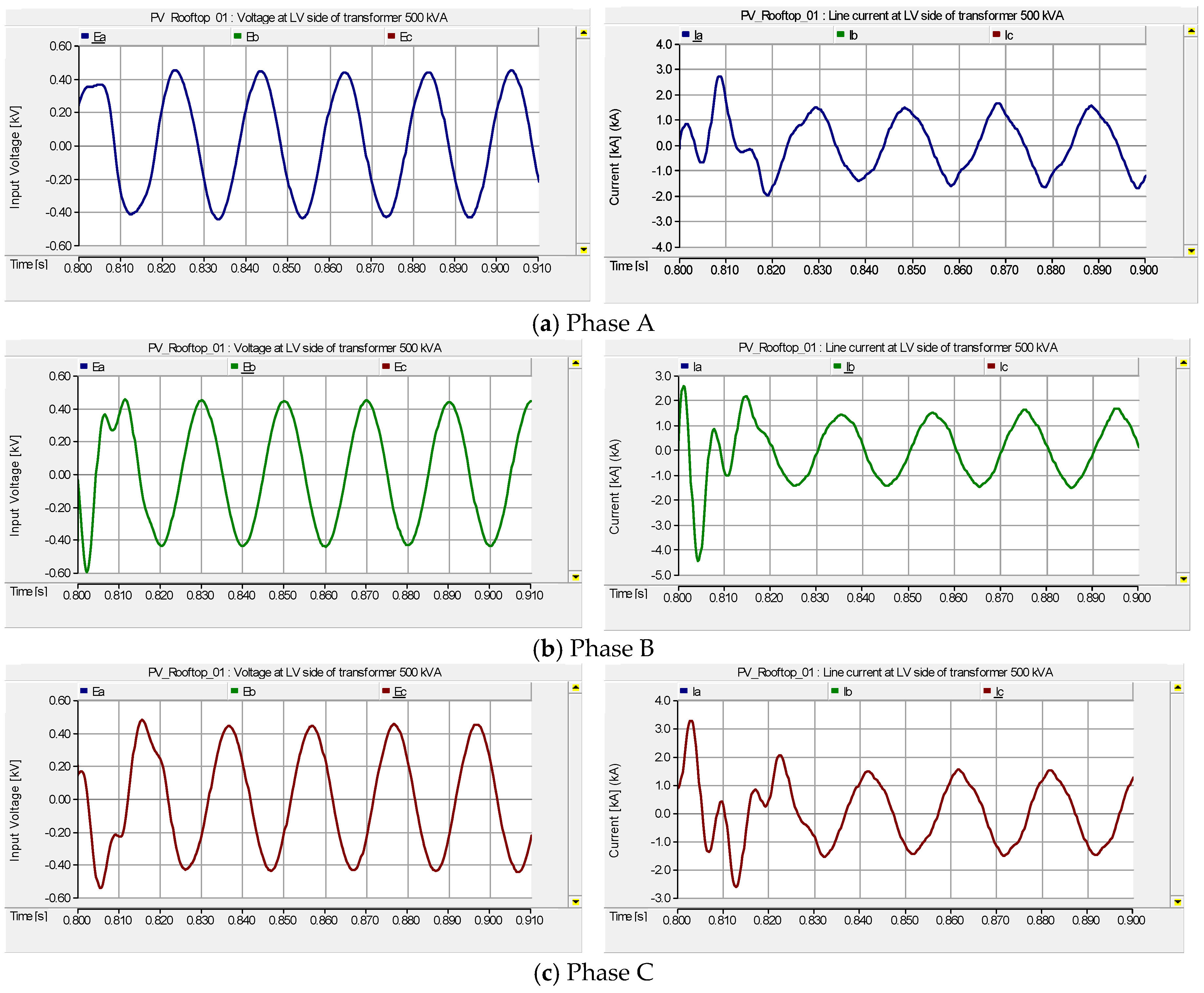
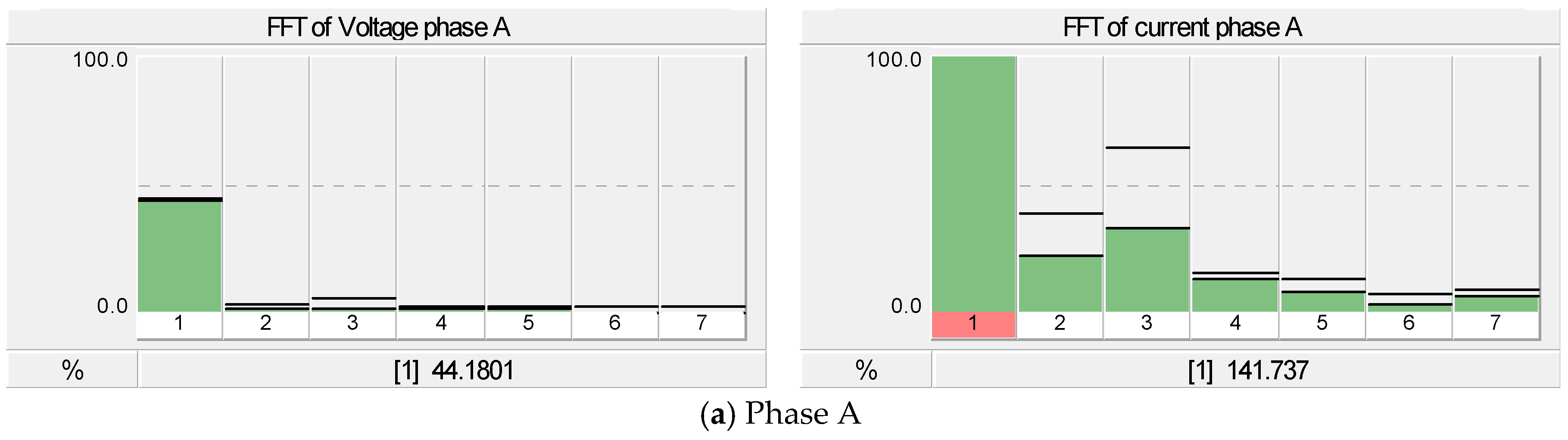
4.2. Case II: The Ferroresonance Effect on the 500 kVA Transformer LV Side with Suburban Home Load and the Total 500 kW Installation Capacity of PV Rooftop Systems
4.3. Case III: The Effect of Ferroresonance When Increasing the Capacity of PV Rooftop Systems from 1 kW to 500 kW
- (1)
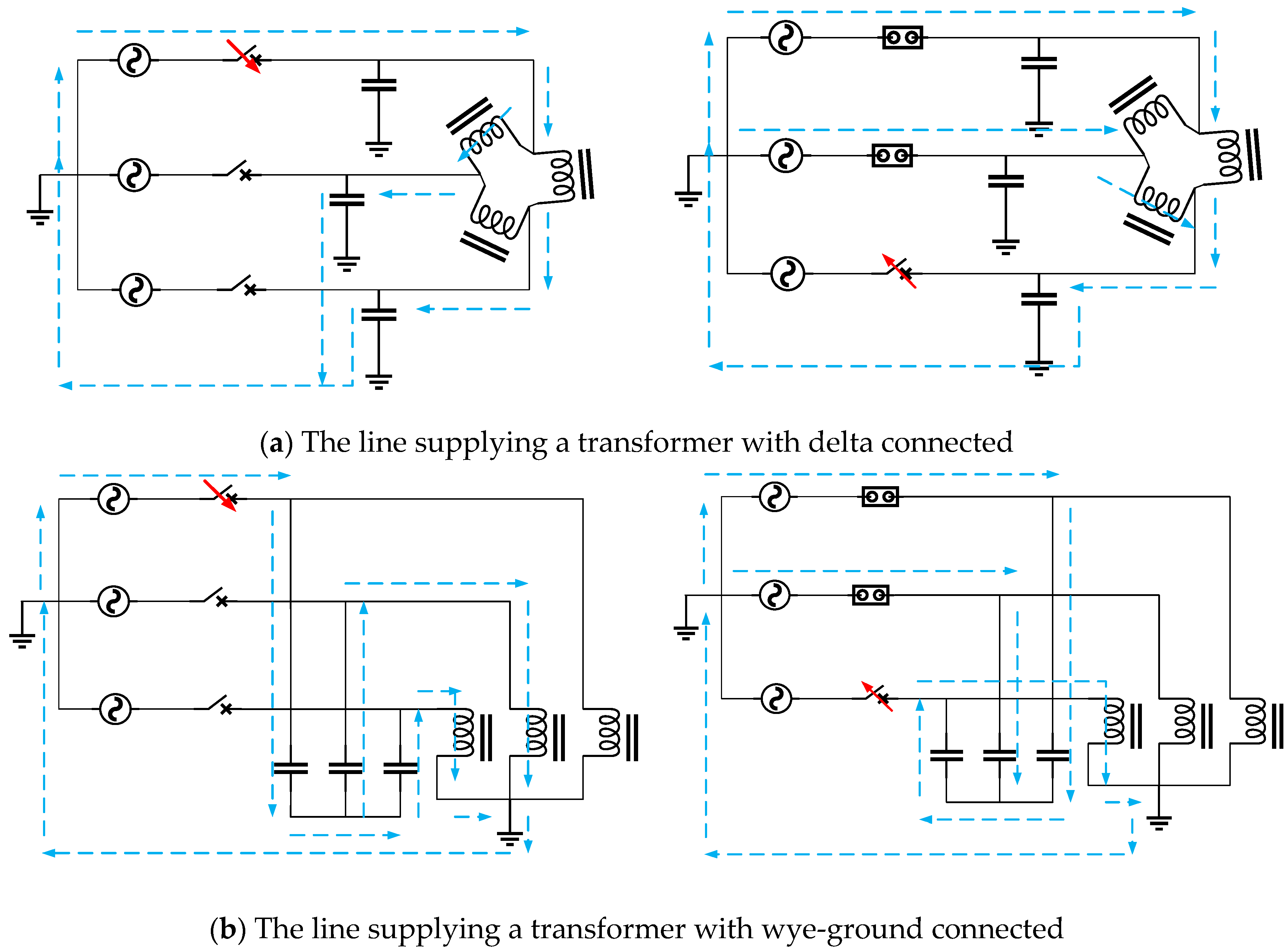
- The effect of the underground cable and distribution transformer configuration.
- (2)
- The effect of magnetizing the core saturation from the distribution transformer used for the voltage divider.
- (3)
- The effect of the supply voltage to a transformer primary winding that is connected to a ground or neutral separated wye or delta connection.
- (4)
- The effect of the increase of the voltage source in the system which, in this case, is the PV rooftop system on the LV side.
- Lowering the value of the capacitance between the circuit breaker and transformer below its critical value by using, for example, a circuit breaker cubicle closer to the transformer or placing circuit breakers just upstream of the transformers and closing them only when the voltage has been restored to all three-phases.
- Avoiding use of the transformers delivering an active power which is lower by 10% than its rated apparent power.
- Avoiding no-load energizing.
- Prohibiting single-phase operations or fuse protection, blowing of which results in single-pole breaking.
- Prohibiting live work on a cable-transformer assembly when the cable length exceeds a certain critical length.
- Resistance-earthing of the neutral of the supply substation.
- Solidly earthing the neutral (permanently or only during energizing and de-energizing operations) of a transformer whose primary is wye-connected (available neutral).
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wareing, J.B.; Perrot, F. Ferroresonance Overvoltages in Distribution Networks. In Proceedings of the IEE Colloquium on Warning! Ferroresonance Can Damage Your Plant (Digest No: 1997/349), Glasgow, UK, 12 November 1997; pp. 5/1–5/7. [Google Scholar]
- Walling, R.A. Ferroresonance in Low-Loss Distribution Transformers. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting, Toronto, ON, Canada, 13–17 July 2003; Volume 2, p. 1222. [Google Scholar]
- Dugan, R.C. Examples of ferroresonance in distribution. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting, Toronto, ON, Canada, 13–17 July 2003; Volume 2, p. 1215. [Google Scholar]
- Dolan, E.J.; Gillies, D.A.; Kimbark, E.W. Ferroresonance in a transformer switched with an EVH line. IEEE Trans. Power Appar. Syst. 1972, PAS-91, 1273–1280. [Google Scholar] [CrossRef]
- Emin, Z.; Zahawi, B.A.T.A.; Auckland, D.W.; Tong, Y.K. Ferroresonance in Electromagnetic Voltage Transformers: A Study Based on Nonlinear Dynamics. IEE Proc. Gener. Transm. Distrib. 1997, 144, 383–387. [Google Scholar] [CrossRef]
- Radmanesh, H.; Abassi, A.; Rostami, M. Analysis of Ferroresonance Phenomena in Power Transformers Including Neutral Resistance Effect. In Proceedings of the IEEE Southeastcon 2009, Atlanta, GA, USA, 5–8 March 2009. [Google Scholar]
- Radmanesh, H.; Gharehpetian, G.B.; Fathi, H. Ferroresonance of Power Transformers Considering Non-linear Core Losses and Metal Oxide Surge Arrester Effects. Electr. Power Compon. Syst. 2012, 40, 463–479. [Google Scholar] [CrossRef]
- Corea-Araujo, J.A.; Barrado-Rodrigo, J.A.; Gonzalez-Molina, F.; Guasch-Pesquer, L. Ferroresonance Analysis on Power Transformers Interconnected to Self-Excited Induction Generators. Electr. Power Compon. Syst. 2016, 44, 359–368. [Google Scholar] [CrossRef]
- Iravani, M.R.; Chaudhary, A.K.S.; Giesbrecht, W.J.; Hassan, I.E.; Keri, A.J.F.; Lee, K.C.; Martinez, J.A.; Morched, A.S.; Mork, B.A.; Parniani, M.; et al. Modeling and analysis guidelines for slow transients. III. The study of ferroresonance. IEEE Trans. Power Deliv. 2000, 15, 255–265. [Google Scholar] [CrossRef]
- Sakarung, P.; Chatratana, S. Application of PSCAD/EMTDC and Chaos Theory to Power System Ferroresonance Analysis. In Proceedings of the International Conference on Power Systems Transients (IPST’05), Montreal, QC, Canada, 19–23 June 2005. Paper No. IPST05-227. [Google Scholar]
- Hernández, J.C.; de la Cruz, J.; Vidal, P.G.; Ogayar, B. Conflicts in the distribution network protection in the presence of large photovoltaic plants: The case of ENDESA. Int. Trans. Electr. Energy Syst. 2013, 23, 669–688. [Google Scholar] [CrossRef]
- Batora, B.; Toman, P. Using of PSCAD software for simulation Ferroresonance Phenomenon in Power system with the three-phase power transformer. Trans. Electr. Eng. 2013, 2, 102–105. [Google Scholar]
- Gonen, T. Electric Power Distribution System Engineering; MaGraw-Hill College Div.: New York, NY, USA, 1985; Volume I. [Google Scholar]
- Buigues, G.; Zamora, I.; Valverde, V.; Mazón, Á. Ferroresonance in three-phase Power Distribution Transformer: Sources, Con sequences and Prevention. In Proceedings of the 19th International Conference on Electricity Distribution, Vienna, Austria, 21–24 May 2007. [Google Scholar]
- Jacobson, D.A.N. Examples of Ferroresonance in a High Voltage Power System. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting, Toronto, ON, Canada, 13–17 July 2003; pp. 1206–1212. [Google Scholar]
- Daily Report. Available online: http://thanyaratthaicenter.com/2017/03/30/ (accessed on 6 June 2017).
- Chaianong, A.; Pharino, C. Outlook and challenges for promoting solar photovoltaic rooftops in Thailand. Renew. Sustain. Energy Rev. 2015, 48, 359–372. [Google Scholar] [CrossRef]
- Energy Policy and Planning Office. IPP, SPP and VSPP Status; Energy Statistic; Energy Policy and Planning Office, Ministry of Energy: Bangkok, Thailand, 2012. [Google Scholar]
- Thanomsat, N.; Plangklang, B. Ferroresonance phenomenon in PV system at LV side of three-phase power transformer using of PSCAD simulation. In Proceedings of the 13th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Mai, Thailand, 28 June–1 July 2016. [Google Scholar]
- Caamano, E.; Thornycroft, J.; de Moor, H.; Cobben, S.; Jantsch, M.; Erge, T.; Laukamp, H.; Suna, D.; Gaiddon, B. State of the Art on Dispersed PV Power Generation: Impact of PV Distributed Generation and Electricity Networks; Intelligent Energy Europe: Brussels, Belgium, 2007. [Google Scholar]
- Papaioannou, I.T.; Bouhouras, A.S.; Marinopoulos, A.G.; Alexiadis, M.C.; Demoulias, C.S.; Labridis, D.P. Harmonic impact of small photovoltaic systems connected to the LV distribution network. In Proceedings of the 2008 5th International Conference on the European Electricity Market, Lisboa, Portugal, 28–30 May 2008; pp. 1–6. [Google Scholar]
- Busrah, A.M.; Ramachandaramurthy, V.K. The Impact of grid connected photovoltaic gereration system to voltage rise in low voltage network. In Proceedings of the 3rd International Conference on Development, Energy, Environment and Economic (DEEE’12), Paris, France, 2–4 December 2012. [Google Scholar]
- Grady, W.M.; Santoso, S. Understanding power system harmonics. IEEE Power Eng. Rev. 2001, 21, 8–11. [Google Scholar] [CrossRef]
- Schlabbach, J. Harmonic current emission of photovoltaic installations under system conditions. In Proceedings of the 2008 5th International Conference on the European Electricity Market, Lisboa, Portugal, 28–30 May 2008; pp. 1–5. [Google Scholar]
- Batrinu, F.; Chicco, G.; Schlabbach, J.; Spertino, F. Impacts of grid-connected photovoltaic plant operation on the harmonic distortion. In Proceedings of the 2006 IEEE Mediterranean Electrotechnical Conference (MELECON), Malaga, Spain, 16–19 May 2006; pp. 861–864. [Google Scholar]
- Menti, A.; Zacharias, T.; Milias-Argitis, J. Harmonic distortion assessment for a single-phase grid-connected photovoltaic system. Renew. Energy 2011, 36, 360–368. [Google Scholar] [CrossRef]
- Chicco, G.; Schlabbach, J.; Spertino, F. Characterisation and assessment of the harmonic emission of grid-connected photovoltaic systems. In Proceedings of the 2005 IEEE Russia Power Tech, St. Petersburg, Russia, 27–30 June 2005; pp. 1–7. [Google Scholar]
- McNeil, B.W.; Mirza, M.A. Estimated power quality for line commutated photovoltaic residential system. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 3288–3295. [Google Scholar] [CrossRef]
- Di Manno, M.; Varilone, P.; Verde, P.; de Santis, M.; di Perna, C.; Salemme, M. User friendly smart distributed measurement system for monitoring and assessing the electrical power quality. In Proceedings of the AEIT International Annual Conference (AEIT), Naples, Italy, 14–16 October 2015. [Google Scholar]
- Ang, S.P. Erroresonance Simulation Studies of Transmission Systems. Ph.D. Thesis, The University of Manchester, Manchester, UK, 2010. [Google Scholar]
- Marti, J.R.; Soudack, A.C. Ferroresonance in power systems: Fundamental solutions. IEE Proc. C Gener. Transm. Distrib. 1991, 138, 321–329. [Google Scholar] [CrossRef]
- Jacobson, D.A.N. Field Testing, Modelling and Analysis of Ferroresonance in a High Voltage Power System. Ph.D. Thesis, The University of Manitoba, Winnipeg, MB, Canada, August 2000. [Google Scholar]
- Valverde, V.; Mazón, A.J.; Zamora, I.; Buigues, G. Ferroresonance in Voltage Transformers: Analysis and Simulations. Renew. Energy Power Qual. J. 2007, 1, 465–471. [Google Scholar] [CrossRef]









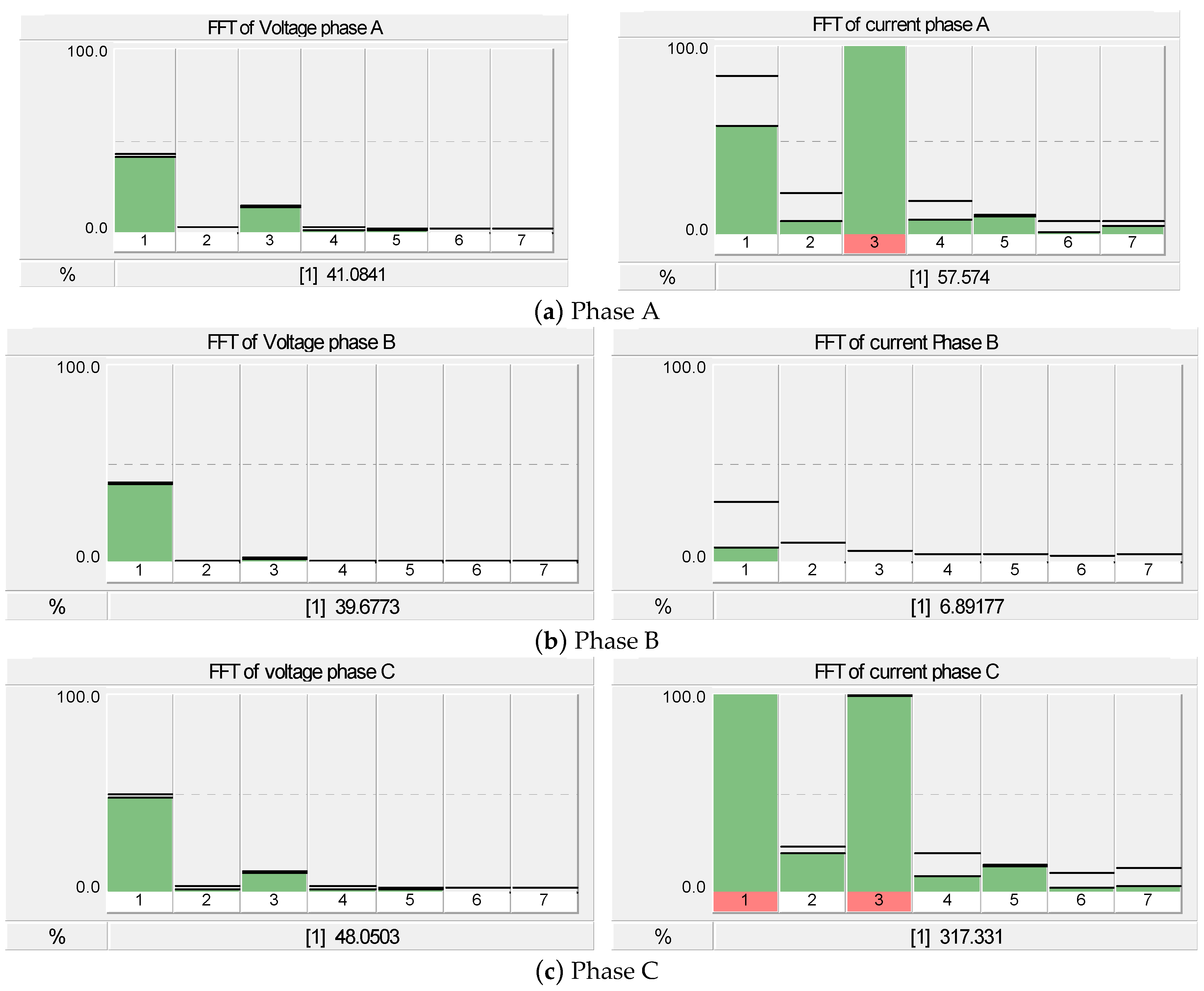
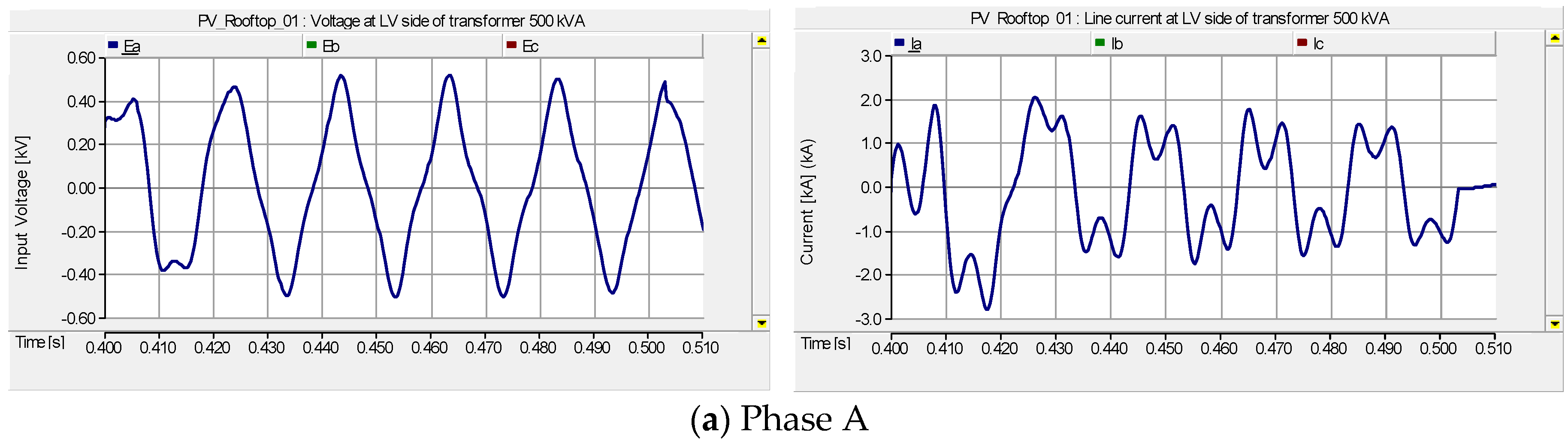
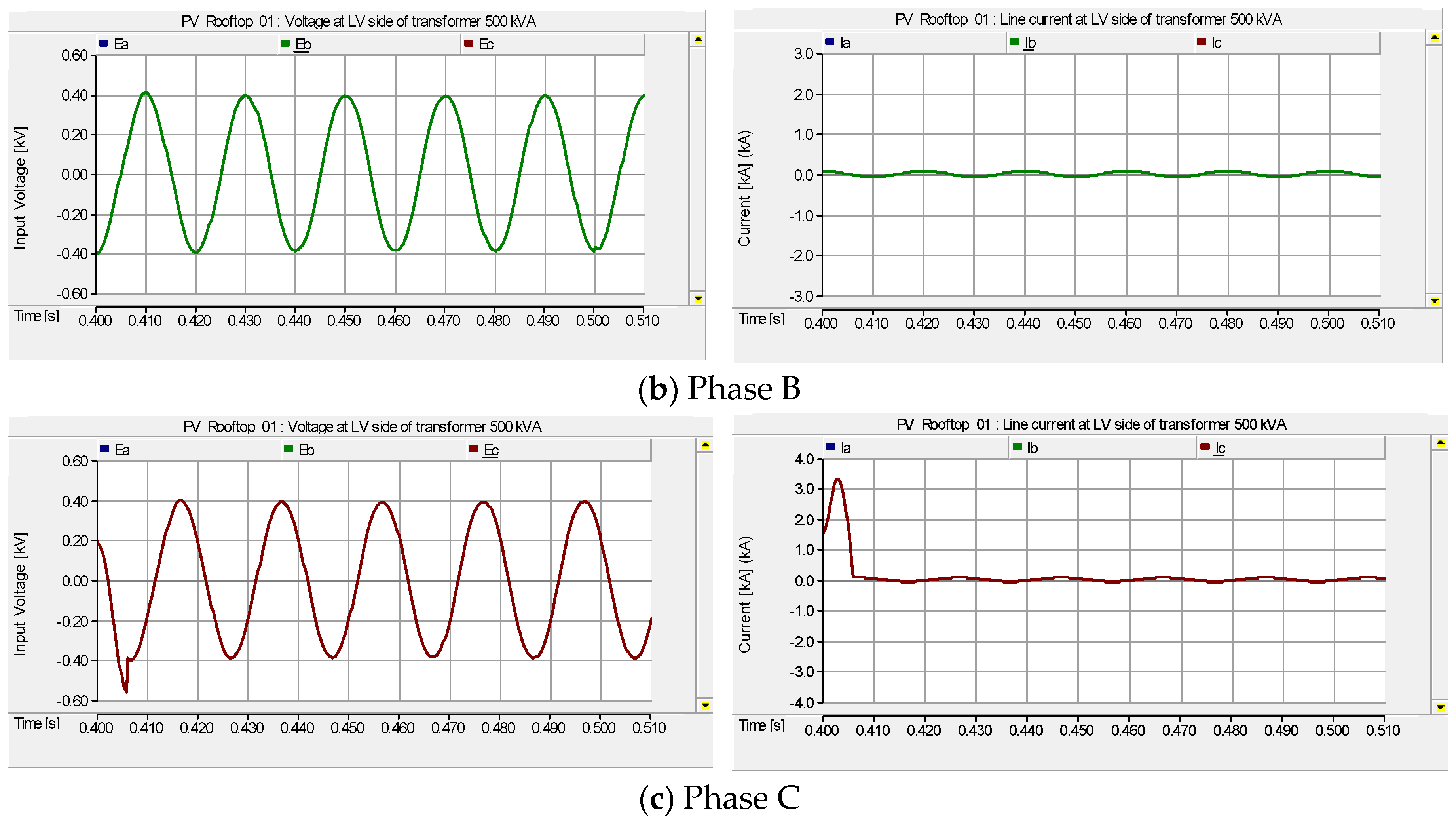

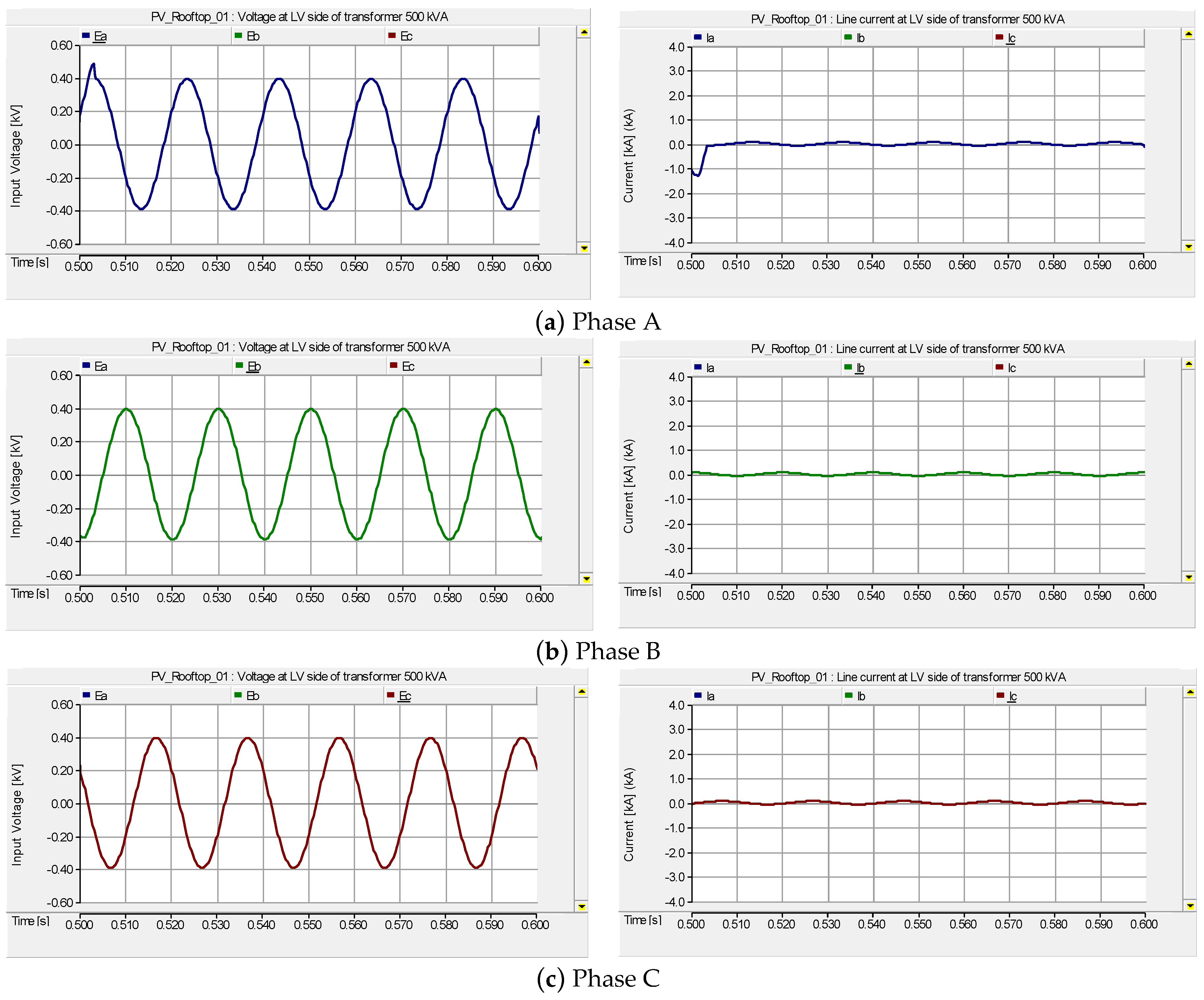


| Name | Parameter | Value |
|---|---|---|
| Vgrid | Base MVA (3 phase) | 10 MVA |
| Base voltage (L-L, RMS) | 32 kV | |
| Base frequency | 50 Hz | |
| Cable 1 | Steady-state frequency | 50 Hz |
| Segment length | 20 km | |
| Cable 2 | Steady-state frequency | 50 Hz |
| Segment length | 20 km | |
| T1 | Transformer MVA | 500 kVA |
| Primary voltage | 22 kV | |
| Secondary voltage | 0.4 kV | |
| Type: Delta-Wye ground | ||
| Base operation frequency | 50 Hz | |
| T2 | Transformer MVA | 1 MVA |
| Primary voltage | 22 kV | |
| Secondary voltage | 0.4 kV | |
| Type: Delta-Wye ground | ||
| Base operation frequency | 50 Hz | |
| Load 1 | Customer Load 1 | 0.01 MW + 0.005 MVAR per phase |
| Load 2 | Customer Load 2 | 0.01 MW + 0.005 MVAR per phase |
| Name | Parameter | Value |
|---|---|---|
| PV module data | Ref. irradiance | 1000 W/m2 |
| Ref. Temperature | 25 °C | |
| Effective area per cell | 0.01 m2 | |
| Series resistance per cell | 0.02 | |
| Shunt resistance per cell | 1000 | |
| Diode ideality factor | 1.5 | |
| Band gap energy | 1.103 eV | |
| Saturation current at reference conditions per cell | 1 × 10−12 kA | |
| Short circuit current at the ref. conditions per cell | 0.0025 kA | |
| Temperature Coefficient of photocurrent | 0.001 A/K | |
| Coupled PI Section | Line Rated Frequency | 50 Hz |
| Line Length | 0.2 km | |
| T3 | Transformer MVA | 500 kVA |
| Primary voltage | 0.4 kV | |
| Secondary voltage | 22 kV | |
| Type: Wye ground—Delta | ||
| Base operation frequency | 50 Hz | |
| Load 3 | Customer Load 3 | 0.01 MW per phase |
| PV Install Capacity (kW) | Vmax (kV, L-L) at Terminal Point of Transformer | Imax (kA) at Terminal Point of Transformer | Vload Max. (kV, L-L) | Iload Max. (kA) | Max. HD of Voltage (%) | Ferroresonance Phenomena |
|---|---|---|---|---|---|---|
| 1 | 0.578 | 3.476 | 0.566 | 0.098 | 27.8 | Y |
| 2 | 0.578 | 3.665 | 0.576 | 0.100 | 31.4 | Y |
| 3 | 0.580 | 3.739 | 0.577 | 0.100 | 33.2 | Y |
| 4 | 0.580 | 3.741 | 0.577 | 0.100 | 33.2 | Y |
| 5 | 0.580 | 3.742 | 0.581 | 0.100 | 33.2 | Y |
| 6 | 0.580 | 3.743 | 0.577 | 0.100 | 34.1 | Y |
| 7 | 0.580 | 3.746 | 0.577 | 0.100 | 33.1 | Y |
| 8 | 0.580 | 3.748 | 0.577 | 0.100 | 33.1 | Y |
| 9 | 0.580 | 3.753 | 0.577 | 0.100 | 33.1 | Y |
| 10 | 0.580 | 3.758 | 0.577 | 0.100 | 33.1 | Y |
| 20 | 0.603 | 3.986 | 0.601 | 0.104 | 32.8 | Y |
| 30 | 0.612 | 4.103 | 0.609 | 0.106 | 32.5 | Y |
| 40 | 0.619 | 4.132 | 0.617 | 0.107 | 33.3 | Y |
| 50 | 0.639 | 4.274 | 0.638 | 0.111 | 33.2 | Y |
| 60 | 0.659 | 4.366 | 0.658 | 0.114 | 32.6 | Y |
| 70 | 0.660 | 4.374 | 0.658 | 0.114 | 31.8 | Y |
| 80 | 0.660 | 4.383 | 0.658 | 0.114 | 33.9 | Y |
| 90 | 0.668 | 4.524 | 0.668 | 0.116 | 34.2 | Y |
| 100 | 0.690 | 4.728 | 0.688 | 0.119 | 34.7 | Y |
| 200 | 0.640 | 4.279 | 0.639 | 0.111 | 31.7 | Y |
| 300 | 0.677 | 4.507 | 0.674 | 0.117 | 35.1 | Y |
| 400 | 0.698 | 4.647 | 0.696 | 0.121 | 36.3 | Y |
| 500 | 0.716 | 5.302 | 0.715 | 0.124 | 37.8 | Y |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thanomsat, N.; Plangklang, B.; Ohgaki, H. Analysis of Ferroresonance Phenomenon in 22 kV Distribution System with a Photovoltaic Source by PSCAD/EMTDC. Energies 2018, 11, 1742. https://doi.org/10.3390/en11071742
Thanomsat N, Plangklang B, Ohgaki H. Analysis of Ferroresonance Phenomenon in 22 kV Distribution System with a Photovoltaic Source by PSCAD/EMTDC. Energies. 2018; 11(7):1742. https://doi.org/10.3390/en11071742
Chicago/Turabian StyleThanomsat, Nattapan, Boonyang Plangklang, and Hideaki Ohgaki. 2018. "Analysis of Ferroresonance Phenomenon in 22 kV Distribution System with a Photovoltaic Source by PSCAD/EMTDC" Energies 11, no. 7: 1742. https://doi.org/10.3390/en11071742
APA StyleThanomsat, N., Plangklang, B., & Ohgaki, H. (2018). Analysis of Ferroresonance Phenomenon in 22 kV Distribution System with a Photovoltaic Source by PSCAD/EMTDC. Energies, 11(7), 1742. https://doi.org/10.3390/en11071742







