Mathematical Thermal Modelling of a Direct-Expansion Solar-Assisted Heat Pump Using Multi-Objective Optimization Based on the Energy Demand
Abstract
:1. Introduction
1.1. Analysis of the Solar Collectors
1.2. Design of the Thermal Storage Unit
1.3. Experimental Validations and Reviews
1.4. Alternative DXSAHP Designs
1.5. DXSAHP Modelling and Simulations
1.6. Scope
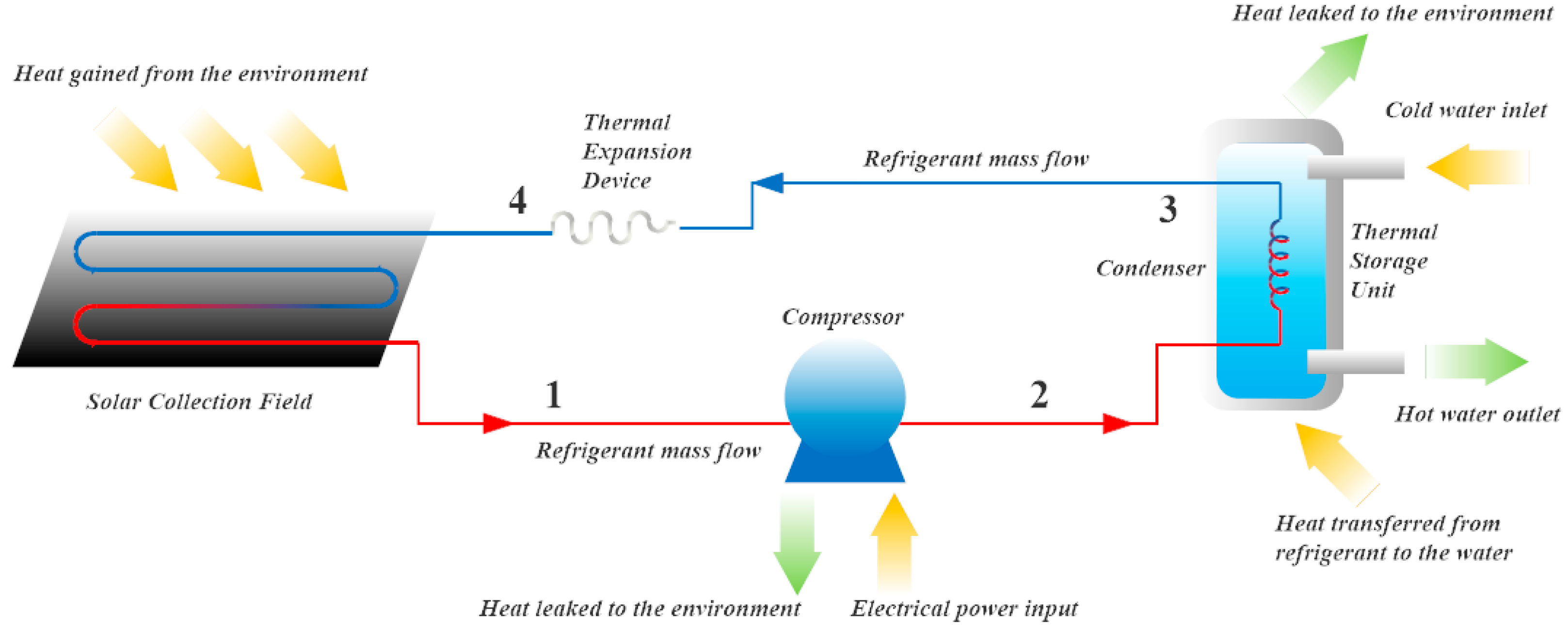
2. Model Development and Structure
- A reciprocating hermetic compressor.
- A flat-plate bare solar collector, which also acts as an evaporator absorbing heat from the environment, with a capillary tube as an expansion device.
- An immersed helical coil heat exchanger, which condenses the working fluid as it transfers the heat gained from the collectors to the final product.
2.1. Modelling and Methodology
2.1.1. Total Heat Collection Model
2.1.2. Thermodynamic Cycle Model
2.1.3. Thermal Storage Capacity Model
3. Results
3.1. Performance on Characteristic Days
3.2. Seasonal Performance
3.3. Continuous Operation
3.4. Model Overview
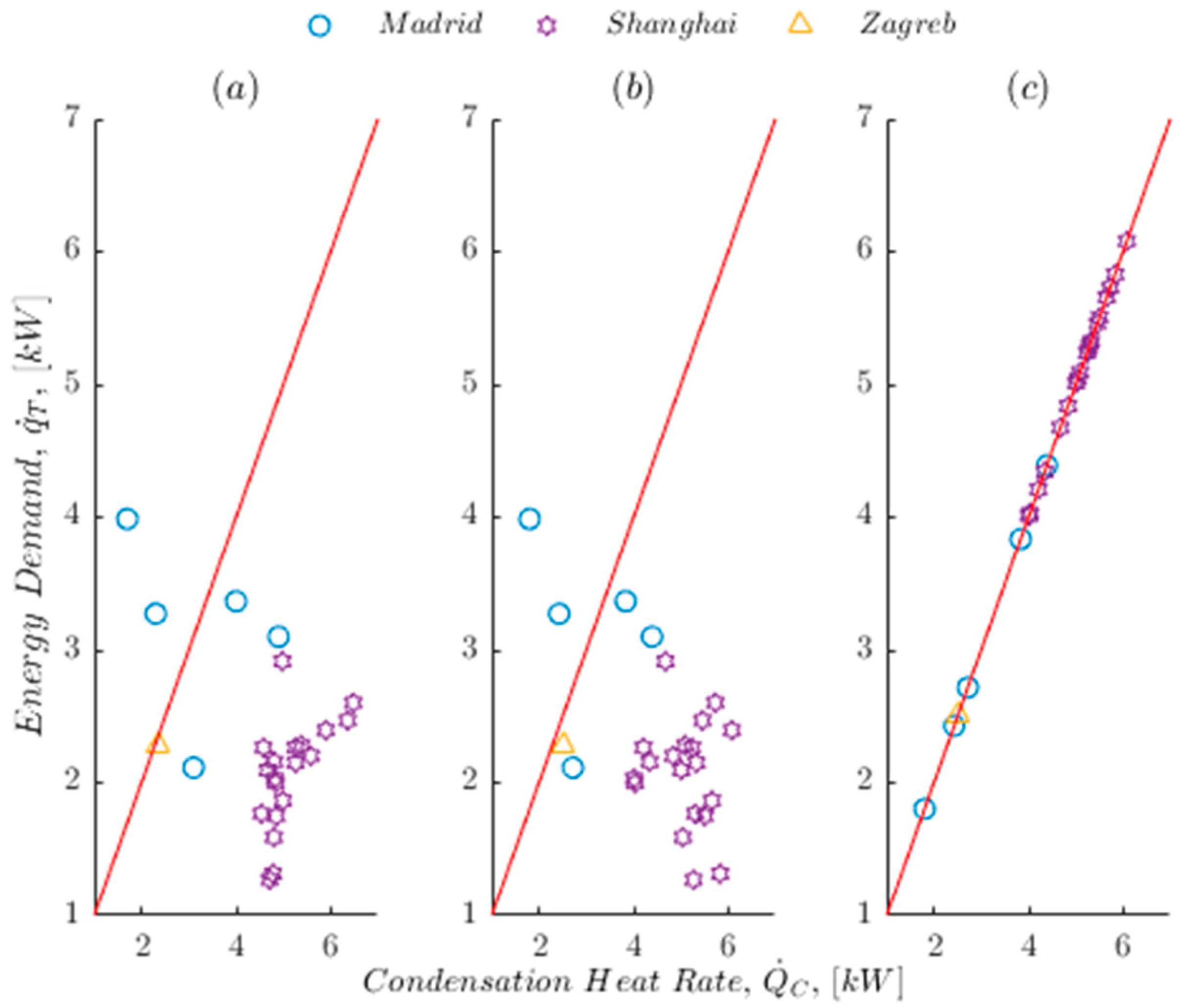
3.5. Statistical Analysis
3.6. Considerations Regarding the Thermal Capacity of the Heat Pump
3.7. Optimization Implementation
4. Conclusions
- The temperature difference in both heat exchangers, and , which needs to be adjusted depending on the specific regional weather conditions as well as for the time of the day the heat pump is working, lowering said temperature gradients considerably during nighttime operation or non-radiation conditions.
- The global efficiency of the compressor, , which drops almost by half during cold nights given the fact that more collectors are needed to achieve the desired outlet temperature which consequentially increases the power input and the heat leaked during the compression stage.
- The shape factor, , which compensates the magnitude of the area of the solar collection field given the fact that the collectors are modelled as a thin layer of fluid between two flat plates, instead of a pipe embedded in a flat plate.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| collector area, m2 | |
| anisotropic index | |
| specific heat, kJ/kg·°C | |
| solar radiation heat flux, kW/m2 | |
| hypothesis | |
| specific enthalpy, kJ/kg | |
| convection heat transfer coefficient, kW/m2·°C | |
| characteristic length, m | |
| thermal conductivity, kW/m·°C | |
| mass flow, kg/s | |
| mass of water, kg | |
| rotational speed, rpm | |
| pressure, kPa | |
| heat transfer rate, kW | |
| energy demand, kW | |
| thermal resistance, °C/kW | |
| tilt factor | |
| relative humidity | |
| radius, m | |
| entropy, kJ/kg·°C | |
| temperature, °C | |
| speed, m/s | |
| volumetric displacement, m3/s | |
| volume, m3 | |
| electrical power input to compressor, kW | |
| Greek letters | |
| significance level | |
| inclination of the flat plate, ° | |
| temperature gradient, °C | |
| work time, s | |
| emissivity of sky | |
| efficiency | |
| incidence angle, ° | |
| mean | |
| density, kg/m3 | |
| standard deviation | |
| variance | |
| Stefan-Boltzmann coefficient, kW/m2·K4 | |
| thermal capacity of the heat pump | |
| complementary altitude angle, ° | |
| shape factor | |
| Non-dimensional numbers | |
| Grashof number | |
| average Nusselt number | |
| Prandtl number | |
| Raleigh number | |
| Reynolds number | |
| Subscripts | |
| 0 | null |
| 1,2,3,4 | process, layer |
| ∞ | air/wind |
| a | alternate |
| atm | atmospheric |
| B | beam |
| C | condensation |
| C-SA | condensation under solar assistance |
| Comp | Compression |
| dp | dew point |
| D | diffuse |
| E | evaporation |
| E-SA | evaporation under solar assistance |
| ex | experiment |
| ext | exterior |
| h | convection |
| h, inf | convection upon the inferior surface |
| h, sup | convection upon the superior surface |
| h, t | total convection |
| i | inlet |
| ins | insulation |
| int | interior |
| L | leaked |
| m | model |
| n, inf | natural on the inferior surface |
| n, sup | natural on the superior surface |
| o | outlet |
| opt | optimum |
| os | outer space |
| ref | refrigerant |
| s | surface |
| SCF | solar collection field |
| T | total |
| V | volume of product |
| w | water |
| σ, t | total radiation |
| Acronyms | |
| confidence interval | |
| coefficient of performance | |
| direct expansion solar-assisted heat pump | |
| GA | genetic algorithm |
| HP | heat pump |
| null hypothesis significance test | |
| thermal storage unit | |
References
- Ibrahim, O.; Fardoun, F.; Younes, R.; Louahlia-Gualous, H. Review of Water Heating Systems: General Selection Approach Based on Energy and Environment Aspects. Build. Environ. 2014, 74, 259–286. [Google Scholar] [CrossRef]
- Sporn, P.; Ambrose, E.R. The Heat Pump and Solar Energy. In Proceedings of the World Symposium on Applied Solar Energy, Phoenix, AZ, USA, 1–5 November 1955. [Google Scholar]
- Chaturvedi, S.K.; Chiang, Y.F.; Roberts, A. Analysis of a Two-Phase Flow Solar Collectors with Application to Heat Pumps. ASME 1980, 104, 358–365. [Google Scholar] [CrossRef]
- Chaturvedi, S.K.; Shen, J.Y. Thermal Performance of a Direct Expansion Solar-Assisted Heat Pump. Sol. Energy 1984, 33, 155–162. [Google Scholar] [CrossRef]
- Chaturvedi, S.K.; Abazeri, M. Transient Simulation of a Capacity-Modulated Direct Expansion Solar-Assisted Heat Pump. Sol. Energy 1987, 39, 421–428. [Google Scholar] [CrossRef]
- Aziz, W.; Chaturvedi, S.K.; Kheireddine, A. Thermodynamic Analysis of Two-Component, Two-Phase Flow in Solar Collectors with Application to a Direct Expansion Solar-Assisted Heat Pump. Energy 1999, 24, 247–259. [Google Scholar] [CrossRef]
- Ito, S.; Miura, N.; Wang, K. Performance of a Heat Pump using Direct Expansion Solar Collectors. Sol. Energy 1999, 65, 189–196. [Google Scholar] [CrossRef]
- Tabatabaei, S.A.; Thilakarathne, D.J.; Treur, J. An Analytical Model for Mathematical Analysis of Smart Daily Energy Management for Air-to-Water Heat Pumps. Energy Procedia 2014, 50, 589–596. [Google Scholar] [CrossRef]
- Zhu, M.; Xie, H.; Zhang, B.; Guan, X. The Characteristics of the Evaporator/Collector for Direct Expansion Solar Assisted Heat Pump System. J. Power Energy Eng. 2013, 1, 73–76. [Google Scholar] [CrossRef]
- Kuang, Y.H.; Sumathy, K.; Wang, R.Z. Study on a Direct-Expansion Solar-Assisted Heat Pump. Int. J. Energy Res. 2003, 27, 531–548. [Google Scholar] [CrossRef]
- Anderson, T.N.; Morrison, G.L.; Behnia, M. Experimental Analysis of a Solar-Boosted Heat Pump Water Heater with Integral Condenser. In Proceedings of the 40th Annual Conference of the Australian and New Zealand Solar Energy Society, Newcastle, Australia, 27–29 November 2002. [Google Scholar]
- Hawlader, M.N.; Chou, S.K.; Ullah, M.Z. The Performance of a Solar Assisted Heat Pump Water Heating System. Appl. Therm. Eng. 2001, 21, 1049–1065. [Google Scholar] [CrossRef]
- Mei, V.C.; Baxter, V.D.; Lamb. Low Cost Heat Pump Water Heater (HPWH). In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 17–20 July 2006. [Google Scholar]
- Moreno-Rodríguez, A. Experimental Validation of a Theoretical Model for a Direct Expansion Solar-Assisted Heat Pump Applied to Heating. Energy 2013, 60, 242–253. [Google Scholar] [CrossRef]
- Soldo, V.; Curko, T.; Balen, I. Thermal Performance of a Direct Expansion Solar-Assisted Heat Pump. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 12–15 July 2004. [Google Scholar]
- Tagliafico, L.A.; Scarpa, F.; Valsuani, F. Direct Expansion Solar-Assisted Heat Pumps—A Clean Steady State Approach for Overall Performnace Analysis. Appl. Therm. Eng. 2014, 66, 216–226. [Google Scholar] [CrossRef]
- Omojaro, P.; Breitkopf, C. Direct Expansion Solar-Assisted Heat Pumps: A Review of Applications and Recent Research. Renew. Sustain. Energy Rev. 2013, 22, 33–45. [Google Scholar] [CrossRef]
- Chaturvedi, S.K.; Abdel-Salam, T.M.; Sreedharan, S.S.; Gorozabel, F.B. Two-Stage Direct Expansion Solar-Assisted Heat Pump for High Temperature Applications. Appl. Therm. Eng. 2009, 29, 2093–2099. [Google Scholar] [CrossRef]
- Cutic, T.; Pasanec, J.; Baleta, J.; Soldo, V.; Curko, T. Mobile Solar-Assisted Heat Pump with Direct Expansion. In Proceedings of the EuroSun 2012—ISES Europe Solar Conference, Rijeka, Croatia, 18–20 September 2012. [Google Scholar]
- Morrison, G.L. Simulation of Packaged Solar Heat Pump Water Heaters. Sol. Energy 1994, 53, 149–257. [Google Scholar] [CrossRef]
- Mehdaoui, F.; Hazami, M.; Naili, N.; Farhat, A. Energetic performances of an Optimized Passive Solar Heating Prototype used for Tunisian Buildings Air Heating Applications. Energy Convers. Manag. 2014, 87, 285–296. [Google Scholar] [CrossRef]
- Bridgeman, A.G. Experimental Analysis of an Indirect Solar Assisted Heat Pump for Domestic Water Heating. Ph.D. Thesis, Queen’s University, Kinsgton, ON, Canada, 2010. [Google Scholar]
- DeGrove, J.M. The Integration of Heat Resources in a Solar Thermal Heat Pump Hydronic System. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2015. [Google Scholar]
- Khalaf, K. Experimental Characterization and Modelling of a Heat Pump Water Heater. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2017. [Google Scholar]
- Fu, Y. Investigation of Solar Assisted Heat Pump System Integrated with High Rise Residential Building. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2014. [Google Scholar]
- Kamel, R.S. Combined Building Integrated Photovoltaic-Thermal Collector with Air Source Heat Pump for Cold Climate. Ph.D. Thesis, Ryerson University, Toronto, ON, Canada, 2015. [Google Scholar]
- Youssef, W.M.K.A. Experimental and Computational Study of Indirect Expansion Solar Assisted Heat Pump System with Latent Heat Storage for Domestic Hot Water Production. Ph.D. Thesis, Brunel University London, London, UK, 2017. [Google Scholar]
- Sterling, S.J.; Collins, M.R. Feasibility Analysis of a Heat Pump Assisted Solar Domestic Hot Water System; Department of Mechanical and Mechatronic Engineering of the University of Waterloo: Waterloo, ON, Canada, 2010. [Google Scholar]
- Li, H.; Yang, H. Study on Performance of Solar Assisted Air Source Heat Pump Systems for Hot Water Production in Hong Kong. Appl. Energy 2010, 87, 2818–2825. [Google Scholar] [CrossRef]
- Ҫağlar, A.; Yamali, C. Performance Analysis of a Solar Assisted Heat Pump with an Evacuated Tubular Collector for Domestic Heating. Energy Build. 2012, 54, 22–28. [Google Scholar]
- Kokila, R.N.; Rajakumar, S. Performance Evaluation of Solar Asisted Heat Pump Water Heating System. IOSR J. Eng. 2013, 3, 12–17. [Google Scholar]
- Gorozabel-Chata, F.B.; Chaturvedi, S.K.; Almogbel, A. Analysis of a Direct Expansion Solar Asisted Heat Pump using Different Refrigerants. Energy Convers. Manag. 2005, 46, 2614–2624. [Google Scholar] [CrossRef]
- Atmaca, I.; Kocak, S. Theoretical Energy and Exergy Analyses of Solar Assisted Heat Pump Sapce Heating System. Therm. Sci. 2014, 18, 417–427. [Google Scholar] [CrossRef]
- Torres-Reyes, E.; Cervantes de Gortari, J. Optimal Performance of an Irreversible Solar Assisted Heat Pump. Exergy Int. J. 2001, 1, 107–111. [Google Scholar] [CrossRef]
- Chyng, J.P.; Lee, C.P.; Huang, B.J. Performance Analysis of a Solar-Assisted Heat Pump Water Heater. Sol. Energy 2003, 74, 33–44. [Google Scholar] [CrossRef]
- Chow, T.T.; Pei, G.; Fong, K.F.; Lin, Z.; Chan, A.S.; He, M. Modeling and Application of Direct-Expansion Solar-Assisted Heat Pump for Water Heating in Subtropical Hong Kong. Appl. Energy 2010, 87, 643–649. [Google Scholar] [CrossRef]
- Sánta, R.; Garbai, L.; Fürstner, I. Optimization of a Heat Pump System. Energy 2015, 89, 45–54. [Google Scholar] [CrossRef]
- Guo, J.J.; Wu, J.Y.; Wang, R.Z.; Li, S. Experimental Research and Operation Optimization of an Air Source Heat Pump Water Heater. Appl. Energy 2011, 88, 4128–4138. [Google Scholar] [CrossRef]
- Khorasaninejad, E.; Hajabdollahi, H. Thermoeconomic and Environmental Optimization of Solar Assisted Heat Pump by Using Multi Objective Particle Swarm Algorithm. Energy 2014, 72, 680–690. [Google Scholar] [CrossRef]
- Rattner, A.; Bohren, J. Heat and Mass Correlations; School of Engineering and Applied Science of the University of Pennsylvania: Philadelphia, PA, USA, 2008. [Google Scholar]
- Hollands, K.G.T.; Unny, T.E.; Raithby, G.D.; Konicek, L. Free Convective Heat Transfer across Inclined Layers. ASME J. Heat Transf. 1976, 98, 189–193. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Free Convection. In Fundamentals of Heat and Mass Transfer; John Wiley & Sons: New York, NY, USA, 2011; pp. 593–652. [Google Scholar]
- Berdahl, P.; Fromberg, R. The Thermal Radiance of Clear Skies. Sol. Energy 1982, 29, 299–314. [Google Scholar] [CrossRef]
- Chen, B.; Kasher, J.; Maloney, J.; Girgis, G.A.; Clark, D. Determination of the Clear Sky Emissivity for Use in Cool Storage and Roof Pond Applications; Passive Solar Research Group of the University of Nebraska at Omaha: Omaha, NE, USA, 1995. [Google Scholar]
- Kalogirou, S. Environmental Characteristics. In Solar Energy Engineering: Processes and Systems; Elsevier Academic Press: Cambridge, MA, USA, 2013; pp. 49–119. [Google Scholar]
- Reindl, D.T.; Beckman, W.A.; Duffie, J.A. Diffuse Fraction Correlations. Sol. Energy 1990, 45, 1–7. [Google Scholar] [CrossRef]
- Reindl, D.T.; Beckman, W.A.; Duffie, J.A. Evaluation of Hourly Tilted Surface Radiation Models. Sol. Energy 1990, 45, 9–17. [Google Scholar] [CrossRef]
- Franco-Lijó, J.M. Evaporador. In Manual de Refrigeración; Reverté: Barcelona, Spain, 2006; pp. 103–127. [Google Scholar]
- Danfoss Manufacturing. Troubleshooting—Fault Location. In Fitters Notes: Hints and Tips for the Installer; Danfoss: Refrigeration and Air Conditioning Division: Nordberg, Denmark, 2006; pp. 155–203. [Google Scholar]
- F-Chart Software. EES: Engineering Equation Solver, version 10.298, F-Chart Software: Madison, WI, USA, 2017.
- Moreno-Rodríguez, A.; González-Gil, A.; Izquierdo, M.; García-Hernando, N. Theoretical Model and Experimental Vlidation of a Direct Expansion Solar-Assisted Heat Pump for Domestic Hot Water Applications. Energy 2012, 45, 704–715. [Google Scholar] [CrossRef]
- Li, Y.W.; Wang, R.Z.; Wu, J.Y.; Xu, Y.X. Experimental Performance Analysis on a Direct-Expansion Solar-Assisted Heat Pump Water Heater. Appl. Therm. Eng. 2007, 27, 2858–2868. [Google Scholar] [CrossRef]
- OriginLab. OriginPro, version 9.3.1.273; OriginLab: Northampton, MA, USA, 2017. [Google Scholar]
- Statgraphics Technologies Inc. STATGRAPHICS 18, version 18.1.01; Statgraphics Technologies Inc.: Fauquier County, VA, USA, 2017. [Google Scholar]
- García-Gutiérrez, A.; Barragán-Reyes, R.M.; Arellano-Gómez, V.M. Research on Heat Pumps in Mexico Operating on Waste Energy as Heat Source. In Proceedings of the Geothermal Resources Council Annual Meeting, Reno, NV, USA, 30 September–3 October 2007. [Google Scholar]
- Eiben, A.E.; Smith, J.E. What is an Evolutionary Algorithm? In Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2003; pp. 15–36. [Google Scholar]
- Sivanandam, S.N.; Deepa, S.N. Evolutionary Computation. In Introduction to Genetic Algorithms; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2008; pp. 1–14. [Google Scholar]
- Charbonneau, P.; Knapp, B. PIKAIA 1.2; National Center for Atmospheric Research—High Altitude Observatory: Boulder, CO, USA, 2002. [Google Scholar]








| Variable | Mean | Std. Deviation | Variance | Ratio of Variance | Difference of Means | Mean Lower Bound | Mean Upper Bound | p-Value |
|---|---|---|---|---|---|---|---|---|
| Characteristic Days | ||||||||
| 3.2 | 1.28 | 1.65 | 0.77 | −0.41 | −2.42 | 1.59 | 0.64 | |
| 3.61 | 1.46 | 2.14 | ||||||
| 1.38 | 0.28 | 0.082 | 3.15 | 0.022 | −0.31 | 0.36 | 0.88 | |
| 1.35 | 0.16 | 0.026 | ||||||
| Seasonal Performance | ||||||||
| 5.13 | 0.57 | 0.327 | 1.21 | 0.17 | −0.17 | 0.53 | 0.31 | |
| 4.95 | 0.51 | 0.269 | ||||||
| 0.99 | 0.176 | 0.031 | 1.93 | 0.062 | −0.03 | 0.16 | 0.22 | |
| 0.93 | 0.126 | 0.016 | ||||||
| Continuous Operation | ||||||||
| 2.34 | 0.37 | 0.137 | 1.47 | −0.027 | −0.34 | 0.29 | 0.86 | |
| 2.37 | 0.30 | 0.093 | ||||||
| 0.41 | 0.06 | 0.0036 | 6 | -0.030 | −0.07 | 0.01 | 0.16 | |
| 0.44 | 0.025 | 0.0006 | ||||||
| Hour | (°C) | (kW) | (kW) | (kW) | (°C) | (s) | ||
|---|---|---|---|---|---|---|---|---|
| 10:00 | 15.8 | 1.946 | 22.18 | −20.23 | 18.6 | 1800 | 0.08 | 5.69 |
| 10:30 | 18.6 | 1.955 | 20.23 | −18.28 | 21.4 | 0.09 | 5.63 | |
| 11:00 | 21.4 | 1.955 | 18.28 | −16.32 | 24.3 | 0.10 | 5.49 | |
| 11:30 | 24.3 | 2.029 | 16.32 | −14.29 | 27.2 | 0.12 | 5.23 | |
| 12:00 | 27.2 | 2.196 | 14.29 | −12.10 | 30.4 | 0.15 | 5.4 | |
| 12:30 | 30.4 | 2.402 | 12.10 | −9.70 | 33.9 | 0.19 | 5.5 | |
| 13:00 | 33.9 | 2.583 | 9.70 | −7.11 | 37.6 | 0.26 | 5.65 | |
| 13:30 | 37.6 | 2.776 | 7.11 | −4.34 | 41.7 | 0.39 | 5.86 | |
| 14:00 | 41.7 | 2.795 | 4.34 | −1.54 | 45.7 | 300 | 0.64 | 5.66 |
| 14:05 | 45.7 | 2.796 | 1.54 | 1.25 | 48.29 | 1.81 | 5.66 |
(°C) | (°C) | (kW) | (s) | (kW) | ||
|---|---|---|---|---|---|---|
| 15.8 | 48 | 2.34 | 1800 | 22.43 | 0.10 | 5.69 |
| 3600 | 11.21 | 0.20 | 5.63 | |||
| 5400 | 7.47 | 0.31 | 5.49 | |||
| 7200 | 5.60 | 0.41 | 5.23 | |||
| 9000 | 4.48 | 0.52 | 5.4 | |||
| 10,800 | 3.73 | 0.62 | 5.5 | |||
| 12,600 | 3.20 | 0.73 | 5.65 | |||
| 14,400 | 2.80 | 0.83 | 5.86 | |||
| 16,200 | 2.49 | 0.93 | 5.66 | |||
| 18,000 | 2.24 | 1.04 | 5.66 |
| Date | (°C) | (°C) | (kW) | (s) | (kW) | ||
|---|---|---|---|---|---|---|---|
| 04/04/2005 | 20.6 | 50 | 6.48 | 7200 | 2.58 | 2.51 | 6.61 |
| 05/04/2005 | 22.1 | 6.36 | 2.44 | 2.59 | 6.36 | ||
| 05/04/2005 | 22.9 | 5.90 | 2.37 | 2.48 | 5.46 | ||
| 15/04/2005 | 25.1 | 5.58 | 2.18 | 2.55 | 5.26 | ||
| 16/04/2005 | 24.2 | 5.38 | 2.26 | 2.37 | 5.49 | ||
| 18/04/2005 | 28.9 | 4.99 | 1.84 | 2.69 | 6.09 | ||
| 20/04/2005 | 25.7 | 5.26 | 2.13 | 2.46 | 5.26 | ||
| 22/04/2005 | 24.4 | 5.26 | 2.24 | 2.34 | 5.21 | ||
| 08/05/2005 | 32.0 | 4.80 | 1.57 | 3.04 | 4.95 | ||
| 10/05/2005 | 24.4 | 4.58 | 2.24 | 2.03 | 4.37 | ||
| 11/05/2005 | 35.1 | 4.78 | 1.30 | 3.66 | 5.56 | ||
| 12/05/2005 | 35.6 | 4.71 | 1.25 | 3.74 | 5.54 | ||
| 14/05/2005 | 17.1 | 4.98 | 2.89 | 1.72 | 3.11 | ||
| 15/05/2005 | 25.6 | 4.81 | 2.14 | 2.24 | 4.63 | ||
| 17/05/2005 | 27.4 | 4.84 | 1.98 | 2.44 | 4.57 | ||
| 19/05/2005 | 27.0 | 4.82 | 2.01 | 2.39 | 4.34 | ||
| 20/05/2005 | 30.2 | 4.85 | 1.73 | 2.79 | 5.91 | ||
| 30/05/2005 | 26.3 | 4.67 | 2.07 | 2.24 | 5.36 | ||
| 31/05/2005 | 30.0 | 4.54 | 1.75 | 2.59 | 5.75 |
| Date | (°C) | (°C) | (kW) | (s) | (kW) | ||
|---|---|---|---|---|---|---|---|
| 4/12/2009 | 13 | 51 | 4.0 | 14400 | 3.25 | 1.23 | 2.5 |
| 7/12/2009 | 14 | 2.3 | 3.16 | 0.72 | 1.9 | ||
| 6/05/2010 | 16 | 4.9 | 2.98 | 1.64 | 2.9 | ||
| 2/09/2010 | 27 | 3.1 | 2.01 | 1.54 | 2.2 | ||
| 2/12/2010 | 6 | 1.7 | 3.87 | 0.43 | 1.7 |
| No. of individuals | 128 |
| No. of generations | 2048 |
| Mutation rate | 0.35 |
| Location | (°C) | (°C) | (s) | (s) | (L) | Residuals | ||
|---|---|---|---|---|---|---|---|---|
| Madrid | 13 | 51 | 14,400 | 12,618 | 300 | 1 | 1 | 2.323 × 10−17 |
| 14 | 19,523 | 2 | 4.146 × 10−20 | |||||
| 16 | 10,117 | 2 | 3.476 × 10−20 | |||||
| 27 | 11,165 | 4 | 8.360 × 10−18 | |||||
| 6 | 32,402 | 4 | 5.603 × 10−17 | |||||
| Shanghai | 20.6 | 50 | 7200 | 3239 | 150 | 4 | 1 | 6.658 × 10−11 |
| 22.1 | 3224 | 4 | 8.666 × 10−13 | |||||
| 22.9 | 2808 | 4 | 5.461 × 10−20 | |||||
| 25.1 | 3246 | 4 | 2.030 × 10−12 | |||||
| 24.2 | 3196 | 4 | 4.778 × 10−11 | |||||
| 28.9 | 2344 | 4 | 8.562 × 10−13 | |||||
| 25.7 | 2874 | 4 | 5.239 × 10−11 | |||||
| 24.4 | 3081 | 4 | 2.109 × 10−11 | |||||
| 32.0 | 2241 | 4 | 1.641 × 10−12 | |||||
| 24.4 | 3842 | 4 | 6.370 × 10−11 | |||||
| 35.1 | 1600 | 4 | 6.780 × 10−12 | |||||
| 35.6 | 1711 | 4 | 2.484 × 10−12 | |||||
| 17.1 | 4459 | 4 | 1.320 × 10−10 | |||||
| 25.6 | 3546 | 4 | 5.705 × 10−12 | |||||
| 27.4 | 3536 | 4 | 8.227 × 10−11 | |||||
| 27.0 | 3618 | 4 | 5.154 × 10−09 | |||||
| 30.2 | 2259 | 4 | 3.556 × 10−11 | |||||
| 26.3 | 2980 | 4 | 3.412 × 10−13 | |||||
| 30.0 | 2369 | 4 | 3.655 × 10−11 | |||||
| Zagreb | 15.8 | 48 | 18,000 | 16,360 | 300 | 1 | 1 | 4.502 × 10−20 |
| Location | COP | ||||
|---|---|---|---|---|---|
| R22 | R134a | R404A | R407C | R410A | |
| Madrid | - | 2.5 | 2.82 | 3.25 | 2.56 |
| - | 1.91 | 2.23 | 2.61 | 2.09 | |
| - | 2.88 | 3.10 | 3.54 | 2.76 | |
| - | 2.21 | 2.20 | 2.59 | 2.12 | |
| - | 1.7 | 1.95 | 2.32 | 1.87 | |
| Shanghai | 6.61 | 10.33 | 7.79 | 8.89 | 6.14 |
| 6.36 | 9.41 | 7.25 | 8.28 | 5.79 | |
| 5.46 | 5.16 | 4.20 | 4.18 | 4.13 | |
| 5.26 | 7.58 | 6.15 | 7.04 | 5.08 | |
| 5.48 | 8.23 | 6.55 | 7.49 | 5.34 | |
| 6.08 | 8.33 | 6.86 | 7.77 | 5.61 | |
| 5.26 | 8.37 | 6.72 | 7.66 | 5.47 | |
| 5.20 | 8.47 | 6.72 | 7.68 | 5.46 | |
| 4.94 | 6.77 | 5.90 | 6.71 | 4.99 | |
| 4.36 | 6.52 | 5.39 | 6.22 | 4.55 | |
| 5.55 | 9.43 | 7.42 | 8.43 | 5.94 | |
| 5.54 | 8.28 | 6.66 | 7.59 | 5.43 | |
| 3.11 | 3.69 | 3.17 | 3.21 | 3.27 | |
| 4.62 | 6.57 | 5.47 | 6.30 | 4.62 | |
| 4.56 | 5.87 | 4.52 | 5.26 | 4.00 | |
| 4.34 | 5.75 | 4.96 | 5.73 | 4.29 | |
| 5.91 | 9.98 | 7.52 | 8.62 | 5.96 | |
| 5.36 | 7.67 | 6.27 | 7.16 | 5.17 | |
| 5.74 | 9.61 | 7.27 | 8.34 | 5.78 | |
| Zagreb | - | 5.61 | 3.92 | 4.49 | 3.72 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De León-Ruiz, J.E.; Carvajal-Mariscal, I. Mathematical Thermal Modelling of a Direct-Expansion Solar-Assisted Heat Pump Using Multi-Objective Optimization Based on the Energy Demand. Energies 2018, 11, 1773. https://doi.org/10.3390/en11071773
De León-Ruiz JE, Carvajal-Mariscal I. Mathematical Thermal Modelling of a Direct-Expansion Solar-Assisted Heat Pump Using Multi-Objective Optimization Based on the Energy Demand. Energies. 2018; 11(7):1773. https://doi.org/10.3390/en11071773
Chicago/Turabian StyleDe León-Ruiz, Jorge E., and Ignacio Carvajal-Mariscal. 2018. "Mathematical Thermal Modelling of a Direct-Expansion Solar-Assisted Heat Pump Using Multi-Objective Optimization Based on the Energy Demand" Energies 11, no. 7: 1773. https://doi.org/10.3390/en11071773






