Design and Experimental Implementation of a Hysteresis Algorithm to Optimize the Maximum Power Point Extracted from a Photovoltaic System
Abstract
1. Introduction
2. Photovoltaic Modeling
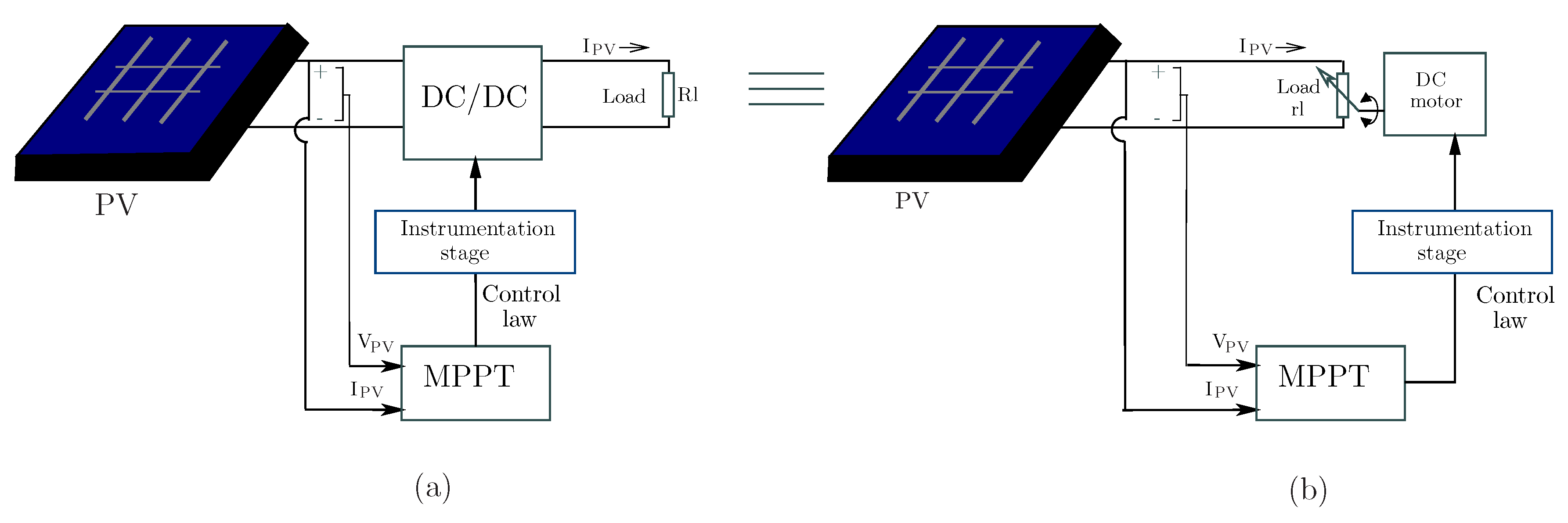
3. An Equivalent Model of the DC/DC Converter in PV-MPPT Systems
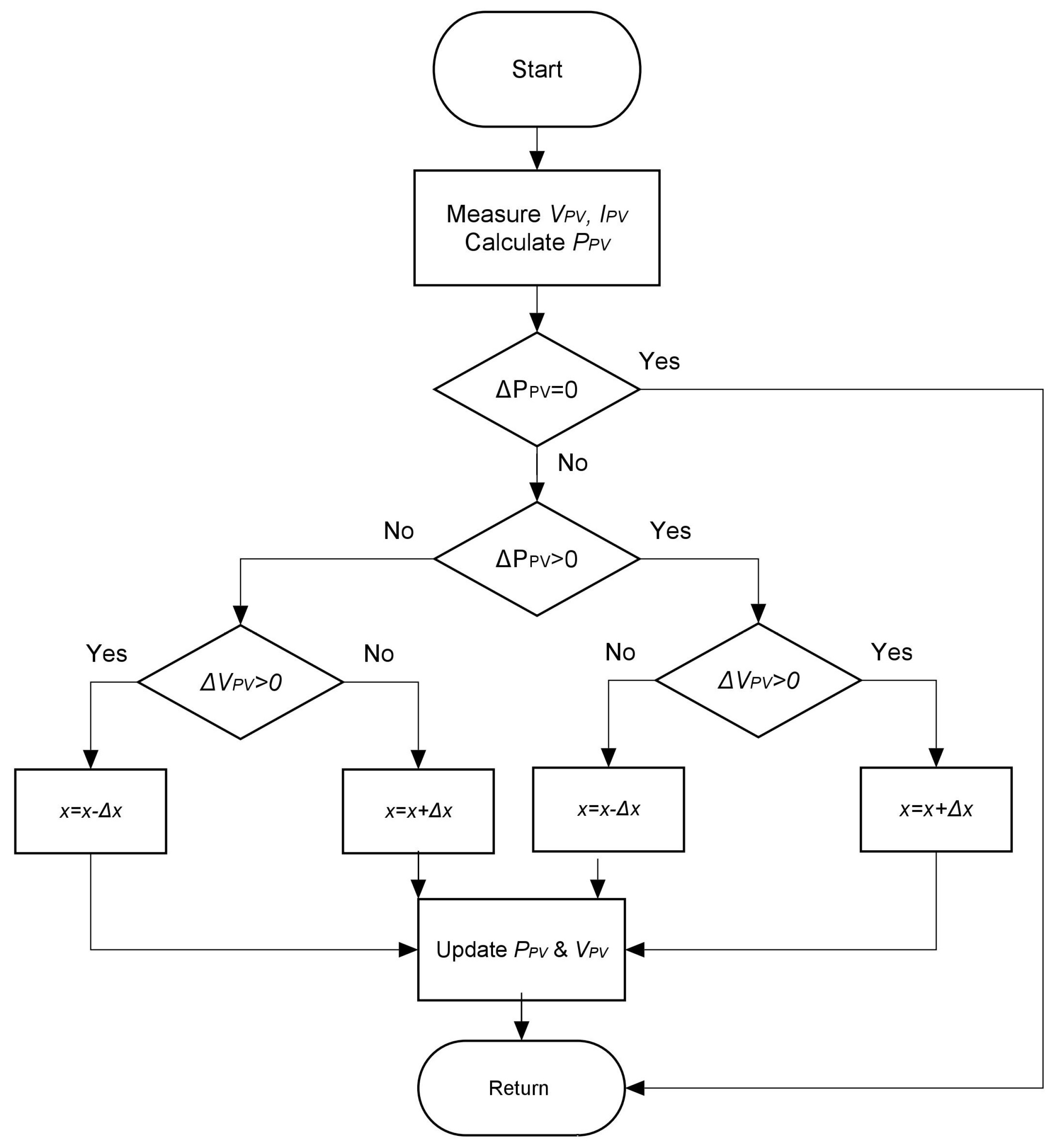
4. The MPPT Perturb and Observer Method
- If both the power and voltage increase ( and ), it means that the operating point has been moved forward and the search of the MPP continues in the same direction.
- On the other hand, if power decreases and voltage decreases ( and ), it indicates that the MPP search is oriented in the wrong direction.
- The third possible case is when the power increases (), but the voltage decreases (). This indicates that the search of the MPP is oriented in the right direction.
- Finally, the last possible situation is presented when the power decreases () and the voltage increases (). This case indicates that the MPP search is incorrectly oriented.
5. The Proposed MPPT Algorithm by Using a Dynamic Hysteresis Model
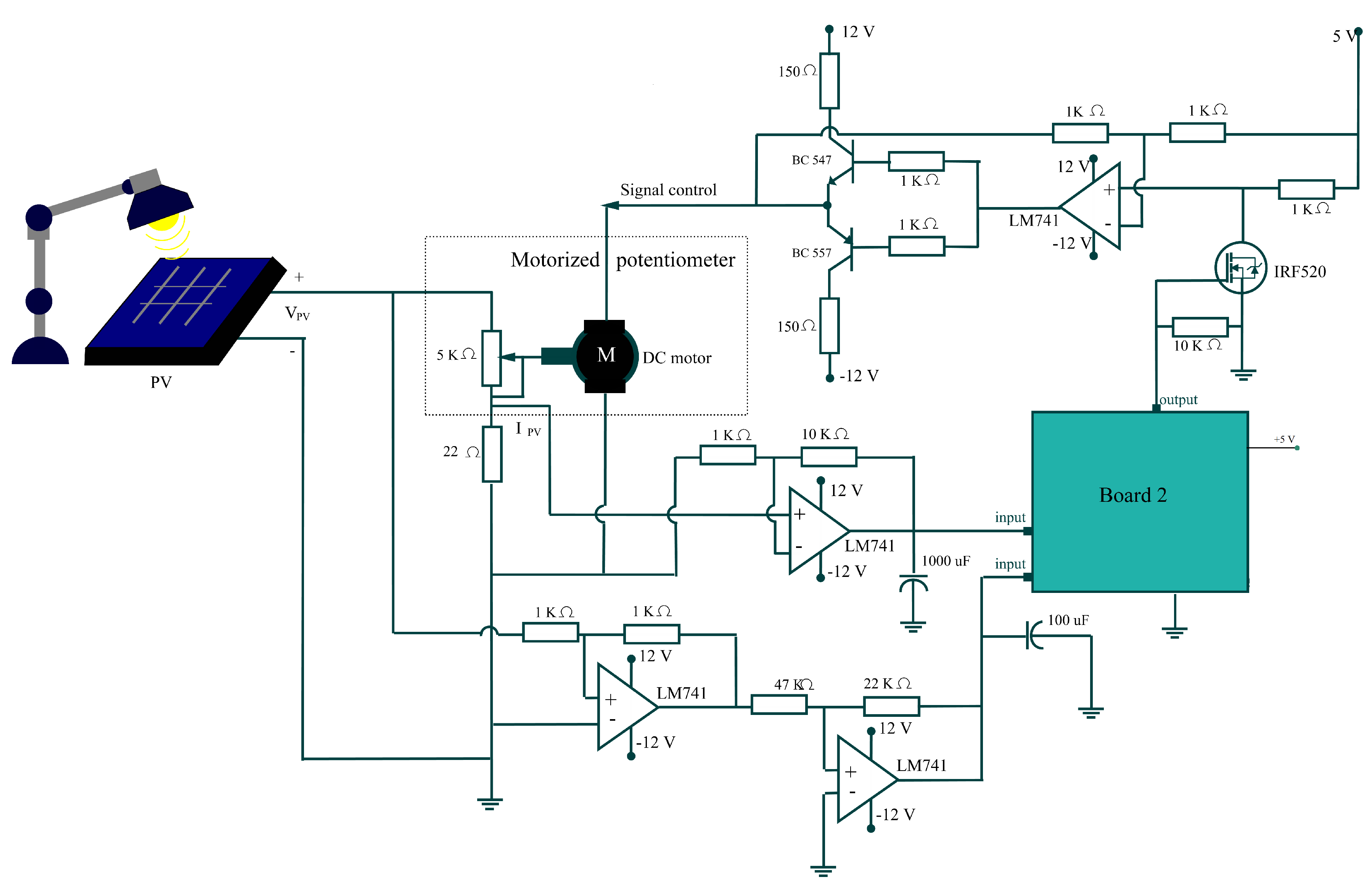
6. A PV-MPPT Experimental Platform
- A 5 W photovoltaic module Intertek IP65-IEC61215 (Intertek, London, UK) supplying a maximum voltage in close-circuit of 17 V and 21 V in open-circuit.
- An Arduino Uno board (labeled here as Board 1) to automatically control the intensity light of the bulb.
- A lamp with a 100 W bulb to emulate the irradiation variation and shading conditions.
- A 22 shunt resistance used to instrument the supplied PV current to the load.
- A motorized-potentiometer constituted by a DC motor mechanically linked to a 5 k potentiometer. This potentiometer emulates the load seen by the PV panel.
- A second Arduino Uno board (labeled here as Board 2) where the MPPT control algorithm is implemented.
- An electronic instrumentation development to couple the inputs and output signals to/from Board 2.
6.1. Technical Specifications
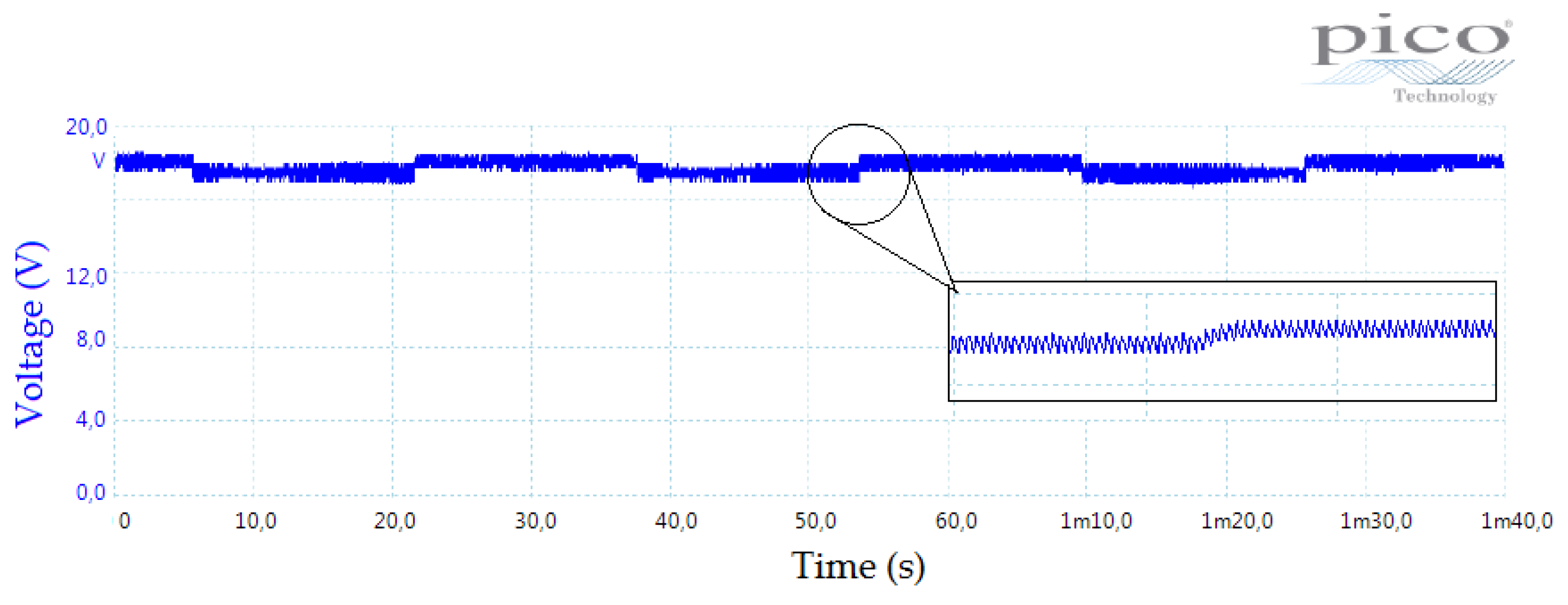
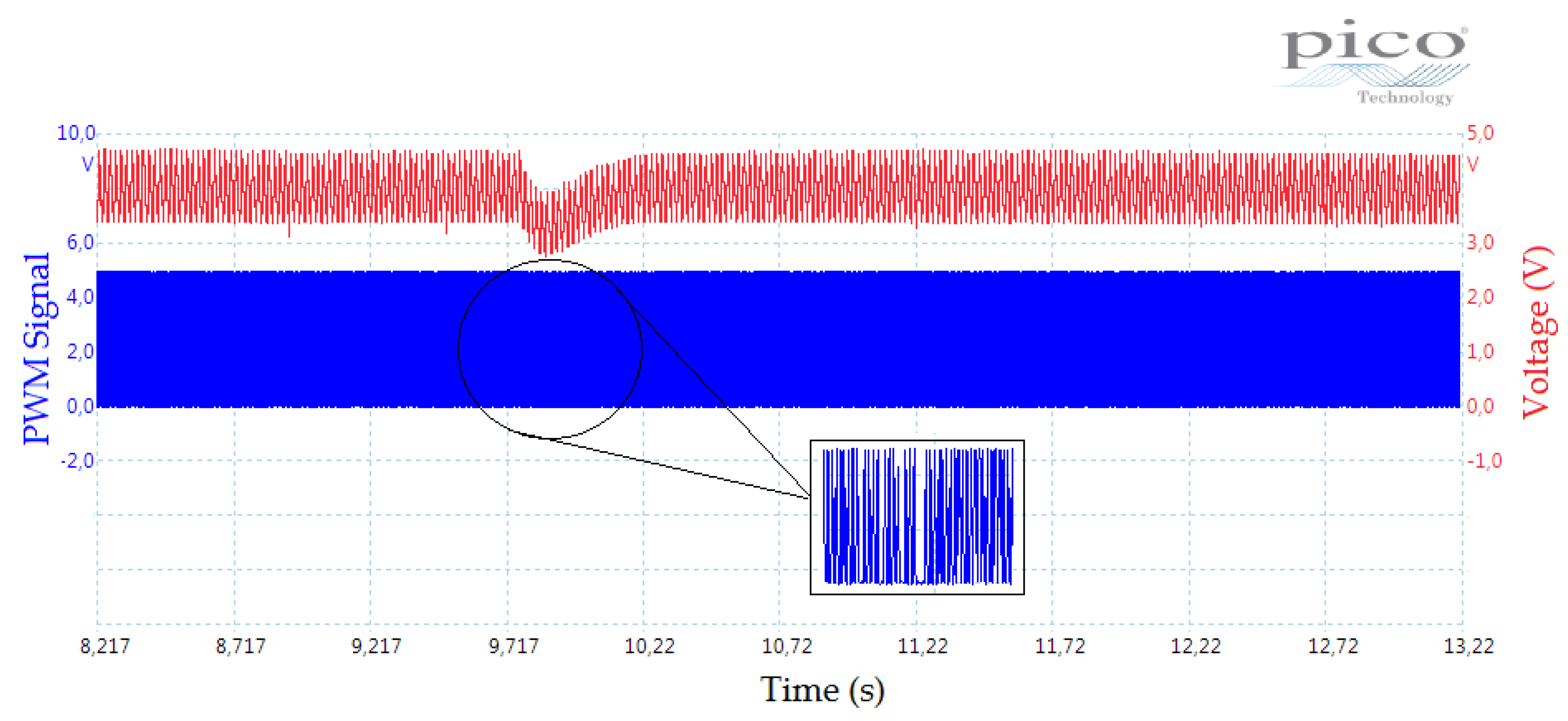
- Stage A: The irradiation control stage consists of Board 1 and an electronic instrumentation system. The general electronic circuit of this stage is presented in Appendix B, Figure A1. In this stage, an intentionally repetitive blinking light phenomenon was induced. Because of a PV panel being too sensitive to this kind of light perturbation, our experiment platform is able to emulate, for instance, a fast shading light condition [25,48]. Specifically, for the experiments shown in this paper, two levels of light intensity were programmed. The PV voltage in open-circuit under the effect of the irradiation changes is shown in Figure 8. Here, the automatic change of these two light intensity levels is made evident. In addition, the effect induced by the blinking phenomenon in the light bulb is clearly perceived. Note that this stage is independently designed from the other stages that integrate our PV-MPPT system.
- Stage 1: This stage consists of an electronic circuit, shown in Appendix B, Figure A2, which allows the PV voltage and PV current signals to be readable by the Arduino (Board 2). This is because the Arduino board reads voltages in the range of 0–5 V and our PV panel can produce up to 17 V.
- Stage 2: This stage involves the Arduino Uno (Board 2) where the MPPT algorithms are coded. The programed codes for experimental implementation are presented in Appendix C. Both algorithms, the P&O method and our hysteresis approach, generate a reference command signal (named here ), which assists with accomplishing the maximum power point tracking. Moreover, in this stage, a classic controller was implemented to stabilize the DC motor [20]. In this case, a proportional-controller (P-controller) that stabilizes the position of the motor around a set point value is employed. Thus, the P-controller was developed in terms of the position of the motor () captured by the potentiometer (see Figure 7). Since the position of the motor is directly related to the resistance of the potentiometer, the P-controller is obtained from the voltage point of view:Therefore, our P-controller is expressed as: , where is the proportional gain and is the set point established by the user. The P-controller coupled to the reference command signal (X) obtained from the MPPT algorithm can then be captured in the following control law (From the closed-loop system stability point of view, it is well known that a DC motor is controllable by a proportional controller):Since the Arduino analog outputs employ a PWM format according to the instrumentation stage, the above control law requires being translated into a PWM signal by using the Arduino instruction analogWrite (version 1.8.5-Windows, Arduino, Turin, Italy). Hence, the Equation (9) is rewritten as follows:where is selected here as the medium value of the Arduino PWM duty cycle range (255/2) since the DC motor must turn both left and right. On the other hand, is actually the duty cycle used by Arduino to generate the PWM output signal. Then, this signal will drive the DC motor through the electronic stage. In consequence, Equation (10) has the following objectives:
- –
- to stabilize the motor around the value through the P-controller,
- –
- to navigate the DC motor position by following the MPPT reference command signal X from the reference.
To successfully complete this stage, it was necessary to modify the Arduino PWM output frequency from 490 Hz to 40 kHz by editing the # PWM Arduino library because of the DC motor dynamics. - Stage 3: This phase consists of an electronic instrumentation to correctly drive the DC motor (see Figure 7). The PWM control signal generated in Stage 2 () is a unipolar one since Arduino outputs are limited to positive voltage values. Nevertheless, the DC motor must be able to turn in both senses to increase or decrease the potentiometer resistance linked mechanically to it. For this reason, this stage converts the unipolar signal to a bipolar one without losing the original control signal information.Figure 9 shows the final developed platform. Clearly, our experimental platform has notable advantages with respect to other experimental realizations [1,6,20,23,37], such as:
- It uses low cost electronic components (about 100 Euros).
- The hardware deployment requires a small area.
- It is easy to build.
- It uses an open-source software.
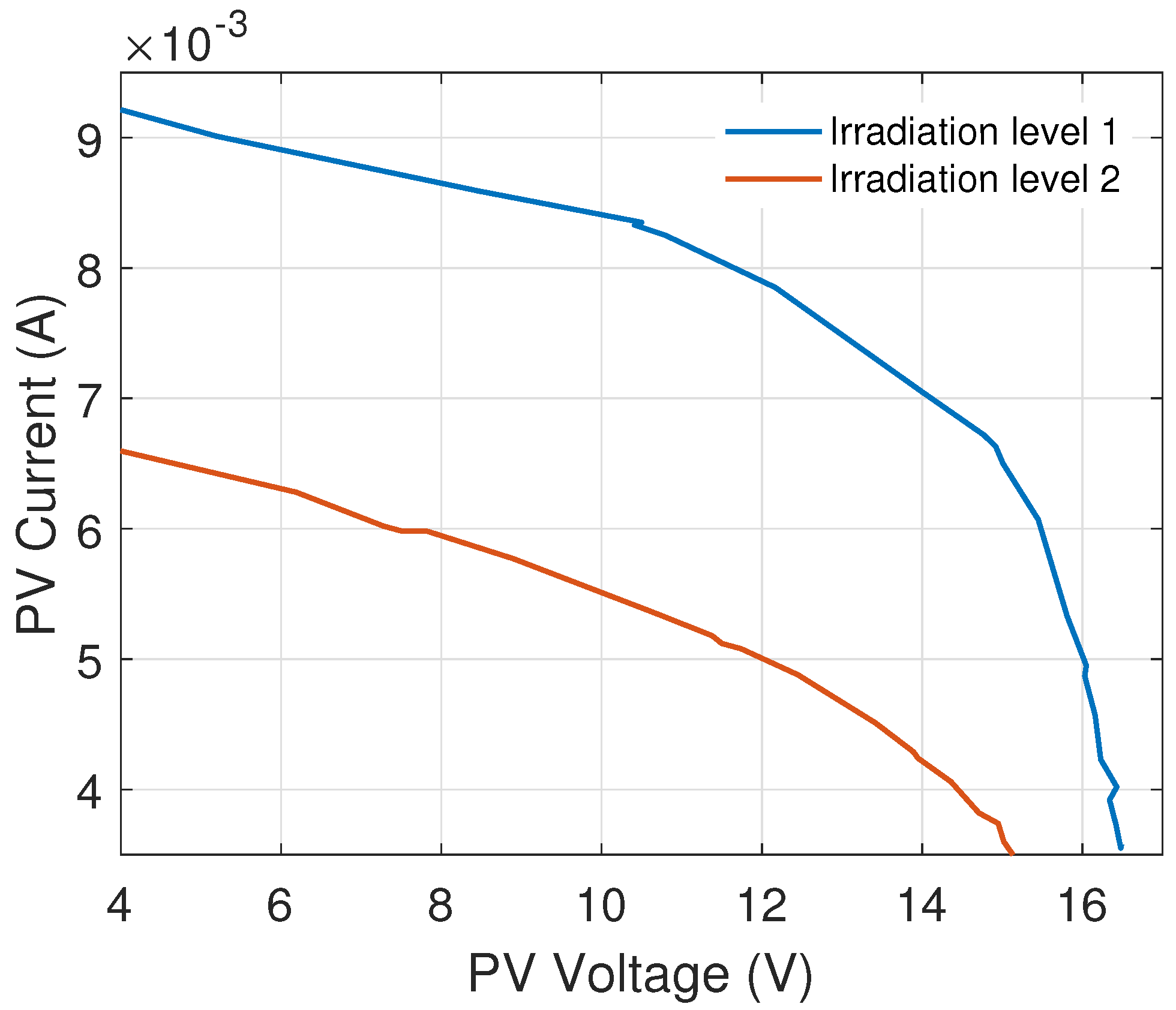
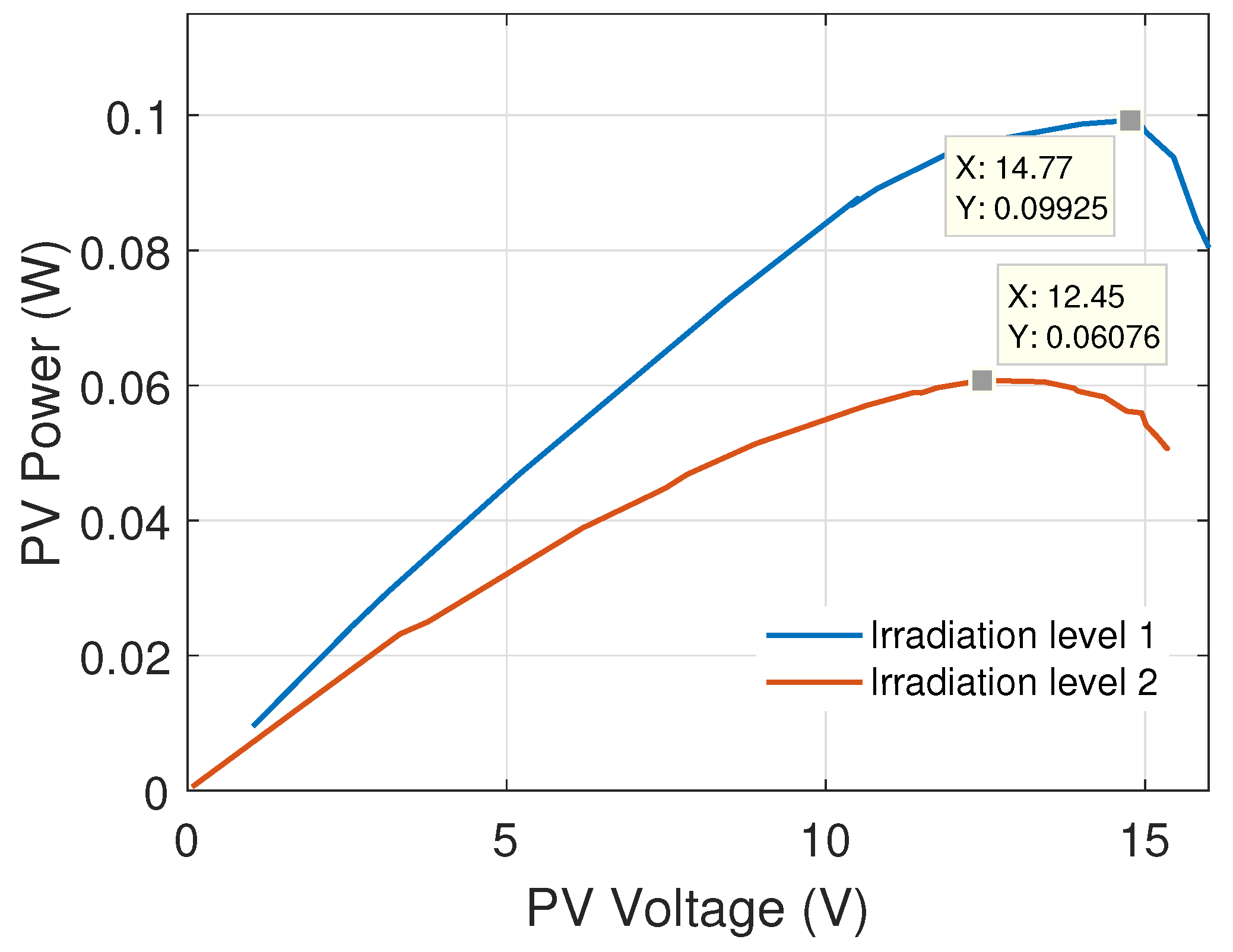
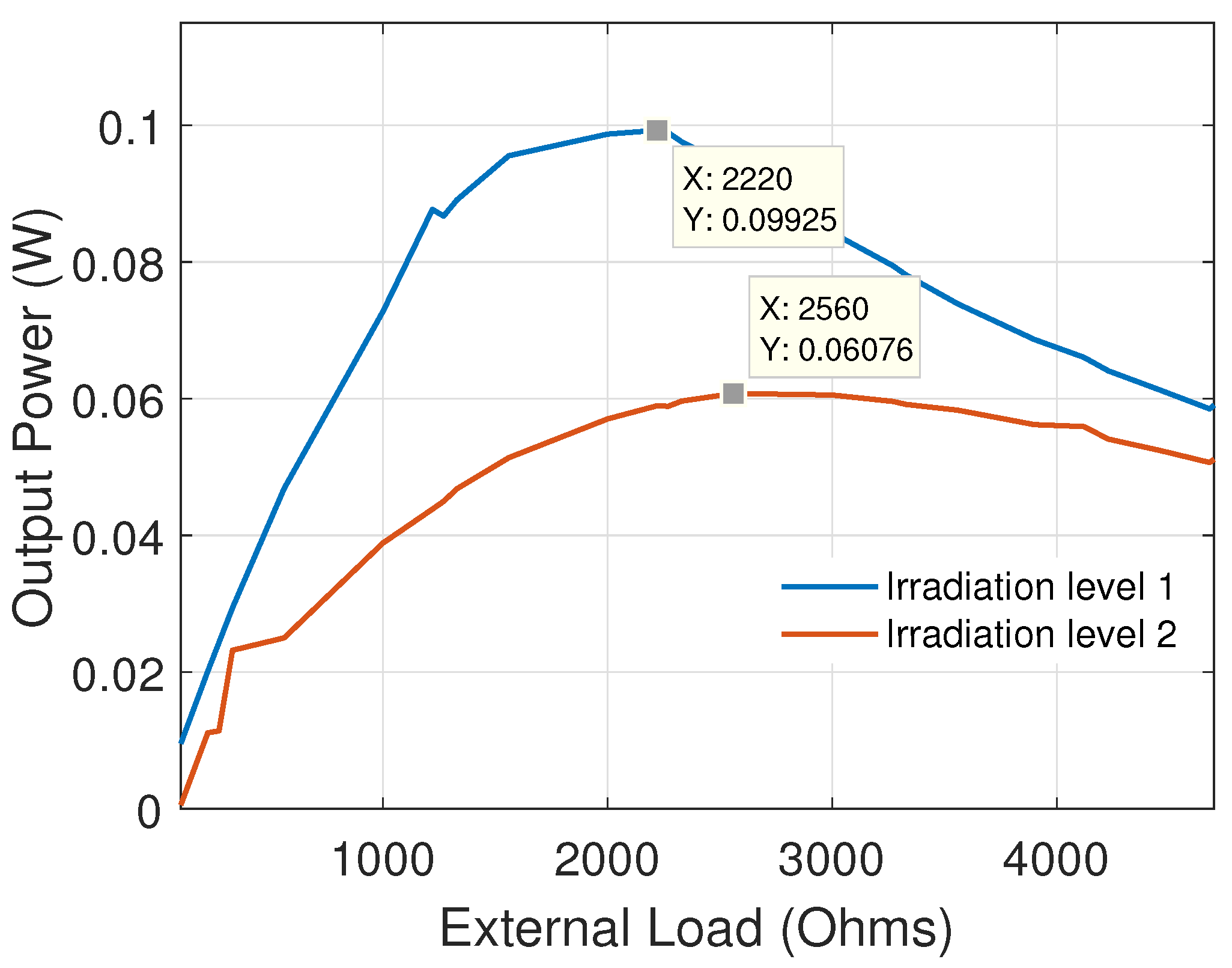
6.2. PV-Panel Characterization
7. Results and Discussion
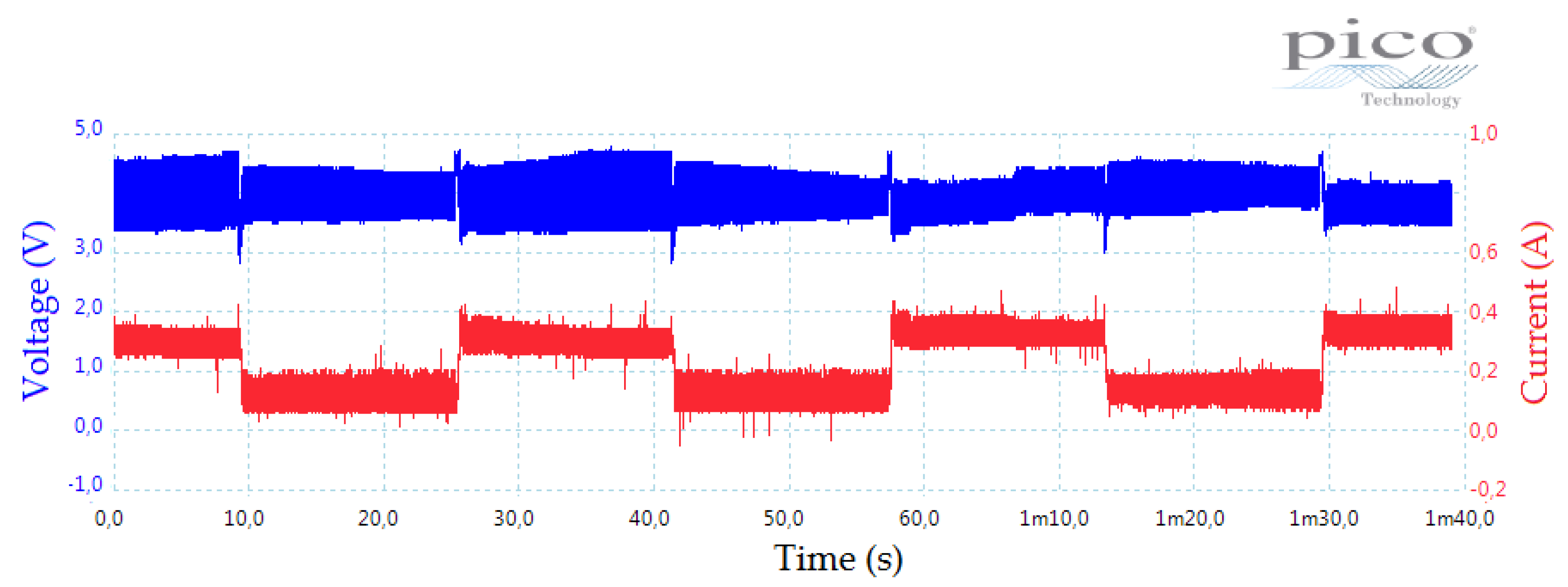
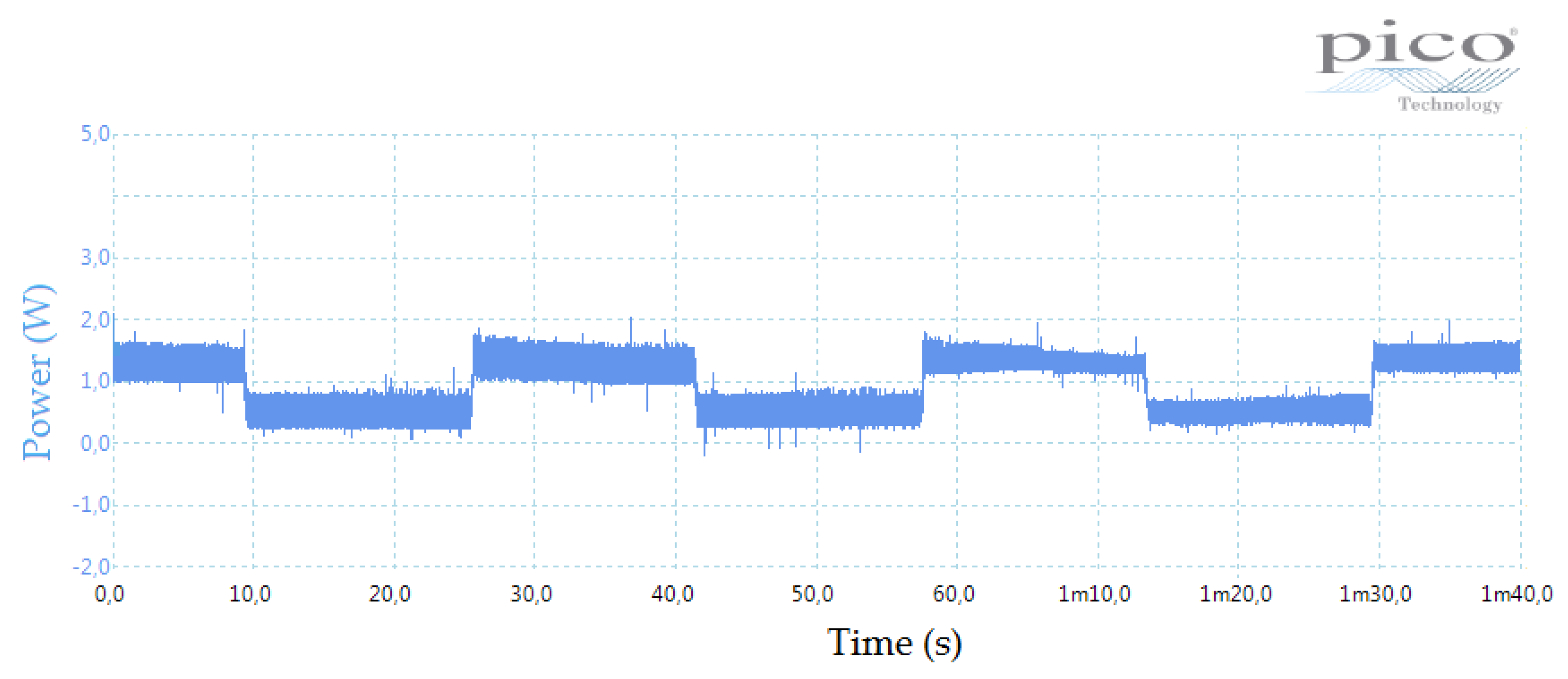
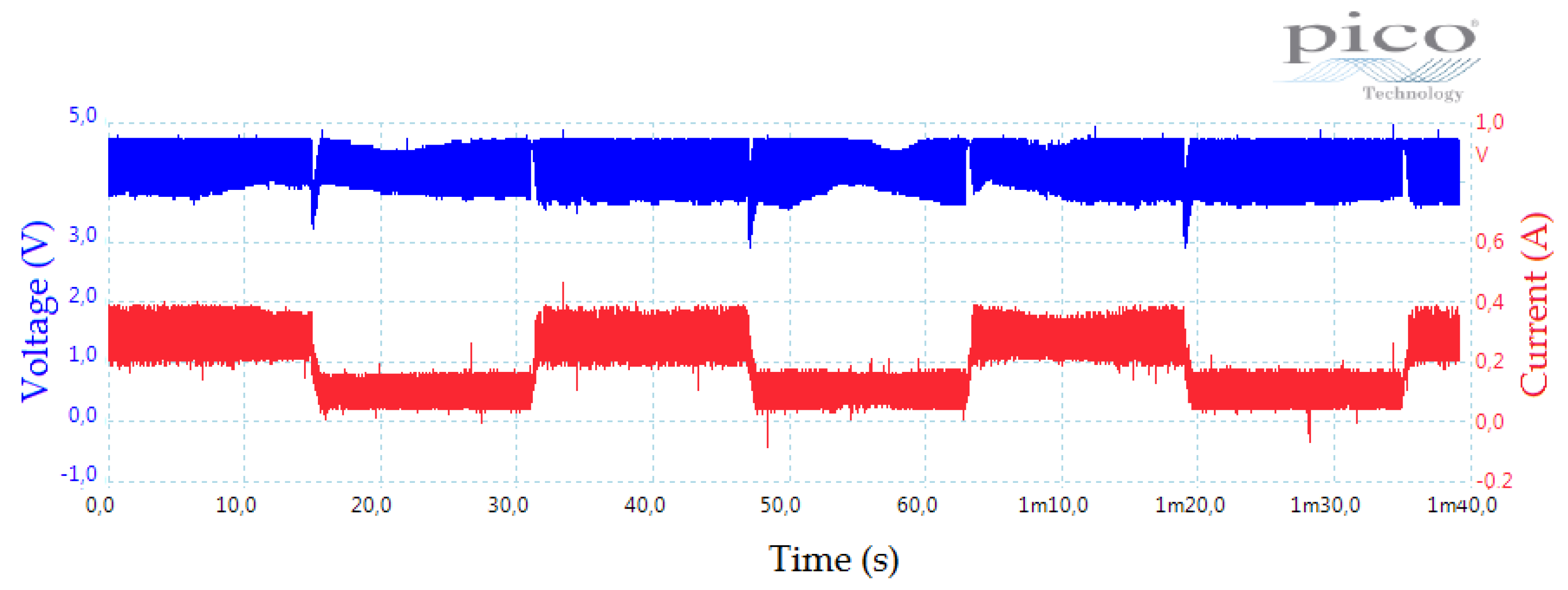
7.1. Experimental Results by Using the MPPT Perturb and Observer Method
7.2. Experimental Results by Using the Hysteresis MPPT Method
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Values for PV Characteristics’ Curves
| External Load () | PV Voltage (V) | PV Current (mA) | PV Power (W) |
|---|---|---|---|
| 100 | 1.03 | 0.0092 | 0.0095 |
| 220 | 2.14 | 0.0094 | 0.0201 |
| 270 | 2.58 | 0.0094 | 0.0243 |
| 330 | 3.14 | 0.0093 | 0.0294 |
| 560 | 5.20 | 0.0090 | 0.0469 |
| 1000 | 8.47 | 0.0085 | 0.0728 |
| 1220 | 10.5 | 0.0083 | 0.0877 |
| 1270 | 10.41 | 0.0083 | 0.0867 |
| 1330 | 10.8 | 0.0082 | 0.0891 |
| 1560 | 12.17 | 0.0078 | 0.0955 |
| 2000 | 14 | 0.0070 | 0.0987 |
| 2220 | 14.77 | 0.0067 | 0.0993 |
| 2227 | 14.92 | 0.0066 | 0.0989 |
| 2330 | 15.01 | 0.0065 | 0.0976 |
| 2560 | 15.45 | 0.0060 | 0.0938 |
| 3000 | 15.81 | 0.0053 | 0.0843 |
| 3270 | 16.05 | 0.0049 | 0.0794 |
| 3330 | 16.03 | 0.0048 | 0.0781 |
| 3560 | 16.16 | 0.0045 | 0.0739 |
| 3900 | 16.23 | 0.0042 | 0.0687 |
| 4120 | 16.34 | 0.0040 | 0.0660 |
| 4230 | 16.34 | 0.0039 | 0.0641 |
| 4460 | 16.42 | 0.0037 | 0.0612 |
| 4680 | 16.48 | 0.0035 | 0.0585 |
| 4700 | 16.47 | 0.0035 | 0.0590 |
| External Load () | PV Voltage (V) | PV Current (mA) | PV Power (W) |
|---|---|---|---|
| 100 | 0.0775 | 0.0071 | 0.0006 |
| 220 | 1.59 | 0.0069 | 0.0111 |
| 270 | 1.63 | 0.0069 | 0.0114 |
| 330 | 2.33 | 0.0069 | 0.0232 |
| 560 | 3.77 | 0.0066 | 0.0250 |
| 1000 | 6.19 | 0.0062 | 0.0389 |
| 1220 | 7.28 | 0.0060 | 0.0438 |
| 1270 | 7.52 | 0.0059 | 0.0450 |
| 1330 | 7.83 | 0.0059 | 0.0468 |
| 1560 | 8.90 | 0.0057 | 0.0514 |
| 2000 | 10.64 | 0.0053 | 0.0570 |
| 2220 | 11.38 | 0.0051 | 0.0589 |
| 2270 | 11.5 | 0.0051 | 0.0589 |
| 2330 | 11.74 | 0.0050 | 0.0596 |
| 2560 | 12.45 | 0.0048 | 0.0608 |
| 3000 | 13.42 | 0.0041 | 0.0605 |
| 3270 | 13.89 | 0.0042 | 0.0596 |
| 3330 | 13.95 | 0.0042 | 0.0591 |
| 3560 | 14.36 | 0.0040 | 0.0583 |
| 3900 | 14.71 | 0.0038 | 0.0562 |
| 4120 | 14.95 | 0.0037 | 0.0559 |
| 4230 | 15.02 | 0.0036 | 0.0541 |
| 4460 | 15.19 | 0.0034 | 0.0524 |
| 4680 | 15.35 | 0.0033 | 0.0507 |
| 4700 | 15.30 | 0.0033 | 0.0511 |
Appendix B. Electronic Diagrams

Appendix C. Program Codes
Appendix C.1. Arduino Program to Implement the Perturb and Observer Algorithm
- //Arduino library included to manipulate the PWM output frequency.
- # include <PWM.h>
- //Variables to process power data.
- float potA=0, pot, deltaPot, deltaPotN;
- //Control variable.
- float uPWM=0;
- //Reference command signal generated by the P&O algorithm.
- float X;
- //Variables to process voltage data.
- float Vref, VrefA=0, deltaVref;
- //Variables to read PV voltage and PV current values.
- float voltage, current;
- //Variables to process the read values.
- float voltajeValue, corrienteValue;
- void setup() {
- pinMode(0,INPUT); //Pin to read voltage.
- pinMode(2,INPUT); //Pin to read current.
- pinMode(9, OUTPUT); //Pin to write output control.
- //Timer initialization.
- InitTimersSafe();
- //Instruction to set the PWM frequency at 40 KHz.
- bool success=SetPinFrequencySafe(9, 40000);
- }
- void loop() {
- //Read the voltage and scale it into the Arduino range (0−1023).
- voltajeValue=analogRead(0);
- voltage=voltajeValue∗(5.0/1023.0);
- //Calculate the real PV voltage according to external electronic instrumentation.
- voltage=voltage/0.468;
- //Read the current and scale it into the Arduino range (0−1023).
- corrienteValue=analogRead(2);
- current=corrienteValue∗(5.0/1023.0);
- //Calculate the real PV current according to external electronic instrumentation.
- current=current/36.96;
- pot=voltage∗current; //Calculate PV power.
- deltaPot=pot-potA; //Calculate power difference.
- //Calculate sign of power difference.
- if (deltaPot > 0){deltaPotN= 1;}
- else {deltaPotN= −1;}
- deltaVref=voltage−VrefA; //Calculate voltage difference.
- //P&O algorithm to obtain the reference command signal.
- X=deltaVref∗deltaPotN;
- uPWM=20∗(voltage−10+X)+127; //Calculate the final control signal.
- analogWrite(9,round(uPWM)); //Writes the final control signal in Pin 9.
- //Update power and voltage.
- potA=pot;
- VrefA=voltage;
- }
Appendix C.2. Arduino Program to Implement Our Hysteresis MPPT Algorithm
- //Arduino library included to operate the PWM output frequency.
- # include <PWM.h>
- //Variables to process power data.
- float potA=0, pot, deltaPot, deltaPotN;
- //Control variable.
- float uPWM=0;
- //Variables to process voltage data.
- double deltaVolt, voltA;
- //Variables to read PV voltage and PV current values.
- int voltage, current;
- //Hysteresis algorithm variables.
- double sgnPot, sgnz, z, xaf, xd;
- //Reference command signal generated by the hysteresis algorithm.
- float X=0.1;
- //Variables to process the read values.
- float voltajeValue, corrienteValue;
- // Hysteresis algorithm constants.
- double timeChange=0.1, a=1, b=1, alpha=10;
- void setup() {
- pinMode(0,INPUT); //Pin to read voltage.
- pinMode(2,INPUT); //Pin to read current.
- pinMode(9, OUTPUT); //Pin to write output control.
- //Timer initialization.
- InitTimersSafe();
- //Instruction to set the output frequency at 40 KHz.
- bool success=SetPinFrequencySafe(9, 40000);
- }
- void loop() {
- //Read the voltage and scale it into the Arduino range (0−1023).
- voltajeValue=analogRead(0);
- voltage=voltajeValue∗(5.0/1023.0);
- //Calculate the real PV voltage according to external electronic instrumentation.
- voltage=voltage/0.468;
- //Read the current and scale it into the Arduino range (0-1023).
- corrienteValue=analogRead(2);
- current=corrienteValue∗(5.0/1023.0);
- //Calculate the real PV current according to external electronic instrumentation.
- current=current/36.96;
- pot=voltage∗current; //Calculate PV power.
- deltaPot=pot-potA; //Calculate power difference.
- deltaVolt=voltage-voltA; //Calculate voltage difference.
- //Calculate sign of power difference.
- if (deltaPot > 0){sgnPot= 1;}
- else {sgnPot= −1;}
- //Hysteresis MPPT algorithm.
- z=deltaVolt∗a∗sgnPot;
- if (z > 0){sgnz= 1;}
- else {sgnz= −1;}
- //Hysteresis dynamic equation to obtain the reference command signal.
- xd=X+timeChange∗(alpha∗(−X+b∗sgnz));
- //Calculate control signal.
- uPWM=20∗(voltage−(10+X))+127;
- //Write the final control signal in Pin 9.
- analogWrite(9,round(uPWM));
- //Update variables.
- potA=pot;
- voltA=voltage;
- X=xd;
- }
References
- De Brito, M.A.G.; Galotto, L.; Sampaio, L.P.; Melo, G.D.A.; Canesin, C.A. Evaluation of the main MPPT techniques for photovoltaic applications. IEEE Trans. Ind. Electron. 2013, 60, 1156–1167. [Google Scholar] [CrossRef]
- Grätzel, M. Solar energy conversion by dye-sensitized photovoltaic cells. Inorg. Chem. 2005, 44, 6841–6851. [Google Scholar] [CrossRef] [PubMed]
- Carreño-Ortega, A.; Galdeano-Gómez, E.; Pérez-Mesa, J.C.; Galera-Quiles, M.D.C. Policy and environmental implications of photovoltaic systems in farming in southeast Spain: Can greenhouses reduce the greenhouse effect? Energies 2017, 10, 761. [Google Scholar] [CrossRef]
- Hassan, A.S.; Cipcigan, L.; Jenkins, N. Optimal battery storage operation for PV systems with tariff incentives. Appl. Energy 2017, 203, 422–441. [Google Scholar] [CrossRef]
- Vieira, F.M.; Moura, P.S.; de Almeida, A.T. Energy storage system for self-consumption of photovoltaic energy in residential zero energy buildings. Renew. Energy 2017, 103, 308–320. [Google Scholar] [CrossRef]
- Boukenoui, R.; Ghanes, M.; Barbot, J.P.; Bradai, R.; Mellit, A.; Salhi, H. Experimental assessment of Maximum Power Point Tracking methods for photovoltaic systems. Energy 2017, 132, 324–340. [Google Scholar] [CrossRef]
- Karami, N.; Moubayed, N.; Outbib, R. General review and classification of different MPPT Techniques. Renew. Sustain. Energy Rev. 2017, 68, 1–18. [Google Scholar] [CrossRef]
- Schwertner, C.D.; Bellinaso, L.V.; Hey, H.L.; Michels, L. Supervisory control for stand-alone photovoltaic systems. In Proceedings of the 2013 Brazilian Power Electronics Conference (COBEP), Gramado, Brazil, 27–31 October 2013; pp. 582–588. [Google Scholar]
- Yang, Y.; Blaabjerg, F.; Wang, H.; Simoes, M.G. Power control flexibilities for grid-connected multi-functional photovoltaic inverters. IET Renew. Power Gener. 2016, 10, 504–513. [Google Scholar] [CrossRef]
- Cucchiella, F.; D’Adamo, I.; Gastaldi, M. Economic analysis of a photovoltaic system: A Resource for residential households. Energies 2017, 10, 814. [Google Scholar] [CrossRef]
- Liu, J.; Long, Y.; Song, X. A study on the conduction mechanism and evaluation of the comprehensive efficiency of photovoltaic power generation in China. Energies 2017, 10, 723. [Google Scholar]
- Hernández, J.C.; Bueno, P.G.; Sanchez-Sutil, F. Enhanced utility-scale photovoltaic units with frequency support functions and dynamic grid support for transmission systems. IET Renew. Power Gener. 2017, 11, 361–372. [Google Scholar] [CrossRef]
- Koutroulis, E.; Blaabjerg, F. A new technique for tracking the global maximum power point of PV arrays operating under partial-shading conditions. IEEE J. Photovolt. 2012, 2, 184–190. [Google Scholar] [CrossRef]
- Hemandez, J.; Garcia, O.; Jurado, F. Photovoltaic devices under partial shading conditions. Int. Rev. Model. Simul. 2012, 5, 414–425. [Google Scholar]
- Rodrigues, E.; Osório, G.; Godina, R.; Bizuayehu, A.; Lujano-Rojas, J.; Catalão, J. Grid code reinforcements for deeper renewable generation in insular energy systems. Renew. Sustain. Energy Rev. 2016, 53, 163–177. [Google Scholar] [CrossRef]
- Cabrera-Tobar, A.; Bullich-Massagué, E.; Aragüés-Peñalba, M.; Gomis-Bellmunt, O. Review of advanced grid requirements for the integration of large scale photovoltaic power plants in the transmission system. Renew. Sustain. Energy Rev. 2016, 62, 971–987. [Google Scholar] [CrossRef]
- Orchi, T.F.; Mahmud, M.A.; Oo, A.M.T. Generalized dynamical modeling of multiple photovoltaic units in a grid-connected system for analyzing dynamic interactions. Energies 2018, 11, 296. [Google Scholar] [CrossRef]
- Ni, Q.; Zhuang, S.; Sheng, H.; Wang, S.; Xiao, J. An optimized prediction intervals approach for short term PV power forecasting. Energies 2017, 10, 1669. [Google Scholar] [CrossRef]
- Kim, D.J.; Kim, B.; Ko, H.S.; Jang, M.S.; Ryu, K.S. A novel supervisory control algorithm to improve the performance of a real-time PV power-hardware-in-loop simulator with Non-RTDS. Energies 2017, 10, 1651. [Google Scholar] [CrossRef]
- Kebir, A.; Woodward, L.; Akhrif, O. Extremum-seeking control with adaptive excitation: Application to a photovoltaic system. IEEE Trans. Ind. Electron. 2018, 65, 2507–2517. [Google Scholar] [CrossRef]
- Marinkov, S.; de Jager, B.; Steinbuch, M. Extremum seeking control with data-based disturbance feedforward. In Proceedings of the 2014 American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; pp. 3627–3632. [Google Scholar]
- Ouoba, D.; Fakkar, A.; El Kouari, Y.; Dkhichi, F.; Oukarfi, B. An improved maximum power point tracking method for a photovoltaic system. Opt. Mater. 2016, 56, 100–106. [Google Scholar] [CrossRef]
- Farhat, M.; Barambones, O.; Sbita, L. A new maximum power point method based on a sliding mode approach for solar energy harvesting. Appl. Energy 2017, 185, 1185–1198. [Google Scholar] [CrossRef]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Power Electronics and Control Techniques for Maximum Energy Harvesting in Photovoltaic Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Belkaid, A.; Colak, I.; Isik, O. Photovoltaic maximum power point tracking under fast varying of solar radiation. Appl. Energy 2016, 179, 523–530. [Google Scholar] [CrossRef]
- Safari, A.; Mekhilef, S. Simulation and hardware implementation of incremental conductance MPPT with direct control method using cuk converter. IEEE Trans. Ind. Electron. 2011, 58, 1154–1161. [Google Scholar] [CrossRef]
- Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of perturb and observe MPPT algorithm implementation techniques for PV pumping applications. IEEE Trans. Sustain. Energy 2012, 3, 21–33. [Google Scholar] [CrossRef]
- Robles Algarín, C.; Taborda Giraldo, J.; Rodríguez Álvarez, O. Fuzzy logic based MPPT controller for a PV system. Energies 2017, 10, 2036. [Google Scholar] [CrossRef]
- Enany, M.A.; Farahat, M.A.; Nasr, A. Modeling and evaluation of main maximum power point tracking algorithms for photovoltaics systems. Renew. Sustain. Energy Rev. 2016, 58, 1578–1586. [Google Scholar] [CrossRef]
- Dochain, D.; Perrier, M.; Guay, M. Extremum seeking control and its application to process and reaction systems: A survey. Math. Comput. Simul. 2011, 82, 369–380. [Google Scholar] [CrossRef]
- Tafticht, T.; Agbossou, K.; Doumbia, M.; Cheriti, A. An improved maximum power point tracking method for photovoltaic systems. Renew. Energy 2008, 33, 1508–1516. [Google Scholar] [CrossRef]
- Dasgupta, N.; Pandey, A.; Mukerjee, A.K. Voltage-sensing-based photovoltaic MPPT with improved tracking and drift avoidance capabilities. Sol. Energy Mater. Sol. Cells 2008, 92, 1552–1558. [Google Scholar] [CrossRef]
- Scarpa, V.V.; Buso, S.; Spiazzi, G. Low-complexity MPPT technique exploiting the PV module MPP locus characterization. IEEE Trans. Ind. Electron. 2009, 56, 1531–1538. [Google Scholar] [CrossRef]
- Hammami, M.; Grandi, G. A single-phase multilevel PV generation system with an improved ripple correlation control MPPT algorithm. Energies 2017, 10, 2037. [Google Scholar] [CrossRef]
- Liu, F.; Kang, Y.; Zhang, Y.; Duan, S. Comparison of P&O and hill climbing MPPT methods for grid-connected PV converter. In Proceedings of the 2008 3rd IEEE Conference on Industrial Electronics and Applications (ICIEA 2008), Singapore, 3–5 June 2008; pp. 804–807. [Google Scholar]
- Liu, F.; Duan, S.; Liu, F.; Liu, B.; Kang, Y. A variable step size INC MPPT method for PV systems. IEEE Trans. Ind. Electron. 2008, 55, 2622–2628. [Google Scholar]
- Loukriz, A.; Haddadi, M.; Messalti, S. Simulation and experimental design of a new advanced variable step size Incremental Conductance MPPT algorithm for PV systems. ISA Trans. 2016, 62, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Leyva, R.; Alonso, C.; Queinnec, I.; Cid-Pastor, A.; Lagrange, D.; Martínez-Salamero, L. MPPT of photovoltaic systems using extremum-seeking control. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 249–258. [Google Scholar] [CrossRef]
- Mao, M.; Duan, Q.; Duan, P.; Hu, B. Comprehensive improvement of artificial fish swarm algorithm for global MPPT in PV system under partial shading conditions. Trans. Inst. Meas. Control 2018, 40, 2178–2199. [Google Scholar] [CrossRef]
- Mellit, A.; Kalogirou, S.A. MPPT-based artificial intelligence techniques for photovoltaic systems and its implementation into field programmable gate array chips: Review of current status and future perspectives. Energy 2014, 70, 1–21. [Google Scholar] [CrossRef]
- Chen, Y.T.; Jhang, Y.C.; Liang, R.H. A fuzzy-logic based auto-scaling variable step-size MPPT method for PV systems. Sol. Energy 2016, 126, 53–63. [Google Scholar] [CrossRef]
- Faranda, R.; Leva, S. Energy comparison of MPPT techniques for PV systems. WSEAS Trans. Power Syst. 2008, 3, 446–455. [Google Scholar]
- Aranda, E.D.; Galan, J.A.G.; De Cardona, M.S.; Marquez, J.M.A. Measuring the IV curve of PV generators. IEEE Ind. Electron. Mag. 2009, 3, 4–14. [Google Scholar] [CrossRef]
- Verneau, G.; Aubard, L.; Crebier, J.C.; Schaeffer, C.; Schanen, J.L. Empirical power MOSFET modeling: Practical characterization and simulation implantation. In Proceedings of the 37th IAS Annual Meeting, Conference Record of the 2012 IEEE Industry Applications Conference, Pittsburgh, PA, USA, 13–18 October 2002; pp. 2425–2432. [Google Scholar]
- Acho, L.; Vidal, Y. Hysteresis modeling of a class of RC-OTA hysteretic-chaotic generators. In Proceedings of the 5th International Conference on Physics and Control, León, Spain, 5–8 September 2011. [Google Scholar]
- Tutivén, C.; Vidal, Y.; Acho, L.; Rodellar, J. Hysteresis-based design of dynamic reference trajectories to avoid saturation in controlled wind turbines. Asian J. Control 2017, 19, 438–449. [Google Scholar] [CrossRef]
- De León, N.I.P.; Acho, L.; Rodellar, J. Adaptive predictive control of a base-isolated hysteretic system. In Proceedings of the 2017 21st International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 19–21 October 2017; pp. 390–395. [Google Scholar]
- Manickam, C.; Raman, G.P.; Raman, G.R.; Ganesan, S.I.; Chilakapati, N. Fireworks enriched P&O algorithm for GMPPT and detection of partial shading in PV systems. IEEE Trans. Power Electron. 2017, 32, 4432–4443. [Google Scholar]
- Das, P.; Mohapatra, A.; Nayak, B. Modeling and characteristic study of solar photovoltaic system under partial shading condition. Mater. Today Proc. 2017, 4, 12586–12591. [Google Scholar] [CrossRef]


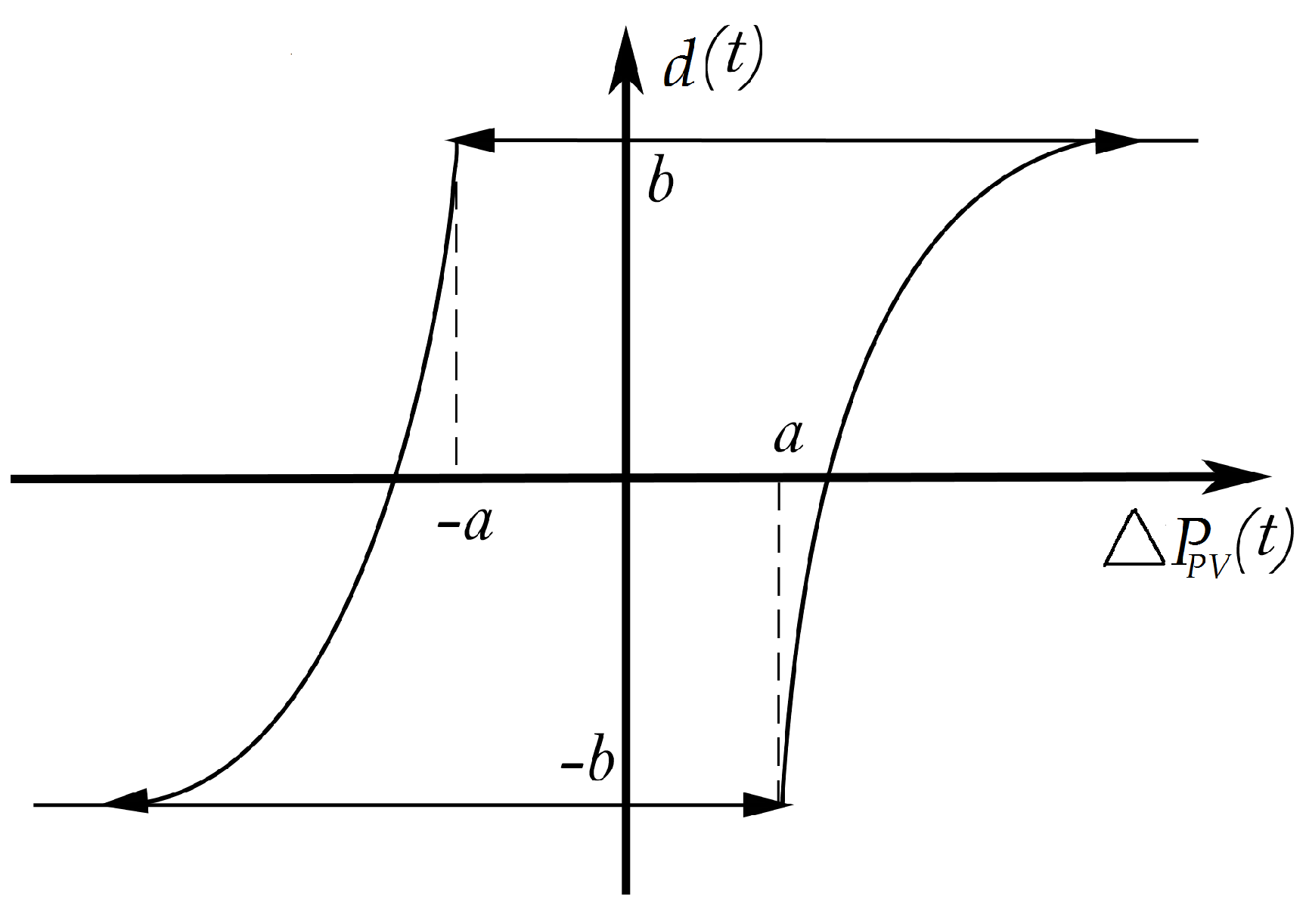







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ponce de León Puig, N.I.; Acho, L.; Rodellar, J. Design and Experimental Implementation of a Hysteresis Algorithm to Optimize the Maximum Power Point Extracted from a Photovoltaic System. Energies 2018, 11, 1866. https://doi.org/10.3390/en11071866
Ponce de León Puig NI, Acho L, Rodellar J. Design and Experimental Implementation of a Hysteresis Algorithm to Optimize the Maximum Power Point Extracted from a Photovoltaic System. Energies. 2018; 11(7):1866. https://doi.org/10.3390/en11071866
Chicago/Turabian StylePonce de León Puig, Nubia Ilia, Leonardo Acho, and José Rodellar. 2018. "Design and Experimental Implementation of a Hysteresis Algorithm to Optimize the Maximum Power Point Extracted from a Photovoltaic System" Energies 11, no. 7: 1866. https://doi.org/10.3390/en11071866
APA StylePonce de León Puig, N. I., Acho, L., & Rodellar, J. (2018). Design and Experimental Implementation of a Hysteresis Algorithm to Optimize the Maximum Power Point Extracted from a Photovoltaic System. Energies, 11(7), 1866. https://doi.org/10.3390/en11071866