1. Introduction
The fuse, as simple overcurrent protection device, is widely used in a range of voltages from 12 V to as high as 66 kV. Being connected in series with the protected equipment, the fuse detects and isolates the faulted equipment from the network. In its simplest form, it consists of a piece of metal wire connected between two terminals on a suitable support; and at its most complex as a cartridge fuselink mounted in a carrier and fuse base. Modern cartridge fuselinks contain fusible elements mounted in rigid housings of insulating material. The housings are filled with suitable exothermal and arc-quenching powders, such as silica, and they are sealed by metal endcaps which carry the conducting tags or end connections. The metal parts, other than the fusible elements, are invariably of copper, brass, steel or composites and they must be capable of operating under the exacting thermal, mechanical and electrical conditions which may arise in service.
A fuse has to operate for up to 20 years with the same electrical performances, supporting the usual load currents and transient overloads [
1]. For this, the fuse has to be thermally and chemically compatible with the environment, but being capable to interrupt the circuit when exposed to overcurrents. This interruption is assured by melting of an element, followed by an arching phenomenon with high energy release, depending on the circuit parameters and characteristics.
Successful fault interruption implies that the arcing is wholly contained within the fuselink and the level at which this can be achieved is termed the breaking or rupturing capacity of the fuselink. The operating time of a fuselink varies inversely with the level of an overcurrent and discrimination is obtained in networks by choosing fuses with the necessary time-current characteristics and current ratings. The time-current characteristic is determined by the design of the fuse itself, in particular but not exclusively, the fuse material and the physical geometry of the fuselink(s). In practice, the fuse current characteristic is chosen to ensure adequate discrimination with other fuses and/or overcurrent relaying devices around the network.
In previous works, a one-dimensional model describing the gas flux and the heat distribution in high breaking capacity (HBC) fuses is presented in [
2]. It used a flow model joined with a porous medium model considering the heat transfer over hot gas and cold silica sand. Also, in [
3] a model to simulate the flow of a compressible fluid in porous media considering a microscopic thermal model to estimate the local thermal process of the solid phase is described. A mathematical model of the fuselink heating, including solid-liquid-vapour phase transitions used to estimate the pre-arcing time in HBC fuses is presented in [
4]. The model estimates the enthalpy formulation for the heat equation with a source term representing the Joule effect jointed with the Laplace equation for the potential and the Ohm’s law.
The physico-chemical processes during the operation of fuselinks under fault currents are very complex. In [
5], some methods to measure the current and voltage arc using analog/digital converters are presented and the observed phenomena investigated. Multiple arcing and a short-duration lowering of the arc voltage have been explained.
The adiabatic assumption usually applied in modelling is considered in [
6]. The influence of the pre-arcing step on the arcing step is analysed via the Joule integral, the energy released in the fuse and the mass and length of the fulgurite.
Manufacturers of HBC fuses need more accurate models of fuse behaviour during the arc time period of breaking the main electric circuit. The models will be obtained if the understanding of fuse arc phenomena will be improved. Therefore, in [
7] some experimental tests such as calorimetry, analysis of fuselink fulgurite, electron spectroscopy for chemical analysis, and determination of produced gas have been performed. The conclusions were that no chemical change takes place during fuse arcing.
A methodology that expresses the thermal process in high voltage current-limiting fuses for currents until the rated value is presented in [
8]. Thus, it solves the transient heating aspects of the fuse to achieve the values of the released power and the heat transfer coefficient, according to the steady state conditions. An empirical model to study the current-limiting fuses utilised in distribution system applications is presented in [
9]. The different phases of fuse operation are modelled using EMTP software. Although the model has limits, it is simple and allows an easy utilisation for a nonexpert.
The effect of the M-effect metal setting over the overload current pre-arcing time for DC current-limiting fuse is described in [
10]. Experimental results have outlined that the M-effect has influence if the overload current is about two times of the rated current.
When function in current-limiting mode, current-limiting fuses can reduce the heat and pressure hazards related on arc events because they limit the current in the first one-quarter cycle. The possibility to estimate the arc current and incident energy for equipment using current-limiting fuses and applying NEC Section 240.67 by general arc models utilisation is presented in [
11].
Temperature distribution on the fuselinks with different type of cross-section fuse elements is presented in [
12]. Some mathematical models are proposed in the case of fuselinks with variable cross-sections. Results of numerical calculations of fuse element heating in transient and steady state, performed with FLUX 2D software are reported in [
13]. The calculations considered the heating of the entire fuse element. A research related to NV melting fuse is presented in [
14]. The calculation was based on the 3D finite element analysis that was performed with the software Vector Fields Opera. Analyses have been carried out for a different melting fuse current and different shape of perforation of melting fuselink. Understanding the thermal behaviour of a fuse is important in order to optimize the design and to choose the correct fuse rating for each application. A model for a fuse based on the Thermal Network Methodology was developed in [
15], including terminals, electrical connections, and a fuse canister. In this case, the thermal behavior of a HBC fuse is dependent just on the design of the fusing element, the material parameters, and the environment conditions. The pre-arcing time estimation for fuselinks operated in industrial protection circuits in case of heavy faults currents, is described in [
16]. An enthalpy method to solve heat-transfer equation with two phase changes was described. The mathematical model joints thermal and electrical equations based on the energy conservation principle and the Ohm’s law, respectively.
Standardised fuse classes are presented in [
17] based on the IEC 60269 and IEC 60282 technical standards. The mistake in selecting of the suitable class is the most usual error and the results are faults in the protected equipment up to a severe fuse blast. Usual cases of wrong selection are discussed, highlighting the problems resulting from this erroneous selection and also the risks. Thus, to avoid errors in selection a profound knowledge of the use methodology of HBC fuses is necessary. The distribution of the temperature in the fuse under usual operating conditions was studied in [
18] and also large experiments with different fuse element types at various thermal stress values have been realised. The result of the environmental temperature rising inside a fuse-box, because of the Joule losses, over the current rating of the fuses is studied in [
19], in connexion with the ampacity of the overhead conductors. The increasing temperature into the fuse box has been estimated in compliance to the IEC 60890 standard with amendment in order to deal with external installation of the switchboard, that is the heat increase due to solar irradiance.
A numerical analysis of the transient temperature rise of the fuse elements in current-limiting fuses for protecting semiconductor devices is described in [
20]. The transient temperature rise was obtained by using 3-D finite element method combining the analysis of current distribution in the fuse with the heat analysis of the fuse. The thermal analysis of a medium voltage fuse by the finite element method is described in [
21] where the model has been designed and simulated under various conditions of ambient temperature with the Cosmos software tool. In [
22,
23], the effect of the current harmonics (with different THD) on the fuse thermal operating conditions, was studied using the software ANSYS. A mathematical model of the fuse time-current characteristic is presented in [
24]. The authors used the Least Square Method and the Residual Sum of Squares as a comparative parameter. Thus, it is possible to identify models with better adjustment in global scope considering the different nominal current ratings, speed ratios and manufacturers. Also, the calculation of the fuse melting point by inrush energy has been described in [
25].
Fuses in parallel may be an alternative to single-type fuses for use in power distribution networks or for semiconductor protection. A conclusion of the work presented in [
26] is that parallel connection of fuses is generally well accepted by the customers in a lot of worldwide markets but use of UL-fuses connected in parallel has special requirements. A novel unsymmetrical faults analysis method with hybrid compensation for microgrid distribution systems is proposed in [
27,
28,
29]. The method employs the actual three-phase models to handle unsymmetrical faults. The new method can be used to solve the various types of single or simultaneous unsymmetrical faults. Power electronic converters are very reliable equipment and are widely used in many activities including industries, services and even residential. However, there is a non-negligible risk of failure of a semiconductor acting to commutate in a leg. In that case, the semiconductor will short-circuit and all the available source energy will pass through the leg in question. There is then a very high risk of the semi-conductor exploding, with occurrence of an electric arc inside the converter and even outside. A more detail aspects related to the protection of these converters under high di/dt’s, using dedicated fuselinks, are presented in [
30]. A proposed modification to IEEE Std. 1584 arc flash incident energy calculations is presented in [
31] which would account for the impact of environmental temperature variation on fuse performance without detailed fuse performance modeling.
The purpose of this work is to analyze the temperature distribution over the fuselinks in the case of an asymmetric ratio of the electric current through fuselinks. The analysis will be performed during steady-state operating conditions of the HBC fuse. The thermal model takes into consideration the thermal overlapping effect of all notches of the fuselink. Also, it includes the temperature variation of the electrical resistivity of the fuselink material. First, it will obtain a mathematical model of the temperature distribution in the case of the HBC fuse with two parallel fuselinks. Then, the theoretical results will be compared with simulated results of a three dimensional thermal model of the same HBC fuse. Finally, experimental tests will be realised in order to validate the proposed model of the HBC fuse.
2. Mathematical Model
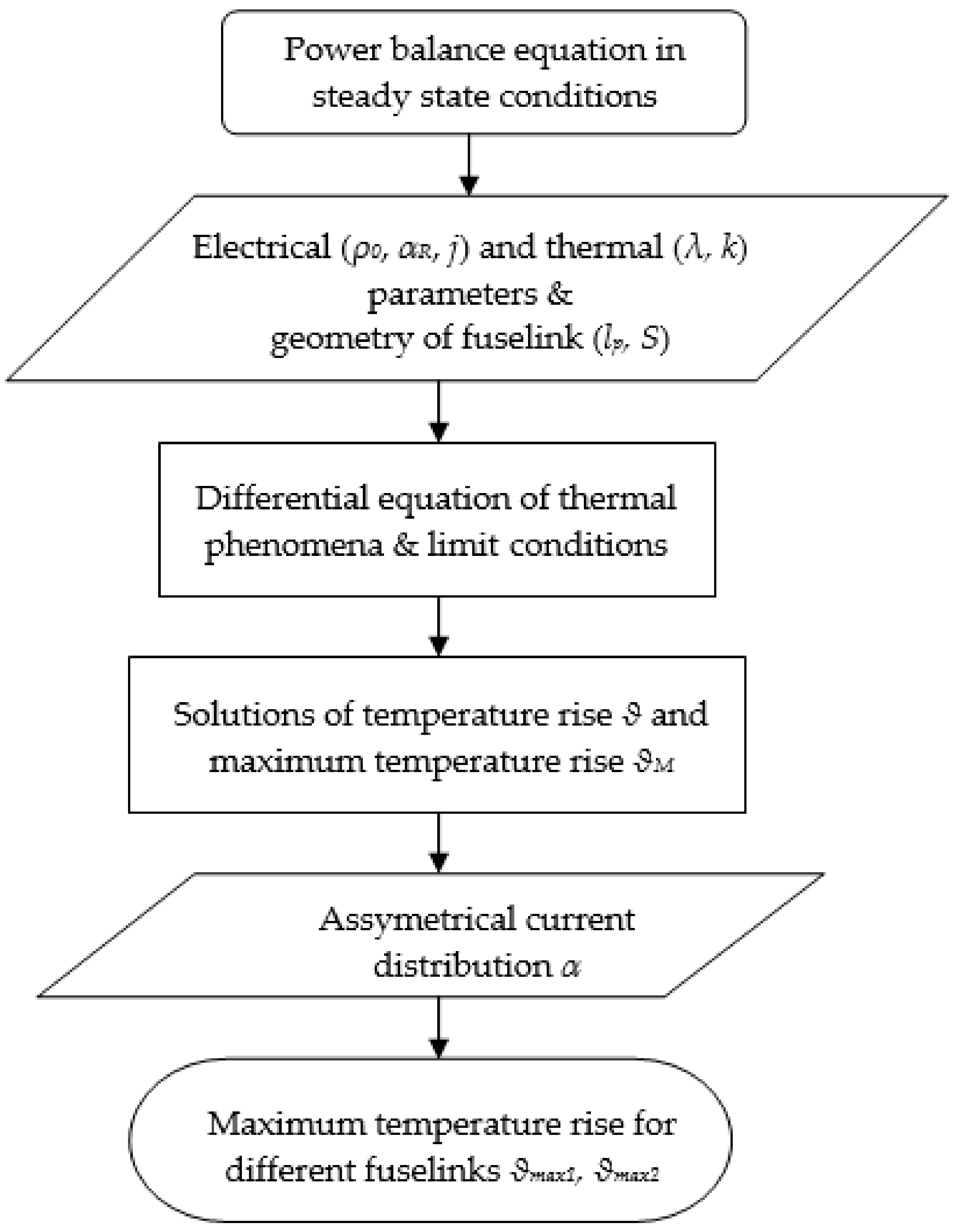
In order to obtain the thermal mathematical model, the flowchart from
Figure 1 has been considered. It starts with the power balance equation in steady-state conditions. Then, taking into account the electrical (
ρ0,
j,
αR) and thermal (
λ,
k) parameters of the fuse, and the geometry (
lp,
S) of the fuselink it will obtain the differential equation of the analuzed thermal phenomena. Together with the limit conditions it can be obtained the solutions for temperature rise distribution
ϑ and maximum temperature rise
ϑM. Taking into account the assymetrical current distribution through the fuselinks, finaly, it provides the maximum temperature rise for different fuselinks.
In the case of HBC fuses, the notches of the fuselink have a very small cross-section and the temperatures in these small areas are higher than the other parts of the fuselink. Actually, the notches are local thermal sources along the fuselink. Therefore, the initial fuselink can be transformed into a series of small fuselinks placed in front junctions where there are identically thermal sources, as presented in
Figure 2.
In every contact junction there is the same power loss
P0x and along the small fuselinks there is the axial heat flux of
Px =
P0x/2. The small fuselinks are actually conductors with the constant cross-sections and in this case, the power balance in steady-state conditions can be considered as [
12,
32]:
The first part of the relation is the thermal flux due to the temperature gradient from the conductor, the second part is the Joule power loss inside the conductor and the third part represents the thermal flux released by the lateral surface of the conductor. The electrical resistivity is estimated by a linear evolution with the temperature:
and, considering:
it results:
or:
The differential equation has the general solution as:
and has the limit condition:
From Equation (7) it follows that the integration constant
A1 has to be equal to zero, and thus the solution results as:
The particular solution
ϑs refers to the steady-state heat of the conductor due to the Joule effect of the electric current with no external thermal source. The expression is valuable for any section of the fuselink,
Figure 2:
;
;
;
;
and
. Because there are five additional thermal sources in the points 0,
x0, 2
x0, 3
x0 and 4
x0,
Figure 2, the study considers the sum of the thermal effects of the additional thermal sources. The temperature increase lengthwise spread is set by the mutual influence of every thermal sources. In compliance with the relation (8), the next relations can be found on each section of the small fuselink:
with the following limit conditions:
and:
where the additional power loss
P0x can be calculated on the basis of the geometry of the notch:
During steady-state conditions, in the area of the notches the temperature rise value
ϑ, reaches the local maximum temperature rise
ϑM. Hence, during steady-state conditions, the additional power loss of a certain notch is directly proportional with the maximum temperature rise of that notch:
The total cross-section of the notches at a certain point (0,
x0, 2
x0, 3
x0 and 4
x0), varies in the range 0 <
s <
S. Within the notches area (0,
x0, 2
x0, 3
x0 and 4
x0), it has been considered that a half of the additional thermal power spreads to the left of the notch area and the other half goes to the right of the notch,
Figure 2. It is to mention the supposition that the fuselink is a homogenous type. Also, for the limit condition (11), the relations in brackets contain only the temperature rise term with the thermal source at
x =
x0,
x = 2
x0,
x = 3
x0, respectively,
x = 4
x0.
During operating conditions of the HBC fuse, it is important to know the maximum temperature of the fuselink because the time-current characteristic, actually the protection characteristic of the fuse depends on this parameter. So, taking into account Equations (9)–(11) and (13), the solutions of the maximum temperature rise values in different points of the fuselink are:
From the above equations it is to notice that the maximum of the temperature rise is according to the ϑM3 expression; hence, ϑM3 > ϑM2 = ϑM4 > ϑM1 = ϑM5.
The mounting mode of the fuselinks inside the fuse gives various values for the dimensions (in length and thickness) of the fuse elements. This results in diverse electrical resistance scenarios of the fuselinks with consequences in an asymmetrical current distribution through the fuselinks when the fuse has mounted in parallel many fuse elements. In the case of the fuse with two parallel fuselinks, the current which flows through the fuse elements, has two different values
I1 and
I2. The sum of these two currents is:
I =
I1 +
I2, and the ratio between them is:
I2 =
αI1, where 0 <
α < 1. It results:
According to the previous Equation (19), it will compute the maximum temperature rise values for both fuselinks in the condition of an asymmetric ratio of the electric current through these fuse elements. Therefore, the formula will be:
and:
In the case of the fuse with more parallel fuselinks, the sum of currents is:
I =
I1 +
I2 … +
In, and the ratio between them is:
I2 =
α1I1,
I3 =
α2I1 …
In =
αn−1I1, where 0 <
α1,
α2…
αn−1 < 1 and the index “
n” means the number of the parallel fuselinks. This results in:
Hence, the maximum temperature rise of all the fuselinks will have the expressions:
3. Three-Dimensional Thermal Model
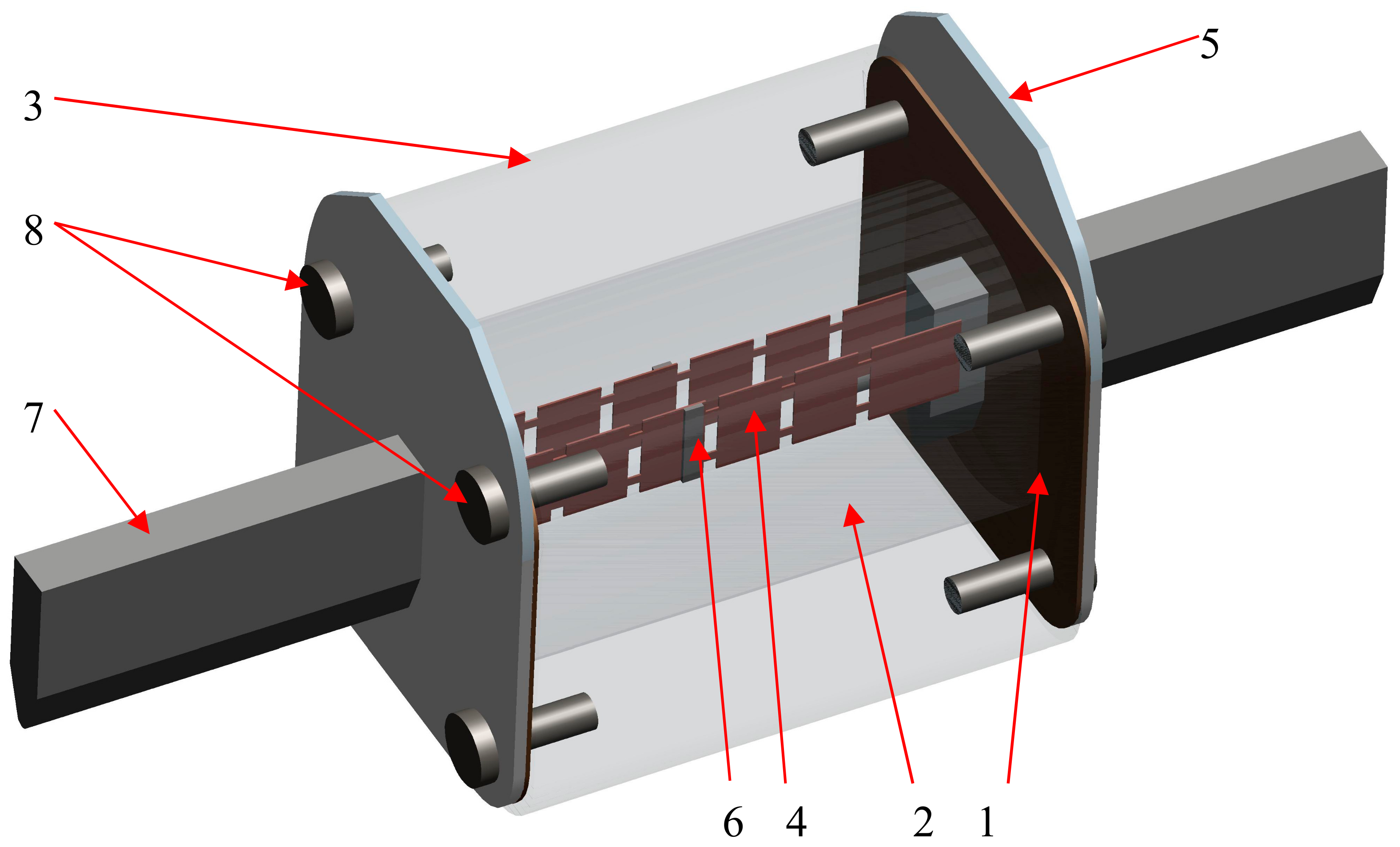
Using the software package Pro-ENGINEER, a 3D model for a HBC fuse has been developed. The analyzed HBC fuse was a gG type, size 2, having a 160 A rated current, a 550 V rated voltage, a 12.8 W rated power losses and a 120 kA rated breaking capacity. The 3D model considered all the component of a HBC fuse, that is: screws, ceramic body, silica sand, inner and outer cap, alloy M-effect attached on fuselinks and knife contacts, as presented in
Figure 3.
All thermal simulations were realised with the 3D finite elements Pro-MECHANICA software. In
Table 1 there are presented the material properties of the components, corresponding to
Figure 3. The heat load has been considered for both fuselink elements in conjunction with the considered asymmetry coefficient. These elements have a uniform spatial distribution. For the mesh of the 3D model tetrahedron solids element types has been used with the next admissible angle limits (degrees): maximum face: 175; minimum face: 5, maximum edge: 175; minimum edge: 5. The maximum aspect ratio is 30 and the maximum edge turn (degrees) is 95. Also, for the tolerance of the geometry were used the next values: minimum edge length: 0.0001; minimum surface dimension: 0.0001; minimum cusp angle: 0.86; merge tolerance: 0.0001. In order to solve the thermal steady-state simulation, it was used the single pass adaptive convergence method.
For the analyzed HBC fuse has been considered the next dimensions: the length of the ceramic body: 61 mm, square cross-section: 50 mm × 50 mm, total length including the knife contacts: 150 mm. The fuse link dimensions are: 55 mm in length, about 10mm width and 0.2 mm thickness. The environment temperature was about 25 °C. Experimental tests give the values for the convection coefficient on the ceramic body as 15.3 W/m2°C. For the metal parts of the fuse, the convection coefficient was of 19.5 W/m2°C. Convection condition was having into attention like boundary condition for the outer boundaries such as knife contacts, outer caps, screws, and ceramic body and it has been applied on surfaces with a uniform spatial variation and a bulk temperature of 25 °C.
Further, steady state thermal simulations have been realised.
Figure 4 represents the spread of the temperature into the fuse by the most thermally loaded fuselink.
Figure 5 presents the spread of the temperature through the least thermally loaded fuse element. In
Figure 6 is depicted the distribution of the temperature on the fuse at a half cross-section of it. From the figure it results higher values of the temperatures on the right side of the fuse cross-section which match to the most thermally loaded fuselink.
Figure 7 depicts only the fuse elements for a better representation of the fuselinks temperature dispense.
4. Discussion of the Results
Considering the solutions for the equations of the maximum temperature rise (20) and (21), the influence of electrical and geometrical parameters on the fuselink heating can be analyzed. A first thermal analysis was carried out for the variation of the asymmetrical coefficient of current distribution through the fuselinks, from 0.2 to 1,
Figure 8.
During this thermal analysis, the electric current through the fuse was 160 A, the total cross-section of the notch was 0.4 mm
2 and the distance between notches
x0,
Figure 2, was about 7 mm. It is to observe that when the asymmetrical coefficient is decreasing, actually, the current imbalance between the two fuselinks increases, the maximum temperature rise of the fuselink crossed by the higher current, increases,
ϑmax1calc = 579.2 °C when
α = 0.2. On the other hand, the maximum temperature rise of the fuselink crossed by the lower current decreases,
ϑmax2calc = 9.8 °C at
α = 0.2. In the situation when the asymmetrical coefficient goes equal with 1, actually, the currents through both fuselinks are equal, the maximum temperature rise of both fuselinks gets the same value of 99.8 °C. Hence, the imbalance current through the fuselinks leads to overheating of one of the fuselink which can reach the melting temperature of the fuselink material during small overloads and finally, this fuselink will be broken. Therefore, the time-current characteristic of HBC fuse will work inappropriately at least in the overload area.
The simulation values of maximum temperature rise are higher than the computed ones,
Figure 8,
ϑmax1sim = 584.3 °C,
ϑmax2sim = 11.8 °C when
α = 0.2 and
ϑmax1sim =
ϑmax2sim = 102.8 °C for
α = 1. This is explained by the fact that thermal simulations takes into account the mutual thermal influences between fuselinks.
The next thermal analysis was carried out for the variation of the notch cross-section from 0.2 mm
2 to 1.6 mm
2,
Figure 9. In this case, the constant parameters are the distance between notches, 7 mm, the asymmetrical coefficient
α = 0.8 and the electric current with the value of 160 A. The variation of the notch cross-section means the variation of the additional power loss which leads to variation of the maximum temperature rise of the fuselink. It can be noticed,
Figure 9, a decreasing of the maximum temperature rise for both fuselinks when the notch cross-section increases. The explanation is that additional power loss depends inversely proportional by the notch cross-section, and finally, the maximum temperature rise of the fuselink has the same variation. The maximum temperature rise of the most leaded fuselink, decreases from
ϑmax1calc = 201.1 °C to 95 °C and the maximum temperature rise of the least loaded fuselink, decreases from
ϑmax2calc = 106.7 °C to 54.3 °C when the notch cross-section goes from 0.2 to 1.6 mm
2.
The simulated values are close to the computed ones,
Figure 9,
ϑmax1sim = 204.7 °C,
ϑmax2sim = 109.2 °C when
s = 0.2 mm
2 and
ϑmax1sim = 98.1 °C,
ϑmax2sim = 56.2 °C for
s = 1.6 mm
2. Anyway, it is to observe that the simulated results are slightly higher than the calculated ones because of the same mutual thermal influences between fuselinks. A third thermal analysis was carried out for the variation of the distance between notches,
Figure 10.
For this analysis, the electric current was 160 A, the asymmetrical coefficient
α = 0.8 and the notch cross-section was about 0.4 mm
2. A decrease of the maximum temperature rise when the distance between notches increases is observed for both fuselinks. This is explained by the fact that the smaller the distance between notches, the greater the thermal influence of the additional power losses because of the notches on the maximum temperature rise. The maximum temperature rise of the fuselink crossed by the higher current, decreases from
ϑmax1calc = 140.8 °C to 123.5 °C and the maximum temperature rise of the fuselink crossed by the lower current, decreases from
ϑmax2calc = 79.2 °C to 69.8 °C when the distance between notches varies from 3 to 12 mm. The same as previous thermal analysis, because of the mutual thermal influence between fuselinks, the simulated values are higher than the calculated ones:
ϑmax1sim = 143.7 °C,
ϑmax2sim = 84.1 °C when
x0 = 3 mm and
ϑmax1sim = 126.4 °C,
ϑmax2sim = 72.5 °C for
x0 = 12 mm,
Figure 10. Another thermal analysis has been considered for the variation of the electric current which flows by whole fuse,
Figure 11.
The asymmetrical coefficient was considered about 0.8, the distance between notches was 7 mm and the notch cross-section had the value of 0.4 mm
2. The electric current has been varied from 140 to 240 A. As assumed, the maximum temperature rise of the fuselink increases with the current increases. Hence, at 140 A the maximum temperature rise of the most loaded fuselink is
ϑmax1calc = 92.8 °C and goes to 579.3 °C when the current reaches 240 A. On the other hand, the maximum temperature rise of the least thermally loaded fuselink, increases from
ϑmax2calc = 54.3 °C to 227.7 °C when the electric current varies from 140 to 240 A. This can be explained by the fact that the maximum temperature rise is directly proportional with the square current through the fuselink. Because of the same explanation as in previous thermal analysis, the simulated values are slightly higher than calculated ones:
ϑmax1sim = 96.1 °C,
ϑmax2sim = 56.2 °C when
I = 140 A and
ϑmax1sim = 584.1 °C,
ϑmax2sim = 231.8 °C for
I = 240 A,
Figure 11.
To validate the results obtained for the maximum temperature rise, experimental tests have been made. In
Figure 12 the electric circuit diagram used for experimental tests is presented.
The ATR auto-transformer adapts the input voltage for the high current supply device CS. From this, the high current flows by the HBC fuse F, which warms. An ammeter A, by a current transformer CT, measures the value of the current. The temperatures in the middle of both fuselinks is measured by a thermocouple Th1 type K. The thermocouples give low voltage signals which are amplified with a signal conditioning board AT2F-16. This signal is the input for a data acquisition board type PC-LPM-16 which can be programmed with LabVIEW software. The measurement points are exactly as for the thermal simulations and calculations.
For technological reasons (specialized workshops equipped with proper dentures in order to obtain fuselinks with different notch cross-sections and different distances between notches) it has been performed experimental tests only in the case of current variation for an asymmetrical coefficient of 0.8. This has been obtained from different welding points, actually a different contact resistance, between fuselinks and knife contact of the fuse.
In
Figure 11 the computed and experimental results are presented. Also, in the next
Table 2, there are presented the values of computed, simulated and experimental temperature rise for different currents.
It can be observed that the experimental temperature rise values are lower than the calculated ones
: ϑmax1exp = 88.5 °C,
ϑmax2exp = 51.6 °C when
I = 140 A and
ϑmax1exp = 576.2 °C,
ϑmax2exp = 224.4 °C for
I = 240 A,
Figure 11. This can be explained by the fact that during the experimental tests, the HBC fuse was mounted on its fuse-carrier and conductors are used to connect the fuse with the main electric circuit. Due to their volume and thermal capacity, these elements act as heat sinks for the fuselinks, with consequences in significant heat dissipation rate. Moreover, the dissimilarity between the temperature from the experimental tests and those resulted from the mathematical model are due to different factors, such as: simplifications of the thermal model, errors during the measurement, and mounting test conditions. However, there is less than 3.5 °C difference between the experimental and computed results.
The proposed mathematical model can be used only in the case of steady-state conditions. During transient conditions, the thermal model has to consider the time-variation of the temperature, or temperature rise. In this situation, the effects of fault currents upon the fuse operation can be analyzed. Also, in the case of fuselinks with different notch shapes or variable cross-section, the mathematical model has to be changed. This analysis would be considered for further research in the HBC fuse field.
5. Conclusions
High breaking capacity fuses are widely used to protect electrical installations and especially power distribution systems against overcurrents. Depending on its rated current, the fuse includes more than one single fuse element. For manufacturing reasons, during fuse operating conditions, there is the possibility that an asymmetrical current distribution between fuselinks appears, which may lead to an improper functioning of the HBC fuse.
This article describes a mathematical model capable of analyzing the maximum temperature rise of a HBC fuse with two parallel mounted fuselinks. The thermal model permits the estimation of the maximum temperature rise of both fuselinks with the current change, the cross-section variation of the notches, the variation of the distance between the notches and for the variation of the imbalance current through the fuselinks. The mathematical model can be used for a HBC fuse with “n” parallel mounted fuselinks. The mathematical expressions to compute the maximum temperature rise for all parallel fuselinks have been obtained. Also, a three dimensional thermal model for the same HBC fuse has been achieved. The thermal simulated values of the maximum temperature rise of both fuselinks are close to the computed ones. The maximum difference between these values is about 5 °C. The 3D thermal model of the HBC fuse can be used as a design tool for the power systems protection, in particular for low voltage power supply.
In order to validate the presented mathematical model and the 3D thermal model, experimental tests have been made. There are close values between computed, experimental and simulated results in the case of current variation through the HBC fuse. The maximum difference between computed and experimental results is about 3.5 °C.
The mathematical model permits one to design new types of fuselink having a suitable thermal distribution with the opportunity to obtain new solutions for a better connection between fuses and the devices to be protected.