1. Introduction
New transport paradigms have been emerging in recent years thanks to the widespread use of connected devices. This is leading to a shift from car ownership to car sharing models of transportation. One-way car sharing services, in which passengers rent a vehicle by the minute wherever it is currently parked and leave it at any other place within a given area, are already common in large cities in Europe [
1]. Autonomous driving technology would allow vehicles to autonomously move to passengers when called, making shared transportation much more convenient and speeding up its adoption [
2].
The introduction of shared autonomous electric vehicles (SAEVs), or robot taxis as they are sometimes referred to, will also transform the transport sector from the perspective of energy use. SAEVs may be an important enabler of transport sector electrification [
3]. It is therefore important to study the impact of this system on the electricity grid. In particular, SAEVs can offer synergies in the framework of a Virtual Power Plant (VPP) or microgrid. Users may sign up for both electricity and transport services from the same provider (the VPP/microgrid and SAEV operator), avoiding the costs of owning a private car. This scheme may lower the total costs of the system and may allow a larger penetration of renewable energy in the grid.
Most studies on the charging of electric vehicles and their interaction with renewable energy have focused on private vehicles, mostly assuming that vehicles are used once or twice a day and charged at night [
4]. In this work, we present a methodology for the optimization of SAEVs charging with distributed dispatchable generators (DG), renewable energy generators, grid electricity with variable pricing, vehicle-to-grid, and considering vehicles’ rebalancing requirements. We investigate the costs and carbon emissions of a SAEV system in the context of a grid-connected VPP and of an isolated microgrid compared to alternative energy storage and transport options. The economic performance of SAEVs would improve in the case of larger fluctuating renewable energy penetration. This is considered to be a synergy effect of SAEVs and renewable energy. Therefore, the aim of this study was to evaluate this synergy effect quantitatively by using the proposed method for optimizing the charging of SAEVs.
The work is organized as follows. In
Section 2, we present an overview of the related work in this field. In
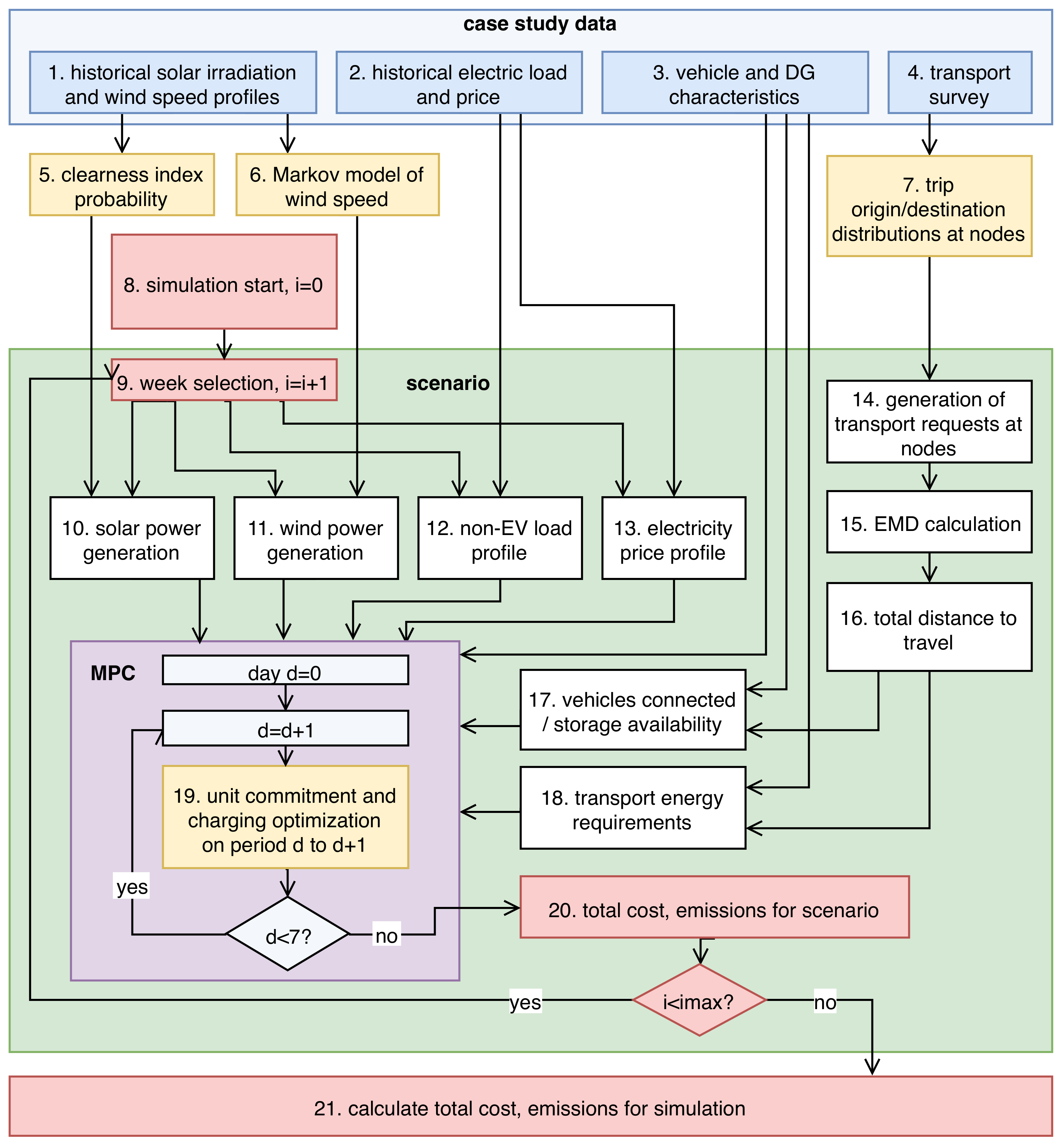
Section 3, we introduce the methodology used, including the transport demand generation, the charging optimization algorithm, and the renewable energy profile generation. In
Section 4, the assumptions and methodology specific to our case studies are presented. In
Section 5, we report and discuss the results of the simulations for the case study. In
Section 6, we present our conclusions and future work.
2. Related Work
The related academic work in this field mainly concerns the integration of renewable energy with electric vehicles and their synergies, and the operation of shared autonomous electric vehicles. There is a vast literature on the interaction of private EVs with renewable energy, and many studies have focused on SAEV operation. Electric vehicles offer great opportunities for grid balancing and integration of renewable energy sources, because of the flexibility of charging [
5,
6]. Vehicle to grid (V2G), or the discharge of vehicle batteries to the grid, has also been proposed as a way to further increasing their benefits by replacing peak generation [
7,
8]. Effective strategies have been developed for the participation of aggregated vehicle fleets with V2G in the electricity markets [
9].
Most studies on electric vehicles and renewable energy consider private vehicles. Liu et al. [
6] presented a review of electric vehicles interacting with renewable energy in the context of the smart grid. They categorized work on EVs into three types depending on the objective: minimization of cost, maximization of efficiency or minimization of emissions. The review also highlights that mixed-integer linear programming (MILP) and stochastic analysis for intermittent renewable energy sources are common in the literature. Liang and Zhuang [
10] discussed the literature on stochastic modeling and optimization in microgrids. Nosratabadi et al. [
11] presented a useful review of distributed energy scheduling in microgrid and virtual power plants, including work that consider EVs. Mwasilu et al. [
12] presented a review of the work on the interaction between EVs with V2G and renewable energy. One of the highlighted problems is the difficulty in implementing V2G in practice with private vehicles.
Wang et al. [
13] studied the impact of electric vehicles and demand response on a power system with wind power generation. The simulations are run over a the period of a week, with 24 h optimization period and the last hour of the previous period used as the first hour of the next optimization period. They modeled the availability of vehicles by estimating the time of arrival of the vehicle at home. They found that electric vehicles can significantly decrease the cost when smart charging of vehicles is employed for the case study of the expected Illinois grid in 2020. Su et al. [
14] proposed a stochastic optimization model for operating cost minimization of a microgrid with EVs, wind and solar power, batteries, and distributed dispatchable generators. They considered both the energy scheduling problem and subsequently iteratively adjusted the results to minimize distribution losses and satisfy grid constraints. Saber and Venayagamoorthy [
15] proposed a method to maximize renewable energy utilization to minimize costs and emissions in smart grid with EVs and V2G. Schuller et al. [
16] formulated a MILP problem for the quantification of load flexibility of EVs for renewable energy integration in the grid. They used driving patterns of full-time employees and retired persons from the German Mobility Panel to simulate two common classes of vehicle usage. Renewable generation is taken from the German grid and scaled to the actual consumption of EVs to quantify the ability of EVs to balance the intermittent generation. They considered backup generators in form of gas turbines. The study analyzes the effect of shorter optimization horizon from a week to one day to test a more realistic limited advanced knowledge. They concluded that optimal smart charging significantly increases the utilization of renewable energy, with the best performance in a solar/wind mixed generation portfolio. They also found that EVs have significant inter-day flexibility. Arslan and Karasan [
17] developed an energy management model for the minimization of VPP costs considering distributed generation, renewable energy sources, and EVs. They evaluated the impact of VPP formation on costs and carbon emissions in a community. They conducted a extensive sensitivity analysis to understand the influence of several parameters on the results for a case study in California. They concluded that VPP are effective at decreasing costs for participants and can represent a solution to several challenges in the electricity market in the future.
Vehicle connection is one of the main problems for coordinating the charging of private electric vehicles [
18,
19]. This has been generally dealt with by estimating the time of arrival of people at home [
13,
18,
19,
20]. Another problem is the determination of the minimum final SOC of private vehicles. Many studies assume that vehicles should have 100% SOC at the beginning of the day [
13,
21], thus limiting the amount of charging flexibility allowed. These problems are mitigated by SAEVs, as vehicles can move to charging stations whenever they are not transporting passengers.
There is limited literature focusing on shared EV systems. Kahlen and Ketter [
22] developed an algorithm for the control of vehicles in a carsharing system. Decisions in this model concern the commitment of vehicles for operating reserve, the charging of vehicles, or the commitment for transport service. The decision is made by comparing expected profits over future time steps for each action, and it is calculated with a multiple linear regression model. By testing the model with data from a free floating carsharing system they found that profits could increase by 7–12% with practically no decrease in vehicle availability. Biondi et al. [
23] developed a method for the optimal positioning of charging station for electric car sharing systems and study the impact of these systems on the electricity grid.
SAEV operations in terms of transport have been the focus of several studies. Zhang et al. [
24] developed a model predictive control approach for the optimization of an autonomous car-sharing system with rebalancing which considers electric charging constraints. Chen et al. [
25] studied the operation of a SAEV system with a model based on Ref. [
2]. The agent-based transport model methodology is similar, but the investigation is expanded by including charging of the electric vehicles serving 10% of trip demand in a medium-sized metropolitan area. Bauer et al. [
26] developed an agent-based model for the simulation of SAEV. They found the optimal battery size and number of charging stations to minimize costs through sensitivity analysis. They concluded that vehicles with 50–90 miles range and 66 chargers per square mile (25 per square km) with a 11 kW connection can provide service with a cost of
$0.29–
$0.61 per mile (
$0.18–
$0.38 per km), about 10 times lower than normal taxis and lower than if the service was provided by any non-electric vehicle. They also calculate that SAEVs would reduce GHG emissions by 73% compared to current taxis with the current power grid. Chen et al. [
27] introduced a methodology for the optimal routing and charging of EVs in a fleet. They included a simplified analysis of the possible impacts of the system on the electricity distribution network. All models considered do not consider “smart” charging, or optimized charging taking into consideration grid-side aspects such as dynamic electricity price or grid constraints. In particular, Chen et al. [
25] found that simultaneous charging of the fleet at peak times may be problematic for the electric grid. This is a known problem of uncoordinated electric vehicles charging [
7].
As shown in this section, the topic of shared vehicles interacting with renewable energy has been largely overlooked. SAEVs present different availability patterns compared to private vehicles. Private vehicles tend to be connected at night and less during the day while owners stay at their destination. In contrast, SAEVs can be connected at any time when they are not serving passengers. Moreover, SAEVs have the potential to replace a large number of vehicles, thus decreasing the total amount of battery storage available. As many studies on SAEVs predict that these systems will soon be commercially available and potentially replace private vehicles in many cases, it is important to understand the impact of this shift on the potential for electrified transportation to integrate renewable energy in the grid.
5. Results and Discussion
In this study, two cases were considered for analysis: grid-connected VPP without DG, and isolated microgrid with DG. Each data point represents 100 week-long simulations, taken from Mondays to Sundays of the load profile.
5.1. VPP Case
We considered five scenarios to compare the cost and emissions performance of SAEV to other options and the effectiveness of the optimization algorithm in the context of a VPP. These are summarized in
Table 5. The Business as usual (BAU) case assumed private vehicles and electricity from utility at a fixed price of 20 yen/kWh and excess generation sold at the marginal price (see
Section 4.4). The battery case assumes that households install a battery and join a VPP with an energy management system that minimizes total costs. The three SAEV scenarios assume that households join a VPP that also provides transport services via SAEV (thus, they avoid buying a private vehicle) without installing a battery. The three scenarios differ with regard to the charging strategy applied, and correspond, respectively, to unscheduled charging, optimized charging without V2G, and optimized charging with V2G.
Total costs for each scenario are shown in
Figure 4. A breakdown of costs and the CO
emissions for each scenario are reported in
Table 6. The cases with transport provided by SAEV (Scenarios 4–6) are the lowest cost options. The cost savings are dominated by capital costs, as vehicles are shared among all participants in the VPP while avoiding the cost of each individual buying a private vehicle. However, the cost of electricity becomes significantly higher in the case of SAEV, although it is still lower than the fuel costs it replaces. The proposed algorithm decreases electricity costs by 32% and 75%, respectively, for the scenario with no V2G and with V2G over the unscheduled charging. The difference would increase with more variable electricity prices in markets with higher penetration of intermittent sources.
Carbon emissions increase significantly in the SAEV cases, due to the combined effect of high carbon intensity of the Japanese grid and the high efficiency of hybrid cars. Another important factor is the higher total distance traveled by SAEV compared to private vehicles due to the need to rebalance empty vehicles, as discussed previously. However, we did not consider the life-cycle emissions, which would likely be significantly lower due to the need for fewer vehicles. The optimization objective function could also be expanded with carbon pricing and hourly carbon intensity to minimize the emissions. This was not considered in this work due to lack of data.
5.1.1. Sensitivity to Autonomous Driving Technology Costs
Autonomous driving technology costs are the most important factor determining the total cost of the system. This is because capital costs dominate the total costs, being about 10 times the variable costs (
Table 6). However, even for the case in which vehicles cost 6 million yen (
$60,000), the SAEV + VPP systems are cheaper than the alternative (
Figure 5a).
5.1.2. Sensitivity to Battery Costs
The sensitivity to battery costs is presented in
Figure 5b. Battery costs are a major factor in determining the operating or variable costs. Costs for SAEV with V2G decrease faster than other cases, as the lower cost of battery cycling allows vehicles to be used for grid storage. It should be noted that battery prices are expected to fall significantly in coming years. Bloomberg New Energy Finance 2017 Lithium-Ion Battery Price Survey gives average pack prices of
$209/kWh (20,900 yen/kWh) in 2017, and they expect these will fall below
$100/kWh (10,000 yen/kWh) by 2025 [
50].
5.1.3. Sensitivity to Fuel Prices and Fuel Efficiency
Operating or variable costs (fuel, electricity and battery) are very sensitive to fuel prices and HEV fuel efficiency. While variable costs for the BAU and battery cases are similar with SAEV cases in the baseline scenario, these costs diverge significantly with less optimistic assumptions for HEV. This is shown in
Figure 6. A fuel efficiency of 20 km/liter is the target for new vehicles sold in Japan in 2020 [
51]. Note that 15, 20 and 23 km/liter are equivalent to 35, 47 and 54 mpg, respectively. This is still very optimistic for HEV, and the average fuel efficiency of vehicles may be towards the lower end of the range, thus favoring SAEVs. Fuel prices may also increase as oil prices increase.
5.1.4. Effect of Increasing Solar Grid Penetration
The value of grid storage is higher with higher grid penetration of intermittent renewable energy. To test the effect of different levels of intermittent renewable energy penetration on the grid, the approximate aggregate cost curve of dispatchable generation in the TEPCO area was estimated by fitting an exponential curve to the demand/price data from JEPX (
Figure 7a). This allows the generation of artificial electricity price profiles depending on load and renewable energy generation profiles. We tested the case of increasing penetration of solar power in the grid, with the results reported in
Figure 7b. Higher solar penetration depresses prices paid for excess solar generation and encourages self-consumption and storage. This especially favours SAEV cases that can charge when prices are lower. The V2G case shows almost no difference with the scheduled case without V2G. This is because this simple analysis neglects some side-effects of higher solar penetration, such as the fast and expensive ramping needed at evenings. This would further increase the value of V2G providing peak generation.
5.2. Microgrid Case
The same transport, load and weather data used for the VPP were used to test the microgrid case. We assumed an isolated microgrid with no grid connection (
). We tested the same scenarios presented in
Table 5 with renewable capacity sized to cover all electrical loads over a year with a 50/50% share of wind and solar power. The results are listed in
Table 7. Total costs are shown in
Figure 8. An example of the results for one week with and without V2G is presented in
Figure 9. In
Figure 10, we report the average utilization and load factors. These are defined, respectively, as the share of time a generator is active over the whole period, and the load level of the generator when active. As generators are less efficient at lower load factors, higher load factors are preferable. The effect of lower load factor on varying the per unit carbon emissions or costs were not considered for simplicity. The cases with batteries and with SAEV + V2G show the highest load factors and the lowest utilization factors. In particular, this implies the possibility to re-size the system with less generators, thus reducing the capital costs. This effect was not considered in this work (the generators are assumed to be already present).
Sensitivity to Renewable Energy Capacity
The sensitivity to renewable energy capacity is shown in
Figure 11. The values of capacity represent the share of yearly load generated by renewable energy. These correspond to RE capacities listed in
Table 7. SAEVs are effective at integrating renewable energy in the system. The total cost for the BAU case with no renewable energy is approximately the same as for the case with SAEV + V2G with 150% renewable energy. As shown in
Figure 11b, this allows a drastic decrease in carbon emissions at the same cost level.
5.3. Implications for Policy and Practice
The results suggest that there would be significant advantages for households shifting from a private vehicle to a SAEV system in the context of a VPP or in a microgrid. This could help accelerate transport electrification, provide large amount of grid storage to integrate intermittent renewable sources, and avoid the problems connected with the introduction of a large amount of non-controlled EVs on the grid. Rapidly decreasing costs of batteries and autonomous driving technology would make the system even more favorable. However, in the current situation, the system may increase carbon emissions in the Japanese context. The introduction of carbon pricing with a real-time carbon intensity signal from the grid may not only solve this problem, but also actively decrease the total carbon emissions. It should also be noted that, even though in this work we considered a constant average carbon intensity, vehicles tend to charge at periods of excess electricity generation and low prices, which often correspond to high renewable energy generation and thus lower carbon intensity.
The results may also apply to non-autonomous car sharing systems, although the cost of manual rebalancing would likely make the system more expensive and the absence of autonomous capability less attractive to users.
6. Conclusions
The synergies between Shared Autonomous Electric Vehicles (SAEV) and renewable energy sources were studied in the context of a grid-connected Virtual Power Plant (VPP) and an isolated microgrid. An optimization methodology was developed for the charge and discharge of the vehicles to minimize costs for the system. We tested the model with several scenarios using weather data and transport patterns for the Tokyo region. The results for the case study show that SAEV with the optimized charging are effective at decreasing the overall costs in the VPP. The proposed algorithm also decreases electricity expenditures by 75% over the unscheduled charging in the case of SAEV + V2G. Total cost savings are however dominated by capital cost savings due to lower number of vehicles needed. Overall, total costs are about 20% lower for households with rooftop solar power shifting from utility power and hybrid private vehicles to the VPP with SAEV. We also show that further electricity savings (and possibly profits) could be attained in a grid with higher penetration of intermittent renewable energy, demonstrating strong synergies existing between SAEVs and renewable energy. In the case of the isolated microgrid, SAEVs with V2G decrease cost by 16% and cut carbon emissions by half. This demonstrates the potential of SAEV to promote the integration of intermittent renewable energy while reducing total costs for the system.
This is an early work on the integration of SAEV with renewable energy, and several other aspects could be investigated in future work. Real-time grid carbon intensity could be used to extend the cost function to include carbon pricing to reduce vehicles’ emissions. In addition, an estimate of the life-cycle carbon emissions of the systems studied would allow assessing more realistically the impact of this technology. A more detailed model of dispatchable generation costs could be used to investigate more realistically the effect of increasing penetration of renewable energy in the grid and the potential for vehicles to provide grid storage. Moreover, the provision by vehicles of high revenue grid services such as frequency control or operating reserves could be included in the optimization.