An Energy-Balanced Geographic Routing Algorithm for Mobile Ad Hoc Networks

Abstract

To mitigate the frequent link breakage and node death caused by node mobility and energy constraints in mobile ad-hoc networks, we propose an energy-balanced routing algorithm for energy and mobility greedy perimeter stateless routing (EM-GPSR) based on geographical location. In the proposed algorithm, the forward region is divided into four sub-regions. Then, according to the remaining lifetime of each node and the distance between the source node and the destination node, we select the next-hop node in the candidate sub-regions. Since the energy consumption rate of the node is taken into account, the next-hop selection favors the nodes with longer remaining lifetimes. Simulation results show that compared with conventional greedy perimeter stateless routing (GPSR) and speed up-greedy perimeter stateless routing (SU-GPSR) routing algorithms, the proposed algorithm can lead to a lower end-to-end delay, longer service time, and higher transmission efficiency for the network.

1. Introduction

A mobile ad-hoc network is a self-organized multi-relay wireless communication network which is composed of a number of mobile nodes with limited volume [1,2,3]. Mobile ad-hoc networks complete the information transmission with multiple hops. With the rapid development of computing, sensor, communication and network technology, mobile ad-hoc networks will play a new role in military and civilian applications, such as search and rescue operations, target detection, prevention of attacks, wind speed estimation, etc [4,5,6,7,8].

Due to the limited energy of nodes, the wide application of mobile ad-hoc networks is restricted. Therefore, the optimization of energy use and network load balancing has been a hot topic in the industry and academia [9]. With the increasing demand for multimedia applications, the energy consumption of nodes increases sharply in particular. If mobile nodes run out of energy, it will directly lead to data transmission interruption. The failure or exit of nodes may split the network and affect the quality of service of the network [10], which leads to higher requirements for the load-handling of the network. Therefore, an efficient energy balance and an accurate and timely perception of the nodes’ remaining energy are crucial for mobile ad-hoc networks to move from theory to practice.

Traditional routing protocols in mobile ad-hoc networks usually use the clustering algorithm to reduce energy consumption. In the cluster structure, nodes with lower energy are used for sensing near the target, while nodes with higher energy are selected as cluster heads for processing and sending information [11]. In Reference [12], the authors propose a hierarchical clustering algorithm (HCAL) and a corresponding protocol for hierarchical routing in large-scale mobile ad-hoc network. HCAL jointly utilizes table-driven and on-demand routing using a combined weight metric to search the dominant set of nodes. Motivated by an energy-efficiency policy for the optimal selection of cluster-heads in the wireless sensor networks, in Reference [13], a modified stable election protocol, named Prolong-SEP (P-SEP), is presented to prolong the stable period of fog-supported sensor networks by maintaining balanced energy consumption.

In cluster-based routing algorithms, data aggregation and fusion are performed to reduce the amount of messages sent to the base station (BS), which greatly improves the extendability of the whole system and effectively reduces the energy consumption. However, the throughput and the packet loss rate of cluster-based routing are not good enough [14]. To gain a better performance for clustered multihop mobile wireless networks, routing must take radio channel access, code scheduling, and channel reservation into account. In Reference [15], the authors propose heuristic routing schemes for clustered multihop mobile wireless networks. Considering that existing active clustering mechanisms require a periodic refresh of neighborhood information and introduce a significantly large amount of communication maintenance overhead, Gerla et al. [16] introduce a passive clustering scheme which is mostly supported/maintained by user data packets instead of explicit control packets.

In Reference [17], it has been shown that if the queue lengths are observed at both servers, the optimal decision is to route jobs to the shorter queue, while if the queue lengths are not observed, it is best to alternate between queues, providing that the initial distribution of the two queue sizes is the same. Reference [18] presents a loop-free, distributed routing protocol for mobile packet radio networks. The routing algorithm adapts asynchronously in a distributed fashion to arbitrary changes in topology in the absence of global topological knowledge. Ahmadi et al. [19] present an energy- and delay-aware routing method which combines Cellular automata (CA) with a Genetic algorithm (GA). The algorithm identifies a set of routes that can fulfill the delay constraints based on CA, and selects a reasonably good one by using the GA.

The geographic position-based routing protocol makes packet forwarding decision according to the positions of nodes. Compared with the cluster-based routing protocol, this kind of routing protocol is especially suitable for mobile ad-hoc networks. In such networks, each node does not need to maintain the routing table and the global network topology, but only needs to know the location information of the neighbor nodes within its communication radius. The routing can be established only by judging the current state of the next-hop node [20].

Greedy perimeter stateless routing (GPSR) [21] is a typical routing protocol based on geographic information. Compared with traditional routing protocols, GPSR takes into account the energy and movement velocity of nodes [22], which has become a hot topic in the research of network routing protocols. The geographic source routing (GSR) protocol proposed in [23] aims to apply GPSR to urban environments. GSR uses the Dijkstra algorithm and forwards packets to the destination via the shortest path between the source and destination. In Reference [24], a forward algorithm called GPSR Divisional Perimeter (GPSR-DP)is proposed, which improves the performance of GPSR by using the right-hand rule and the left-hand rule. Specifically, in the GPSR-DP protocol, if a routing void occurs, a forwarding node on the left or right side of the sending node is selected according to a heuristic algorithm.

As in GPSR, the proposed algorithm in Reference [20] does not change the forwarding behavior when reaching a dead end, and the packets are simply discarded. On the basis of the GPSR algorithm, a congestion control based routing algorithm is proposed in Reference [25] to solve the network congestion problem caused by high network node density under heavy load. It balances the network load and reduces the packet transmission delay. In Reference [26], an improved GPSR routing algorithm, ferry-assisted GPSR protocol (FA-GPSR), is designed to solve the problem of network connection disruption caused by the continuous movement of combat units in military scenarios. The patrol nodes are deployed in the perimeter of the combat scope. When the plane perimeter forwarding fails, the patrol node is used to transmit the data packets until the destination node or the next greedy node is reached.

However, References [20,21,22,23,24,25,26] do not take into account node energy consumption and node mobility in the actual environment. The influence of vehicle movement velocity on the GPSR protocol is mentioned in Reference [27], and a method to overcome this effect is proposed, but the mobility of nodes is not considered. The GPSR routing through movement awareness (GPSR-MA) protocol is proposed in reference [28] for vehicular ad-hoc networks, which adds speed and direction parameters to the basic GPSR packet header format. Therefore, it extends the perception of routing protocols to the mobility state of nodes and uses additional information in subsequent routing decisions. However, the proposed algorithm in Reference [28] only considers node mobility and does not consider node energy consumption. In Reference [29], an enhanced and more energy-efficient resource management method are proposed through a joint interest, physical and energy-aware clustering and resource management framework, capitalizing on the wireless powered communication technique in Machine-to-Machine-driven Internet of Things. In Reference [30], the problem of coalition formation among Machine-to-Machine (M2M) communication type devices and the resource management problem is addressed. Each M2M device is characterized by its energy availability, as well as by differentiated interests for communicating with other devices based on the Internet of Things (IoT) application that they jointly serve. While in References [29] and [30], the node mobility is not considered.

In Reference [31], an energy-balanced routing algorithm based on a probabilistic transmission model (EGPSR) is proposed. This algorithm divides the forward region into four parts with equal area, thus prolonging the network’s lifetime. Although the proposed algorithm considers the energy consumption of the nodes in mobile ad-hoc networks, it ignores mobility, the most basic feature of mobile ad-hoc networks. In Reference [32], a routing algorithm considering node energy and mobility, SU-GPSR, is proposed to solve the node mobility problem ignored by Reference [31]. However, the SU-GPSR algorithm does not take into account the relationship between the remaining energy and the energy consumption rate of the node, and the node energy is therefore not balanced.

In this paper, we propose an improved GPSR algorithm named EM-GPSR (Energy and Mobility GPSR), by integrating the node mobility and the node remaining energy. With respect to the node mobility, this work firstly divides the forward region according to the remaining lifetime of the link. Then, it selects the next-hop node in the candidate region according to the remaining lifetime of the node, the distance from the node to the destination node, etc.. Regarding the node energy balance, when taking the energy consumption rate into account, the selection of the next hop favors the node with the longest remaining lifetime. Simulation results show that, compared with conventional greedy perimeter stateless routing (GPSR) and the SU-GPSR routing algorithms, the proposed algorithm can lead to a lower end-to-end delay, longer service time, and higher transmission efficiency for the network.

2. GPSR

The GPSR protocol is a geographic routing protocol that takes into account nodes energy and speed of mobility. In the GPSR protocol, nodes are uniformly distributed and know their geographical positions. Firstly, the greedy algorithm is used to forward the data along a straight line, and the nodes forward the data to the nearest neighbor node (using the Euclidean distance). However, if the node is too far from the destination node, the data can not be transferred through a single hop. In this case, there appears a routing void, with the result that the data can not be transmitted. Under this situation, the protocol uses the boundary forwarding algorithm to forward data to the nodes on the void’s region boundary. The routing algorithm mainly uses two modes: The greedy algorithm mode and the perimeter forwarding mode. The principles of these two patterns are described as follows.

GPSR uses a greedy algorithm to establish routing, tag packet with positional information, forward packets according to the position of the destination node, and greedily select the next-hop node. When the source node forwards the data packet to the destination node, the node with the shortest distance to the destination node is selected as the next hop from the neighbor nodes within the communication range of the source node. The process is iterated until there is no node closer to the destination node than the current node (there is a routing void).

The perimeter forwarding mode mainly uses the right-hand rule for perimeter traversal. However, the right-hand rule cannot be used on non-planar graphs, so the prerequisite for perimeter forwarding is the construction of a planar graph within the communication range, in which any two edges do not intersect [33]. In GPSR, two algorithms, Relative Neighborhood Graph (RNG) and Gabriel Graph (GG), are used to remove the intersecting edges [34,35]. In the RNG algorithm, the condition for the existence of a link between nodes u and v is that the distance between u and v is not greater than the maximum distance between u and w or v to w for any node w. In the GG algorithm, the condition for the existence of edges between nodes u and v is that there are no other nodes in the circle where the diameter is $d(u,v)$.

If the next-hop node can not be found within the range of the communication radius R when using the greedy forwarding mode, the routing will be automatically switched to planar perimeter forwarding. When the source node S has data to transmit to the destination node D, it uses the right-hand rule to find the next-hop node a, as shown in Figure 1. Then, the node position of the switching mode is recorded. If the distance between the next-hop node a and the destination node is still larger than the distance between S and D, then the planar perimeter forwarding is continued, otherwise, the greedy forwarding is applied. As shown in Figure 2, when a routing void appears at S, the planar peripheral forwarding is applied. When the node with the plane peripheral forwarding is closer to the destination node than the node with the routing void, it will turn to the greedy forwarding mode, according to the data forwarding rules of the GPSR algorithm. Then, the final path is $S\to a\to b\to c\to e\to f\to D$.

3. EM-GPSR

According to the data forwarding rules of the GPSR algorithm, the closer to the destination node, the faster the energy of the node is consumed. The node energy depletion may lead to network fragmentation, affecting the overall performance of the network. Therefore, balancing the energy consumption of nodes is an important challenge in the design of routing algorithms for mobile ad-hoc networks. In order to explain the research motivation and ideas of the routing algorithm proposed in this paper, the related SU-GPSR algorithm is introduced first. By introducing the specific steps of the SU-GPSR algorithm, this paper summarizes the problems and defects of the SU-GPSR algorithm. On this basis, we propose an improved GPSR algorithm that comprehensively considers node mobility and residual energy, namely EM-GPSR.

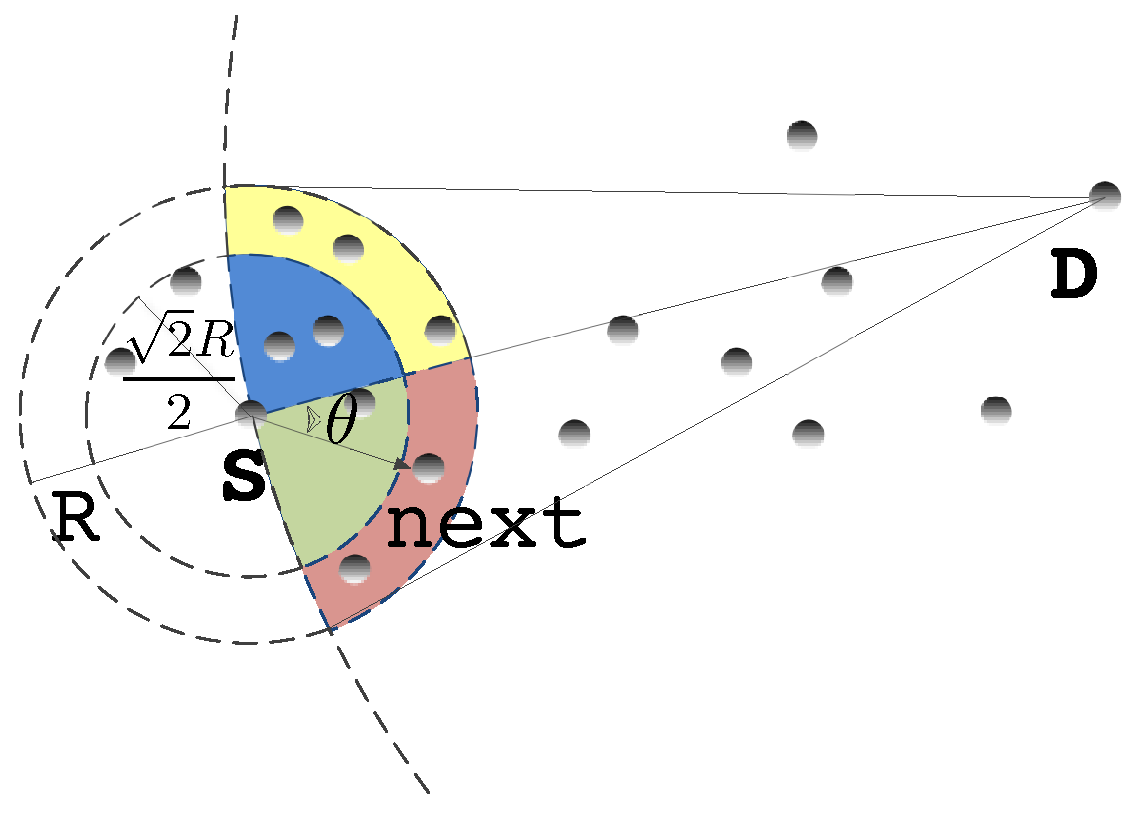
3.1. SU-GPSR

For the problem of node energy limitation in ad-hoc networks, Reference [31] proposes an energy-balanced routing algorithm, EGPSR, based on a probabilistic transmission model. The algorithm categorizes the next-hop region into four parts with equal area, calculates the average remaining energy of each region, and takes the region with the highest average remaining energy as the next-hop candidate region. Although the proposed algorithm considers the energy consumption of nodes for mobile ad-hoc network scenarios, it ignores the mobility of mobile ad-hoc networks.

Regarding the disadvantage of Reference [31], Sun et al. [32] design the SU-GPSR routing algorithm, which considers the node energy and the node mobility. The algorithm improves the method of dealing with routing voids. Similar to EGPSR, the number of nodes in each sub-region is different. According to the average energy, a sub-region is selected as the next-hop candidate region. The SU-GPSR algorithm considers the remaining energy of the node after this forwarding instead of the current remaining energy. The remaining energy after forwarding can be expressed as

$$E_i^{{}^{\prime }}=E_i-E_{R\_elec}·k-E_{T\_elec}·k·L_i+H{E}_i$$

(1)

where k indicates the number of bits received or transmitted, $E_i$ is the remaining energy of the next-hop node i, $E_{R\_elec}$ is the energy consumed by receiving one bit of data, $E_{T\_elec}$ denotes the energy consumed by sensing one bit of data and the destination node, respectively. $H{E}_i$ represents the energy harvested by node i through energy harvesting, and can be expressed as

$$H{E}_i=E_i·\rho ·(-e^{-k_i/n}+1)$$

(2)

with

$$k_i={\displaystyle \frac{u_i^{pv}·v_i^{pv}}{c_i}}$$

(3)

Here, $\rho$ represents the energy harvesting efficiency, $u_i^{pv}$ and $v_i^{pv}$ are the output voltage and output current, and $c_i$ indicates the remaining energy of node i. Among different regions, the next-hop candidate region is selected by comparing the average prediction of the remaining energy. On this basis, SU-GPSR considers the mobility of the node and selects the next-hop node according to Equation (4) in the candidate sub-region.

$$p_j=\left\{\begin{array}{cc}{\displaystyle \frac{\alpha E_j}{{\displaystyle \sum _{i=0}^q}{E}_i}}·{\displaystyle \frac{N_j}{{\displaystyle \sum _{i=0}^q}{N}_i}}·\left(1-{\displaystyle \frac{L_j}{{\displaystyle \sum _{i=0}^q}{L}_i}}\right)·cos\theta ·F,\hfill & q\ge 2\\ 1,\hfill & q=1\\ 0,\hfill & q=0\end{array}\right.$$

(4)

where $N_i$ is the number of adjacent nodes of the next-hop node i, and $L_i$ is the distance from the next-hop node to the destination node. The symbol $\theta$ denotes the angle formed by the next-hop node, the current node and the destination node. The smaller the value of $\theta$ is, the closer the next-hop node is to the destination node. q and $\alpha$ are the number of nodes in the candidate region and the weight of the energy factor, respectively. Hence $\alpha$ can be expressed as

$$\alpha ={(1+H)}^{1+\rho }$$

(5)

where H indicates whether the node has the capability of harvesting energy, as shown in Equation (6).

$$H=\left\{\begin{array}{cc}0,& \mathrm{next}\mathrm{node}\mathrm{without}\mathrm{harvesting}\hfill \\ 1,& \mathrm{next}\mathrm{node}\mathrm{with}\mathrm{harvesting}\hfill \end{array}\right.$$

(6)

The function F in Equation (4) is defined in Equation (7), which indicates the weight for the selection of a static or mobile node.

$$F={(M+1)}^{\frac{T_L-(T_{now}-T_0)}{T_L}-\frac{1}{2}}$$

(7)

where, $T_L$ represents the maximum survival time of the data packet, $T_{now}$ indicates the current time and $T_0$ represents the data packet generation time. M indicates whether the selected node is mobile or static and can be expressed as

$$M=\left\{\begin{array}{cc}0,& \mathrm{if}\mathrm{static}\mathrm{node}\hfill \\ 1,& \mathrm{if}\mathrm{mobile}\mathrm{node}\hfill \end{array}\right.$$

(8)

3.2. Energy-Balanced Model

The SU-GPSR algorithm takes into account the remaining energy and the mobility of the node, the distance to the destination node and the remaining time of the packet. The OPNET simulations show that SU-GPSR has a longer network lifetime than GPSR under different network densities. When some nodes in the network are mobile, the delay of SU-GPSR is lower and the number of hops is less. However, the algorithm has the following defects:

• The best next-hop node cannot be selected according to geographical location. If the node with the most energy and the least energy is in the same area, the selection may not fall in this region;
• The mobility of nodes is only distinguished by zero and one. Obviously, it cannot reflect the motion characteristics of nodes;
• Although the prediction model of energy consumption is proposed, the energy consumption rate of nodes is not taken into account.
• Energy harvesting is not a common function of mobile ad-hoc network nodes at present. Harvesting devices bring additional cost and the energy harvesting efficiency is not clearly stated.

Aiming at the problems of SU-GPSR, an improved GPSR algorithm, EM-GPSR, is proposed in this paper, which comprehensively considers the mobility and the remaining energy of the node. The EM-GPSR algorithm categorizes the next-hop region into four sub-regions with equal area, then calculates the average remaining energy of each sub-region, integrating the node energy consumption rate and the node remaining energy.

First of all, the four sub-regions categorized on the basis of SU-GPSR, shown in Figure 3, have the same area, thus the radius of inner circle equals $\sqrt{2}R/2$.

The number of nodes in each sub-region is different. Each node in the same area has its own movement velocity. According to the information of node velocity and position, we calculate the remaining lifetime of the perimeter node leaving the current communication range. If the remaining lifetime is below the threshold, it means this node does not belong to the candidate set. The threshold value is set to ensure that $25\%$ of the nodes have a remaining lifetime larger than the threshold value. Finally, the next-hop node is selected in the candidate set according to Equation (9):

$${\psi }_j={\displaystyle \frac{N_j}{{\displaystyle \sum _{i=0}^q}{N}_i}}·\left(1-{\displaystyle \frac{L_j}{{\displaystyle \sum _{i=0}^q}{L}_i}}\right)·cos\theta ·{\displaystyle \frac{TN{L}_j}{{\displaystyle \sum _{i=0}^q}TN{L}_i}}$$

(9)

where $TN{L}_i$ represents the remaining life-time of node i, which can be expressed as

$$TN{L}_i={\displaystyle \frac{E_i}{r_i}}$$

(10)

where $E_i$ represents the remaining energy of node i and $r_i$ the energy consumption rate. We use the HELLO packet in the EM-GPSR algorithm to update the position and velocity periodically. The remaining lifetime of the node link is calculated by the velocity and distance of the node. The next-hop node is selected according to the weight ${\psi }_j$.

When node S is ready to transmit data to node D, we first select the candidate set according to the node state information (speed and distance) in the routing table. As shown in Figure 4, the candidate set selected according to the link remaining lifetime and the threshold value are yellow nodes $a,b$ and c. Then, from Equation (9) we select c as the best next-hop node in the candidate set and repeat this strategy in further selections, until the packet reaches the destination node or there appears a routing void. The selection example can be demonstrated in Figure 5. When a routing void is encountered, the data are forwarded according to GPSR’s planar perimeter forwarding mode (right-hand rule).

3.3. Flow of the EM-GPSR Algorithm

In terms of the features of EM-GPSR, we extend the HELLO packet format of the GPSR protocol [36], including node ID, position, velocity and remaining lifetime, as shown in Figure 6. Note that the signaling overhead of our algorithm is more than twice that of the most basic hello protocols [37], while our routing performance is greatly improved, at the cost of overhead.

The EM-GPSR routing protocol is designed according to the energy balance optimization model. The concrete steps are listed as follows.

• Step 1: Network initialization, where all nodes periodically send HELLO packets to neighbor nodes.
• Step 2: If node i receives a HELLO packet from a neighbor node, it checks whether the node ID in the HELLO packet already exists in its local memory.
• Step 3: When the source node S is ready to transmit data to the destination node D, according to the routing table node state information (movement speed and distance), it selects the candidate set first. Then, according to Equation (9), it further selects the best next-hop node c from the candidate set and sends the packet to the node c.
• Step 4: The node c receives the data packet, determines whether it is the destination node, if so, ends the routing process; otherwise, it determines whether the selected region is void, and if not, employs planar forwarding (right-hand rule), otherwise it returns to step 3.

A flowchart of the EM-GPSR routing protocol is shown in Figure 7.

4. Simulation

In this section, we compared the performance of the proposed strategy with several geographic routing algorithms. Among them, GPSR is a classic ad-hoc routing algorithm based on the geographic location. SU-GPSR is a routing protocol that considers energy consumption balance and the mobility of nodes. Firstly, on the basis of the mobility of nodes and the remaining lifetime of the link, the candidate nodes are divided by the threshold, and then the node above the threshold is selected according to the weight of the measurement.

GPSR, SU-GPSR, Improved Energy and Mobility ACO (IEMACO) and the proposed EM-GPSR routing strategy are simulated and analyzed with the OPNET network simulation tool, and the simulation parameters are set up as shown in

Table 1. Simulation parameters.

Parameter	Value	Parameter	Value
Scene size	1000 m × 1000 m	Mobile nodel	Random Way Point
Node Velocity	0–50 m/s	Node number of network	40
Initial node energy	1000 J	Packet rate	1–10 packets/s
MAC protocal	IEEE 802.11	Data rate	1 Mbps
Communication range	250 m	Packet size	512 Bytes
Simulation time	200 s	HELLO packet size	15 Bytes
Max waiting time of HELLO packet	12 s	Update cycle of HELLO packet	3.5–4.5 s

.

Figure 8 shows how the average end-to-end delay of different routing algorithms varies with the speed at which the node moves. It can be seen from Figure 8 that as the node moves faster, the average end-to-end delay increases. Moreover, the end-to-end delay of the topology-based routing protocol is obviously higher than that of the protocol based on geographic location. This is because topology-based routing protocols are passive, where routing discovery is only carried out when data transmission is needed. Moreover, when the node has mobility, the routing information obtained by the neighboring node may be outdated, and the node has to rediscover the route before the data transmission. In the three geographic routing protocols, GPSR has the best latency performance when the node moves at a low speed. This is because GPSR uses greedy forwarding, and the criterion for each selection is to pick the node closest to the destination node, while for SU-GPSR and EM-GPSR, in addition, the mobility and energy of the node are also considered. Therefore, the next hop is not necessarily the closest to the destination node, and so the delay is increased. However, with the increase of node movement speed, the delay performance of the EM-GPSR algorithm proposed in this paper is obviously better than SU-GPSR and IEMACO. This is because EM-GPSR fully considers the mobility and energy consumption rate of nodes. The “area” is divided according to the remaining lifetime of the link, and a link with a longer lifetime is selected to ensure the stability and continuity of data transmission and to reduce the end-to-end delay.

Figure 9 shows the curve of the packet delivery rate for different routing protocols with varying node movement velocity. It can be seen from the figure that the packet delivery rate in the network decreases with the increase of the node movement speed. The GPSR packet delivery rate is the lowest since GPSR only uses greedy forwarding, and the stability of the selected link may not be as good as other algorithms. When the node movement speed is less than 20 m/s, the packet delivery rate of IEMACO is slightly higher than that of EM-GPSR. When the node movement speed is greater than 20 m/s, the IEMACO packet delivery rate drops significantly and is smaller than EM-GPSR. As in the topological routing protocol IEMACO, when a node finds that the next hop does not exist, the process of routing rediscovery is longer. Moreover, the faster the topology changes, the more frequently the routing is discovered, which can cause packets to be discarded. However, with the increase of node movement speed, the packet delivery rate of the EM-GPSR algorithm can be significantly higher than SU-GPSR and IEMACO. This is because EM-GPSR takes the mobility of the node as the primary consideration, and chooses the link with a long remaining lifetime to transmit the data, which improves the packet delivery rate. The long-lived link of the road carries out data transmission, which improves the packet delivery rate.

Figure 10 shows the variation of death time of the first node in the network with the movement speed of the node under different routing algorithms. It can be seen from the figure that as the node moves faster, the death time of the first node in the network also increases. The first node of GPSR has the lowest dead time. This is because when the node moves at a lower speed, the greedy forwarding selects the node closest to the destination node as the next hop for data transmission. Only when the node energy on the link is exhausted, which causes the current node to leave the network, are other nodes selected for data transmission. The IEMACO curve is higher than the other three curves. This is because the routing of IEMACO is based on the topology and the node status of the whole network. In terms of energy consumption, not only the next-hop node but also the energy state of all nodes on the path to the destination node are considered, and so the performance is better in terms of energy balance. With the increase of node movement speed, the EM-GPSR algorithm proposed in this paper can guarantee link stability and predict the residual lifetime of the node according to the node energy consumption rate in the next-hop selection. The balance of energy consumption is achieved.

Figure 11 shows the number of dead nodes at different node velocities under different routing algorithms. As can be seen from Figure 11, as the node moves faster, the number of node deaths also increases. The number of node deaths in GPSR is significantly higher than that of SU-GPSR and EM-GPSR. This is because the algorithm does not consider node energy. When the current node cannot provide service because it has exhausted its energy, it will continue to select the node closest to the destination node as the next hop to continue transmission until the end of energy consumption. The number of node deaths in EM-GPSR proposed in this paper is small. This is because the concept of the remaining lifetime of nodes is proposed in this paper. On the basis of ensuring the stability of data transmission, the EM-GPSR algorithm tries to select nodes with more remaining energy to ensure the balance of energy consumption.

Figure 12 shows the average end-to-end delay varying with node-sending speed for different routing algorithms. It can be seen that with the increase of network load, the average end-to-end delay in the network is on the rise, which is due to the limited data processing capacity and bandwidth of the nodes. The end-to-end delay of GPSR grows fastest because the link breaks often occur when the node is moving constantly, which makes the node need to choose the next hop again, and so the re-transmission increases the end-to-end delay. The SU-GPSR partly considers the mobility of nodes, that is, distinguishing between mobile and static nodes, so the delay is relatively low. The proposed EM-GPSR algorithm takes the mobility of nodes fully into account, and takes it as the primary condition for selecting the next hop. Comparing the remaining lifetime of the link to select the candidate set, this can improve the stability of the data transmission link, reduce the frequency of re-transmission, and thus reduce the end-to-end delay.

Figure 13 shows the curve of the packet delivery rate varies with node packet delivery speed for different routing algorithms. As can be seen from Figure 13, the packet delivery rate decreases with the increase of the node’s packet delivery rate, since the network load increases as the packet delivery rate increases, while the node’s transmission capacity and cache are limited. Therefore, some packets are dropped or outdated due to waiting longer than the maximum lifetime. The performance of the GPSR algorithm is the worst, mainly due to the fact that GPSR does not consider the mobility of nodes. When the data transmission link suddenly breaks, the node needs to send data packets again, and if the number of re-transmissions reaches the upper limit, the data packets are discarded. The proposed EM-GPSR algorithm gives priority to the next-hop node with the more stable link, which can reduce the number of re-transmissions, and so the packet delivery rate is the highest and the performance is better.

Figure 14 shows the curve of the death time of the first node in the network versus the packet transmitting rate under different routing algorithms. It can be seen from the figure that as the packet transmitting rate increases, the dead time of the first node in the network decreases. It also shows that the GPSR has the worst performance because the GPSR does not take into account the energy consumption of a node. When a node is selected as the next hop, the link will continue to be used until the node is not reachable or the link is broken. A single node consequently consumes energy too fast and fails. However, SU-GPSR and EM-GPSR proposed in this paper are obviously superior to GPSR, mainly because the next-hop selection takes into account the remaining energy of nodes, and nodes with more remaining energy are preferentially selected. The first node death time of EM-GPSR is a little longer than that of SU-GPSR, owing to a more accurate measurement of the energy consumption of nodes.

Figure 15 compares the number of dead nodes at different packet delivery rates under different routing algorithms. As can be seen from the figure, the number of dead nodes increases with the increase of the packet delivery rate. Because GPSR does not consider energy balance, the number of dead nodes is the largest. Besides, the proposed EM-GPSR further introduces the remaining lifetime of the node and makes the energy consumption of the network more balanced, thus, reduces the number of dead nodes.

5. Conclusions

In order to solve the problem of frequent link breakage and node death caused by node mobility and energy constraints in mobile ad-hoc networks, an energy-balanced routing algorithm based on geographical location, EM-GPSR, is proposed in this paper. The conventional geographic routing algorithm does not fully consider the imbalance of energy consumption caused by the continuous movement of nodes and energy constraints, while the proposed EM-GPSR algorithm takes into account the mobility, the energy status and the remaining lifetime of the node in the selection of the next hop. The region division method is employed to reduce the computational complexity. The simulation results show that the proposed algorithm has a lower end-to-end delay, higher packet delivery rate and a longer network lifetime.