Applied Research on Distributed Generation Optimal Allocation Based on Improved Estimation of Distribution Algorithm
Abstract
:1. Introduction
2. Optimal Configuration Model of DG
3. Algorithm Principle
3.1. Estimation of Distribution Algorithm
- (1)
- Initialize the population
- (2)
- Execute cycle-body
- Selecting: Select several individuals to form a dominant group according to a certain selection mechanism.
- Modeling: Establish a probability model according to a certain criteria.
- Sampling: Use the proposed probability model to generate the next generation; determine whether the termination condition is met. if it is satisfied, output the optimal individual. If not, continue to execute the loop body.
3.2. The Principle of Bayesian Statistical Inference
3.3. The EDA with Bayesian Inference Improved
3.3.1. Establishment of IEDA Probability Model
3.3.2. Update of Probability Model
3.3.3. Population Regeneration
3.4. Algorithm Steps
4. Load Flow Analysis
5. Power Calculation
6. Case Studies
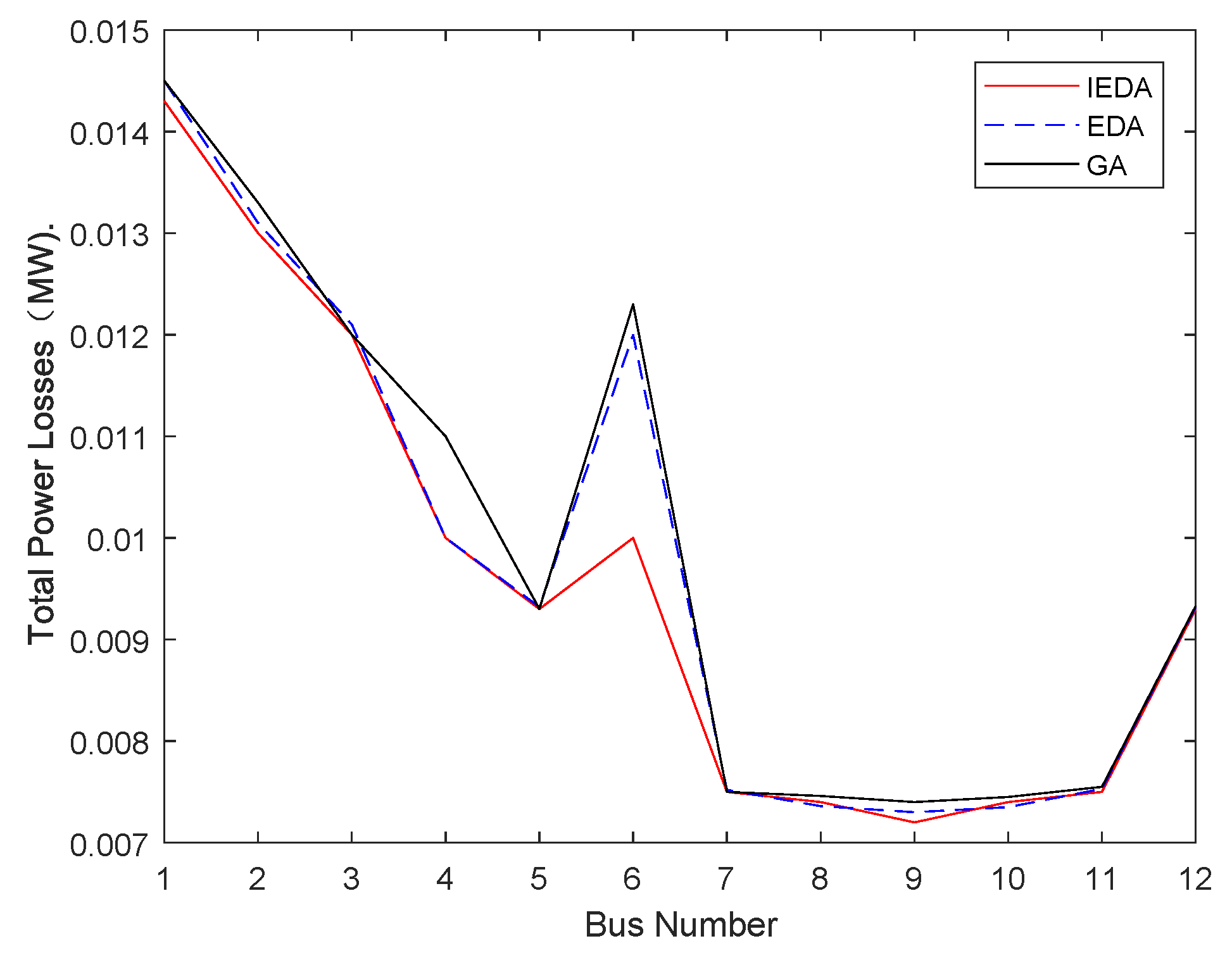
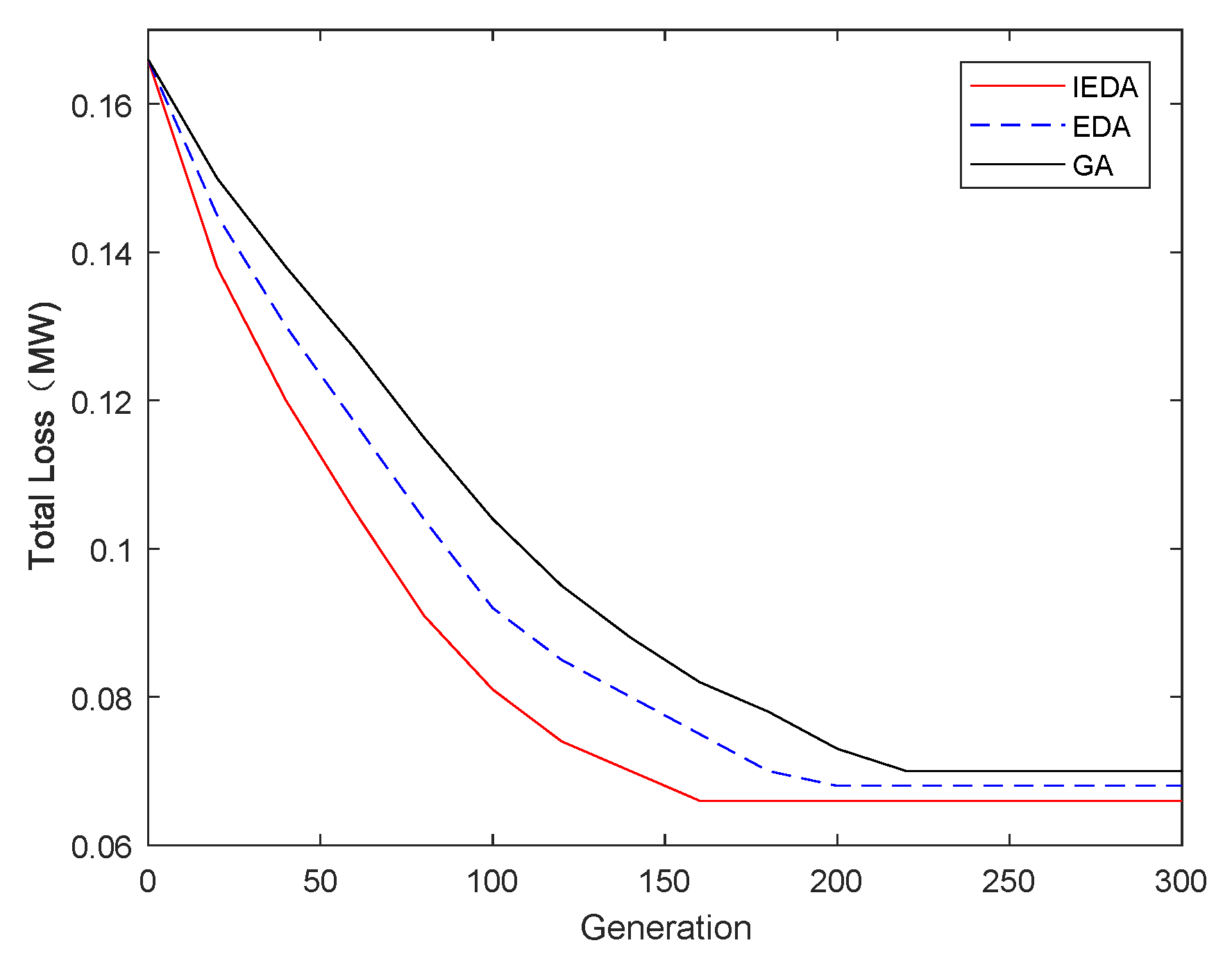
6.1. Test System 1: 12 Bus Radial Distribution System
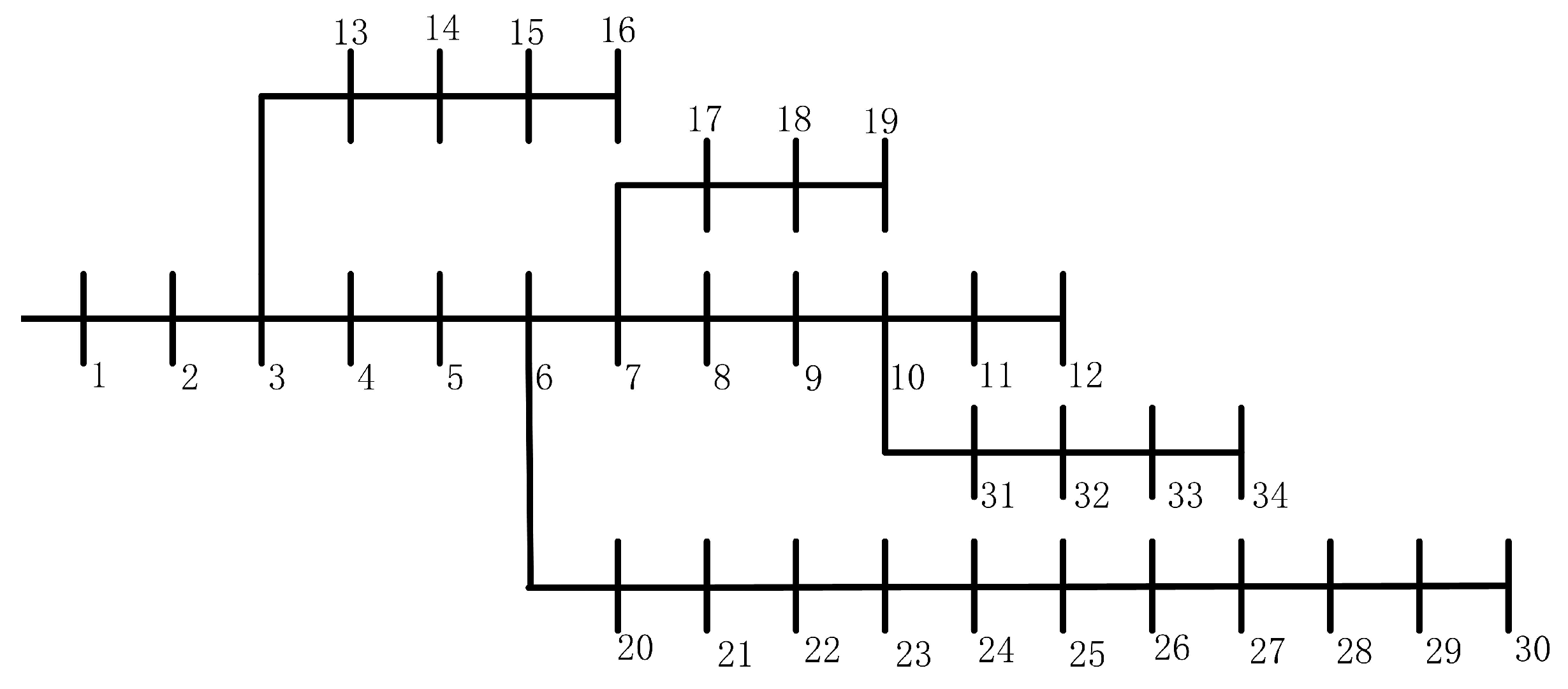
6.2. Test System 2: 34 Bus Radial Distribution System
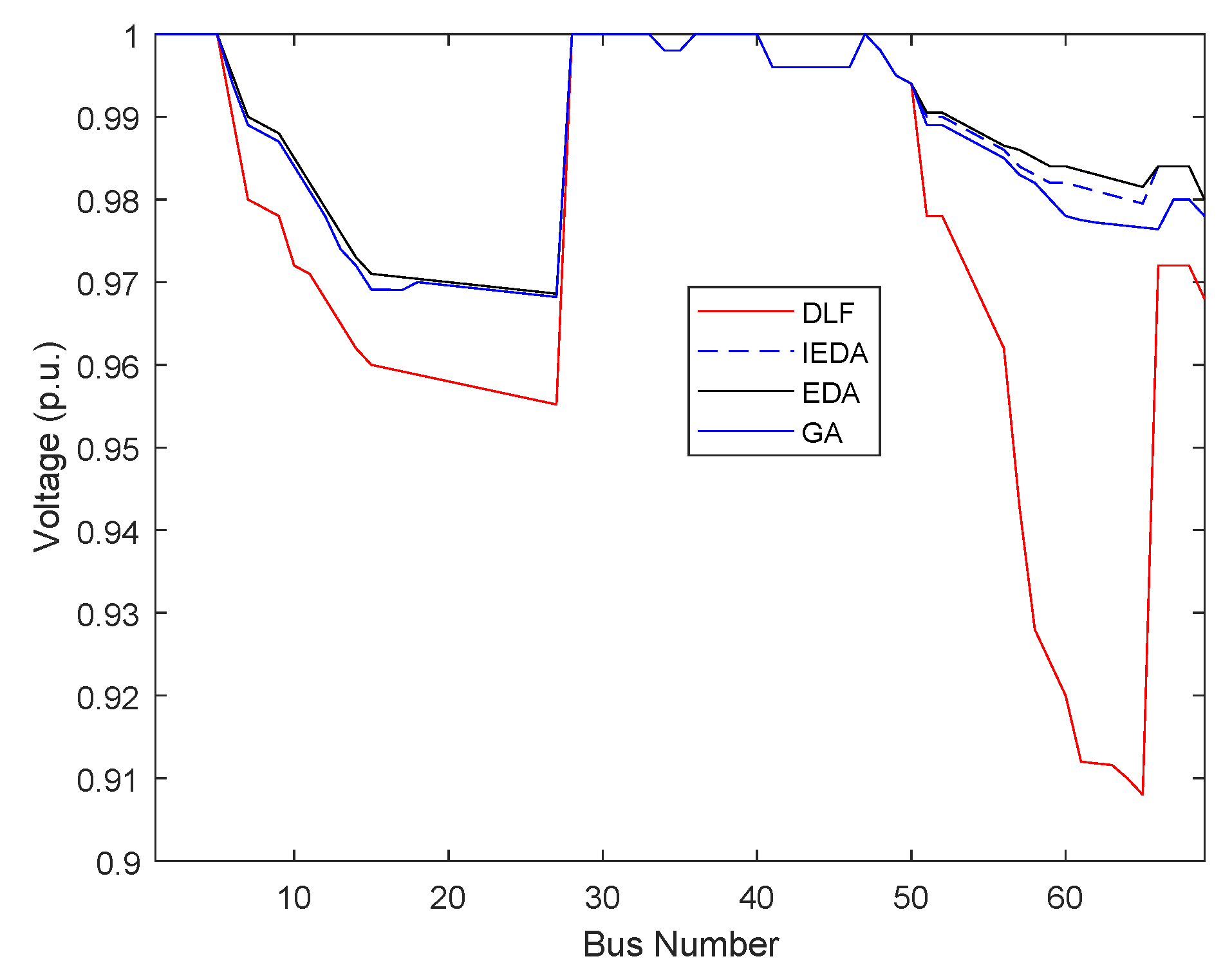
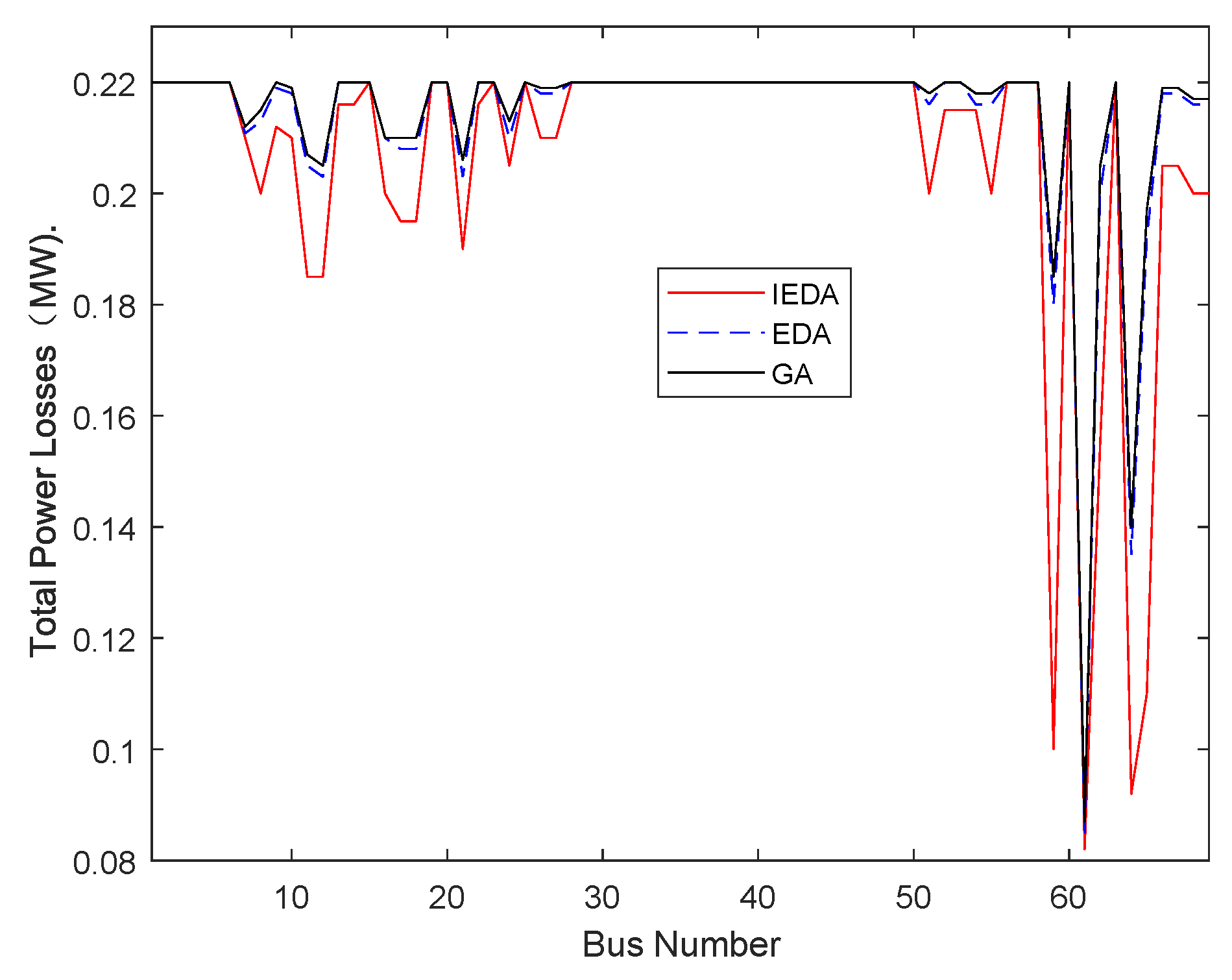
6.3. Test System 3: 69 Bus Radial Distribution System
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| DG | Distributed generation |
| IEDA | Improved estimation of distribution algorithm |
| EDA | Estimation of distribution algorithm |
| GA | Genetic algorithm |
| The total power loss of the radial distribution system | |
| The real power generation using DG at bus i | |
| The power demand at bus i | |
| The line loss on the bus i | |
| The lower limits of voltages at bus i | |
| The upper limits of voltages at bus i | |
| The maximum current value of branch i | |
| The apparent power of bus i | |
| The active power of bus i | |
| The reactive power of bus i | |
| BCBV | The branch–current to bus–voltage matrix |
| BIBC | The bus–injections to branch–currents matrix |
| The active load powers on bus i | |
| The reactive load powers on bus i |
References
- Cano, E.B. Utilizing fuzzy optimization for distributed generation allocation. In Proceedings of the TENCON 2007 IEEE Region 10 Conference, Taipei, Taiwan, 30 October–2 November 2007; pp. 1–4. [Google Scholar]
- Keane, A.; Ochoa, L.F.; Borges, C.L.; Ault, G.W.; Alarcon-Rodriguez, A.D.; Currie, R.A.; Pilo, F.; Dent, C.; Harrison, G.P. State-of-the-art techniques and challenges ahead for distributed generation planning and optimization. IEEE Trans. Power Syst. 2013, 28, 1493–1502. [Google Scholar] [CrossRef]
- Naderi, E.; Seifi, H.; Sepasian, M.S. A dynamic approach for distribution system planning considering distributed generation. IEEE Trans. Power Deliv. 2012, 27, 1313–1322. [Google Scholar] [CrossRef]
- Peng, X.; Lin, L.; Zheng, W.; Liu, Y. Crisscross optimization algorithm and monte carlo simulation for solving optimal distributed generation allocation problem. Energies 2015, 8, 13641–13659. [Google Scholar] [CrossRef]
- Devi, S.; Geethanjali, M. Application of modified bacterial foraging optimization algorithm for optimal placement and sizing of distributed generation. Expert Syst. Appl. 2014, 41, 2772–2781. [Google Scholar] [CrossRef]
- Sheng, W.; Liu, K.Y.; Liu, Y.; Meng, X.; Li, Y. Optimal placement and sizing of distributed generation via an improved nondominated sorting genetic algorithm II. IEEE Trans. Power Deliv. 2015, 30, 569–578. [Google Scholar] [CrossRef]
- Prakash, P.; Khatod, D.K. Optimal sizing and siting techniques for distributed generation in distribution systems: A review. Renew. Sustain. Energy Rev. 2016, 57, 111–130. [Google Scholar] [CrossRef]
- Aman, M.; Jasmon, G.; Mokhlis, H.; Bakar, A. Optimal placement and sizing of a DG based on a new power stability index and line losses. Int. J. Electr. Power Energy Syst. 2012, 43, 1296–1304. [Google Scholar] [CrossRef]
- Gitizadeh, M.; Vahed, A.A.; Aghaei, J. Multistage distribution system expansion planning considering distributed generation using hybrid evolutionary algorithms. Appl. Energy 2013, 101, 655–666. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Bansal, R. Analytical strategies for renewable distributed generation integration considering energy loss minimization. Appl. Energy 2013, 105, 75–85. [Google Scholar] [CrossRef]
- Acharya, N.; Mahat, P.; Mithulananthan, N. An analytical approach for DG allocation in primary distribution network. Int. J. Electr. Power Energy Syst. 2006, 28, 669–678. [Google Scholar] [CrossRef]
- Keane, A.; O’Malley, M. Optimal utilization of distribution networks for energy harvesting. Int. J. Electr. Power Energy Syst. 2007, 22, 467–475. [Google Scholar] [CrossRef]
- Peng, X.; Lin, L.; Liu, Y.; Wang, X.; Meng, A. Optimal Dis-tributed Generator Allocation Method Based on Correlation Latin Hypercube Sampling Monte Carlo Simulation Embedded Crisscross Optimization Algorithm. Proc. CSEE 2015, 16, 4077–4085. [Google Scholar]
- Atwa, Y.M.; El-Saadany, E.F. Probabilistic approach for optimal allocation of wind-based distributed generation in distribution systems. IET Renew. Power Gener. 2011, 5, 79–88. [Google Scholar] [CrossRef]
- Atwa, Y.; El-Saadany, E.; Salama, M.; Seethapathy, R. Optimal renewable resources mix for distribution system energy loss minimization. IEEE Trans. Power Syst. 2010, 25, 360–370. [Google Scholar] [CrossRef]
- Gandomkar, M.; Vakilian, M.; Ehsan, M. A genetic–based tabu search algorithm for optimal DG allocation in distribution networks. Electr. Power Compon. Syst. 2005, 33, 1351–1362. [Google Scholar] [CrossRef]
- Wang, R.; Li, K.; Zhang, C.; Du, C.; Chu, X. Distributed Generation Planning Based on Multi-Objective Chaotic Quantum Genetic Algorithm. Power Syst. Technol. 2011, 12, 183–189. [Google Scholar]
- Yammani, C.; Maheswarapu, S.; Matam, S.K. A Multi-objective Shuffled Bat algorithm for optimal placement and sizing of multi distributed generations with different load models. Int. J. Electr. Power Energy Syst. 2016, 79, 120–131. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Devabalaji, K.; Ravi, K. Optimal Allocation of DG in the Radial Distribution Network Using Bat Optimization Algorithm. In Advances in Power Systems and Energy Management; Springer: Berlin, Germany, 2018; pp. 563–569. [Google Scholar]
- Seker, A.A.; Hocaoglu, M.H. Artificial Bee Colony algorithm for optimal placement and sizing of distributed generation. In Proceedings of the 2013 8th International Conference on Electrical and Electronics Engineering, Amman, Jordan, 28–30 November 2013; pp. 127–131. [Google Scholar]
- Johan, N.F.M.; Azmi, A.; Rashid, M.A.; Yaakob, S.B.; Rahim, S.R.A.; Zali, S.M. Multi-objective using Artificial Bee Colony optimization for distributed generation placement on power system. In Proceedings of the 2013 IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 29 November–1 December 2013; pp. 117–121. [Google Scholar]
- Zhao, F.; Si, J.; Wang, J. Research on optimal schedule strategy for active distribution network using particle swarm optimization combined with bacterial foraging algorithm. Int. J. Electr. Power Energy Syst. 2016, 78, 637–646. [Google Scholar] [CrossRef]
- Kowsalya, M. Optimal size and siting of multiple distributed generators in distribution system using bacterial foraging optimization. Swarm Evolut. Comput. 2014, 15, 58–65. [Google Scholar]
- Chen, Y.; Liu, L.G. Sizing and Locating of Distributed Generations Based on Chaos Particle Swarm Optimization Algorithm. In Applied Mechanics and Materials; Trans Tech Publications: Zurich, Switzerland, 2013; Volume 291, pp. 2119–2123. [Google Scholar]
- Jamian, J.J.; Mustafa, M.W.; Mokhlis, H. Optimal multiple distributed generation output through rank evolutionary particle swarm optimization. Neurocomputing 2015, 152, 190–198. [Google Scholar] [CrossRef]
- Dharageshwari, K.; Nayanatara, C. Multiobjective optimal placement of multiple distributed generations in IEEE 33 bus radial system using simulated annealing. In Proceedings of the 2015 International Conference on Circuits, Power and Computing Technologies (ICCPCT-2015), Nagykoyle, India, 19–20 March 2015; pp. 1–7. [Google Scholar]
- Popović, Ž.; Kerleta, V.D.; Popović, D. Hybrid simulated annealing and mixed integer linear programming algorithm for optimal planning of radial distribution networks with distributed generation. Electr. Power Syst. Res. 2014, 108, 211–222. [Google Scholar] [CrossRef]
- Salhi, A.; Rodríguez, J.A.V.; Zhang, Q. An estimation of distribution algorithm with guided mutation for a complex flow shop scheduling problem. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation, London, UK, 7–11 July 2007; pp. 570–576. [Google Scholar]
- Li, D.; Peng, F.; Zhou, X.; Liu, C. Research of Batch Scheduling with Arrival Time Based on Estimation of Distribution Algorithm. In Proceedings of the 2014 Seventh International Symposium on Computational Intelligence and Design, Hangzhou, China, 13–14 December 2014; Volume 2, pp. 125–130. [Google Scholar]
- Cai, C.; Yan, G.; Tang, J. Detection of fatigue cracks under environmental effects using Bayesian statistical inference. Int. J. Appl. Electromagn. Mech. 2016, 52, 1015–1021. [Google Scholar] [CrossRef]
- Teng, J.H. A direct approach for distribution system load flow solutions. IEEE Trans. Power Deliv. 2003, 18, 882–887. [Google Scholar] [CrossRef]









| Algorithm | Advantage | Shortcoming |
|---|---|---|
| Analytical method | The method is simple and less workload | Dealing with single objective optimization problem only |
| Classical optimization algorithm | The model is accurate and the method is simple | The computation is large and the computation speed is slow |
| Genetic algorithm | The convergence speed is fast and the versatility is strong | It is more complex, easy to fall into premature convergence, and depends on the initial population |
| Bat algorithm | Simple structure, few parameters and strong robustness | The speed of convergence is slow and the precision of optimization is low |
| Artificial bee colony algorithm | The global search ability is strong and the convergence speed is fast | it is easy to fall into the local optimum, and the search speed slows down later |
| Bacterial foraging algorithm | Strong parallel search ability and easy to get out of local minimum | The convergence speed is slow and the computation is large |
| Particle swarm optimization | The training speed is fast, the efficiency is high, and the algorithm is simple | It is easy to fall into local optimal solution and poor handling of discrete optimization problems |
| Simulated annealing algorithm | Strong global search capability | Convergence speed is slow and parallel computing is difficult |
| Test System | Total Load (MVA) | without DG (MW) | Algorithm | Optimum Place (bus no) | Optimum Size (MW) | (MW) | Voltage (p.u) |
|---|---|---|---|---|---|---|---|
| IEDA | 9 | 0.2335 | 0.0072 | 0.992 | |||
| 12 bus | 0.435 + 0.3900i | 0.145 | EDA | 9 | 0.2378 | 0.0073 | 0.993 |
| GA | 9 | 0.2385 | 0.0074 | 0.991 | |||
| IEDA | 21 | 2.9506 | 0.066 | 0.968 | |||
| 34 bus | 4.6365 + 2.8735i | 0.1638 | EDA | 21 | 3.0023 | 0.068 | 0.969 |
| GA | 21 | 3.0112 | 0.070 | 0.967 | |||
| IEDA | 61 | 1.8705 | 0.082 | 0.9815 | |||
| 69 bus | 3.8021 + 2.6945i | 0.2254 | EDA | 61 | 2.0661 | 0.085 | 0.9835 |
| GA | 61 | 2.0845 | 0.087 | 0.9775 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Yang, X.; Wu, Y.; Liu, X. Applied Research on Distributed Generation Optimal Allocation Based on Improved Estimation of Distribution Algorithm. Energies 2018, 11, 2363. https://doi.org/10.3390/en11092363
Yang L, Yang X, Wu Y, Liu X. Applied Research on Distributed Generation Optimal Allocation Based on Improved Estimation of Distribution Algorithm. Energies. 2018; 11(9):2363. https://doi.org/10.3390/en11092363
Chicago/Turabian StyleYang, Lei, Xiaohui Yang, Yue Wu, and Xiaoping Liu. 2018. "Applied Research on Distributed Generation Optimal Allocation Based on Improved Estimation of Distribution Algorithm" Energies 11, no. 9: 2363. https://doi.org/10.3390/en11092363
APA StyleYang, L., Yang, X., Wu, Y., & Liu, X. (2018). Applied Research on Distributed Generation Optimal Allocation Based on Improved Estimation of Distribution Algorithm. Energies, 11(9), 2363. https://doi.org/10.3390/en11092363




