Evaluation of the Vertical Producing Degree of Commingled Production via Waterflooding for Multilayer Offshore Heavy Oil Reservoirs
Abstract
:1. Introduction
2. Multilayer Reservoir Commingling Production Waterflood Model
2.1. Multilayer Water Flooding Model under One-Dimensional Linear Seepage Flow
2.1.1. Assumptions
- The left boundary is the supply boundary with constant injection, and the right boundary is the production ends, which creates a balance between injection and production.
- The media is rigid and porous, and the fluid is incompressible.
- There are stable interlayers between layers, regardless of inter-layer cross flow.
- Non-piston water displacement oil is present, and there are two phases of oil and water.
2.1.2. Modeling
2.2. Multilayer Water Flooding Model under Planar Radial Flow
2.2.1. Assumptions
- The boundary is the supply boundary with constant injection and creates a balance between injection and production.
- The media is rigid and porous, and the fluid is incompressible.
- There are stable interlayers between layers, regardless of inter-layer cross flow.
- Non-piston water displacement oil is present, and there are two phases of oil and water.
2.2.2. Modeling
3. Model Solving
4. Model Validation
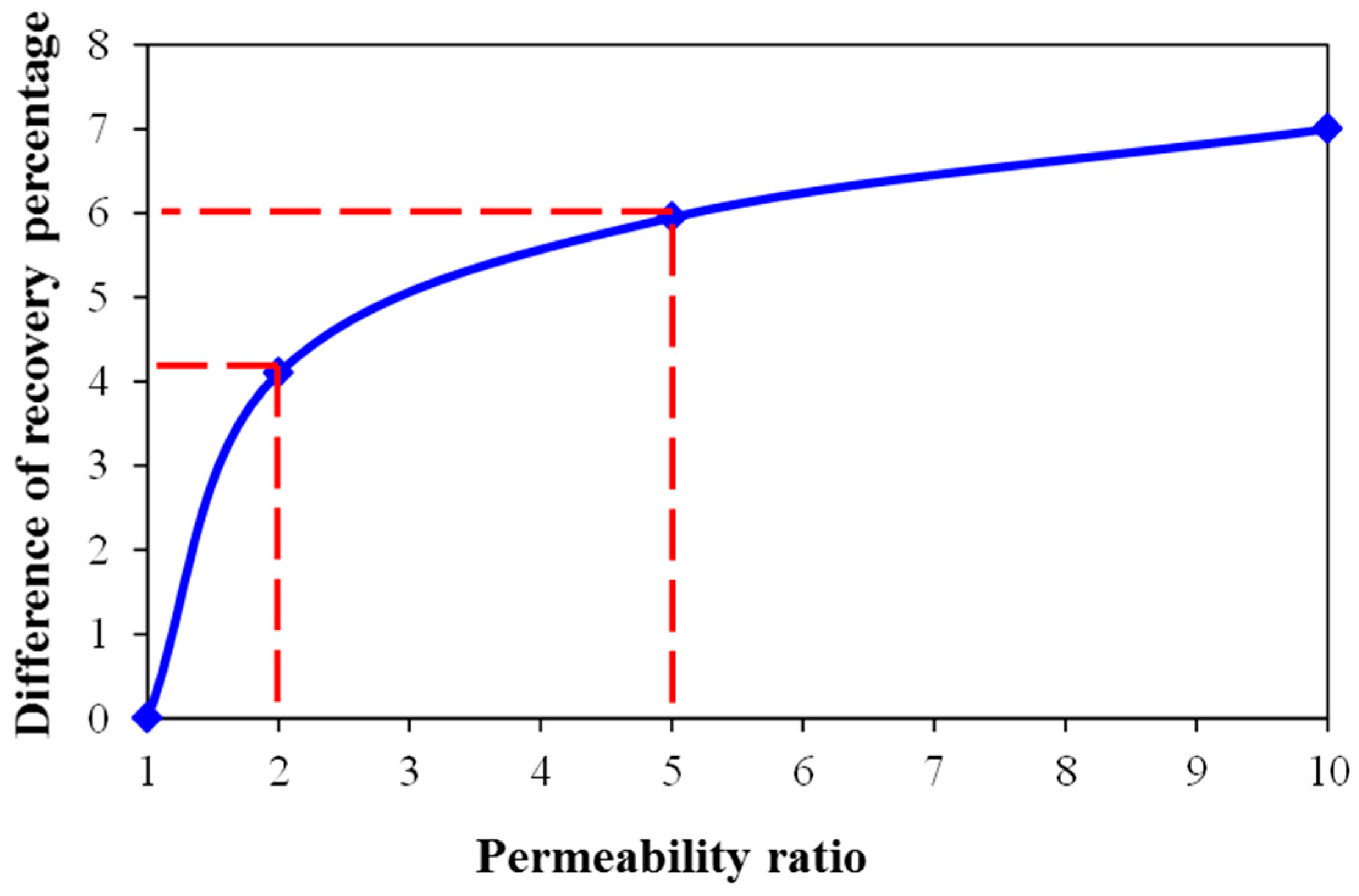
5. Model Application and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| position of waterflood front in layer i, m; | |
| initial oil edge radius, m; | |
| thickness of layer i, m; | |
| porosity of layer i, dimensionless; | |
| water saturation of the waterflood front of layer i, dimensionless; | |
| the derivative of the fractional flow corresponding to the water saturation of the waterflood front in layer i, dimensionless; | |
| liquid production rate in layer i, m3/d; | |
| total liquid production rate, m3/d; | |
| the permeability of layer i, 10−3µm2; | |
| relative permeability of oil, fraction; | |
| relative permeability of water, fraction; | |
| wellbore radius, m; | |
| displacement pressure in layer i, MPa; | |
| oil viscosity in layer i, mPa·s; | |
| total pore volume of the reservoir, m3; | |
| resistance of layer i, mPa·s/(d·m); | |
| reservoir recovery percent of the multilayer commingling production, dimensionless; | |
| sweep efficiency of the multilayer commingling production, dimensionless; | |
| average water saturation in two-phase region, fraction; | |
| irreducible water saturation, fraction; | |
| M | number of water-breakthrough layers, dimensionless; |
| N | total number of model layers, dimensionless; |
| i, j | serial number of layers. |
References
- Warner, G.E. Waterflooding a Highly Stratified Reservoir. J. Pet. Technol. 1968, 10, 1179–1186. [Google Scholar] [CrossRef]
- Hatzignatiou, D.G.; Ogbe, D.O.; Dehghani, K.; Economides, M.J. Interference Pressure Behavior in Multilayered Composite Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 27–30 September 1987; pp. 245–260. [Google Scholar]
- Pan, Y.; Kamal, M.; Kikani, J. Field Applications of a Semianalytical Model of Multilateral Wells in Multilayer Reservoirs. SPE Reserv. Eval. Eng. 2010, 13, 861–872. [Google Scholar]
- Tang, Z.X.; Liu, H.; Jiang, C.Z. Technical Measures for Improving Oilfield Development by Waterflooding in a Large Multi-Layered Heterogeneous Sandstone Reservoir. In Proceedings of the International Meeting on Petroleum Engineering, Beijing, China, 17–25 March 1986; pp. 287–298. [Google Scholar]
- Hong, L.; Jin, P.; Xiaolu, W.; Xinan, Y.; Qing, L. Analysis of Interlayer Interference and Research of Development Strategy of Multilayer Commingled Production Gas Reservoir. Energy Procedia 2012, 16, 1341–1347. [Google Scholar] [CrossRef]
- Du, Q.L.; Zhao, Y.; Lu, Y.; Zhu, L. Study on Genetic Type and Potential Tapping Measures of the Remaining Oil in Multi-layered and Heterogeneous Sandstone Reservoir. J. Dermatol. Surg. Oncol. 1999, 17, 865–868. [Google Scholar]
- Huang, S.J.; Kang, B.T.; Cheng, L.S.; Zhou, W.S.; Chang, S.P. Quantitative Characterization of Interlayer Interference and Productivity Prediction of Directional Wells in the Multilayer Commingled Production of Ordinary Offshore Heavy Oil Reservoirs. Pet. Explor. Dev. 2015, 42, 533–540. [Google Scholar] [CrossRef]
- Su, Y.C. A Set of Techniques to Describe Quantitatively Remaining Oil in Offshore Heavy Oilfields under Commingling Production in Large Well Spacing. China Offshore Oil Gas 2012, 24, 82–85. [Google Scholar]
- Wang, F.Y.; Liu, Z.C.; Jiao, L.; Wang, C.L.; Guo, H. A Fractal Permeability Model Coupling Boundary-layer Effect for Tight Oil Reservoirs. Fract. Complex Geom. Patterns Scaling Nat. Soc. 2017, 25, 1750042. [Google Scholar] [CrossRef]
- Li, C.X.; Shen, Y.H.; Ge, H.K.; Su, S.; Yang, Z. Analysis of Spontaneous Imbibition in Fractal Tree-like Network System. Fract. Complex Geom. Patterns Scaling Nat. Soc. 2016, 24, 1650035. [Google Scholar] [CrossRef]
- Qiu, L.; Yang, S.; Qu, C.; Xu, N.; Gao, Q.; Zhang, X.; Liu, X.; Wang, D. A Comprehensive Porosity Prediction Model for the Upper Paleozoic Tight Sandstone Reservoir in the Daniudi Gas Field, Ordos Basin. J. Earth Sci. 2017, 28, 1086–1096. [Google Scholar] [CrossRef]
- Brice, B.W.; Renouf, G. Increasing Oil Recovery from Heavy Oil Waterfloods. In Proceedings of the SPE International Thermal Operations and Heavy Oil Symposium, Calgary, AB, Canada, 20–23 October 2008; pp. 1–13. [Google Scholar]
- Miller, K.A. Improving the State of the Art of Western Canadian Heavy Oil Waterflood Technology. J. Can. Pet. Technol. 2006, 45, 7–11. [Google Scholar] [CrossRef]
- Pari, M.N.; Kabir, A. Viability Study of Implementing Smart/Intelligent Completion in Commingled Wells in an Australian Offshore Oil Field. Soc. Pet. Eng. 2009, 49, 441. [Google Scholar]
- Buckley, S.E.; Leverett, M.C. Mechanism of Fluid Displacement in Sands. Trans. AIME 1942, 146, 107–116. [Google Scholar] [CrossRef]
- Stiles, W.E. Use of Permeability Distribution in Water-flood Calculations. Trans. AIME 1949, 186, 9–13. [Google Scholar] [CrossRef]
- Dykstra, H.; Parsons, R.L. The Prediction of Oil Recovery by Waterflooding in Secondary Recovery of Oil in the United States, 2nd ed.; API: Washington, DC, USA, 1950; pp. 160–174. [Google Scholar]
- Hiatt, N.W. Injected–fluid Coverage of Multi–well Reservoirs with Permeability Stratification. Drill Prod. Prac. 1958, 165, 165–194. [Google Scholar]
- Dyes, A.B.; Caudle, B.H. Oil Production after Breakthrough as Influenced by Mobility Ratio. AIME 1954, 201, 81–86. [Google Scholar] [CrossRef]
- Osman, M.E.; Tiab, D. Waterflooding Performance and Pressure Analysis of Heterogeneous Reservoirs. In Proceedings of the Middle East Technical Conference and Exhibition, Manama, Bahrain, 9–12 March 1981; pp. 773–779. [Google Scholar]
- Johnson, C.E. Prediction of Oil Recovery by Waterflood—A Simplified Graphical Treatment of the Dykstra-Parsons Method. J. Pet. Technol. 2013, 8, 55–56. [Google Scholar] [CrossRef]
- Lefkovits, H.C.; Hazebroek, P.; Allen, E.; Matthews, C.S. A Study of the Behavior of Bounded Reservoirs Composed of Stratified Layers. Soc. Pet. Eng. J. 1961, 1, 43–58. [Google Scholar] [CrossRef]
- Kucuk, F.; Ayestaran, L. Well Testing and Analysis Techniques for Layered Reservoirs. SPE Form. Eval. 1984, 8, 342–354. [Google Scholar] [CrossRef]
- Bourdet, D. Pressure Behavior of Layered Reservoirs with Crossflow. In Proceedings of the SPE California Regional Meeting, Bakersfield, CA, USA, 27–29 March 1985; pp. 405–412. [Google Scholar]
- Tompang, R.; Kelkar, B.G. Prediction of Waterflood Performance in Stratified Reservoirs. Chest 1988, 92, 657–662. [Google Scholar]
- Tang, X.; Liu, S. A New Vertical Interference Test Method in a Three Layer Reservoir with an Unstable Impermeable Interlayer. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 6–9 October 1996; pp. 725–736. [Google Scholar]
- El-Khatib, N.A.F. The Application of Buckley-Leverett Displacement to Waterflooding in Non-Communicating Stratified Reservoirs. In Proceedings of the SPE Middle East Oil Show, Manama, Bahrain, 17–20 March 2001; pp. 1–12. [Google Scholar]
- El-Khatib, N.A.F. Waterflooding Performance in Inclined Communicating Stratified Reservoirs. SPE J. 2012, 17, 31–42. [Google Scholar] [CrossRef]
- El-Khatib, N.A.F. The Modification of the Dykstra-Parsons Method for Inclined Stratified Reservoirs. SPE J. 2012, 17, 1029–1040. [Google Scholar] [CrossRef]
- Guo, P.; Wang, J.; Liu, Q.; Zhang, M. Study on Development Mechanism of Commingling Production in Low-Permeability Gas Reservoirs. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010; pp. 1–20. [Google Scholar]
- Li, L.R.; Yuan, S.Y.; Hu, Y.L. Quantitative Rules for the Subdivision and Recombination of Layer Series in Water-displacement Reservoirs, The Innovation and Practice of Seepage Mechanics and Engineering. In Proceedings of the 11th National Conference on Seepage Mechanics, Chongqing, China, 28–30 April 2011; pp. 216–222. [Google Scholar]
- Zhou, Y.F.; Fang, Y.J.; Wang, X.D. Study on non-piston water displacement efficiency for layered reservoir. J. Pet. Geol. Recov. Effic. 2009, 16, 86–89. [Google Scholar]
- An, W.Y. Interference Mechanism of Multilayer Heterogeneous Reservoir in High Water cut Stage. J. North East Pet. Univ. 2012, 36, 72–75. [Google Scholar]
- Zhang, S.K.; Liu, B.G.; Zhong, S.Y. Theoretical Model for Waterflooding Development of Multi-Zone Reservoir. J. Xinjiang Pet. Geol. 2009, 30, 734–737. [Google Scholar]
- Zhang, J.G.; Lei, G.L.; Zhang, Y.Y. Seepage Mechanics; China University of Petroleum Press: Beijing, China, 1998; pp. 148–160. [Google Scholar]
- Li, S.X.; Gu, J.W. Foundation of Reservoir Numerical Simulation; China University of Petroleum Press: Beijing, China, 2009; pp. 147–148. [Google Scholar]
- Corey, A.T. The Interrelation between Gas and Oil Relative Permeabilities. Prod. Mon. 1954, 19, 38–41. [Google Scholar]
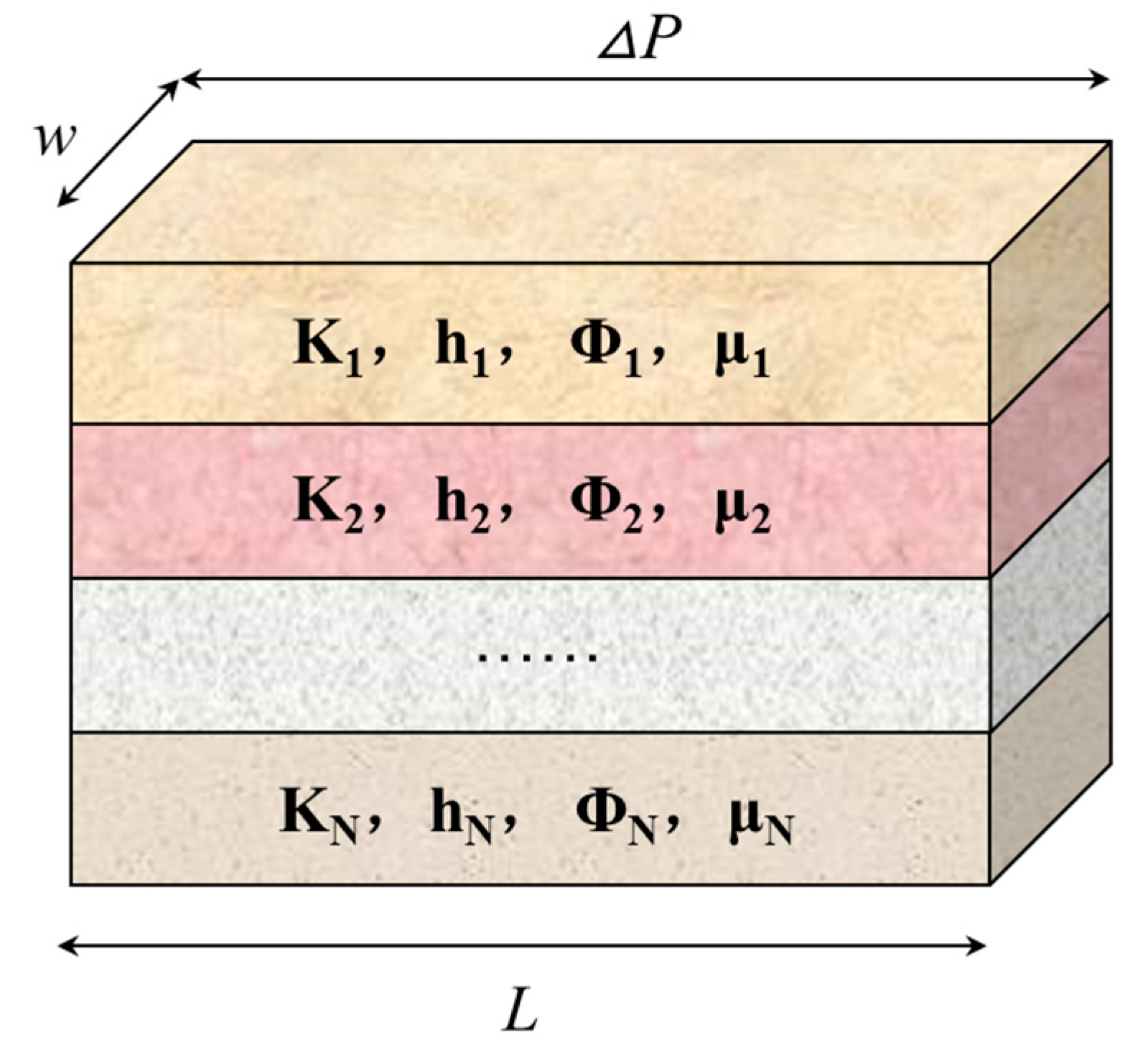







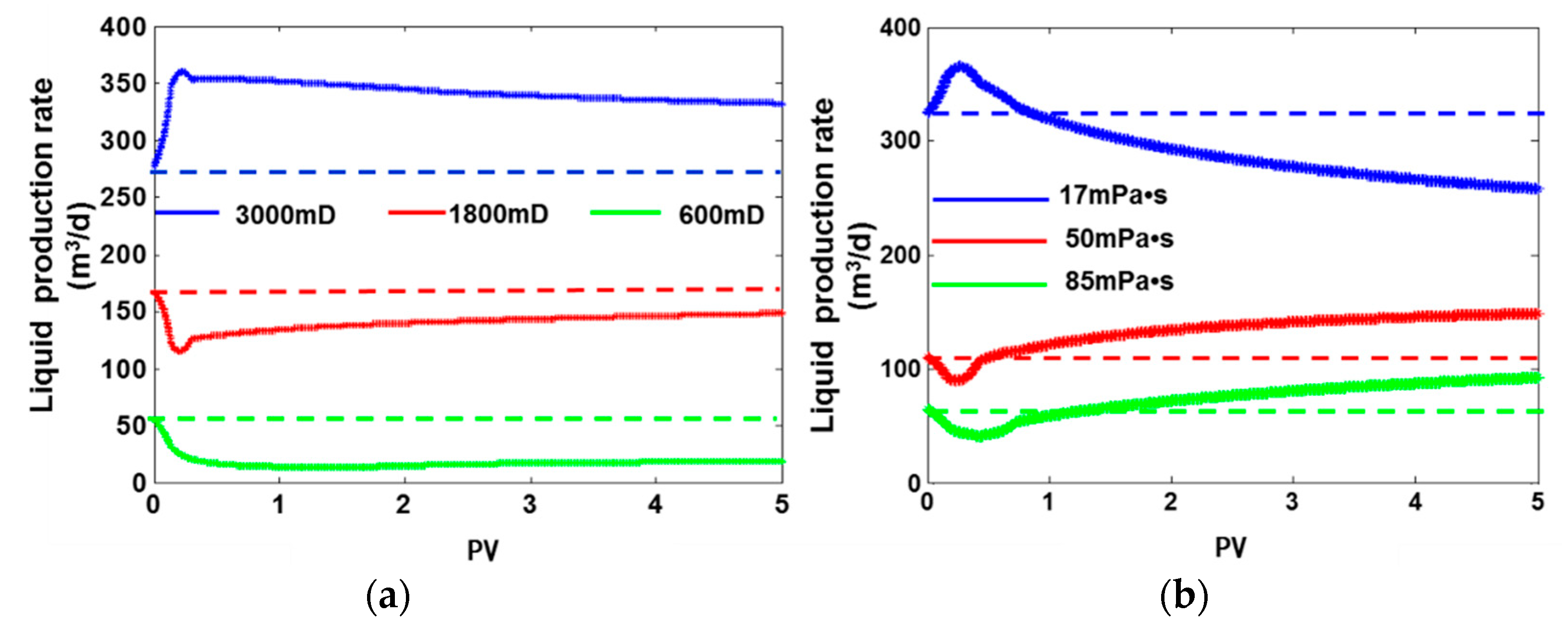

| Model Parameters | Value | Model Parameters | Value |
|---|---|---|---|
| Reservoir radius (m) | 350 | Layer 1 permeability (10−3 µm2) | 3000 |
| Reservoir thickness (m) | 5 | Layer 2 permeability (10−3 µm2) | 1800 |
| Reservoir porosity (%) | 25 | Layer 3 permeability (10−3 µm2) | 600 |
| Water injection rate (m3/d) | 500 | Oil viscosity (mPa·s) | 50 |
| Model Parameters | Value | Model Parameters | Value |
|---|---|---|---|
| Reservoir radius (m) | 350 | Oil viscosity in Layer 1 (mPa·s) | 17 |
| Reservoir thickness (m) | 5 | Oil viscosity in Layer 2 (mPa·s) | 50 |
| Reservoir porosity (%) | 25 | Oil viscosity in Layer 3 (mPa·s) | 85 |
| Water injection rate (m3/d) | 500 | Layers’ permeability (10−3 µm2) | 1800 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, F.; Cheng, L.; Sun, Q.; Huang, S. Evaluation of the Vertical Producing Degree of Commingled Production via Waterflooding for Multilayer Offshore Heavy Oil Reservoirs. Energies 2018, 11, 2428. https://doi.org/10.3390/en11092428
Shen F, Cheng L, Sun Q, Huang S. Evaluation of the Vertical Producing Degree of Commingled Production via Waterflooding for Multilayer Offshore Heavy Oil Reservoirs. Energies. 2018; 11(9):2428. https://doi.org/10.3390/en11092428
Chicago/Turabian StyleShen, Fei, Linsong Cheng, Qiang Sun, and Shijun Huang. 2018. "Evaluation of the Vertical Producing Degree of Commingled Production via Waterflooding for Multilayer Offshore Heavy Oil Reservoirs" Energies 11, no. 9: 2428. https://doi.org/10.3390/en11092428
APA StyleShen, F., Cheng, L., Sun, Q., & Huang, S. (2018). Evaluation of the Vertical Producing Degree of Commingled Production via Waterflooding for Multilayer Offshore Heavy Oil Reservoirs. Energies, 11(9), 2428. https://doi.org/10.3390/en11092428





