1. Introduction
Building energy management systems (BEMS) are gaining popularity due to their ability to maximize profit for building owners. This objective is achieved by BEMS through monitoring and controlling various services within the building, ensuring increased efficiency of energy usage and optimizing the utilization of the building equipment. Generally, buildings use various energy forms such as electricity, heat energy, and cooling energy. Therefore, efficient conversion technologies of devices like combined heat and power units, optimal sizing of conventional and renewable sources, and integration of new devices are important ways to improve energy efficiency and economic benefit. Various studies have been conducted on maximizing the energy efficiency, sizing and integration of equipment, and improving economic benefits as discussed in the following paragraphs.
A deterministic demand side management program as a mixed integer linear programming problem is developed in reference [
1], where the impact of EV integration on operation costs in smart buildings is analyzed. A new energy management strategy for a dc distribution system in buildings is proposed by reference [
2]. The authors in reference [
3] have studied integrating of combined heat and power and heat pumps in buildings to improve their economic benefits, performance, flexibility, and stability. A method for generating maps indicating minimum battery and photovoltaics sizes for self-sufficient single-family houses in rural areas at the border between Germany and the Czech Republic has been proposed in reference [
4]. A control strategy for the management of a polygeneration system considering fuel cells and conventional energies technologies is proposed in reference [
5]. In reference [
6], a distributed optimization algorithm for residential users equipped with individual controllable loads, energy storage systems, and shared renewable energy sources is proposed. A scheduling approach for the minimization of energy costs in a smart home with storage devices, power generators, and renewable sources is proposed by reference [
7]. In reference [
8], an AC multi-period optimal power flow model for distribution systems with energy storage system considering uncertainties in wind and solar power generation is proposed. In reference [
9], a real-time strategy based on model predictive control for the energy scheduling of a grid-connected smart residential users with deferrable and non-deferrable electrical appliances is proposed.
Meanwhile, due to increases in the standard of living, a limited availability of arable land, and growth in population has resulted in the deployment of greenhouses. Smart greenhouses can provide high-quality fruits and vegetables even in the off-season by controlling indoor environmental conditions. The environmental factors of the greenhouse such as temperature, CO
2 concentration, light intensity, and humidity are important factors for plant growth [
10]. However, these control parameters are coupled with each other and require significant amounts of energy to maintain within acceptable bounds. Control of these factors is a difficult and challenging issue and different studies are conducted to control the environmental factors in greenhouses, as discussed below.
The authors of reference [
11] conducted a study to improve the energy performance of commercial greenhouses through a dual heat screen and double glazed glass in northern European climatic conditions. The authors in reference [
12] have provided solutions for photovoltaic greenhouses to coordinate solar panels and energy production by using agricultural production. The authors have also studied internal parameters (temperature, relative humidity, and solar radiation) and the optimal range of parameters for efficient plant growth. In reference [
13], a PID controller was used to adjust the various environmental conditions of the greenhouse to operate within the normal range and to effectively solve the interaction between the parameters. However, the fulfillment of these control parameters requires a significant amount of energy (electrical and thermal). Manual or sub-optimal operations can result in increased operation costs and ultimately reduce the profit for the greenhouse owners. Therefore, energy management of greenhouses has been considered by various researchers, as discussed below.
The concept of energy management for closed greenhouses integrated with thermal energy storage systems is presented in reference [
14]. In reference [
15], the temperature of the greenhouse is controlled by heating, natural ventilation, and energy conservation of the greenhouse by combining model predictive control with particle swarm optimization to solve non-linear optimization problems. In reference [
16], various techniques are used for the energy management of greenhouses and their efficiencies are analyzed by using building energy simulations. In reference [
17], a mathematical model for optimal operation of greenhouses is developed to minimize the operation cost of the energy generation units for a grid-connected mode. However, during emergencies, all the control parameters cannot be met due to disconnection from the utility grid. Therefore, both grid-connected and islanded modes have been considered in reference [
18], where the islanded mode is more focused.
Recently, rooftop greenhouses have also been considered in various studies to enhance the self-sufficiency of cities. In the case of rooftop greenhouses, they can be deployed on the rooftops of buildings, which is otherwise a non-productive space. In reference [
19], a residential building with a rooftop greenhouse is analyzed to quantify environmental impacts while considering the indoor temperatures of building households. In reference [
20], a new agricultural production system considering sustainability in Mediterranean urban areas through the integration of a greenhouse on the roof of buildings is analyzed. In reference [
21], optimal operation of building microgrids with rooftop greenhouses is considered for a building having n households and a rooftop greenhouse.
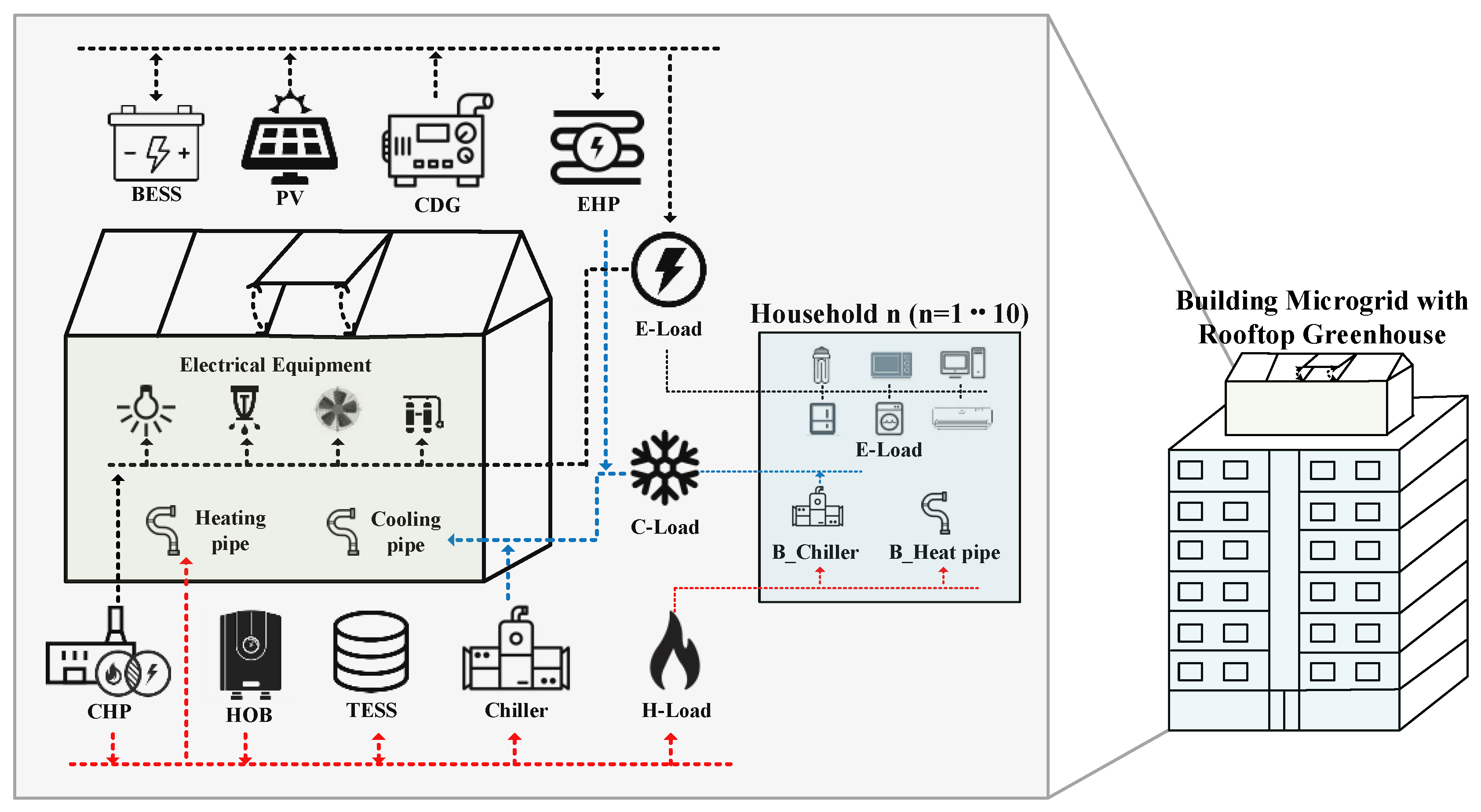
The BEMS can be utilized to collectively control the equipment of the greenhouse and the building. This cooperative optimization can further increase the profit for building owners due to difference in energy consumption patterns of the building residents and the greenhouse. Therefore, coordinated operation of building microgrids with rooftop greenhouses has been studied. However, in reference [
19], only control of indoor temperature of building and rooftop greenhouse using heat and cooling energy is considered. Similarly, indoor temperature control of building and rooftop greenhouse is studied in reference [
20], where energy transfer between greenhouse and the building is considered. The amount of electricity needed to harvest crops and the potential profit from the crop is analyzed in reference [
22]. In reference [
23], the improvement in the crop yield and environmental benefits obtained through energy and gas exchange, water exchange, and waste energy exchange between building and rooftop are analyzed. However, the growth of plants is influenced by various other environmental factors also such as humidity, light intensity, and CO
2 concentration, which are ignored in these studies. A huge amount of energy is required in building microgrids with a rooftop greenhouse to fulfil energy demands, thus an energy management system for improving crops yield and energy efficiency is required. An energy management system for building microgrids is also needed. In addition, in the islanded mode, due to the absence of connection with the utility grid, local resources may not be sufficient to fulfill the entire energy demands of the network. The situation becomes worse if any equipment failure occurs during the islanded period. Therefore, in this study, the islanded operation of building microgrid with rooftop greenhouse is studied considering optimal control environments, component outage, and component recovery.
This paper is an extension of reference [
21], where only the grid-connected mode was considered. In this study, optimal operation of building microgrid with rooftop greenhouse in the islanded mode is considered. In addition, the outage and recovery of different components in the system during islanded mode are also considered. Both the building and greenhouse have electrical, thermal, and cooling energy loads. The greenhouse has additional constraints to control the indoor environmental parameters such as indoor temperature, humidity, CO
2 concentration, and light intensity. The load in the building is decomposed into critical and non-critical loads to ensure service reliability to critical loads during emergency operation of the microgrid. The normal operation bounds of control parameters in the greenhouse are relaxed to a set of additional bounds to maximize the growth of plants under resource scarcity. Different penalties are defined for violation of different bounds, i.e., higher penalties are set for higher deviations from the normal bounds. A priority weight matrix is defined to control the violation of parameters while considering the importance of each parameter to the plant growth. The performance of the proposed method is evaluated by carrying out various simulations in islanded mode. In addition to the operation of the islanded mode, the outage and recovery of CHP, EHP, and the fogging system are also considered during different intervals of the scheduling horizon. In addition, simultaneous outage of equipment is also analyzed to validate the performance of the proposed operation scheme under extreme cases of equipment outage.
5. Conclusions
In this paper, an optimal operation method for a building microgrid with a rooftop greenhouse considering equipment outages is proposed. The proposed operational strategy defines the priority of various control parameters through the weight matrix and considers the optimum growth of the plants. If the control parameters are out of the acceptable bounds, additionally relaxed bounds are utilized and a violation cost is imposed. The performance of the proposed method is evaluated by considering seven equipment outages cases. It has been observed that during an equipment outage, replaceable equipment has been operated to fulfill the energy deficit, i.e., DG and HOB has been utilized in case of a CHP outage. In case of absence of replaceable equipment or inability of the replaceable equipment to fulfill the energy demand, violation of acceptable bounds is considered for the greenhouse. Similarly, the shedding of non-critical loads is considered in the case of building households. For example, in the case of an EHP outage, cooling is provided through the chiller but due to insufficient heat, temperature violations occur. It also has been observed that, after equipment restoration, the control parameters have gradually been restored to their normal bounds. However, in the final case, the CO2 concentration was unable to reach the acceptable bound in the current scheduling horizon due to limited capacity of the CO2 generator, i.e., it requires more time.
The formulated problem is subjected to environmental uncertainties and uncertainties in energy usage patterns of building residents. Consideration of uncertainties in loads and renewables will be a valuable extension of this paper.