Assessment of Primary Energy Conversion of a Closed-Circuit OWC Wave Energy Converter
Abstract
1. Introduction
2. Numerical Models From Wave to Pneumatic Power
2.1. Hydrodynamics
2.2. Thermodynamics
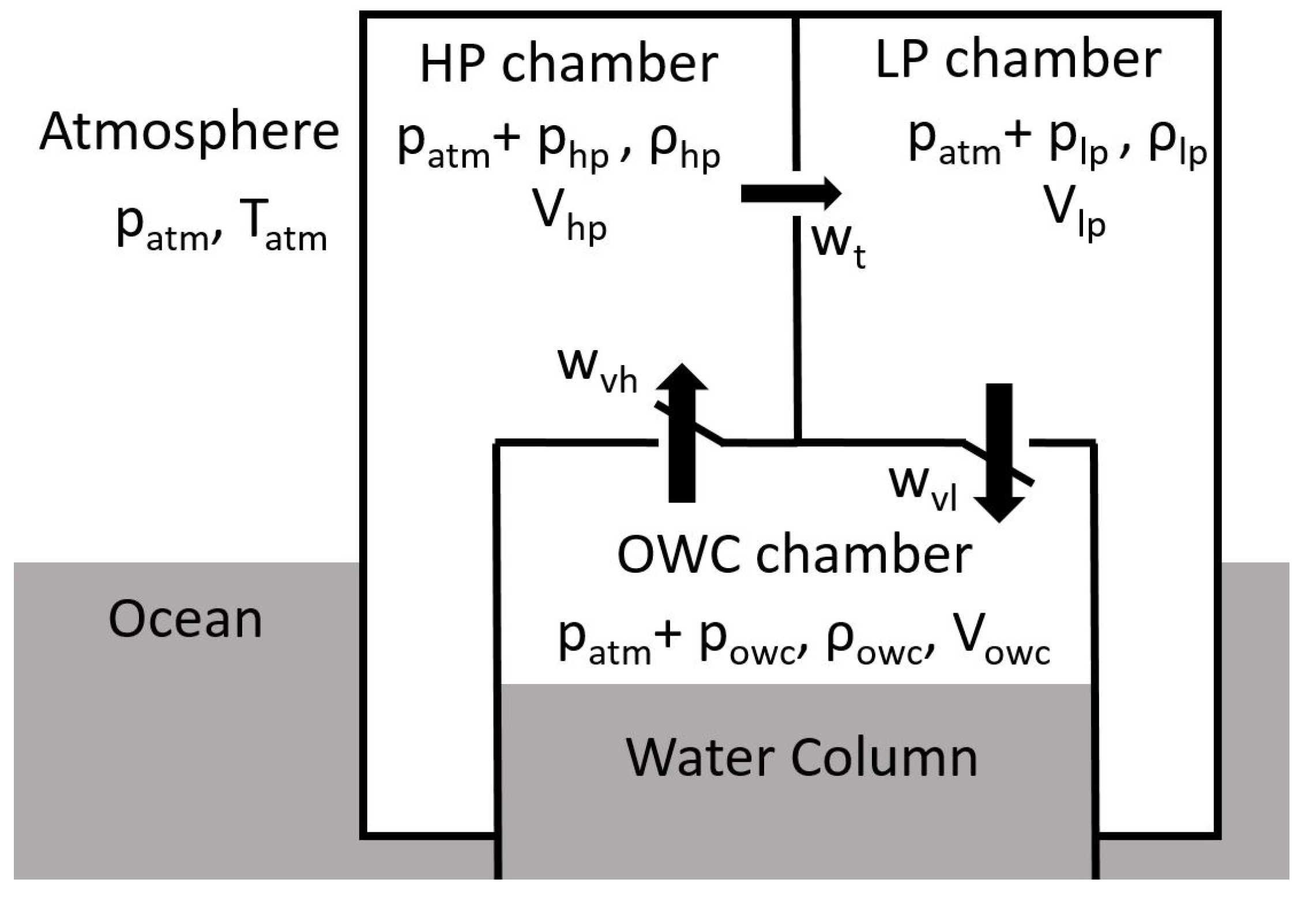
2.2.1. General Equations
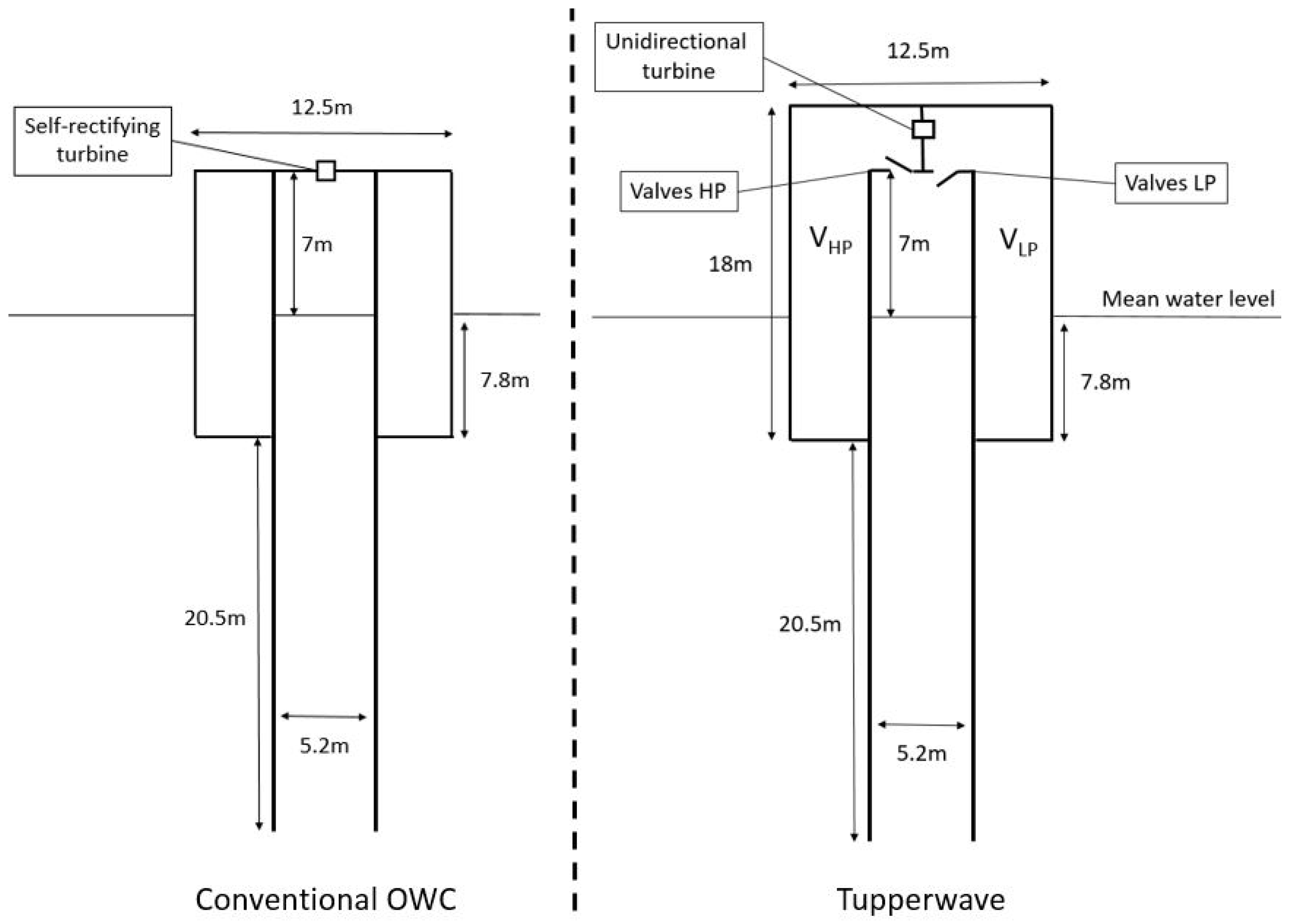
2.2.2. Conventional OWC Thermodynamics
2.2.3. Tupperwave Device Thermodynamics
2.3. Numerical Solution
3. Physical Modelling in the Wave Tank
3.1. Physical Models Design and Fabrication
3.1.1. Scaling
3.1.2. Turbines
3.1.3. Valves
3.2. Experimental Setup and Test Plan
4. Results and Numerical Model Validation
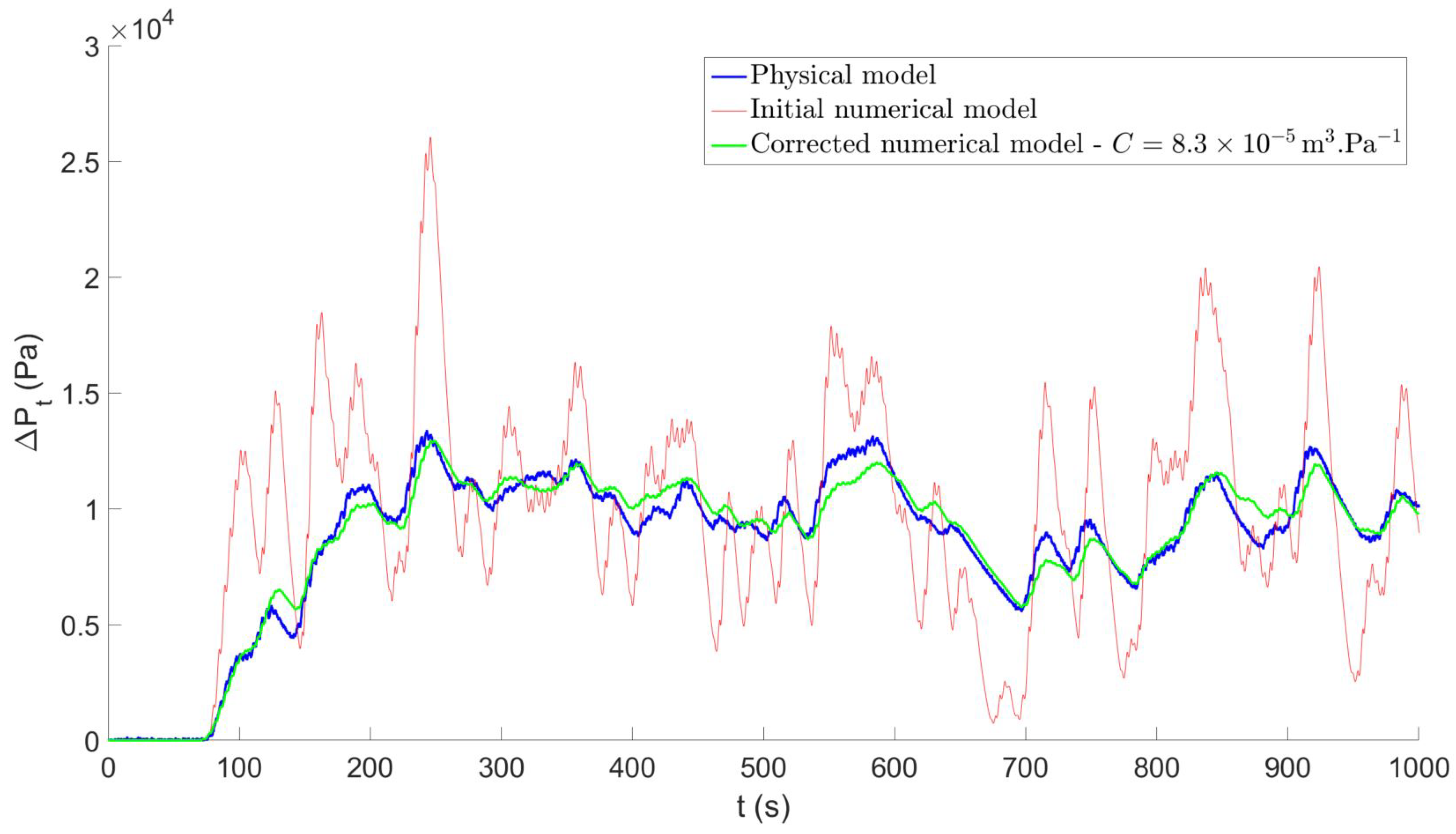
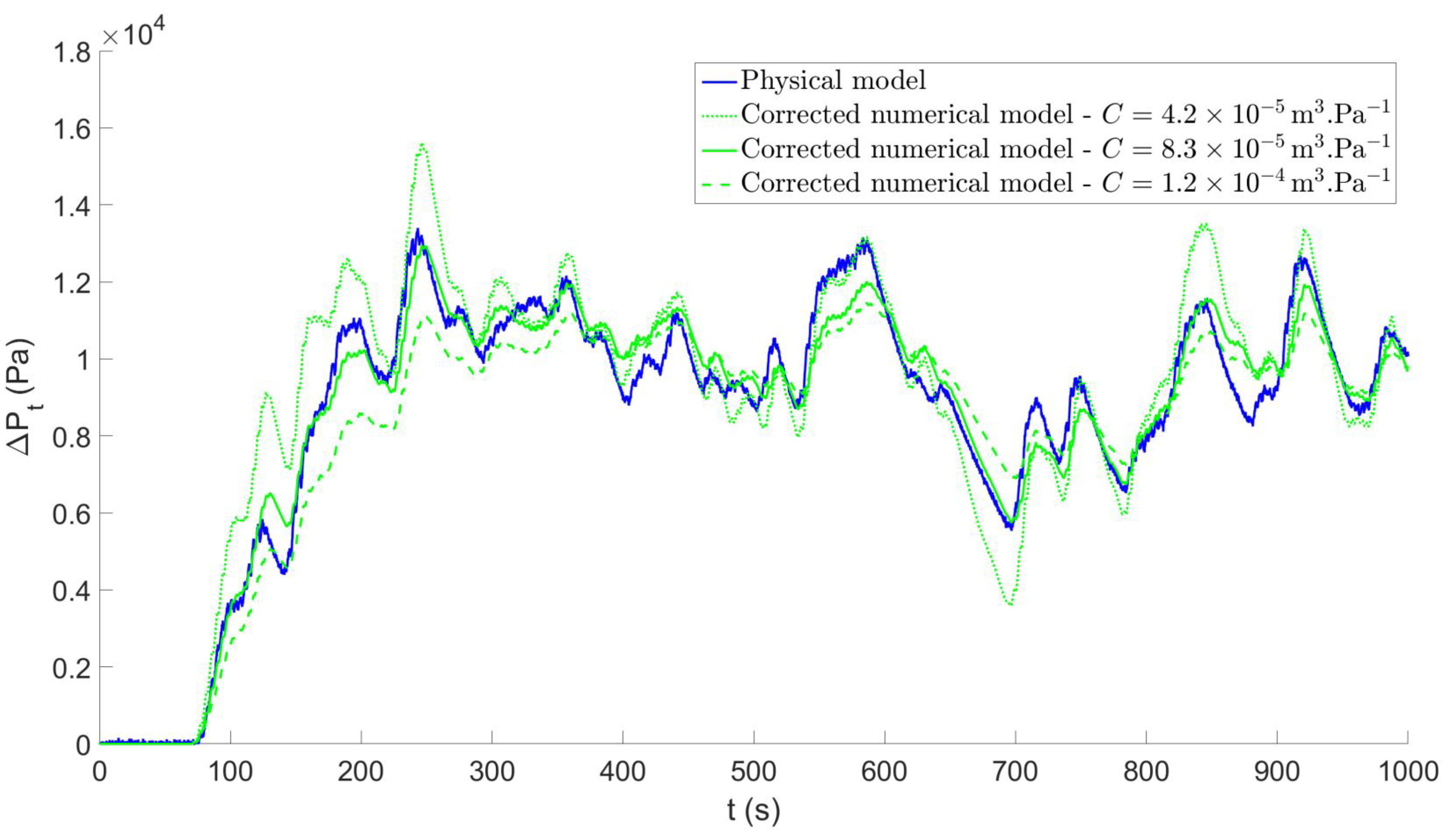
4.1. Correction in the Tupperwave Numerical Model
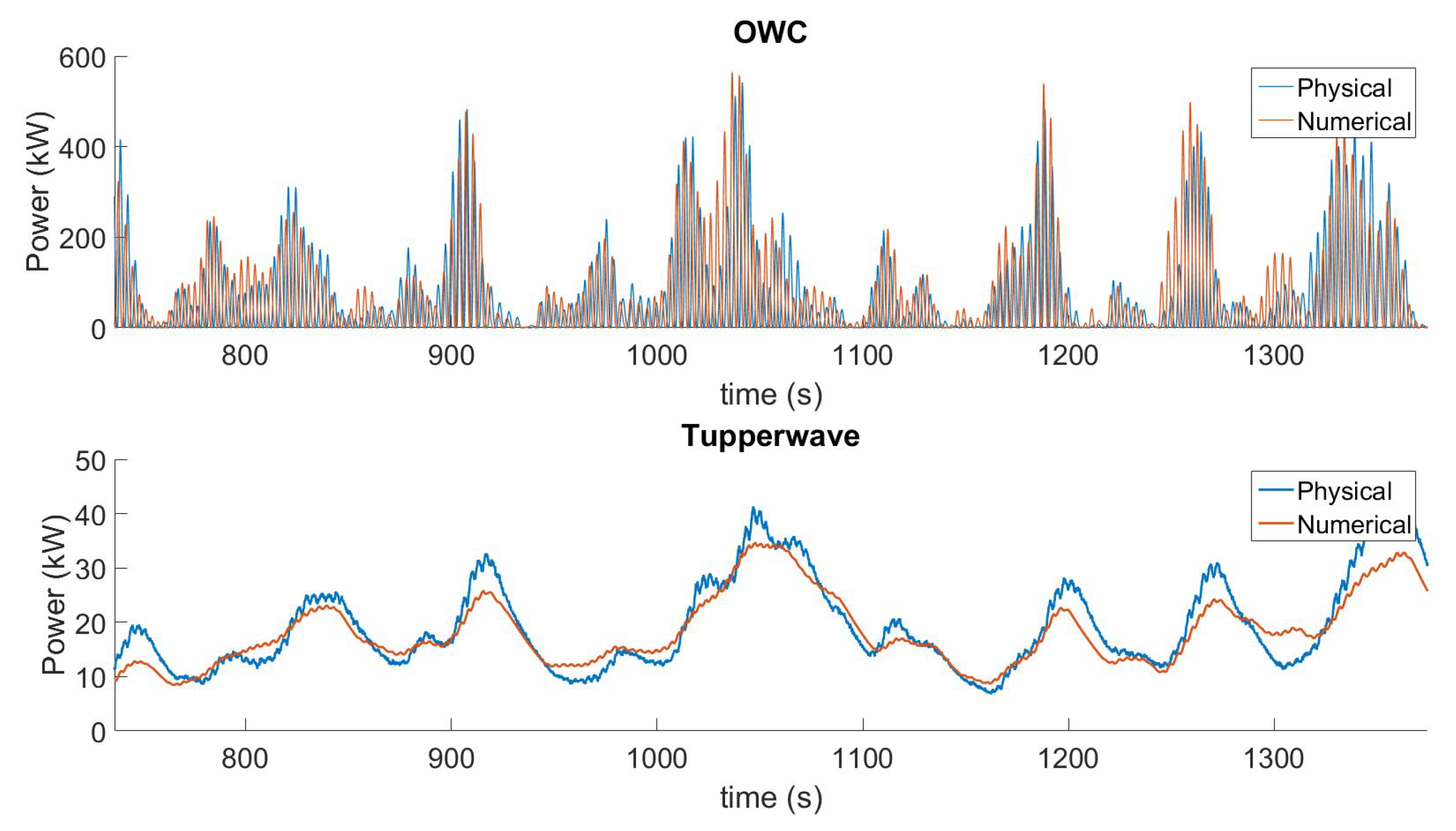
4.2. Numerical Model Validation
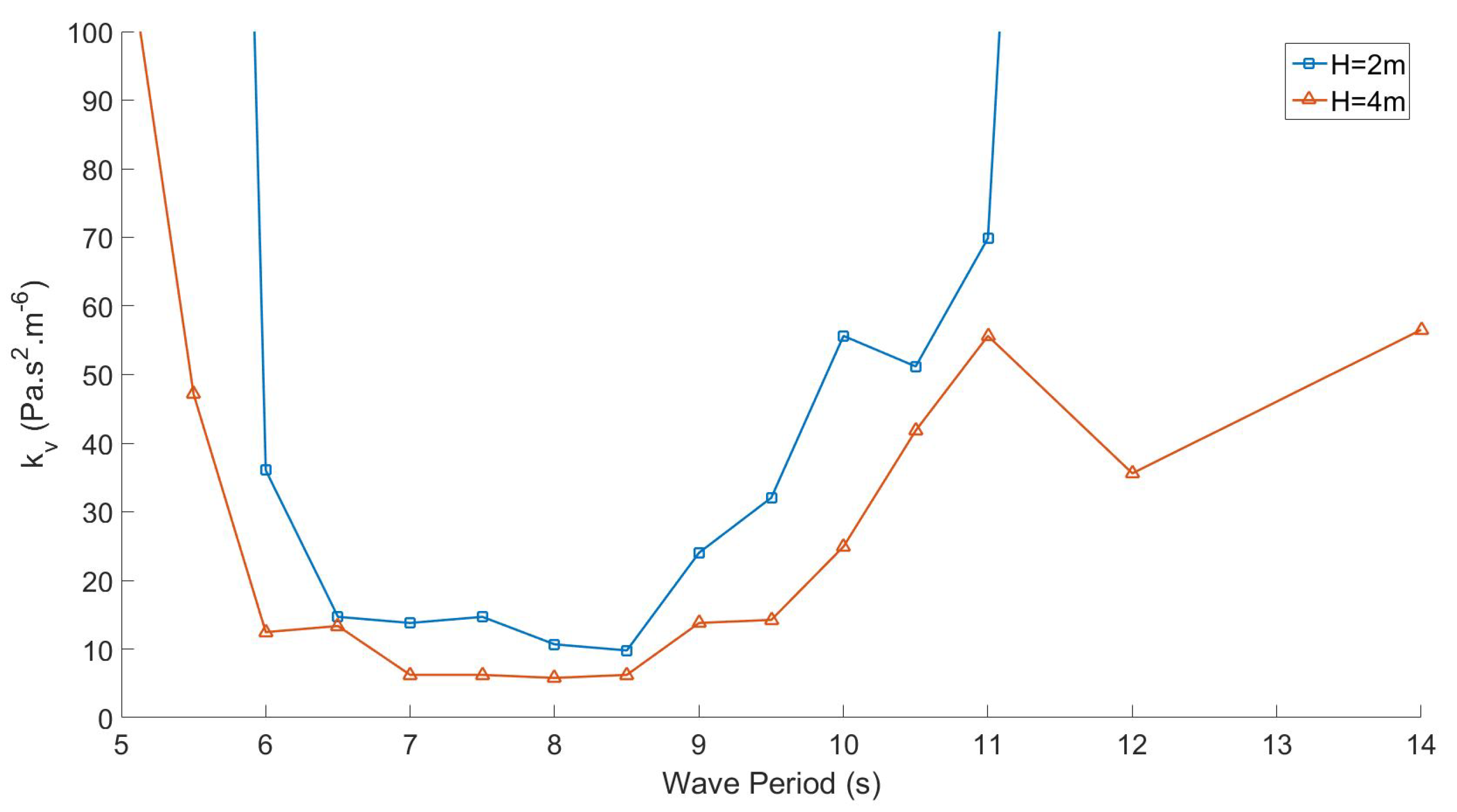
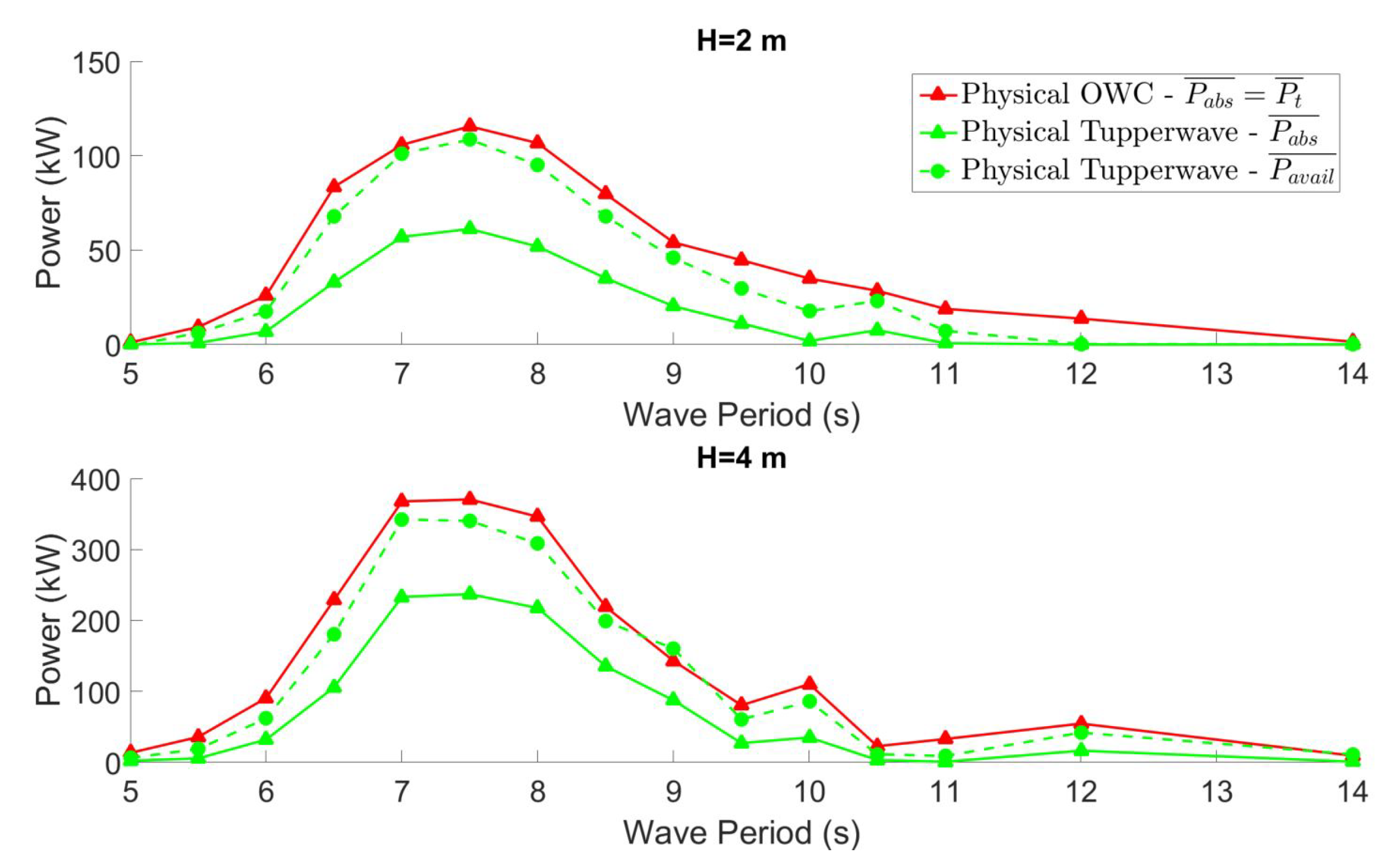
4.3. Power Performance Comparison
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Prony’s Method
References
- Bellamy, N. The circular sea clam wave energy converter. In Hydrodynamics of Ocean Wave-Energy Utilization; Springer: Berlin/Heidelberg, Germany, 1986; pp. 69–79. [Google Scholar]
- Ryan, S.; Algie, C.; Macfarlane, G.J.; Fleming, A.N.; Penesis, I.; King, A. The Bombora wave energy converter: A novel multi-purpose device for electricity, coastal protection and surf breaks. In Proceedings of the Australasian Coasts & Ports Conference 2015: 22nd Australasian Coastal and Ocean Engineering Conference and the 15th Australasian Port And Harbour Conference, Auckland, New Zealand, 15–18 September 2015; Engineers Australia and IPENZ: Auckland, New Zealand, 2015; p. 541. [Google Scholar]
- Falcão, A.F.O.; Henriques, J.C.C.; Gato, L.M.C. Self-rectifying air turbines for wave energy conversion: A comparative analysis. Renew. Sustain. Energy Rev. 2018, 91, 1231–1241. [Google Scholar] [CrossRef]
- Lopes, B. Construction and Testing of a Double Rotor Self-Rectifying Air Turbine Model for Wave Energy Recovery Systems. Master’s Thesis, Tecnico Lisboa, Lisboa, Portugal, 2017. (In Portuguese). [Google Scholar]
- Borges, J. Three-Dimensional Design of Turbomachinery. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 1986. [Google Scholar]
- Falcão, A.F.O.; Henriques, J.C.C. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar] [CrossRef]
- Masuda, Y.; McCormick, M.E. Experiences in pneumatic wave energy conversion in Japan. In Utilization of Ocean Waves—Wave to Energy Conversion; ASCE: Reston, VA, USA, 1986; pp. 1–33. [Google Scholar]
- Falcão, A.F.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Vicente, M.; Benreguig, P.; Crowley, S.; Murphy, J. Tupperwave-preliminary numerical modelling of a floating OWC equipped with a unidirectional turbine. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC), Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Penalba, M.; Ringwood, J. A review of wave-to-wire models for wave energy converters. Energies 2016, 9, 506. [Google Scholar] [CrossRef]
- Penalba, M.; Sell, N.; Hillis, A.; Ringwood, J. Validating a wave-to-wire model for a wave energy converter—Part I: The Hydraulic Transmission System. Energies 2017, 10, 977. [Google Scholar] [CrossRef]
- Penalba, M.; Cortajarena, J.A.; Ringwood, J. Validating a wave-to-wire model for a wave energy converter—Part II: The electrical system. Energies 2017, 10, 1002. [Google Scholar] [CrossRef]
- Kelly, J.F.; Wright, W.M.; Sheng, W.; O’Sullivan, K. Implementation and verification of a wave-to-wire model of an oscillating water column with impulse turbine. IEEE Trans. Sustain. Energy 2016, 7, 546–553. [Google Scholar] [CrossRef]
- Evans, D. Wave-power absorption by systems of oscillating surface pressure distributions. J. Fluid Mech. 1982, 114, 481–499. [Google Scholar] [CrossRef]
- Evans, D. The oscillating water column wave-energy device. IMA J. Appl. Math. 1978, 22, 423–433. [Google Scholar] [CrossRef]
- Cheng, A.H.D.; Cheng, D.T. Heritage and early history of the boundary element method. Eng. Anal. Bound. Elem. 2005, 29, 268–302. [Google Scholar] [CrossRef]
- Sheng, W.; Alcorn, R.; Lewis, A. Assessment of primary energy conversions of oscillating water columns. I. Hydrodynamic analysis. J. Renew. Sustain. Energy 2014, 6, 053113. [Google Scholar] [CrossRef]
- Falcão, A.F.; Henriques, J.C.; Cândido, J.J. Dynamics and optimization of the OWC spar buoy wave energy converter. Renew. Energy 2012, 48, 369–381. [Google Scholar] [CrossRef]
- Henriques, J.; Falcao, A.; Gomes, R.; Gato, L. Air turbine and primary converter matching in spar-buoy oscillating water column wave energy device. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; p. V008T09A077. [Google Scholar]
- Taghipour, R.; Perez, T.; Moan, T. Hybrid frequency–time domain models for dynamic response analysis of marine structures. Ocean Eng. 2008, 35, 685–705. [Google Scholar] [CrossRef]
- Cummins, W. The Impulse Response Function and Ship Motions; Technical Report; David Taylor Model Basin: Washington, DC, USA, 1962. [Google Scholar]
- Lee, C.H. WAMIT Theory Manual; Massachusetts Institute of Technology, Department of Ocean Engineering: Cambridge, MA, USA, 1995. [Google Scholar]
- Giorgi, G.; Ringwood, J.V. Consistency of viscous drag identification tests for wave energy applications. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC), Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Morison, J.; Johnson, J.; Schaaf, S. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Falcao, A.F.O.; Justino, P.A.P. OWC wave energy devices with air flow control. Ocean Eng. 1999, 26, 1275–1295. [Google Scholar] [CrossRef]
- Sheng, W.; Alcorn, R.; Lewis, A. On thermodynamics in the primary power conversion of oscillating water column wave energy converters. J. Renew. Sustain. Energy 2013, 5, 023105. [Google Scholar] [CrossRef]
- López, I.; Pereiras, B.; Castro, F.; Iglesias, G. Optimisation of turbine-induced damping for an OWC wave energy converter using a RANS–VOF numerical model. Appl. Energy 2014, 127, 105–114. [Google Scholar] [CrossRef]
- Benreguig, P.; Murphy, J.; Vicente, M.; Crowley, S. Wave-to-Wire model of the Tupperwave device and performance comparison with conventional OWC. In Proceedings of the RENEW 2018 3rd International Conference on Renewable Energies Offshore, Lisbon, Portugal, 8–10 October 2018. [Google Scholar]
- Duclos, G.; Clément, A.H.; Chatry, G. Absorption of outgoing waves in a numerical wave tank using a self-adaptive boundary condition. Int. J. Offshore Polar Eng. 2001, 11, 168–175. [Google Scholar]
- Sheng, W.; Alcorn, R.; Lewis, A. A new method for radiation forces for floating platforms in waves. Ocean Eng. 2015, 105, 43–53. [Google Scholar] [CrossRef]
- MATLAB. Version 7.10.0 (R2010a); The MathWorks Inc.: Natick, MA, USA, 2010. [Google Scholar]
- Falcão, A.F.O.; Henriques, J.C.C. Model-prototype similarity of oscillating-water-column wave energy converters. Int. J. Mar. Energy 2014, 6, 18–34. [Google Scholar] [CrossRef]
- Kurniawan, A.; Chaplin, J.; Greaves, D.; Hann, M. Wave energy absorption by a floating air bag. J. Fluid Mech. 2017, 812, 294–320. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Henriques, J.C.C. The Spring-Like Air Compressibility Effect in OWC Wave Energy Converters: Hydro-, Thermo-and Aerodynamic Analyses. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018. [Google Scholar]
- SOLIDWORKS. Version 2017; Dassault Systèmes SE. Available online: https://www.solidworks.com/ (accessed on 21 May 2019).
- Benreguig, P.; Thiebaut, F.; Murphy, J. Pneumatic orifice calibration, investigation into the influence of test rig characteritics on calibration results. In Proceedings of the CORE Conference, Glasgow, UK, 12–14 September 2016. [Google Scholar]
- Capricorn, HypAir Balance, Product Technical Data Sheet (ver. 001/08.2013). 2013. Available online: http://www.capricorn.pl/upload/files/20150904/napowietrzacz-hipair-balance-karta-techniczna-en.pdf (accessed on 21 May 2019).
- Benreguig, P.; Murphy, J.; Sheng, W. Model scale testing of the Tupperwave device with comparison to a conventional OWC. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering OMAE2018, Madrid, Spain, 17–22 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018. [Google Scholar]
- Hodgins, N.; Keysan, O.; McDonald, A.S.; Mueller, M.A. Design and testing of a linear generator for wave-energy applications. IEEE Trans. Ind. Electron. 2012, 59, 2094–2103. [Google Scholar] [CrossRef]
- Prudell, J.; Stoddard, M.; Amon, E.; Brekken, T.K.; Von Jouanne, A. A permanent-magnet tubular linear generator for ocean wave energy conversion. IEEE Trans. Ind. Appl. 2010, 46, 2392–2400. [Google Scholar] [CrossRef]
- Baker, N.; Mueller, M.A. Direct drive wave energy converters. Rev. Energy Renew. Power Eng. 2001, 1, 1–7. [Google Scholar]
- Benreguig, P.; Vicente, M.; Dunne, A.; Murphy, J. Modelling Approaches of a Closed-Circuit OWC Wave Energy Converter. J. Mar. Sci. Eng. 2019, 7, 23. [Google Scholar] [CrossRef]











| Model Scale | Full Scale | |
|---|---|---|
| Total mass (kg) | 58.4 | |
| Distance device bottom, COG(m) | 0.892 | 21.49 |
| Distance device bottom, COB(m) | 0.961 | 23.16 |
| Ixx () | 23 | |
| Iyy () | 23.5 | |
| Izz () | 2 |
| Model Scale | Full Scale | ||||
|---|---|---|---|---|---|
| Orifice | Diameter (mm) | () | () | () | () |
| OWC1 | 22.6 | 21.1 | |||
| OWC2 | 20.6 | 30.9 | |||
| OWC3 | 17.5 | 58.3 | |||
| T1 | 11.5 | 209 | |||
| T2 | 9.2 | 552 | |||
| T3 | 7 | 1439 |
| Sea State | Pearson Correlation Coefficient (-) | ||
|---|---|---|---|
| (m) | (s) | Initial Model | Corrected Model |
| 2 | 5.7 | 0.72 | 0.85 |
| 3 | 7.1 | 0.68 | 0.93 |
| 3 | 8.5 | 0.69 | 0.93 |
| 5 | 8.5 | 0.65 | 0.94 |
| 3 | 10.6 | 0.70 | 0.94 |
| 5 | 10.6 | 0.65 | 0.93 |
| 5 | 12.7 | 0.62 | 0.93 |
| 3 | 14.1 | 0.70 | 0.86 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benreguig, P.; Pakrashi, V.; Murphy, J. Assessment of Primary Energy Conversion of a Closed-Circuit OWC Wave Energy Converter. Energies 2019, 12, 1962. https://doi.org/10.3390/en12101962
Benreguig P, Pakrashi V, Murphy J. Assessment of Primary Energy Conversion of a Closed-Circuit OWC Wave Energy Converter. Energies. 2019; 12(10):1962. https://doi.org/10.3390/en12101962
Chicago/Turabian StyleBenreguig, Pierre, Vikram Pakrashi, and Jimmy Murphy. 2019. "Assessment of Primary Energy Conversion of a Closed-Circuit OWC Wave Energy Converter" Energies 12, no. 10: 1962. https://doi.org/10.3390/en12101962
APA StyleBenreguig, P., Pakrashi, V., & Murphy, J. (2019). Assessment of Primary Energy Conversion of a Closed-Circuit OWC Wave Energy Converter. Energies, 12(10), 1962. https://doi.org/10.3390/en12101962






