A Multi-Scale Analysis of the Fire Problems in an Urban Utility Tunnel
Abstract
1. Introduction
2. Experimental Method
2.1. Bench-Scale Tests
2.2. Full-Scale Tests
2.3. Model-Scale Tests
3. Results and Discussion
3.1. Fire Behaviour of Accommodated Cables
3.1.1. Burning Characteristics and Phenomena
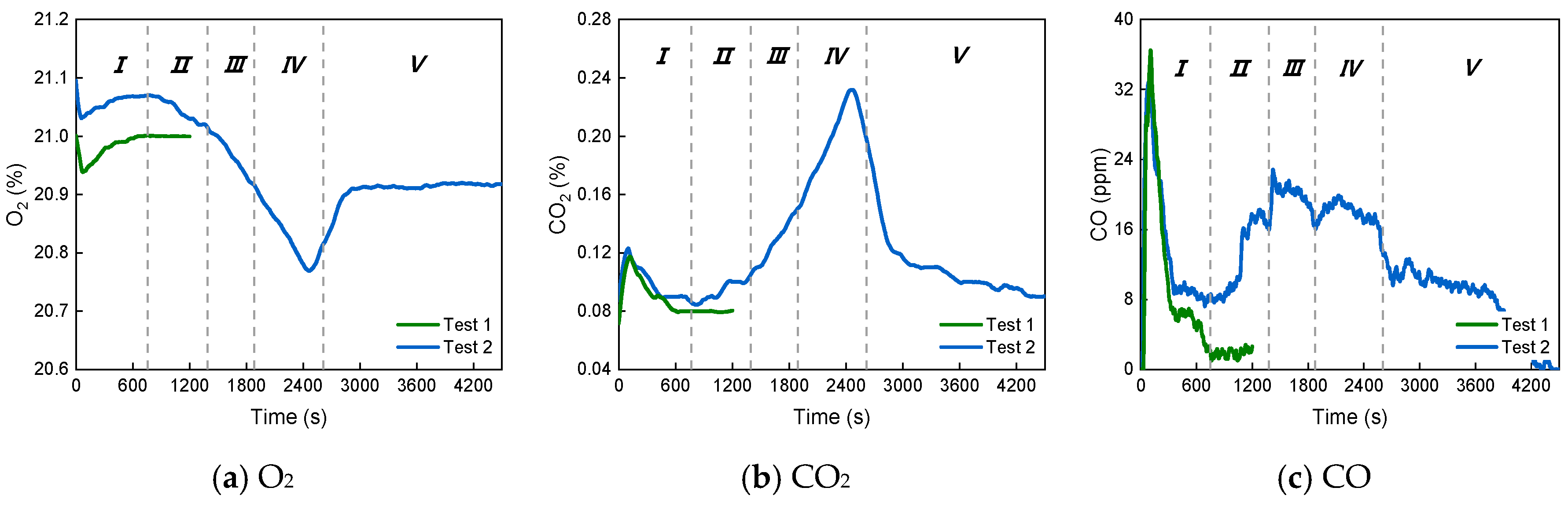
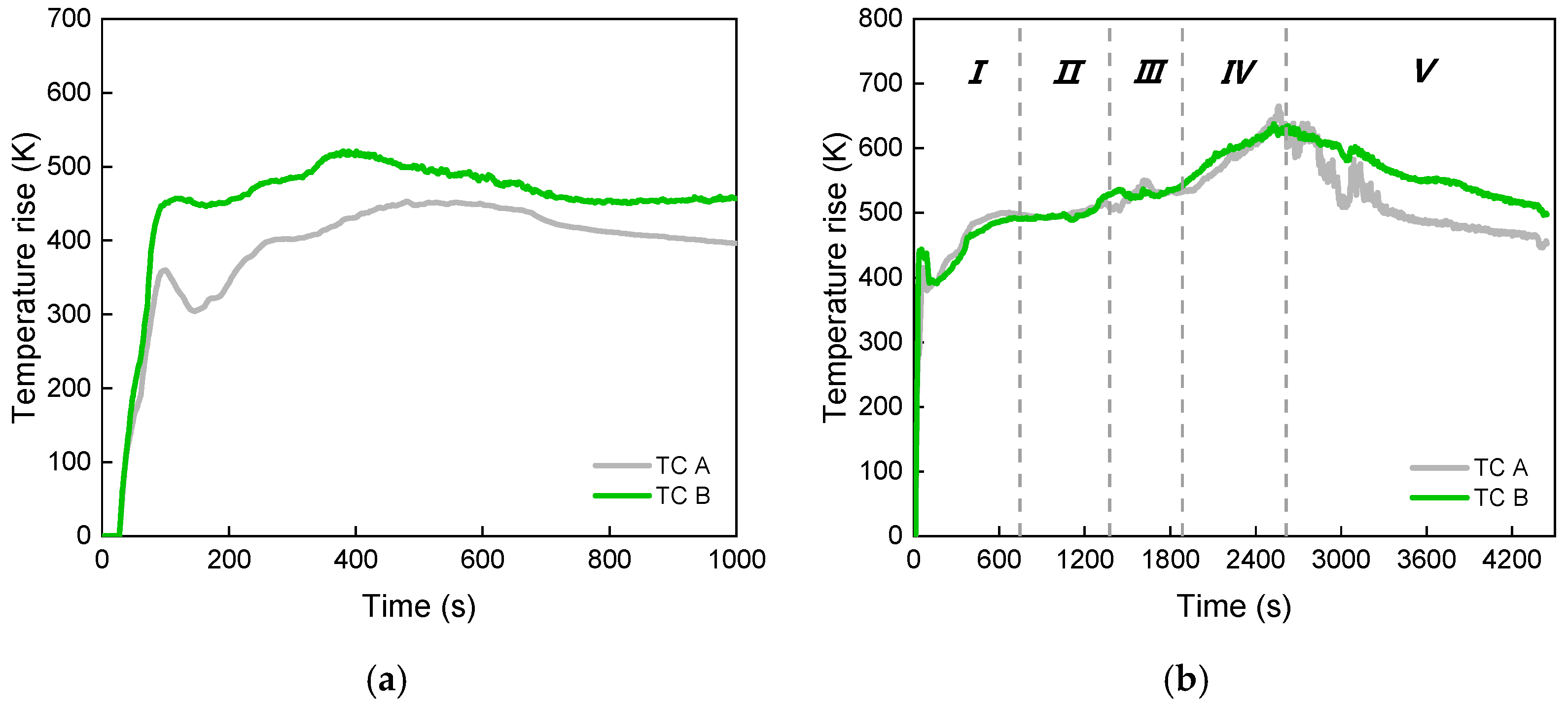
3.1.2. Combustion Gas Concentration and Cable Surface Temperature
3.2. Temperature Field within the Hot Gas Layer
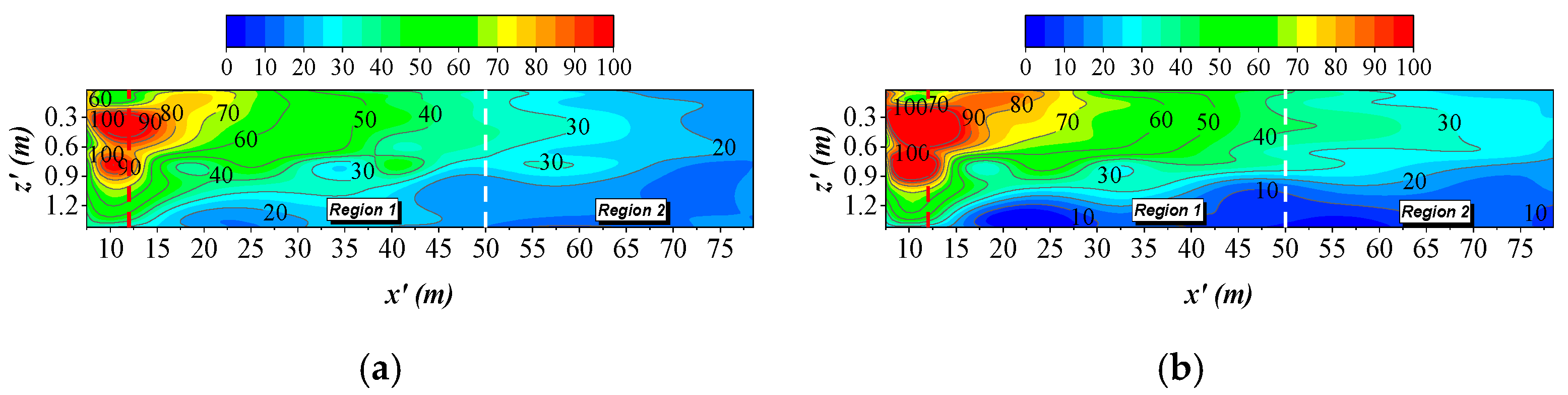
3.2.1. Two-Dimensional Temperature Field
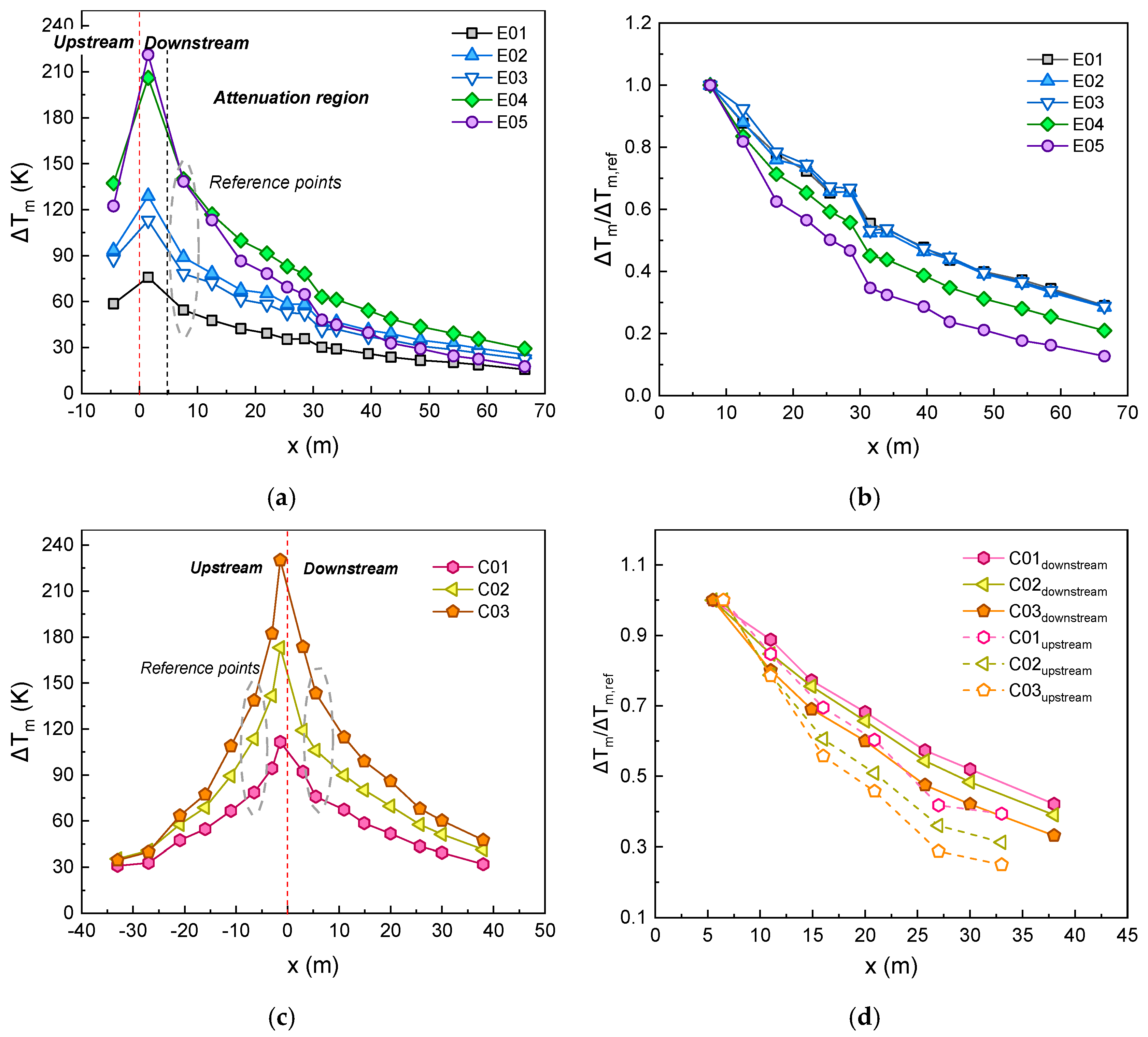
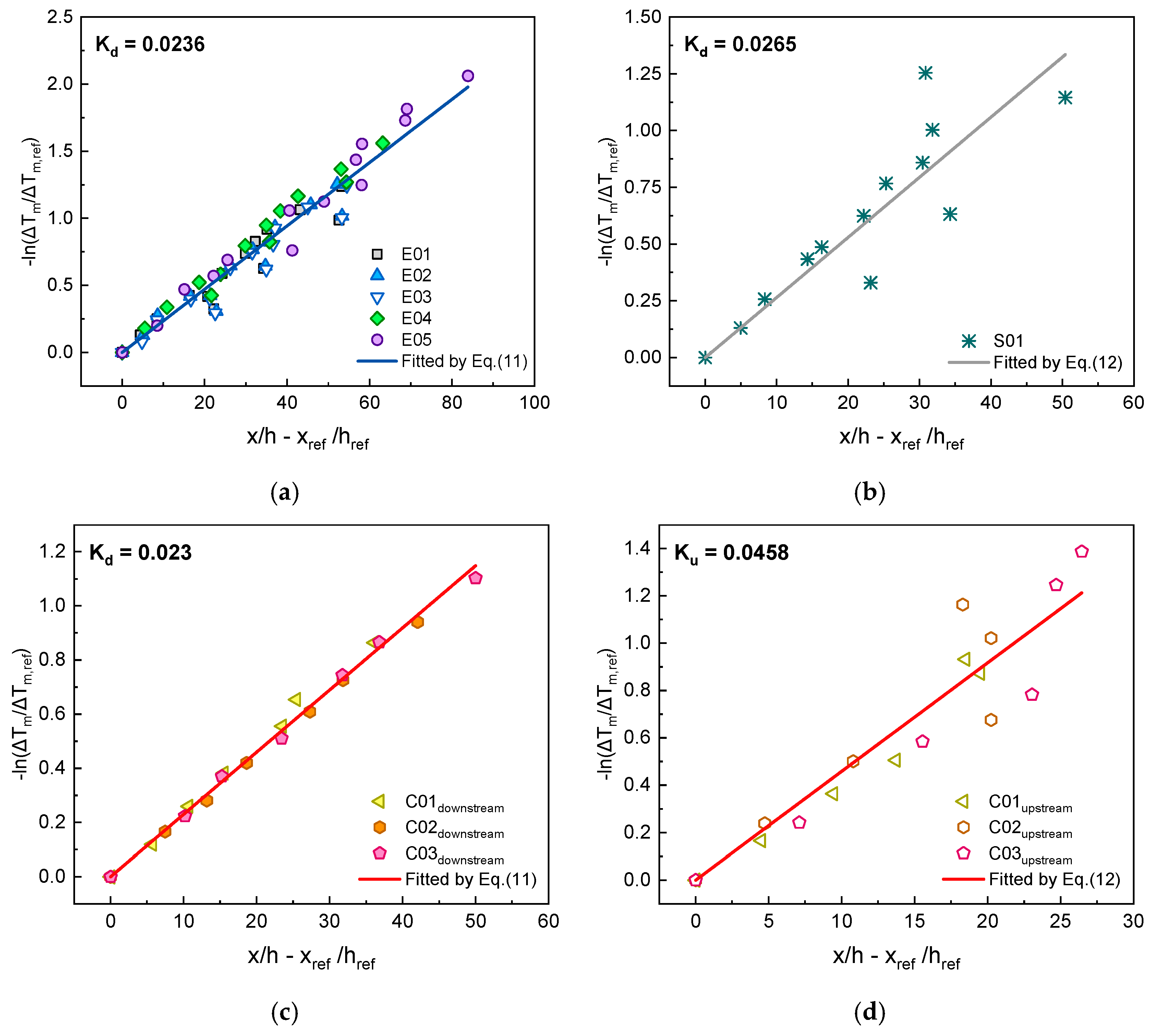
3.2.2. Longitudinal Maximum Gas Temperature Decay
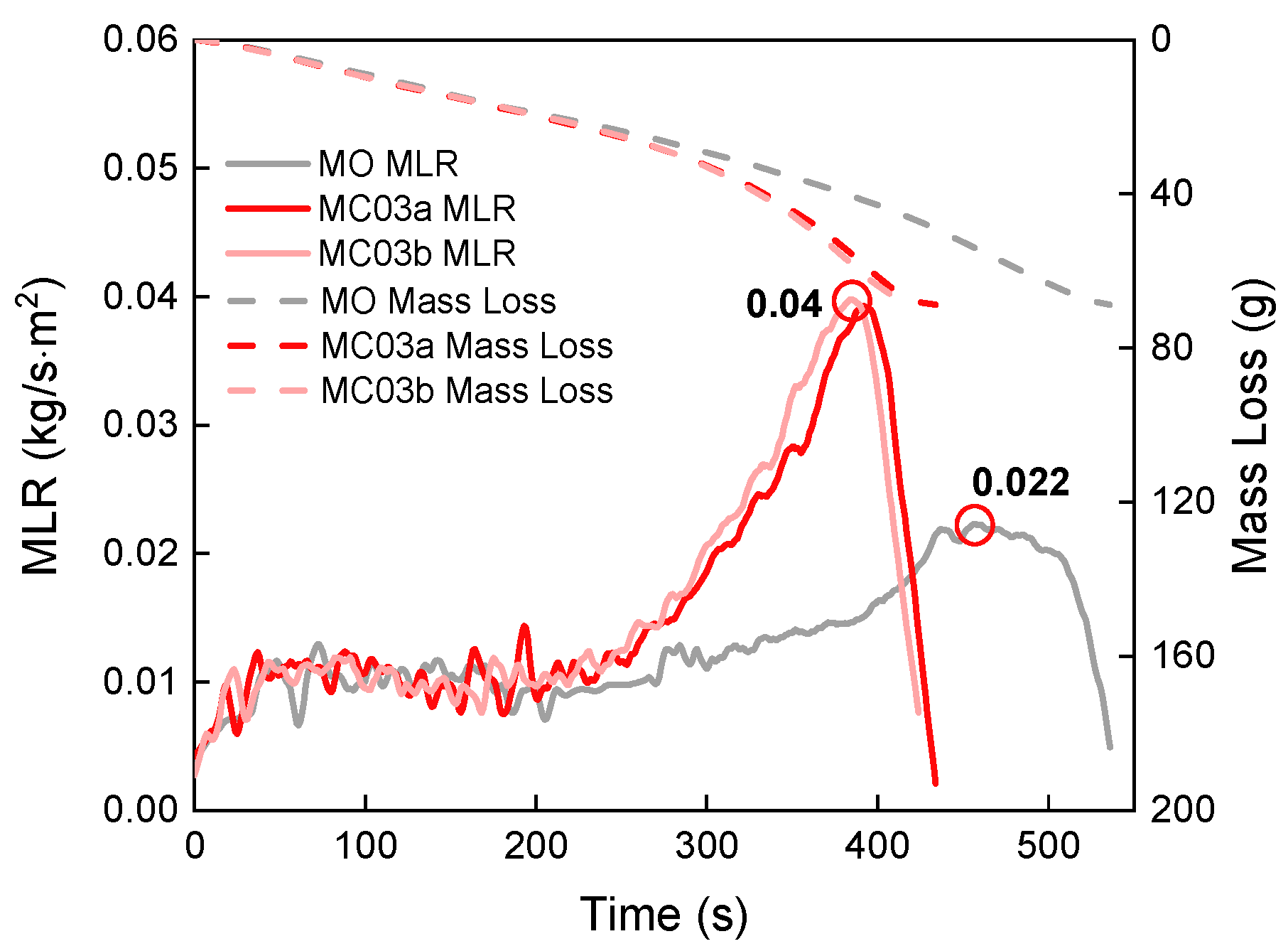
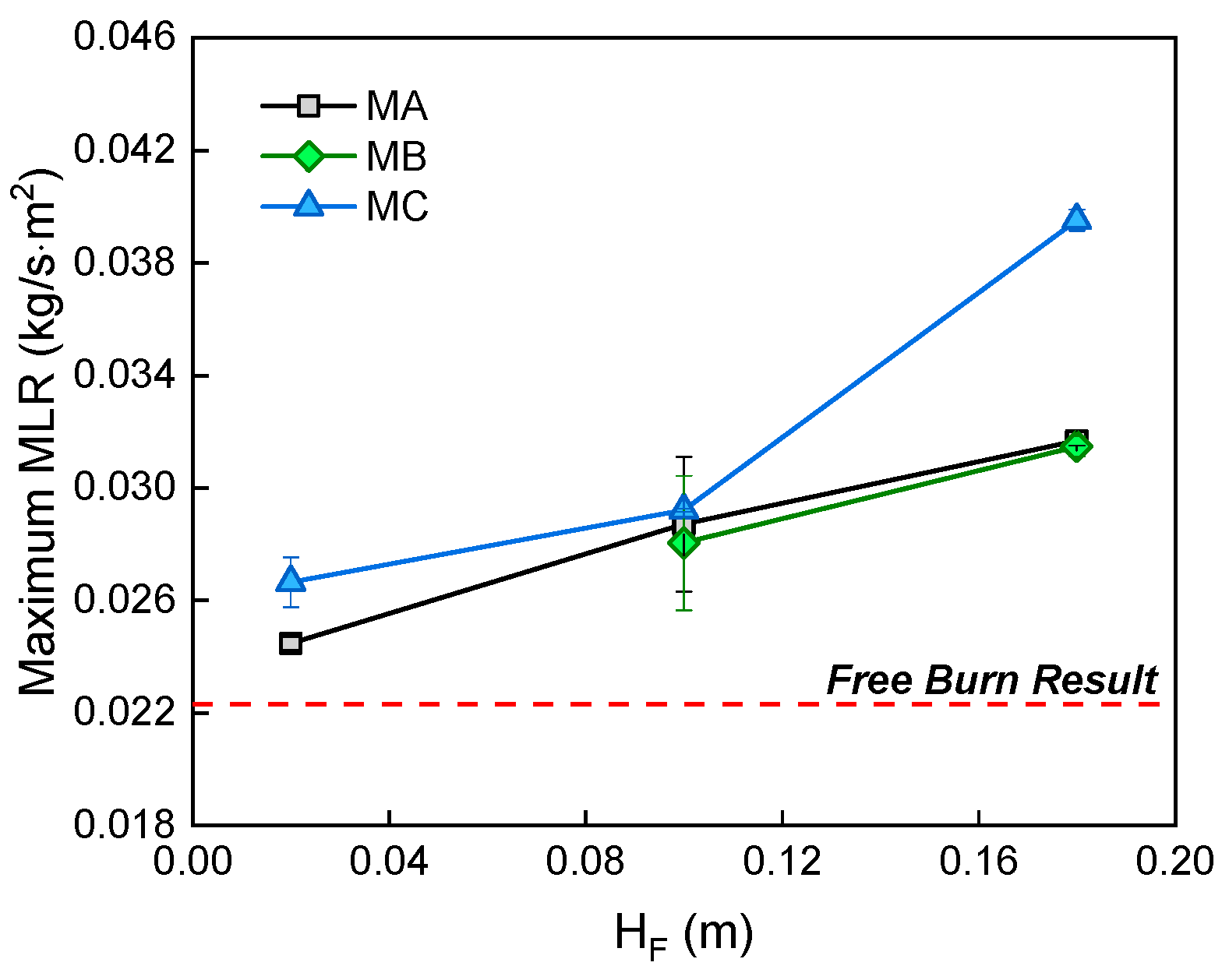
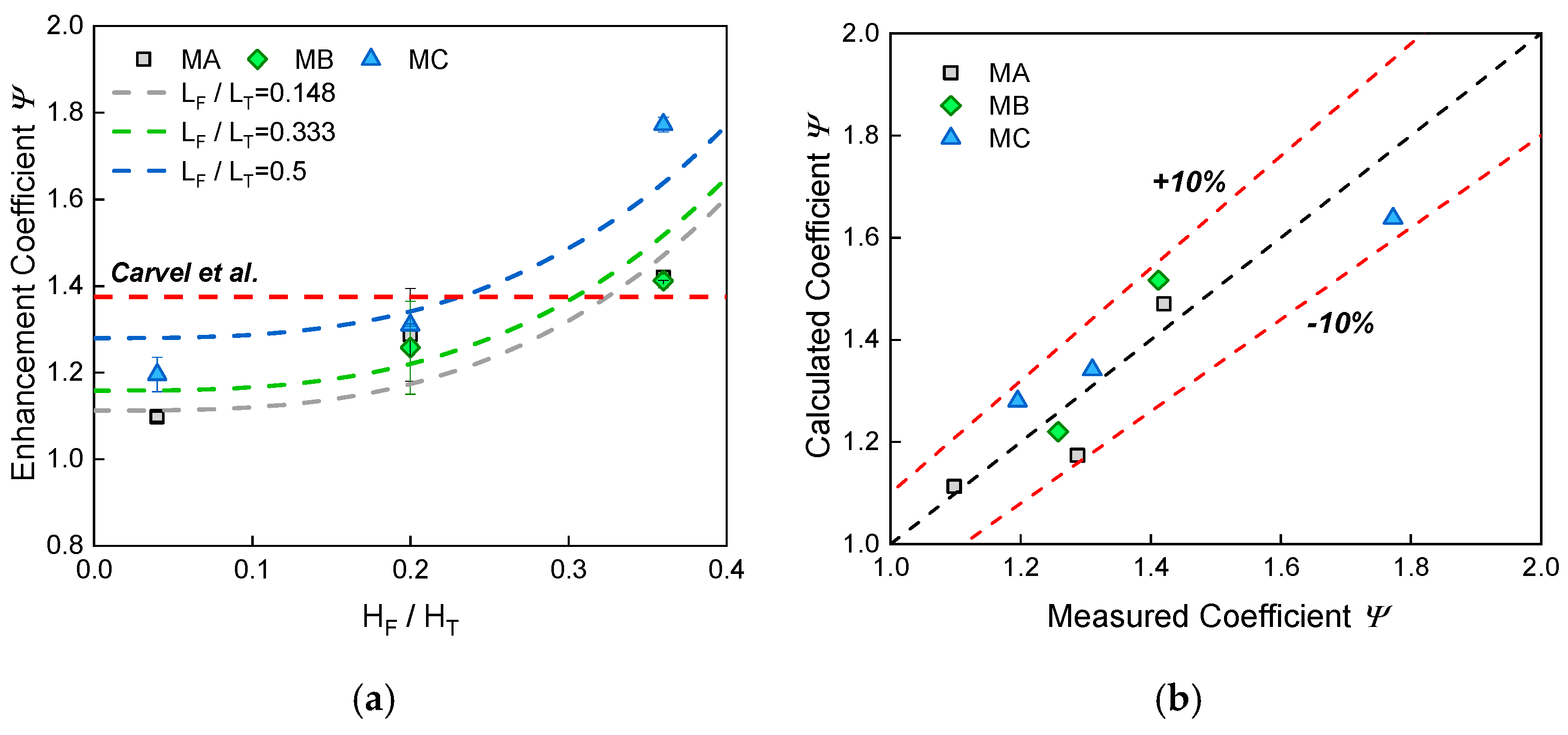
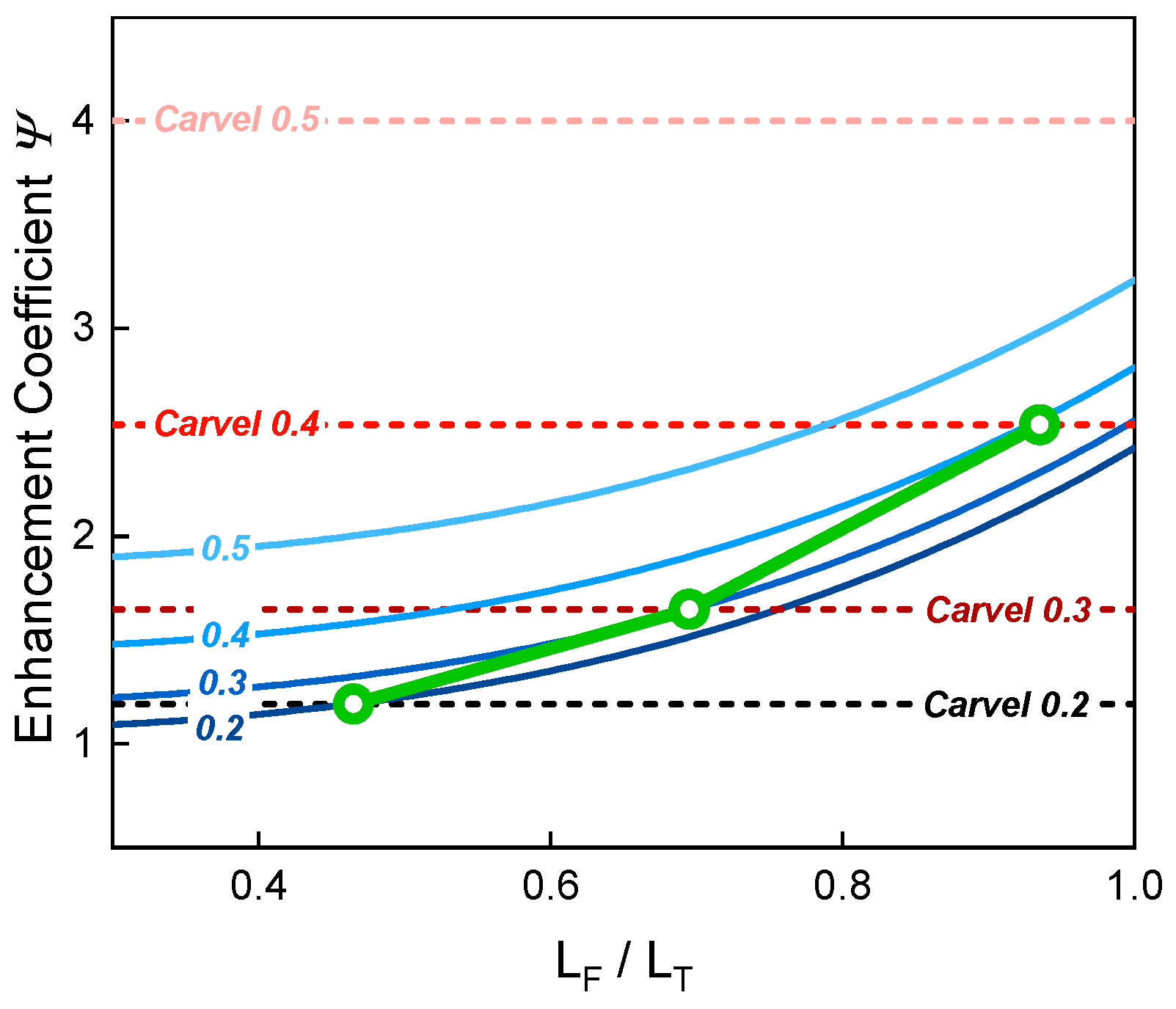
3.3. Enhanced Fuel Burning Rates in a Utility Tunnel
4. Conclusions
- (1)
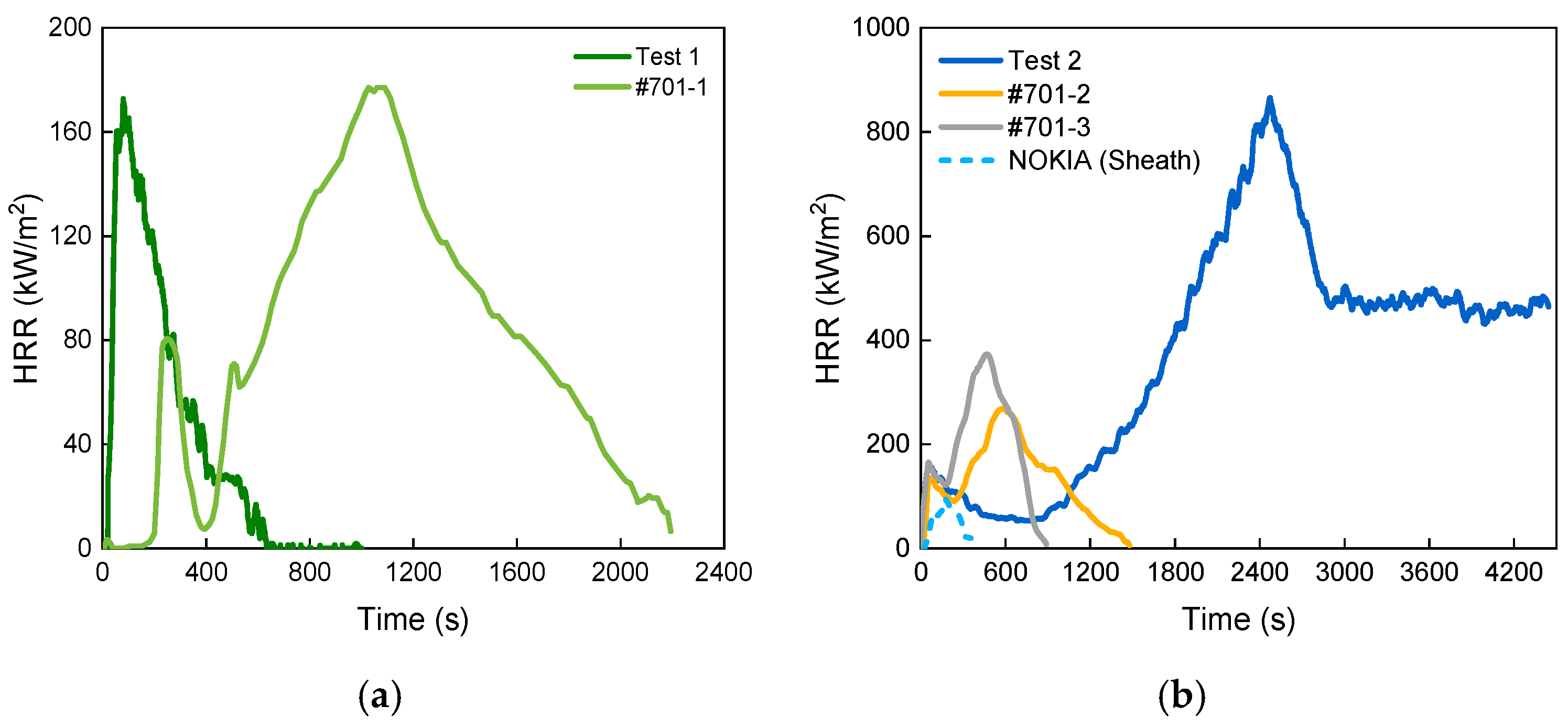
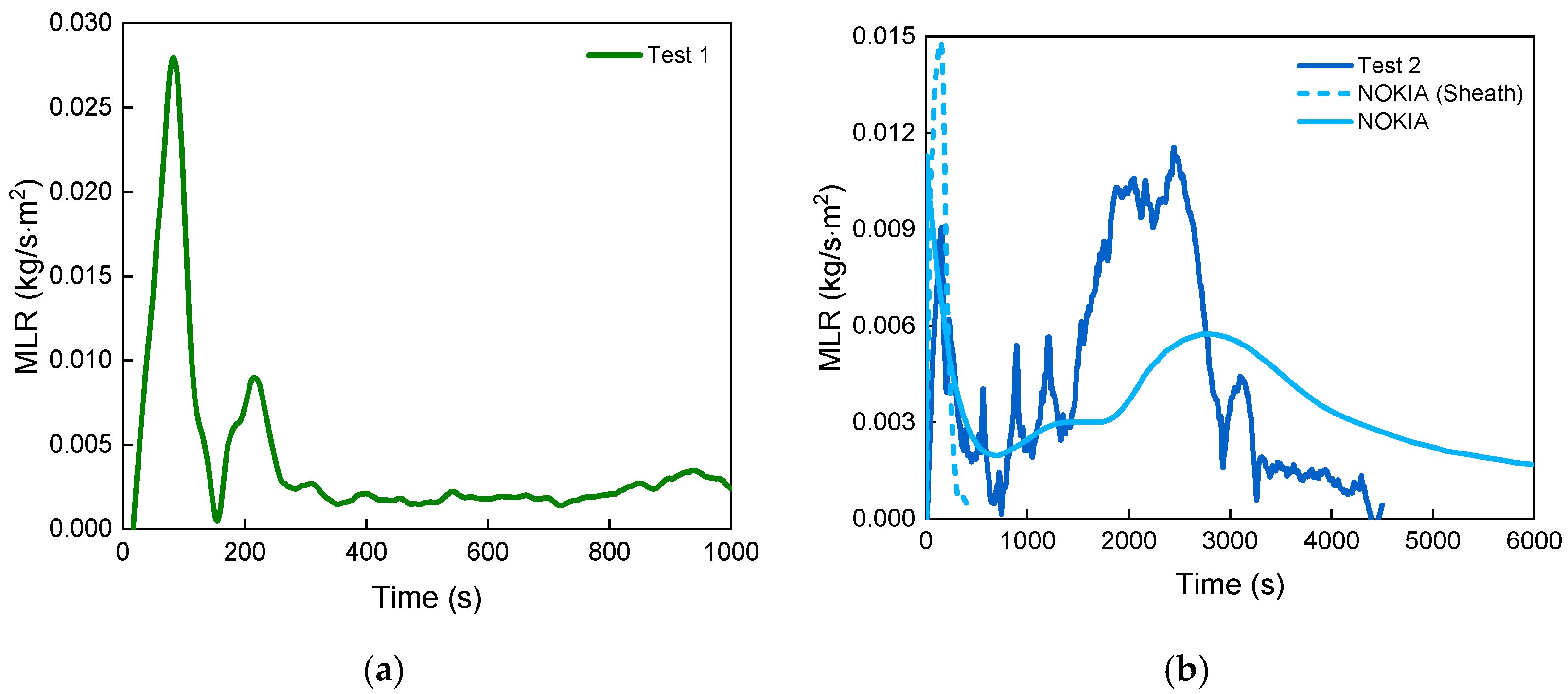
- The critical exposed radiative heat flux for the ZRC-YJV-8.7/10 3 × 95 mm2 power cable to achieve complete combustion lies in the range from 24.9 kW/m2 to 28.3 kW/m2. Compared with incomplete burning, its burning duration was more than four times longer and the peak HRR was five times as high (865.6 kW/m2). The incomplete burning was similar to the initial stage of the complete burning. Compared with other cables, i.e., NOKIA AHXCMK 10 kV 3 × 95/70 mm2 and 7/C #12AWG 600V, the ZRC-YJV-8.7/10 3 × 95 mm2 cable has a generally similar HRR/MLR evolving trend but with significantly greater hazard, even under a lower heat flux.
- (2)
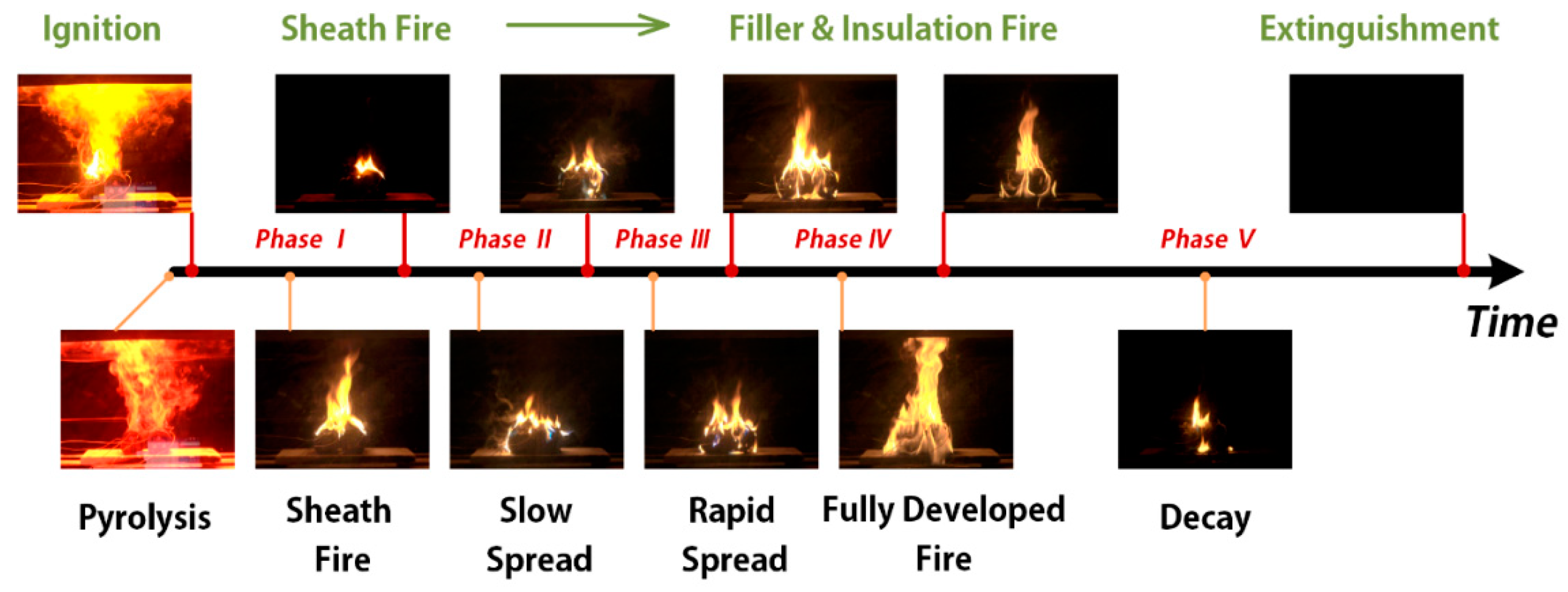
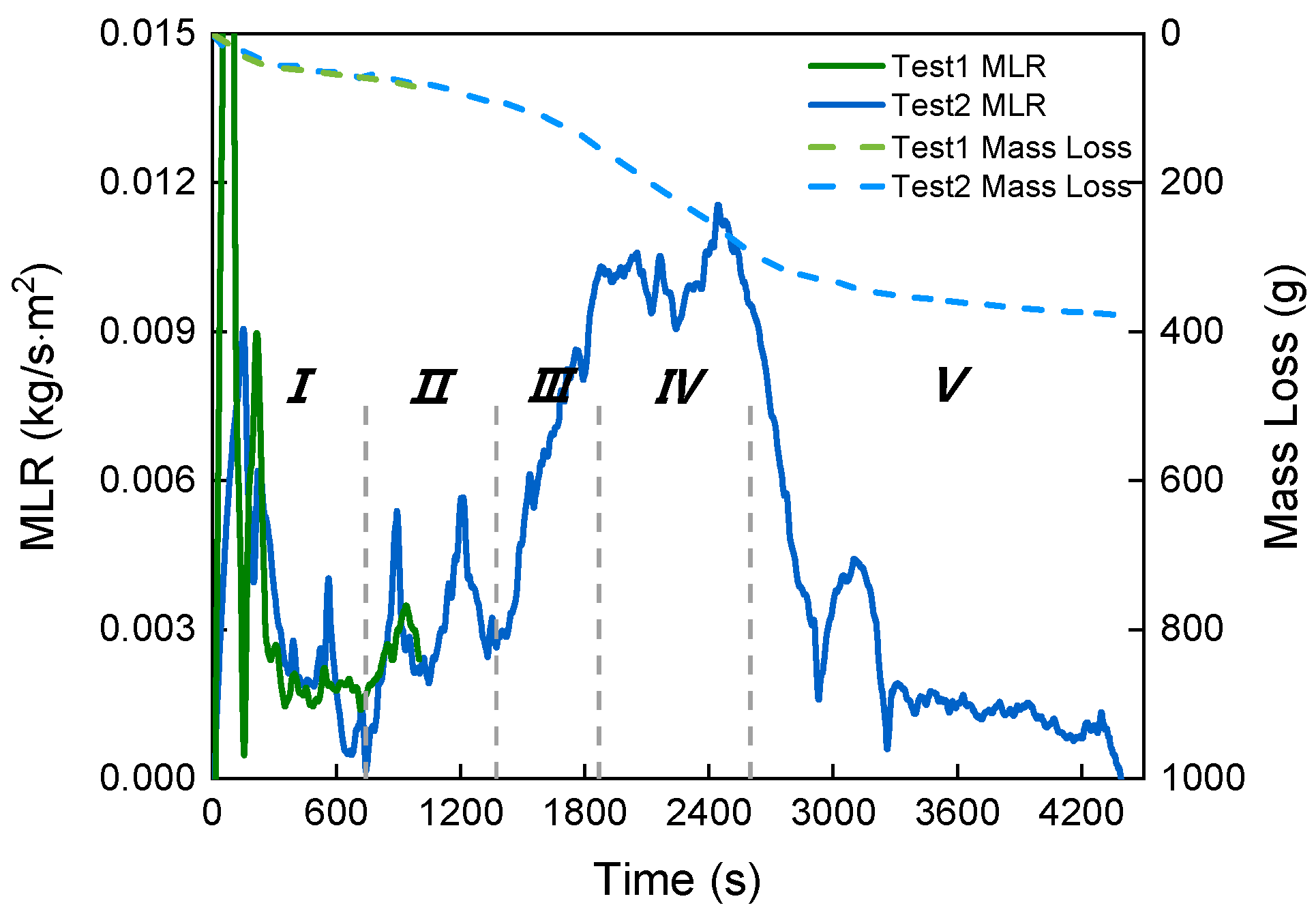
- The whole burning process was gradual from the outside to the inside and can be divided into five phases: the sheath fire, slow spread, rapid spread, full developed fire and decay. The dripping and burning behaviours of the thermoplastic filler promoted the combustion, increased the burning area and led to a fully developed stage. The PVC sheath and XLPE insulation provided significant thermal protection in the second phase. The toxic CO was rapidly produced in the first phase.
- (3)
- When the ceiling clearance H increased, the gas layer became thinner and the maximum gas temperature attenuated more quickly. The closed end interrupted the symmetry in the flow field, wherein the upstream flow became thicker and the related temperature decayed faster.
- (4)
- With the different behaviours of upstream flow and downstream flow considered, an analytical model was developed. The exponent model took fire size and ceiling clearance into account and is able to predict the maximum gas temperature attenuation of both flows reasonably well. The fully-closed case has also been estimated.
- (5)
- The phenomenon of enhanced fuel burning in a utility tunnel should be carefully treated. This enhancement is affected by , and simultaneously. Carvel et al.’s model was modified to integrate the effects of these factors. and are further found to have a comparable effect on the enhancement while the influence of is much smaller. The closed end restricts the ventilation available for combustion but should have no effect as the fuel moves close to the open portal. The current model is thus believed to work within a suitable range of
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cano-Hurtado, J.; Canto-Perello, J. Sustainable development of urban underground space for utilities. Tunn. Undergr. Space Technol. 1999, 14, 335–340. [Google Scholar] [CrossRef]
- Canto-Perello, J.; Curiel-Esparza, J. An analysis of utility tunnel viability in urban areas. Civ. Eng. Environ. Syst. 2006, 23, 11–19. [Google Scholar] [CrossRef]
- Beard, A.; Carvel, R. The Handbook of Tunnel Fire Safety; Thomas Telford Ltd.: London, UK, 2005. [Google Scholar]
- Ingason, H.; Li, Y.Z.; Lönnermark, A. Tunnel Fire Dynamics; Springer: Berlin, Germany, 2014. [Google Scholar]
- Ko, J. Study on the Fire Risk Prediction Assessment due to Deterioration contact of combustible cables in Underground Common Utility Tunnels. J. Korean Soc. Disaster Inf. 2015, 11, 135–147. [Google Scholar] [CrossRef]
- Liang, K.; An, W.; Tang, Y.; Cong, Y. Study on cable fire spread and smoke temperature distribution in T-shaped utility tunnel. Case Stud. Therm. Eng. 2019, 14, 100433. [Google Scholar] [CrossRef]
- Hurley, M.J.; Gottuk, D.T.; Hall, J.R., Jr.; Harada, K.; Kuligowski, E.D.; Puchovsky, M.; Watts, J.M., Jr.; Wieczorek, C.J. SFPE Handbook of Fire Protection Engineering; Springer: Berlin, Germany, 2015. [Google Scholar]
- Grayson, S.J. Fire Performance of Electric Cables-New Test Methods and Measurement Techniques; Final report of EU SMT project SMT4- CT96-2059; Interscience Communications Ltd.: London, UK, 2000. [Google Scholar]
- Commission, University of Nevada. Reno Cable Response to Live Fire (CAROLFIRE); NCR: Rockville, MD, USA, 2008; Volume 1–3. [Google Scholar]
- McGrattan, K.B.; Lock, A.J.; Marsh, N.D.; Nyden, M.R. Cable Heat Release, Ignition, and Spread in Tray Installations During Fire (CHRISTIFIRE): Phase 1-Horizontal Trays; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2012.
- McGrattan, K.B.; Bareham, S.D. Cable Heat Release, Ignition, and SPREAD in Tray Installations during Fire (CHRISTIFIRE) Phase 2: Vertical Shafts and Corridors| NIST; NIST: Gaithersburg, MD, USA, 2013.
- Matala, A.; Hostikka, S. Probabilistic simulation of cable performance and water based protection in cable tunnel fires. Nucl. Eng. Des. 2011, 241, 5263–5274. [Google Scholar] [CrossRef]
- Matala, A.; Hostikka, S. Pyrolysis modelling of PVC cable materials. Fire Saf. Sci. 2011, 10, 917–930. [Google Scholar] [CrossRef]
- Delichatsios, M.A. The flow of fire gases under a beamed ceiling. Combust. Flame 1981, 43, 1–10. [Google Scholar] [CrossRef]
- Hu, L.; Huo, R.; Chow, W.K.; Wang, H.; Yang, R. Decay of buoyant smoke layer temperature along the longitudinal direction in tunnel fires. J. Appl. Fire Sci. 2004, 13, 53–77. [Google Scholar] [CrossRef]
- Hu, L.; Huo, R.; Li, Y.; Wang, H.; Chow, W. Full-scale burning tests on studying smoke temperature and velocity along a corridor. Tunn. Undergr. Space Technol. 2005, 20, 223–229. [Google Scholar] [CrossRef]
- Ingason, H.; Li, Y.Z. Model scale tunnel fire tests with longitudinal ventilation. Fire Saf. J. 2010, 45, 371–384. [Google Scholar] [CrossRef]
- Carvel, R.; Beard, A.; Jowitt, P.; Drysdale, D. The influence of tunnel geometry and ventilation on the heat release rate of a fire. Fire Technol. 2004, 40, 5–26. [Google Scholar] [CrossRef]
- Lönnermark, A.; Ingason, H. The Effect of Cross-sectional Area and Air Velocity on the Conditions in a Tunnel during a Fire; SP Technical Research Institute of Sweden: Borås, Sweden, 2007. [Google Scholar]
- Li, Y.Z.; Fan, C.G.; Ingason, H.; Lönnermark, A.; Ji, J. Effect of cross section and ventilation on heat release rates in tunnel fires. Tunn. Undergr. Space Technol. 2016, 51, 414–423. [Google Scholar] [CrossRef]
- Huggett, C. Estimation of rate of heat release by means of oxygen consumption measurements. Fire Mater. 1980, 4, 61–65. [Google Scholar] [CrossRef]
- International Standard Organization. Reaction-to-Fire Tests-Heat Release, Smoke Production and Mass Loss Rate-Part 1: Heat Release Rate (Cone Calorimeter Method); ISO: Geneva, Switzerland, 2002. [Google Scholar]
- Babrauskas, V. Heat release rates. In SFPE Handbook of Fire Protection Engineering; Springer: Berlin, Germany, 2016; pp. 799–904. [Google Scholar]
- Ji, J.; Zhong, W.; Li, K.; Shen, X.; Zhang, Y.; Huo, R. A simplified calculation method on maximum smoke temperature under the ceiling in subway station fires. Tunn. Undergr. Space Technol. 2011, 26, 490–496. [Google Scholar] [CrossRef]
- Oka, Y.; Oka, H.; Imazeki, O. Ceiling-jet thickness and vertical distribution along flat-ceilinged horizontal tunnel with natural ventilation. Tunn. Undergr. Space Technol. 2016, 53, 68–77. [Google Scholar] [CrossRef]
- Davis, W.D.; Cooper, L.Y. Estimating the Environment and the Response of Sprinkler Links in Compartment Fires with Draft Curtains and Fusible-Link-Actuated Ceiling Vents: User Guide for the Computer Code LAVENT; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 1989.
- Motevalli, V.; Marks, C.H. Characterizing the unconfined ceiling jet under steady-state conditions: A reassessment. Fire Saf. Sci. 1991, 3, 301–312. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, Z.; Wan, H.; Zhu, J. Experimental study on longitudinal and transverse temperature distribution of sidewall confined ceiling jet plume. Appl. Therm. Eng. 2016, 107, 583–590. [Google Scholar] [CrossRef]
- Haerter, A. Fire tests in the Ofenegg-Tunnel in 1965. In Proceedings of the International Conference on Fires in Tunnels, SP REPORT, London, UK, 15 December 1998; pp. 195–214. [Google Scholar]
- Ingason, H. Fire testing in road and railway tunnels. In Flammability Testing of Materials Used in Construction, Transport and Mining; Elsevier: Amsterdam, The Netherlands, 2006; pp. 231–274. [Google Scholar]

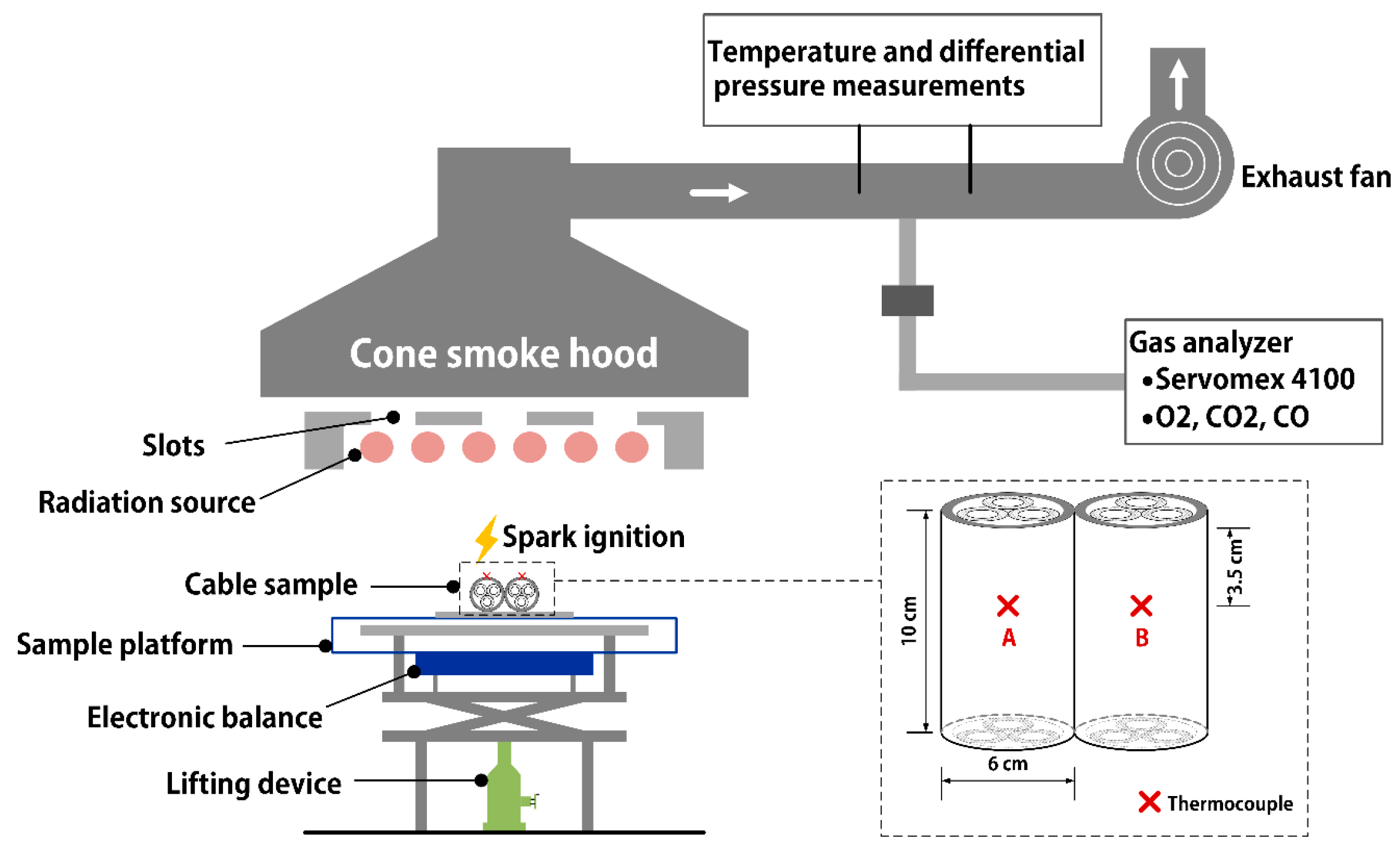


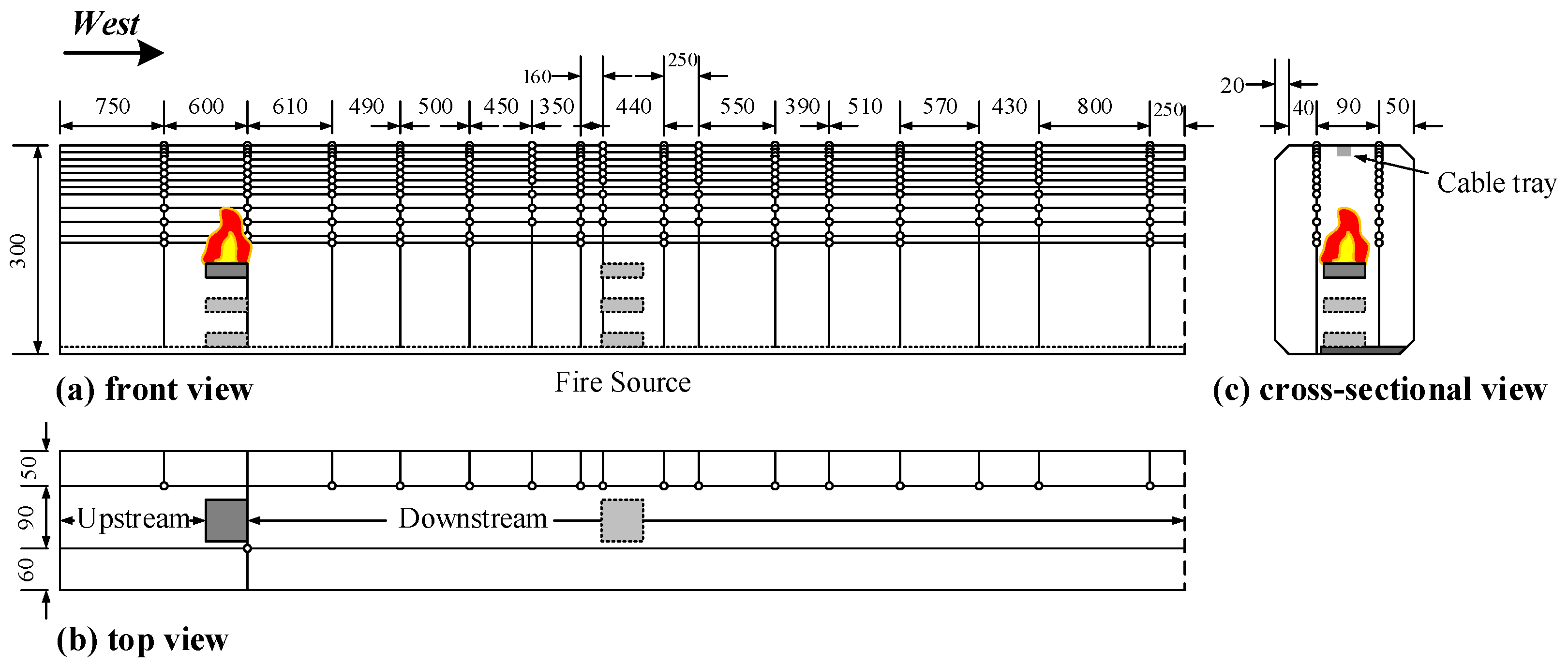

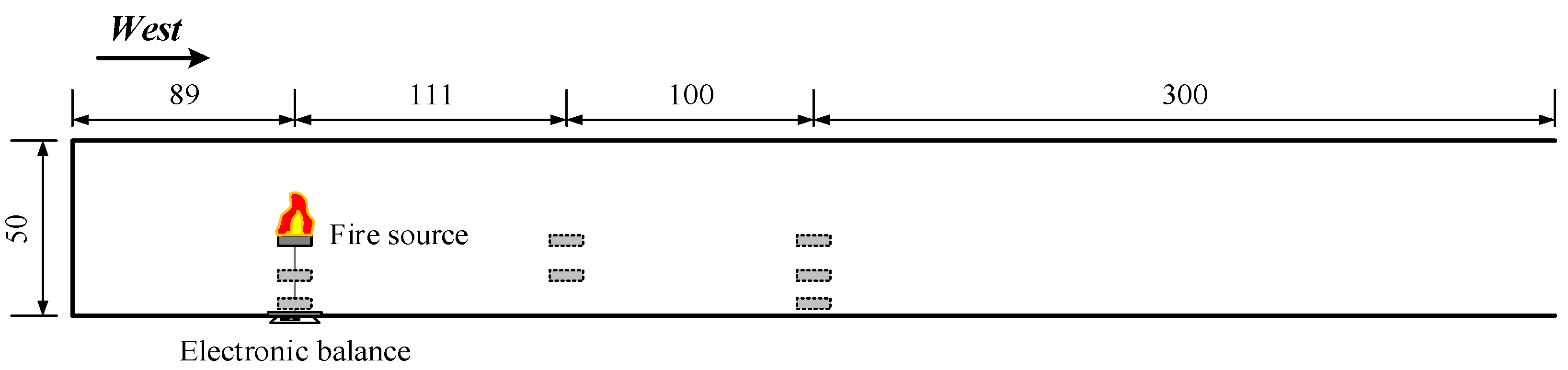



| Test No. | Ambient Temperature T∞ (°C) | Fuel Type | Fuel Pan Size (cm × cm × cm) | Horizontal Distance from East End (m) | Ceiling Clearance, H (m) | East End | West End |
|---|---|---|---|---|---|---|---|
| E01 | 13.5 | Heptane | 40 × 40 × 20 | 12 | 2.9 | Closed | Open |
| E02 | 13.3 | Heptane | 60 × 60 × 20 | 12 | 2.9 | Closed | Open |
| E03 | 11.9 | Heptane | 60 × 60 × 20 | 12 | 2.9 | Closed | Open |
| E04 | 12.6 | Heptane | 60 × 60 × 20 | 12 | 2.4 | Closed | Open |
| E05 | 13.0 | Heptane | 60 × 60 × 20 | 12 | 1.9 | Closed | Open |
| C01 | 13.3 | Heptane | 60 × 60 × 20 | 40.5 | 2.9 | Closed | Open |
| C02 | 14.3 | Heptane | 60 × 60 × 20 | 40.5 | 2.4 | Closed | Open |
| C03 | 15.1 | Heptane | 60 × 60 × 20 | 40.5 | 1.9 | Closed | Open |
| S01 | 13.8 | Diesel | 60 × 60 × 20 | 12 | 2.9 | Closed | Closed |
| MA01 | - | Heptane | 10 × 10 × 3 | 0.89 | 0.48 | Closed | Open |
| MA02 | - | Heptane | 10 × 10 × 3 | 0.89 | 0.4 | Closed | Open |
| MA03 | - | Heptane | 10 × 10 × 3 | 0.89 | 0.32 | Closed | Open |
| MB02 | - | Heptane | 10 × 10 × 3 | 2 | 0.4 | Closed | Open |
| MB03 | - | Heptane | 10 × 10 × 3 | 2 | 0.32 | Closed | Open |
| MC01 | - | Heptane | 10 × 10 × 3 | 3 | 0.48 | Closed | Open |
| MC02 | - | Heptane | 10 × 10 × 3 | 3 | 0.4 | Closed | Open |
| MC03 | - | Heptane | 10 × 10 × 3 | 3 | 0.32 | Closed | Open |
| MO | - | Heptane | 10 × 10 × 3 | - | - | - | - |
| Test No. | Cable Markings | Diameter (mm) | Sheath | Filler | Insulation | Conductor | Radiative Heat Flux (kW/m2) | Peak Heat Release Rate HRR (kW/m2) |
|---|---|---|---|---|---|---|---|---|
| Test 1 | ZRC-YJV-8.7/10 3 × 95 mm2 | 60 | PVC | PE | XLPE | Copper | 24.9 | 172.6 |
| Test 2 | ZRC-YJV-8.7/10 3 × 95 mm2 | 60 | PVC | PE | XLPE | Copper | 28.3 | 865.6 |
| NOKIA | NOKIA AHXCMK 10 kV 3 × 95/70 mm2 | 54 | PVC | PE | XLPE | Cooper & Aluminium | 50 | 94.5 1 |
| #701-1 | 7/C #12AWG 600V | 14 | PVC | - | PE | Copper | 25 | 177.1 |
| #701-2 | 7/C #12AWG 600V | 14 | PVC | - | PE | Copper | 50 | 269.3 |
| #701-3 | 7/C #12AWG 600V | 14 | PVC | - | PE | Copper | 75 | 373.4 |
| Phase No. | Phase | Duration | Description |
|---|---|---|---|
| - | Pyrolysis and ignition | 12 s (pyrolysis) | The exposed surface of sheath smoked rapidly. After 6 s, the surface was ignited but no sustained ignition was observed. Then, 6 s after, the spark re-ignited the left sample and a part of the flame then jumped onto the right. Two flames merged quickly. |
| I | Sheath fire | 0–744 s | Popping of pieces off the surface occurred on and off. Rapid flashing occurred right under the upper sheath. The samples deformed greatly while burning, with the char surface forming blisters. The burning itself started to decay soon. |
| II | Slow spread | 745–1374 s | The flame on the upper sheath was weak. Flashing under the upper sheath became unobtrusive. The sheath and insulation provided significant thermal protection. In the end, the flame started penetrating the underlying material and blue flames were noted. |
| III | Rapid spread | 1375–1870 s | Filler was on fire, with a large amount of dripping and burning out the bottom. The flame spread fairly deep and the whole surface was touched. Blue flames were inside. |
| V | Fully developed fire | 1871–2600 s | Blue flames became unnoticeable. The whole cable was burning steadily and vigorously. Occasional melted liquid was noticed and the burning area at the bottom became larger. |
| VI | Decay | 2601–4390 s | The fire decayed gradually. Then, flames appeared only on the upper surface and bottom for a while and extinguished finally. |
| Test No. | ||||
|---|---|---|---|---|
| E01–05 | 0.0236 | 0.985 | - | - |
| C01–03 | 0.0230 | 0.998 | 0.0458 | 0.964 |
| S01 | 0.0265 | 0.935 | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, K.; Zhou, X.; Yang, L.; Tang, X.; Zheng, Y.; Cao, B.; Peng, Y.; Liu, H.; Ni, Y. A Multi-Scale Analysis of the Fire Problems in an Urban Utility Tunnel. Energies 2019, 12, 1976. https://doi.org/10.3390/en12101976
Ye K, Zhou X, Yang L, Tang X, Zheng Y, Cao B, Peng Y, Liu H, Ni Y. A Multi-Scale Analysis of the Fire Problems in an Urban Utility Tunnel. Energies. 2019; 12(10):1976. https://doi.org/10.3390/en12101976
Chicago/Turabian StyleYe, Kai, Xiaodong Zhou, Lizhong Yang, Xiao Tang, Yuan Zheng, Bei Cao, Yang Peng, Hong Liu, and Yong Ni. 2019. "A Multi-Scale Analysis of the Fire Problems in an Urban Utility Tunnel" Energies 12, no. 10: 1976. https://doi.org/10.3390/en12101976
APA StyleYe, K., Zhou, X., Yang, L., Tang, X., Zheng, Y., Cao, B., Peng, Y., Liu, H., & Ni, Y. (2019). A Multi-Scale Analysis of the Fire Problems in an Urban Utility Tunnel. Energies, 12(10), 1976. https://doi.org/10.3390/en12101976






