Multi-Input ?uk-Derived Buck-Boost Voltage Source Inverter for Photovoltaic Systems in Microgrid Applications
Abstract
:1. Introduction
2. The Operation Principle of the Proposed Topology
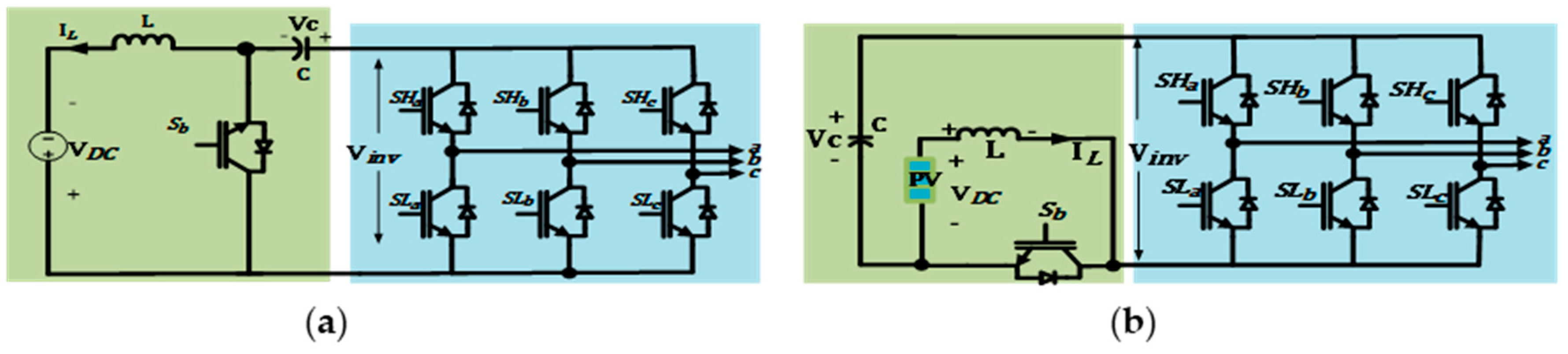
2.1. The Operation of the Single-Input CBBVSI Topology
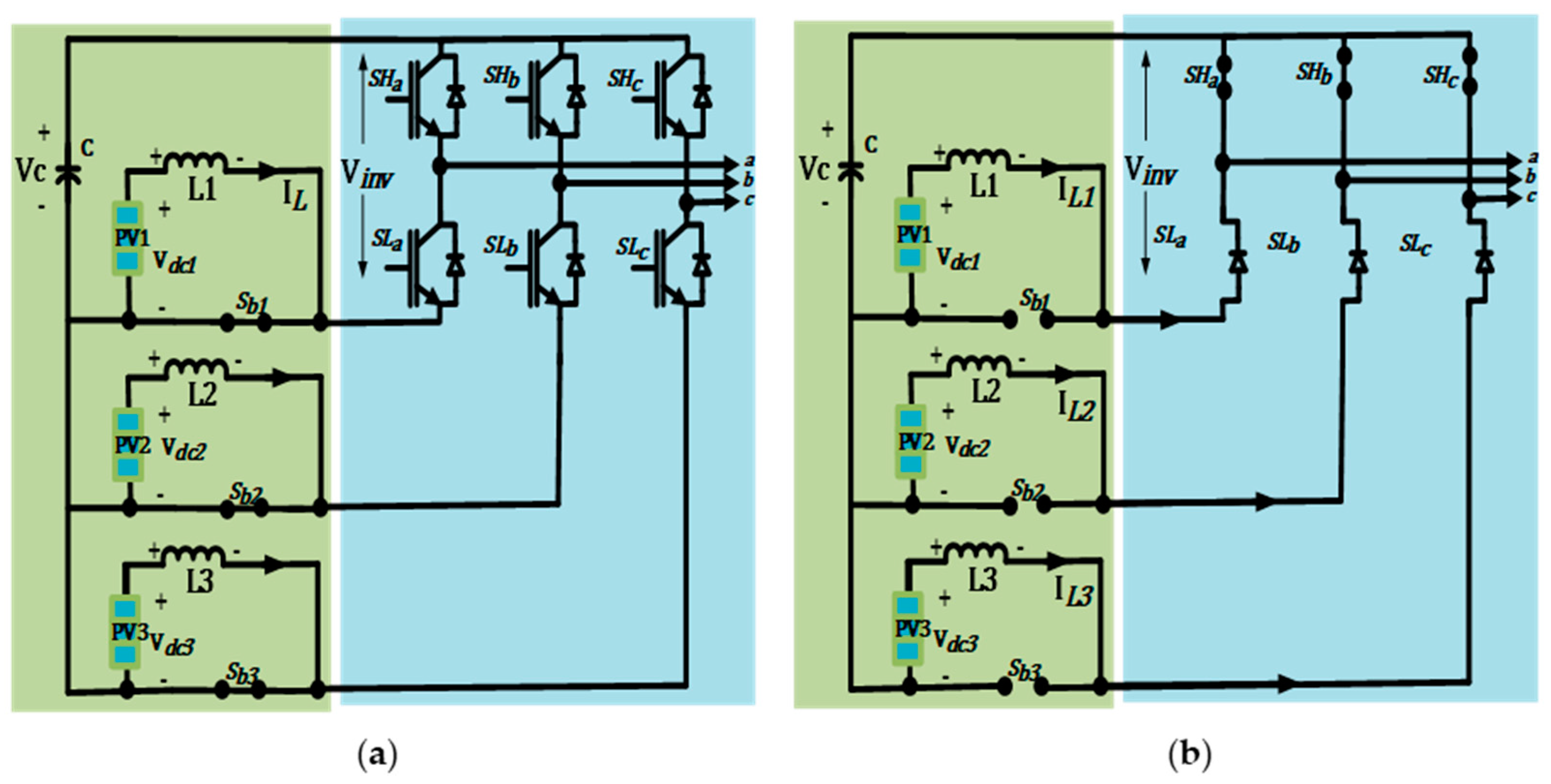
2.2. The Operation of the Multi-Input CBBVSI Topology
3. Analysis of the Modulation of the Proposed Topology
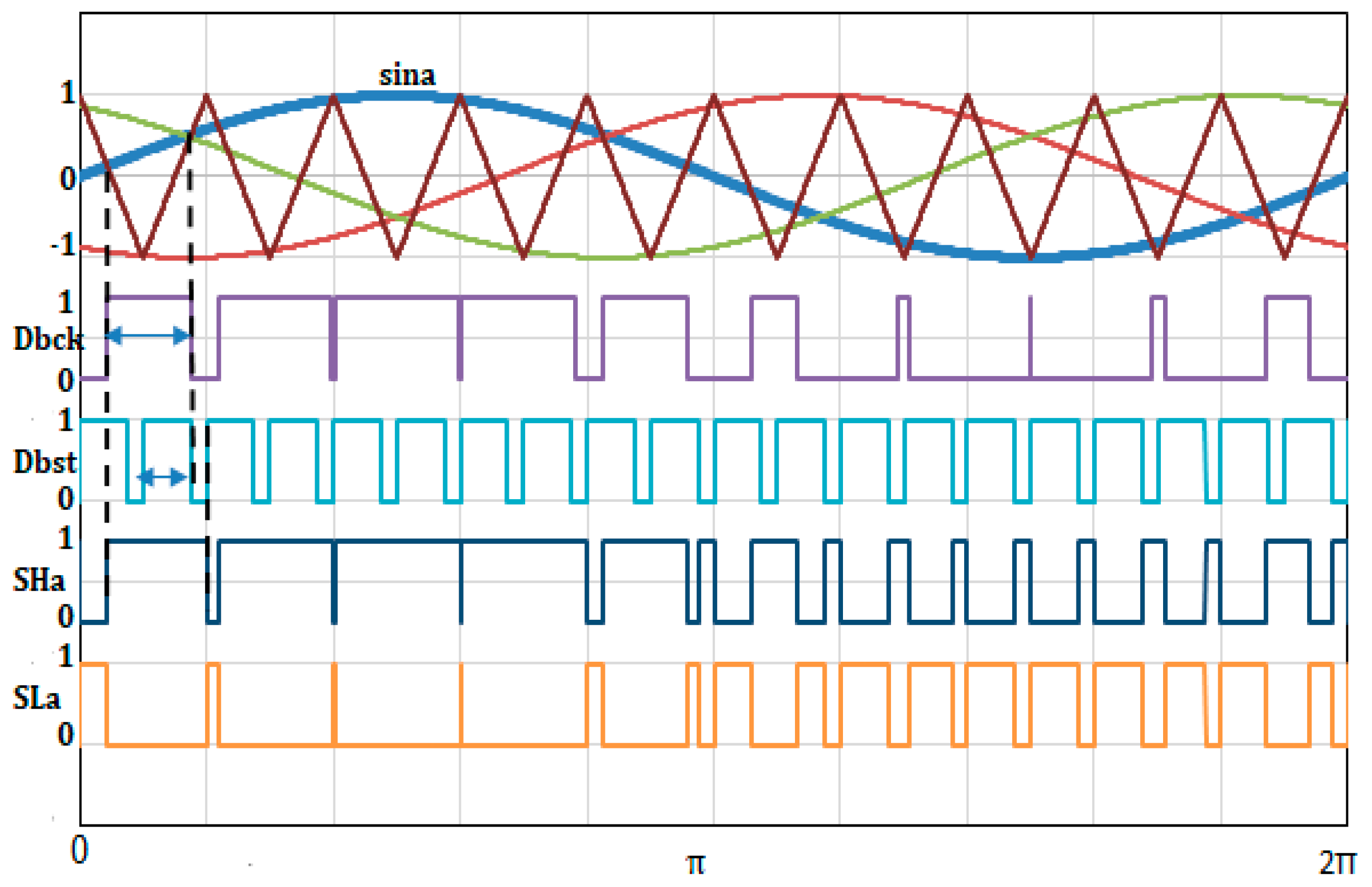
3.1. Sinusoidal Pluse Width Modualtion
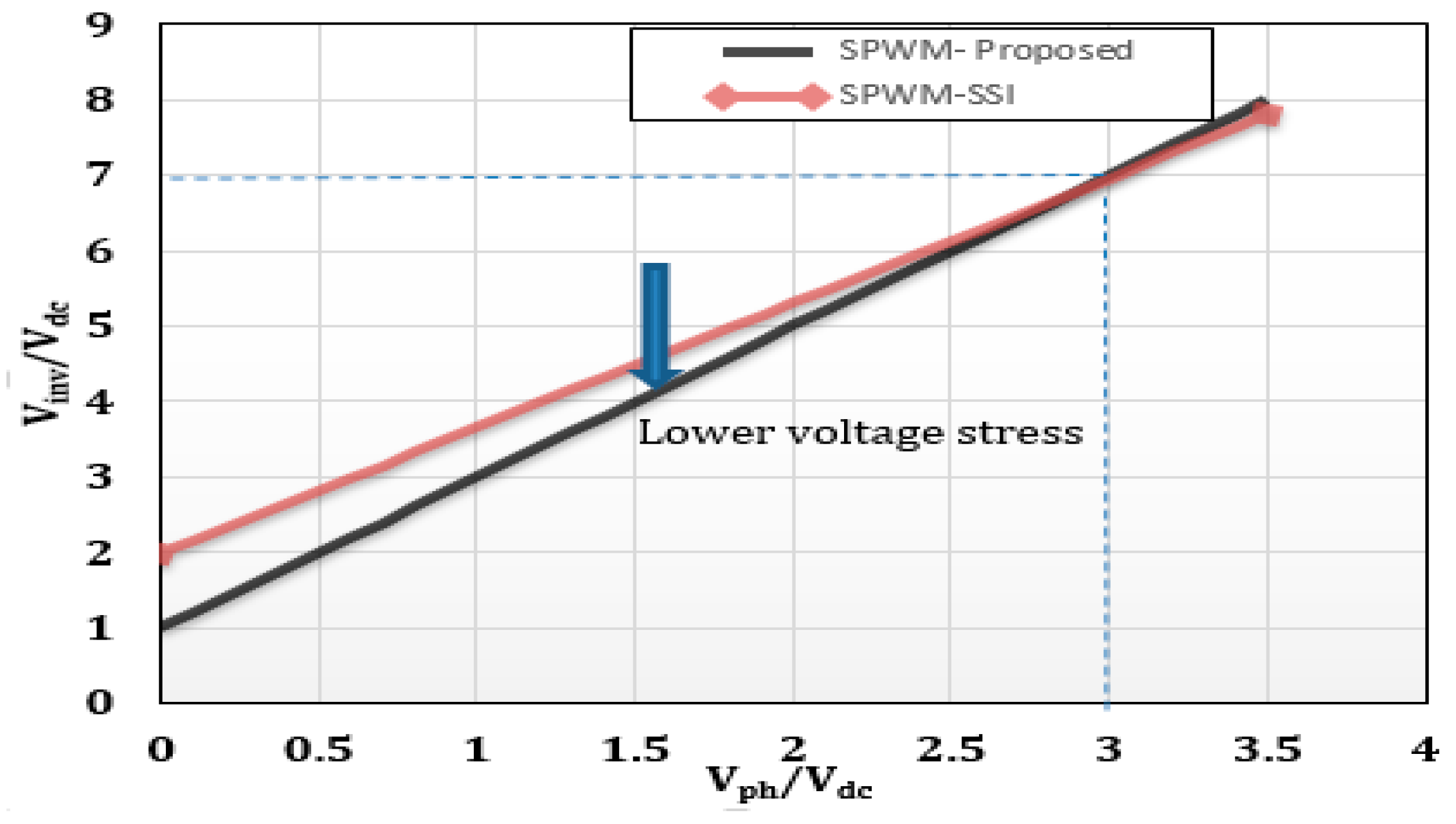
3.2. The Conversion Ratio
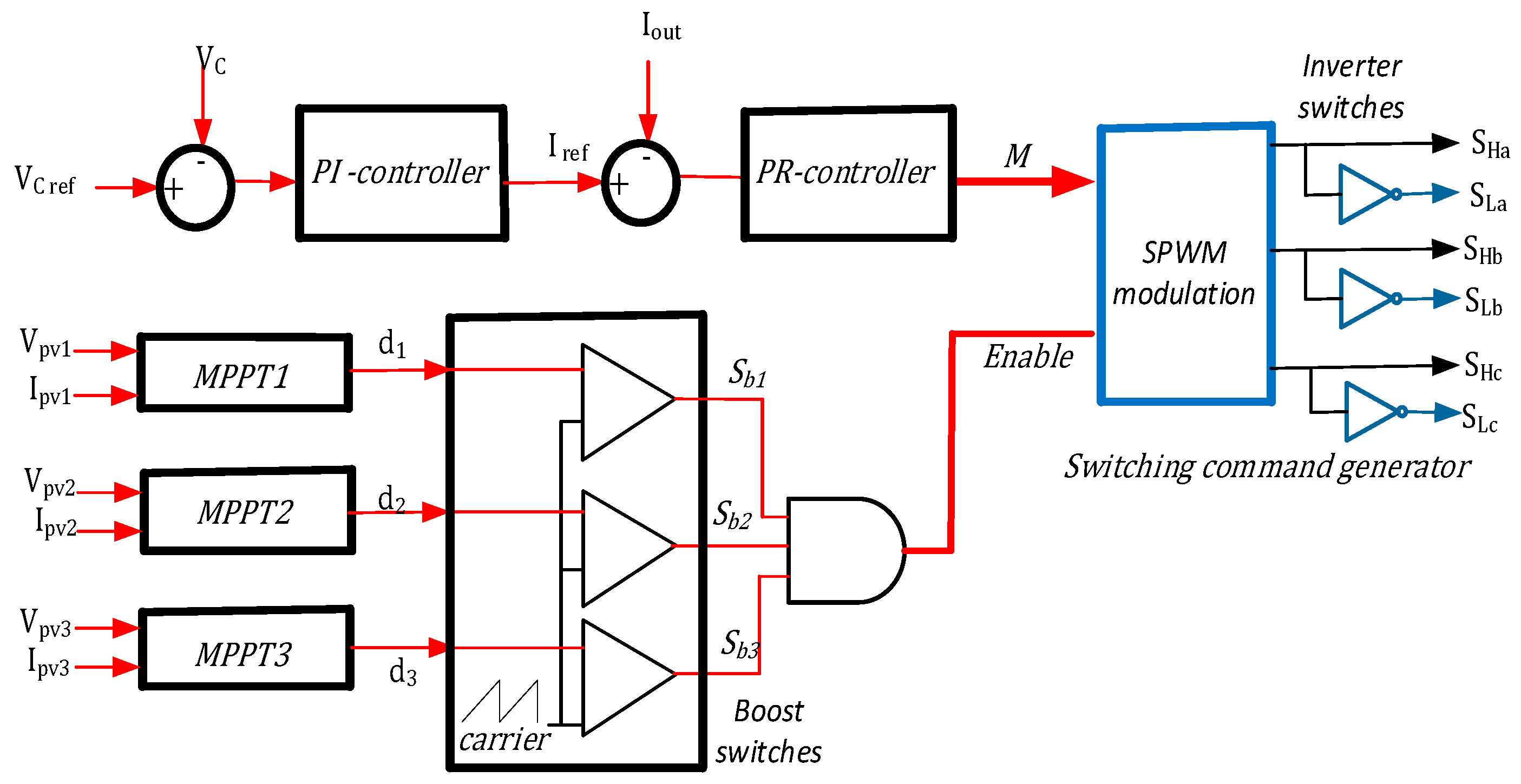
4. Control of the Proposed Multi-Input Three Phase Inverter
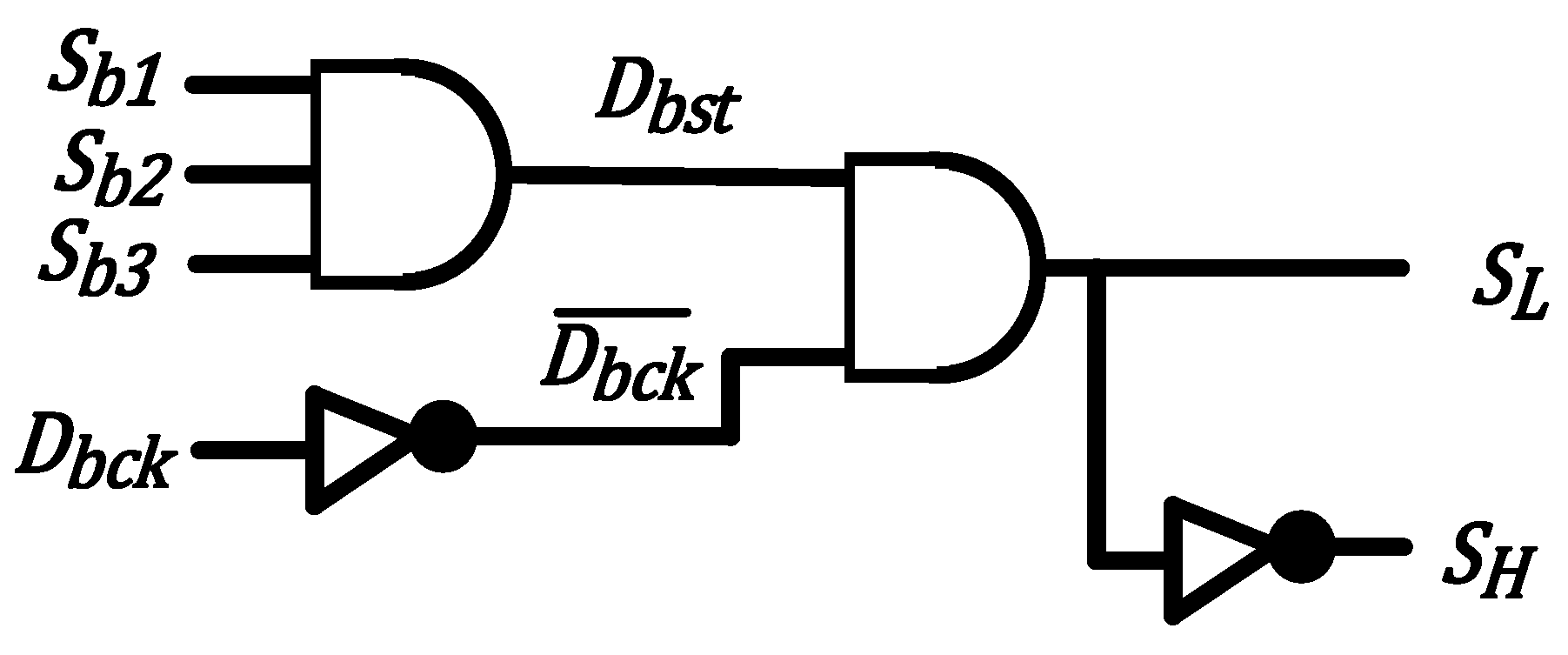
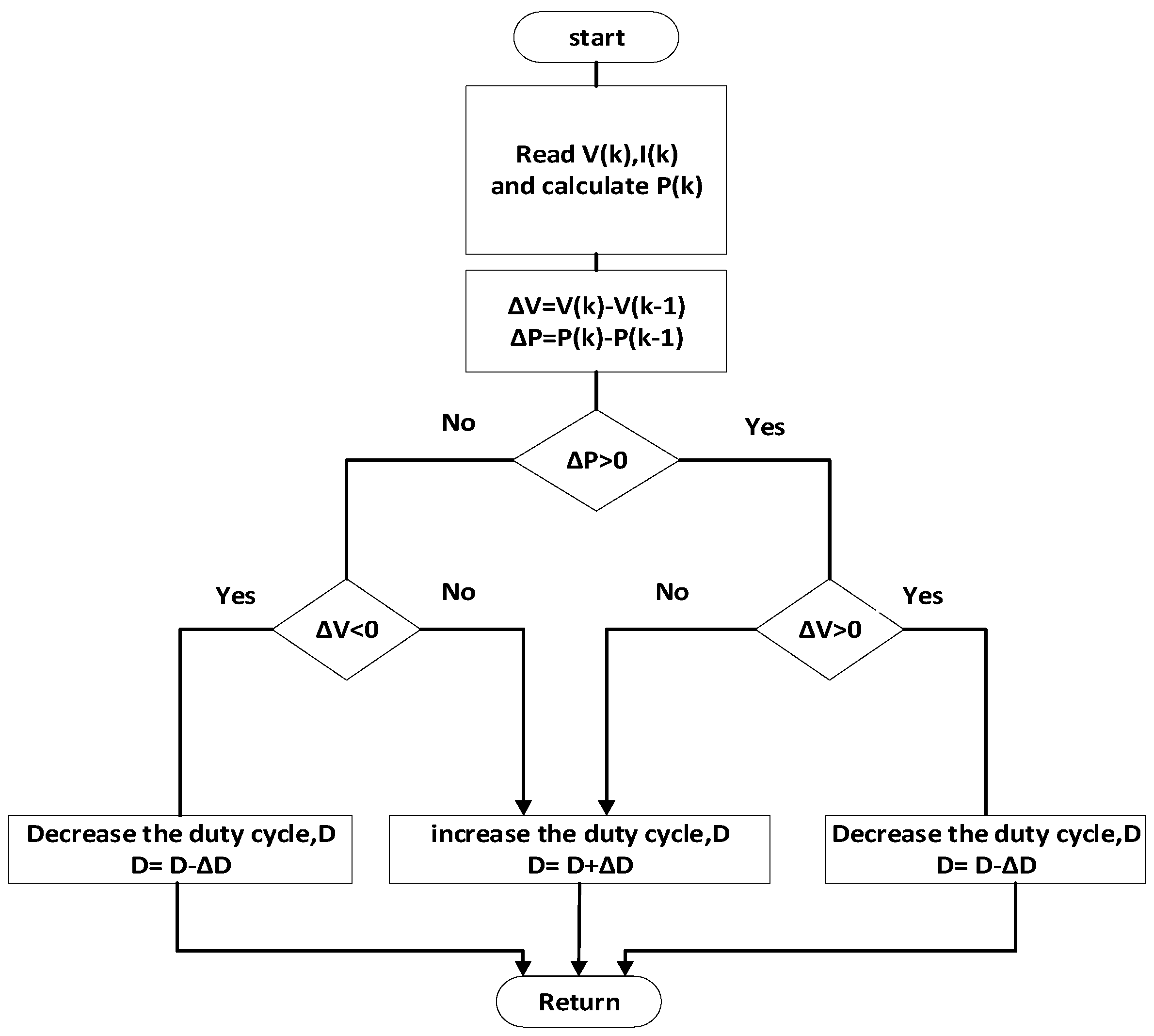
- MPPT algorithm to harvest the maximum power from the PV sources. Any MPPT algorithm can be used for the proposed inverter. The waveforms of the PV voltage strongly depend on the type of MPPT controller used and the values of its parameters. If we restrict ourselves to a Perturb and Observe (P and O) MPPT controller, which is the one used in this paper, many variants of this algorithm exist. Namely, the output of the MPPT block could be a current reference that should be tracked by the PV current, a voltage reference that should be tracked by the PV voltage, or it could be the duty cycle that must be directly applied to the converter. In the first two cases, PI compensators are used to process the error between the controlled variables and their references. In the third case, the duty cycle is applied without any compensation scheme. Since the focus of the paper is not on this particular aspect, the simplest P and O MPPT controller providing the duty cycle directly is used in this paper. Its flowchart is shown in Figure 8. Each PV input has its own MPPT controller. For the proposed multi-input inverter, the output of this block determines the state of the corresponding boost switches (Sb1, Sb2, Sb3). Therefore, any change in the duty cycle of one of these boost switches, and the other two switches are not affected. Thus, the states are logically processed through a logic date of AND type to identify the maximum inverter modulation index, i.e., the inverter can be operated only if all the boost switches are ON.
- The second control block is used to regulate the DC link voltage. The DC reference (Vcref) should be determined based on the required boost voltage. A Proportional Integral (PI) controller is applied to this block. The Laplace domain transfer function of this controller can be expressed as follows:The output of this block determines the reference current for the third control loop.
- The third block controls the converter output current. The Proportional plus Resonant (PR) controller is adopted here. Its Laplace domain transfer function is given by the following expression:where ω is the fundamental frequency.
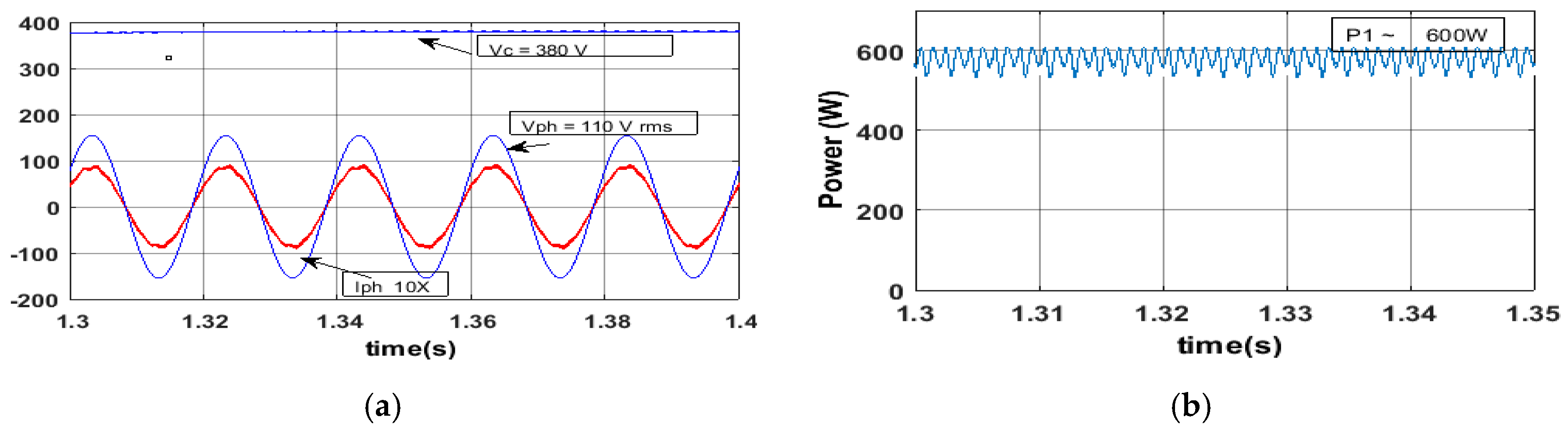
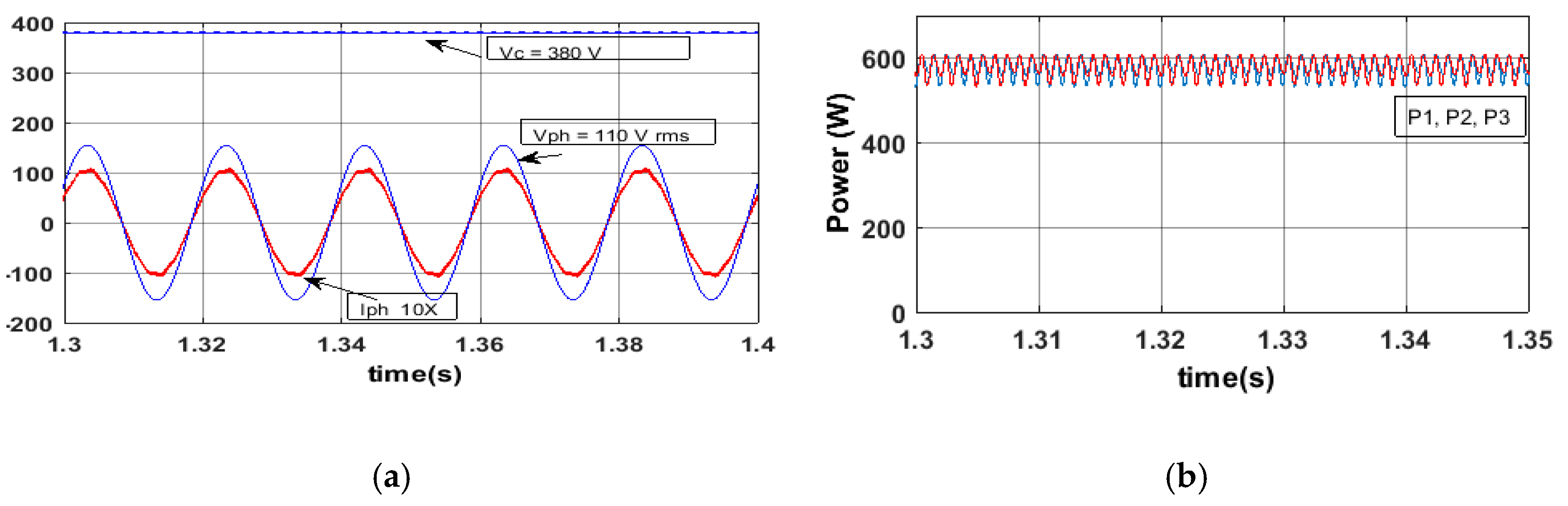
5. Simulation Results
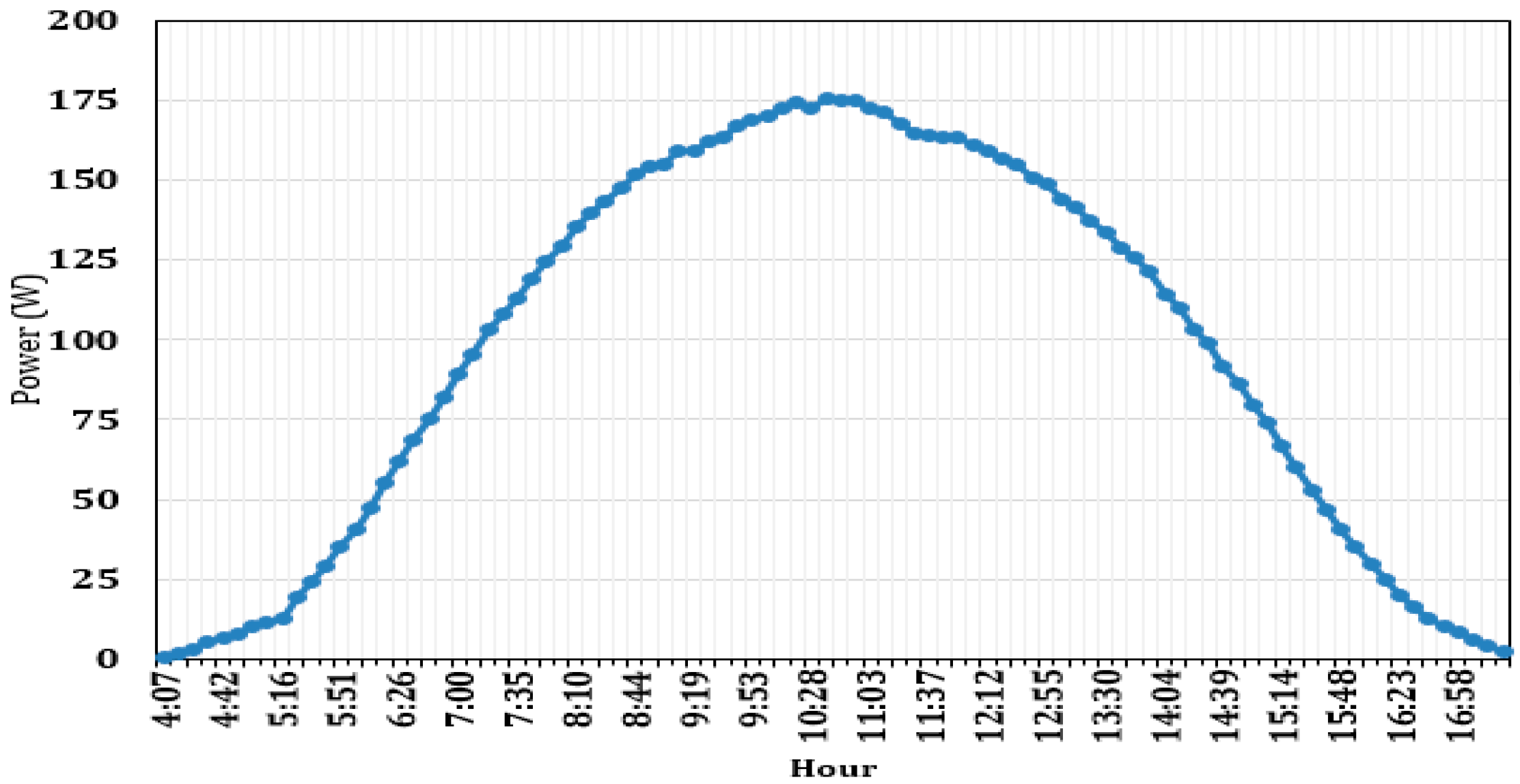
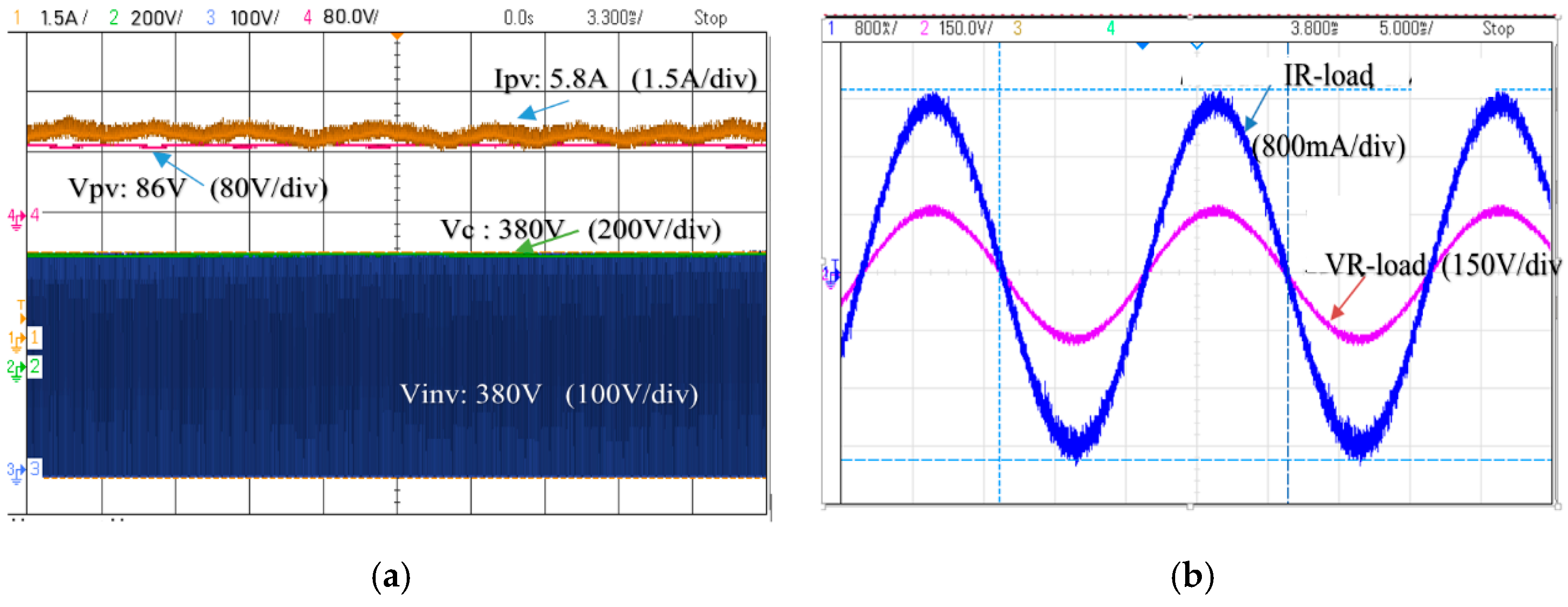
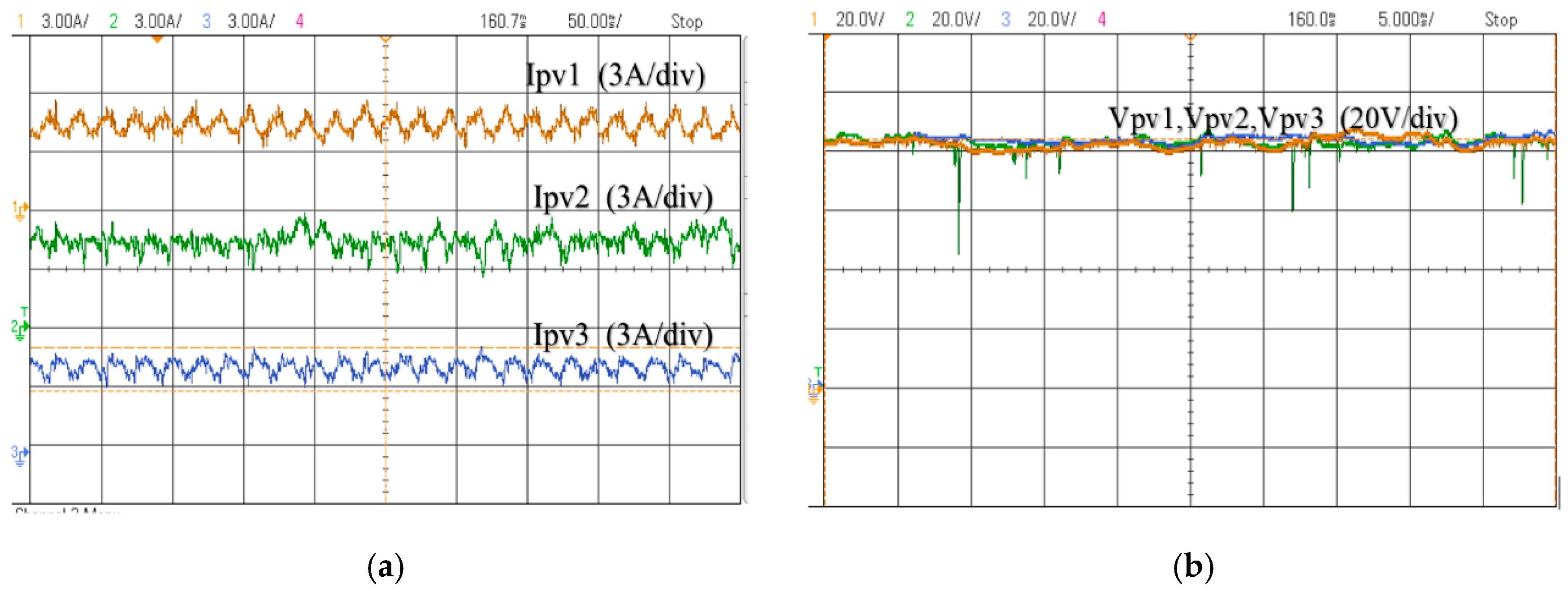
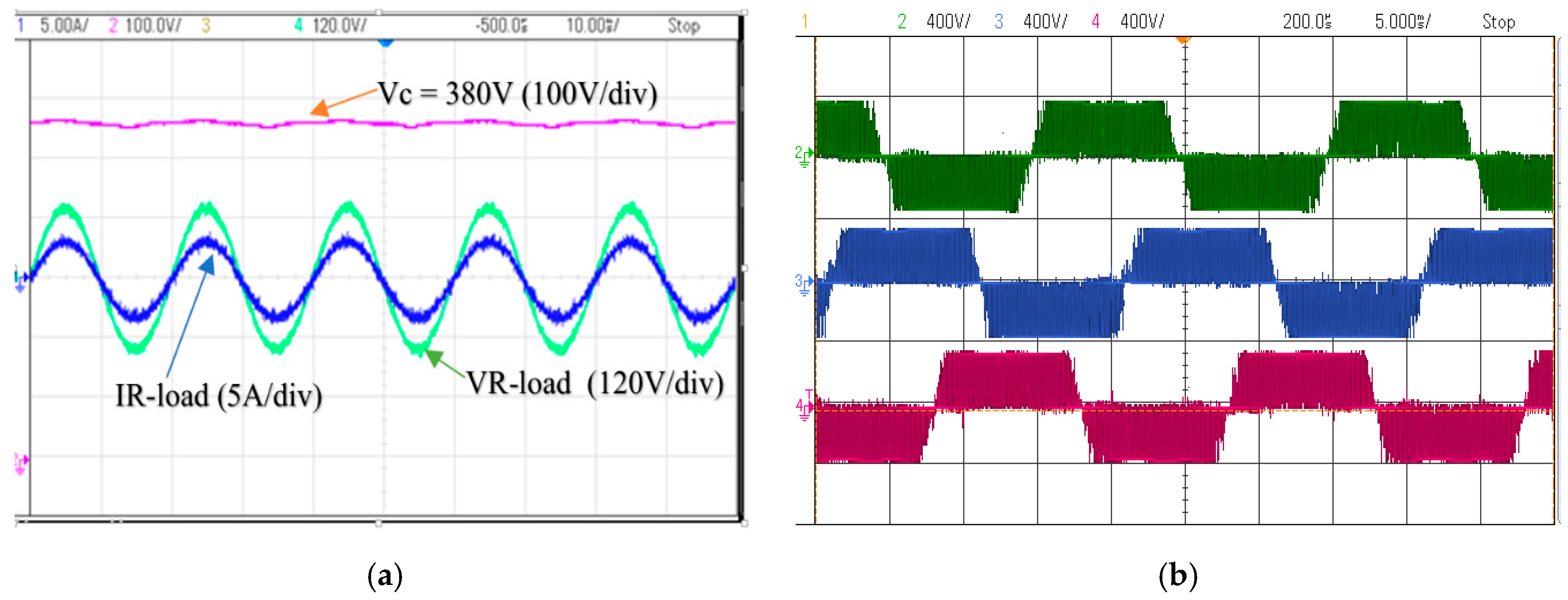
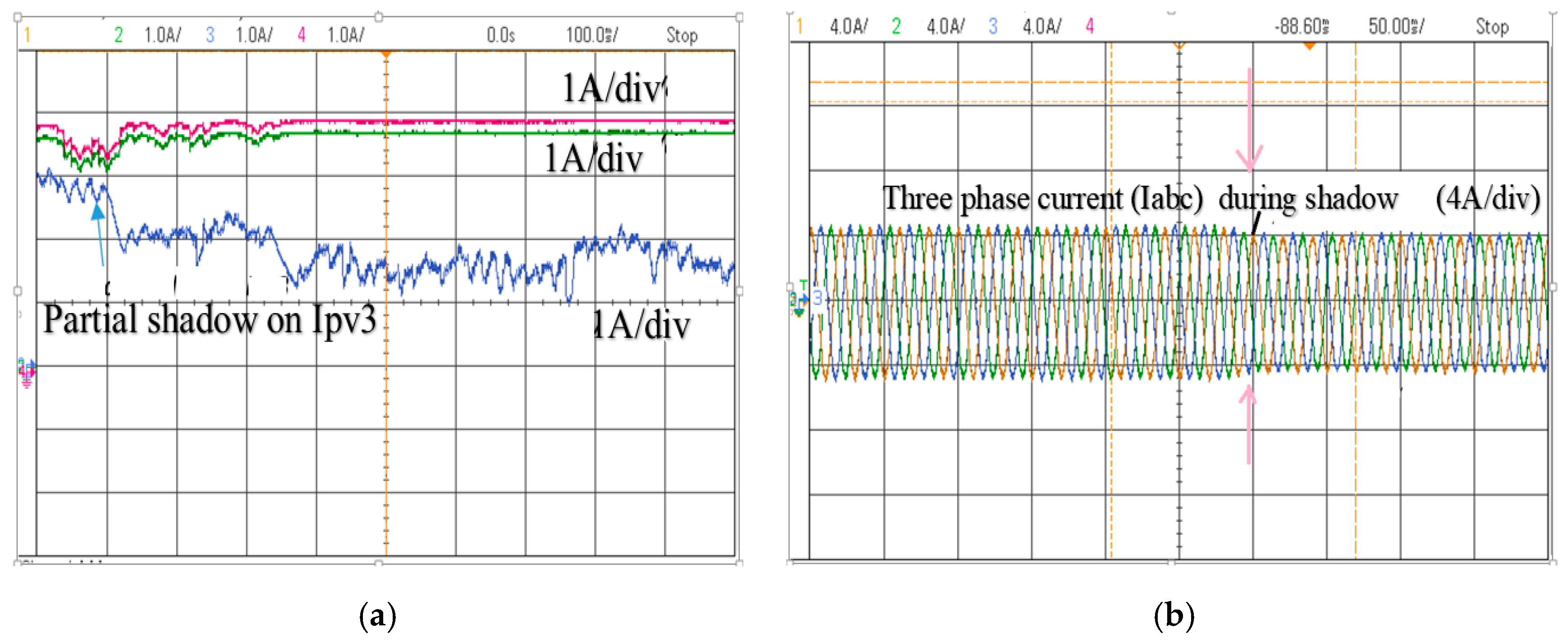
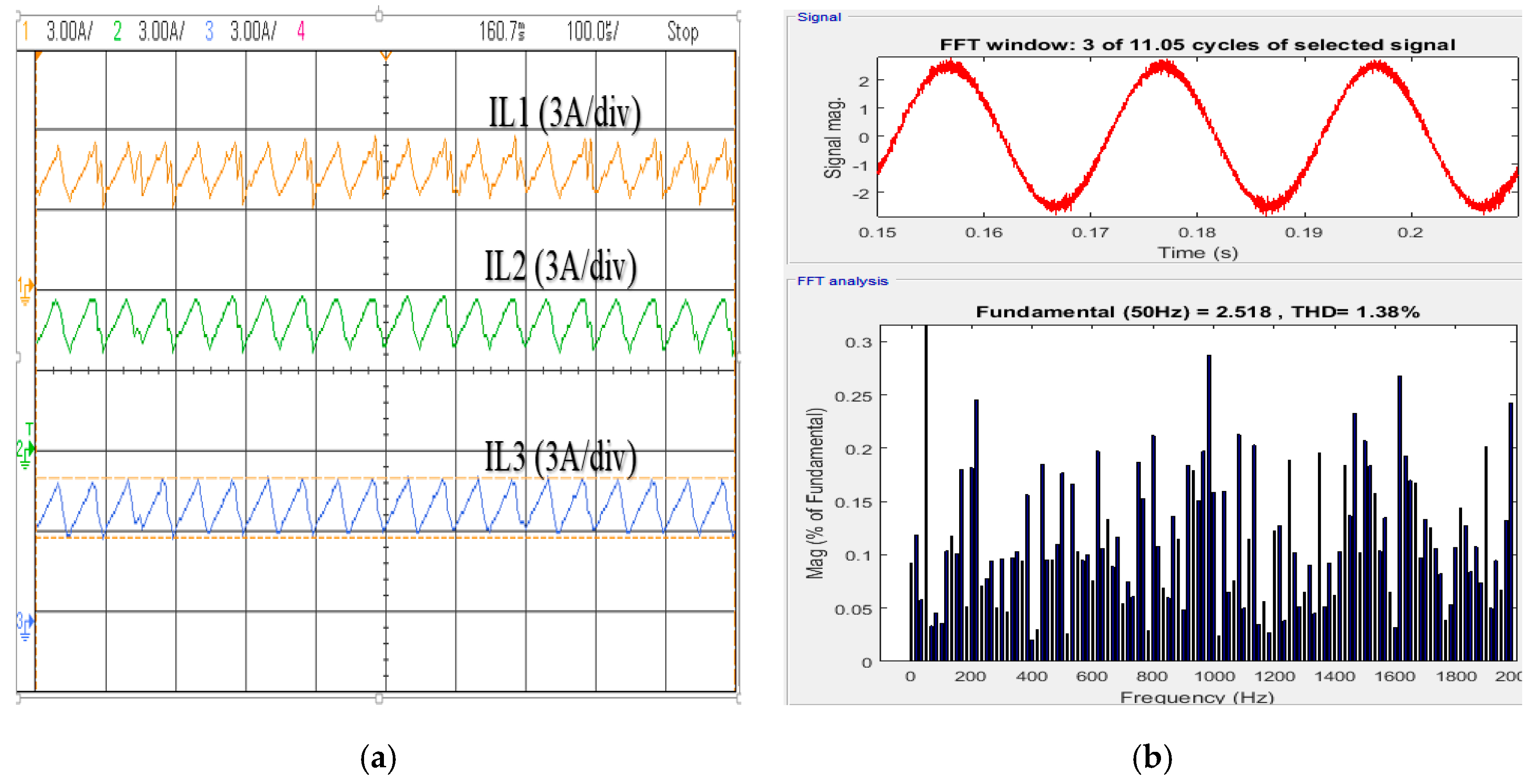
6. Experimental Result
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CBBVSI | Ćuk-derived Buck-Boost voltage source inverter |
| MPPT | Maximum Power Point Tracking |
| PV | Photovoltaic |
| ZSI | Z-Source Inverter |
| qZSI | Quasi-Z-Source Inverter |
| SBBVSI | SEPIC-derived Buck-Boost voltage source inverter |
| SPWM | Sinusoidal Pulse Width Modulation |
| SSI | Split Source Inverter |
References
- Schimpf, F.; Norum, L.E. Grid connected Converters for Photovoltaic, State of the Art, Ideas for Improvement of Transformerless Inverters. In Proceedings of the Nordic Workshop on Power and Industrial Electronics (NORPIE/2008), Espoo, Finland, 9–11 June 2008; Volume 6. [Google Scholar]
- Kjaer, S.B.; Pedersen, J.K.; Blaabjerg, F. A review of single-phase grid-connected inverters for photovoltaic modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
- Bayhan, S.; Trabelsi, M.; Abu-Rub, H.; Malinowski, M. Finite-Control-Set Model-Predictive Control for a Quasi-Z-Source Four-Leg Inverter Under Unbalanced Load Condition. IEEE Trans. Ind. Electron. 2017, 64, 2560–2569. [Google Scholar] [CrossRef]
- Shen, M.; Joseph, A.; Wang, J.; Peng, F.Z.; Adams, D.J. Comparison of traditional inverters and Z-source inverter for fuel cell vehicles. IEEE Trans. Power Electron. 2007, 22, 1453–1463. [Google Scholar] [CrossRef]
- Mohr, M.; Franke, W.T.; Wittig, B.; Fuchs, F.W. Converter systems for fuel cells in the medium power range-a comparative study. IEEE Trans. Ind. Electron. 2010, 57, 2024–2032. [Google Scholar] [CrossRef]
- Chen, Y.; Smedley, K.M. A cost-effective single-stage inverter with maximum power point tracking. IEEE Trans. Power Electron. 2004, 19, 1289–1294. [Google Scholar] [CrossRef]
- González, R.; López, J.; Sanchis, P.; Marroyo, L. Transformerless inverter for single-phase photovoltaic systems. IEEE Trans. Power Electron. 2007, 22, 693–697. [Google Scholar] [CrossRef]
- Fortunato, M.; Giustiniani, A.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Maximum power point tracking in a one-cycle-controlled single-stage photovoltaic inverter. IEEE Trans. Ind. Electron. 2008, 55, 2684–2693. [Google Scholar] [CrossRef]
- El Aamri, F.; Maker, H.; Sera, D.; Spataru, S.; Guerrero, J.M.; Mouhsen, A. A Direct Maximum Power Point Tracking Method for Single-Phase Grid Connected PV Inverters. IEEE Trans. Power Electron. 2018, 33, 8961–8971. [Google Scholar] [CrossRef]
- Anurag, A.; Deshmukh, N.; Maguluri, A.; Anand, S. Integrated DC-DC Converter Based Grid-Connected Transformerless Photovoltaic Inverter with Extended Input Voltage Range. IEEE Trans. Power Electron. 2018, 33, 8322–8330. [Google Scholar] [CrossRef]
- Peng, F.Z. Z-source inverter. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Peng, F.Z.; Shen, M.; Qian, Z. Maximum boost control of the Z-source inverter. IEEE Trans. Power Electron. 2005, 20, 833–838. [Google Scholar]
- Tang, Y.; Xie, S.; Zhang, C.; Xu, Z. Improved Z-source inverter with reduced Z-source capacitor voltage stress and soft-start capability. IEEE Trans. Power Electron. 2009, 24, 409–415. [Google Scholar]
- Zhu, M.; Yu, K.; Luo, F.L. Switched inductor Z-source inverter. IEEE Trans. Power Electron. 2010, 25, 2150–2158. [Google Scholar]
- Aghdam, S.R.; Babaei, E.; Zadeh, S.G. Improvement the performance of switched-inductor Z-source inverter. In Proceedings of the Industrial Electronics Conference (IECON), Venna, Austria, 10–13 November 2013; pp. 876–881. [Google Scholar]
- Nguyen, M.K.; Lim, Y.C.; Cho, G.B. Switched-inductor quasi-Z-source inverter. IEEE Trans. Power Electron. 2011, 26, 3183–3191. [Google Scholar]
- Ho, A.V.; Chun, T.W.; Kim, H.G. Extended boost active-switched-capacitor/switched-inductor quasi-Z-source inverters. IEEE Trans. Power Electron. 2015, 30, 5681–5690. [Google Scholar]
- Siwakoti, Y.P.; Town, G.E.; Loh, P.C.; Blaabjerg, F. Y-source inverter. In Proceedings of the 2014 IEEE 5th International Symposium on Power Electronics for Distributed Generation Systems, Galway, Ireland, 24–27 June 2014; pp. 1–6. [Google Scholar]
- Siwakoti, Y.P.; Blaabjerg, F.; Loh, P.C. Quasi-Y-source inverter. In Proceedings of the 2015 Australasian Universities Power Engineering Conference, Wollongong, Australia, 27–30 September 2105; pp. 1–5. [Google Scholar]
- Siwakoti, Y.P.; Blaabjerg, F.; Loh, P.C. Quasi-Y-Source Boost DC-DC Converter. IEEE Trans. Power Electron. 2015, 30, 6514–6519. [Google Scholar]
- Ribeiro, H.; Pinto, A.; Borges, B. Single-stage DC-AC converter for photovoltaic systems. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 12–16 September 2010; pp. 604–610. [Google Scholar]
- Abdelhakim, A.; Mattavelli, P.; Spiazzi, G. Three-Phase Split-Source Inverter (SSI): Analysis and Modulation. IEEE Trans. Power Electron. 2016, 31, 7451–7461. [Google Scholar]
- Lee, S.S.; Heng, Y.E. Improved Single-Phase Split-Source Inverter with Hybrid Quasi-Sinusoidal and Constant PWM. IEEE Trans. Ind. Electron. 2017, 64, 2024–2031. [Google Scholar]
- Lee, S.S.; Theam Tan, A.S.; Ishak, D.; Mohd-Mokhtar, R. Single-Phase Simplified Split-Source Inverter (S3I) for Boost DC-AC Power Conversion. IEEE Trans. Ind. Electron. 2018, 1. [Google Scholar] [CrossRef]
- Gao, F.; Loh, P.C.; Blaabjerg, R.F.; Teodorescu, D.; Vilathgamuwa, M. Component-minimized buck-boost voltage source inverters. In Proceedings of the 2007 IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 23–27 September 2007; pp. 2311–2318. [Google Scholar]
- Abdelhakim, A. Analysis and modulation of the buck-boost voltage source inverter (BBVSI) for lower voltage stresses. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 926–934. [Google Scholar]
- Abdeen, E.; Gaafar, M.A.; Orabi, M. Performance Analysis for Single-Stage Buck-Boost Inverter. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 587–592. [Google Scholar]
- Azizi, M.; Mohamadian, M.; Beiranvand, R. A New Family of Multi-Input Converters Based on Three Switches Leg. IEEE Trans. Ind. Electron. 2016, 63, 6812–6822. [Google Scholar] [CrossRef]
- Abdeen, E.; Orabi, M.; Hasaneen, E.S. Optimum tilt angle for photovoltaic system in desert environment. Sol. Energy 2017, 155, 267–280. [Google Scholar] [CrossRef]




| Symbol | The Maximum Current | The Maximum Voltage |
|---|---|---|
| SHa,b,c, SLa,b,c | Iph | Vinv |
| Sb1,2,3 | IL + Iph | Vinv |
| Symbol | Quantity | Value |
|---|---|---|
| Vph | Grid voltage | 110 V RMS |
| Voc | Open circuit voltage of PV array | 112 V |
| Isc | Short circuit current of PV array | 7 A |
| Vmax | Voltage at MPP of PV array | 100 V |
| Imax | Current at MPP of PV array | 6 A |
| C | DC link capacitor | 47 uF |
| L | Inductor Li of boost circuit | 1 mH |
| Fsw | Switching frequency | 10 kHz |
| Kp/Ki | PI and PR controller gains | 0.5/10 and 50/8000 |
| Symbol | Quantity | Value |
|---|---|---|
| Voc | Open circuit voltage of PV modules | 3 × 37 V |
| Isc | Short circuit current of PV modules | 9 A |
| Vmax | Voltage at MPP of PV module | 3 × 30 V |
| Imax | Current at MPP of PV module | 8 A |
| R load | Resistor load (single-multi input) | 40–77 |
| L filter | Output current filter | 5 mH |
| C | DC link capacitor | 47 uF |
| L | Inductor Li of boost circuit | 1.2 mH |
| fsw | Switching frequency | 10 kHz |
| Symbol | SSI [21] | ZSI [10,12] | The Proposed Inverter | [26] Dual | |
|---|---|---|---|---|---|
| Single | Multi | ||||
| No. of input source | 1 | 1 | 1 | 3 | 2 |
| No. of switches | 6 | 6 | 7 | 9 | 8 |
| No. of diodes | 3 | 1 | 0 | 0 | 0 |
| No. of Inductors | 1 | 2 | 1 | 3 | 2 |
| No. of Capacitors | 1 | 2 | 1 | 1 | 1 |
| Capacitor value | 380 | 590 | 47 | 47 | Not reported |
| Measured voltage gain | 1.56 | 1.13 | 1.86 | 1.86 | 3.75 |
| Measured peak efficiency | Not reported | 93% | 92.4% | Not reported | |
| Maximum current stress for the inverter bridge | 3 × (IL + Iph) | 3 × (2IL/3 + Iph) | 3 × (Iph) | 3 × (Iph) | 3 × (Iph) |
| 3 × (Iph) | 3 × (2IL/3 + Iph) | 3 × (Iph) | 3 × (Iph) | 3 × (Iph) | |
| Boost switch | - | - | 1 × (IL + Iph)) | 3 × (IL + Iph) | 2 × (IL + Iph)) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdeen, E.; Gaafar, M.A.; Orabi, M.; Ahmed, E.M.; El Aroudi, A. Multi-Input ?uk-Derived Buck-Boost Voltage Source Inverter for Photovoltaic Systems in Microgrid Applications. Energies 2019, 12, 2007. https://doi.org/10.3390/en12102007
Abdeen E, Gaafar MA, Orabi M, Ahmed EM, El Aroudi A. Multi-Input ?uk-Derived Buck-Boost Voltage Source Inverter for Photovoltaic Systems in Microgrid Applications. Energies. 2019; 12(10):2007. https://doi.org/10.3390/en12102007
Chicago/Turabian StyleAbdeen, Eltaib, Mahmoud A. Gaafar, Mohamed Orabi, Emad M. Ahmed, and Abdelali El Aroudi. 2019. "Multi-Input ?uk-Derived Buck-Boost Voltage Source Inverter for Photovoltaic Systems in Microgrid Applications" Energies 12, no. 10: 2007. https://doi.org/10.3390/en12102007
APA StyleAbdeen, E., Gaafar, M. A., Orabi, M., Ahmed, E. M., & El Aroudi, A. (2019). Multi-Input ?uk-Derived Buck-Boost Voltage Source Inverter for Photovoltaic Systems in Microgrid Applications. Energies, 12(10), 2007. https://doi.org/10.3390/en12102007






