Improving Microgrid Frequency Regulation Based on the Virtual Inertia Concept while Considering Communication System Delay
Abstract
:1. Introduction
- To reduce the installation costs, the size of the installed equipment should be minimal, so that the system will not face high costs during its long operation time.
- To enhance the frequency behavior of the microgrid, communicational infrastructure with minimum delays is required to update information quickly.
2. Case Study
2.1. Modeling the Power Source of Diesel Generator
2.2. Fuel Cell
2.3. Electrolyze Unit
2.4. Model of Renewable Energy Sources
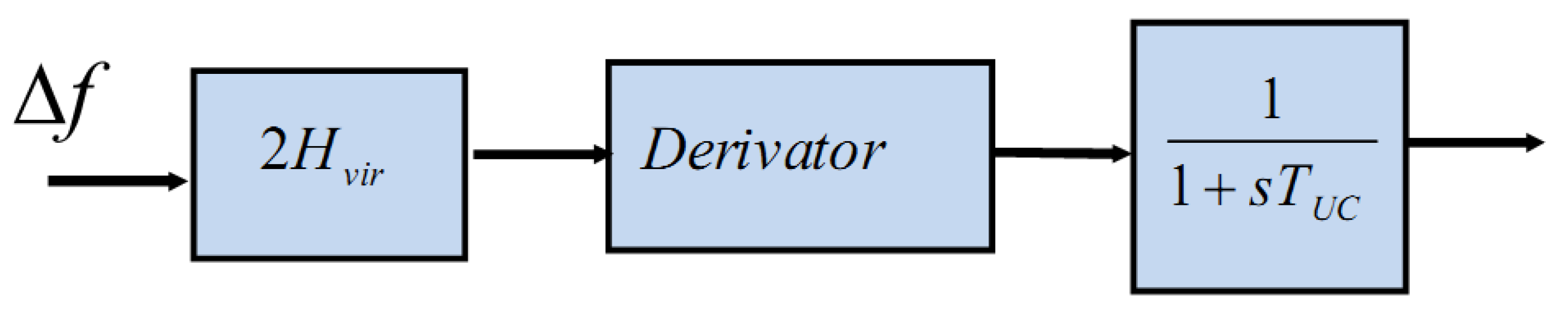
2.5. Ultra-Capacitor
2.6. Telecommunication System Delay
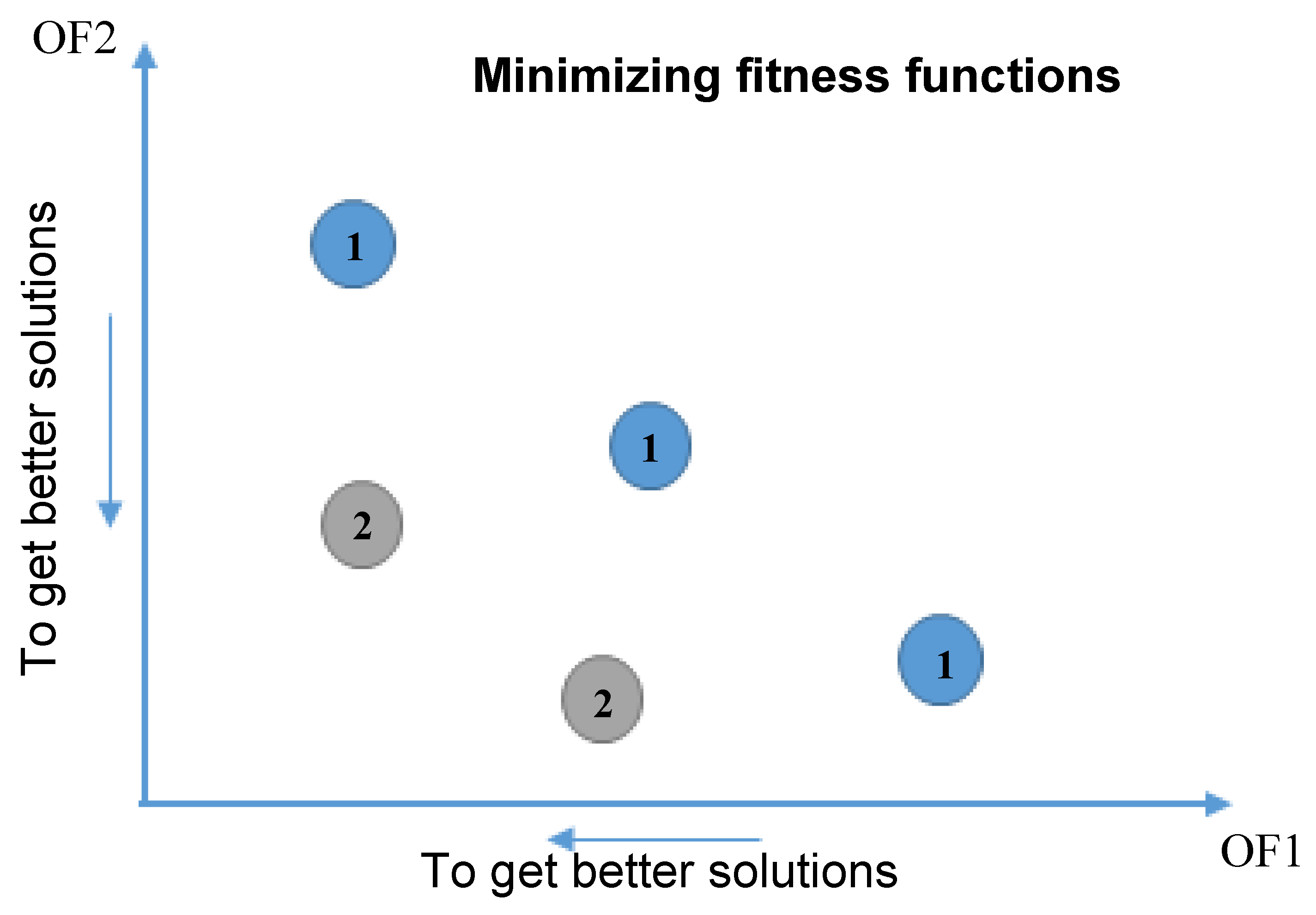
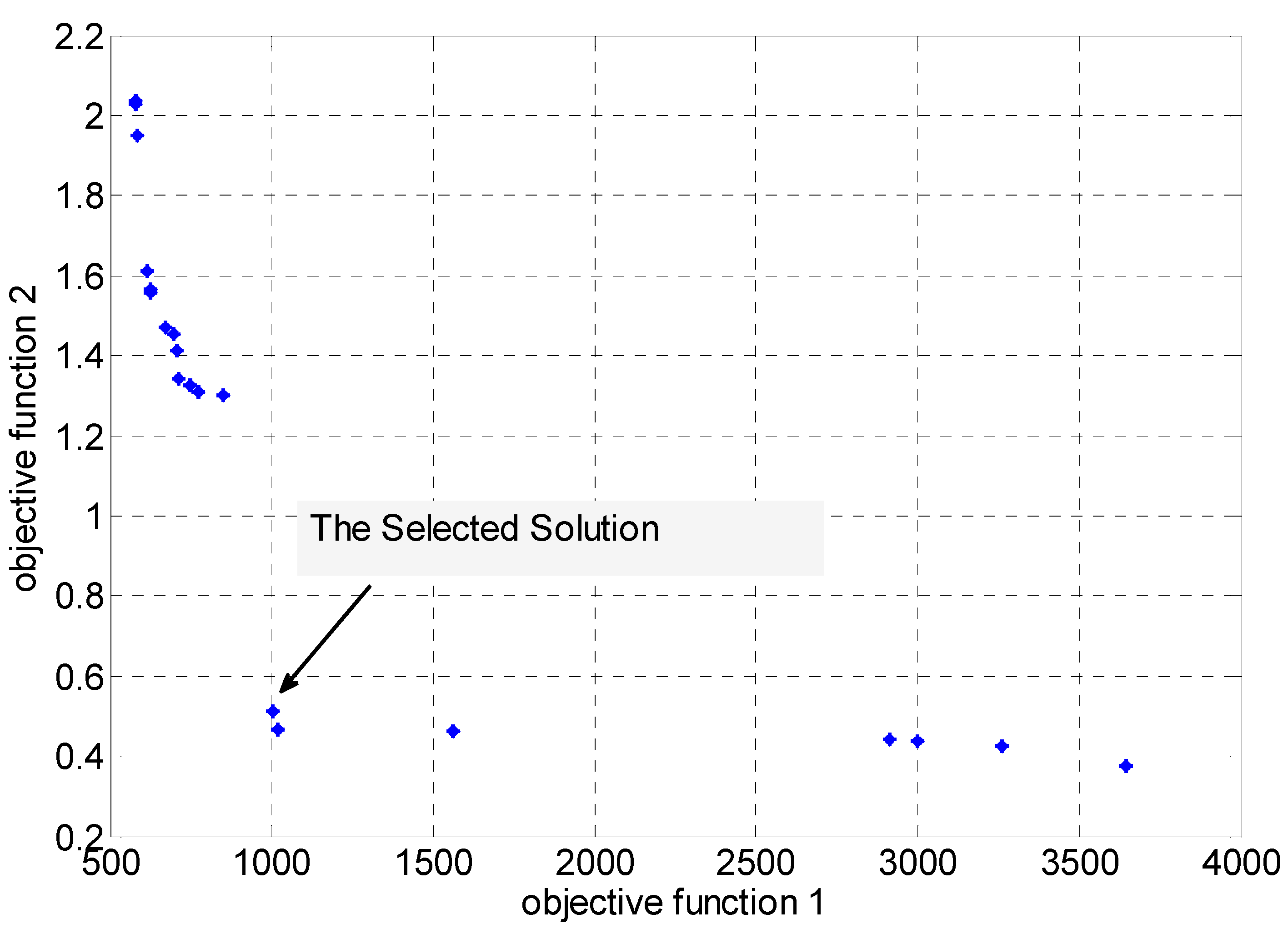
2.7. Optimization Algorithm
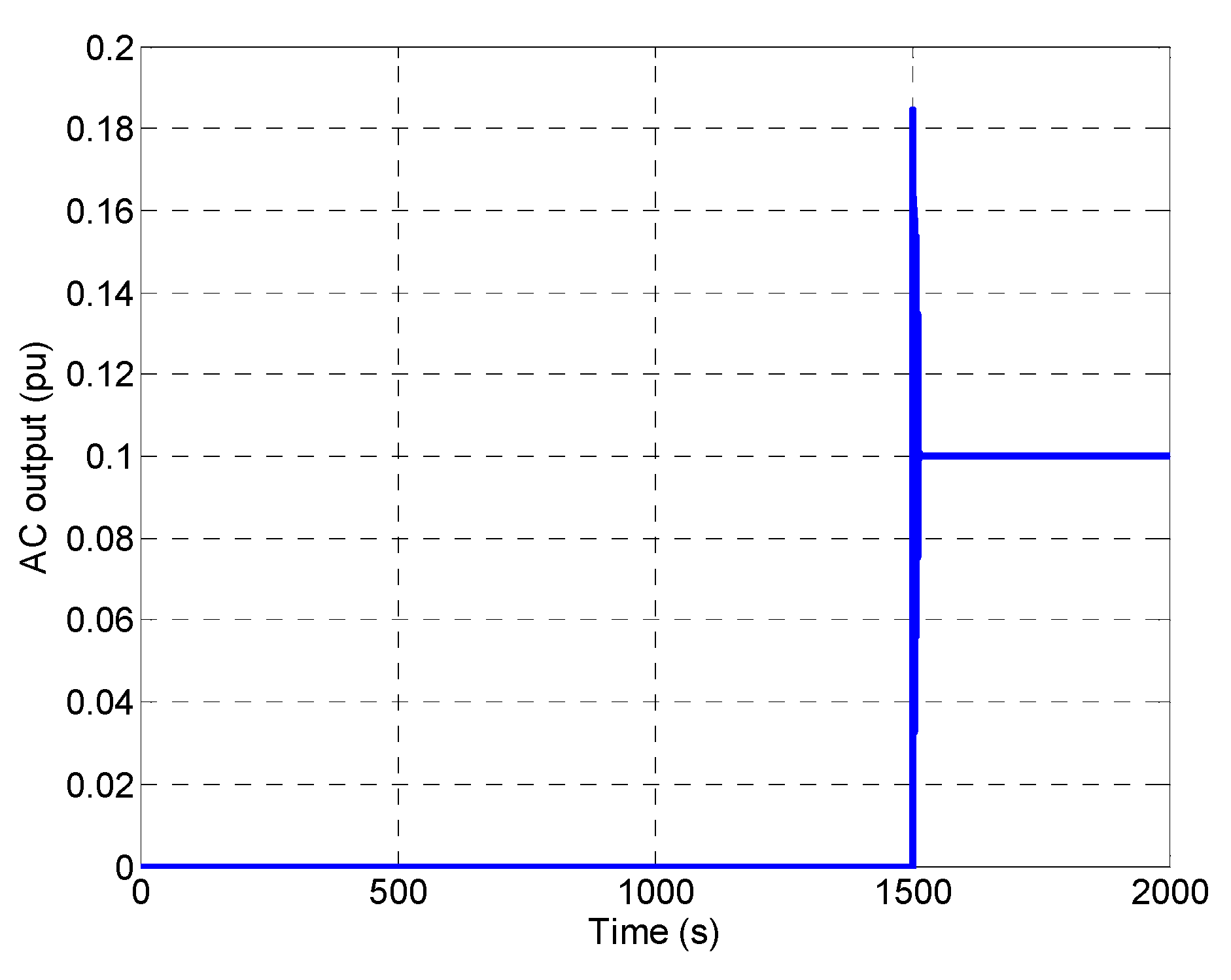
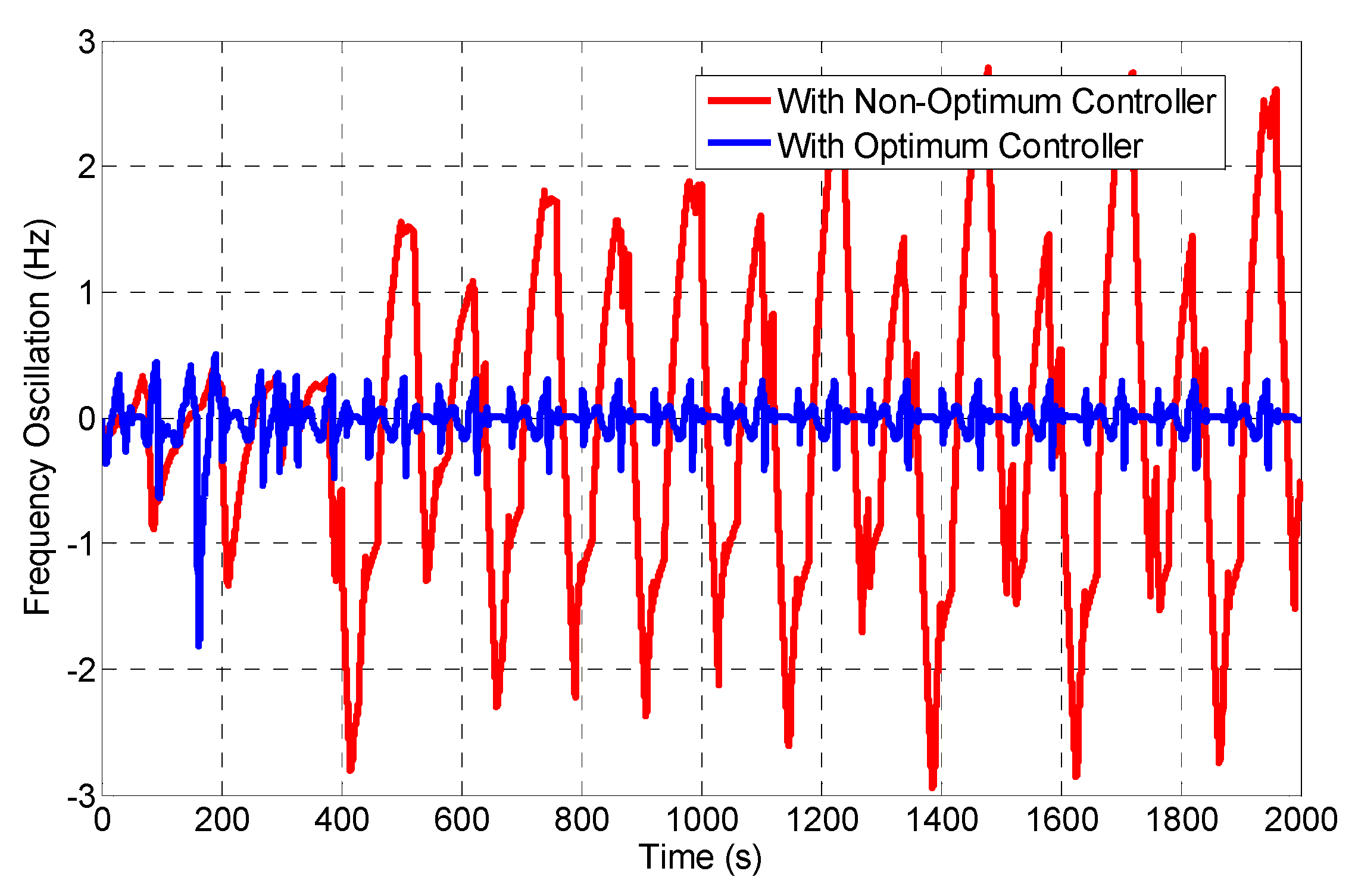
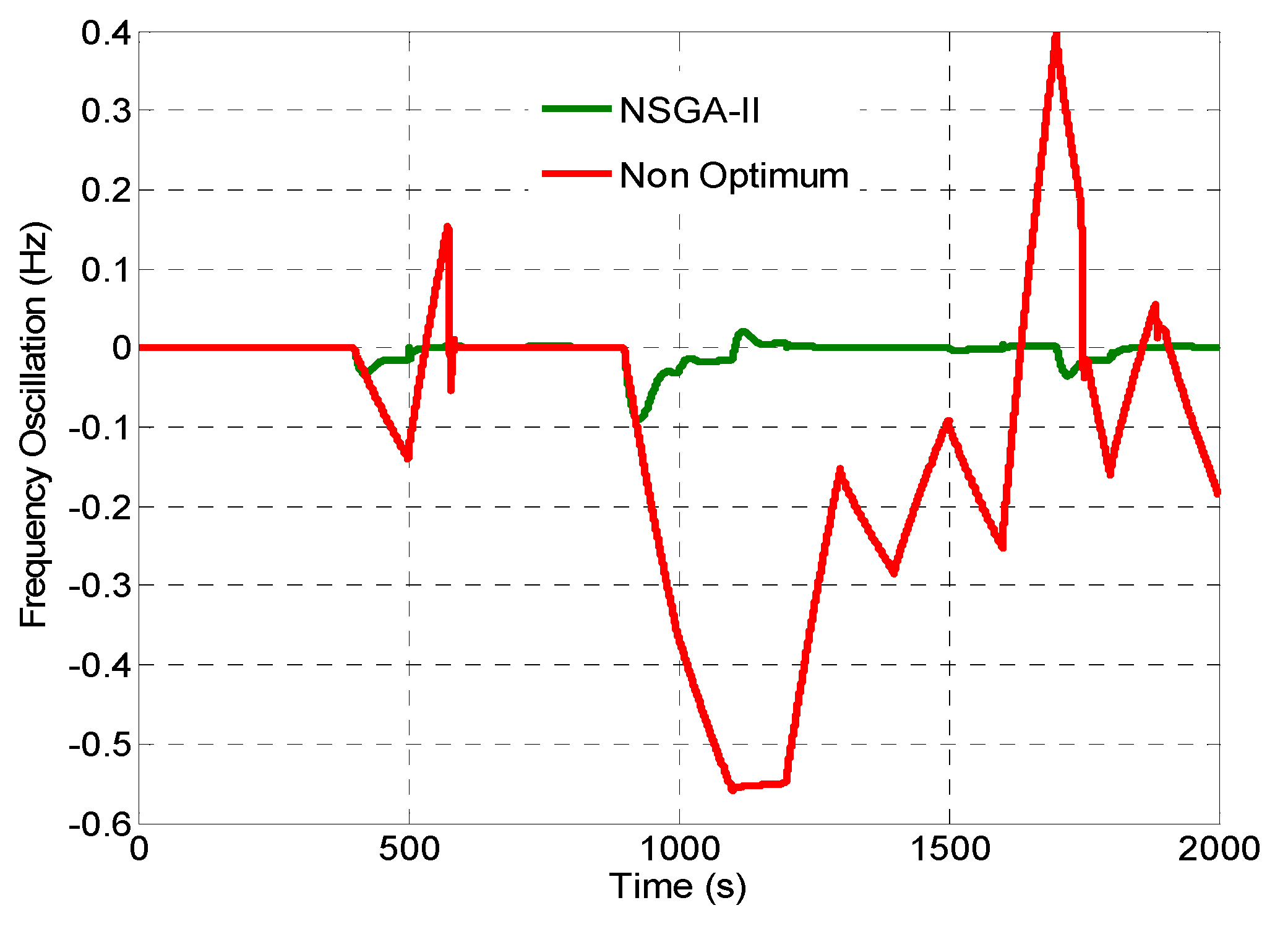
3. Simulation Results
- ✓
- Scenario I: In the first scenario, the performance of the microgrid was simulated through the application of a telecommunication networks delay with non-optimum parameter values.
- ✓
- Scenario II: In the second scenario, the performance of the microgrid with the optimum control parameters, virtual inertia and telecommunication systems delay values is verified through simulation setups.
- ✓
- Scenario III: In the third scenario, the delay of the telecommunication system is not considered while the optimum parameters are applied in the simulated system.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hatziargyriou, N. (Ed.) Microgrids: Architectures and Control; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Liu, W.; Gu, W.; Sheng, W.; Meng, X.; Wu, Z.; Chen, W. Decentralized multi-agent system-based cooperative frequency control for autonomous microgrids with communication constraints. IEEE Trans. Sustain. Energy 2014, 5, 446–456. [Google Scholar] [CrossRef]
- Abdel-Hamed, A.M.; Ellissy, A.E.E.K.; El-Wakeel, A.S.; Abdelaziz, A.Y. Optimized control scheme for frequency/power regulation of microgrid for fault tolerant operation. Electr. Power Compon. Syst. 2016, 44, 1429–1440. [Google Scholar] [CrossRef]
- Venkataramanan, G.; Marnay, C. A larger role for microgrids. IEEE Power Energy Mag. 2008, 6, 78–82. [Google Scholar] [CrossRef]
- Chen, C.; Wang, J.; Qiu, F.; Zhao, D. Resilient distribution system by microgrids formation after natural disasters. IEEE Trans. Smart Grid 2016, 7, 958–966. [Google Scholar] [CrossRef]
- Tani, A.; Camara, M.B.; Dakyo, B. Energy management in the decentralized generation systems based on renewable energy—Ultracapacitors and battery to compensate the wind/load power fluctuations. IEEE Trans. Ind. Appl. 2015, 51, 1817–1827. [Google Scholar] [CrossRef]
- Ahmed, N.A.; Miyatake, M.; Al-Othman, A.K. Power fluctuations suppression of stand-alone hybrid generation combining solar photovoltaic/wind turbine and fuel cell systems. Energy Convers. Manag. 2008, 49, 2711–2719. [Google Scholar] [CrossRef]
- Chen, Z.; Spooner, E. Grid power quality with variable speed wind turbines. IEEE Trans. Energy Convers. 2001, 16, 148–154. [Google Scholar] [CrossRef]
- Liang, X. Emerging power quality challenges due to integration of renewable energy sources. IEEE Trans. Ind. Appl. 2017, 53, 855–866. [Google Scholar] [CrossRef]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]
- Shim, J.W.; Cho, Y.; Kim, S.J.; Min, S.W.; Hur, K. Synergistic control of SMES and battery energy storage for enabling dispatchability of renewable energy sources. IEEE Trans. Appl. Supercond. 2013, 23, 5701205. [Google Scholar] [CrossRef]
- Onar, O.C.; Uzunoglu, M.; Alam, M.S. Dynamic modeling, design and simulation of a wind/fuel cell/ultra-capacitor-based hybrid power generation system. J. Power Sources 2006, 161, 707–722. [Google Scholar] [CrossRef]
- Jing, W.; Lai, C.H.; Wong, W.S.; Wong, M.D. Dynamic power allocation of battery-supercapacitor hybrid energy storage for standalone PV microgrid applications. Sustain. Energy Technol. Assess. 2017, 22, 55–64. [Google Scholar] [CrossRef]
- Chandrakala, V.; Sukumar, B.; Sankaranarayanan, K. Load frequency control of multi-source multi-area hydro thermal system using flexible alternating current transmission system devices. Electr. Power Compon. Syst. 2014, 42, 927–934. [Google Scholar] [CrossRef]
- Arani, M.F.M.; Mohamed, Y.A.R.I. Cooperative control of wind power generator and electric vehicles for microgrid primary frequency regulation. IEEE Trans. Smart Grid 2018, 9, 5677–5686. [Google Scholar] [CrossRef]
- Liu, Y.; You, S.; Tan, J.; Zhang, Y.; Liu, Y. Frequency Response Assessment and Enhancement of the US Power Grids toward Extra-High Photovoltaic Generation Penetrations—An Industry Perspective. IEEE Trans. Power Syst. 2018, 33, 3438–3449. [Google Scholar] [CrossRef]
- Kalantar, M. Dynamic behavior of a stand-alone hybrid power generation system of wind turbine, microturbine, solar array and battery storage. Appl. Energy 2010, 87, 3051–3064. [Google Scholar] [CrossRef]
- Gao, L.; Jiang, Z.; Dougal, R.A. An actively controlled fuel cell/battery hybrid to meet pulsed power demands. J. Power Sources 2004, 130, 202–207. [Google Scholar] [CrossRef]
- Nayeripour, M.; Hoseintabar, M.; Niknam, T. Frequency deviation control by coordination control of FC and double-layer capacitor in an autonomous hybrid renewable energy power generation system. Renew. Energy 2011, 36, 1741–1746. [Google Scholar] [CrossRef]
- Khooban, M.H.; Niknam, T.; Blaabjerg, F.; Dragičević, T. A new load frequency control strategy for micro-grids with considering electrical vehicles. Electr. Power Syst. Res. 2017, 143, 585–598. [Google Scholar] [CrossRef] [Green Version]
- Sigrist, L.; Egido, I.; Miguélez, E.L.; Rouco, L. Sizing and controller setting of ultracapacitors for frequency stability enhancement of small isolated power systems. IEEE Trans. Power Syst. 2015, 30, 2130–2138. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, Y.; Wang, Z.; Pen, H. Secondary frequency stochastic optimal control in independent microgrids with virtual synchronous generator-controlled energy storage systems. Energies 2018, 11, 2388. [Google Scholar] [CrossRef]
- Hammad, E.; Farraj, A.; Kundur, D. On Effective Virtual Inertia of Storage-Based Distributed Control for Transient Stability. IEEE Trans. Smart Grid 2019. Accepted for publications. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Power system stabilization using virtual synchronous generator with alternating moment of inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.; Mitani, Y.; Hongesombut, K.; Küfeoğlu, S. Virtual inertia control-based model predictive control for microgrid frequency stabilization considering high renewable energy integration. Sustainability 2017, 9, 773. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. Distributed power system virtual inertia implemented by grid-connected power converters. IEEE Trans. Power Electron. 2018, 33, 8488–8499. [Google Scholar] [CrossRef]
- Jiang, L.; Yao, W.; Wu, Q.H.; Wen, J.Y.; Cheng, S.J. Delay-dependent stability for load frequency control with constant and time-varying delays. IEEE Trans. Power Syst. 2012, 27, 932–941. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.; Liu, P.X. Impact of Communication Delays on Secondary Frequency Control in an Islanded Microgrid. IEEE Trans. Ind. Electron. 2015, 62, 2021–2031. [Google Scholar] [CrossRef]
- Singh, V.P.; Kishor, N.; Samuel, P. Load frequency control with communication topology changes in smart grid. IEEE Trans. Ind. Inform. 2016, 12, 1943–1952. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, G.; Dai, Y.; Bi, D.; Sun, J.; Xie, X. Design of a Fractional Order Frequency PID Controller for an Islanded Microgrid: A Multi-Objective Extremal Optimization Method. Energies 2017, 10, 1502. [Google Scholar] [CrossRef]
- Chaine, S.; Tripathy, M.; Satpathy, S. NSGA-II based optimal control scheme of wind thermal power system for improvement of frequency regulation characteristics. Ain Shams Eng. J. 2015, 6, 851–863. [Google Scholar] [CrossRef] [Green Version]
- Kamjoo, A.; Maheri, A.; Dizqah, A.M.; Putrus, G.A. Multi-objective design under uncertainties of hybrid renewable energy system using NSGA-II and chance constrained programming. Int. J. Electr. Power Energy Syst. 2016, 74, 187–194. [Google Scholar] [CrossRef]
- Mishra, S.; Mallesham, G.; Jha, A.N. Design of controller and communication for frequency regulation of a smart microgrid. IET Renew. Power Gener. 2012, 6, 248–258. [Google Scholar] [CrossRef]
- Abazari, A.; Monsef, H.; Wu, B. Coordination strategies of distributed energy resources including FESS, DEG, FC and WTG in load frequency control (LFC) scheme of hybrid isolated micro-grid. Int. J. Electr. Power Energy Syst. 2019, 1, 535–547. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]










| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Tuc | 0.2 (s) | TFC | 4 (s) |
| H | 5 (s) | TAC | 0.2 (s) |
| D | 0.012 (pu/Hz) | Tdt | 20 (s) |
| Tdg | 2 (s) | fbase | 50 Hz |
| Parameter | Limitation | Parameter | Limitation |
|---|---|---|---|
| HVir_average | 5–8 | Bfc | 0.05–0.3 |
| kpdg | 0.1–1 | Rfc | 10–20 |
| kidg | 0.001–0.005 | kpac | 60–80 |
| Bdg | 0.07–0.2 | kiac | 0.01–0.5 |
| Rdg | 10–20 | Bac | 0.1–3 |
| kpfc | 0.01–0.3 | Tac | 10–20 |
| kifc | 0.001–0.005 | Td | 1–10 |
| Non-Optimum Parameters | Optimum Parameters | ||
|---|---|---|---|
| Parameter | Value | Parameter | Value |
| Hvir | 1 | Hvir | 0.2005 |
| kpdg | 0.244 | kpdg | 0.7167 |
| kidg | 0.0032 | kidg | 0.0024 |
| Bdg | 0.1386 | Bdg | 0.1687 |
| Rdg | 19.93 | Rdg | 17.084 |
| kpfc | 0.0298 | kpfc | 0.0764 |
| kifc | 0.0043 | kifc | 0.0025 |
| Bfc | 0.1878 | Bfc | 0.2338 |
| Rfc | 17.09 | Rfc | 12.7212 |
| kpac | 57.7635 | kpac | 75.3 |
| kiac | 7.08 | kiac | 0.4 |
| Bac | 0.5923 | Bac | 0.1 |
| Rac | 28.1 | Rac | 16.1 |
| Td | 3 | Td | 4.8 |
| 1.2 | 0.513 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alizadeh, G.A.; Rahimi, T.; Babayi Nozadian, M.H.; Padmanaban, S.; Leonowicz, Z. Improving Microgrid Frequency Regulation Based on the Virtual Inertia Concept while Considering Communication System Delay. Energies 2019, 12, 2016. https://doi.org/10.3390/en12102016
Alizadeh GA, Rahimi T, Babayi Nozadian MH, Padmanaban S, Leonowicz Z. Improving Microgrid Frequency Regulation Based on the Virtual Inertia Concept while Considering Communication System Delay. Energies. 2019; 12(10):2016. https://doi.org/10.3390/en12102016
Chicago/Turabian StyleAlizadeh, Gholam Ali, Tohid Rahimi, Mohsen Hasan Babayi Nozadian, Sanjeevikumar Padmanaban, and Zbigniew Leonowicz. 2019. "Improving Microgrid Frequency Regulation Based on the Virtual Inertia Concept while Considering Communication System Delay" Energies 12, no. 10: 2016. https://doi.org/10.3390/en12102016
APA StyleAlizadeh, G. A., Rahimi, T., Babayi Nozadian, M. H., Padmanaban, S., & Leonowicz, Z. (2019). Improving Microgrid Frequency Regulation Based on the Virtual Inertia Concept while Considering Communication System Delay. Energies, 12(10), 2016. https://doi.org/10.3390/en12102016








