Improvement of Combustion Process of Spark-Ignited Aviation Wankel Engine
Abstract
:1. Introduction
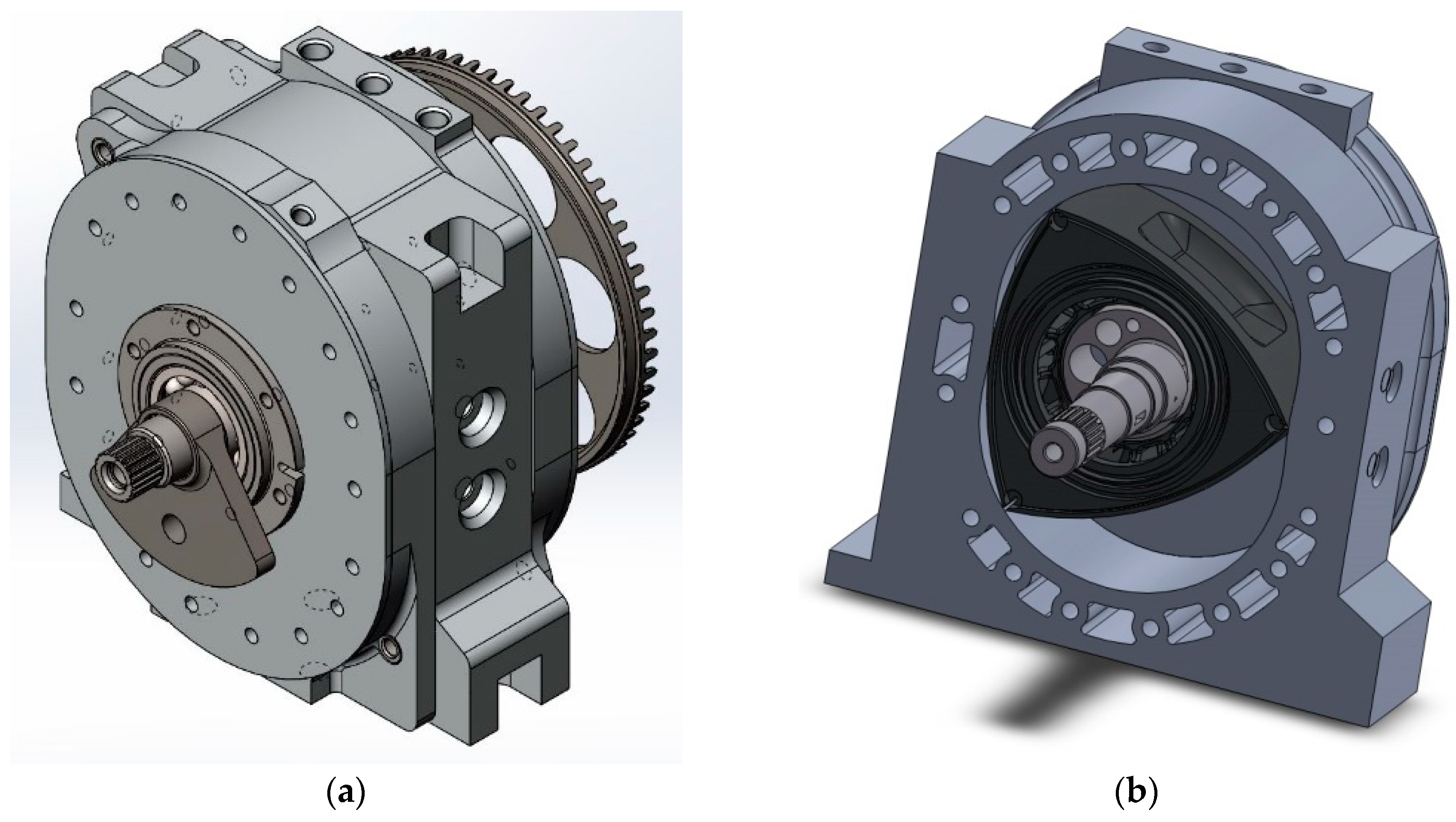
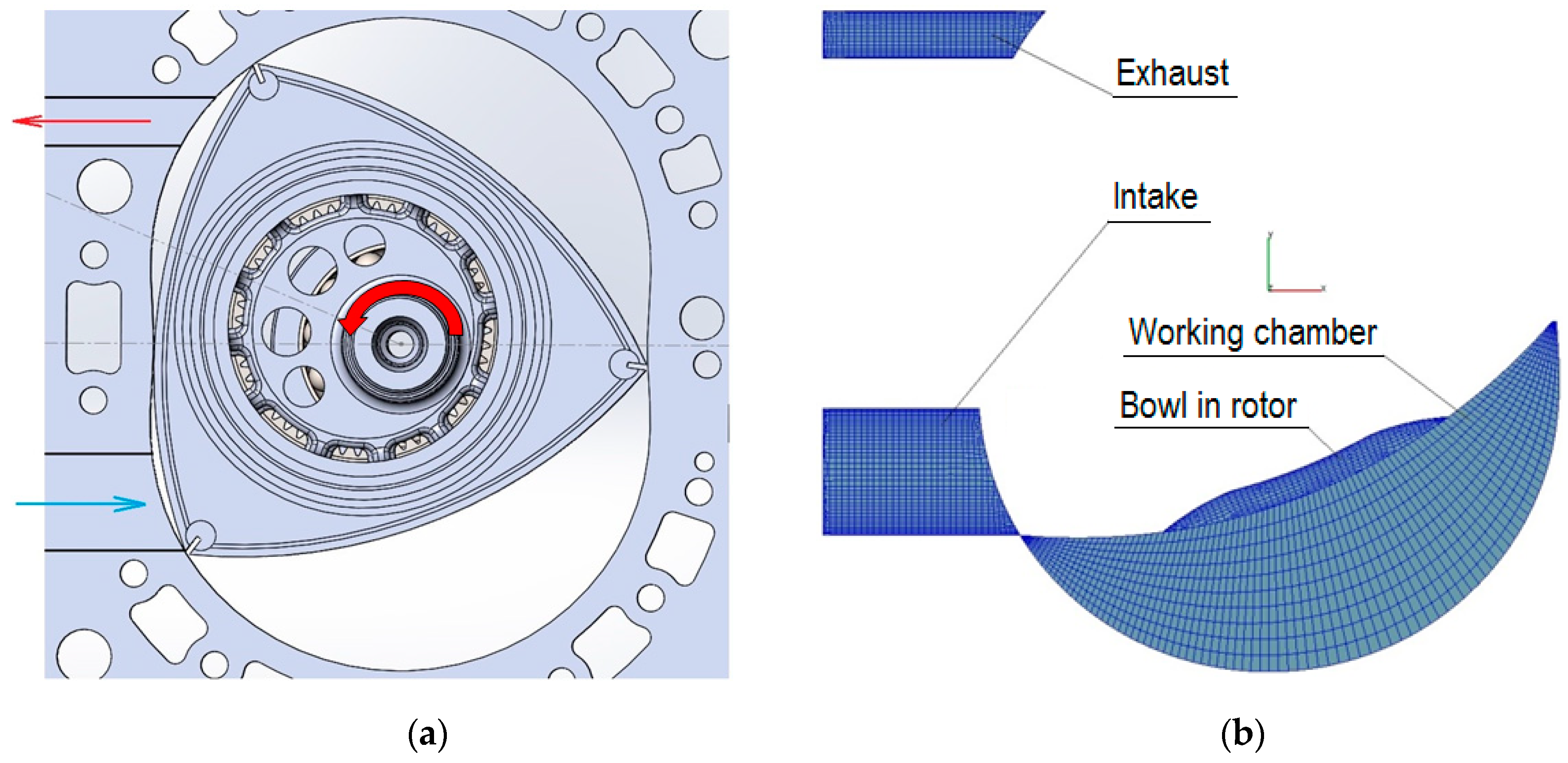
2. Mathematical Model
3. Results and Discussion
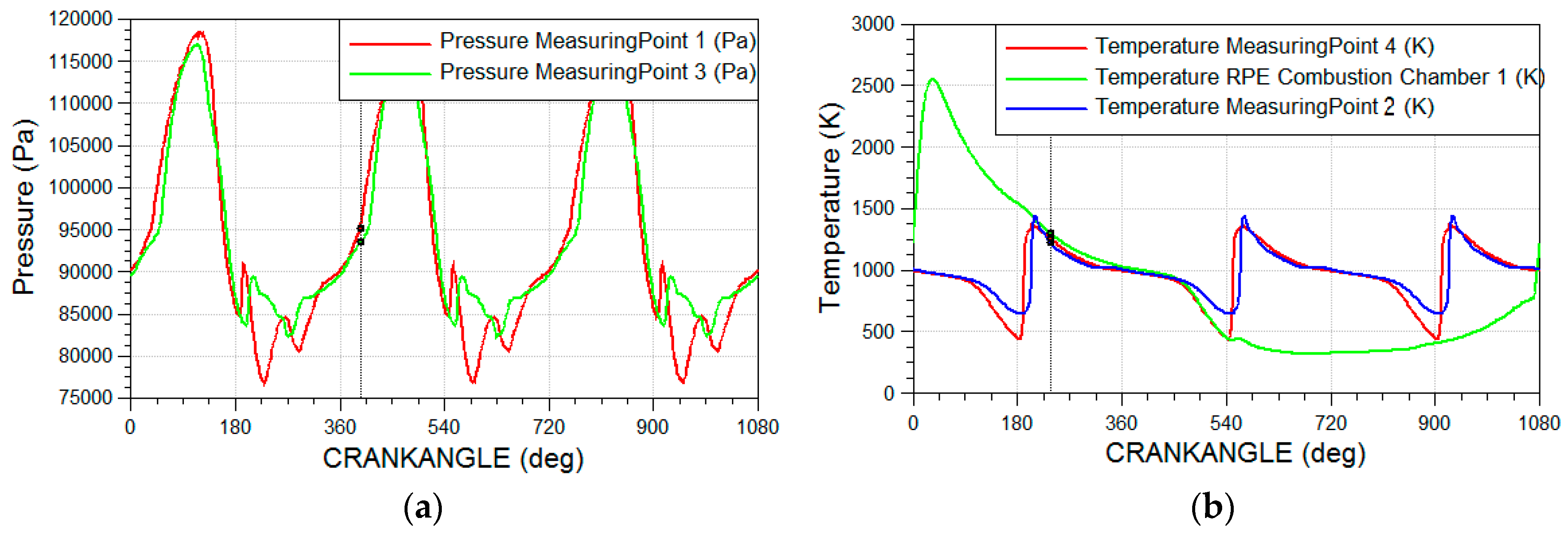
3.1. Validation
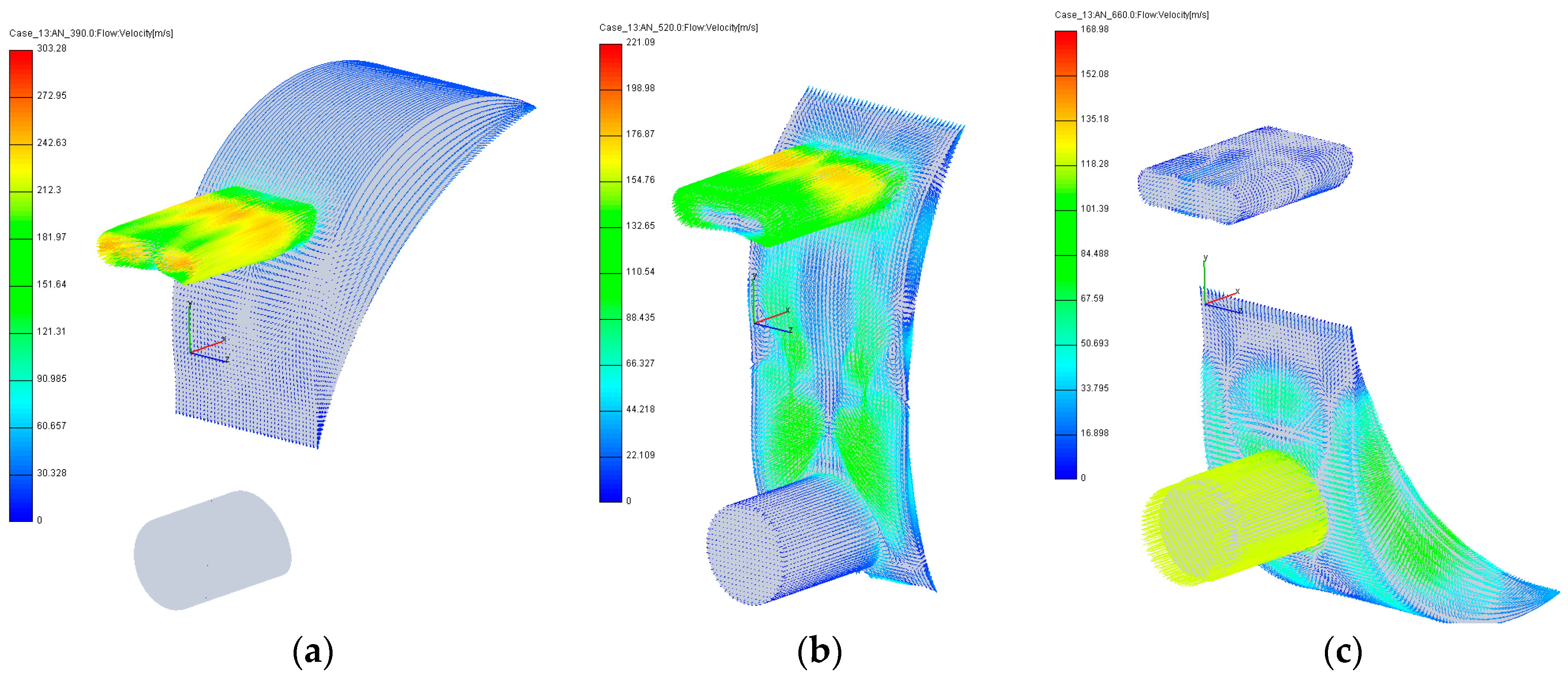
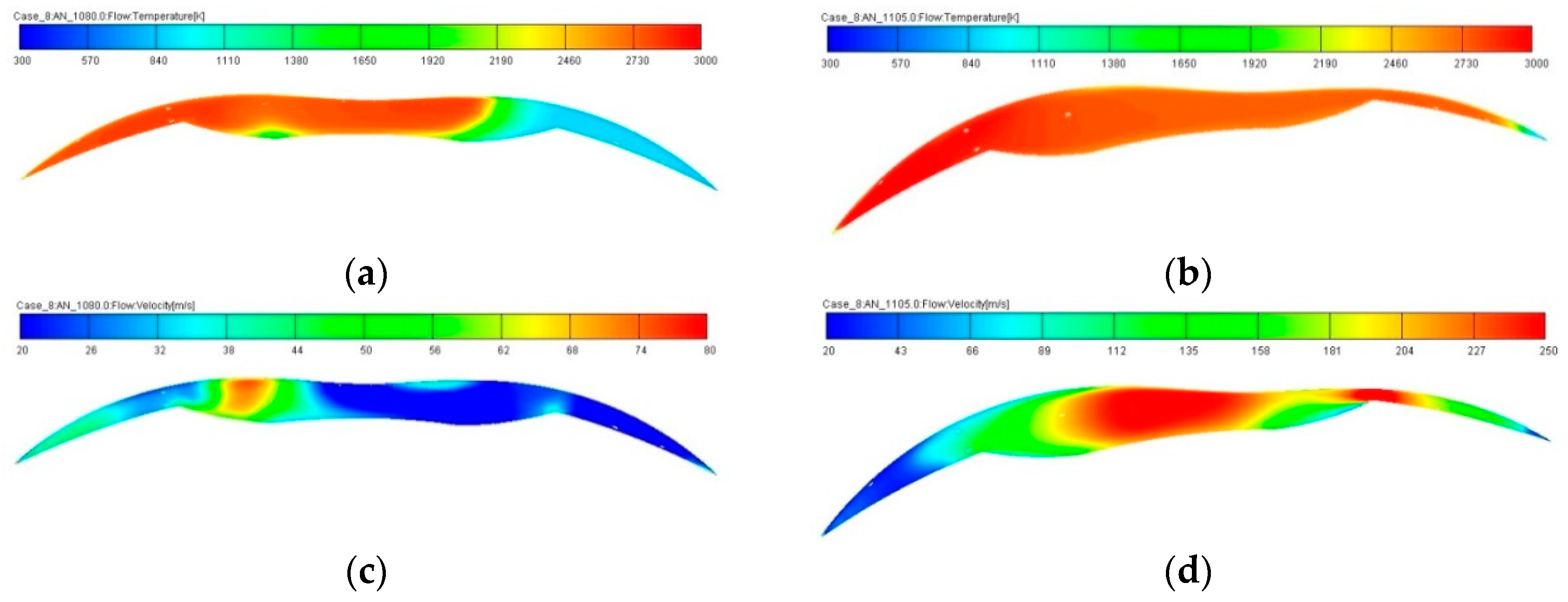
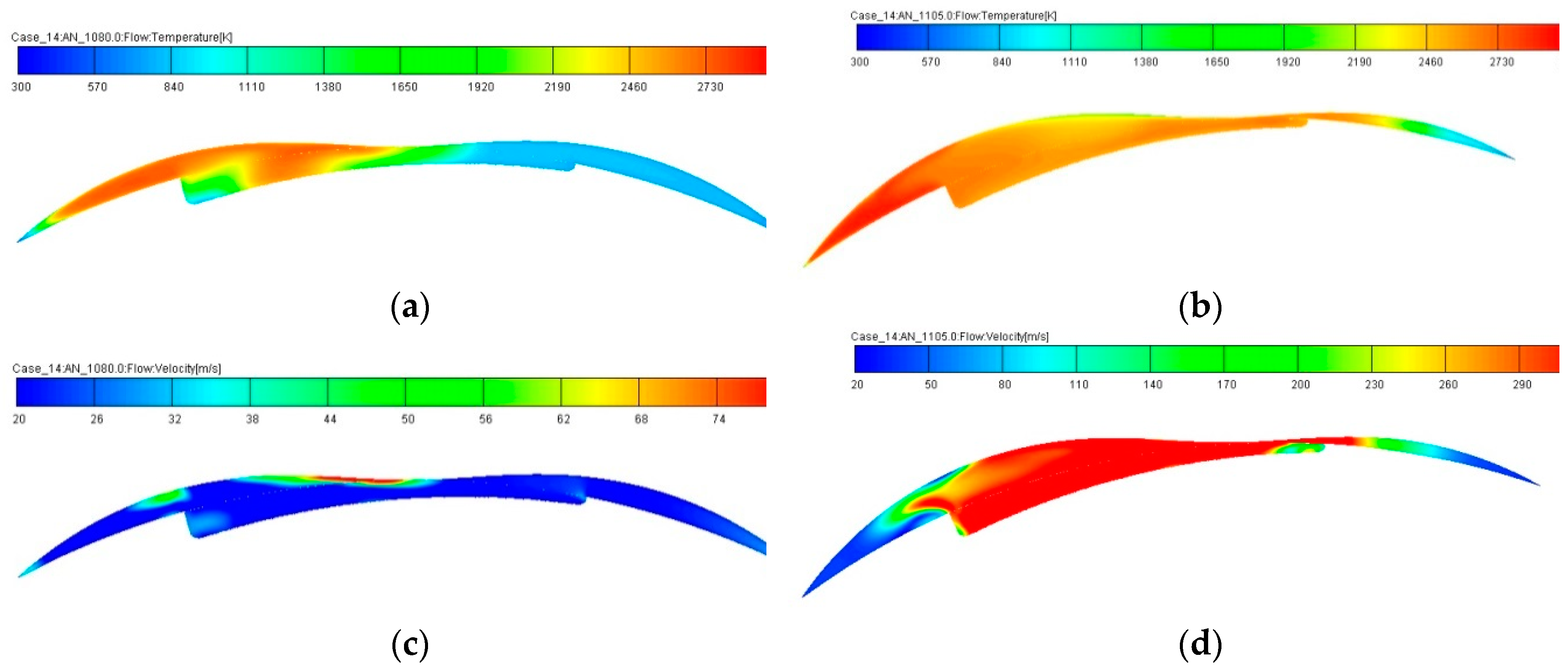
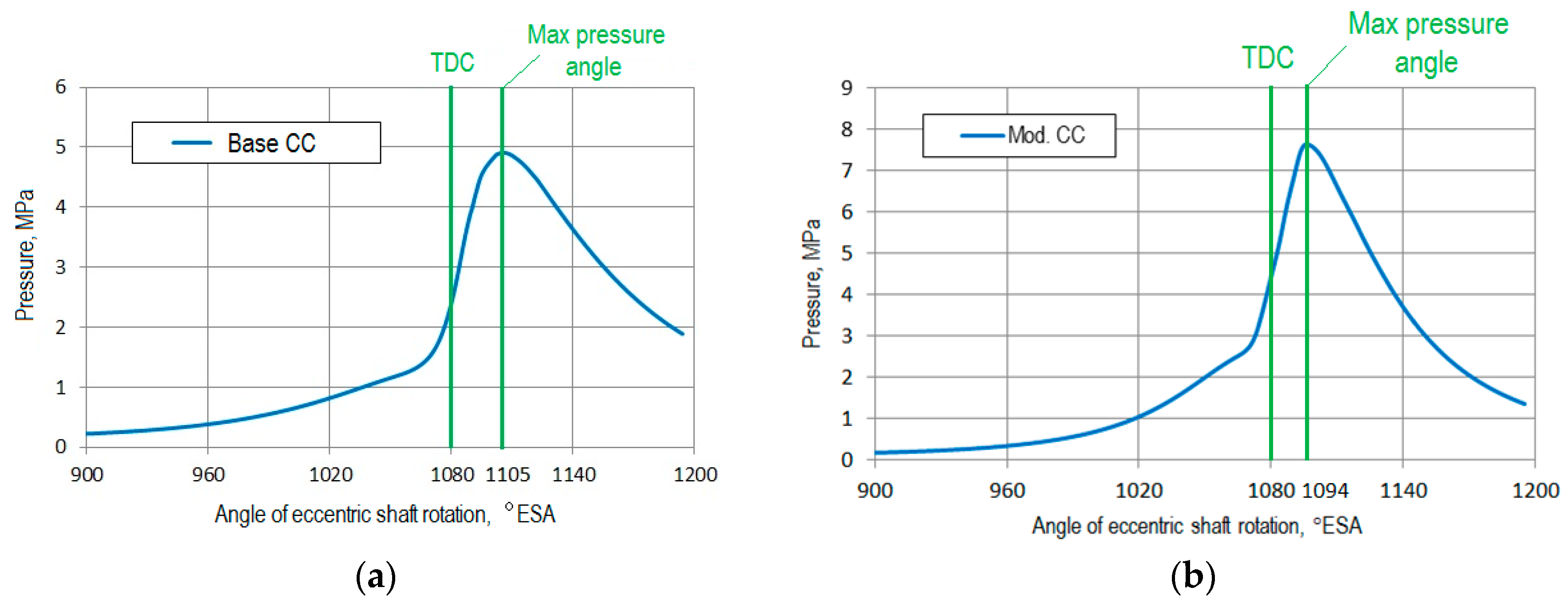
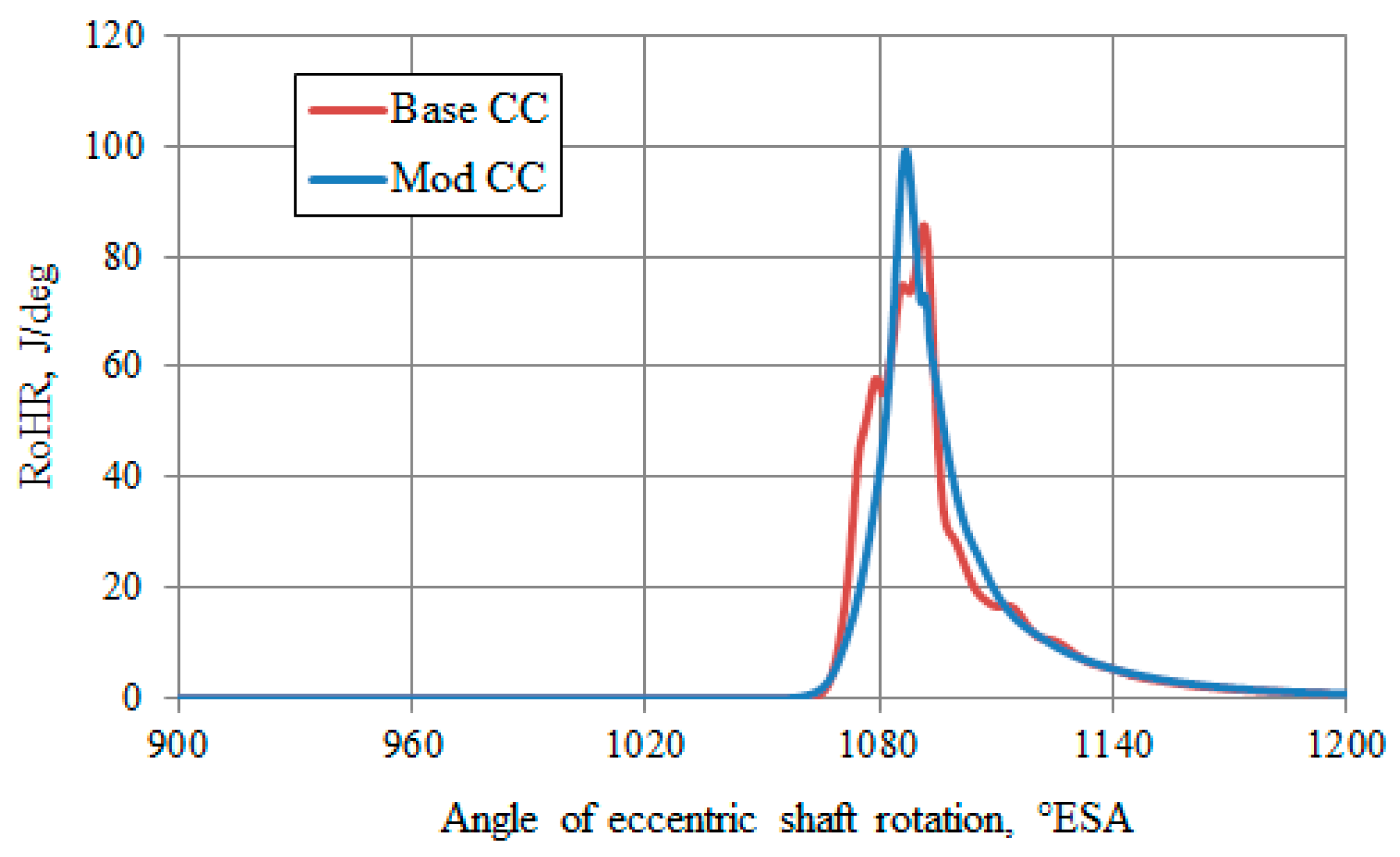
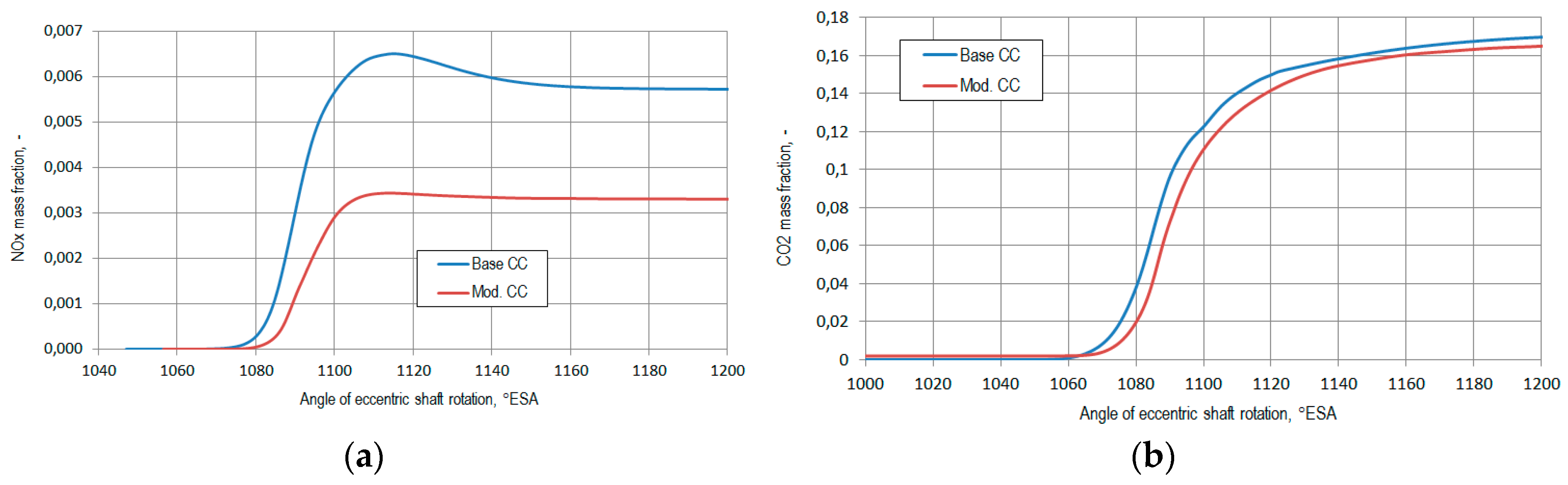
3.2. Results of Numerical Experiments
4. Conclusions
- A mathematical model of the Wankel engine has been developed, one which allows three-dimensional determining of the parameters of the working fluid in the entire calculated volume, taking into account inlet and exhaust processes. This model also takes into account the geometric features of the WE combustion chamber and allows for the determination of the best design in terms of improving the engine efficiency.
- A later ignition of the trailing spark plug was proposed (the interval between spark plug actuation is 15 °ESA), which reduced the irregularity of flame propagation in the direction of the rotor movement.
- According to the results of modeling the processes of turbulent combustion and transfer in the WE working chamber, a significant influence of the shape of the recess in the rotor on the engine performance has been determined. An alternative design of the chamber shape in the rotor, which allows increasing the efficiency of the WE operation, has been offered.
- It has been shown that lower values of maximum gas temperature (Tmax = 2821 K for modified CC and 2967 K for base CC) lead to 42% improvement in the engine environmental performance of nitrogen oxide (NOx) emissions and an increase in its efficiency in regard to the reduction of carbon dioxide (CO2) emissions (by 5%).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stone, R. Introduction to Internal Combustion Engines, 4th ed.; Palgrave Macmillan Press: Basingstoke, UK, 2012; 516p. [Google Scholar]
- The New Generation of Wankel Rotary Engines; Wankel Super-Tec GmbH: Cottbus, Germany, 2004; p. 30.
- Kostyuchenkov, A.N.; Zelentsov, A.A.; Semenov, P.V.; Minin, V.P. Development of a Single-Section Demonstrator Rotary Engine on the Basis of a Modern Complex Design Procedure. Vestn. Samara Gos. Aerocosm. Univ. 2014, 2, 173–181. (In Russian) [Google Scholar] [CrossRef]
- Beniovich, V.S.; Apazidi, G.D.; Boyko, A.M. Rotary Engines; Mashinostroenie Publ.: Moscow, Russia, 1968; p. 153. (In Russian) [Google Scholar]
- Yamamoto, K. Rotary Engine; Sankaido Co., Ltd.: Tokyo, Japan, 1981; p. 68. [Google Scholar]
- Poojitganont, T.; Izweik, H.T.; Berg, H.P. The Simulation of Flow Field inside the Wankel Combustion Chamber. In Proceedings of the 20th Conference of Mechanical Engineering Network, Nakhon Ratchasima, Thailand, 18–20 October 2006. [Google Scholar]
- Kavtaradze, R.Z. Theory of Piston Engines: Special Chapters; Mosk. Gos. Tekh. Univ. im. N.E. Baumana: Moscow, Russia, 2016; pp. 467–496. (In Russian) [Google Scholar]
- Kavtaradze, R.Z. Three-Dimensional Simulation of Non-steady Thermophysical Processes in Piston Engines; Mosk. Gos. Tekh. Univ. im. N.E. Baumana: Moscow, Russia, 2012; pp. 5–33. (In Russian) [Google Scholar]
- Merker, G.; Schwarz, C.; Teichmann, R. Grundlagen Verbrennungsmotoren: Funktionsweise, Simulation, Messtechnik (Fundamentals of Internal Combustion Engines: Mode of Operation, Simulation, Measurement Technology), 9th ed.; Springer: Wiesbaden, Germany, 2019; p. 1117. [Google Scholar]
- Basshuysen, R.; Schäfer, F. (Hrsg.) Handbuch Verbrennungsmotor. 4. Auflage; Vieweg und Sohn Verlag: Wiesbaden, Germany, 2007; p. 1032. [Google Scholar]
- Kavtaradze, R.; Zelentsov, A.; Gladyshev, S.P.; Kavtaradze, Z.; Onishchenko, D. Heat insulating effect of soot deposit on local transient heat transfer in diesel engine combustion chamber. SAE Int. Pap. 2012. [Google Scholar] [CrossRef]
- Kavtaradze, R.Z. Local Heat Transfer in Piston Engines; Mosk. Gos. Tekh. Univ. im. N.E. Baumana: Moscow, Russia, 2016; pp. 189–226. (In Russian) [Google Scholar]
- Tatschl, R.; Schneider, J.; Basara, D.; Brohmer, A.; Mehring, A.; Hanjalić, K. Progress in the 3D-CFD calculation of the gas and water side heat transfer in engines, in Verfahren 10 Tagung der Arbeitsprozess des Verbrennungsmotors. In Proceedings of the 10th Meeting on the Working Process of the Internal Combustion Engine, Graz, Austria, 23–25 September 2005. [Google Scholar]
- Hanjalić, K.; Popovać, M.; Hadziabdić, M. A Robust Near-Wall Elliptic-Relaxation Eddy-Viscosity Turbulence Model for CFD. Int. J. Heat Fluid Flow 2004, 25, 897–901. [Google Scholar] [CrossRef]
- Tatschl, R.; Basara, B.; Schneider, J.; Hanjalic, K.; Popovac, M.; Brohmer, A.; Mehring, J. Advanced Turbulent Heat Transfer Modeling for IC-Engine Applications Using AVL FIRE. In Proceedings of the International Multidimensional Engine Modeling User’s Group Meeting, Detroit, MI, USA, 2 April 2006. [Google Scholar]
- Popovać, M.; Hanjalić, K. Compound Wall Treatment for RANS Computation of Complex Turbulent Flow. In Proceedings of the 3rd M.I.T. Conference, Boston, MA, USA, 14–17 June 2005. [Google Scholar]
- Candel, S.; Poinsot, T. Flame Stretch and the Balance Equation for the Flame Area. Combust. Sci. Technol. 1990, 70, 1–15. [Google Scholar] [CrossRef]
- Delhaye, B.; Cousyn, B. Computation of Flow and Combustion in Spark Ignition Engine and Comparison with Experiment. SAE Technol. Pap. 1996, 961960. [Google Scholar] [CrossRef]
- Meneveau, C.; Sreenivasan, K.R. The Multifractal Nature of Turbulent Energy Dissipation. J. Fluid Mech. 1991, 224, 429–484. [Google Scholar] [CrossRef]
- Kavtaradze, R.Z.; Onishchenko, D.O.; Zelentsov, A.A.; Sergeev, S.S. The influence of rotational charge motion intensity on nitric oxide formation in gas-engine cylinder. Int. J. Heat Mass Transf. 2009, 52, 4308–4316. [Google Scholar] [CrossRef]
- Kavtaradze, R.Z.; Onishchenko, D.O.; Golosov, A.S. Modeling of Processes into the Intake System of Aircraft Piston Engine with Intake Port Injection. Vestn. Mosk. Gos. Tekh. Univ. im. N.E. Baumana. Mashinostr. [Herald of the Bauman Moscow State Technical Univ. Mech. Eng. 2012, 4, 3–16. (In Russian) [Google Scholar]
- Lanshin, A.I.; Finkelberg, L.A.; Kostuchenkov, A.N.; Zelentsov, A.A.; Bakanov, M.A. Investigation of Inlet Flow Swirl Influence on the Aviation Piston Engine Characteristics. Vestn. Voronezh Gos. Tekh. Univ. [Herald of Voronezh State Technical Univ.] 2012, 2, 96–99. (In Russian). Available online: https://elibrary.ru/item.asp?id=17335022 (accessed on 14 June 2019).
- Zelentsov, A.A. Analysis of Influence of Working Process Features on Effective Characteristics of Aircraft Piston Engines. Vestn. Mosk. Gos. Tekh. Univ. im. N.E. Baumana. Mashinostr. [Herald of the Bauman Moscow State Technol. Univ., Mech. Eng.] 2013, 4, 81–93. (In Russian). Available online: http://vestnikmach.ru/articles/177/177.pdf (accessed on 14 June 2019).
- Kavtaradze, Z.; Onishchenko, D.O.; Zelentsov, L.A.; Finkel’berg, L.A.; Kostyuchenkov, A. Modeling of Processes of Transfer, Combustion and Nitric Oxides Formation in the Aircraft Piston Engine with Duplicated Ignition System. Izv. Akad. Nauk. Energetik 2012, 6, 135–152. (In Russian) [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Finkelberg, L.; Kostuchenkov, A.; Zelentsov, A.; Minin, V. Improvement of Combustion Process of Spark-Ignited Aviation Wankel Engine. Energies 2019, 12, 2292. https://doi.org/10.3390/en12122292
Finkelberg L, Kostuchenkov A, Zelentsov A, Minin V. Improvement of Combustion Process of Spark-Ignited Aviation Wankel Engine. Energies. 2019; 12(12):2292. https://doi.org/10.3390/en12122292
Chicago/Turabian StyleFinkelberg, Lev, Alexander Kostuchenkov, Andrei Zelentsov, and Vladimir Minin. 2019. "Improvement of Combustion Process of Spark-Ignited Aviation Wankel Engine" Energies 12, no. 12: 2292. https://doi.org/10.3390/en12122292
APA StyleFinkelberg, L., Kostuchenkov, A., Zelentsov, A., & Minin, V. (2019). Improvement of Combustion Process of Spark-Ignited Aviation Wankel Engine. Energies, 12(12), 2292. https://doi.org/10.3390/en12122292




