Dual 3-Phase Bridge Multilevel Inverters for AC Drives with Voltage Sag Ride-through Capability
Abstract
:1. Introduction
2. AC VSD with a Multilevel Inverter Based in Dual 3-Phase VSIs
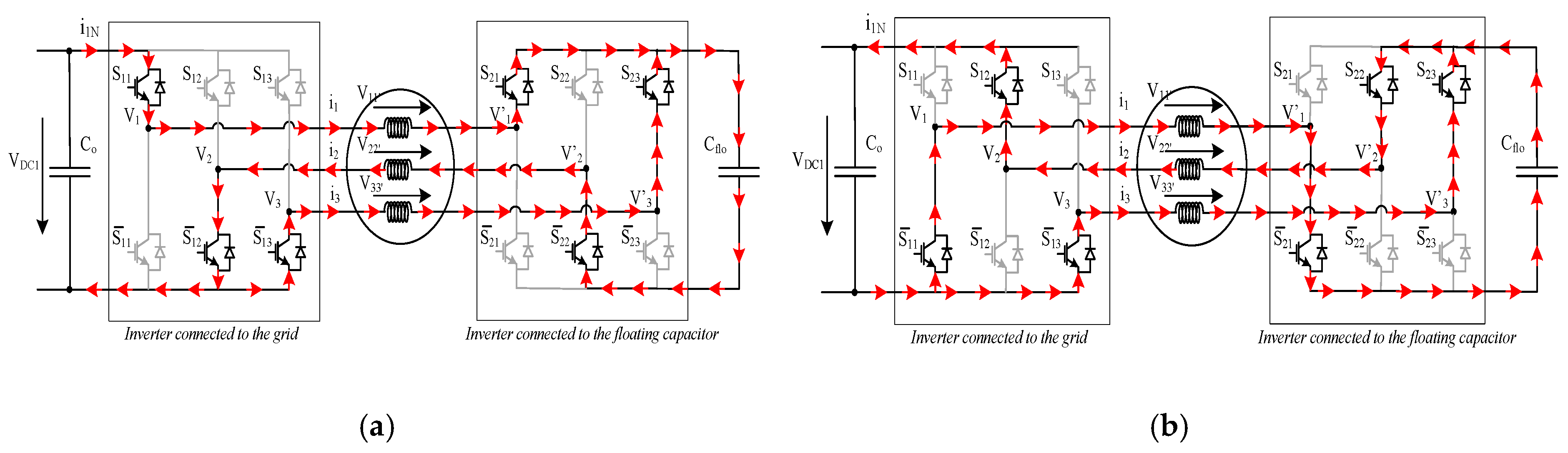
2.1. Proposed Multilevel Inverter with Voltage Sag Ride-through Capability
2.2. Comparison with Other Topologies
2.3. AC VSD Model with the Proposed Multilevel Inverter
3. Control System
3.1. Field Oriented Control
3.2. Current Controller
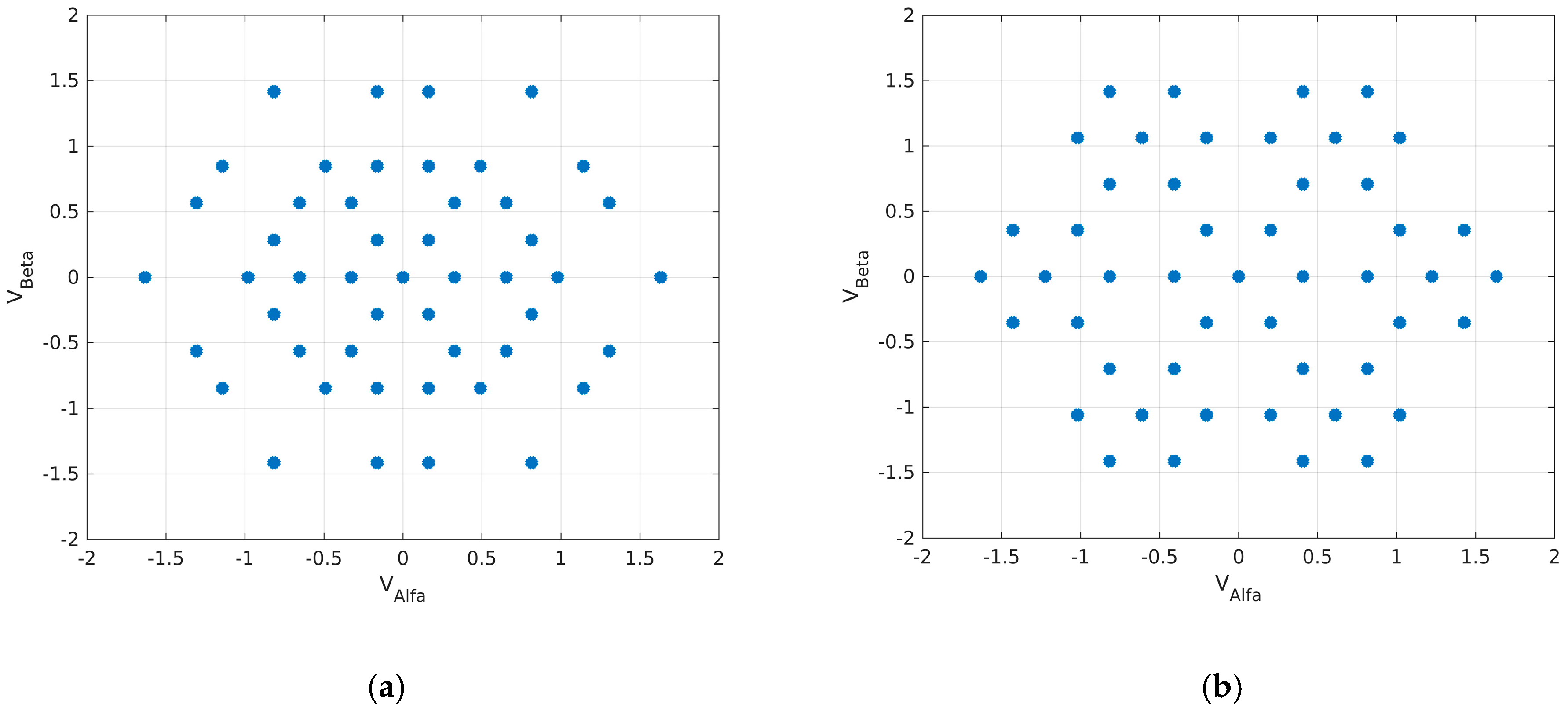
3.3. Impact of a Voltage Sag on the Voltage Vectors
3.4. Voltage Vector Modulator Implementation
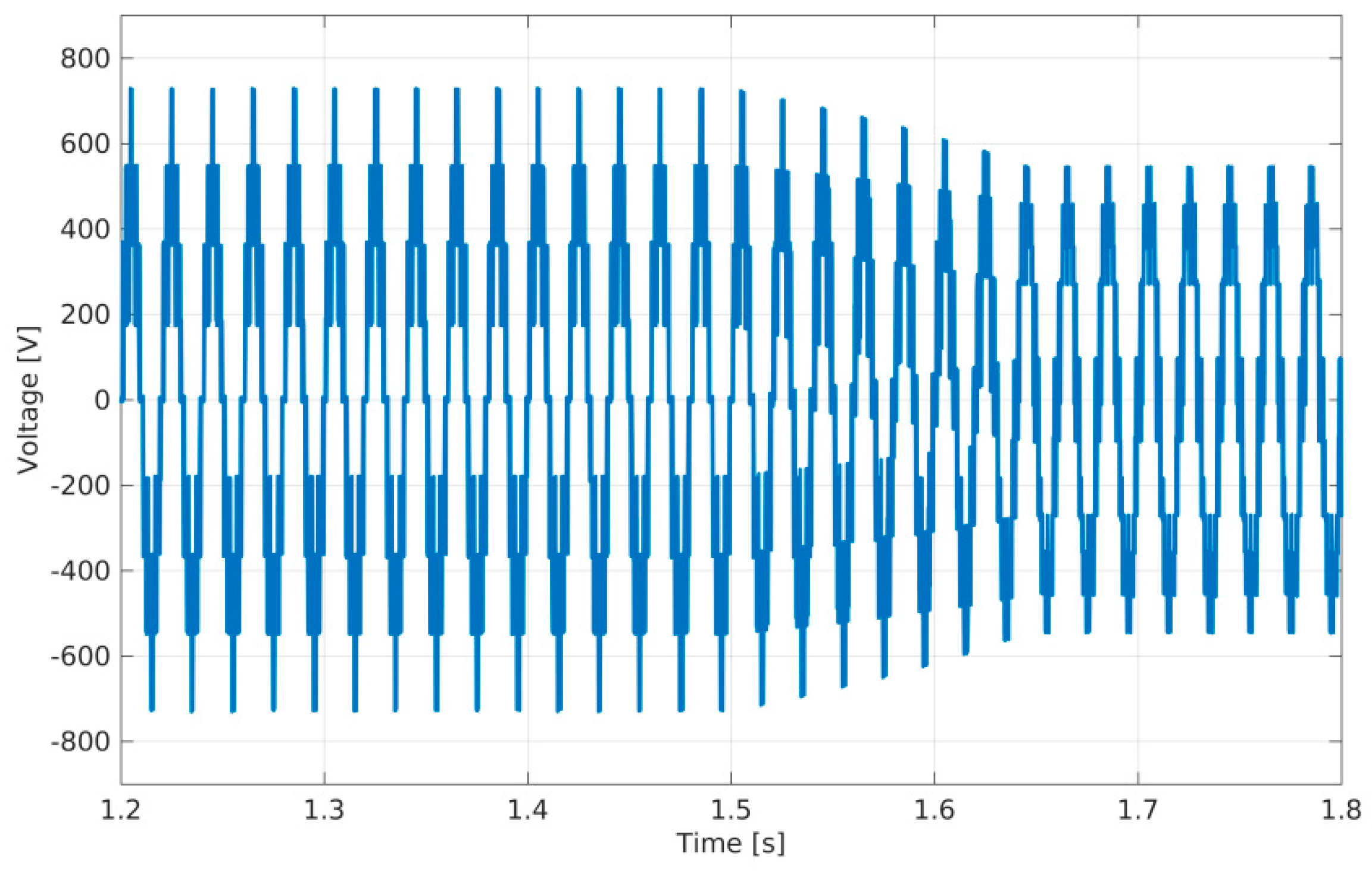
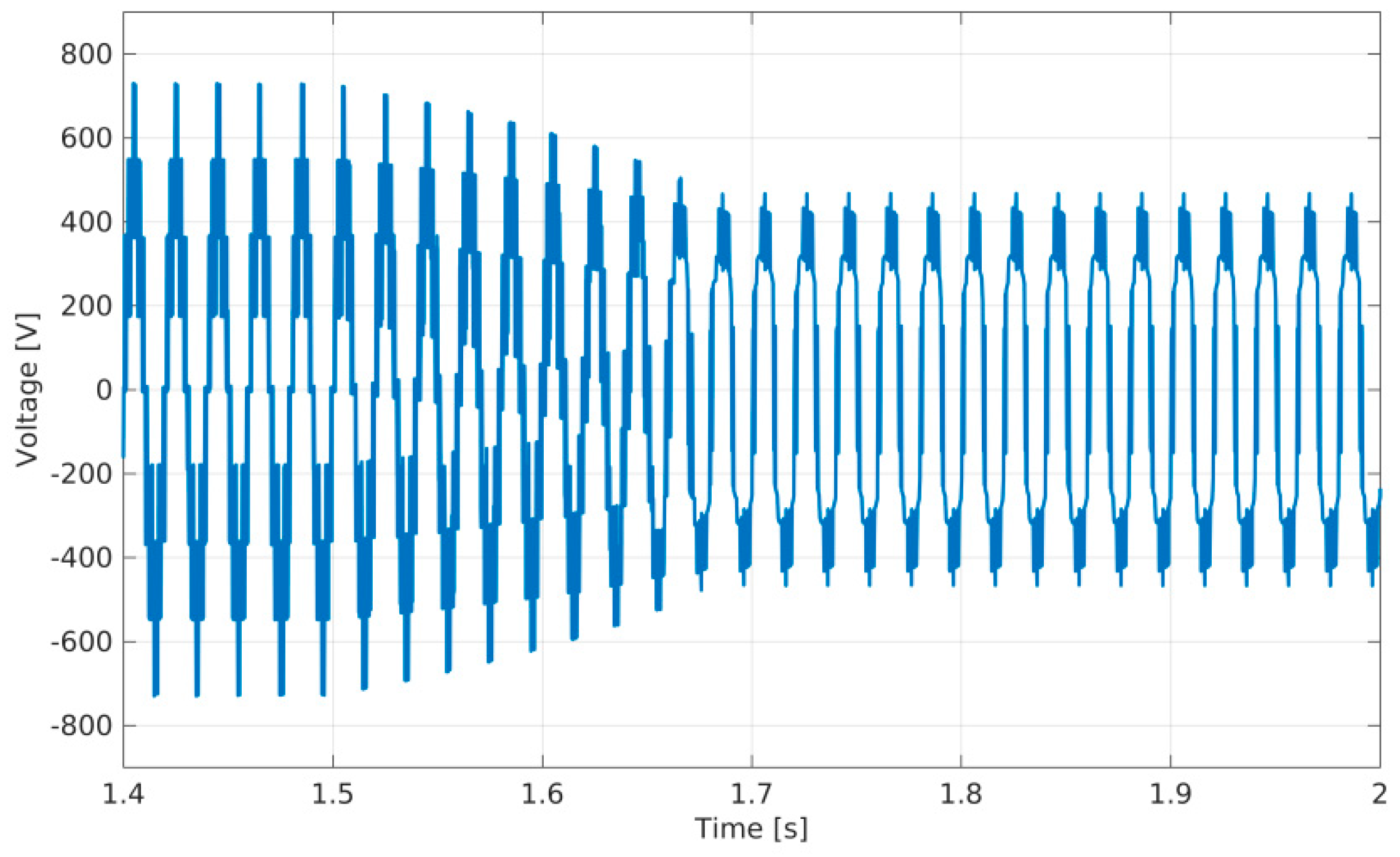
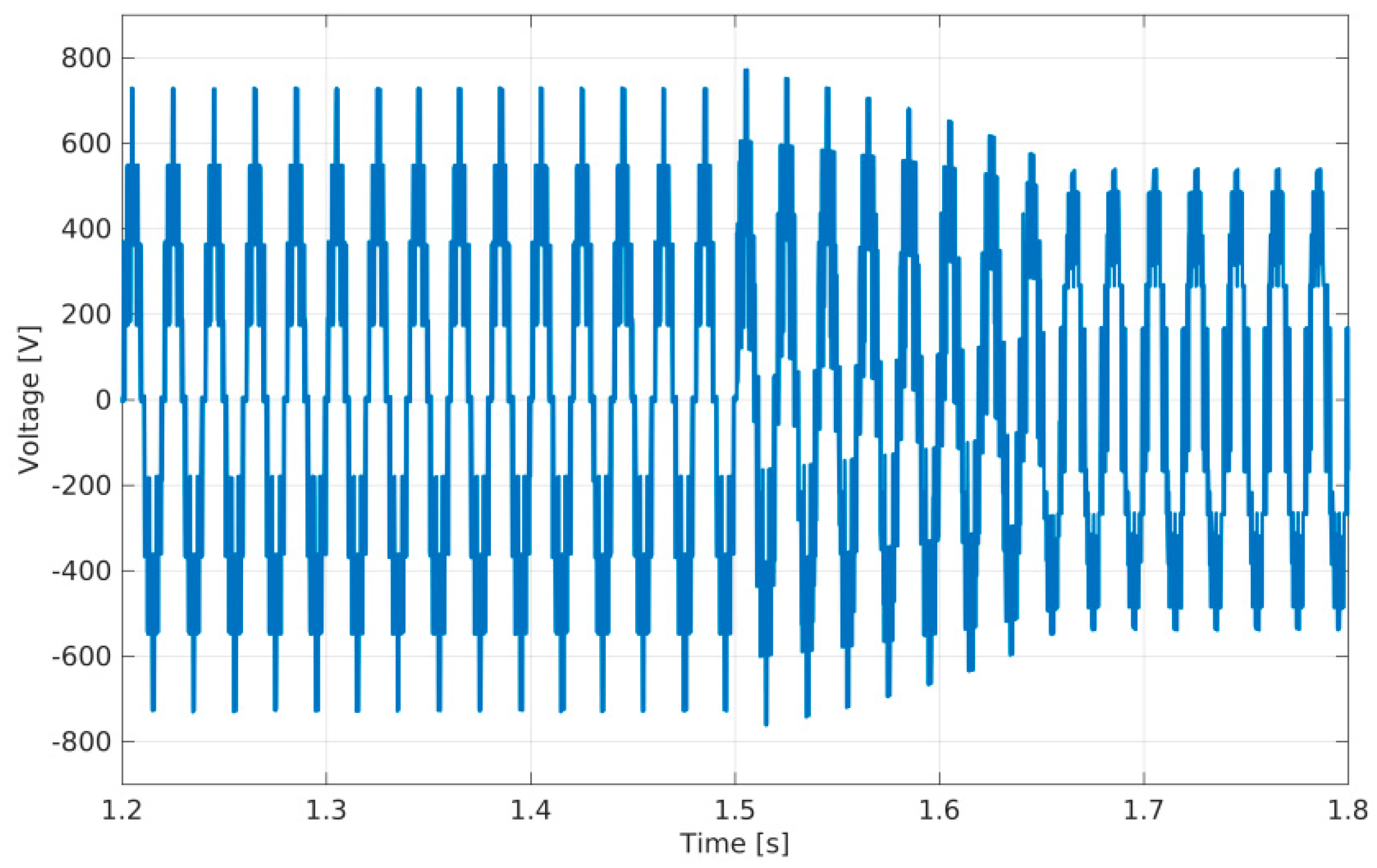
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bollen, M.H. Understanding Power Quality Problems—Voltages and Interruptions; IEEE Press: Piscataway, NJ, USA, 1999. [Google Scholar]
- Electric Power Research Institute. The Cost of Power Disturbances to Industrial and Digital Economy Companies; EPRI: Palo Alto, CA, USA, 2001. [Google Scholar]
- Almeida, A.; Ferreira, F.; Both, D. Technical and Economical Considerations in The Application of Variable-Speed Drives With Electric Motor Systems. IEEE Trans. Ind. Appl. 2005, 41, 188–199. [Google Scholar] [CrossRef]
- IEEE Std. 1159-1995. Recommended Practice for Monitoring Electric Power Quality; IEEE PRESS: New York, NY, USA, 1995. [Google Scholar]
- IEC 1000-2-1-1990-Part 2: Environment-Sedion 1. Description of the environment-Electromagnetic environment for low-frequency conduded disturbances and signaling in public low-voltage power supply systems. In Proceedings of the 1999 IEEE Transmission and Distribution Conference, New Orleans, LA, USA, 11–16 April 1999.
- SEMI F47-0706. Specification for Semiconductor Processing Equipment Voltage Sag Immunity, August 2012. Available online: http://www.semi.org (accessed on 12 March 2019).
- IEC 61000-4-34, Ed. 1.0. Electromagnetic Compatibility–Part 4-34: Testing and Measurement Techniques-Voltage Dips, Short Interruptions and Voltage Variations Immunity Tests for Equipment with Input Current More Than 16 a Per Phase; IEC: Geneva, Switzerland, 2005. [Google Scholar]
- IEC 61800-3, Ed. 2.1. Adjustable Speed Electrical Power Drive Systems-Part 3: EMC Requirements and Specific Test Methods; IEC: Geneva, Switzerland, 2012. [Google Scholar]
- Lee, K.; Jahns, T.M.; Lipo, T.A.; Venkataramanan, G.; Berkopec, W.E. Impact of Input Voltage Sag and Unbalance on DC-Link Inductor and Capacitor Stress in Adjustable-Speed Drives. IEEE Trans. Ind. Appl. 2008, 44, 495–504. [Google Scholar] [CrossRef]
- Lee, K.; Jahns, T.M.; Novotny, D.W.; Lipo, T.A.; Berkopec, W.E.; Blasko, V. Impact of Inductor Placement on the Performance of Adjustable-Speed Drives Under Input Voltage Unbalance and Sag Conditions. IEEE Trans. Ind. Appl. 2006, 42, 1230–1240. [Google Scholar] [CrossRef]
- Llerena, M.T.; Homrich, R.P.; Filho, A.F.F. Estimation of the Induction Machine Behaviour Subjected to Voltage Sags. In Proceedings of the 3rd IET International Conference on Power Electronics, Machines and Drives, London, UK, 4–6 April 2006; pp. 286–290. [Google Scholar]
- Pietilainen, K.; Harnefors, L.; Petersson, A.; Nee, H. DC-Link Stabilization and Voltage Sag Ride-Through of Inverter Drives. IEEE Trans. Ind. Electron. 2006, 53, 1261–1268. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, F.J.T.E.; Almeida, A.T.; Baoming, G. Impact of Voltage Sags and Continuous Unbalance on Variable-Speed Drives. In Proceedings of the XIX International Conference on Electrical Machines, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar]
- Petronijević, M.; Veselić, B.; Mitrović, N.; Kostić, V.; Jeftenić, B. Comparative Study of Unsymmetrical Voltage Sag Effects on Adjustable Speed Induction Motor Drives. ET Electr. Power Appl. 2011, 5, 432–442. [Google Scholar] [CrossRef]
- Tallam, R.M.; Lukaszewski, R.A. Voltage Sag and Unbalance Generator for Power Quality Testing of Adjustable Speed Drives. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 4565–4571. [Google Scholar]
- Bogarra, S.; Monjo, L.; Saura, J.; Córcoles, F.; Pedra, J. Comparison of simplified models for voltage-source-inverter-fed adjustable-speed drive during voltage sags when the during-event continue mode of operation is active. IET Electr. Power Appl. 2014, 8, 329–341. [Google Scholar] [CrossRef]
- Córcoles, F.; Bogarra, S.; Pedra, J.; Luna, A. Discrete Fault-Clearing Instant Influence on the Simulation of Voltage-Source-Inverter-Fed Adjustable-Speed Drives Subjected to Voltage Sags. IET Electr. Power Appl. 2011, 5, 465–477. [Google Scholar] [CrossRef]
- Martin, P.; Jiří, F. Electric Drive with Voltage-Fed Inverter with Regard to Influence of Voltage Sag. In Proceedings of the 16th International Conference on Mechatronics, Brno, Czech Republic, 3–5 December 2014; pp. 666–671. [Google Scholar]
- Epperly, R.; Hoadley, F. Considerations when applying ASD’s in continuous processes. IEEE Trans. Ind. Appl. 1997, 33, 389–395. [Google Scholar] [CrossRef]
- Fatu, M.; Blaabjerg, F.; Boldea, I. Grid to Standalone Transition Motion-Sensorless Dual-Inverter Control of PMSG With Asymmetrical Grid Voltage Sags and Harmonics Filtering. IEEE Trans. Power Electron. 2014, 29, 3463–3472. [Google Scholar] [CrossRef]
- Van Zyl, A.; Spee, R.; Faveluke, A.; Bhowmik, S. Voltage sag ride through for adjustable-speed drives with active rectifiers. IEEE Trans. Ind. Appl. 1997, 34, 1270–1277. [Google Scholar] [CrossRef]
- Ramela, K.R.; Kumar, V.S. Simulation of ride through capability of adjustable speed drive for type A and type B voltage sags and well using Buck-Boost converter. In Proceedings of the International Conference on Recent Advancements in Electrical, Electronics and Control Engineering, Sivakasi, India, 15–17 December 2011; pp. 506–511. [Google Scholar]
- Zhou, Y.; Huang, W.; Hong, F. Single-Phase Input Variable-Speed AC Motor System Based on an Electrolytic Capacitor-Less Single-Stage Boost Three-Phase Inverter. IEEE Trans. Power Electron. 2016, 31, 7043–7052. [Google Scholar] [CrossRef]
- Yin, Z.; Han, M.; Du, Y.; Zhang, Z. A Practical Approach for Ride Through of Super Capacitor Energy Storage Based ASD System. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exhibition, Dallas, TX, USA, 2–5 May 2006; pp. 744–746. [Google Scholar]
- Deswal, S.; Dahiya, R.; Jain, D. Ride-through capability of adjustable-speed drive during various power quality events using supercapacitor. In Proceedings of the IEEE Electrical Power & Energy Conference, Montreal, QC, Canada, 22–23 October 2009; pp. 1–6. [Google Scholar]
- Rodriguez, J.; Lai, J.S.; Peng, F.Z. Multilevel inverters: A survey of topologies, control and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef]
- Alavi, O.; Viki, A.H.; Shamlou, S. A Comparative Reliability Study of Three Fundamental Multilevel Inverters Using Two Different Approaches. Electronics 2016, 5, 18. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J. Optimized Modeling and Control Strategy of the Single-Phase Photovoltaic Grid-Connected Cascaded H-bridge Multilevel Inverter. Electronics 2018, 7, 207. [Google Scholar] [CrossRef]
- Yang, D.; Yin, L.; Wu, S.X.N. Power and Voltage Control for Single-Phase Cascaded H-Bridge Multilevel Converters under Unbalanced Loads. Energies 2018, 11, 2435. [Google Scholar] [CrossRef]
- Leng, S.; Haque, A.; Perera, N.; Knight, A.M.; Salmon, J. Smart Grid Connection of an Induction Motor Using a Three-Phase Floating H-bridge System as a Series Compensator. IEEE Trans. Power Electron. 2016, 31, 7053–7064. [Google Scholar] [CrossRef]
- Stemmler, H.; Guggenbach, P. Configurations of high-power voltage source inverter drives. In Proceedings of the European Conference on Power Electronics and Applications, Brighton, UK, 13–16 September 1993; pp. 7–14. [Google Scholar]
- Chu, L.; Jia, Y.; Chen, D.; Xu, N.; Wang, Y.; Tang, X.; Xu, Z. Research on Control Strategies of an Open-End Winding Permanent Magnet Synchronous Driving Motor (OW-PMSM)-Equipped Dual Inverter with a Switchable Winding Mode for Electric Vehicles. Energies 2017, 10, 616. [Google Scholar] [CrossRef]
- Pires, V.F.; Martins, J.F.; Hao, C. Dual-Inverter for Grid-Connected Photovoltaic System: Modeling and Sliding Mode Control. Sol. Energy 2012, 86, 2106–2115. [Google Scholar] [CrossRef]
- Baiju, M.R.; Mohapatra, K.K.; Kanchan, R.S.; Gopakumar, K. A dual two-level inverter scheme with common mode voltage elimination for an induction motor drive. IEEE Trans. Power Electron. 2004, 19, 794–805. [Google Scholar] [CrossRef]
- Somasekhar, V.T.; Srinivas, S.; Kumar, K.K. Effect of Zero-Vector Placement in a Dual-Inverter Fed Open-End Winding Induction-Motor Drive With a Decoupled Space-Vector PWM Strategy. IEEE Trans. Ind. Electron. 2008, 55, 2497–2505. [Google Scholar] [CrossRef]
- Pires, V.F.; Foito, D.; Silva, J.F. Fault-Tolerant Multilevel Topology Based on Three Phase H-Bridge Inverters for Open-End Winding Induction Motor Drives. IEEE Trans. Energy Convers. 2017, 32, 895–902. [Google Scholar] [CrossRef]
- Rajeevan, P.P.; Sivakumar, K.; Gopakumar, K.; Patel, C.; Abu-Rub, H. A Nine-Level Inverter Topology for Medium-Voltage Induction Motor Drive With Open-End Stator Winding. IEEE Trans. Ind. Electron. 2013, 60, 3627–3636. [Google Scholar] [CrossRef]
- Kieferndorf, F.; Basler, M.; Serpa, L.A.; Fabian, J.-H.; Coccia, A.; Scheuer, G.A. ANPC-5L Technology Applied to Medium Voltage Variable Speed Drives Applications. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Pisa, Italy, 14–16 June 2010; pp. 1718–1725. [Google Scholar]
- Krause, P.; Wasynczuk, O.; Sudhoff, S.D.; Pekarek, S. Analysis of Electric Machinery and Drive Systems; IEEE Press: Piscataway, NJ, USA, 2013. [Google Scholar]
- Blaschke, F. The principle of field-orientation as applied to the new transvector closed-loop control system for rotating machines. Siemens Rev. 1972, 39, 217–220. [Google Scholar]
- Gao, W.; Hung, J. Variable structure control of nonlinear systems: A new approach. IEEE Trans. Ind. Electron. 1993, 40, 45–55. [Google Scholar]
- Silva, J.F. Sliding mode control design of drive and regulation electronics for power converters. Power Electron. J. Circuits Syst. Comput. 1995, 5, 355–371. [Google Scholar] [CrossRef]











| Topology | Structure | Extra Converter | Storage Elements | Boost Capability | Multilevel Operation | Immunity to Voltage Sag |
|---|---|---|---|---|---|---|
| Diode Rectifier | Diode Rectifier (4 or 6 Diodes) + Three-Phase Classical Inverter (6 Switches) | No | Very Large DC Electrolytic Capacitor or Supercapacitor or Batteries | No | No | Dependent or the Capacity of the extra storage elements |
| From Ref. [22] | Diode Rectifier (4 or 6 Diodes + DC–DC Buck-Boost Converter (1 Diode + 1 Switch) + Three-Phase Inverter (6 Switches) | Yes | Extra 1 Inductor | Yes | No | High |
| Active Rectifier (Bask-to-Back Inverters) | Single or Three-Phase Rectifier (4 or 6 Switches) + Two-level Three phase Inverters (6 Switches) | No | No | Yes | No | High |
| ANPC-5L [38] | Multilevel Rectifier (24 Switches) + Multilevel Inverter (24 Switches) | No | Four Capacitors | No | Yes | High |
| Proposed | Diode Rectifier (4 or 6 diodes) or active rectifier (4 or 6 Switches) + Two two-level Three-Phase Inverters (12 Switches) | No | One Classical DC Capacitor | Yes | Yes | Very High |
| S11 | S12 | S13 | S21 | S22 | S23 | Vector | Vα | Vβ |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 2 | 0.482 VDC | 0.707 VDC |
| 0 | 1 | 0 | 0 | 1 | 1 | 20 | 0.482 VDC | 0.707 VDC |
| 1 | 0 | 0 | 1 | 0 | 1 | 38 | 0.482 VDC | 0.707 VDC |
| 1 | 1 | 0 | 0 | 0 | 0 | 49 | 0.482 VDC | 0.707 VDC |
| 1 | 1 | 0 | 1 | 1 | 1 | 56 | 0.482 VDC | 0.707 VDC |
| 1 | 1 | 1 | 0 | 0 | 1 | 58 | 0.482 VDC | 0.707 VDC |
| S11 | S12 | S13 | S21 | S22 | S23 | Vector | Vα | Vβ |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 2 | 0.326 VDC | 0.565 VDC |
| 0 | 1 | 0 | 0 | 1 | 1 | 20 | 0.245 VDC | 0.707 VDC |
| 1 | 0 | 0 | 1 | 0 | 1 | 38 | 0.489 VDC | 0.565 VDC |
| 1 | 1 | 0 | 0 | 0 | 0 | 49 | 0.408 VDC | 0.707 VDC |
| 1 | 1 | 0 | 1 | 1 | 1 | 56 | 0.408 VDC | 0.707 VDC |
| 1 | 1 | 1 | 0 | 0 | 1 | 58 | 0.326 VDC | 0.565 VDC |
| −3 | −2 | −1 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|---|
| −2 | 21, 30 | 22 | 22 | 18, 54 | 50 | 50 | 34, 52 |
| −1 | 21, 30 | 21, 30 | 6, 17, 24 26, 52, 62 | 18, 54 | 2, 20, 38 49, 56, 58 | 34, 52 | 34, 52 |
| 0 | 29 | 5, 14, 23 25, 32, 61 | 5, 14, 23 25, 32, 61 | 1, 8, 10, 19, 28, 37 46, 55, 57, 64 | 4, 33, 40 42, 51, 60 | 4, 33, 40 42, 51, 60 | 36 |
| 1 | 13, 31 | 13, 31 | 7, 9, 16 27, 45, 63 | 11, 47 | 3, 12, 39 41, 48, 59 | 35, 44 | 35, 44 |
| 2 | 13, 31 | 15 | 15 | 11, 47 | 43 | 43 | 35, 44 |
| Parameters | Value |
|---|---|
| rs | 0.21 Ω |
| rr | 1.32 Ω |
| Lm | 64.2 mH |
| Ls | 65.2 mH |
| Lr | 65.2 mH |
| J | 0.08 Kg m2 s−1 |
| p | 2 |
| Parameters | Value |
|---|---|
| Grid phase-neutral RMS voltage (Vs) | 230 V |
| Input filter (L) | 0.1 mH |
| Inputfilter (R) | 0.1 Ω |
| Capacitor of the grid connected inverter (Co) | 9.2 mF |
| Capacitor of the floating inverter (Cflo) | 9.2 mF |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pires, V.F.; Monteiro, J.; Silva, J.F. Dual 3-Phase Bridge Multilevel Inverters for AC Drives with Voltage Sag Ride-through Capability. Energies 2019, 12, 2324. https://doi.org/10.3390/en12122324
Pires VF, Monteiro J, Silva JF. Dual 3-Phase Bridge Multilevel Inverters for AC Drives with Voltage Sag Ride-through Capability. Energies. 2019; 12(12):2324. https://doi.org/10.3390/en12122324
Chicago/Turabian StylePires, Vitor Fernão, Joaquim Monteiro, and José Fernando Silva. 2019. "Dual 3-Phase Bridge Multilevel Inverters for AC Drives with Voltage Sag Ride-through Capability" Energies 12, no. 12: 2324. https://doi.org/10.3390/en12122324





