Investigation of Analysis Methods for Pulse Decay Tests Considering Gas Adsorption
Abstract
:1. Introduction
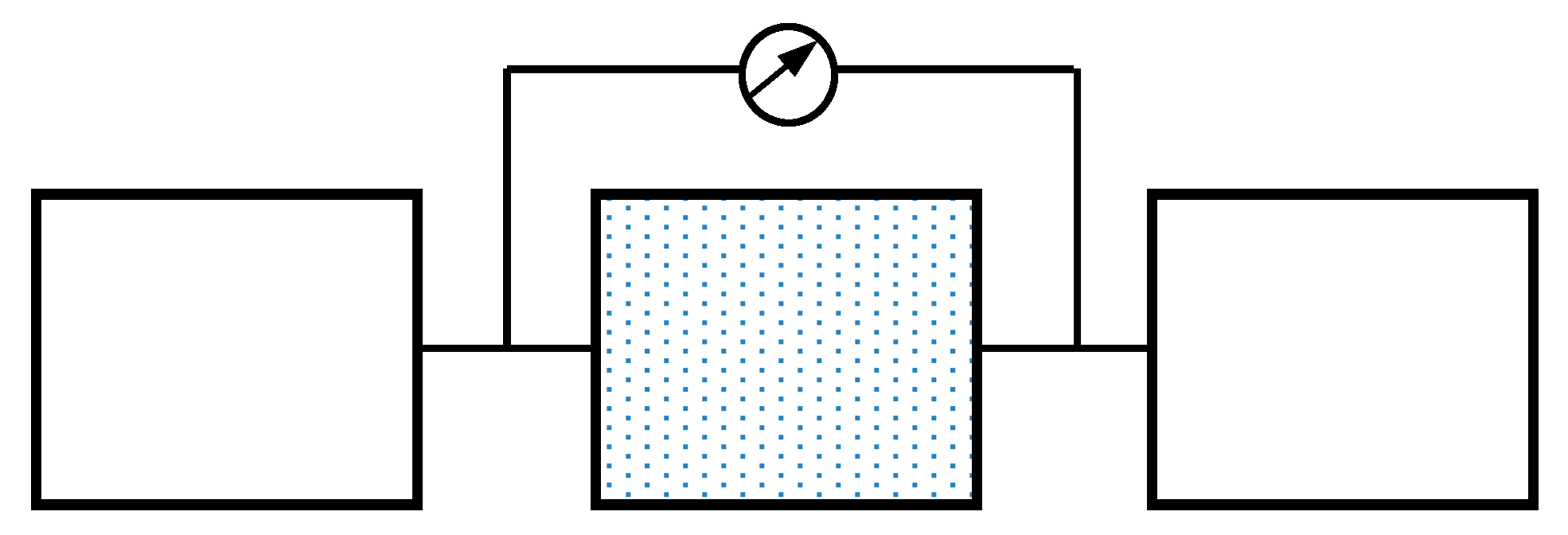
2. Mathematical Models and the Numerical Method
2.1. Equilibrium Sorption Model
2.2. Non-Equilibrium Sorption Model
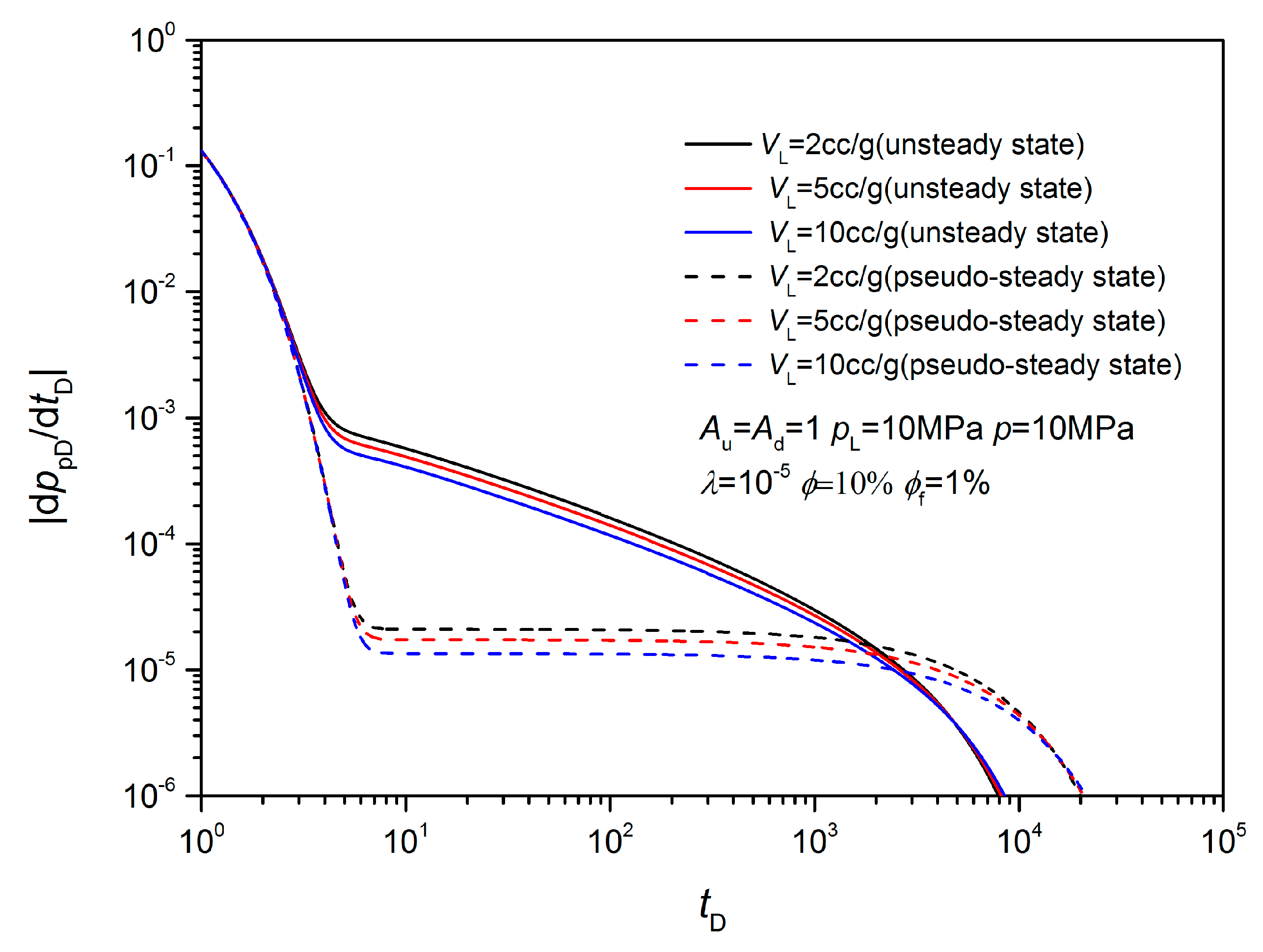
3. Sensitivity Analysis
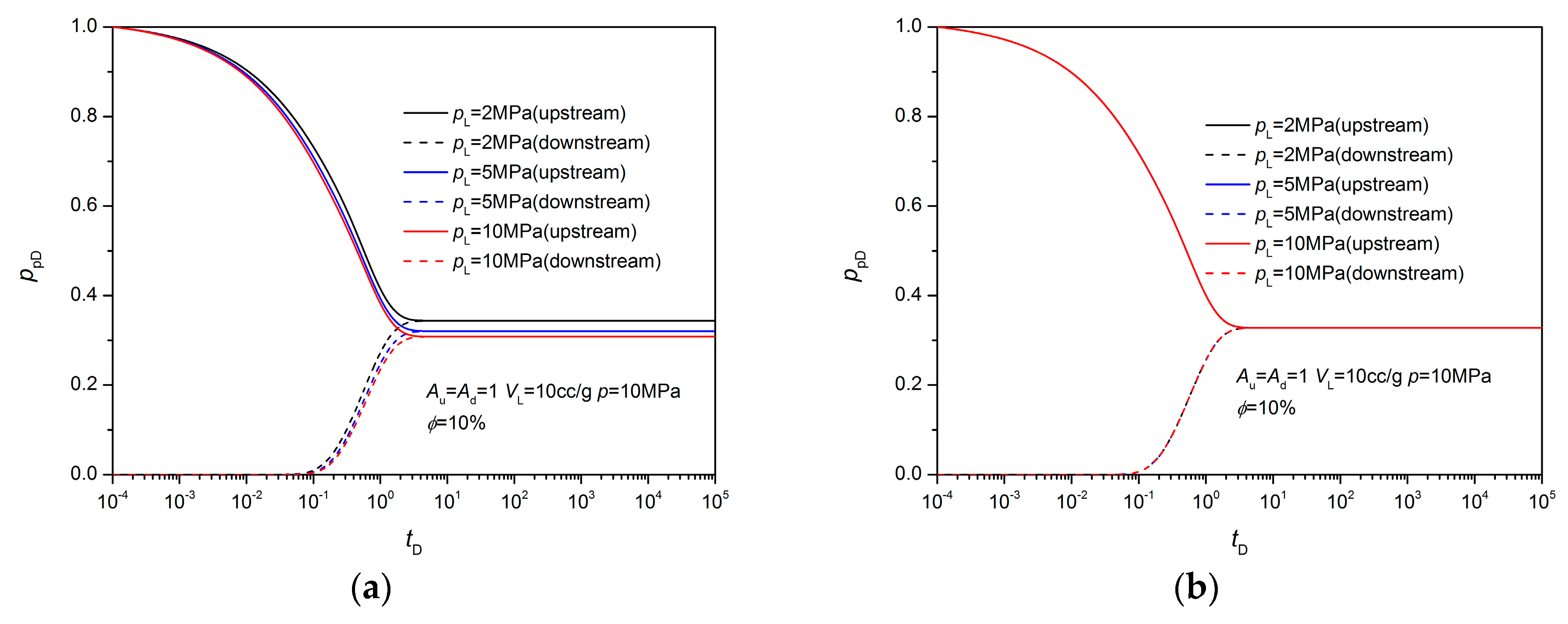
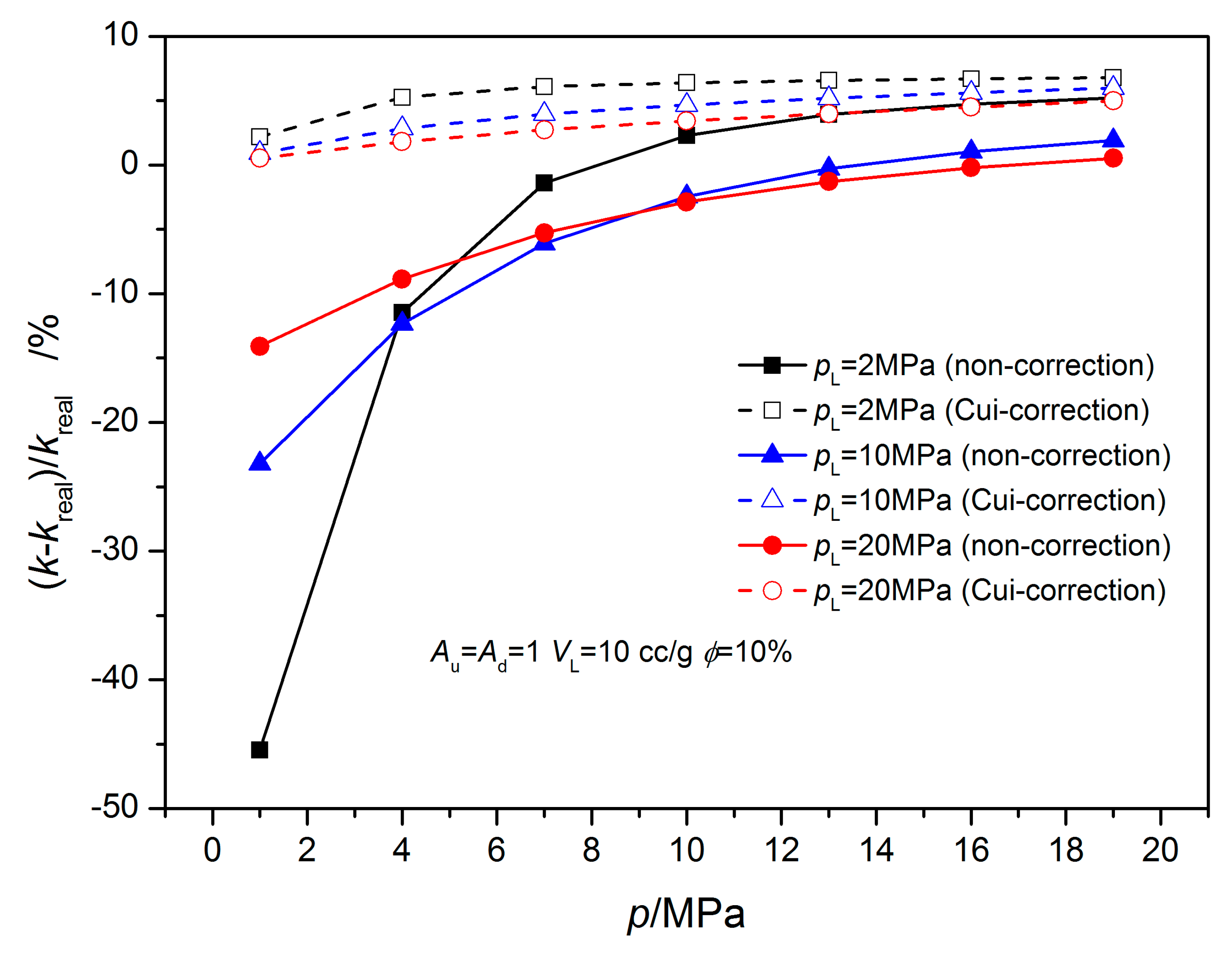
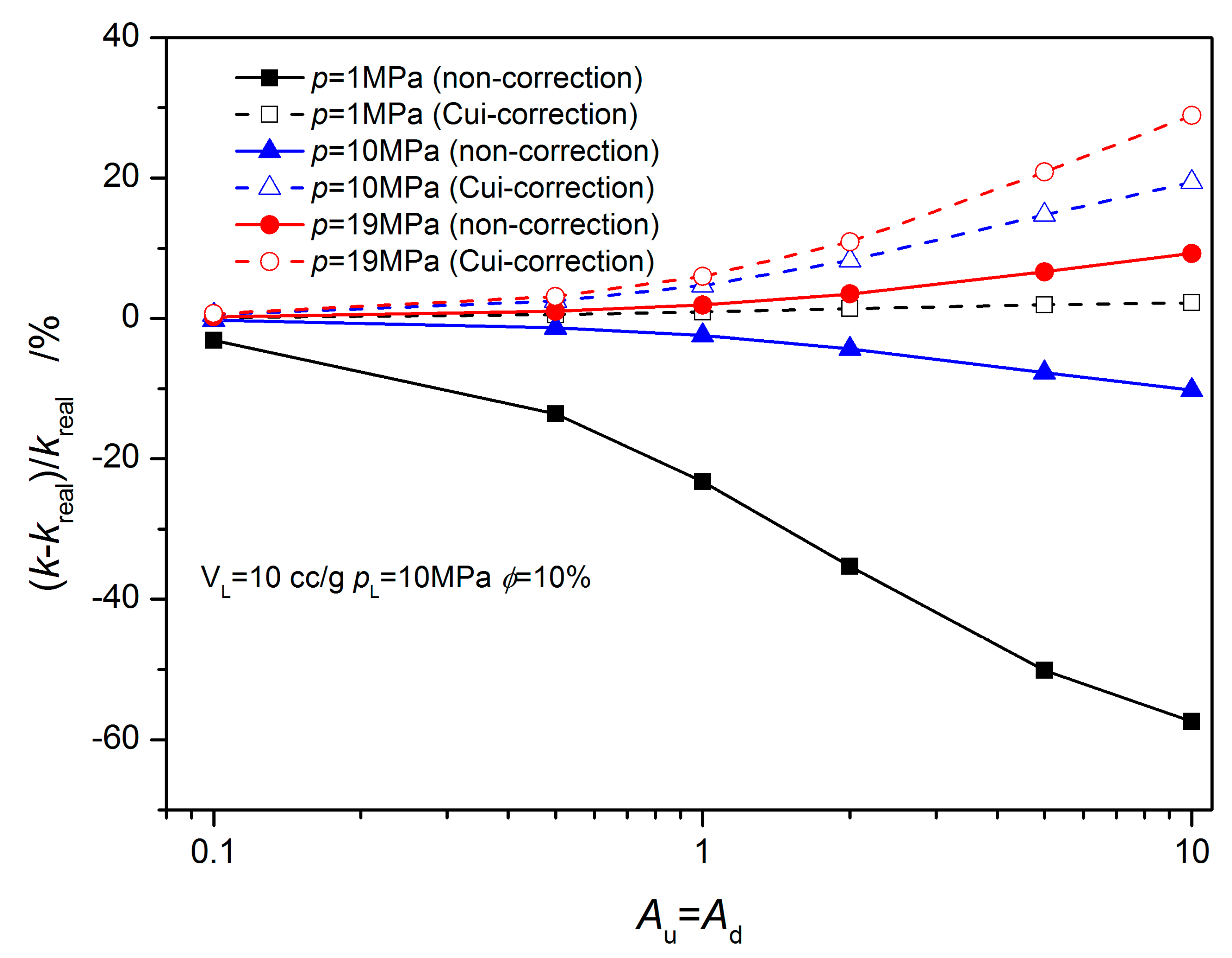
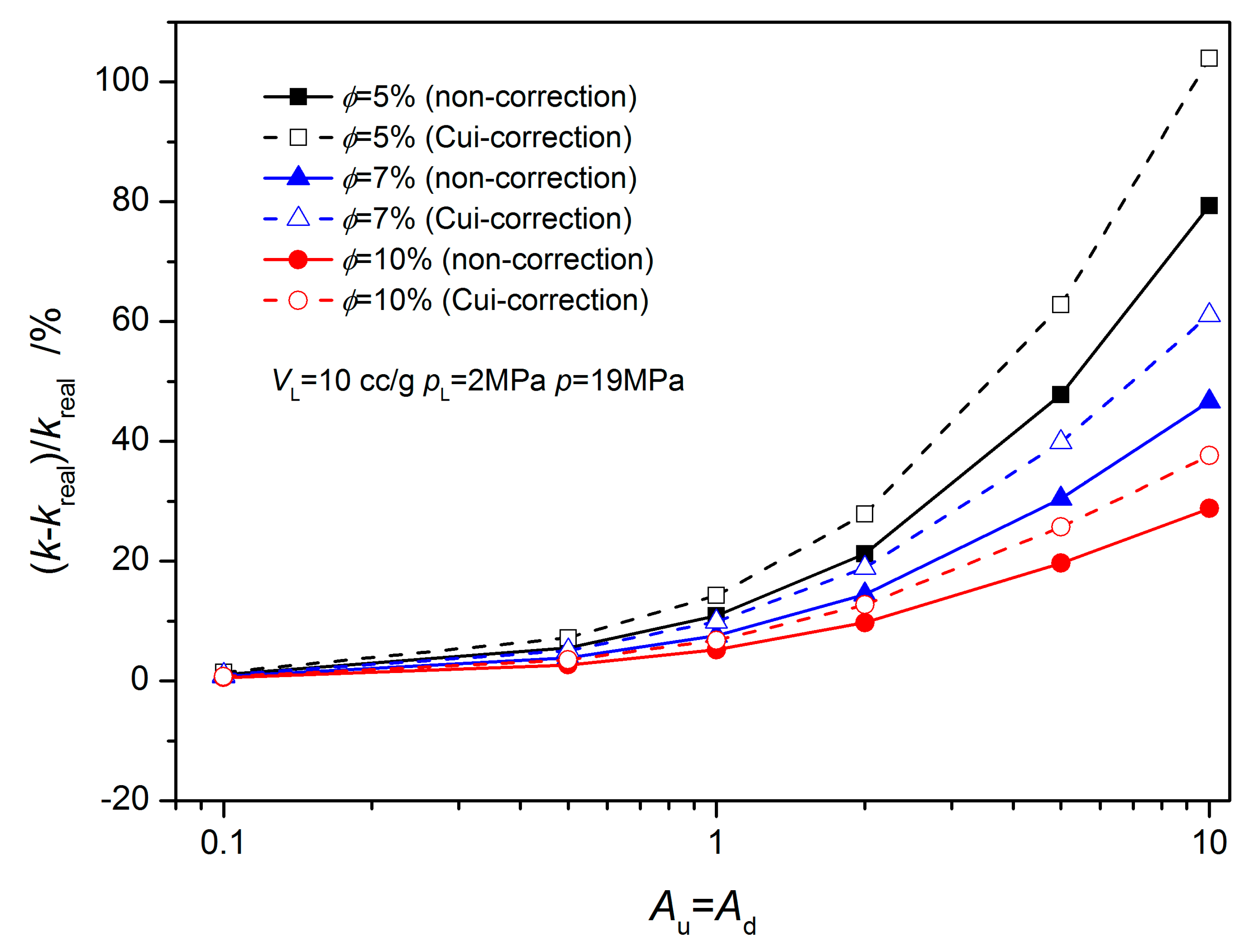
3.1. Equilibrium Sorption Model
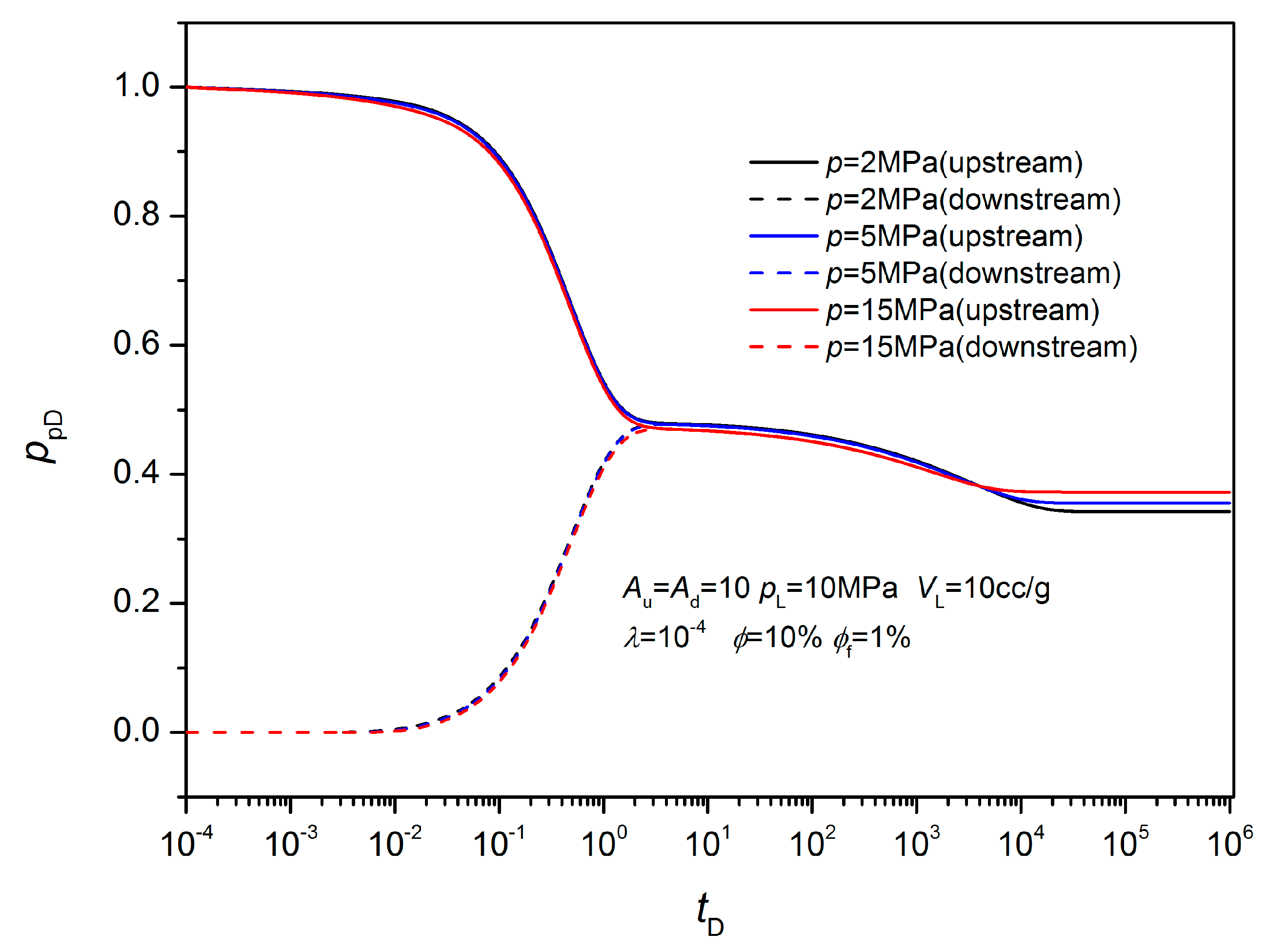
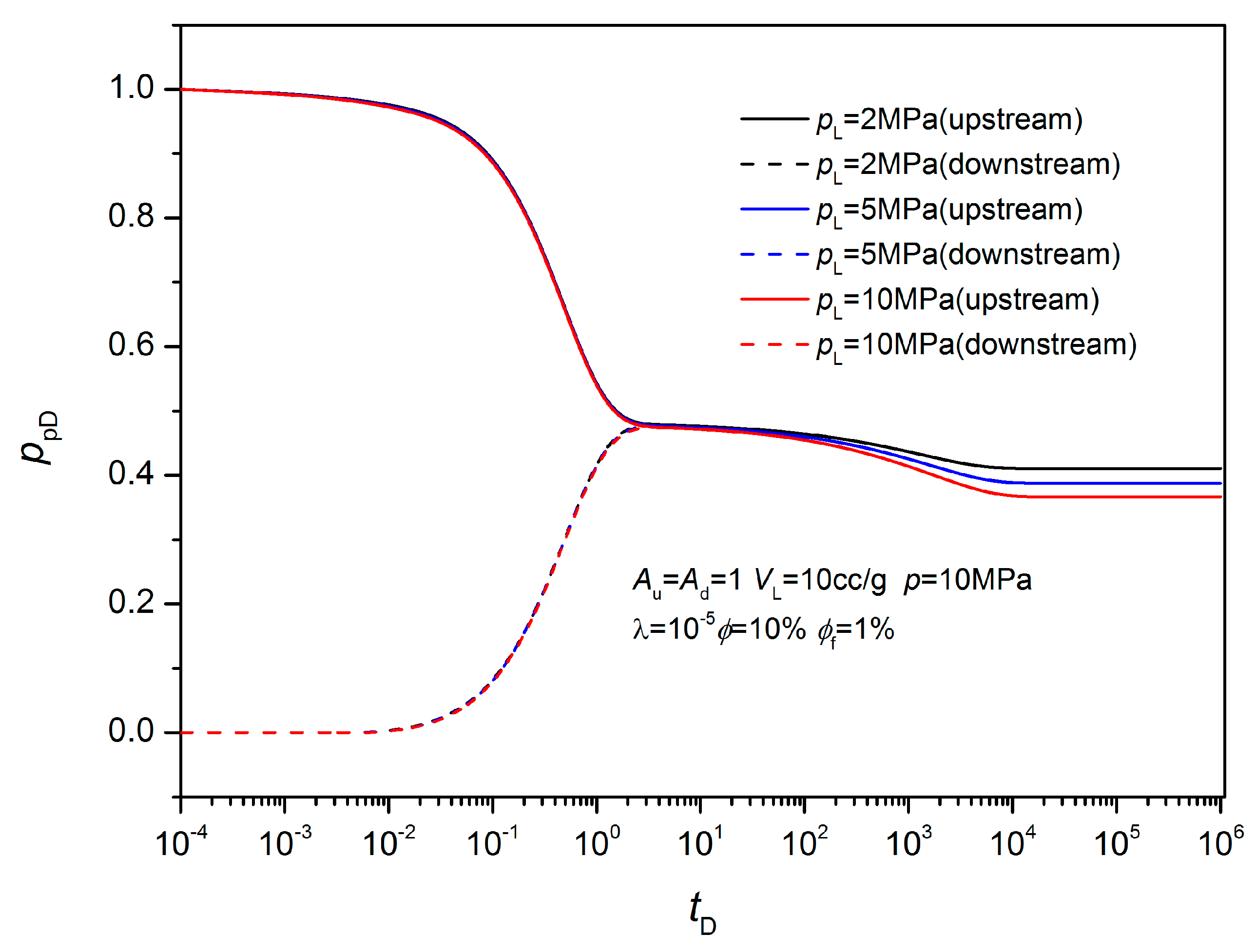
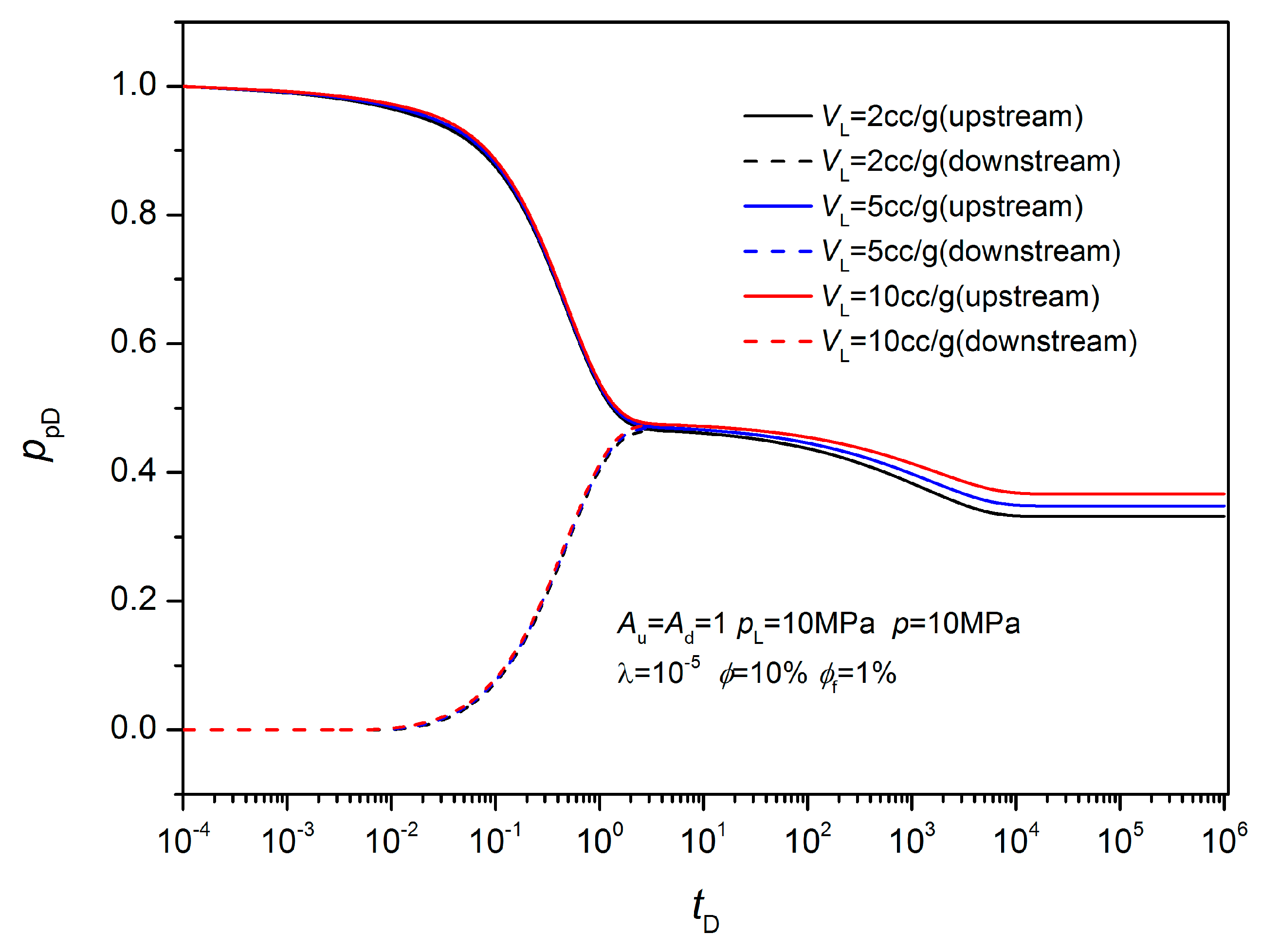
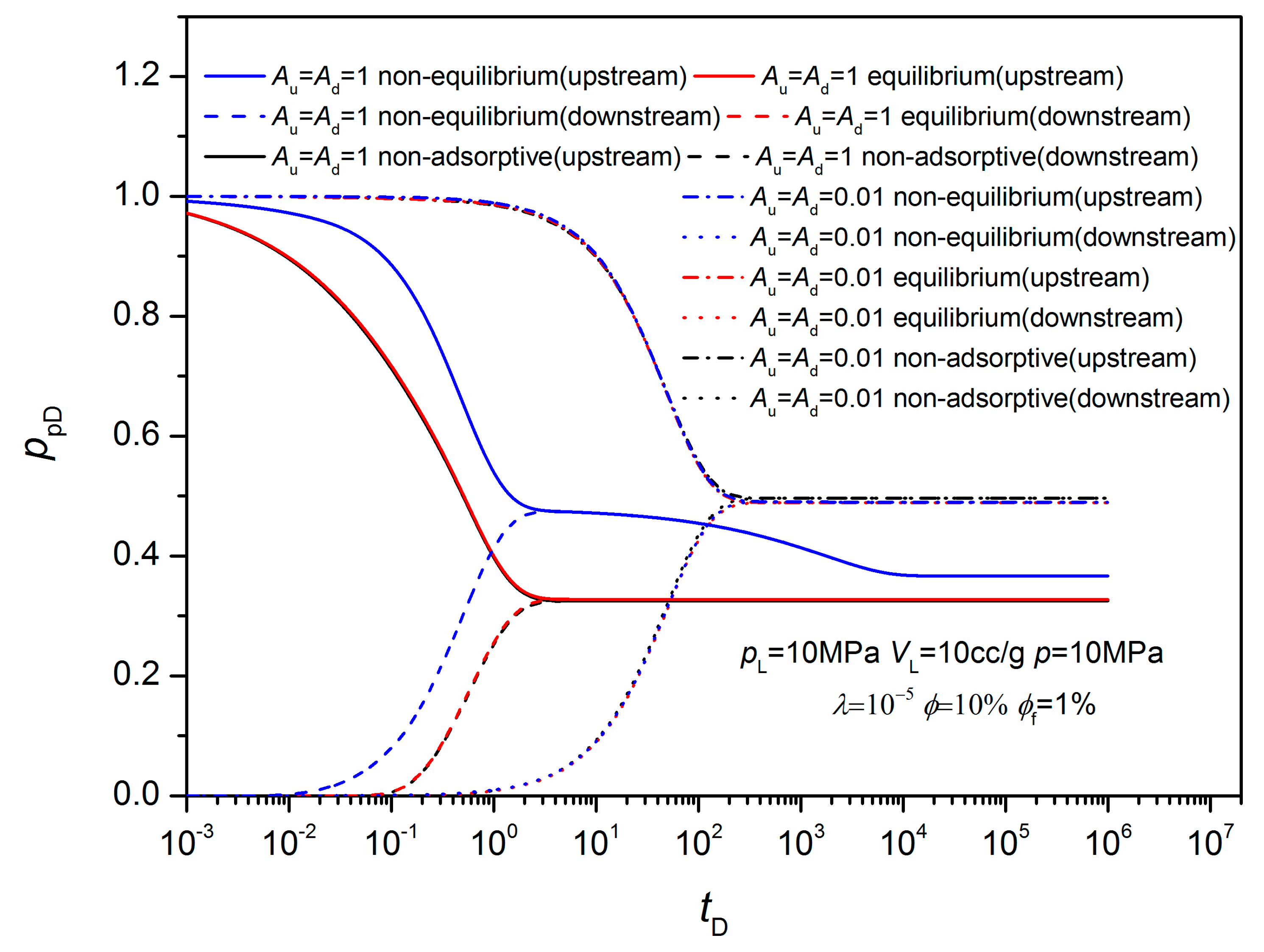
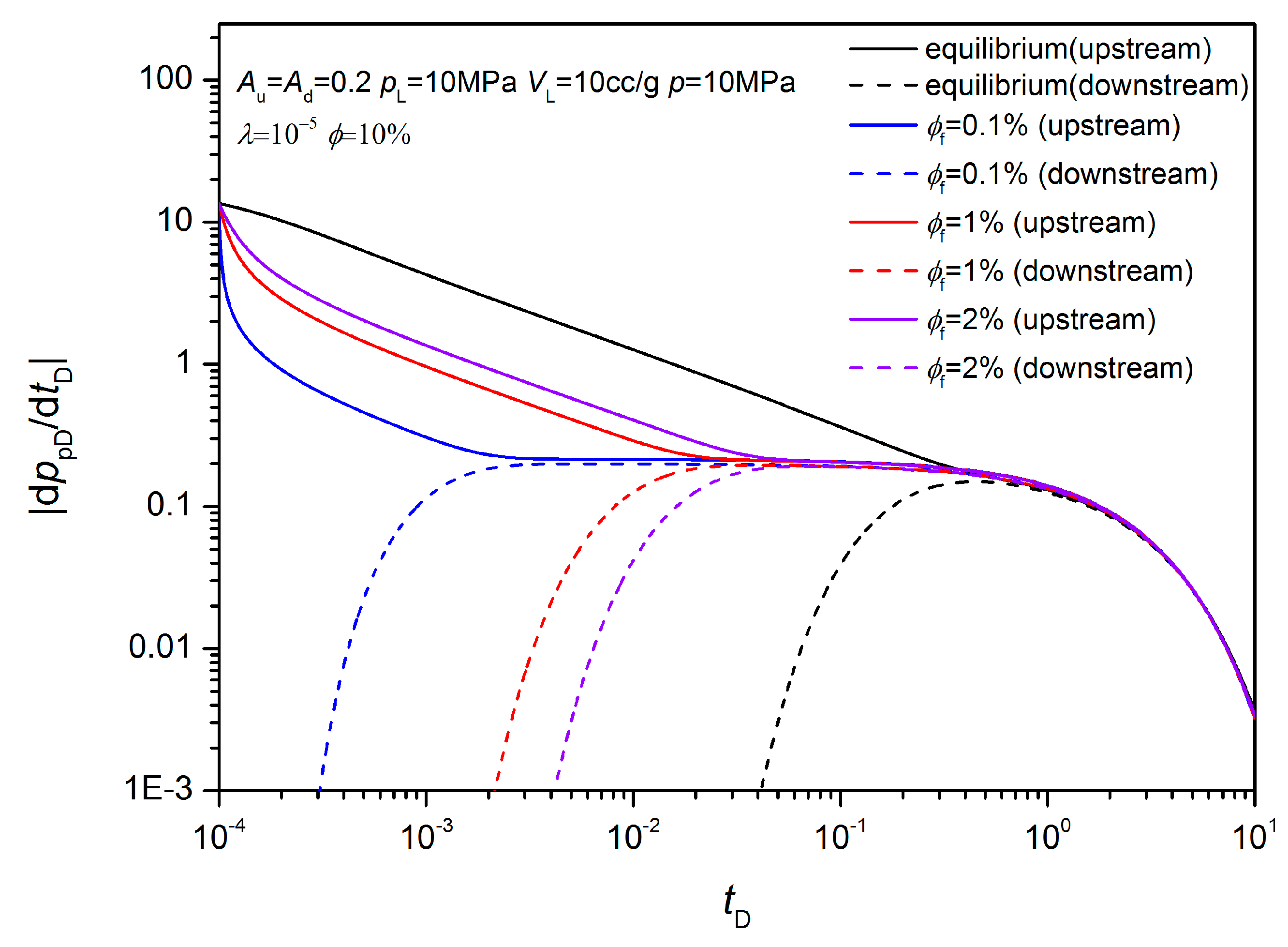
3.2. Non-Equilibrium Sorption Model
4. The Analysis Method for Adsorptive Gas
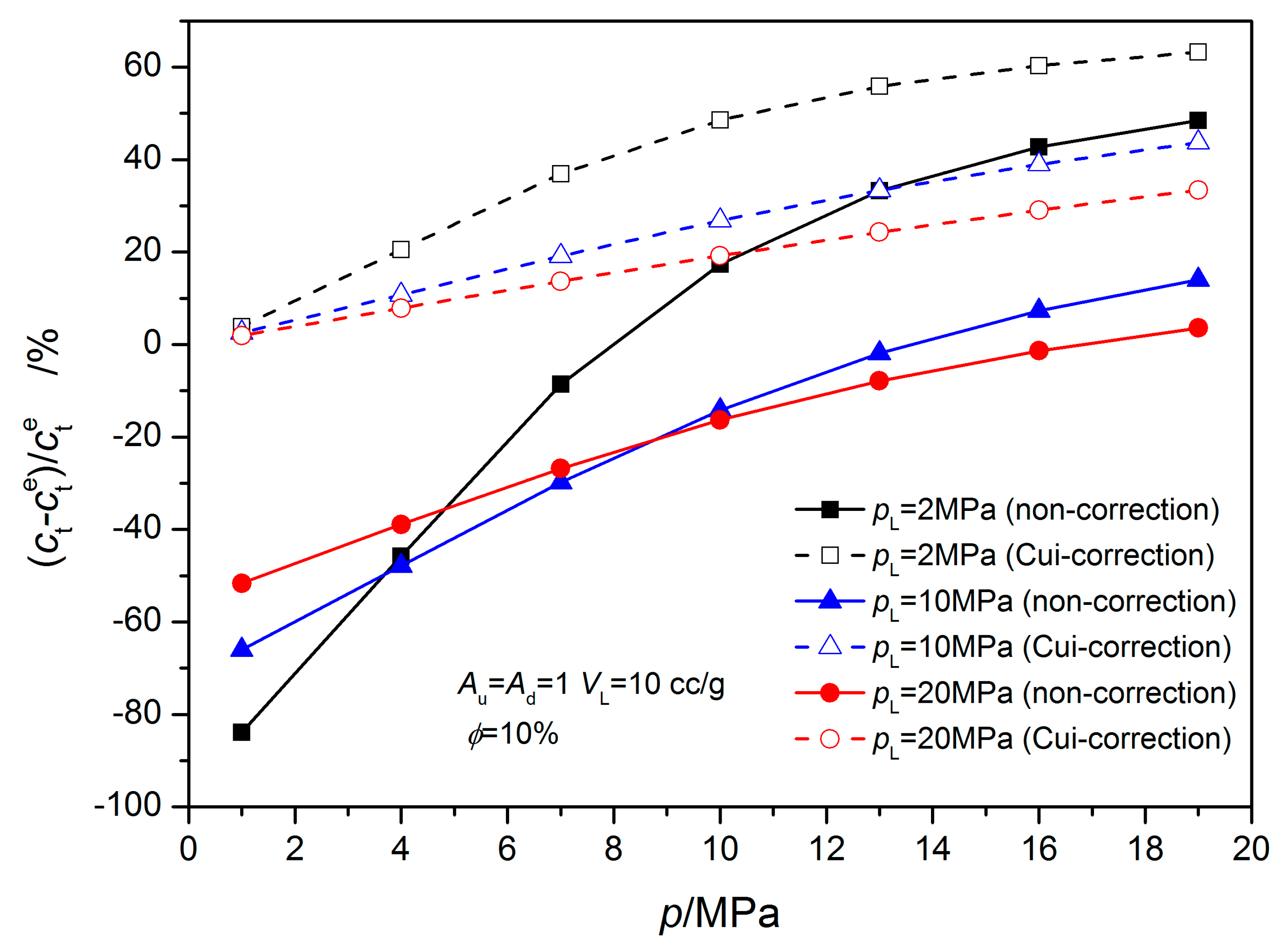
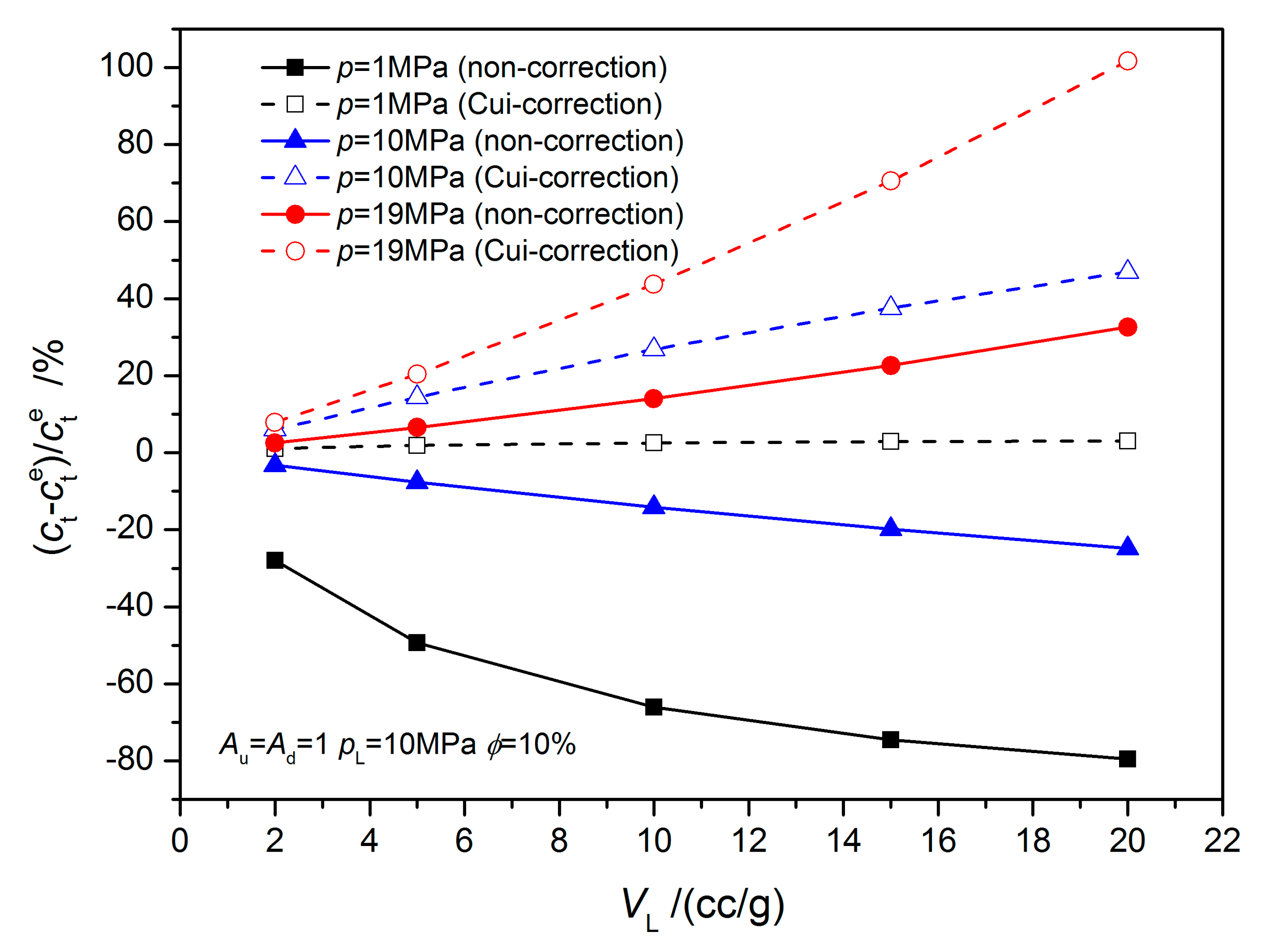
4.1. Equilibrium Sorption Model
4.2. Non-Equilibrium Sorption Model
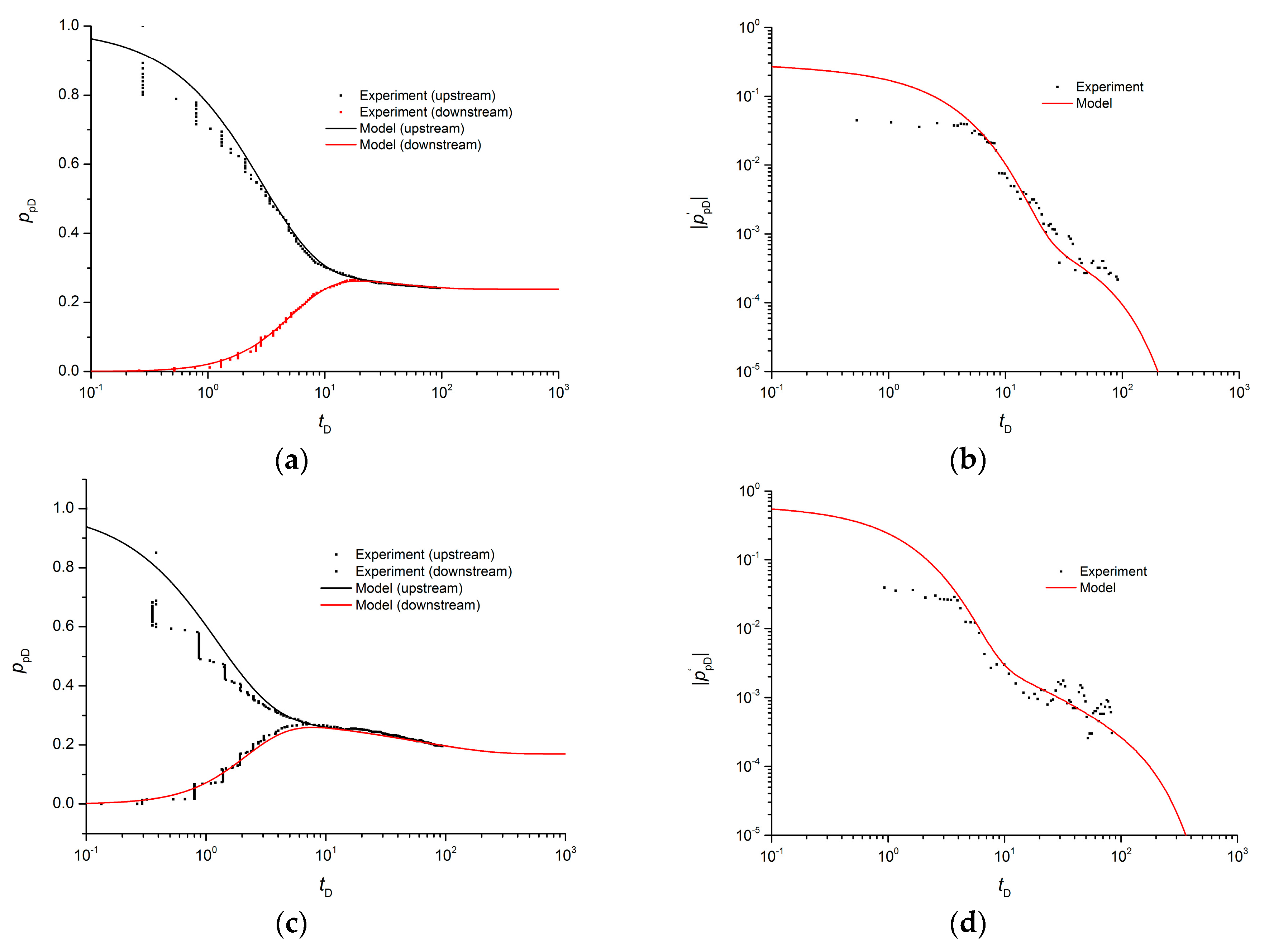
5. Case Study
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| p,pf | pressure and fracture pressure [Pa]; |
| t | time [s]; |
| x | coordinate along the sample, takes the upstream vessel as the origin [m]; |
| L | length of the sample [m]; |
| Vu, Vd, Vp | the volume of the upstream vessel, downstream vessels and the sample pore, respectively [m3]; |
| V, Vic | total gas mass occurred and initial total gas mass occurred in the matrix [kg/m3]; |
| C, CE | gas concentration in the matrix and equivalent gas concentration in the fracture, respectively [kg/m3]; |
| VL, pL | Langmuir volume and pressure respectively [m3/kg, Pa]; |
| cg, cf | compressibility of testing gas and pore volume, respectively [Pa−1]; |
| ct, | sample total compressibility and equivalent total compressibility [Pa−1]; |
| cVd, cVu | compressibilities of upstream and downstream vessels respectively [Pa−1]; |
| k, kf, km | permeability, permeabilities of fractures and matrix respectively [m2]; |
| Dm | gas diffusion coefficient [m2/s]; |
| Rm, rm | the radius and coordinate of the spherical matrix respectively [m]; |
| M | molecular molar mass [kg/mol]; |
| Z | gas deviator factor; |
| R | Universal Gas Constant [J/(mol∙K)]; |
| T | temperature [K] |
| Greeks | |
| φ, φa, φf, φm | porosity, porosity of the adsorbed phased, fracture and matrix, respectively [%]; |
| μ | viscosity [Pa∙s]; |
| ρ, ρa, ρsc, ρs | density of the testing gas, adsorbed gas, gas at the standard condition and apparent density of samples [kg/m3]; |
| λD | pseudo-interporosity flow coefficient; |
| ω | pseudo-storativity ratio; |
| Subscripts | |
| f, m | macropores and micropores respectively; |
| u, d | upstream and downstream vessels respectively; |
| a | adsorbed phase; |
| i | reference status; |
| 0 | initial status; |
| p | normalized pseudo-pressure; |
| D | dimensionless variable |
Appendix A. Numerical Solution for Equilibrium Sorption Model
Appendix B. Numerical Solution for the Pseudo-Steady-State Non-Equilibrium Sorption Model
Appendix C. Numerical Solution for the Unsteady State Non-Equilibrium Sorption Model
References
- Brace, W.F.; Walsh, J.B.; Frangos, W.T. Permeability of granite under high pressure. J. Geophys. Res. 1968, 73, 2225–2236. [Google Scholar] [CrossRef]
- Bourbie, T.; Walls, J. Pulse decay permeability: Analytical solution and experimental test. SPE J. 1982, 22, 719–921. [Google Scholar] [CrossRef]
- Hsieh, P.A.; Tracy, J.V.; Neuzil, C.E.; Bredehoeft, J.D.; Silliman, S.E. A transient laboratory method for determining the hydraulic properties of ‘tight’ rocks—I. Theory. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 245–252. [Google Scholar] [CrossRef]
- Chen, T.; Stagg, P.W. Semilog analysis of the pulse decay technique of permeability measurement. SPE J. 1984, 24, 639–642. [Google Scholar] [CrossRef]
- Jones, S.C. A technique for faster pulse-decay permeability measurements in tight rocks. SPE Form. Eval. 1997, 12, 19–25. [Google Scholar] [CrossRef]
- Pan, Z.; Ma, Y.; Connell, L.D.; Down, D.I.; Camilleri, M. Measuring anisotropic permeability using a cubic shale sample in a triaxial cell. J. Nat. Gas Sci. Eng. 2015, 26, 336–344. [Google Scholar] [CrossRef]
- Jang, H.; Lee, W.; Kim, J.; Lee, J. Novel apparatus to measure the low-permeability and porosity in tight gas reservoir. J. Pet. Sci. Eng. 2016, 142, 1–12. [Google Scholar] [CrossRef]
- Firouzi, M.; Alnoaimi, K.; Kovscek, A.; Wilcox, J. Klinkenberg effect of predicting and measuring helium permeability in gas shales. Int. J. Coal Geol. 2014, 123, 62–68. [Google Scholar] [CrossRef]
- Heller, R.; Vermylen, J.; Zoback, M. Experimental investigation of matrix permeability of gas shales. AAPG Bull. 2014, 98, 975–995. [Google Scholar] [CrossRef]
- Mokhtari, M.; Tutuncu, A.N. Characterization of anisotropy in the permeability of organic-rich shales. J. Pet. Sci. Eng. 2015, 133, 496–506. [Google Scholar] [CrossRef]
- Zhang, R.; Ning, Z.; Yang, F.; Wang, X.; Zhao, H.; Wang, Q. Impacts of nanopore structure and elastic properties on stress-dependent permeability of gas shales. J. Nat. Gas Sci. Eng. 2015, 26, 1663–1672. [Google Scholar] [CrossRef]
- Cronin, M.B.; Flemings, P.B.; Bhandari, A.R. Dual-permeability microstratigraphy in the Barnett Shale. J. Pet. Sci. Eng. 2016, 142, 119–128. [Google Scholar] [CrossRef]
- Cao, C.; Li, T.; Shi, J.; Zhang, L.; Fu, S.; Wang, B.; Wang, H. A new approach for measuring the permeability of shale featuring adsorption and ultra-low permeability. J. Nat. Gas Sci. Eng. 2016, 30, 548–556. [Google Scholar] [CrossRef]
- Zhang, R.; Ning, Z.; Yang, F.; Zhao, H.; Wang, Q. A laboratory study of the porosity-permeability relationships of shale and sandstone under effective stress. Int. J. Rock Mech. Min. Sci. 2016, 81, 19–27. [Google Scholar] [CrossRef]
- Alnoaimi, K.R.; Duchateau, C.; Kovscek, A.R. Characterization and measurement of multiscale gas transport in shale-core samples. SPE J. 2016, 21, 573–588. [Google Scholar] [CrossRef]
- Aljamaan, H.; Al Ismail, M.; Kovscek, A.R. Experimental investigation and Grand Canonical Monte Carlo simulation of gas shale adsorption from the macro to the nano scale. J. Nat. Gas Sci. Eng. 2017, 48, 119–137. [Google Scholar] [CrossRef]
- Alnoaimi, K.R.; Kovscek, A.R. Influence of microcracks on flow and storage capacities of gas shales at core scale. Transp. Porous Media 2019, 127, 53–84. [Google Scholar] [CrossRef]
- Ghanizadeh, A.; Gasparik, M.; Amann-Hildenbrand, A.; Gensterblum, Y.; Krooss, B.M. Experimental study of fluid transport processes in the matrix system of the European organic-rich shales: I. Scandinavian Alum Shale. Mar. Pet. Geol. 2014, 51, 79–99. [Google Scholar] [CrossRef]
- Ghanizadeh, A.; Amann-Hildenbrand, A.; Gasparik, M.; Gensterblum, Y.; Krooss, B.M.; Littke, R. Experimental study of fluid transport processes in the matrix system of the European organic-rich shales: II. Posidonia Shale (Lower Toarcian, northern Germany). Int. J. Coal Geol. 2014, 123, 20–33. [Google Scholar] [CrossRef]
- Gensterblum, Y.; Ghanizadeh, A.; Krooss, B.M. Gas permeability measurements on Australian subbituminous coals: Fluid dynamic and poroelastic aspects. J. Nat. Gas Sci. Eng. 2014, 19, 202–214. [Google Scholar] [CrossRef]
- Cui, X.; Bustion, A.M.M.; Bustion, R.M. Measurements of gas permeability and diffusivity of tight reservoir rocks: Different approaches and their applications. Geofluids 2009, 9, 208–223. [Google Scholar] [CrossRef]
- Civan, F.; Rai, C.S.; Sondergeld, C.H. Shale permeability determined by simultaneous analysis of multiple pressure-pulse measurements obtained under different conditions. In Proceedings of the North American Unconventional Gas Conference and Exhibition, The Woodlands, TX, USA, 14–16 June 2011. [Google Scholar] [CrossRef]
- Anbarci, K.; Ertekin, T. A comprehensive study of pressure transient analysis with sorption phenomena for single-phase gas flow in coal seams. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 23–26 September 1990. [Google Scholar] [CrossRef]
- Kolesar, J.E.; Ertekin, T.; Obut, S.T. The unsteady-state nature of sorption and diffusion phenomena in the micropore structure of coal: Part 1-theroy and mathematical formulation. SPE Form. Eval. 1990, 5, 81–97. [Google Scholar] [CrossRef]
- Yuan, W.; Pan, Z.; Li, X.; Yang, Y.; Zhao, C.; Connell, L.D.; Li, S.; He, J. Experimental study and modelling of methane adsorption and diffusion in shale. Fuel 2014, 117, 509–519. [Google Scholar] [CrossRef]
- Jia, B.; Tsau, J.S.; Barati, R. Evaluation of core heterogeneity effect on pulse-decay experiment. In Proceedings of the International Symposium of the Society of Core Analysts, Vienna, Austria, 27 August–1 September 2017. [Google Scholar]
- Jia, B.; Tsau, J.S.; Barati, R. Experimental and numerical investigations of permeability in heterogeneous fractured tight porous media. J. Nat. Gas Sci. Eng. 2018, 58, 216–233. [Google Scholar] [CrossRef]
- Han, G.; Sun, L.; Liu, Y.; Zhou, S. Analysis method of pulse decay tests for dual-porosity cores. J. Nat. Gas Sci. Eng. 2018, 59, 274–286. [Google Scholar] [CrossRef]
- Haydel, J.J.; Kobayashi, R. Adsorption equilibria in the Methane-Propane-Silica gel system at high pressures. Ind. Eng. Chem. Fundam. 1967, 6, 546–554. [Google Scholar] [CrossRef]
- Ding, D.Y.; Farah, N.; Bourbiaux, B.; Wu, Y.S.; Mestiri, I. Simulation of matrix/fracture interaction in low-permeability fractured unconventional reservoirs. SPE J. 2018, 23, 1–389. [Google Scholar] [CrossRef]
- Noetinger, B.; Estebenet, T.; Landereau, P. A direct determination of the transient exchange term of fractured media using a continuous time random walk method. Transp. Porous Media 2001, 44, 539–557. [Google Scholar] [CrossRef]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, G.; Chen, Y.; Liu, X. Investigation of Analysis Methods for Pulse Decay Tests Considering Gas Adsorption. Energies 2019, 12, 2562. https://doi.org/10.3390/en12132562
Han G, Chen Y, Liu X. Investigation of Analysis Methods for Pulse Decay Tests Considering Gas Adsorption. Energies. 2019; 12(13):2562. https://doi.org/10.3390/en12132562
Chicago/Turabian StyleHan, Guofeng, Yang Chen, and Xiaoli Liu. 2019. "Investigation of Analysis Methods for Pulse Decay Tests Considering Gas Adsorption" Energies 12, no. 13: 2562. https://doi.org/10.3390/en12132562
APA StyleHan, G., Chen, Y., & Liu, X. (2019). Investigation of Analysis Methods for Pulse Decay Tests Considering Gas Adsorption. Energies, 12(13), 2562. https://doi.org/10.3390/en12132562





