A Super-Twisting Sliding-Mode Stator Flux Observer for Sensorless Direct Torque and Flux Control of IPMSM
Abstract
:1. Introduction
2. Direct Torque and Flux Control
3. Active Flux-Based Sensorless Control
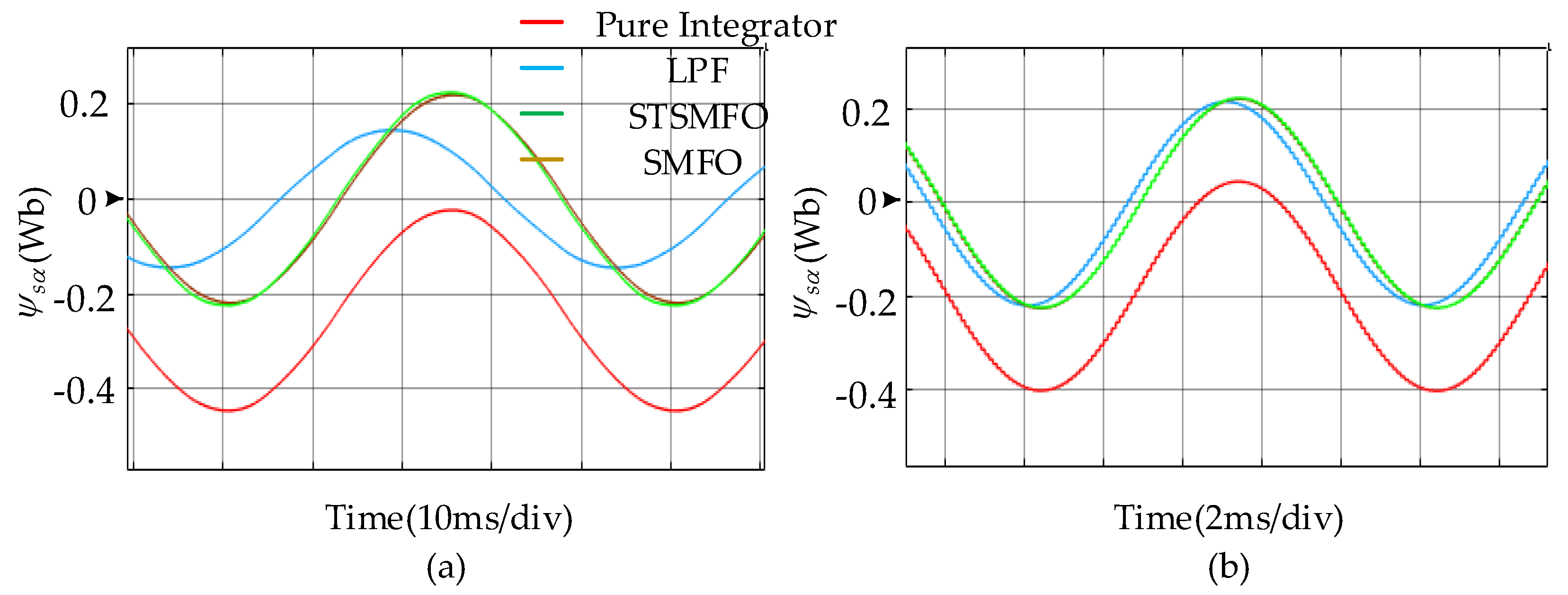
3.1. Pure Integrator-Based Observer
3.2. Low-Pass Filter (LPF)-Based Observer
3.3. First-Order Sliding-Mode Stator Flux Observer (SMFO)
4. Super-Twisting Sliding-Mode Stator Flux Observer
4.1. Super-Twisting Algorithm
4.2. Super-Twisting Sliding-Mode Stator Flux Observer
5. Evaluation via Simulation and Experiment
5.1. Simulation Results
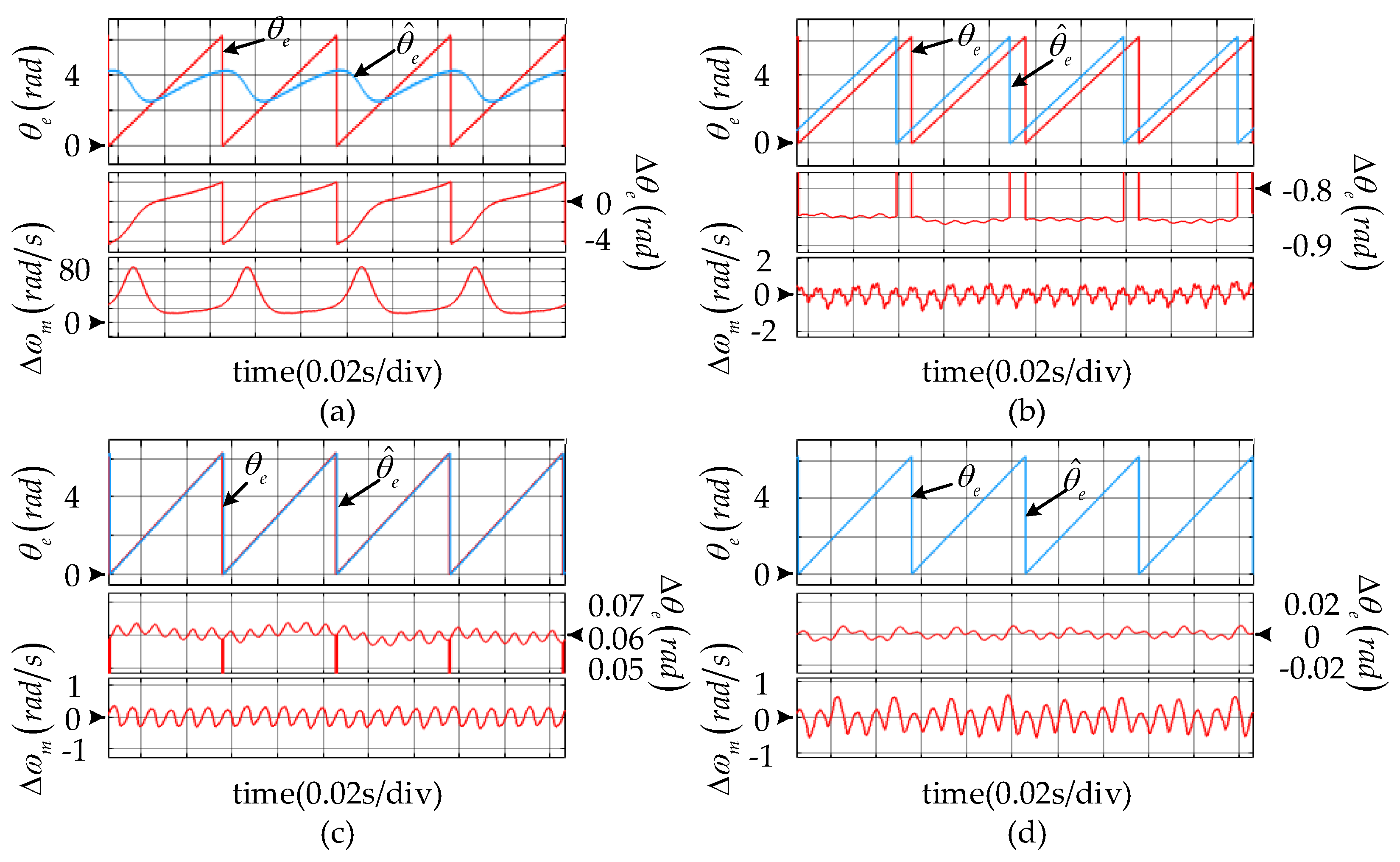
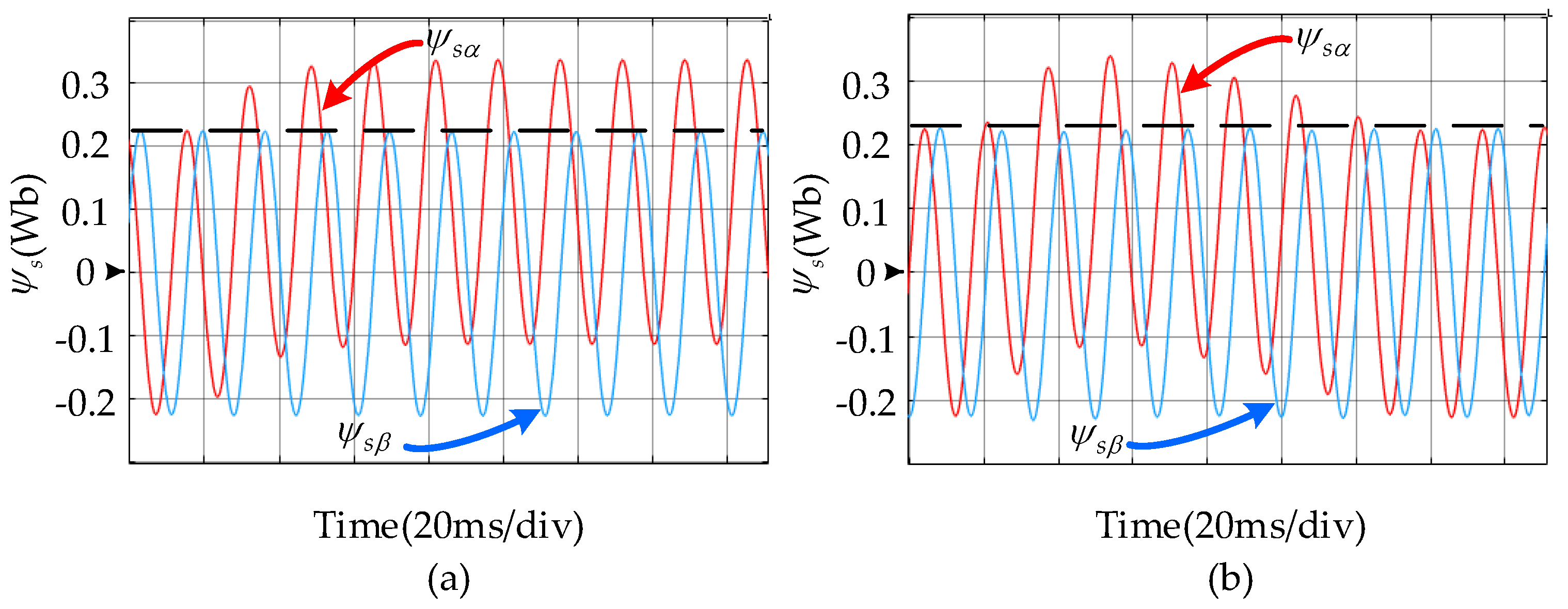
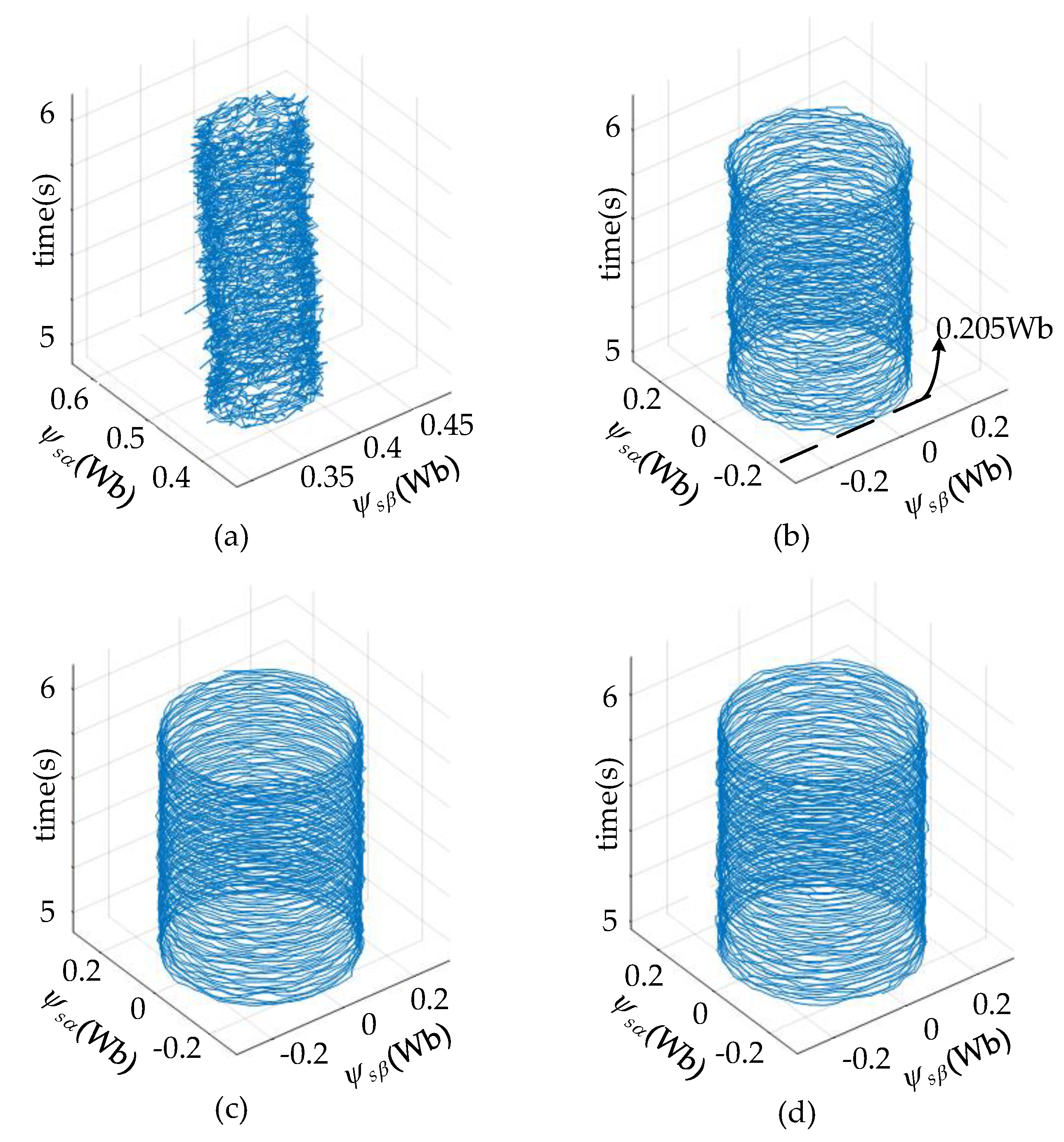
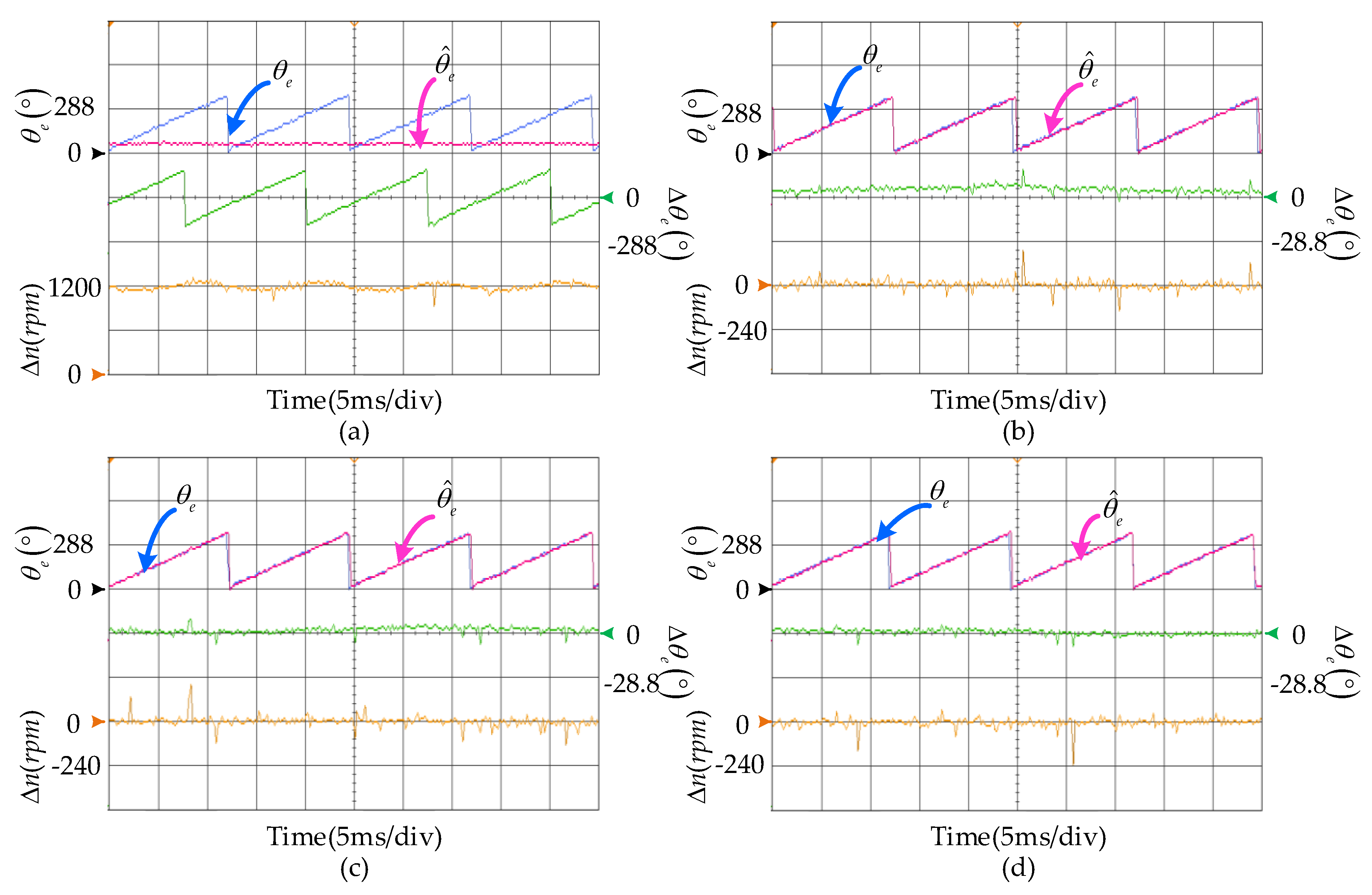
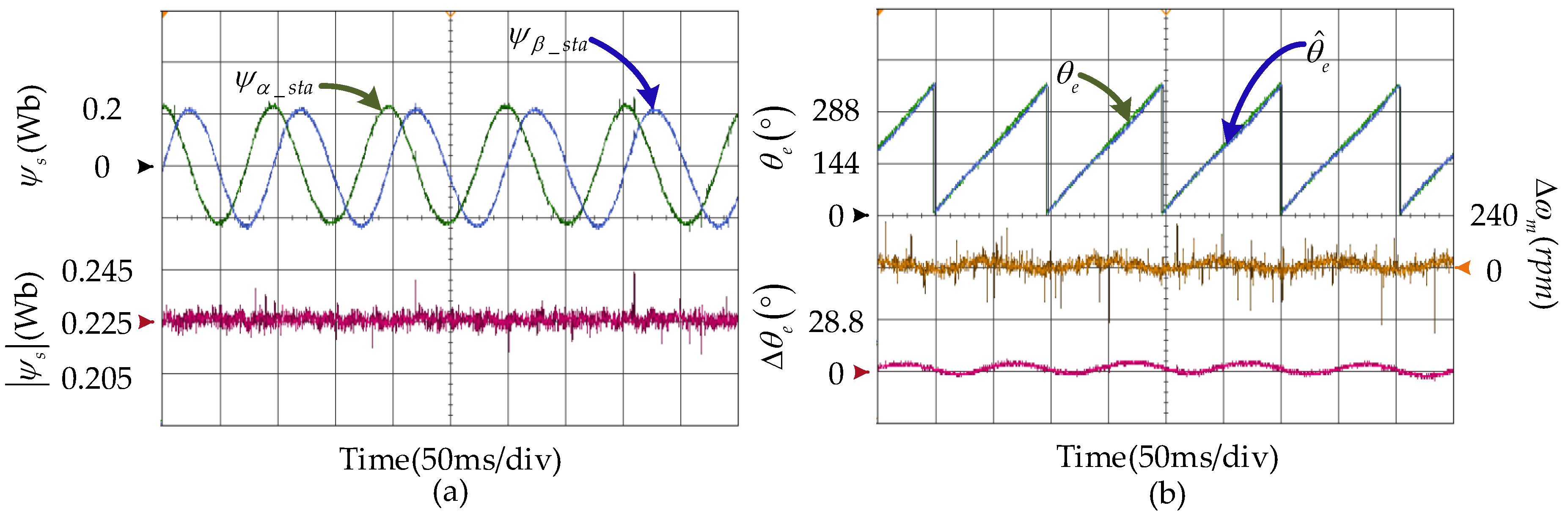
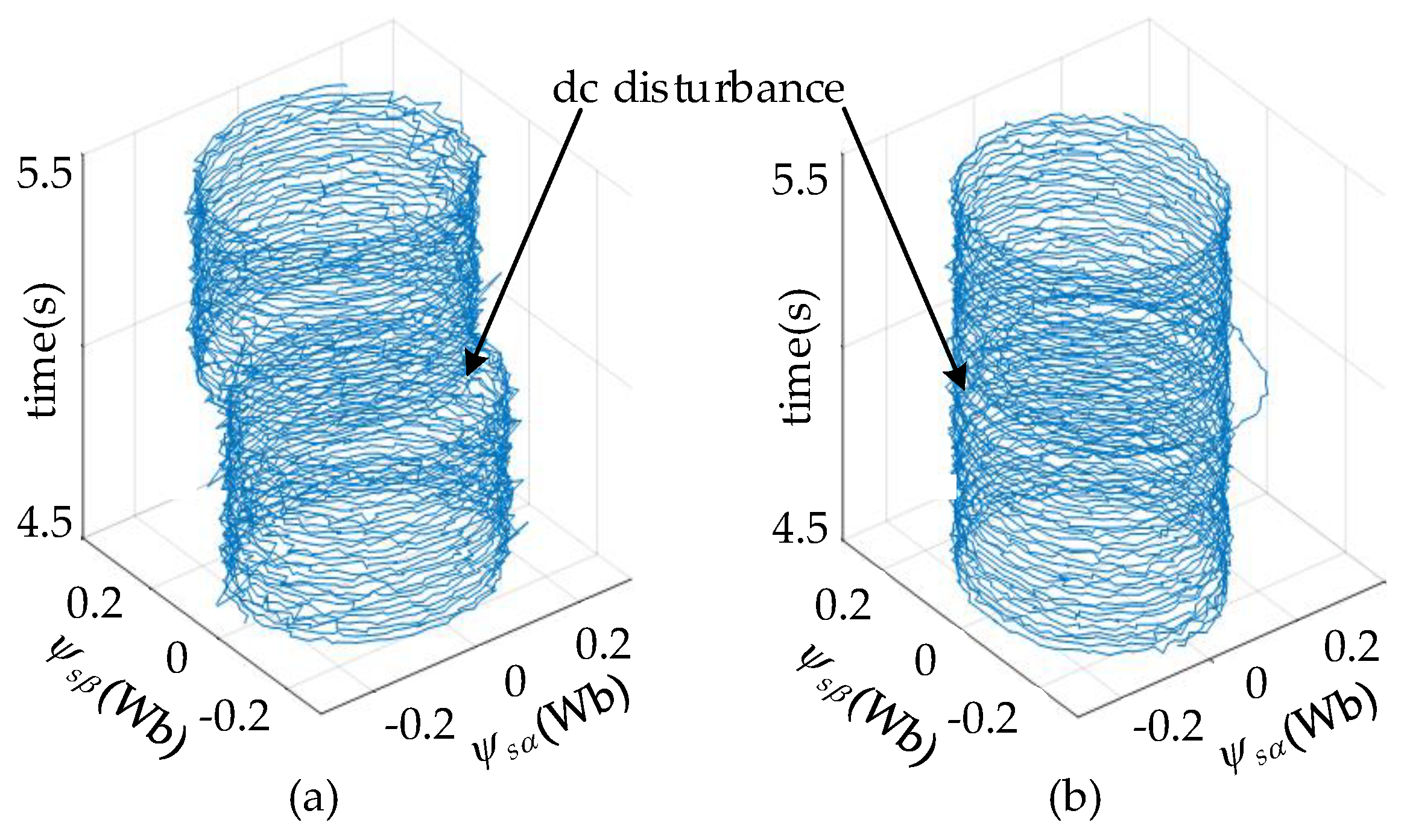
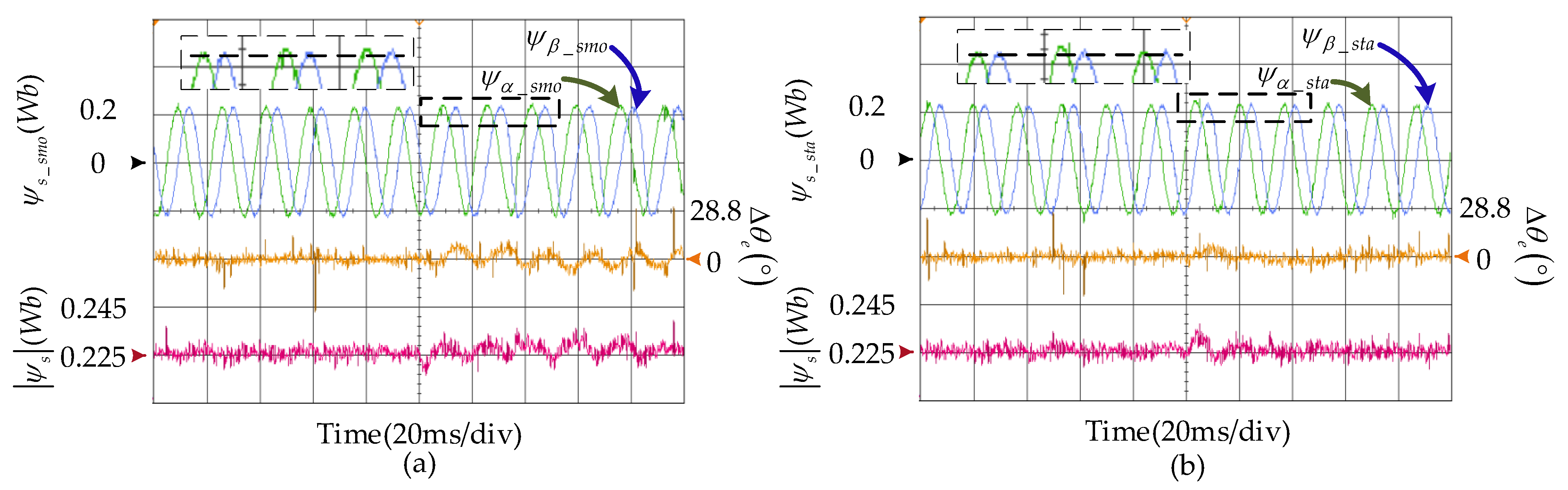
5.2. Experimental Results
5.2.1. Steady-State Performance
5.2.2. DC Disturbance Rejection
5.2.3. Dynamic Capability
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, J.; Huang, X.; Niu, F.; You, C.; Wu, L.; Fang, Y. Prediction Error Analysis of Finite-Control-Set Model Predictive Current Control for IPMSMs. Energies 2018, 11, 2051. [Google Scholar] [CrossRef]
- Lara, J.; Xu, J.; Chandra, A. Effects of Rotor Position Error in the Performance of Field Oriented Controlled PMSM Drives for Electric Vehicle Traction Applications. IEEE Trans. Ind. Electron. 2016, 63, 4738–4751. [Google Scholar] [CrossRef]
- Rahman, M.M.; Uddin, M.N. Third Harmonic Injection Based Nonlinear Control of IPMSM Drive for Wide Speed Range Operation. IEEE Trans. Ind. Appl. 2014, 55, 3174–3184. [Google Scholar] [CrossRef]
- Takahashi, I.; Noguchi, T. A New Quick-Response and High-Efficiency Control Strategy of an Induction Motor. IEEE Trans. Ind. Appl. 1986, 22, 820–827. [Google Scholar] [CrossRef]
- Ouanjli, N.E.; Derouich, A.; Ghzizal, A.E.; Motahhir, S.; Chebabhi, A.; Mourabit, Y.E.; Taoussi, M. Modern improvement techniques of direct torque control for induction motor drives—A review. Prot. Control Mod. Power Syst. 2019, 4, 136–147. [Google Scholar] [CrossRef]
- Choi, Y.; Choi, H.H.; Jung, J. Feedback Linearization Direct Torque Control with Reduced Torque and Flux Ripples for IPMSM Drives. IEEE Trans. Power Electron. 2016, 31, 3728–3737. [Google Scholar] [CrossRef]
- Tang, L.; Zhong, L.; Rahman, M.F.; Hu, Y. A Novel Direct Torque Controlled Interior Permanent Magnet Synchronous Machine Drive with Low Ripple in Flux and Torque and Fixed Switching Frequency. IEEE Trans. Power Electron. 2004, 19, 346–354. [Google Scholar] [CrossRef]
- Foo, G.; Rahman, M.F. Sensorless Direct Torque and Flux-Controlled IPM Synchronous Motor Drive at Very Low Speed Without Signal Injection. IEEE Trans. Ind. Electron. 2010, 57, 395–403. [Google Scholar] [CrossRef]
- Chen, J.; Yang, S.; Tu, J. Comparative Evaluation of a Permanent Magnet Machine Saliency-Based Drive with Sine-Wave and Square-Wave Voltage Injection. Energies 2018, 11, 2189. [Google Scholar] [CrossRef]
- Yousefi-Talouki, A.; Pescetto, P.; Pellegrino, G.; Boldea, I. Combined Active Flux and High Frequency Injection Methods for Sensorless Direct Flux Vector Control of Synchronous Reluctance Machines. IEEE Trans. Power Electron. 2018, 33, 2447–2457. [Google Scholar] [CrossRef]
- Yoon, Y.; Sul, S.; Morimoto, S.; Ide, K. High-Bandwidth Sensorless Algorithm for AC Machines Based on Square-Wave-Type Voltage Injection. IEEE Trans. Ind. Appl. 2011, 47, 1361–1370. [Google Scholar] [CrossRef]
- Shi, Y. Online Identification of Permanent Magnet Flux Based on Extended Kalman Filter for IPMSM Drive with Position Sensorless Control. IEEE Trans. Ind. Electron. 2012, 59, 4169–4178. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, X.; Wu, X.; Tan, G.; Chen, X. Sensorless Control for IPMSM Based on Adaptive Super-Twisting Sliding-Mode Observer and Improved Phase-Locked Loop. Energies 2019, 12, 1225. [Google Scholar] [CrossRef]
- Vieira, R.P.; Gastaldini, C.C.; Azzolin, R.Z.; Gründling, H.A. Sensorless Sliding-Mode Rotor Speed Observer of Induction Machines Based on Magnetizing Current Estimation. IEEE Trans. Ind. Electron. 2014, 61, 4573–4582. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, L.; Cheng, M.; Chau, K.T. Sensorless SVPWM-FADTC of a New Flux-Modulated Permanent-Magnet Wheel Motor Based on a Wide-Speed Sliding Mode Observer. IEEE Trans. Ind. Electron. 2015, 62, 3143–3151. [Google Scholar] [CrossRef]
- Gadoue, S.M.; Giaouris, D.; Finch, J.W. MRAS Sensorless Vector Control of an Induction Motor Using New Sliding-Mode and Fuzzy-Logic Adaptation Mechanisms. IEEE Trans. Energy Convers. 2010, 25, 394–402. [Google Scholar] [CrossRef]
- Boldea, I.; Paicu, M.C.; Andreescu, G. Active Flux Concept for Motion-Sensorless Unified AC Drives. IEEE Trans. Power Electron. 2008, 23, 2612–2618. [Google Scholar] [CrossRef]
- Boldea, I.; Paicu, M.C.; Andreescu, G.; Blaabjerg, F. “Active Flux” DTFC-SVM Sensorless Control of IPMSM. IEEE Trans. Energy Convers. 2009, 24, 314–322. [Google Scholar] [CrossRef]
- Zhao, R.; Xin, Z.; Loh, P.C.; Blaabjerg, F. A Novel Flux Estimator Based on Multiple Second-Order Generalized Integrators and Frequency-Locked Loop for Induction Motor Drives. IEEE Trans. Power Electron. 2017, 32, 6286–6296. [Google Scholar] [CrossRef]
- Xu, W.; Jiang, Y.; Mu, C.; Blaabjerg, F. Improved Nonlinear Flux Observer-Based Second-Order SOIFO for PMSM Sensorless Control. IEEE Trans. Power Electron. 2019, 34, 565–579. [Google Scholar] [CrossRef]
- Choi, J.; Nam, K.; Bobtsov, A.A.; Pyrkin, A.; Ortega, R. Robust Adaptive Sensorless Control for Permanent-Magnet Synchronous Motors. IEEE Trans. Power Electron. 2017, 32, 3989–3997. [Google Scholar] [CrossRef]
- Lin, T.C.; Zhu, Z.Q.; Liu, J.M. Improved Rotor Position Estimation in Sensorless-Controlled Permanent-Magnet Synchronous Machines Having Asymmetric-EMF with Harmonic Compensation. IEEE Trans. Ind. Electron. 2015, 62, 6131–6139. [Google Scholar] [CrossRef]
- Roberto, M.; Edmundo, B.; Marco, A.A.; Hernández, C. Sensorless Predictive DTC of a Surface-Mounted Permanent-Magnet Synchronous Machine Based on Its Magnetic Anisotrogy. IEEE Trans. Ind. Electron. 2013, 60, 3016–3024. [Google Scholar]
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Liang, D.; Li, J.; Qu, R. Sensorless Control of Permanent Magnet Synchronous Machine Based on Second-Order Sliding-Mode Observer with Online Resistance Estimation. IEEE Trans. Ind. Appl. 2017, 53, 3672–3682. [Google Scholar] [CrossRef]
- Liang, D.; Li, J.; Qu, R.; Kong, W. Adaptive Second-Order Sliding-Mode Observer for PMSM Sensorless Control Considering VSI Nonlinearity. IEEE Trans. Power Electron. 2018, 33, 8994–9004. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, S.; Xiao, Y.; Wang, L. Sensorless Vector Control of Permanent Magnet Synchronous Linear Motor Based on Self-adaptive Super-twisting Sliding Mode Controller. IEEE Access 2019, 7, 44998–45011. [Google Scholar] [CrossRef]
- Holakooie, M.H.; Ojaghi, M.; Taheri, A. Modified DTC of a Six-Phase Induction Motor with a Second-Order Sliding-Mode MRAS-Based Speed Estimator. IEEE Trans. Power Electron. 2019, 34, 600–611. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second-order sliding mode controlers and observer. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2856–2861. [Google Scholar]
- Moreno, J.A.; Osorio, M. Strict Lyapunov Functions for the Super-Twisting Algorithm. IEEE Trans. Autom. Control 2012, 57, 1035–1040. [Google Scholar] [CrossRef]
- Zhong, L.; Rahman, M.F.; Hu, W.; Lim, K.W. Analysis of Direct Torque Control in Permanent Magnet Synchronous Motor Drives. IEEE Trans. Power Electron. 1997, 12, 528–536. [Google Scholar] [CrossRef]
- Wu, X.; Tan, G.; Ye, Z.; Liu, Y.; Xu, S. Optimized Common-Mode Voltage Reduction PWM for Three-Phase Voltage Source Inverters. IEEE Trans. Power Electron. 2016, 31, 2959–2969. [Google Scholar] [CrossRef]
- Xia, Y.; Gou, B.; Xu, Y. Anew ensemble-based classifier for IGBT open-circuit fault diagnosis in three-phase PWM converter. Prot. Control Mod. Power Syst. 2018, 3, 364–372. [Google Scholar] [CrossRef]











| Parameter | Value |
|---|---|
| rated speed | 3000 rpm |
| rated power | 60 kW |
| rated voltage | 380 V |
| rated current | 130 A |
| rotational inertia | 0.2 kg·m2 |
| pn | 4 |
| Rs | 0.1 Ω |
| Ld/Lq | 0.95/2.05 mH |
| ψf | 0.225 Wb |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Chen, S.; Wu, X.; Tan, G.; Hao, J. A Super-Twisting Sliding-Mode Stator Flux Observer for Sensorless Direct Torque and Flux Control of IPMSM. Energies 2019, 12, 2564. https://doi.org/10.3390/en12132564
Chen J, Chen S, Wu X, Tan G, Hao J. A Super-Twisting Sliding-Mode Stator Flux Observer for Sensorless Direct Torque and Flux Control of IPMSM. Energies. 2019; 12(13):2564. https://doi.org/10.3390/en12132564
Chicago/Turabian StyleChen, Junlei, Shuo Chen, Xiang Wu, Guojun Tan, and Jianqi Hao. 2019. "A Super-Twisting Sliding-Mode Stator Flux Observer for Sensorless Direct Torque and Flux Control of IPMSM" Energies 12, no. 13: 2564. https://doi.org/10.3390/en12132564
APA StyleChen, J., Chen, S., Wu, X., Tan, G., & Hao, J. (2019). A Super-Twisting Sliding-Mode Stator Flux Observer for Sensorless Direct Torque and Flux Control of IPMSM. Energies, 12(13), 2564. https://doi.org/10.3390/en12132564






