An Efficient Method to Predict Compressibility Factor of Natural Gas Streams
Abstract
:1. Introduction
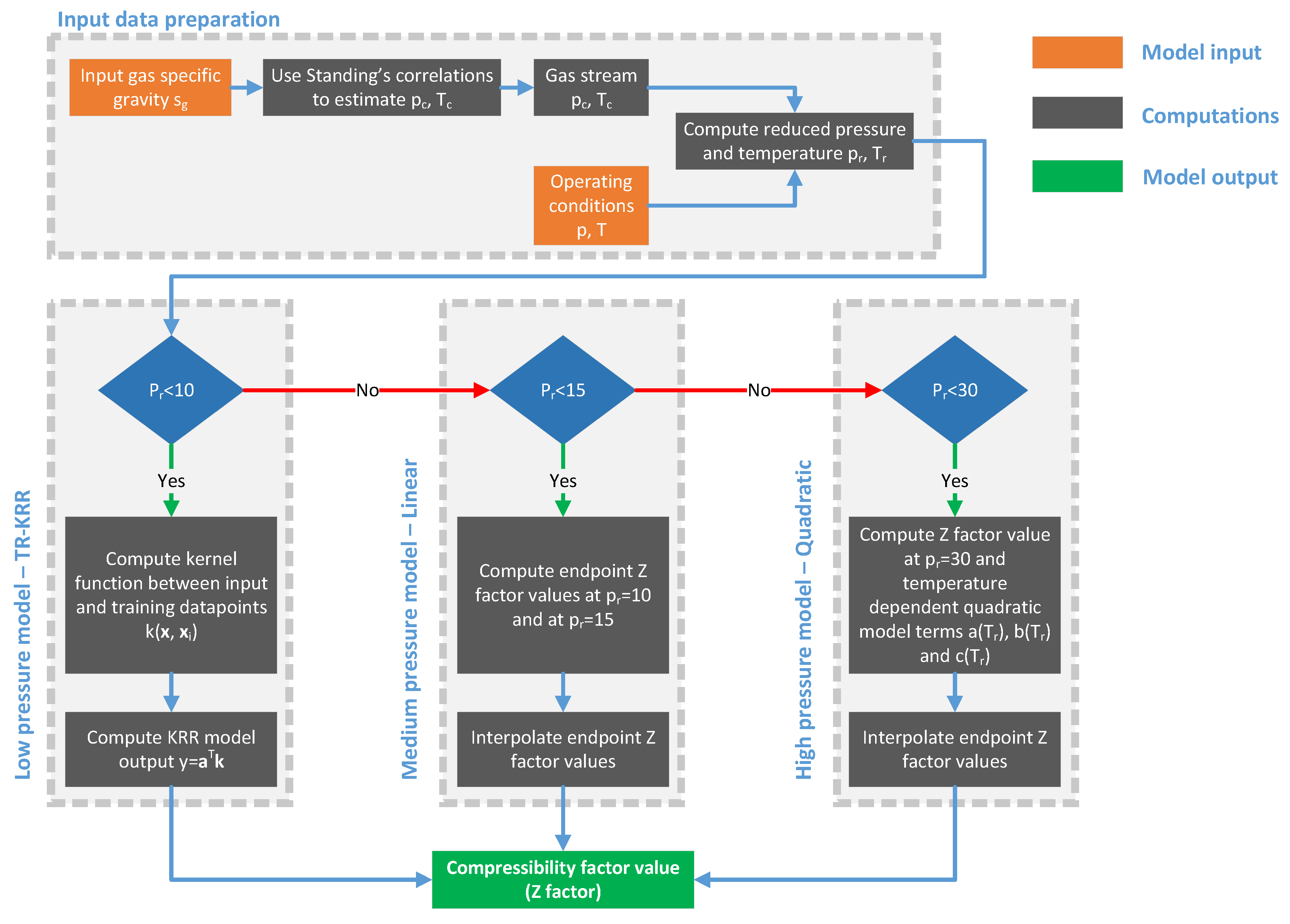
2. Methodology
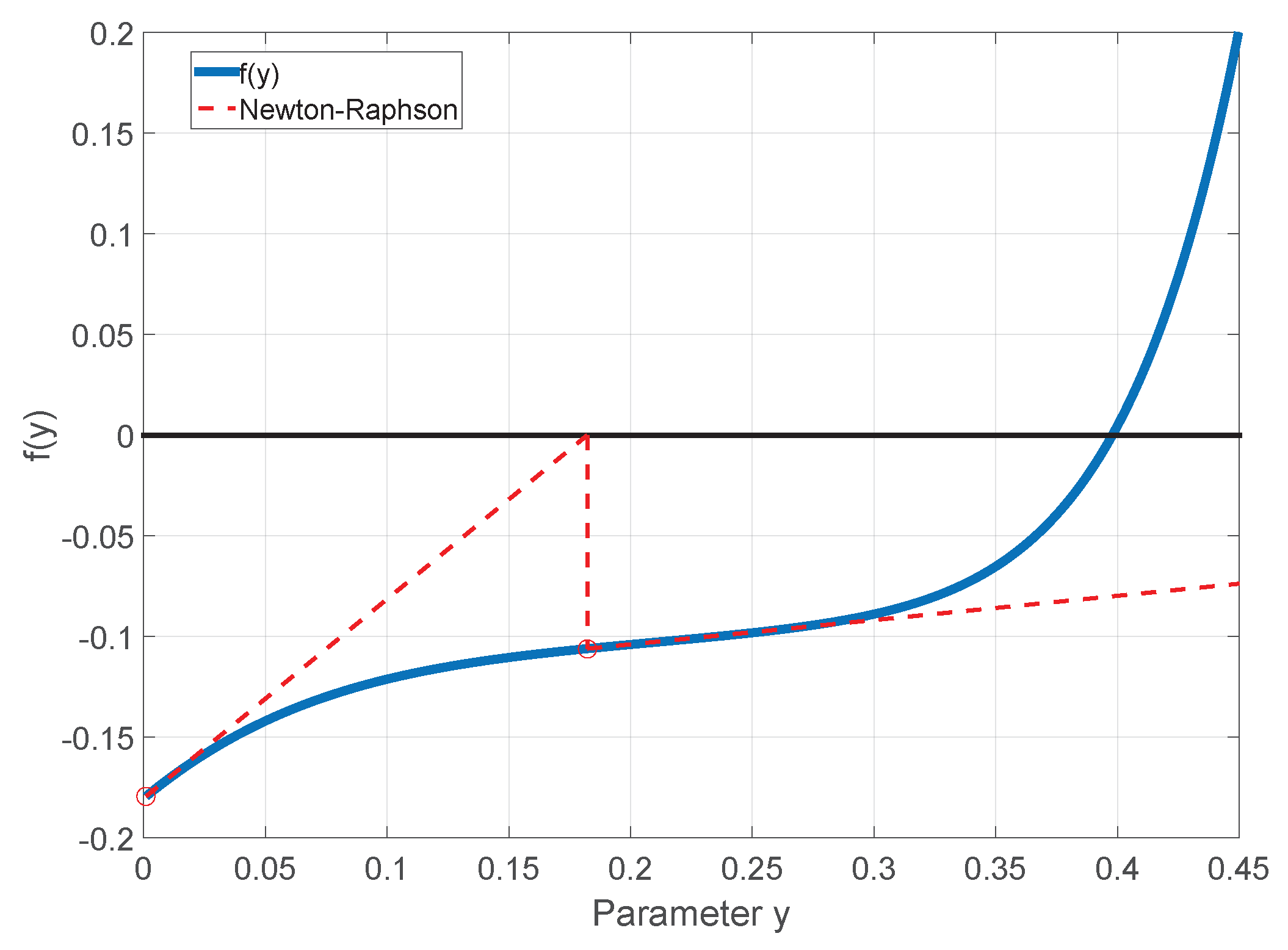
2.1. The Low Pressure Range
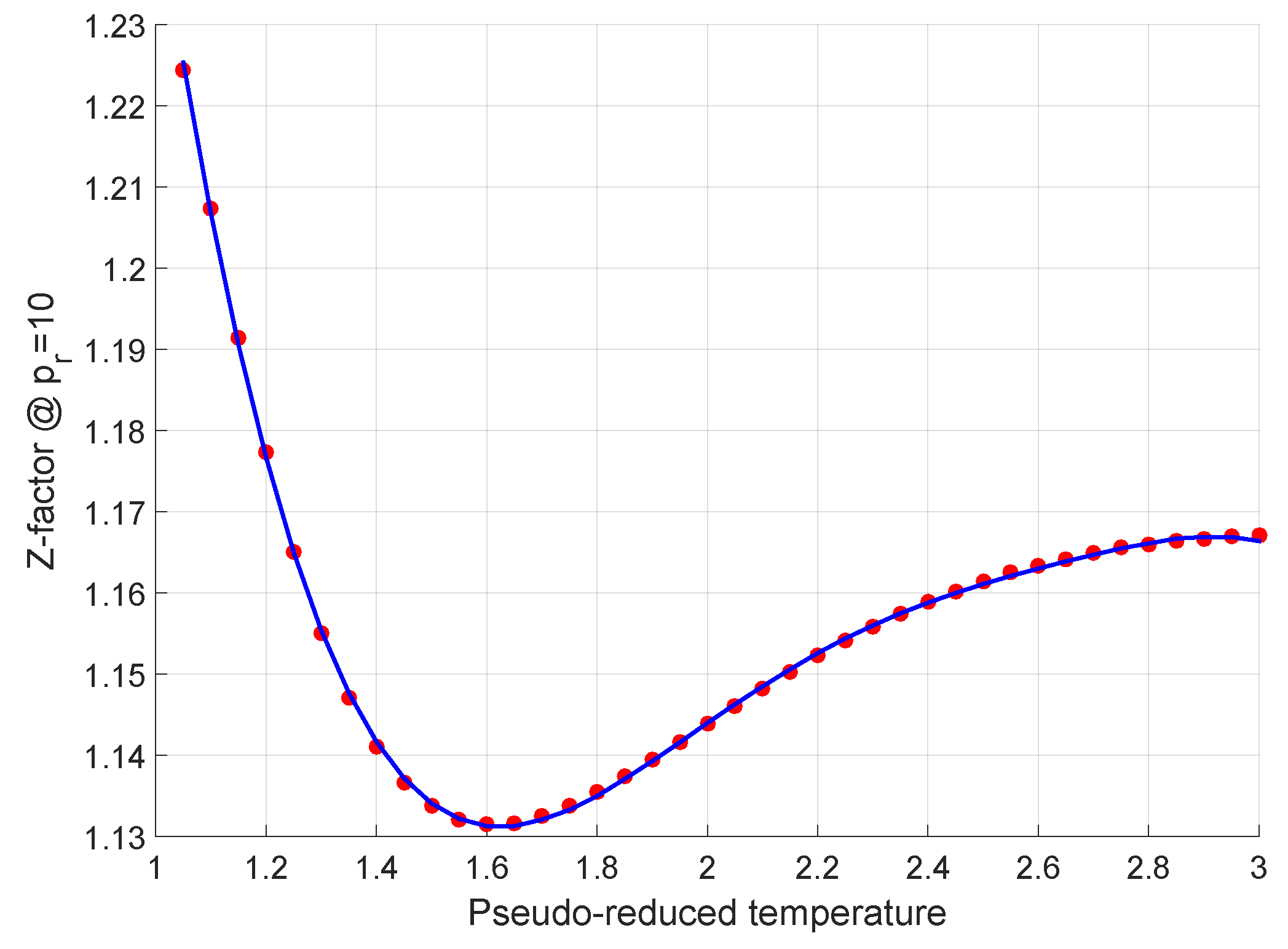
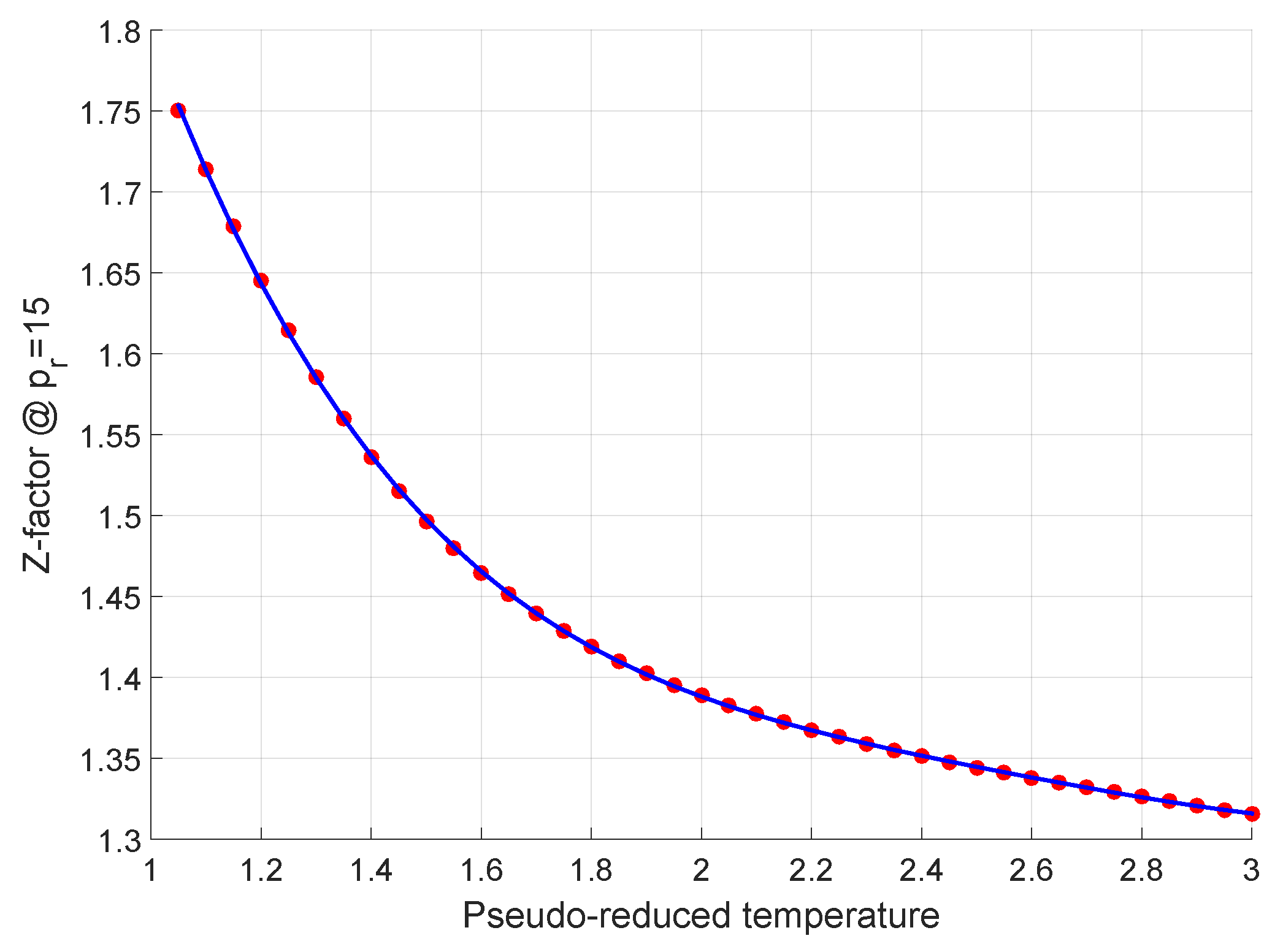
2.2. The Medium Pressure Range
2.3. The High Pressure Range
2.4. The Combined Model
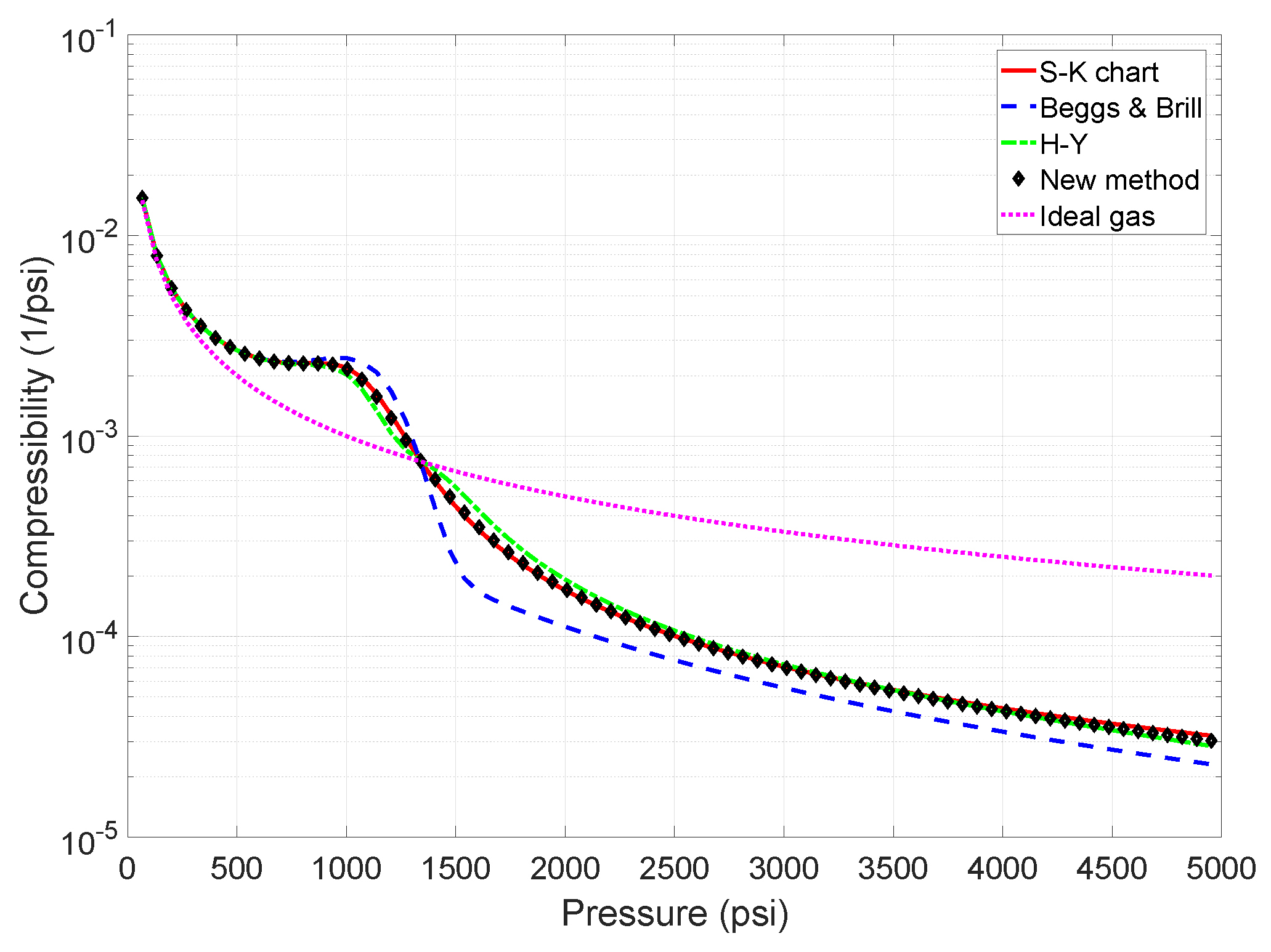
3. Results and Discussion
4. Case Studies
4.1. Case Study 1
4.2. Case Study 2
4.3. Case Study 3
5. Conclusions
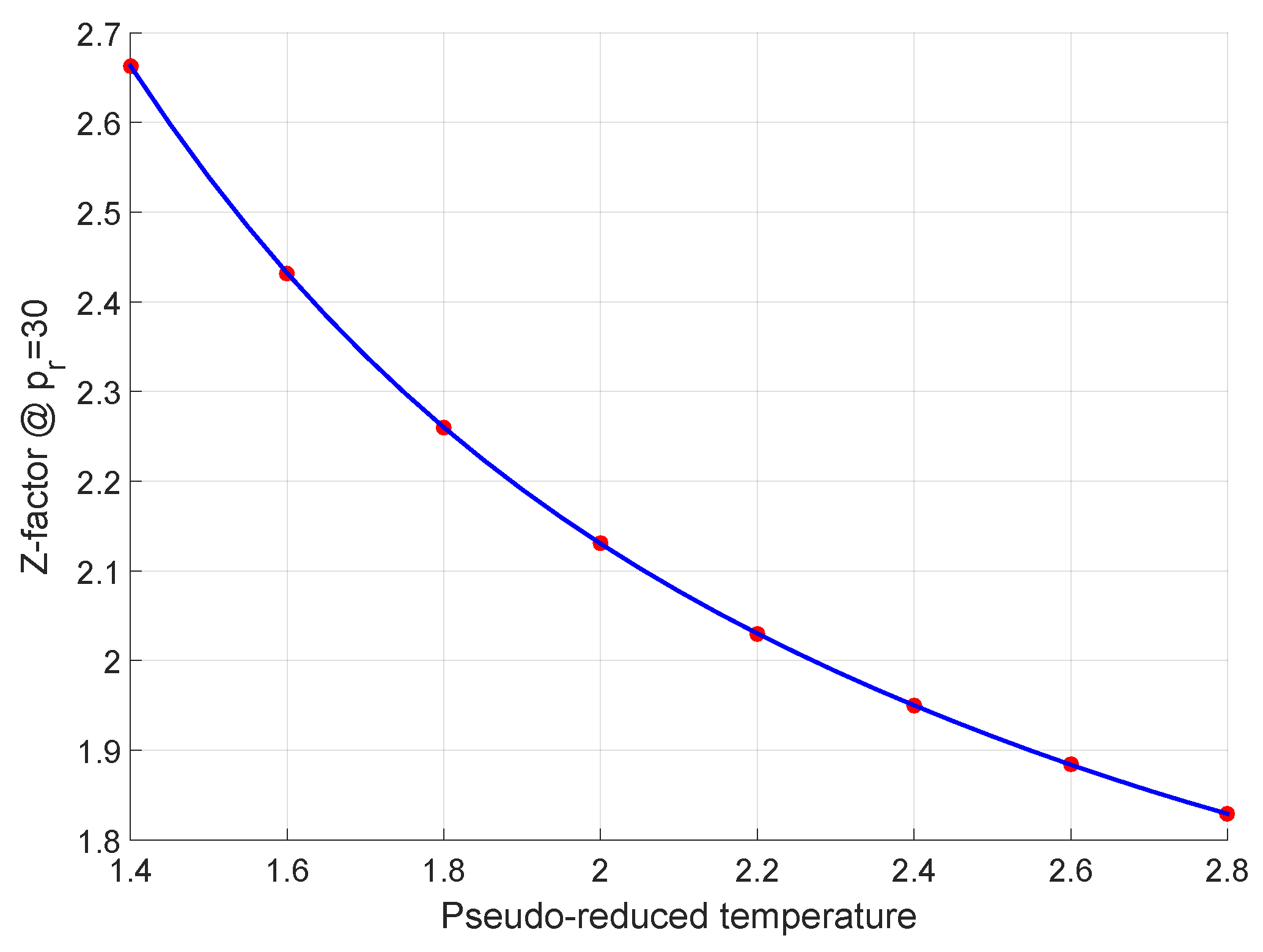
- At low reduced pressures where critical behavior might be observed and dependency on pressure is quite complex, the proposed method utilized the non-linear regression TR-KRR modeling technique to predict the gas compressibility factor.
- Our results indicated that despite the abruptly changing slope of the Z-factor isotherms, the TR-KRR model was highly accurate and efficient at predicting Z-factor.
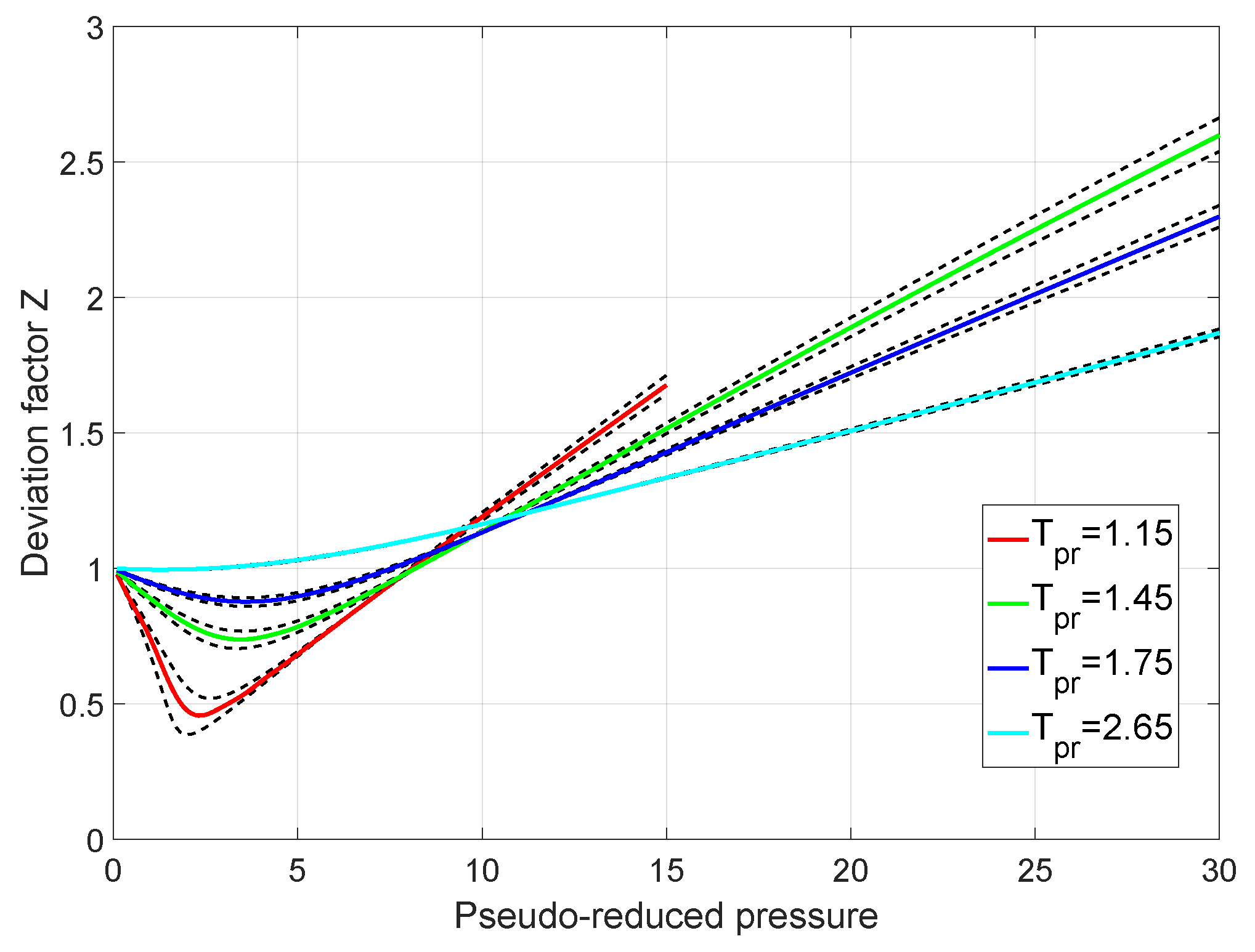
- The simplicity of the original S-K chart and its extension at medium and high pressures was directly inherited by the corresponding linear and quadratic submodels developed for the prediction of the Z-factor.
- Special attention has been paid to ensure a natural model derivative behavior, so as to end up with reliable isothermal compressibility values.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Details of the Z L Model
| Algorithm 1: Linear CG for computing . , |
 |
Appendix B. Details of the Z M Model
Appendix C. Details of the Z H Model
References
- Tan, S.P.; Qiu, X.; Dejam, M.; Adidharma, H. Critical point of fluid confined in nanopores: Experimental detection and measurement. J. Phys. Chem. C 2019, 123, 9824–9830. [Google Scholar] [CrossRef]
- Qiu, X.; Tan, S.P.; Dejam, M.; Adidharma, H. Simple and accurate isochoric differential scanning calorimetry measurements: Phase transitions for pure fluids and mixtures in nanopores. Phys. Chem. Chem. Phys. 2019, 21, 224–231. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Tan, S.P.; Dejam, M.; Adidharma, H. Novel isochoric measurement of the onset of vapor-liquid phase transition using differential scanning calorimetry. Phys. Chem. Chem. Phys. 2018, 20, 26241–26248. [Google Scholar] [CrossRef] [PubMed]
- Nikpoor, M.H.; Dejam, M.; Chen, Z.; Clarke, M. Chemical-gravity-thermal diffusion equilibrium in two-phase non-isothermal petroleum reservoirs. Energy Fuels 2016, 30, 2021–2034. [Google Scholar] [CrossRef]
- Standing, M. Volumetric and Phase Behavior of Oil Field Hydrocarbon Systems: PVT for Engineers; California Research Corporation: Vancouver, BC, Canada, 1951. [Google Scholar]
- Amyx, J.W.; Bass, D.M.; Whiting, R.L. Petroleum Reservoir Engineering: Physical Properties; McGraw-Hill: New York, NY, USA, 1960. [Google Scholar]
- Redlich, O.; Kwong, J.N. On the thermodynamics of solutions. v. an equation of state. Fugacities of gaseous solutions. Chem. Rev. 1949, 44, 233–244. [Google Scholar] [CrossRef] [PubMed]
- Whitson, C.; Brule, M. Phase Behavior; SPE: Richardson, TX, USA, 2000. [Google Scholar]
- Reid, R.C.; Prausnitz, J.M.; Poling, B.E. The Properties of Gases and Liquids, 4th ed.; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Zudkevitch, D.; Joffe, J. Correlation and prediction of Vapor-Liquid Equilibrium with the Redlich-Kwong Equation of State. AIChE J. 1970, 16, 112. [Google Scholar] [CrossRef]
- Hayden, J.G.; O’Connell, J.P. A generalized method for predicting second virial coefficients. Ind. Eng. Chem. Proc. Des. Dev. 1975, 14, 209–216. [Google Scholar] [CrossRef]
- Katz, D.L.; Cornell, D.; Kobayashi, R.; Poettmann, F.H.; Vary, J.A.; Elenbaas, J.R.; Weinaug, C.F. Handbook of Natural Gas Engineering; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Wichert, E.; Aziz, K. Compressibility Factor of Sour Natural Gases. Cdn. J. Chem. Eng. 1975, 49, 267. [Google Scholar] [CrossRef]
- Kay, W. Gases and vapors at high temperature and pressure-density of hydrocarbon. Ind. Eng. Chem. 1936, 28, 1014–1019. [Google Scholar] [CrossRef]
- Stewart, W.; Burkhardt, S.; Voo, D. Prediction of pseudo-critical parameters for mixtures. In Proceedings of the AIChE Meeting, Kansas City, MO, USA, 18 May 1959; Volume 18. [Google Scholar]
- Sutton, R. Compressibility factors for high-molecular-weight reservoir gases. In Proceedings of the SPE Annual Technical Conference and Exhibition, Las Vegas, NV, USA, 22–26 September 1985; Society of Petroleum Engineers: London, UK, 1985. [Google Scholar]
- Danesh, A. Pvt and Phase Behaviour of Petroleum Reservoir Fluids; Developments in Petroleum Science, Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Hall, K.R.; Yarborough, L. A New EOS for Z-factor Calculations. Oil Gas J. 1973, 71, 82–92. [Google Scholar]
- Dranchuk, P.; Abou-Kassem, H. Calculation of z factors for natural gases using equations of state. J. Can. Pet. Technol. 1975, 14. [Google Scholar] [CrossRef]
- Brill, J.P.; Beggs, H.D. Two-Phase Flow in Pipes; University of Tulsa INTERCOMP Course: The Hague, The Netherlands, 1974. [Google Scholar]
- Azizi, N.; Behbahani, R.; Isazadeh, M. An efficient correlation for calculating compressibility factor of natural gases. J. Nat. Gas Chem. 2010, 19, 642–645. [Google Scholar] [CrossRef]
- Kumar, N. Compressibility Factor for Natural and Sour Reservoir Gases by Correlations and Cubic Equations of State. Master’s Thesis, Texas Tech University, Lubbock, TX, USA, 2004. [Google Scholar]
- Heidaryan, E.; Moghadasi, J.; Rahimi, M. New correlations to predict natural gas viscosity and compressibility factor. Fluid Phase Equilibria 2009, 218, 1–13. [Google Scholar] [CrossRef]
- Kareem, L.; Iwalewa, T.; Al-Marhoun, M. New explicit correlation for the compressibility factor of natural gas: linearized z-factor isotherms. J. Petrol Explor. Prod. Technol. 2016, 6, 481–492. [Google Scholar] [CrossRef]
- Elsharkawy, A.M. Efficient methods for calculations of compressibility, density and viscosity of natural gases. Fluid Phase Equilibria 2004, 218, 1–13. [Google Scholar] [CrossRef]
- Moghadassi, A.; Parvizian, F.; Hosseini, S.; Fazlali, A. A new approach for estimation of pvt properties of pure gases based on artificial neural network model. Braz. J. Chem. Eng. 2009, 26, 199–206. [Google Scholar] [CrossRef]
- Irene, A.I.; Sunday, I.S.; Orodu, O.D. Forecasting Gas Compressibility Factor Using Artificial Neural Network Tool for Niger-Delta Gas Reservoir. Soc. Pet. Eng. 2016. [Google Scholar] [CrossRef] [Green Version]
- Kamyab, M.; Sampaio, J.H.; Qanbari, F.; Eustes, A.W. Using artificial neural networks to estimate the z-factor for natural hydrocarbon gases. J. Pet. Sci. Eng. 2010, 73, 248–257. [Google Scholar] [CrossRef]
- Sanjari, E.; Lay, E.N. Estimation of natural gas compressibility factors using artificial neural network approach. J. Nat. Gas Sci. Eng. 2012, 9, 220–226. [Google Scholar] [CrossRef]
- Fayazi, A.; Arabloo, M.; Mohammadi, A.H. Efficient estimation of natural gas compressibility factor using a rigorous method. J. Nat. Gas Sci. Eng. 2014, 16, 8–17. [Google Scholar] [CrossRef]
- Kamari, A.; Hemmati-Sarapardeh, A.; Mirabbasi, S.-M.; Nikookar, M.; Mohammadi, A.H. Prediction of sour gas compressibility factor using an intelligent approach. Fuel Process. Technol. 2013, 116, 209–216. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Mohamadi-Baghmolaei, M.; Azin, R.; Osfouri, S.; Mohamadi-Baghmolaei, R.; Zarei, Z. Prediction of gas compressibility factor using intelligent models. Nat. Gas Ind. B 2015, 2, 283–294. [Google Scholar] [CrossRef] [Green Version]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Maalouf, M.; Homouz, D. Kernel ridge regression using truncated newton method. Knowl.-Based Syst. 2014, 71, 339–344. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall/CRC: Vancouver, BC, Canada, 1994. [Google Scholar]
- Rencher, A. Methods of Multivariate Analysis; Wiley Interscience: Hoboken, NJ, USA, 2002. [Google Scholar]
- Shores, T. Applied Linear Algebra and Matrix Analysis; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]

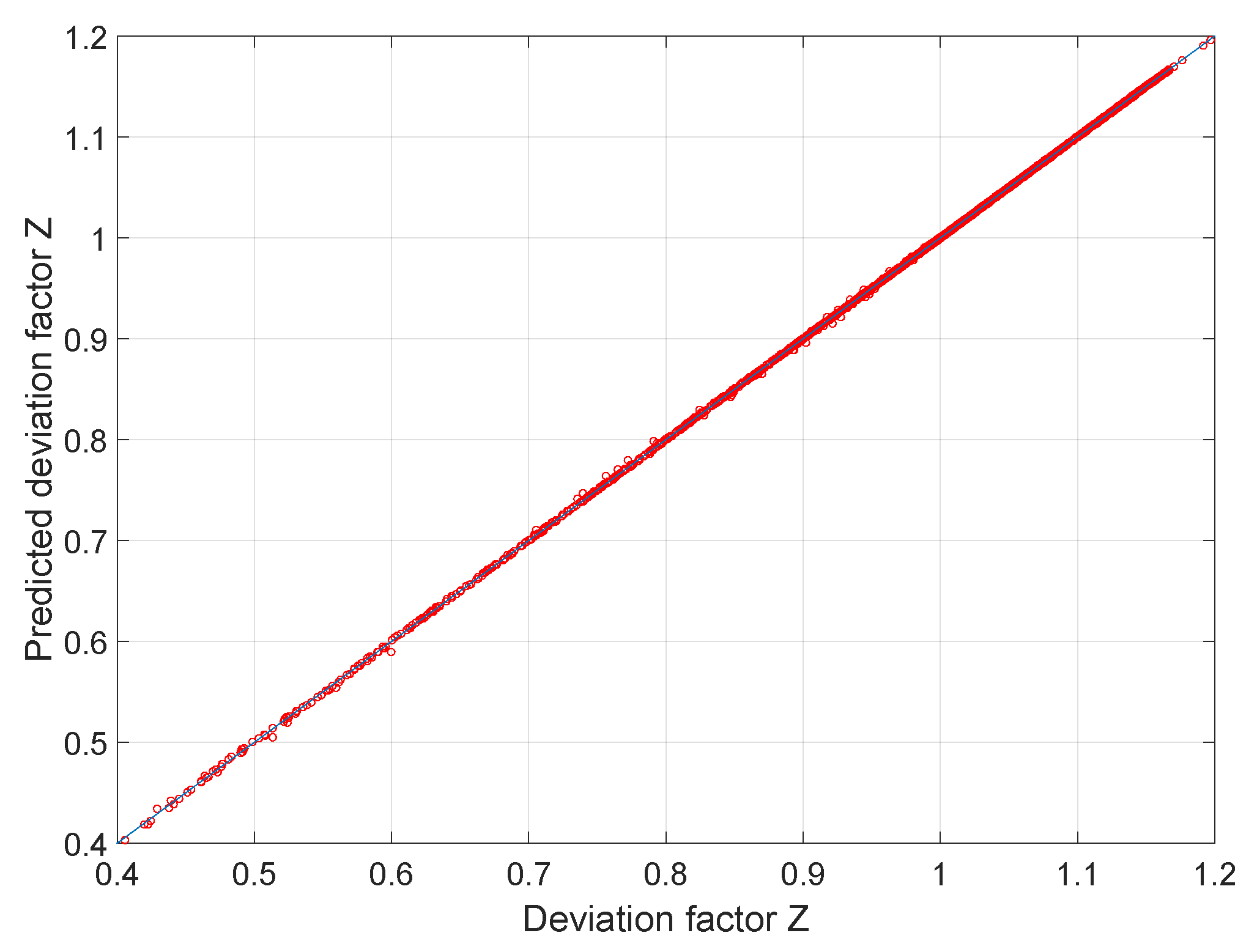
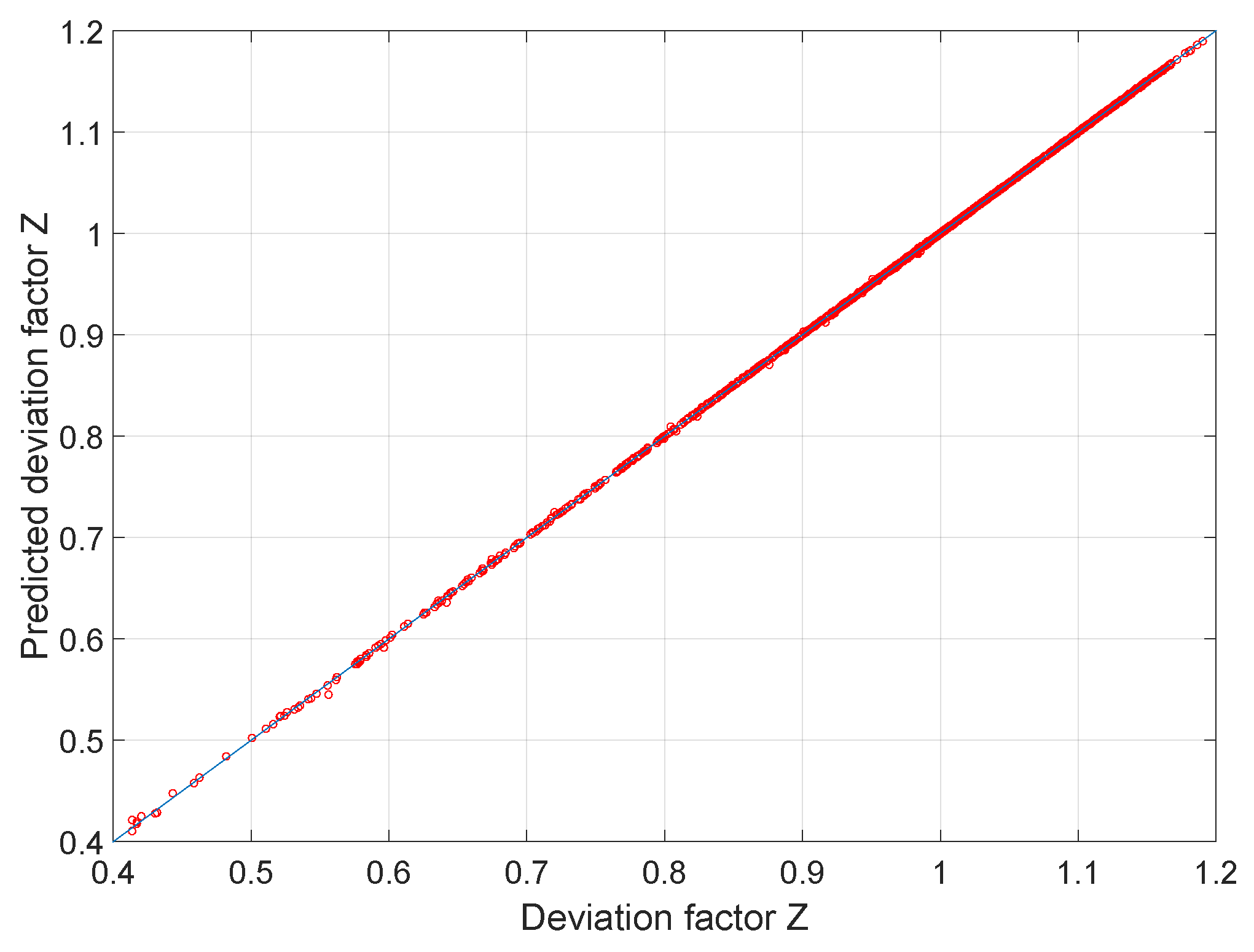

| Training Dataset | Validation Dataset | |
|---|---|---|
| Mean error | 0.00 | 0.00 |
| Mean relative error (%) | 0.00 | 0.00 |
| Mean absolute relative error (%) | 0.04 | 0.04 |
| Max error | 0.01 | 0.01 |
| Max relative error (%) | 1.70 | 1.98 |
| 0.99997 | 0.99996 |
| Method | Z-Factor | (psi) | Deviation (psi) |
|---|---|---|---|
| Standing–Katz | 0.6950 | 337 | - |
| Beggs and Brill | 0.7137 | 278 | 59 |
| Hall and Yarborough | 0.7071 | 300 | 37 |
| This method | 0.6912 | 347 | 10 |
| P (psi) | T (F) | Z (B-B) | Z (H-Y) | Z (S-K Chart) | Z (This Work) | |||
|---|---|---|---|---|---|---|---|---|
| 3600 | 150 | 0.00 | 5.48 | 1.51 | 0.826 | 0.842 | 0.833 | 0.832 |
| 3450 | 150 | 4.78 | 5.25 | 1.51 | 0.814 | 0.830 | 0.822 | 0.820 |
| 3300 | 150 | 12.65 | 5.02 | 1.51 | 0.804 | 0.820 | 0.811 | 0.809 |
| 3150 | 150 | 20.48 | 4.79 | 1.51 | 0.795 | 0.810 | 0.800 | 0.798 |
| 2850 | 150 | 38.25 | 4.34 | 1.51 | 0.781 | 0.794 | 0.785 | 0.783 |
| 2685 | 150 | 44.01 | 4.09 | 1.51 | 0.776 | 0.788 | 0.780 | 0.778 |
| Method | Reserves Estimate (Bscf) | Deviation (Bscf) |
|---|---|---|
| Beggs and Brill | 224.4 | 4.36 |
| Hall and Yarborough | 227.7 | 1.05 |
| Standing–Katz chart | 228.7 | - |
| This work | 229.3 | 0.61 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaganis, V.; Homouz, D.; Maalouf, M.; Khoury, N.; Polychronopoulou, K. An Efficient Method to Predict Compressibility Factor of Natural Gas Streams. Energies 2019, 12, 2577. https://doi.org/10.3390/en12132577
Gaganis V, Homouz D, Maalouf M, Khoury N, Polychronopoulou K. An Efficient Method to Predict Compressibility Factor of Natural Gas Streams. Energies. 2019; 12(13):2577. https://doi.org/10.3390/en12132577
Chicago/Turabian StyleGaganis, Vassilis, Dirar Homouz, Maher Maalouf, Naji Khoury, and Kyriaki Polychronopoulou. 2019. "An Efficient Method to Predict Compressibility Factor of Natural Gas Streams" Energies 12, no. 13: 2577. https://doi.org/10.3390/en12132577
APA StyleGaganis, V., Homouz, D., Maalouf, M., Khoury, N., & Polychronopoulou, K. (2019). An Efficient Method to Predict Compressibility Factor of Natural Gas Streams. Energies, 12(13), 2577. https://doi.org/10.3390/en12132577






