A New Outer-Rotor Hybrid-Excited Flux-Switching Machine Employing the HTS Homopolar Topology
Abstract
:1. Introduction
- (1)
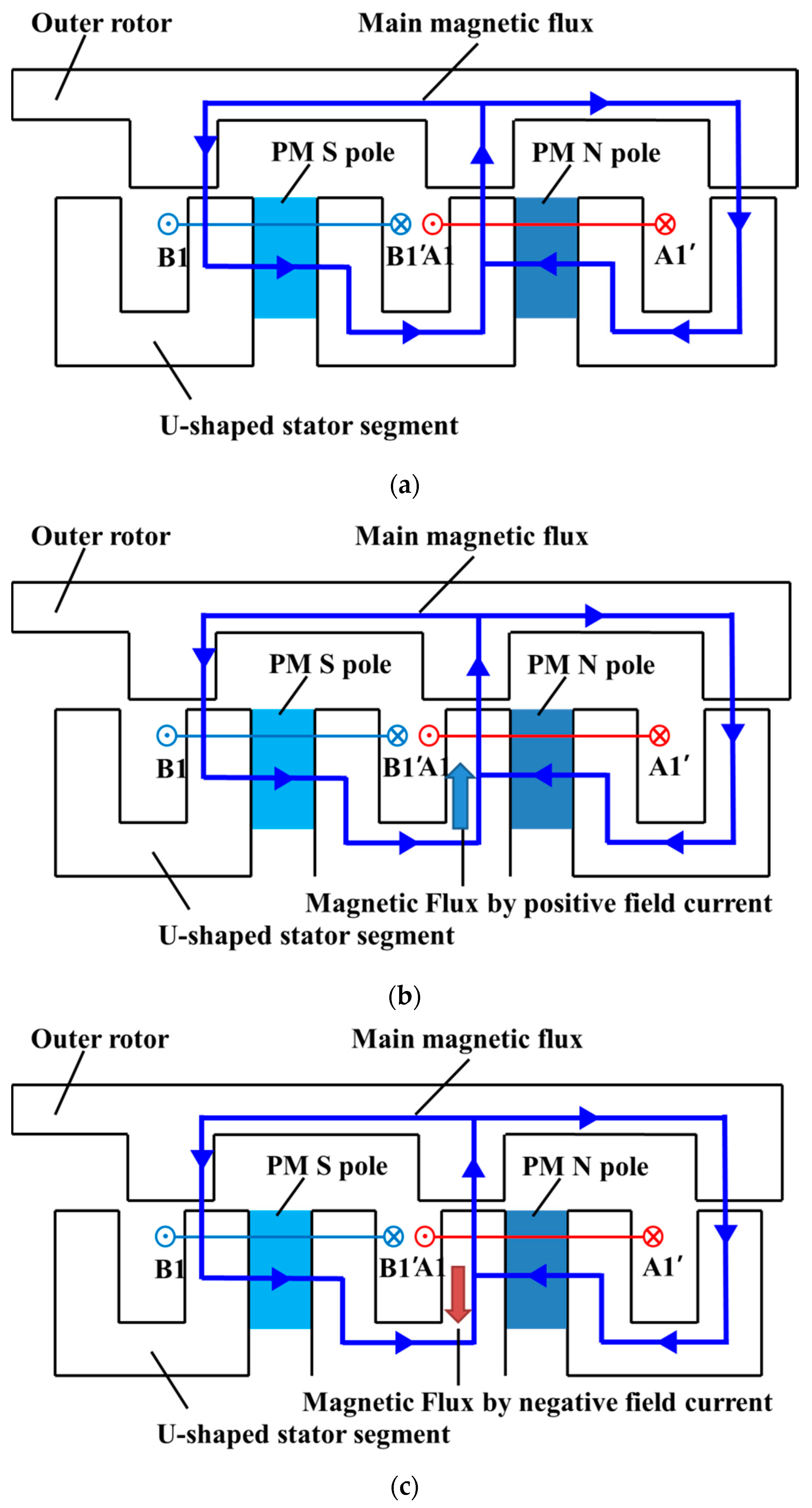
- The main magnetic flux is generated by the PMs and switching of the field polarities in the rotor tooth, for the rotating magnetic field is realized through the flux-switching topology.
- (2)
- It adopts HTS coil excitation and homopolar topology for flux regulation.
- (3)
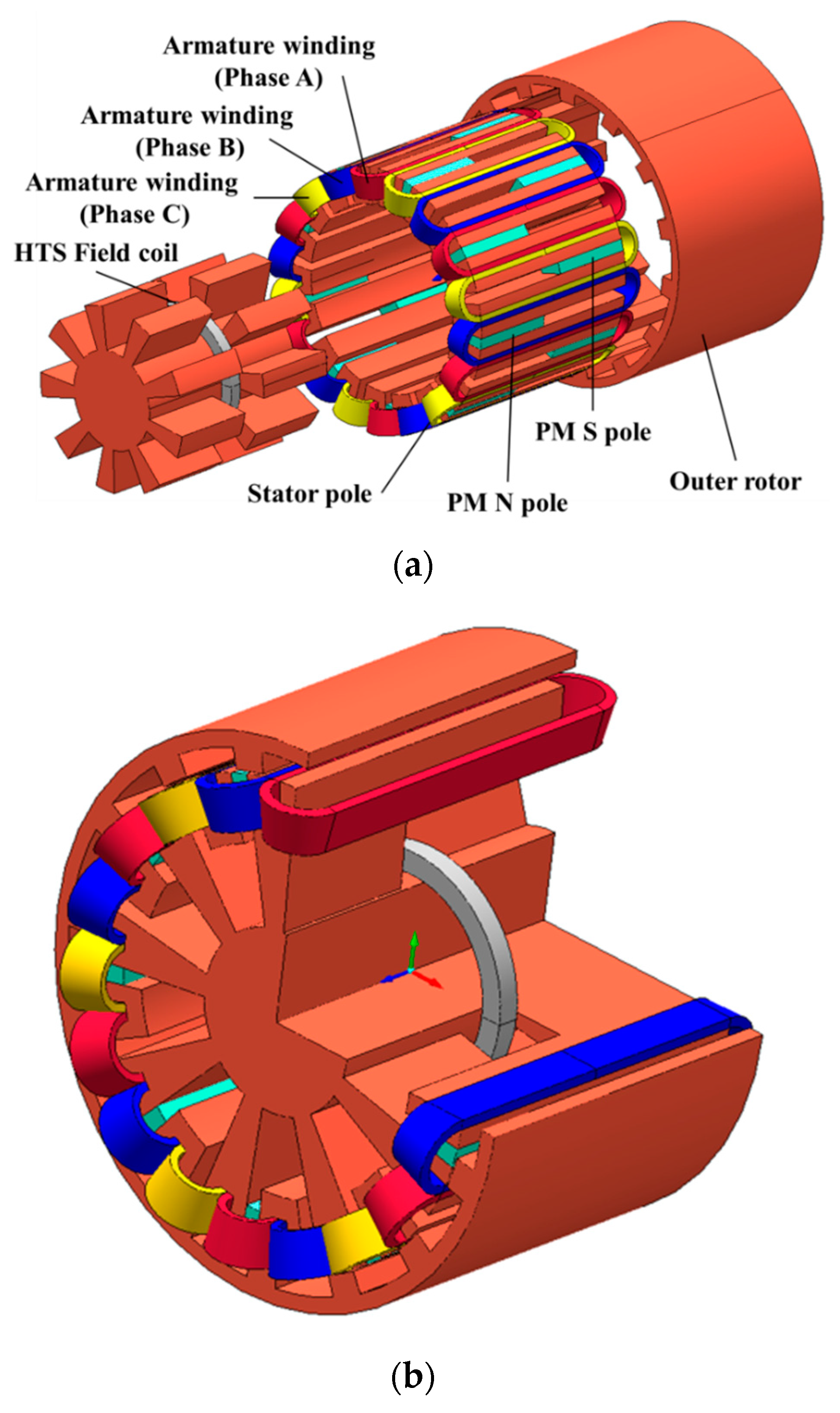
- All components such as armature winding, HTS field coil, and PMs, except outer-rotor, are located in the inner stator.
- (4)
- The outer rotor consists only of the iron-core with tooth.
2. Machine Topology, Operating Principle, and Design of the Proposed FSM
2.1. Machine Topology of the Proposed FSM
2.2. Operating Principle of the Proposed FSM
2.3. Design Methodology of the Proposed FSM and HTS Field Coil
2.4. Machine Design and Optimization
2.5. Design of the HTS Field Coil and Cryostat
3. Characteristic Analysis of the Proposed FSM
3.1. Characteristics Analysis Method Using FEM Software
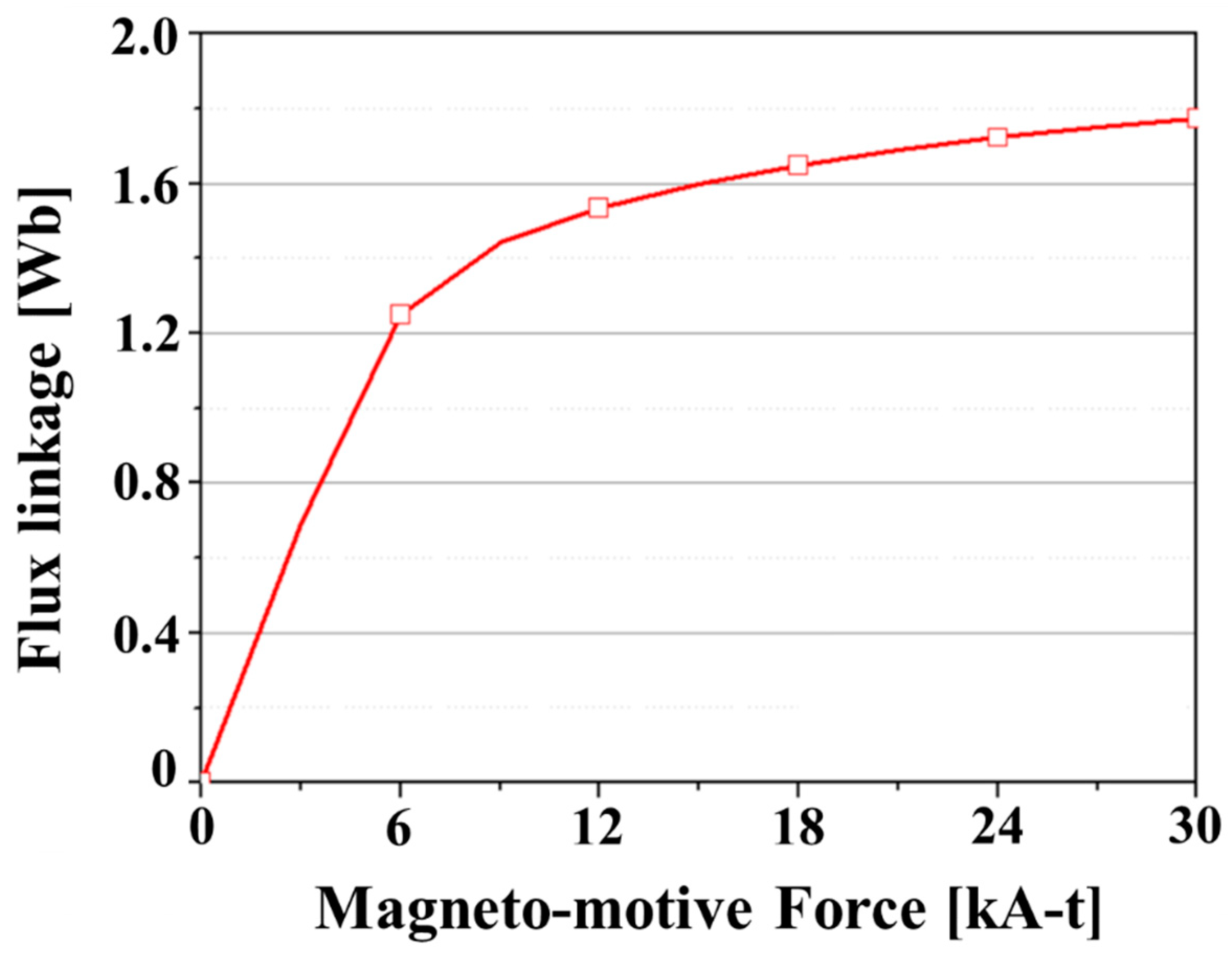
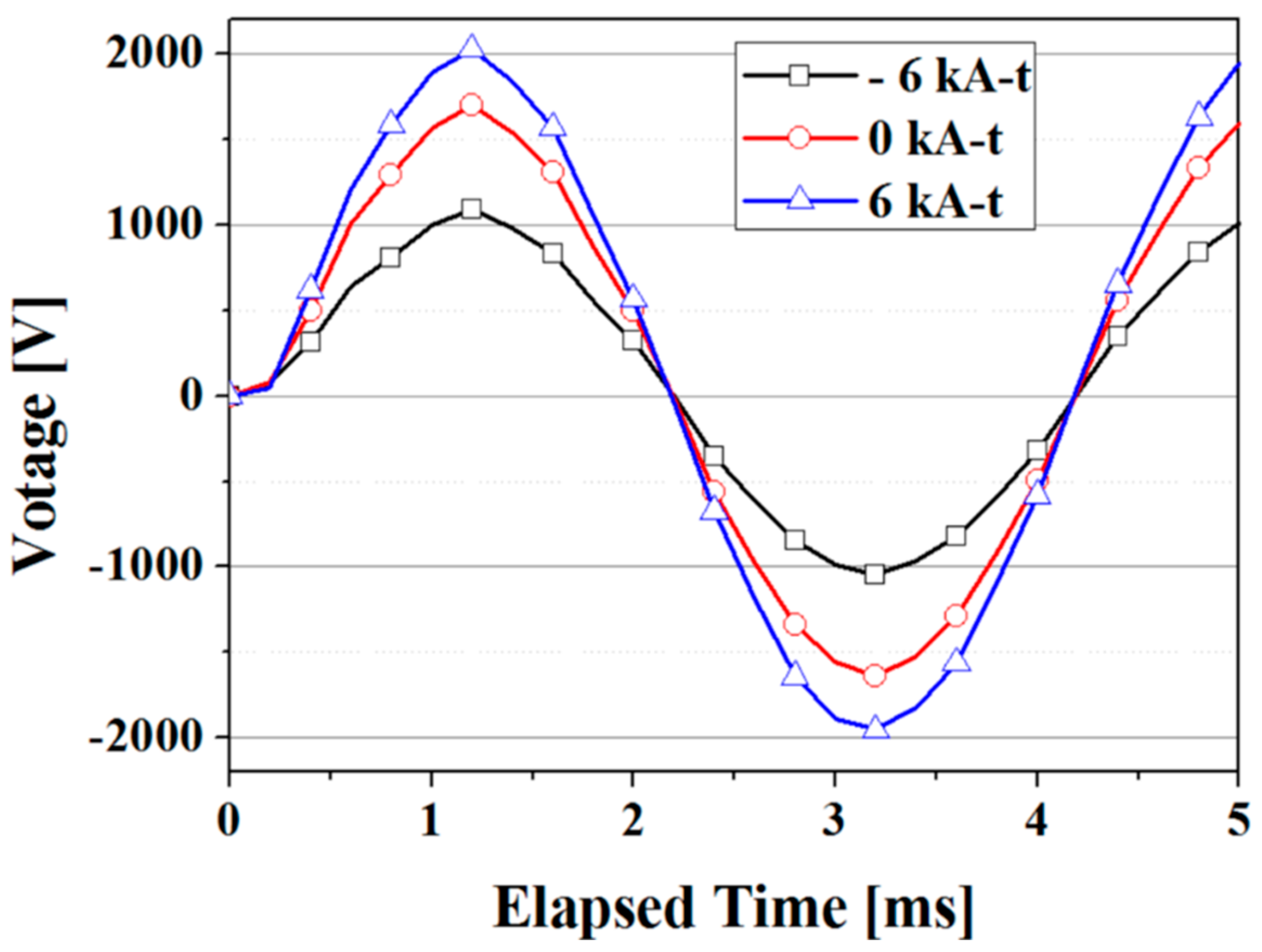
3.2. Field Distribution of the Proposed FSM
3.3. Transient Motion Analysis of the Proposed FSM
3.4. Perfomance Comparisons of the Proposed FSM with Other Outer-Rotor Brushless Machines [35,36]
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| HTS | high-temperature superconductor |
| FSM | flux switching machine |
| MMF | magneto-motive force |
| DPC | double-pancake coil |
| SPC | single-pancake coil |
| MLI | multi-layer insulation |
| FEM | finite element method |
| ρcl | electrical resistivity of the current lead |
| lcl | length of the current lead |
| I | transport current through the current lead |
| Acl | cross-sectional area of the current lead |
| kcl | thermal conductivity of the current lead |
| TH | temperature at the high-temperature part |
| TL | temperature at the low-temperature part |
| Nl | No. of signal lines or leading-in tubes |
| Al | cross-sectional area of a signal line or a leading-in tube |
| kl | thermal conductivity of a signal line or a leading-in tube |
| Ll | length of a signal line or a leading-in tube |
| σ | Stefan-Boltzmann constant (5.67 × 10-8 W·m-2·K-4) |
| εH | emissivity of the vessel |
| εN | emissivity of MLI |
| N | No. of MLI |
| AH | surface area of the high-temperature part |
| AL | surface area of the low-temperature part |
References
- Lee, C.H.T.; Chau, K.T.; Liu, C.; Lin, F. Design and Analysis of a Magnetless Flux-Switching DC-Excited Machine for Wind Power Generation. J. Int. Counc. Electr. Eng. 2014, 4, 80–87. [Google Scholar] [CrossRef] [Green Version]
- Pellegrino, G.; Vagati, A.; Guglielmi, P.; Boazzo, B. Performance comparison between surface-mounted and interior PM motor drives for electric vehicle application. IEEE Trans. Ind. Electron. 2012, 59, 803–811. [Google Scholar] [CrossRef]
- Pellegrino, G.; Armando, E.; Guglielmi, P. Direct-flux vector control of IPM motor drives in the maximum torque per voltage speed range. IEEE Trans. Ind. Electron. 2012, 59, 3780–3788. [Google Scholar] [CrossRef]
- Gieras, J.F. Permanent Magnet Motors Technology: Design and Applications, 3rd ed.; CRC Press Taylor & Francis Group: New York, NY, USA, 2010. [Google Scholar]
- Morimoto, S.; Takeda, Y.; Hirasa, T.; Taniguchi, K. Expansion of operating limits for permanent magnet motor by current vector control considering inverter capacity. IEEE Trans. Ind. Appl. 1990, 26, 866–871. [Google Scholar] [CrossRef]
- Le, W.; Ching, T.W.; Chau, K.T. Design and Analysis of an Outer-Rotor Parallel-Hybrid-Excited Vernier Machine. Chin. J. Electr. Eng. 2017, 3, 27–32. [Google Scholar]
- Hoang, E.; Lecrivain, M.; Gabsi, M. A new structure of a switching flux synchronous polyphased machine with hybrid excitations. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–8. [Google Scholar]
- Hua, W.; Cheng, M.; Zhang, G. A novel hybrid-excitation flux switching motor for hybrid vehicles. IEEE Trans. Magn. 2009, 45, 4728–4731. [Google Scholar] [CrossRef]
- Zhang, C.; Hua, W.; Cheng, M.; Liao, J.; Wang, K.; Zhang, J. Investigation of an Improved Hybrid-Excitation Flux-Switching Brushless Machine. IEEE Trans. Ind. Appl. 2015, 51, 3791–3799. [Google Scholar] [CrossRef]
- Gaussens, B.; Hoang, E.; Lécrivain, M.; Manfe, P.; Gabsi, M. A hybrid-excited flux-switching machine for high-speed DC-alternator applications. IEEE Trans. Ind. Electron. 2014, 61, 2076–2989. [Google Scholar] [CrossRef]
- Rahimi, S.K.; Sulaiman, E. Design investigation of hybrid excitation flux switching machine for high-speed electric vehicles. In Proceedings of the 2014 IEEE 8th International Power Engineering and Optimization Conference (PEOCO2014), Langkawi, Malaysia, 24–25 March 2014; pp. 303–307. [Google Scholar]
- Zhang, G.; Cheng, M.; Hua, W.; Dong, J.N. Analysis of the oversaturated effect in hybrid excited flux-switching machines. IEEE Trans. Magn. 2011, 47, 2827–2830. [Google Scholar] [CrossRef]
- Hua, W.; Cheng, M.; Zhang, G. Electromagnetic performance analysis of hybrid-excited flux-switching machines by a nonlinear magnetic network model. IEEE Trans. Magn. 2011, 47, 3216–3219. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, J.; Zhang, Y.; Guo, Y.; Lei, G. New axial laminated structure flux-switching permanent magnet machine with 6/7 poles. IEEE Trans. Magn. 2011, 47, 2823–2826. [Google Scholar] [CrossRef]
- Rauch, S.E.; Johnson, L.J. Design principles of flux-switching alternators. AIEE Trans. Power App. Syst. 1995, 74, 1261–1268. [Google Scholar]
- Zhu, Z.Q.; Chen, J.T. Advanced flux-switching permanent magnet brushless machines. IEEE Trans. Magn. 2010, 46, 1447–1453. [Google Scholar] [CrossRef]
- Hoang, E.; Ben-Ahmed, A.H.; Lucidarme, J. Switching flux permanent magnet polyphased synchronous machines. In Proceedings of the 7th European Conference on Power Electronics and Applications, Trondheim, Norway, 8–10 September 1997; pp. 903–908. [Google Scholar]
- Zhu, Z.Q.; Howe, D. Electrical machines and drives for electric, hybrid, and fuel cell vehicles. Proc. IEEE 2007, 95, 746–765. [Google Scholar] [CrossRef]
- Kim, J.M.; Jang, J.Y.; Lee, S.-G.; Hwang, Y.J. Characteristics Analysis of an HTS Flux-Switching Synchronous Generator with NI-Type HTS Field Coils. IEEE Trans. Appl. Supercond. 2018, 28, 5202705. [Google Scholar] [CrossRef]
- Li, W.; Chau, K.T.; Ching, T.W.; Wang, Y.; Chen, M. Design of a High-Speed Superconducting Bearlingless Machine for Flywheel Energy Storage Systems. IEEE Trans. Appl. Supercond. 2015, 25, 5700204. [Google Scholar]
- Lee, S.-H.; Hong, J.-P.; Kwon, Y.-K.; Jo, Y.-S.; Baik, S.-K. Study on Homopolar Superconductivity Synchronous Motors for Ship Propulsion Applications. IEEE Trans. Appl. Supercond. 2008, 18, 717–720. [Google Scholar]
- Sivasubramaniam, K.; Zhang, T.; Lokhandwalla, M.; Laskaris, E.T.; Bray, J.W.; Gerstler, B.; Shah, M.R.; Alexander, J.P. Development of a High Speed HTS Generator for Airborne Applications. IEEE Trans. Appl. Supercond. 2009, 19, 1656–1661. [Google Scholar] [CrossRef]
- Nasr, A.; Hlioui, S.; Gabsi, M.; Mairie, M.; Lalevee, D. Design Optimization of a Hybrid-Excited Flux-Switching Machine for Aircraft Safe DC Power Generation Using a Diode Bridge Rectifier. IEEE Trans. Ind. Elect. 2017, 64, 9896–9904. [Google Scholar] [CrossRef]
- Farrok, O.; Islam, M.R.; Guo, Y.; Zhu, J.; Xu, W. A Novel Design Procedure for Designing Linear Generators. IEEE Trans. Ind. Elect. 2018, 65, 1846–1854. [Google Scholar] [CrossRef]
- Farrok, O.; Islam, M.R.; Sheikh, M.R.I.; Xu, W. A new optimization methodology of the linear generator for wave energy conversion systems. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT2016), Taipei, Taiwan, 14–17 March 2016; pp. 1412–1417. [Google Scholar]
- Fei, W.; Luk, P.C.; Shen, J.X.; Wang, Y.; Jin, M.J. A Novel Permanent Magnet Flux Switching Machine with an Outer-Rotor Configuration for In-Wheel Light Traction Applications. IEEE Trans. Ind. Appl. 2012, 48, 1496–1506. [Google Scholar] [CrossRef]
- Kumar, R.; Sulaiman, E.; Jenal, M.; Bahrim, F.S. Parametric Optimization and Performance Analysis of Outer Rotor Permanent Magnet Flux Switching Machine for Downhole Application. J. Magn. 2017, 22, 69–77. [Google Scholar] [CrossRef] [Green Version]
- Hwang, Y.J.; Ahn, M.C.; Lee, J.; Yoon, Y.S.; Kim, H.M.; Chung, Y.D.; Jo, Y.-S.; Kim, T.J.; Ko, T.K. Electromagnetic design of a 15 MW-class HTS flux switching synchronous machine considering mechanical stress of the rotor core. IEEE Trans. Appl. Supercond. 2014, 24, 5202305. [Google Scholar]
- Pooke, D.M.; Chamritski, V.; Gibson, S.; Staines, M.P.; Fee, M.; Buckley, R.G. A versatile laboratory electromagnet with HTS coils. IEEE Trans. Appl. Supercond. 2004, 14, 1202–1205. [Google Scholar] [CrossRef]
- Hwang, Y.J.; Jang, J.Y.; Park, S.-Y.; Choi, Y.S. Feasibility Study of a Multipole Electromagnet Using a Parallel Iron-Core Structure. IEEE Trans. Appl. Supercond. 2018, 28, 4902005. [Google Scholar] [CrossRef]
- Kang, M.; Koo, M.; Lee, H.; Cha, G. Current estimation of an HTS BSCCO magnet having multiple power sources based on the field dependent E-J relation. IEEE Trans. Appl. Supercond. 2009, 19, 1257–1261. [Google Scholar] [CrossRef]
- Jo, H.C.; Choi, S.; Na, J.B.; Jang, J.Y.; Hwang, Y.J.; Kim, H.J.; Ahn, M.C.; Chung, Y.D.; Kim, H.M.; Ryu, K.-S.; et al. Characteristics comparison for the various winding methods of HTS magnets. IEEE Trans. Appl. Supercond. 2012, 22, 4902907. [Google Scholar]
- Sulaiman, E.; Khan, F.; Kosaka, T. Field-Excited Flux Switching Motor Design, Optimization and Analysis for Future Hybrid Electric Vehicle Using Finite Element Analysis. Prog. Electromagn. Res. B 2016, 71, 153–166. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Kim, M.S.; Choi, Y.S.; Kim, D.L. Variable Temperature Cryostat for Cryogenic Temperature Sensor Calibration. Supercond. Cryog. 2012, 14, 46–49. [Google Scholar] [CrossRef]
- Moon, H.; Kim, Y.-C.; Park, H.-J.; Park, M.; Yu, I.-K. Development of a MW-Class 2G HTS Ship Propulsion Motor. IEEE Trans. Appl. Supercond. 2016, 26, 5203805. [Google Scholar] [CrossRef]
- Maguire, J.F.; Winn, P.M.; Sidi-Yekhlef, A.; Yuan, J. Cooling System for HTS Machine. U.S. Patent 6 347 522 B1, 19 February 2002. [Google Scholar]
- Kim, Y.H.; Jang, J.Y.; Jo, H.C.; Choi, S.; Na, J.B.; Lee, C.Y.; Song, J.-B.; Lee, H.; Ko, T.K.; Hwang, Y.J. A Study on the Loss in a Superconducting Magnet by the Control Current in a Hybrid Electro-Magnetic Suspension System. IEEE Trans. Appl. Supercond. 2012, 22, 3600105. [Google Scholar] [CrossRef]
- Rabbers, J.J.; Haken, B.T.; Shevchenko, O.A.; ten Kate, H.H.J. An Engineering Formula to Describe the AC Loss of BSCCO/Ag Tape. IEEE Trans. Appl. Supercond. 2001, 11, 2623–2626. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, C.; Lee, C.H.T. Quantitative Comparisons of Six-Phase Outer-Rotor Permanent-Magnet Brushless Machines for Electric Vehicles. Energies 2018, 11, 2141. [Google Scholar] [CrossRef]
- Li, W.; Ching, T.W.; Chau, K.T.; Lee, C.H.T. A Superconducting Vernier Motor for Electric Ship Propulsion. IEEE Trans. Appl. Supercond. 2018, 28, 5201706. [Google Scholar] [CrossRef]












| Parameters | Value |
|---|---|
| No. of stator slot | 18 mm |
| No. of rotor pole | 15 mm |
| Rotor outer radius | 370 mm |
| Rotor inner radius | 318 mm |
| Stator outer radius | 315 mm |
| Active stack length | 480 mm |
| Air gap distance | 3 mm |
| Permanent magnet arc width, βpm | 3.3° |
| Rotor pole arc width, βr | 3.3° |
| Stator tooth arc width, βs | 3.3° |
| Rated rotating speed | 1000 rpm |
| Phases | 3 |
| Machines | Permanent Arc Width | Rotor Pole Arc Width | Stator Tooth Arc Width | THD of No-Load Voltage | Output Power |
|---|---|---|---|---|---|
| Initial design | 3.3° | 3.3° | 3.3° | 11.2% | 167.2 kW |
| Optimal design | 5° | 8° | 5° | 3.1% | 200.4 kW |
| Item | Value |
|---|---|
| HTS wire | Bi-2223 wire |
| Winding structure | Double pancake coil × 2EA |
| Inner radius | 130 mm |
| Outer radius | 170 mm |
| No. of turns per SPC | 50 |
| Total winding turns | 200 |
| Operating temperature | 77 K |
| Estimated Ic @ 77K | 69 A |
| Parameter | Value | |
|---|---|---|
| Conductive Heat Loss | Current Lead | 2.926 [W] |
| Signal Line | 0.045 [W] | |
| Leading-in Tube | 7.602 [W] | |
| Radiation Heat Loss | Vessel Wall | 3.557 [W] |
| Item | Value |
|---|---|
| Relative permeability | 1.06015 |
| Coercivity | −813,242 A/m |
| Residual induction Br | 1.08 T |
| Parameter | Proposed FSM | Typical PMFSM |
|---|---|---|
| Output power | 59–200 kW (Controllable) | 120 kW |
| Mass | 134 kg | 94.5 kg |
| Core loss in solely PM excitation mode | 55.7 W | 48.3 W |
| Parameter | PMVM | PMFSM | HTSVM | HEFSM |
|---|---|---|---|---|
| Efficiency | 92.89% | 86.73% | − | 87.86% |
| Base speed | 600 rpm | 1000 rpm | 230 rpm | 1000 rpm |
| Output power | 13.68 kW | 13.69 kW | 1000 kW | 200.4 kW |
| Power density | 3.6 MW/m3 | 3.6 MW/m3 | 168 kW/m3 | 3.9 MW/m3 |
| Outer rotor diameter | 220 mm | 220 mm | 3200 mm | 370 mm |
| Stack length | 100 mm | 100 mm | 740 mm | 480 mm |
| Field excitation | PM | PM | HTS | PM + HTS |
| Flux controllability | x | x | controllable | controllable |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.M.; Jang, J.Y.; Chung, J.; Hwang, Y.J. A New Outer-Rotor Hybrid-Excited Flux-Switching Machine Employing the HTS Homopolar Topology. Energies 2019, 12, 2654. https://doi.org/10.3390/en12142654
Kim JM, Jang JY, Chung J, Hwang YJ. A New Outer-Rotor Hybrid-Excited Flux-Switching Machine Employing the HTS Homopolar Topology. Energies. 2019; 12(14):2654. https://doi.org/10.3390/en12142654
Chicago/Turabian StyleKim, Jong Myung, Jae Young Jang, Jaewon Chung, and Young Jin Hwang. 2019. "A New Outer-Rotor Hybrid-Excited Flux-Switching Machine Employing the HTS Homopolar Topology" Energies 12, no. 14: 2654. https://doi.org/10.3390/en12142654
APA StyleKim, J. M., Jang, J. Y., Chung, J., & Hwang, Y. J. (2019). A New Outer-Rotor Hybrid-Excited Flux-Switching Machine Employing the HTS Homopolar Topology. Energies, 12(14), 2654. https://doi.org/10.3390/en12142654





