Thermal Response Testing of Large Diameter Energy Piles
Abstract
:1. Introduction
2. Energy Pile Design and Characterization
2.1. Design Approaches and Parameters
2.2. In-situ Characterization
2.3. Alternative Approaches
3. Methods
3.1. General Approach
3.2. Test Site Details
3.3. Pile TRT Field Trials
3.4. 3D Finite Element Analysis
3.4.1. Model Description
3.4.2. Initial and Boundary Conditions
3.5. Analytical Models for GHE Temperature Response
3.5.1. Steady State Models
3.5.2. Transient Pile Models
3.5.3. Implementation
4. Results
4.1. Numerical Simulation
4.1.1. Parameter Estimation of Ground Properties
4.1.2. Forward Simulation
4.1.3. Estimation of Steady State Thermal Resistance
4.2. Application of Analytical Models
4.2.1. Experimental Data
4.2.2. Synthetic TRT Data
4.3. Alternative Determination of Thermal Resistance
5. Discussion: Viability of Pile TRTs
5.1. Testing Time
5.2. Interpretation Methods
5.3. Construction Programme Implications
5.4. Pile versus Borehole Testing
5.5. Cost Analysis
6. Recommendations
6.1. Pile TRT Test Duration
6.2. Pile TRT Power Control
- Use of a dedicated generator rather than fluctuating site electricity supply.
- Carefully insulate the TRT casing and above ground piping, minimise surface piping lengths and attempt to keep the unit out of the sun and wind.
- Apply the highest power possible that will not cause over heating at later times to maximise the SNR in the late time part of the test. Analytical models can be used to estimate the late time temperature to help choose a power level.
- Where there is flexibility in running a heating (traditional) or cooling TRT, the difference between the initial ground temperature and the late time fluid temperature can be exploited to maximise the allowable temperature change over time. For example, if the ground temperature was 20+ °C, it may be beneficial to run a cooling test and target late time fluid temperatures around 3–4 °C instead of potentially overheating the pile with a heating test, as this maximises the temperature change in relation to maximising SNR.
- Include a recovery period in the TRT, which generally gives a better estimate of [67] and will be less susceptible to noise effects. However, this will also increase the time and cost required for the test.
6.3. Borehole Tests
7. Conclusions
- 3D numerical simulation can provide a good match to the TRT test data, providing a reliable means of parameter estimation. Subsequent forward simulation suggests no heating-cooling hysteresis, although the fit to field data does reduce with complex thermal loading cycles.
- Steady state analytical models can be used for interpretation of the test data, providing the test duration is at least 10.
- However, for tests longer than 5, high signal to noise ratio in captured field data is essential, increasing the importance of controlling the power supply to the test. Power fluctuations significantly below those required by ASHRAE are recommended to avoid loss of accuracy. Combined with 2, this makes obtaining reliable soil and pile parameters challenging.
- Alternatively, a transient analytical pile model was able to produce reliable estimates of and from much earlier in the test. This could reduce testing times and hence costs, as well as avoid the difficulties of obtaining high SNR data.
- Further cost savings can be obtained from testing a borehole on the same site and estimating the pile properties from other methods. However, consideration is required regarding the test borehole length and laboratory assessment for concrete thermal properties, both of which can add uncertainty to the results obtained.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Main symbols used | |
| α | thermal diffusivity [m2/s] |
| γ | Euler’s constant |
| λ | thermal conductivity [W/(mK)] |
| ρ | density [kg/m3] |
| A | cross sectional area [m2] |
| c | concrete cover [m] |
| Cp | specific heat capacity [kJ/(kgK)] |
| d | diameter [m] |
| dh | hydraulic diameter [m] |
| fD | Darcy friction factor |
| F | flow rate [L/s] |
| Fo | Fourier number |
| Fsc | short circuit heat loss factor |
| G | G-function |
| H | ground heat exchanger length [m] |
| J | Bessel function |
| m | gradient |
| p | pressure [kPa] |
| q | power [W/m] |
| Q | power [W] |
| r | radius [m] |
| R | resistance [mK/W] |
| s | shank spacing [m] |
| t | time [s] |
| T | temperature [°C or K] |
| v | velocity |
| Y | Bessel function |
| Subscripts | |
| 0 | initial or undisturbed |
| b | borehole or pile |
| c | concrete |
| cond | conductive |
| conv | convective |
| f | fluid |
| g | ground |
| i | inner pipe dimension |
| in | inlet |
| m | solid material (in numerical model) |
| o | outer pipe dimension |
| out | outlet |
| p | pipes |
References
- Australian Government. Australia’s 2030 Climate Change Target; Australian Government, Department of the Environment and Energy: Canberra, Australia, 2015.
- Bureau of Resources and Energy Economics. Australian Energy Update; Australian Government: Canberra, Australia, 2014.
- Lund, J.W.; Freeston, D.H.; Boyd, T.L. Direct utilization of geothermal energy 2010 worldwide review. Geothermics 2011, 40, 159–180. [Google Scholar] [CrossRef]
- Lund, J.W.; Boyd, T.L. Direct utilization of geothermal energy 2015 worldwide review. Geothermics 2016, 60, 66–93. [Google Scholar] [CrossRef]
- Brandl, H. Energy foundations and other thermo-active ground structures. Géotechnique 2006, 56, 81–122. [Google Scholar] [CrossRef]
- Loveridge, F.; Powrie, W. Temperature response functions (G-functions) for single pile heat exchangers. Energy 2013, 57, 554–564. [Google Scholar] [CrossRef]
- Bozis, D.; Papakostas, K.; Kyriakis, N. On the evaluation of design parameters effects on the heat transfer efficiency of energy piles. Energy Build. 2011, 43, 1020–1029. [Google Scholar] [CrossRef]
- Sekine, K.; Ooka, R.; Yokoi, M.; Shiba, Y.; Hwang, S. Development of a ground source heat pump system with ground heat exchanger utilizing the cast-in-place concrete pile foundations of a building. ASHRAE Trans. 2007, 113, 741–753. [Google Scholar]
- Park, S.; Sung, C.; Jung, K.; Sohn, B.; Chauchois, A.; Choi, H. Constructability and heat exchange efficiency of large diameter cast-in-place energy piles with various configurations of heat exchange pipe. Appl. Eng. 2015, 90, 1061–1071. [Google Scholar] [CrossRef]
- Lu, Q.; Narsilio, G.A. Economic analysis of utilising energy piles for residential buildings. Renew. Energy 2019. under review. [Google Scholar]
- Amis, A.; Loveridge, F.A. Energy piles and other thermal foundations for GSHP—developments in UK practice and research. REHVA J. 2014, 2014, 32–35. [Google Scholar]
- Austin, W.A., III. Development of an in Situ System for Measuring Ground Thermal Properties. Doctoral Thesis, Oklahoma State University, Stillwater, OK, USA, 1998. [Google Scholar]
- Gehlin, S.; Eklof, C. TED: A Mobile Equipment for Thermal Response Test. Master’s Thesis, Luleå University of Technology, Luleå, Sweden, 1996. [Google Scholar]
- VDI. VDI 4640 Blatt 3 Utilization of the Subsurface for Thermal Purposes; Underground Thermal Energy Storage; VDI-Gessellschaft Energie Und Umwelt (GEU): Berlin, Germany, 2001. [Google Scholar]
- Mikhaylova, O.; Johnston, I.W.; Narsilio, G.A. Uncertainties in the design of ground heat exchangers. Environ. Geotech. 2016, 3, 253–264. [Google Scholar] [CrossRef]
- Loveridge, F. The Thermal Performance of Foundation Piles Used as Heat Exchangers in Ground Energy Systems. Ph.D. Thesis, University of Southampton, Southampton, UK, 2012. [Google Scholar]
- Franco, A.; Moffat, R.; Toledo, M.; Herrera, P. Numerical sensitivity analysis of thermal response tests (TRT) in energy piles. Renew. Energy 2016, 86, 985–992. [Google Scholar] [CrossRef]
- GSHPA. Thermal Pile Design Installation and Materials Standards; Ground Source Heat Pump Association: Milt Keynes, UK, 2012. [Google Scholar]
- Hu, P.; Zha, J.; Lei, F.; Zhu, N.; Wu, T. A composite cylindrical model and its application in analysis of thermal response and performance for energy pile. Energy Build. 2014, 84, 324–332. [Google Scholar] [CrossRef]
- Loveridge, F.; Powrie, W.; Nicholson, D. Comparison of two different models for pile thermal response test interpretation. ACTA Geotech. 2014, 9, 367–384. [Google Scholar] [CrossRef] [Green Version]
- Loveridge, F.A.; Brettmann, T.; Olgun, C.G.; Powrie, W. Assessing the applicability of thermal response testing to energy piles. In Global Perspectives on the Sustainable Execution of Foundations Works; Infrastructure Group: Stockholm, Sweden, 2014; Volume 0044, p. 10. [Google Scholar]
- Badenes, B.; de Santiago, C.; Nope, F.; Magraner, T.; Urchueguia, J.F.; de Groot, M.; de Santayana, F.P.; Arcoset, J.L.; Martín, F. Thermal characterization of a geothermal precast pile in Valencia (Spain). In Proceedings of the European Geothermal Congress (EGC 2016), Strasbourg, France, 19–24 September 2016. [Google Scholar]
- Bourne-Webb, P.; Burlon, S.; Javed, S.; Kürten, S.; Loveridge, F.A. Analysis and design methods for energy geostructures. Renew. Sustain. Energy Rev. 2016, 65, 402–419. [Google Scholar] [CrossRef]
- Pahud, D. Simulation Tool for Heating/Cooling Systems with Heat Exchanger Piles or Boreholes Heat Exchangers; PileSim User’s Manual Swiss Fed Off Energy: Lausanne, Switzerland, 1999. [Google Scholar]
- Loveridge, F.; Powrie, W. 2D thermal resistance of pile heat exchangers. Geothermics 2014, 50, 122–135. [Google Scholar] [CrossRef]
- Spitler, J.D.; Gehlin, S.E.A. Thermal response testing for ground source heat pump systems—An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Witte, H.J.L. In situ estimation of ground thermal properties. In Advances in Ground-Source Heat Pump Systems; Rees, S., Ed.; Woohosue Publishing: Duxford, UK, 2016. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Beier, R.A.; Smith, M.D. Borehole thermal resistance from line-source model of in-situ tests. ASHRAE Trans. 2002, 108, 212–219. [Google Scholar]
- Vieira, A.; Alberdi-Pagola, M.; Christodoulides, P.; Javed, S.; Loveridge, F.; Nguyen, F.; Florides, G.; Radioti, G.; Cecinato, F.; Prodan, I.; et al. Characterisation of ground thermal and thermo-mechanical behaviour for shallow geothermal energy applications. Energies 2017, 10, 2044. [Google Scholar] [CrossRef]
- Eskilson, P. Thermal Analysis of Heat Extraction Boreholes. Doctoral Thesis, University of Lund, Lund, Sweden, 1987. [Google Scholar]
- Beier, R.A.; Smith, M.D. Minimum Duration of In-Situ Tests on Vertical Boreholes. ASHRAE Trans. 2003, 109, 475–486. [Google Scholar]
- Loveridge, F.; Low, J.; Powrie, W. Site investigation for energy geostructures. Q. J. Eng. Geol. Hydrogeol. 2017, 50, 158–168. [Google Scholar] [CrossRef]
- Loveridge, F.; Olgun, C.G.; Brettmann, T.; Powrie, W. The thermal behaviour of three different auger pressure grouted piles used as heat exchangers. Geotech. Geol. Eng. 2014, 33, 273–289. [Google Scholar] [CrossRef]
- Franco, A.; Fantozzi, F. Experimental analysis of a self consumption strategy for residential building: The integration of PV system and geothermal heat pump. Renew. Energy 2016, 86, 1075–1085. [Google Scholar] [CrossRef]
- Alberdi-Pagola, M.; Poulsen, S.E.; Loveridge, F.; Madsen, S.; Jensen, R.L. Comparing heat flow models for interpretation of precast quadratic pile heat exchanger thermal response tests. Energy 2018, 145, 721–733. [Google Scholar] [CrossRef]
- Bouazza, A.; Wang, B.; Singh, R.M. Soil effective thermal conductivity from energy pile thermal tests. In Proceedings of the International Congress on Environmental Geotechnics, Torino, Italy, 1–3 July 2013; pp. 211–219. [Google Scholar]
- Lennon, D.J.; Watt, E.; Suckling, T.P. Energy piles in Scotland. In Proceedings of the Fifth International Conference Deep Found Bored Auger Piles, Frankfurt, Germany, 15 May 2009. [Google Scholar]
- Ozudogru, T.; Brettmann, T.; Olgun, G.; Martin, J.; Senol, A. Thermal conductivity testing of energy piles: Field testing and numerical modeling. In Proceedings of the Geo-Congress, Oakland, CA, USA, 25–29 March 2012; pp. 25–29. [Google Scholar]
- Jensen-Page, L.; Narsilio, G.A.; Johnston, I.W.; Aditya, G.A.; Mikhaylova, O. Uncertainty in Ground Thermal Conductivity. Energies 2019. under review. [Google Scholar]
- Hellström, G. Ground Heat Storage: Thermal analyses of Duct Storage Systems. Ph.D. Thesis, Lund University, Lund, Sweden, 1991. [Google Scholar]
- Bennet, J.; Claesson, J.; Hellström, G. Multipole method to compute the conductive heat flows to and between pipes in a composite cylinder. In Notes Heat Transfer; Lund University Publications: Cambridge, MA, USA, 1987; Volume 3. [Google Scholar]
- Lamarche, L.; Kajl, S.; Beauchamp, B. A review of methods to evaluate borehole thermal resistances in geothermal heat-pump systems. Geothermics 2010, 39, 187–200. [Google Scholar] [CrossRef]
- Colls, S.; Johnston, I.; Narsillo, G. Experimental study of ground energy systems in Melbourne, Australia. Aust. Geomech. J. 2012, 47, 15–20. [Google Scholar]
- Colls, S. Ground Heat Exchanger Design for. Direct Geothermal Energy Systems. Ph.D. Thesis, The University of Melbourne, Melbourne, Australia, 2013. [Google Scholar]
- Peck, W.A.; Neilson, J.L.; Olds, R.J.; Seddon, K.D. Engineering Geology of Melbourne; Balkema: Rotterdam, The Netherlands, 1992. [Google Scholar]
- Barry-Macaulay, D.; Colls, S.; Wang, B. Thermal properties of the Melbourne Mudstone. In Proceedings of the 12th Australia New Zealand Conference on Geomechanics, Wellington, New Zealand, 22–25 February 2015; pp. 183–190. [Google Scholar]
- Jensen-Page, L.; Narsilio, G.A. Geothermal Testing—Estimation of Thermal Conductivity of Soil and Rock Using a Borehole Heat Exchanger and Laboratory Testing; Golder Associates Pty Ltd.: Melbourne, Australia, 2016. [Google Scholar]
- Gehlin, S.E.A.; Nordell, B. Determining undisturbed ground temperature for thermal response test. Trans. Soc. Heat Refrig. Air Cond. Eng. 2003, 109, 151–156. [Google Scholar]
- ASHRAE. Geothermal energy. HVAC Appl.—Chapter 34 Geotherm. 2011. Available online: https://energy-pe.com/geothermal.htm (accessed on 21 January 2018).
- Narsilio, G.; Bidarmaghz, A.; Colls, S.; Johnston, I. Geothermal energy, detailed modelling of ground heat exchangers. Comput. Geotech. 2019. under review. [Google Scholar]
- Bidarmaghz, A.; Makasis, N.; Narsilio, G.A.; Francisca, F.M.; Carro Pérez, M.E. Geothermal energy in loess. Environ. Geotech. 2016, 3, 225–236. [Google Scholar] [CrossRef]
- Bidarmaghz, A. 3D Numerical Modelling of Vertical Ground Heat Exchangers. Ph.D. Thesis, The University of Melbourne, Melbourne, Australia, 2014. [Google Scholar]
- Barnard, A.C.L.; Hunt, W.A.; Timlake, W.P.; Varley, E. A theory of fluid flow in compliant tubes. Biophys. J. 1966, 6, 717–724. [Google Scholar] [CrossRef]
- Lurie, M.V. Modeling and Calculation of Stationary Operating Regimes of Oil and Gas. Pipelines; Wiley: Weinheim, Germany, 2008. [Google Scholar]
- Zarrella, A.; Emmi, G.; Graci, S.; De Carli, M.; Cultrera, M.; Santa, G.D.; Galgaro, A.; Bertermann, D.; Müller, J.; Pockelé, L.; et al. Thermal Response Testing Results of Different Types of Borehole Heat Exchangers: An Analysis and Comparison of Interpretation Methods. Energies 2017, 10, 801. [Google Scholar] [CrossRef]
- Ingersoll, L.R.; Zabel, O.J.; Ingersoll, A.C. Heat Conduction: With Engineering Geological and Other Applications; Oxford And IBH Publishing Co.: Calcutta/Bombay/New Delhi, India, 1954. [Google Scholar]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools for Python. 2014. Available online: https://www.bibsonomy.org/bibtex/21b37d2cc741af879d7958f2f7c23c420/microcuts (accessed on 15 July 2019).
- Zeng, H.Y.; Diao, N.R.; Fang, Z.H. A finite line-source model for boreholes in geothermal heat exchangers. Heat Transf. Asian Res. 2002, 31, 558–567. [Google Scholar] [CrossRef]
- Zeng, H.; Diao, N.; Fang, Z. Heat transfer analysis of boreholes in vertical ground heat exchangers. Int. J. Heat Mass. Transf. 2003, 46, 4467–4481. [Google Scholar] [CrossRef]
- Lamarche, L.; Beauchamp, B. A new contribution to the finite line-source model for geothermal boreholes. Energy Build. 2007, 39, 188–198. [Google Scholar] [CrossRef]
- Choi, W.; Ooka, R. Interpretation of disturbed data in thermal response tests using the infinite line source model and numerical parameter estimation method. Appl. Energy 2015, 148, 476–488. [Google Scholar] [CrossRef]
- Loveridge, F.; Powrie, W. Performance of piled foundations used as heat exchangers. In Proceedings of the 18th International Conference on Soil Mechanics Geotechnical Engineering, Paris, France, 2–6 September 2013. [Google Scholar]
- Fujii, H.; Okubo, H.; Nishi, K.; Itoi, R.; Ohyama, K.; Shibata, K. An improved thermal response test for U-tube ground heat exchanger based on optical fiber thermomefters. Geothermics 2009, 38, 399–406. [Google Scholar] [CrossRef]
- Acuña, J.; Mogensen, P.; Palm, B. Distributed thermal response test on a U-pipe borehole heat exchanger. In Proceedings of the Effstock 2009, 11th International Conference on Thermal Energy Storage, Stockholm, Sweden, 14–17 June 2009. [Google Scholar]
- Lu, Q.; Narsilio, G.A.; Aditya, G.R.; Johnston, I.W. Economic analysis of vertical ground source heat pump systems in Melbourne. Energy 2017, 125, 107–117. [Google Scholar] [CrossRef]
- Marcotte, D.; Pasquier, P. On the estimation of thermal resistance in borehole thermal conductivity test. Renew. Energy 2008, 33, 2407–2415. [Google Scholar] [CrossRef]
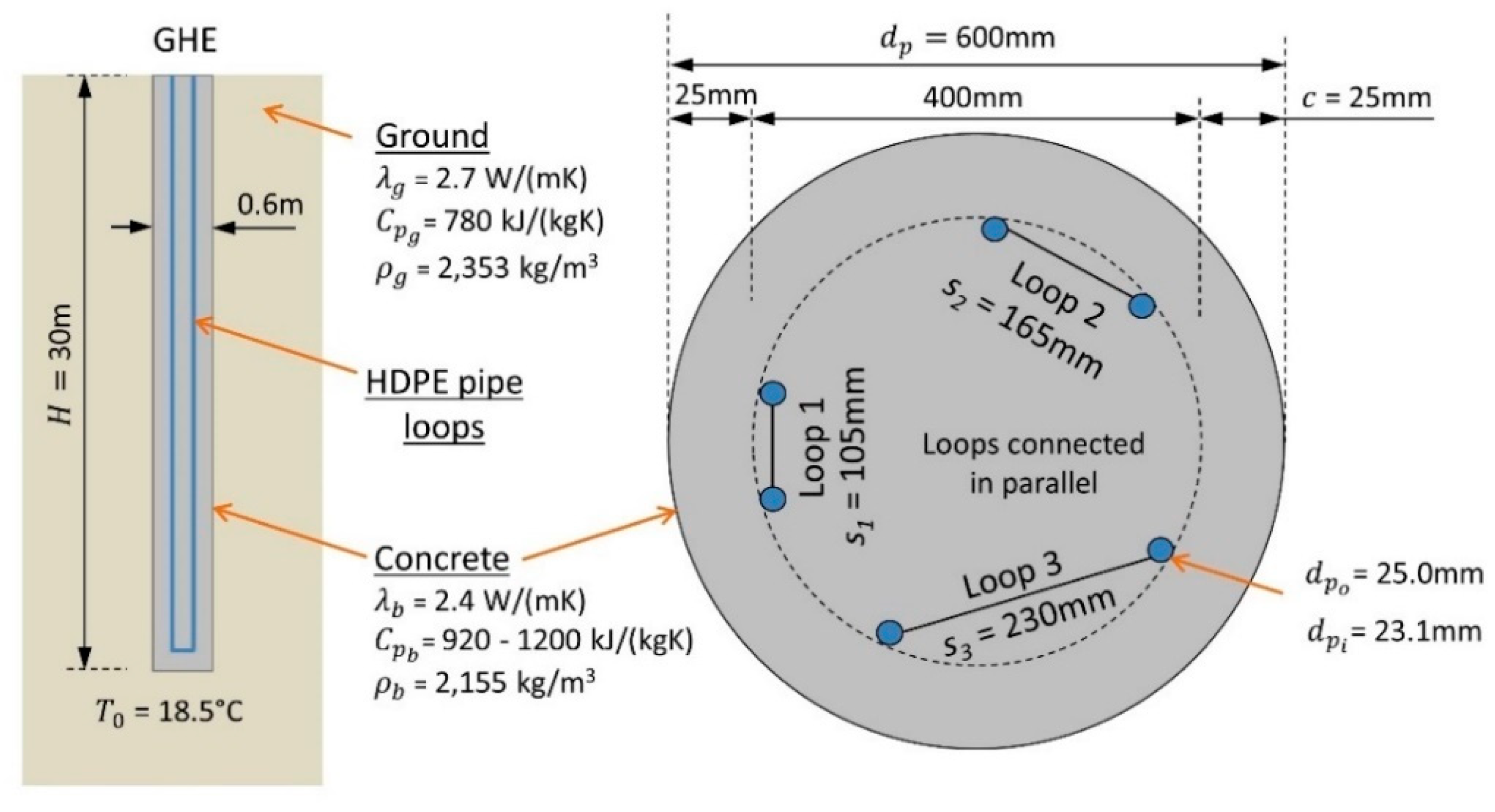












| Parameter | Symbol | Value | Source | Details |
|---|---|---|---|---|
| Geometry | ||||
| Pile length | 30 m | [45] | ||
| Pile diameter | 0.6 m | [45] | ||
| Concrete cover | 0.2 m | [45] | ||
| Loop shank spacing (m) | See Figure 1 | [45] | ||
| Pipe outer diameter | 0.025 m | [45] | ||
| Pipe inner diameter | 0.0213 m | [45] | ||
| Flow rate (total) | 0.75 L/s | |||
| Thermal Properties | ||||
| Pipe thermal conductivity | 0.4 W/(mK) | |||
| Fluid thermal conductivity | 0.582 W/(mK) | |||
| Ground thermal conductivity | 2.7 W/(mK) | [45,47] | Adjacent borehole TRT; laboratory tests using TCi sensor and divided bar method. | |
| Concrete thermal conductivity | 2.4 W/(mK) | [45] | ||
| Fluid heat capacity | 4180 kJ/(kgK) | |||
| Ground heat capacity | 780 kJ/(kgK) | [48] | TCi sensor test on >50 rock cores from different sites with same geology | |
| Concrete heat capacity | 920–1200 kJ/(kgK) | [45] | ||
| Fluid density | 1000 kg/m3 | |||
| Ground density (dry) | 2353 kg/m3 | [45] | Measured on core before thermal tests | |
| Concrete density (dry) | 2155 kg/m3 | [45] | Measured on core before thermal tests | |
| Undisturbed ground temperature | 18.5 °C | [44] | ||
| Test | Type | Start | Length | Q *-Mean | Q-Standard Deviation | |
|---|---|---|---|---|---|---|
| (kW) | (kW) | (%) | ||||
| TRT1 | Heating | 25/05/17 | 14 d | 1.8 | 0.058 | 3.2 |
| - | Rest Period | 9/06/17 | 33 d | |||
| TRT2 | Heating | 11/07/17 | 4 d | 2.8 | 1.08 | 46.7 |
| - | Rest Period | 15/07/17 | 14 d | |||
| Fail 1 | - | 30/07/17 | 1 h | |||
| Fail 2 | - | 31/07/17 | 4.5 h | |||
| TRT3 | Cooling | 3/08/17 | 3.5 d | −3.6 | 0.077 | 2.4 |
| - | Recovery | 7/08/17 | 2 d | |||
| TRT4 | Heating | 11/08/17 | 19 h | 2.5 | 1.3 | 51.2 |
| TRT5 | Cooling | 14/08/17 | 13 h | −3.8 | 0.28 | 7.4 |
| TRT6 | Heating | 15/08/17 | 17 h | 3.7 | 0.81 | 21.7 |
| TRT7 | Cooling | 16/08/17 | 29 h | −4.2 | 0.26 | 6.2 |
| Parameter | Independent Estimate | This Parameter Estimation |
|---|---|---|
| (W/(mK)) | 2.69 [45,47] | 2.7 |
| (W/(mK)) | 2.4 [45] | 2.5 |
| (kJ/(m3K)) | 1835 [45,48] | 1872 |
| (kJ/(m3K)) | 1940–2580 [45] | 2280 |
| TRT | Test Type | RMSE of Numerical Model Fit (°C) |
|---|---|---|
| TRT1 | Heating | 0.048 |
| TRT2 | Heating | 1.744 |
| Fail 1 | - | 0.314 |
| Fail 2 | - | 0.102 |
| TRT3 | Cooling | 1.503 |
| TRT4 | Heating | 0.382 |
| TRT5 | Cooling | 0.484 |
| TRT6 | Heating | 0.386 |
| TRT7 | Cooling | 0.930 |
| Model | Source | |
|---|---|---|
| Empirical 2D resistance | Loveridge & Powrie [25] | 0.0913 + |
| PILESIM Manual recommendations based on Multipole | Pahud [24] | 0.07–0.08 * |
| Multipole method | Bennet, et al. [42] | 0.0514 + |
| Numerical analysis | Equation (4) | 0.056 |
| Factor | Working Pile TRT | Bespoke Borehole TRT | Existing Borehole TRT |
|---|---|---|---|
| Description | Test on working pile | Test on specially drilled borehole after pile design complete | Test on site investigation borehole converted to GHE |
| Programme | Severe programme implications | Minimal programme implications | Minimal to no programme implications |
| Cost (see also Table 7) | High cost | Low cost | Lowest cost |
| Results- | Potentially less accurate than borehole TRT | Potentially more accurate than pile TRT | Increase in accuracy offset against unknown pile length at this stage |
| Results- | Additional benefit is mainly in determining in-situ, although often less accurately than | Reliable methods to estimate analytically are not very accessible. Independent assessment of thermal properties required which comes with additional uncertainty and cost | |
| Costs (AU$) | Working Pile | Bespoke Borehole | Existing Borehole |
|---|---|---|---|
| Drilling | 0 | 30 m @ $80/m = $2400 | 0 |
| Materials 1 | 0 | 30 m @ $30/m = $900 | 30 m @ $30/m = $900 |
| Additional 2 programme time | $$$ (depends on project) | 0 | 0 |
| Running Test 3 | 14 days @ $2000/day = $28,000 | 3 days @ $2000/day = $6000 | 3 days @ $2000/day = $6000 |
| Lab Testing | 0 | $1000 | $1000 |
| TOTAL | $28,000 (minimum) | $10,300 | $7900 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jensen-Page, L.; Loveridge, F.; Narsilio, G.A. Thermal Response Testing of Large Diameter Energy Piles. Energies 2019, 12, 2700. https://doi.org/10.3390/en12142700
Jensen-Page L, Loveridge F, Narsilio GA. Thermal Response Testing of Large Diameter Energy Piles. Energies. 2019; 12(14):2700. https://doi.org/10.3390/en12142700
Chicago/Turabian StyleJensen-Page, Linden, Fleur Loveridge, and Guillermo A. Narsilio. 2019. "Thermal Response Testing of Large Diameter Energy Piles" Energies 12, no. 14: 2700. https://doi.org/10.3390/en12142700
APA StyleJensen-Page, L., Loveridge, F., & Narsilio, G. A. (2019). Thermal Response Testing of Large Diameter Energy Piles. Energies, 12(14), 2700. https://doi.org/10.3390/en12142700





