Near Field Wireless Powering of Deep Medical Implants
Abstract
:1. Introduction
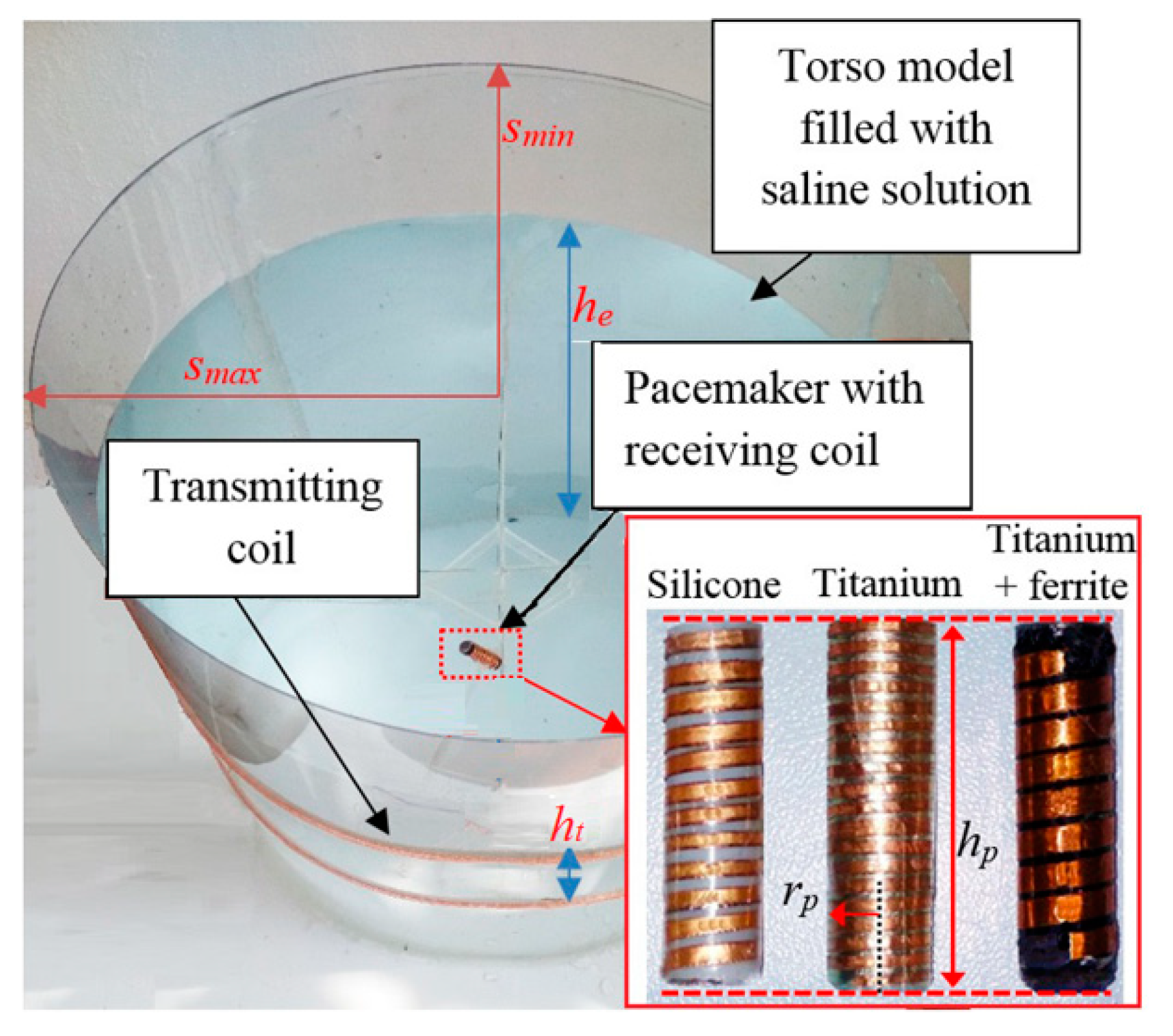
2. Wireless Power Transfer (WPT) System Design
2.1. Electromagnetic Field Model
2.2. Transmitting Side Design
- (1)
- design of the primary coil that maximizes the working area inside the human body where the AIMD is located;
- (2)
- definition of the most suitable operational frequency that allows a deep penetration of the time-varying magnetic field without exceeding the EMF safety limits.
- -
- the excitation is given by two series-connected elliptical solenoids with top-bottom configuration assuming the human body in upright position;
- -
- the human body is assumed to be a simple multilayer cylinder with vertical axis.
2.3. Receiving Side Design
- -
- Test case #1: silicone;
- -
- Test case #2: titanium;
- -
- Test case #3: titanium covered with an external layer of ferrite with thickness tfe = 0.4 mm.
2.4. WPT Electrical Performances
- -
- N2 = 12 for the test case #1 (silicone);
- -
- N2 = 20 for the test case #2 (titanium housing);
- -
- N2 = 8 for the test case #3 (titanium housing + ferrite).
2.5. Thermal Analysis
3. WPT System Demonstrator
3.1. Electrogeometrical Configuration
- -
- Test case #1: N2 = 12, rc = 4.5 mm, ws = 1.9 mm, hc = 28 mm.
- -
- Test case #2: N2 = 20, rc = 4.5 mm, ws = 0.9 mm, hc = 28 mm.
- -
- Test case #3: N2 = 8, rc = 4.5 mm, ws = 3 mm, hc = 28 mm, MnZn ferrite [11] with thickness tfe = 0.4 mm.
3.2. Numerical and Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Campi, T.; Cruciani, S.; Palandrani, F.; De Santis, V.; Hirata, A.; Feliziani, M. Wireless Power Transfer Charging System for AIMDs and Pacemakers. IEEE Trans. Microw. Theory Tech. 2016, 64, 633–642. [Google Scholar] [CrossRef]
- Campi, T.; Cruciani, S.; De Santis, V.; Feliziani, M. EMF Safety and Thermal Aspects in a Pacemaker Equipped with a Wireless Power Transfer System Working at Low Frequency. IEEE Trans. Microw. Theory Tech. 2016, 64, 375–382. [Google Scholar] [CrossRef]
- Xiao, C.; Wei, K.; Cheng, D.; Liu, Y. Wireless Charging System Considering Eddy Current in Cardiac Pacemaker Shell: Theoretical Modeling, Experiments, and Safety Simulations. IEEE Trans. Ind. Electron. 2017, 64, 3978–3988. [Google Scholar] [CrossRef]
- Monti, G.; Arcuti, P.; Tarricone, L. Resonant Inductive Link for Remote Powering of Pacemakers. IEEE Trans. Microw. Theory Tech. 2015, 63, 3814–3822. [Google Scholar] [CrossRef]
- Campi, T.; Cruciani, S.; De Santis, V.; Maradei, F.; Feliziani, M. Feasibility Study of a Wireless Power Transfer System Applied to a Leadless Pacemaker. In Proceedings of the IEEE Wireless Power Transfer Conference (WPTC), Montreal, Canada, 3–7 June 2018. [Google Scholar]
- Yang, C.-L.; Chang, C.-K.; Lee, S.-Y.; Chang, S.-J.; Chiou, L.-Y. Efficient Four-Coil Wireless Power Transfer for Deep Brain Stimulation. IEEE Trans. Microw. Theory Tech. 2017, 65, 2496–2507. [Google Scholar] [CrossRef]
- Puers, R.; Carta, R.; Thoné, J. Wireless power and data transmission strategies for next-generation capsule endoscopes. J. Micromech. Microeng. 2011, 21, 054008. [Google Scholar] [CrossRef]
- Basar, M.R.; Ahmad, M.Y.; Cho, J.; Ibrahim, F. An Improved Wearable Resonant Wireless Power Transfer System for Biomedical Capsule Endoscope. IEEE Trans. Ind. Electron. 2018, 65, 7772–7781. [Google Scholar] [CrossRef]
- Poon, A.S.Y.; O’Driscoll, S.; Meng, T.H. Optimal Frequency for Wireless Power Transmission Into Dispersive Tissue. IEEE Trans. Antennas Propag. 2010, 58, 1739–1750. [Google Scholar] [CrossRef]
- Ho, J.S.; Kim, S.; Poon, A.S.Y. Midfield Wireless Powering for Implantable Systems. Proc. IEEE 2013, 101, 1369–1378. [Google Scholar] [CrossRef]
- International Commission on Non-Ionizing Radiation Protection. Guidelines for limiting exposure to time-varying electric and magnetic fields for low frequencies (1 Hz–100 kHz). Health Phys. 2010, 99, 818–836. [Google Scholar]
- International Commission on Non-Ionizing Radiation Protection. Guidelines for limiting exposure to time-varying electric, magnetic, and electromagnetic fields (up to 300 GHz). Health Phys. 1998, 74, 494–522. [Google Scholar]
- IEEE.Std.C95.1-2005. IEEE standard for safety levels with respect to human exposure to radio frequency electromagnetic fields, 3 kHz to 300 GHz. 2006. Available online: http://dx.doi.org/10.1109/ieeestd.1999.89423 (accessed on 25 May 2019).
- Basar, M.R.; Yazed, A.M.; Cho, J.; Fatimah, I. A wireless power transmission system for robotic capsule endoscopy: Design and optimization. In Proceedings of the 2014 IEEE MTT-S International Microwave Workshop Series on RF and Wireless Technologies for Biomedical and Healthcare Applications (IMWS-Bio2014), London, UK, 8–10 December 2014. [Google Scholar]
- Hasgall, P.A.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.C.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for thermal and electromagnetic parameters of biological tissues. Version 4.0. 15 May 2018. Available online: http://www.itis.swiss/database (accessed on 10 December 2018).
- Bronaugh, E.L. Helmholtz coils for calibration of probes and sensors: Limits of magnetic field accuracy and uniformity. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Atlanta, GA, USA, 14–18 August 1995. [Google Scholar]
- Chen, X.L.; Umenei, A.E.; Chavannes, N.; De Santis, V.; Mosig, J.; Kuster, N. Human Exposure to Close-Range Resonant Wireless Power Transfer Systems as a Function of Design Parameters. IEEE Tran. Electromagn. Compat. 2014, 56, 1027–1034. [Google Scholar] [CrossRef]
- De Santis, V.; Chen, X.L.; Laakso, I.; Hirata, A. An equivalent skin conductivity model for low-frequency magnetic field dosimetry. Biomed. Phys. Eng. Express 2015, 1, 015201. [Google Scholar] [CrossRef]
- Christ, A.; Kainz, W.; Hahn, E.G.; Honegger, K.; Zefferer, M.; Neufeld, E.; Rascher, W.; Janka, R.; Bautz, W.; Chen, J.; et al. The Virtual Family—Development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys. Med. Biol. 2010, 55, N23–N38. [Google Scholar] [CrossRef] [PubMed]
- Sim4Life-v3.2. SIMulation 4 LIFE Science Platform. Available online: http://www.zurichmedtech.com/sim4life (accessed on 10 November 2018).
- De Santis, V.; Chen, X.L. On the issues related to compliance assessment of ICNIRP 2010 basic restrictions. J. Radiol. Prot. 2014, 34, N31–N39. [Google Scholar] [CrossRef] [PubMed]
- ANSI/AAMI/ISO 14117:2012. Active Implantable Medical Devices—Electromagnetic Compatibility—Emc Test Protocols for Implantable Cardiac Pacemakers, Implantable Cardioverter Defibrillators and Cardiac Resynchronization Device. Available online: https://www.iso.org/obp/ui/#iso:std:iso:14117:ed-1:v1:en (accessed on 25 May 2019).
- Campi, T.; Cruciani, S.; Feliziani, M. Magnetic shielding of Wireless Power Transfer systems. In Proceedings of the International Symposium Electromagnetic Compatibility (EMC’14), Tokyo, Japan, 12–16 May 2014; pp. 422–425. [Google Scholar]
- Campi, T.; Cruciani, S.; Maradei, F.; Feliziani, M. Magnetic shielding design of Wireless Power Transfer systems. In Proceedings of the 2015 IEEE Applied Computational Electromagnetics (ACES), Williamsburg, VA, USA, 22–26 March 2015; pp. 1–2. [Google Scholar]
- Campi, T.; Cruciani, S.; Maradei, F.; Feliziani, M. Near-Field Reduction in a Wireless Power Transfer System Using LCC Compensation. IEEE Trans. Electromagn. Compat. 2017, 59, 686–694. [Google Scholar] [CrossRef]
- Kim, D.-H.; Kim, J.; Park, Y.-J. Optimization and Design of Small Circular Coils in a Magnetically Coupled Wireless Power Transfer System in the Megahertz Frequency. IEEE Trans. Microw. Theory Tech. 2016, 64, 2652–2663. [Google Scholar] [CrossRef]
- Abiri, P.; Abiri, A.; Sevag Packard, R.R.; Ding, Y.; Yousefi, A.; Ma, J.; Bersohn, M.; Nguyen, K.-L.; Markovic, D.; Moloudi, S.; et al. Inductively powered wireless pacing via a miniature pacemaker and remote stimulation control system. Sci. Rep. 2017, 7, 6180. [Google Scholar] [CrossRef] [PubMed]
- Das, R.; Yoo, H. Biotelemetry and Wireless Powering for Leadless Pacemaker Systems. IEEE Microw. Wirel. Compon. Lett. 2015, 25, 262–264. [Google Scholar] [CrossRef]
- Stogryn, A. Equations for Calculating the Dielectric Constant of Saline Water (Correspondence). IEEE Trans. Microw Theory Tech. 1971, 19, 733–736. [Google Scholar] [CrossRef]



















| Avg 2 × 2 × 2 mm3 E (V/m) | Avg 5 mm E (V/m) | 10 g avg SAR (W/kg) | |
|---|---|---|---|
| Calculated | 324 | 484 | 1.98 |
| BR Limit | 540 (ICNIRP) | 835 (IEEE) | 2.00 (ICNIRP-IEEE) |
| Angle θ | Silicone | Titanium | Titanium + Ferrite Cover |
|---|---|---|---|
| 0° | 3.62 × 10−10 | 1.15 × 10−10 | 2.69 × 10−9 |
| 30° | 3.16 × 10−10 | 1.01 × 10−10 | 2.34 × 10−9 |
| 60° | 1.90 × 10−10 | 6.54 × 10−10 | 1.36 × 10−9 |
| 80° | 0.76 × 10−10 | 0.33 × 10−10 | 0.48 × 10−9 |
| Test Case | L2 (μH) | M (nH) | R2 (mΩ) | |
|---|---|---|---|---|
| #1 | Numerical | 430 | 18 | 120 |
| Measured | 480 | 17 | 180 | |
| #2 | Numerical | 540 | 13 | 630 |
| Measured | 490 | 10 | 540 | |
| #3 | Numerical | 1420 | 84 | 840 |
| Measured | 1220 | 77 | 920 | |
| Test Case | Primary Coil Current (A) | Efficiency η | ||
|---|---|---|---|---|
| Numerical | Measured | Numerical | Measured | |
| #1 | 0.20 | 0.23 | 0.40 | 0.34 |
| #2 | 0.49 | 0.61 | 0.09 | 0.07 |
| #3 | 0.14 | 0.15 | 0.60 | 0.58 |
| dpx (mm) | dpz (mm) | Efficiency η | Primary Coil Current (A) |
|---|---|---|---|
| 0 | 0 | 0.47 | 0.25 |
| 50 | 0 | 0.51 | 0.20 |
| 100 | 0 | 0.52 | 0.18 |
| 0 | 50 | 0.55 | 0.20 |
| 50 | 50 | 0.58 | 0.16 |
| 100 | 50 | 0.58 | 0.15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campi, T.; Cruciani, S.; De Santis, V.; Maradei, F.; Feliziani, M. Near Field Wireless Powering of Deep Medical Implants. Energies 2019, 12, 2720. https://doi.org/10.3390/en12142720
Campi T, Cruciani S, De Santis V, Maradei F, Feliziani M. Near Field Wireless Powering of Deep Medical Implants. Energies. 2019; 12(14):2720. https://doi.org/10.3390/en12142720
Chicago/Turabian StyleCampi, Tommaso, Silvano Cruciani, Valerio De Santis, Francesca Maradei, and Mauro Feliziani. 2019. "Near Field Wireless Powering of Deep Medical Implants" Energies 12, no. 14: 2720. https://doi.org/10.3390/en12142720
APA StyleCampi, T., Cruciani, S., De Santis, V., Maradei, F., & Feliziani, M. (2019). Near Field Wireless Powering of Deep Medical Implants. Energies, 12(14), 2720. https://doi.org/10.3390/en12142720







