Application of Ordinal Optimization to Reactive Volt-Ampere Sources Planning Problems
Abstract
1. Introduction
2. Mathematical Formulation
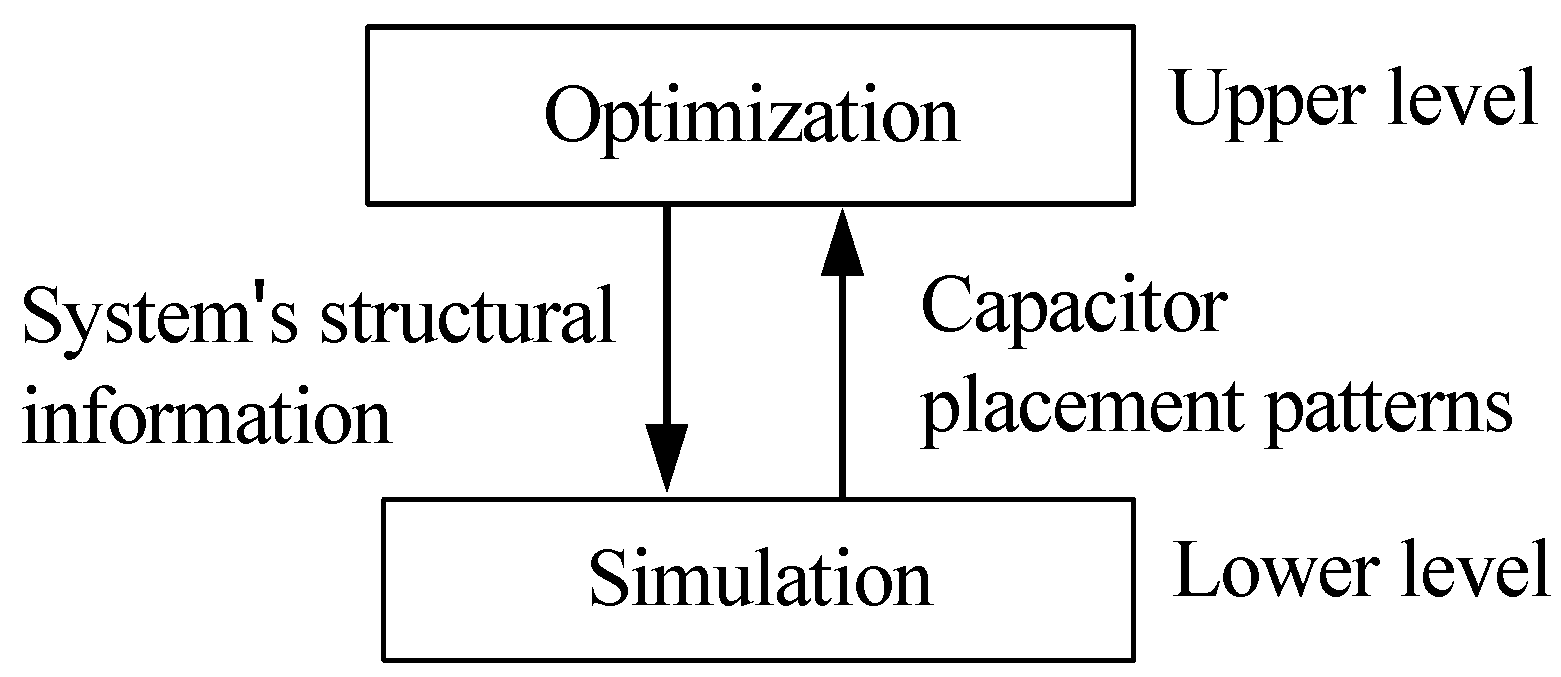
3. Simulation Optimization
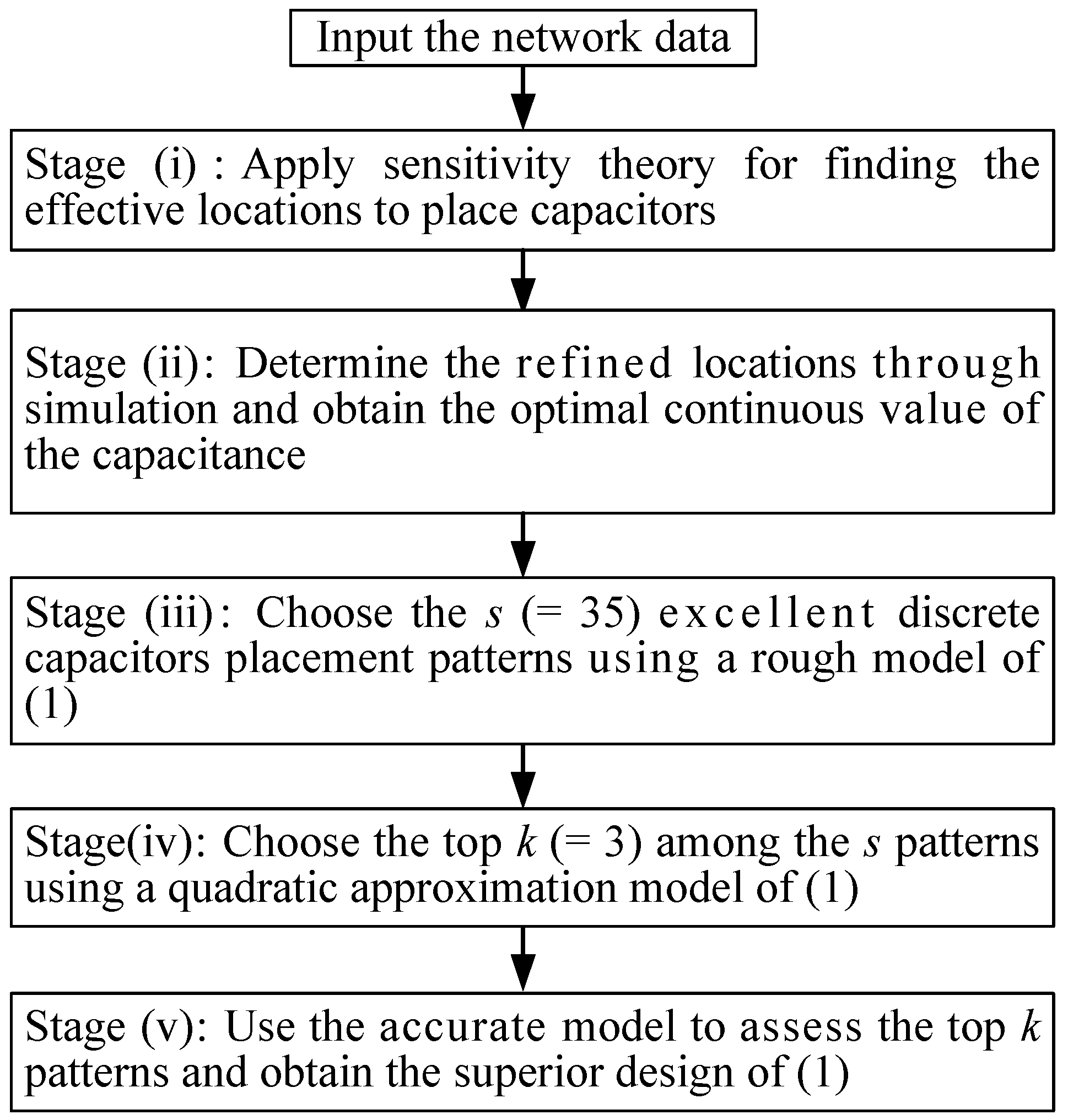
3.1. Five Stages in the OS Algorithm
3.2. Flow Diagram of the Ordinal Search (OS) Algorithm
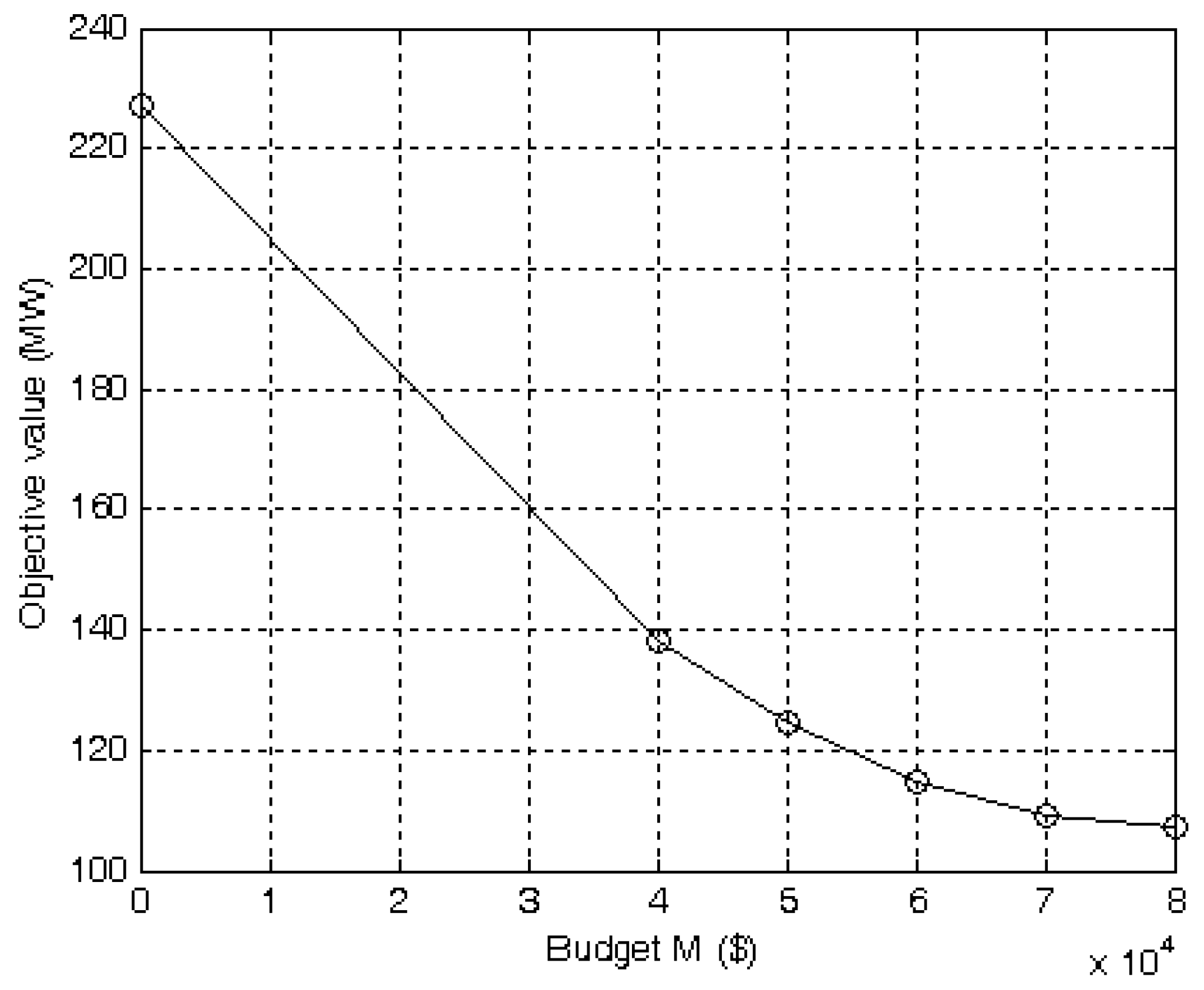
4. Experiment Results
4.1. Test Examples and Results
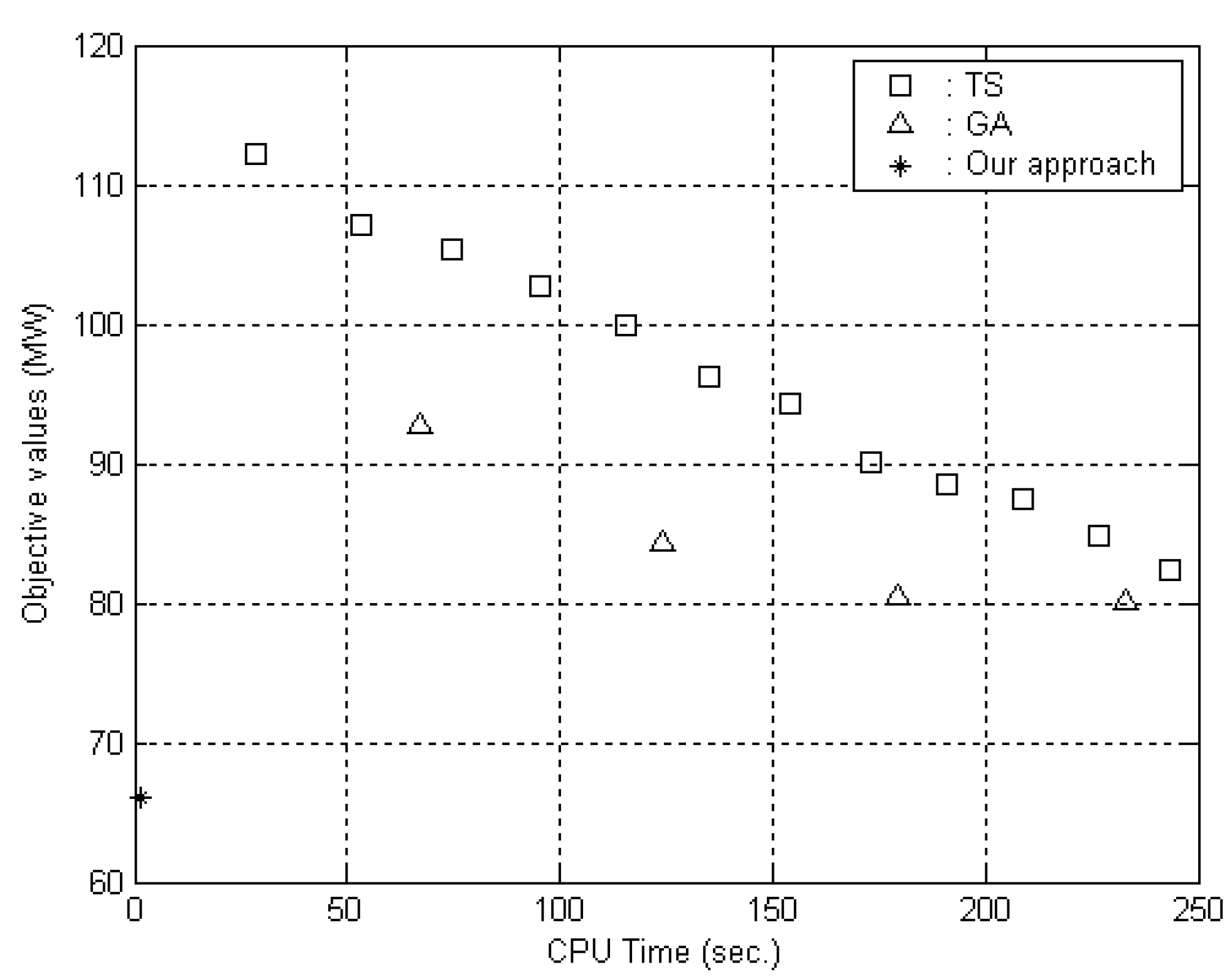
4.2. Comparison with the Competing Methods
4.3. Multiplicity of Configurations
4.4. Discussion About System Losses and Actual Investment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shaheen, A.M.; El-Sehiemy, R.A.; Farrag, S.M. A reactive power planning procedure considering iterative identification of VAR candidate buses. Neural Comput. Appl. 2019, 31, 653–674. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, H.Z.; Liu, L.; Zhang, S.X.; Zhou, Q.; Jiang, L. Coordination of generation, transmission and reactive power sources expansion planning with high penetration of wind power. Int. J. Electr. Power Energy Syst. 2019, 108, 191–203. [Google Scholar] [CrossRef]
- Raj, S.; Bhattacharyya, B. Optimal placement of TCSC and SVC for reactive power planning using Whale optimization algorithm. Swarm Evol. Comput. 2018, 40, 131–143. [Google Scholar] [CrossRef]
- Shen, Y.W.; Shen, F.F.; Chen, Y.L.; Liang, L.Q.; Zhang, B.; Ke, D.P. Reactive power planning for regional power grids based on active and reactive power adjustments of DGS. Energies 2018, 11, 1606. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Babu, R. Teaching learning based optimization algorithm for reactive power planning. Int. J. Electr. Power Energy Syst. 2016, 81, 48–253. [Google Scholar] [CrossRef]
- Birchfield, A.B.; Xu, T.; Overbye, T.J. Power flow convergence and reactive power planning in the creation of large synthetic grids. IEEE Trans. Power Syst. 2018, 33, 6667–6674. [Google Scholar] [CrossRef]
- Karbalaei, F.; Abbasi, S. L-index based contingency filtering for voltage stability constrained reactive power planning. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 3156–3167. [Google Scholar] [CrossRef]
- Liu, Z.H.; Yang, J.H.; Zhang, Y.J.; Ji, T.Y.; Zhou, J.H.; Cai, Z.X. Multi-objective coordinated planning of active-reactive power resources for decentralized droop-controlled islanded Microgrids based on probabilistic load flow. IEEE Access 2018, 6, 40267–40280. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Spea, S.R.; Farrag, S.M.; Abido, M.A. A review of meta-heuristic algorithms for reactive power planning problem. AIN Shams Eng. J. 2018, 9, 215–231. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Raj, S. Swarm intelligence based algorithms for reactive power planning with Flexible AC transmission system devices. Int. J. Electr. Power Energy Syst. 2016, 78, 158–164. [Google Scholar] [CrossRef]
- Huang, W.H.; Sun, K.; Qi, J.J.; Ning, J.X. Optimisation of dynamic reactive power sources using mesh adaptive direct search. IET Gener. Transm. Distrib. 2017, 11, 3675–3682. [Google Scholar] [CrossRef]
- Amaran, S.; Sahinidis, N.V.; Sharda, B.; Bury, S.J. Simulation optimization: A review of algorithms and applications. Ann. Oper. Res. 2016, 240, 351–380. [Google Scholar] [CrossRef]
- De Sousa Junior, W.T.; Montevechi, J.A.B.; Miranda, R.C.; Campos, A.T. Discrete simulation-based optimization methods for industrial engineering problems: A systematic literature review. Comput. Ind. Eng. 2019, 128, 526–540. [Google Scholar] [CrossRef]
- Zhu, Y.L.; Liu, C.X.; Sun, K.; Shi, D.; Wang, Z.W. Optimization of battery energy storage to improve power system oscillation damping. IEEE Trans. Sustain. Energy 2018, in press. [Google Scholar] [CrossRef]
- Abdelaziz, M.; Moradzadeh, M. Monte-Carlo simulation based multi-objective optimum allocation of renewable distributed generation using OpenCL. Electr. Power Syst. Res. 2019, 170, 81–91. [Google Scholar] [CrossRef]
- Roberts, J.J.; Cassula, A.M.; Silveira, J.L.; Bortoni, E.D.; Mendiburu, A.Z. Robust multi-objective optimization of a renewable based hybrid power system. Appl. Energy 2018, 223, 52–68. [Google Scholar] [CrossRef]
- Ebrahimzadeh, E.; Blaabjerg, F.; Wang, X.F.; Bak, C.L. Optimum design of power converter current controllers in large-scale power electronics based power systems. IEEE Trans. Ind. Appl. 2019, 55, 2792–2799. [Google Scholar] [CrossRef]
- Lin, S.S.; Horng, S.C. A more general parallel dual-type method and application to state estimation. Int. J. Electr. Power Energy Syst. 2011, 33, 799–804. [Google Scholar] [CrossRef]
- Lin, S.S.; Lin, C.H.; Horng, S.C. A parallel dual-type algorithm for a class of quadratic programming problems and applications. Expert Syst. Appl. 2009, 36, 5190–5199. [Google Scholar] [CrossRef]
- Lin, S.S. An efficient graph technique based dual-type algorithm for NMNF problems with large capacity constraints. Appl. Math. Comput. 2007, 190, 309–320. [Google Scholar] [CrossRef]
- Yang, D.; Cheng, H.Z.; Ma, Z.L.; Yao, L.Z.; Zhu, Z.L. Dynamic VAR planning methodology to enhance transient voltage stability for failure recovery. J. Mod. Power Syst. Clean Energy 2018, 6, 712–721. [Google Scholar] [CrossRef]
- Yang, D.; Hong, S.Y.; Cheng, H.Z.; Yao, L.Z. A novel dynamic reactive power planning methodology to enhance transient voltage stability. Int. Trans. Electr. Energy Syst. 2017, 27, 2390. [Google Scholar] [CrossRef]
- Ho, Y.C.; Zhao, Q.C.; Jia, Q.S. Ordinal Optimization: Soft Optimization for Hard Problems; Springer: New York, NY, USA, 2007. [Google Scholar]
- Shin, D.W.; Broadie, M.; Zeevi, A. Tractable sampling strategies for ordinal optimization. Oper. Res. 2018, 66, 1693–1712. [Google Scholar] [CrossRef]
- Horng, S.C.; Lin, S.S. Merging crow search into ordinal optimization for solving equality constrained simulation optimization problems. J. Comput. Sci. 2017, 23, 44–57. [Google Scholar] [CrossRef]
- Horng, S.C.; Lin, S.S. Embedding advanced harmony search in ordinal optimization to maximize throughput rate of flow line. Arab. J. Sci. Eng. 2018, 43, 1015–1031. [Google Scholar] [CrossRef]
- Horng, S.C.; Lin, S.S. Ordinal optimization based metaheuristic algorithm for optimal inventory policy of assemble-to-order systems. Appl. Math. Model. 2017, 42, 43–57. [Google Scholar] [CrossRef]
- Horng, S.C.; Lin, S.S. Embedding ordinal optimization into tree–seed algorithm for solving the probabilistic constrained simulation optimization problems. Appl. Sci. 2018, 8, 2153. [Google Scholar] [CrossRef]
- Wu, J.; Han, W.Q.; Chen, T.; Zhao, J.Q.; Li, B.B.; Xu, D.G. Resonance characteristics analysis of grid-connected inverter systems based on sensitivity theory. J. Power Electron. 2018, 18, 746–756. [Google Scholar]
- Pena, I.; Martinez-Anido, C.B.; Hodge, B.M. An extended IEEE 118-Bus test system with high renewable penetration. IEEE Trans. Power Syst. 2018, 33, 281–289. [Google Scholar] [CrossRef]
- Lin, S.S.; Horng, S.C.; Lin, C.H. Distributed quadratic programming problems of power systems with continuous and discrete variables. IEEE Trans. Power Syst. 2013, 28, 472–481. [Google Scholar] [CrossRef]
- Alcayde, A.; Banos, R.; Arrabal-Campos, F.M.; Montoya, F.G. Optimization of the contracted electric power by means of genetic algorithms. Energies 2019, 12, 1270. [Google Scholar] [CrossRef]
- IMSL C Math Library. IMSL C Numerical Libraries 2016.1 for Windows; Rogue Wave Software, Inc.: Louisville, CO, USA, 2016. [Google Scholar]

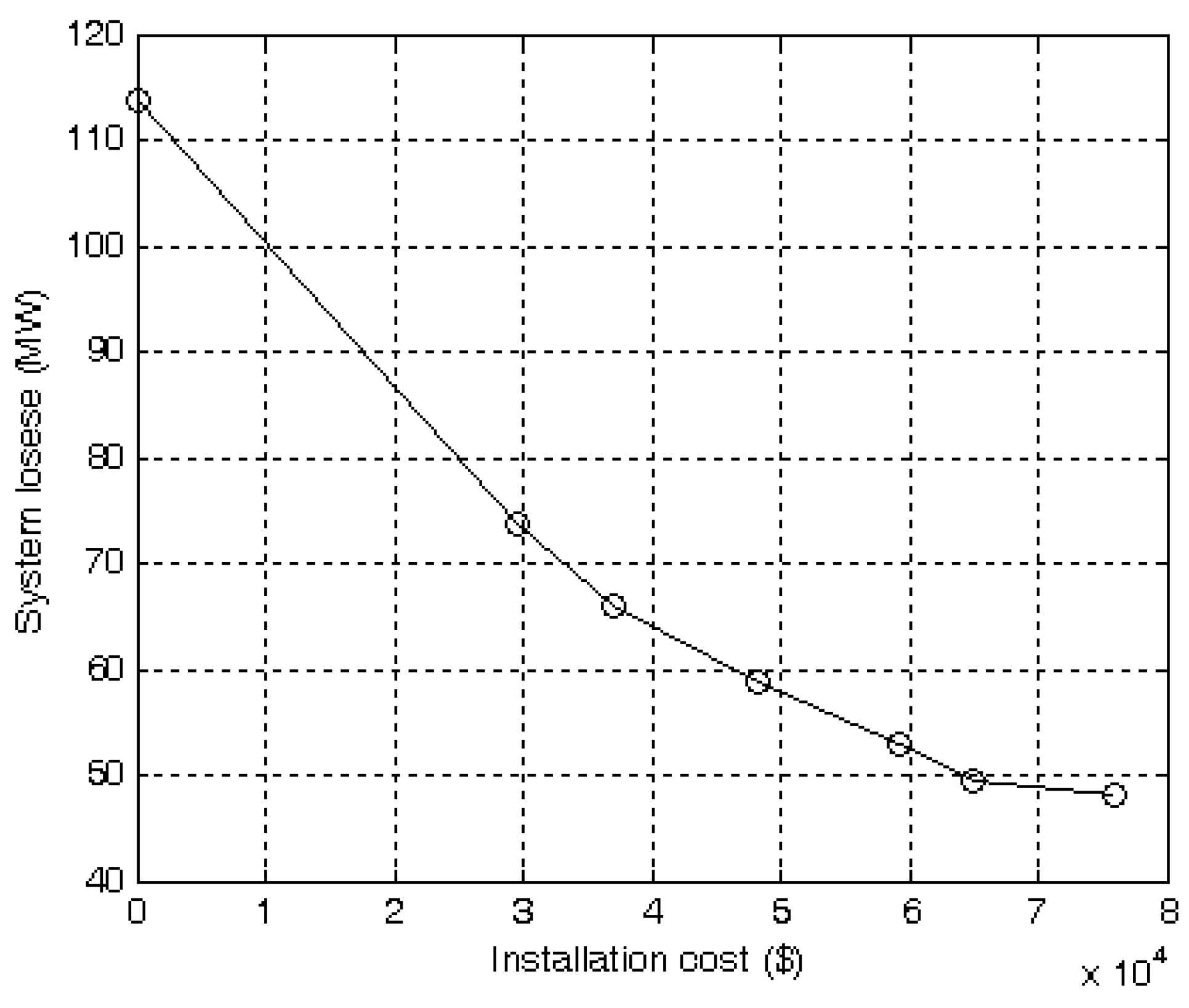
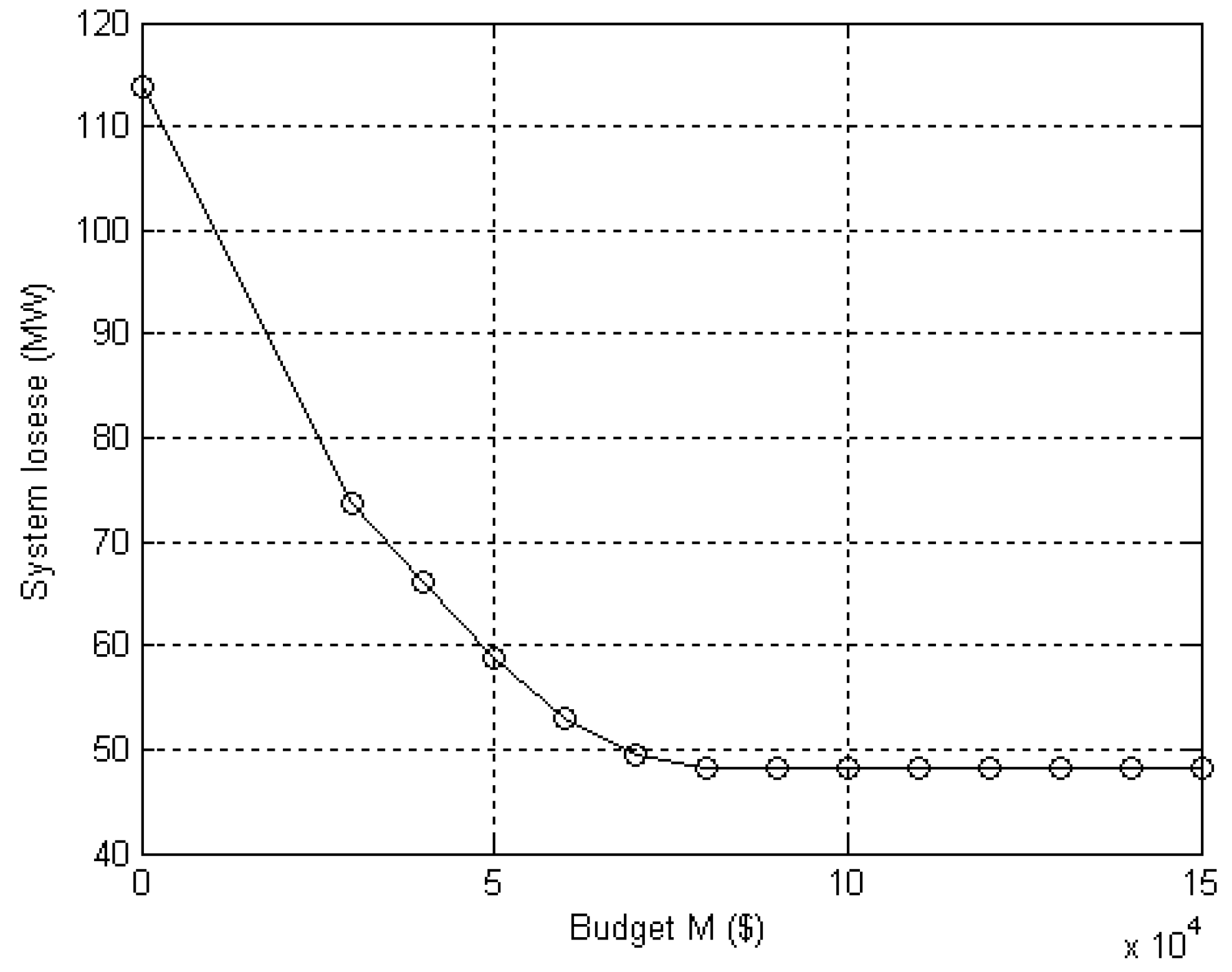
| Budget M ($) | Actual Investment ($) | Objective Values O1 (MW) | CPU Time (seconds) | |
|---|---|---|---|---|
| 40,000 | 37,100 | 66.1228 | 1.65 | 11 |
| 50,000 | 48,200 | 58.8867 | 1.68 | 14 |
| 60,000 | 59,300 | 52.9694 | 1.78 | 17 |
| 70,000 | 64,900 | 49.5524 | 1.79 | 19 |
| 80,000 | 76,000 | 48.1205 | 1.82 | 22 |
| Budget M ($) | Actual Investment ($) | Objective Values O1 (MW) | CPU Time (seconds) | |
|---|---|---|---|---|
| 40,000 | 39,800 | 138.3324 | 7.56 | 11 |
| 50,000 | 48,100 | 124.7231 | 7.74 | 13 |
| 60,000 | 59,200 | 114.9530 | 8.22 | 16 |
| 70,000 | 69,500 | 109.0737 | 8.30 | 20 |
| 80,000 | 79,600 | 107.1801 | 8.45 | 22 |
| Budget M ($) | 40,000 | 50,000 | 60,000 | 70,000 | 80,000 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Location no. | Bus no. | Installed Banks | Bus no. | Installed Banks | Bus no. | Installed Banks | Bus no. | Installed Banks | Bus no. | Installed Banks |
| 1 | 11 | 3 | 11 | 3 | 11 | 3 | 11 | 3 | 11 | 3 |
| 2 | 19 | 2 | 19 | 2 | 19 | 3 | 19 | 3 | 19 | 3 |
| 3 | 23 | 2 | 23 | 3 | 23 | 3 | 23 | 3 | 23 | 3 |
| 4 | 27 | 3 | 27 | 3 | 27 | 3 | 27 | 3 | 27 | 3 |
| 5 | 37 | 3 | 37 | 3 | 37 | 3 | 37 | 3 | 37 | 3 |
| 6 | 56 | 3 | 56 | 3 | 56 | 3 | 56 | 3 | 56 | 3 |
| 7 | 62 | 2 | 62 | 2 | 62 | 2 | 62 | 2 | 62 | 3 |
| 8 | 77 | 3 | 77 | 3 | 77 | 3 | 77 | 3 | 77 | 3 |
| 9 | 92 | 3 | 92 | 3 | 92 | 3 | 92 | 3 | 92 | 3 |
| 10 | 96 | 2 | 96 | 3 | 96 | 3 | 96 | 3 | 96 | 3 |
| 11 | 106 | 3 | 106 | 3 | 106 | 3 | 106 | 3 | 106 | 3 |
| 12 | – | – | 5 | 2 | 5 | 2 | 5 | 2 | 5 | 3 |
| 13 | – | – | 64 | 2 | 64 | 3 | 64 | 3 | 64 | 3 |
| 14 | – | – | 88 | 3 | 88 | 3 | 88 | 3 | 88 | 3 |
| 15 | – | – | – | – | 70 | 2 | 70 | 2 | 70 | 3 |
| 16 | – | – | – | – | 68 | 3 | 68 | 3 | 68 | 3 |
| 17 | – | – | – | – | 105 | 2 | 105 | 2 | 105 | 2 |
| 18 | – | – | – | – | – | – | 12 | 2 | 12 | 2 |
| 19 | – | – | – | – | – | – | 51 | 2 | 51 | 2 |
| 20 | – | – | – | – | – | – | – | – | 48 | 2 |
| 21 | – | – | – | – | – | – | – | – | 75 | 2 |
| 22 | – | – | – | – | – | – | – | – | 110 | 2 |
| Budget M ($) | 40,000 | 50,000 | 60,000 | 70,000 | 80,000 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Location no. | Bus no. | Installed Banks | Bus no. | Installed Banks | Bus no. | Installed Banks | Bus no. | Installed Banks | Bus no. | Installed Banks |
| 1 | 30 | 3 | 30 | 3 | 30 | 3 | 30 | 3 | 30 | 3 |
| 2 | 51 | 3 | 51 | 3 | 51 | 3 | 51 | 3 | 51 | 3 |
| 3 | 61 | 3 | 61 | 3 | 61 | 3 | 61 | 3 | 61 | 3 |
| 4 | 77 | 3 | 77 | 3 | 77 | 3 | 77 | 3 | 77 | 3 |
| 5 | 91 | 3 | 91 | 3 | 91 | 3 | 91 | 3 | 91 | 3 |
| 6 | 92 | 3 | 92 | 3 | 92 | 3 | 92 | 3 | 92 | 3 |
| 7 | 111 | 3 | 111 | 3 | 111 | 3 | 111 | 3 | 111 | 3 |
| 8 | 166 | 2 | 166 | 3 | 166 | 3 | 166 | 3 | 166 | 3 |
| 9 | 216 | 3 | 216 | 3 | 216 | 3 | 216 | 3 | 216 | 3 |
| 10 | 225 | 3 | 225 | 3 | 225 | 3 | 225 | 3 | 225 | 3 |
| 11 | 227 | 3 | 227 | 3 | 227 | 3 | 227 | 3 | 227 | 3 |
| 12 | – | – | 79 | 3 | 79 | 3 | 79 | 3 | 79 | 3 |
| 13 | – | – | 236 | 2 | 236 | 3 | 236 | 3 | 236 | 3 |
| 14 | – | – | – | – | 1 | 3 | 1 | 3 | 1 | 3 |
| 15 | – | – | – | – | 102 | 3 | 102 | 3 | 102 | 3 |
| 16 | – | – | – | – | 106 | 3 | 106 | 3 | 106 | 3 |
| 17 | – | – | – | – | – | – | 189 | 2 | 189 | 3 |
| 18 | – | – | – | – | – | – | 224 | 1 | 224 | 3 |
| 19 | – | – | – | – | – | – | 53 | 2 | 53 | 3 |
| 20 | – | – | – | – | – | – | 173 | 2 | 173 | 3 |
| 21 | – | – | – | – | – | – | – | – | 130 | 2 |
| 22 | – | – | – | – | – | – | – | – | 209 | 2 |
| Methods | Objective Values O1 (MW) | Actual Investment ($) | Power Loss Reduced Rate |
|---|---|---|---|
| Without capacitors | 113.7812 | 0 | – |
| Random selection | 72.8300 | 76,000 | 35.99% |
| Proposed approach | 48.1205 | 76,000 | 57.71% |
| Methods | Objective Values O1 (MW) | Actual Investment ($) | Power Loss Reduced Rate |
|---|---|---|---|
| Without capacitors | 227.0201 | 0 | – |
| Random selection | 150.6278 | 79,600 | 33.65% |
| Porposed approach | 107.1801 | 79,600 | 52.79% |
| Budget M ($) | Actual Investment ($) | Objective Value OG (MW) | Object. Value red. | CPU Time (Sec.) |
|---|---|---|---|---|
| 40,000 | 25,200 | 80.0159 | 21.01% | 232.73 |
| 50,000 | 28,200 | 80.1924 | 36.18% | 209.50 |
| 60,000 | 31,000 | 78.3342 | 47.89% | 258.92 |
| 70,000 | 34,600 | 75.4880 | 52.34% | 250.65 |
| 80,000 | 33,800 | 77.9135 | 61.91% | 255.84 |
| Budget M ($) | Actual Investment ($) | Objective Value OT (MW) | Object. Value red. | CPU Time (Sec.) |
|---|---|---|---|---|
| 40,000 | 18600 | 87.4152 | 32.20% | 209.00 |
| 50,000 | 11200 | 96.6673 | 64.16% | 206.06 |
| 60,000 | 9400 | 99.7849 | 88.38% | 237.86 |
| 70,000 | 7500 | 101.2972 | 104.42% | 202.18 |
| 80,000 | 7500 | 100.0942 | 109.69% | 239.31 |
| IEEE Systems | Budget M ($) | Final Obj. Value (MW) | CPU Time (Sec.) | Speed-up Ratio (II/I) | |||
|---|---|---|---|---|---|---|---|
| Our App. | IMSL | Our App. (I) | IMSL (II) | ||||
| 6-bus | 5000 | 2 | 41.95 | 41.95 | 0.04 | 0.13 | 3.25 |
| 9-bus | 7000 | 2 | 33.65 | 33.65 | 0.11 | 0.39 | 3.54 |
| 11-bus | 7000 | 2 | 27.32 | 27.32 | 0.12 | 1.13 | 9.41 |
| 30-bus | 11,000 | 3 | 22.97 | 22.97 | 0.24 | 8.21 | 34.21 |
| 57-bus | 20,000 | 6 | 37.04 | 37.04 | 0.28 | 23.58 | 84.21 |
| 118-bus | 40,000 | 11 | 66.12 | - | 0.83 | - | - |
| 244-bus | 40,000 | 11 | 138.33 | - | 3.78 | - | - |
| Budget M ($) | Objective Values O1 (MW) | Case 1 Line 14-15 | Case 2 Line 23-32 | Case 3 Line 62-66 | Case 4 Line 101-102 |
|---|---|---|---|---|---|
| 40,000 | 66.1228 | 67.3026 | 66.4918 | 66.2439 | 67.8421 |
| 50,000 | 58.8867 | 60.7235 | 58.9831 | 60.2090 | 60.4789 |
| 60,000 | 52.9694 | 54.5842 | 53.0359 | 55.5249 | 54.7753 |
| Budget M ($) | Objective Values O1 (MW) | Case 1 Line 14-15 Line 23-32 | Case 2 Line 23-32 Line 62-66 | Case 3 Line 62-66 Line 101-102 | Case 4 Line 101-102 Line 14-15 |
|---|---|---|---|---|---|
| 40,000 | 66.1228 | 66.4842 | 66.1123 | 67.8220 | 68.3532 |
| 50,000 | 58.8867 | 59.7301 | 58.9490 | 61.6985 | 62.8257 |
| 60,000 | 52.9694 | 54.5448 | 53.3249 | 54.7271 | 56.2231 |
| Budget M ($) | Objective Values O1 (MW) | Case 1 Line 14-15 Line 23-32 Line 62-66 | Case 2 Line 23-32 Line 62-66 Line 101-102 | Case 3 Line 14-15 Line 62-66 Line 101-102 | Case 4 Line 14-15 Line 23-32 Line 101-102 |
|---|---|---|---|---|---|
| 40,000 | 66.1228 | 66.6751 | 68.0312 | 68.0976 | 68.5908 |
| 50,000 | 58.8867 | 60.3298 | 60.8323 | 62.6996 | 63.0502 |
| 60,000 | 52.9694 | 54.3795 | 54.3238 | 56.1794 | 55.2237 |
| Budget M | Actual Investment | Objective Values (System Losses) | The Classical Objective Values (System Losses + (1/Ke) ×Actual Investment) | |||||
|---|---|---|---|---|---|---|---|---|
| Ke = 10,000 | Ke = 2500 | Ke = 1667 | Ke = 1250 | Ke = 833 | Ke = 625 | |||
| 0 | 0 | 113.7812 | 113.7812 | 113.7812 | 113.7812 | 113.7812 | 113.7812 | * 113.7812 |
| 30,000 | 29,600 | 73.75 | 76.71 | 85.59 | 91.51 | 97.43 | * 109.27 | 121.11 |
| 40,000 | 37,100 | 66.1228 | 69.8328 | 80.9628 | 88.3828 | * 95.8028 | 110.6428 | 125.4828 |
| 50,000 | 48,200 | 58.8867 | 63.7067 | 78.1667 | * 87.8067 | 97.4467 | 116.7267 | 136.0067 |
| 60,000 | 59,300 | 52.9694 | 58.8994 | 76.6894 | 88.5494 | 100.4094 | 124.1294 | 147.8494 |
| 70,000 | 64,900 | 49.5524 | 56.0424 | * 75.5124 | 88.4924 | 101.4724 | 127.4324 | 153.3924 |
| 80,000 | 76,000 | 48.1205 | * 55.7205 | 78.5205 | 93.7205 | 108.9205 | 139.3205 | 169.7205 |
| 90,000 | 76,000 | 48.1205 | * 55.7205 | 78.5205 | 93.7205 | 108.9205 | 139.3205 | 169.7205 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, W.-T.; Horng, S.-C.; Lin, C.-F. Application of Ordinal Optimization to Reactive Volt-Ampere Sources Planning Problems. Energies 2019, 12, 2746. https://doi.org/10.3390/en12142746
Lee W-T, Horng S-C, Lin C-F. Application of Ordinal Optimization to Reactive Volt-Ampere Sources Planning Problems. Energies. 2019; 12(14):2746. https://doi.org/10.3390/en12142746
Chicago/Turabian StyleLee, Wen-Tung, Shih-Cheng Horng, and Chi-Fang Lin. 2019. "Application of Ordinal Optimization to Reactive Volt-Ampere Sources Planning Problems" Energies 12, no. 14: 2746. https://doi.org/10.3390/en12142746
APA StyleLee, W.-T., Horng, S.-C., & Lin, C.-F. (2019). Application of Ordinal Optimization to Reactive Volt-Ampere Sources Planning Problems. Energies, 12(14), 2746. https://doi.org/10.3390/en12142746





