Accuracy Comparison of Coastal Wind Speeds between WRF Simulations Using Different Input Datasets in Japan
Abstract
1. Introduction
2. Observation Data and Evaluation Method
2.1. In-Situ Observation Data
2.2. JMA GPVs
2.3. WRF Configuration
2.4. Evaluation Methods
3. Accuracy Comparison of Wind Speeds
3.1. Comparison between GPV Wind Speeds
3.2. Comparison between GPV and WRF Wind Speeds
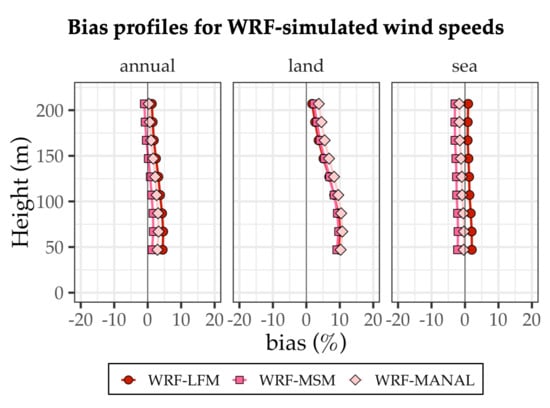
3.3. Comparison between WRF Wind Speeds
4. Discussion on Overestimation for Wind Speeds over Land
4.1. Effect from Nudging Method
4.2. Effect from PBL Scheme
4.3. Other Possible Causes
5. Conclusions
- From the accuracy comparisons between the three JMA datasets, the LFM–GPV exhibited the most accurate wind speeds at the heights from 40 to 200 m. This result is the same as that of our previous study [23], which examined only the surface wind speed, and is reasonable as the LFM–GPV has a higher spatio–temporal resolution than the other datasets.
- The dynamical downscaling simulations with WRF were performed, and we found that the WRF simulations yielded more accurate wind speeds than the input datasets. This was attributed to the ability of WRF to mitigate the negative biases found in the input datasets, especially for the winds blowing from the sea sectors.
- However, we discovered that although the LFM–GPV exhibited the highest accuracy, using the LFM–GPV as an input did not always yield the most accurate wind speeds in the WRF simulation. This was primarily owing to the tendency of WRF to overestimate the wind speed over land that consequently obscured the high accuracy of the LFM–GPV.
- Moreover, it was shown that the overestimation tendency could not be improved by only changing the nudging methods or PBL schemes in the WRF simulation. These results indicated that it may be difficult to utilize the LFM–GPV in the WRF wind simulation, unless the overestimation tendency of WRF is improved first.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| AGL | Above Ground Level |
| AIST | National Institute of Advanced Industrial Science and Technology |
| AMeDAS | Automated Meteorological Data Acquisition System |
| AMSL | Above Mean Sea Level |
| ARW | Advanced Research WRF |
| ASTER GDEM | Advanced Spaceborne Thermal. Emission and Reflection Radiometer Global Digital Elevation Model |
| FDDA | Four-Dimensional Data Assimilation |
| FDDA–DYNAMIC | The method that grid nudging is enabled for the entire outer domain, while it is excluded in the PBL in the inner domain |
| FDDA–STATIC | The method that grid nudging is enabled for the entire outer domain, while it is excluded within the PBL defined below a specified height (set to 1500 m AGL) in the inner domain |
| FNL | Final Operational Global Analysis |
| GPV | Grid Point Value |
| GTOPO30 | Global digital elevation model with a horizontal grid spacing of 30 arc seconds produced by USGS |
| JMA | Japan Meteorological Agency |
| JMBSC | Japan Meteorological Business Support Center |
| KF | Kain–Frisch |
| LANAL | Local Analysis |
| LFM | Local Forecast Model |
| MANAL | Mesoscale Analysis |
| METI | Ministry of Economy, Trade and Industry |
| MLIT | Ministry of Land, Infrastructure, Transport and Tourism |
| MOSST | SST based on a moderate resolution imaging spectroradiometer |
| MSM | Meso Scale Model |
| MYJ | Mellor-Yamada-Janjic |
| MYNN3 | Mellor-Yamada-Nakanishi-Niino Level-3 |
| NASA | National Aeronautics and Space Administration |
| NCEP | National Center for Environmental Prediction |
| NEDO | New Energy and Industrial Technology Development Organization |
| NeoWins | NEDO Offshore Wind Information System |
| NLNI | National Land Numerical Information |
| PARI | Port and Airport Research Institute |
| PBL | Planetary Boundary Layer |
| RMSE | Root Mean Square Error |
| SST | Sea Surface Temperature |
| USGS | United States Geological Survey |
| WRF | Weather Research and Forecasting model |
| WRF–LFM | WRF simulation using the LFM–GPV as input |
| WRF–MANAL | WRF simulation using the MANAL as input |
| WRF–MSM | WRF simulation using the MSM–GPV as input |
| YSU | Yonsei University |
References
- NEDO. The NEDO Offshore Wind Information System. Available online: http://app10.infoc.nedo.go.jp/Nedo_Webgis/top.html (accessed on 29 June 2019).
- Skamarock, W.; Klemp, J.; Dudhia, J.; Gill, D.; Barker, D.; Duda, M.; Huang, X.; Wang, W.; Powers, J. A description of the advanced research WRF version 3. NCAR Tech. Note NCAR/TN-475+ STR. 2008. [Google Scholar]
- Sempreviva, A.M.; Barthelmie, R.J.; Pryor, S.C. Review of methodologies for offshore wind resource assessment in European seas. Surv. Geophys. 2008, 29, 471–497. [Google Scholar] [CrossRef]
- Jimenez, B.; Durante, F.; Lange, B.; Kreutzer, T.; Tambke, J. Offshore wind resource assessment with WAsP and MM5: Comparative study for the German Bight. Wind Energy 2007, 10, 121–134. [Google Scholar] [CrossRef]
- Peña, A.; Hahmann, A.; Hasager, C.; Bingöl, F.; Karagali, I.; Badger, J.; Badger, M.; Clausen, N. South Baltic Wind Atlas. Available online: http://www.southbaltic-offshore.eu/reports-studies/img/SBO_Wind-Atlas.pdf (accessed on 29 June 2019).
- Hahmann, A.N.; Lennard, C.; Badger, J.; Vincent, C.L.; Kelly, M.C.; Volker, P.J.; Argent, B.; Refslund, J. Mesoscale modeling for the Wind Atlas of South Africa (WASA) project. DTU Wind Energy 2014, 50, 80. [Google Scholar]
- Chang, R.; Zhu, R.; Badger, M.; Hasager, C.B.; Xing, X.; Jiang, Y. Offshore wind resources assessment from multiple satellite data and WRF modeling over South China Sea. Remote Sens. 2015, 7, 467–487. [Google Scholar] [CrossRef]
- Mattar, C.; Borvarán, D. Offshore wind power simulation by using WRF in the central coast of Chile. Renew. Energy 2016, 94, 22–31. [Google Scholar] [CrossRef]
- Ohsawa, T.; Kozai, K.; Nakamura, S.; Kawaguchi, K.; Shimada, S.; Takeyama, Y.; Kogaki, T. Accuracy of WRF simulation in the NEDO offshore wind resource map. Proc. Jpn. Wind Energy Symp. 2016, 38, 17–20. (In Japanese) [Google Scholar]
- Ohsawa, T.; Uede, H.; Misaki, T.; Kato, M. Accuracy of WRF Simulations Used for Japanese Offshore Wind Resource Maps. International Conference on Energy and Meteorology 2017. Available online: http://www.wemcouncil.org/ICEMs/ICEM2017_PRES/ICEM_20170629_1120_Sala_2_Ohsawa.pptx (accessed on 29 June 2019).
- Kato, M.; Ohsawa, T.; Uede, H.; Shimada, S. Verification of spatial characteristics of WRF-simulated wind speed in Japanese coastal waters. Proc. Jpn. Wind Energy Symp. 2017, 39, 253–256. (In Japanese) [Google Scholar]
- Hong, S.Y.; Dudhia, J. Next-generation numerical weather prediction: Bridging parameterization, explicit clouds, and large eddies. Bull. Am. Meteorol. Soc. 2012, 93, ES6–ES9. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M. Ocean surface wind simulation forced by different reanalyses: Comparison with observed data along the Iberian Peninsula coast. Ocean Model. 2012, 56, 31–42. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M.; Santos, C.S. Offshore wind energy resource simulation forced by different reanalyses: Comparison with observed data in the Iberian Peninsula. Appl. Energy 2014, 134, 57–64. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M.; Santos, C.S. WRF wind simulation and wind energy production estimates forced by different reanalyses: Comparison with observed data for Portugal. Appl. Energy 2014, 117, 116–126. [Google Scholar] [CrossRef]
- Hahmann, A.N.; Vincent, C.L.; Peña, A.; Lange, J.; Hasager, C.B. Wind climate estimation using WRF model output: Method and model sensitivities over the sea. Int. J. Climatol. 2015, 35, 3422–3439. [Google Scholar] [CrossRef]
- Chadee, X.T.; Seegobin, N.R.; Clarke, R.M. Optimizing the Weather Research and Forecasting (WRF) Model for Mapping the Near-Surface Wind Resources over the Southernmost Caribbean Islands of Trinidad and Tobago. Energies 2017, 10, 931. [Google Scholar] [CrossRef]
- JMBSC. MANAL. Available online: http://www.jmbsc.or.jp/jp/offline/cd0380.html (accessed on 29 June 2019).
- Akimoto, Y.; Kusaka, H. Sensitivity of the WRF Regional Meteorological Model to Input Datasets and Surface Parameters for the Kanto Plain on Fine Summer Days. Geogr. Rev. Jpn. Ser. A 2010, 83, 324–340. (In Japanese) [Google Scholar] [CrossRef]
- NCEP. FNL Operational Model Global Tropospheric Analyses, Continuing from July 1999. Available online: https://doi.org/10.5065/D6M043C6 (accessed on 29 June 2019).
- JMBSC. LFM-GPV. Available online: http://www.jmbsc.or.jp/jp/online/file/f-online10300.html (accessed on 29 June 2019).
- JMBSC. MSM-GPV. Available online: http://www.jmbsc.or.jp/jp/online/file/f-online10200.html (accessed on 29 June 2019).
- Misaki, T.; Ohsawa, T. Evaluation of LFM-GPV and MSM-GPV as input data for wind simulation. J. Jpn. Wind Energy Assoc. 2019, 42, 72–79. [Google Scholar]
- ZephIR Lidar. ZephIR 300. Available online: https://s.campbellsci.com/documents/ca/product-brochures/zephir300_br.pdf (accessed on 29 June 2019).
- Gottschall, J.; Courtney, M. Verification Test for Three WindCube WLS7 LiDARs at the Høvsøre Test Site; Danmarks Tekniske Universitet, Risø Nationallaboratoriet for Bæredygtig Energi: Roskilde, Denmark, 2010. [Google Scholar]
- PARI. Hazaki Oceanographical Research Station (HORS). Available online: https://www.pari.go.jp/unit/edosy/en/main-facility/2.html (accessed on 29 June 2019).
- Mito, T.; Kato, H.; Konagaya, M.; Matsuoka, Y. Accuracy comparison between multiple models of vertical wind Doppler LIDAR. Proc. Jpn. Wind Energy Symp. 2016, 38, 209–211. (In Japanese) [Google Scholar]
- Shimada, S.; Takeyama, Y.; Kogaki, T.; Ohsawa, T.; Nakamura, S. Investigation of the fetch effect using onshore and offshore vertical LIDAR devices. Remote Sens. 2018, 10, 1408. [Google Scholar] [CrossRef]
- JMA. Joint WMO Technical Progress Report on the Global Data Processing and Forecasting System and Numerical Weather Prediction Research Activities for 2016. Available online: http://www.jma.go.jp/jma/jma-eng/jma-center/nwp/report/2016_Japan.pdf (accessed on 29 June 2019).
- NLNI. Land Utilization Segmented Mesh Data. Available online: http://nlftp.mlit.go.jp/ksj-e/jpgis/datalist/KsjTmplt-L03-b.html (accessed on 29 June 2019).
- Sertel, E.; Robock, A.; Ormeci, C. Impacts of land cover data quality on regional climate simulations. Int. J. Climatol. 2010, 30, 1942–1953. [Google Scholar] [CrossRef]
- Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.A.; Mitchell, K.; Ek, M.; Gayno, G.; Wegiel, J.; Cuenca, R.H. Implementation and verification of the unified NOAH land surface model in the WRF model. In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction, Seattle, WA, USA, 10–15 January 2004; pp. 11–15. [Google Scholar]
- Shimada, S.; Ohsawa, T.; Kogaki, T.; Steinfeld, G.; Heinemann, D. Effects of sea surface temperature accuracy on offshore wind resource assessment using a mesoscale model. Wind Energy 2015, 18, 1839–1854. [Google Scholar] [CrossRef]
- Janjić, Z.I. The step-mountain eta coordinate model—Further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Shimada, S.; Ohsawa, T. Accuracy and characteristics of offshore wind speeds simulated by WRF. SOLA 2011, 7, 21–24. [Google Scholar] [CrossRef]
- Shimada, S.; Ohsawa, T.; Chikaoka, S.; Kozai, K. Accuracy of the wind speed profile in the lower PBL as simulated by the WRF model. SOLA 2011, 7, 109–112. [Google Scholar] [CrossRef]
- Draxl, C.; Hahmann, A.N.; Peña, A.; Giebel, G. Evaluating winds and vertical wind shear from Weather Research and Forecasting model forecasts using seven planetary boundary layer schemes. Wind Energy 2014, 17, 39–55. [Google Scholar] [CrossRef]
- Hu, X.M.; Nielsen-Gammon, J.W.; Zhang, F. Evaluation of three planetary boundary layer schemes in the WRF model. J. Appl. Meteorol. Climatol. 2010, 49, 1831–1844. [Google Scholar] [CrossRef]
- Floors, R.; Vincent, C.L.; Gryning, S.E.; Peña, A.; Batchvarova, E. The wind profile in the coastal boundary layer: Wind lidar measurements and numerical modelling. Boundary-Layer Meteorol. 2013, 147, 469–491. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An improved Mellor-Yamada Level-3 model: Its numerical stability and application to a regional prediction of advection fog. Boundary-Layer Meteorol. 2006, 119, 397–407. [Google Scholar] [CrossRef]
- Varquez, A.C.G.; Nakayoshi, M.; Makabe, T.; Kanda, M. WRF Application of High Resolution Urban Surface Parameters on Some Major Cities of Japan. J. Jpn. Soc. Civil Eng. Ser. B1 (Hydraul. Eng.) 2014, 170, I_175–I_180. [Google Scholar] [CrossRef]
- Jimenez, P.A.; Dudhia, J. Improving the representation of resolved and unresolved topographic effects on surface wind in the WRF model. J. Appl. Meteorol. Climatol. 2012, 51, 300–316. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.A.; Arbizu-Barrena, C.; Santos-Alamillos, F.J.; Tovar-Pescador, J.; Pozo-Vázquez, D. Assessing the surface solar radiation budget in the WRF model: A spatiotemporal analysis of the bias and its causes. Mon. Weather Rev. 2016, 144, 703–711. [Google Scholar] [CrossRef]
- Shimada, S.; Liu, Y.Y.; Xia, H.; Yoshino, J.; Kobayashi, T.; Itagaki, A.; Utsunomiya, T.; Hashimoto, J. Accuracy of solar irradiance simulation using the WRF-ARW model. J. Jpn. Sol. Energy Soc. 2012, 38, 41–48. (In Japanese) [Google Scholar]
- Mahrt, L. The early evening boundary layer transition. Q. J. R. Meteorol. Soc. 1981, 107, 329–343. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Alapaty, K.; Herwehe, J.A.; Otte, T.L.; Nolte, C.G.; Bullock, O.R.; Mallard, M.S.; Kain, J.S.; Dudhia, J. Introducing subgrid-scale cloud feedbacks to radiation for regional meteorological and climate modeling. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Zheng, Y.; Alapaty, K.; Herwehe, J.A.; Del Genio, A.D.; Niyogi, D. Improving high-resolution weather forecasts using the Weather Research and Forecasting (WRF) model with an updated Kain–Fritsch scheme. Mon. Weather Rev. 2016, 144, 833–860. [Google Scholar] [CrossRef]













| Site | Niigata | Ibaraki |
|---|---|---|
| Manufacturer | ZephIR Lidar | Leosphere |
| Measurement | ZephIR 300 | WindCube WLS7-86 |
| Vertical Level | 40, 58, 80, 95, 145 m | 47, 67, 87, 107, 127, 147, 167, 187, 207 m |
| Sector | Niigata | Ibaraki |
|---|---|---|
| land | 3937 (55%) | 2276 (32%) |
| sea | 2603 (37%) | 4177 (59%) |
| other | 580 (8%) | 615 (9%) |
| annual | 7120 (100%) | 7068 (100%) |
| GPV | LFM–GPV | MSM–GPV | MANAL | |
|---|---|---|---|---|
| Horizontal Resolution | Surface Level | 0.025° × 0.020° (1201 × 1261 grids) | 0.0625° × 0.0500° (481 × 505 grids) | 5 km × 5 km (721 × 577 grids) |
| Pressure Level | 0.050° × 0.040° (601 × 631 grids) | 0.1250° × 0.1000° (241 × 253 grids) | 5 km × 5 km (721 × 577 grids) | |
| Vertical Layers | 17 levels | 17 levels | 16 levels | |
| Temporal Resolution | 1 hourly (00, 01, ..., 23 UTC) | 3 hourly (00, 03, ..., 21 UTC) | 3 hourly (00, 03, ..., 21 UTC) | |
| Forecast Range | 9 h | 39 h | none | |
| Method | Advanced Research WRF (ARW) Version 3.8.1 | |
|---|---|---|
| Period | 1 year (from October 2015 to September 2016) | |
| Input Data | Soil: NCEP-FNL (6 hourly, 1° × 1°) SST: AIST-Kobe Univ. MOSST (daily, 0.02° × 0.02°) | |
| Terrain Data | Domain 1 | Elevation: USGS GTOPO30 Land use: USGS 24 land-use categories data (30″ × 30″) |
| Domain 2 | Elevation: METI-NASA ASTER GDEM (1″ × 1″) Land use: MLIT NLNI (0.1 km × 0.1 km) | |
| Vertical Levels | 40 levels (Surface to 100 hPa) Lowest half levels: 23 m, 73 m, 130 m, 199 m, 287 m, ... | |
| FDDA | Domain 1 | Enabled (u, v, θ, q) |
| Domain 2 | Enabled (u, v, θ, q), excluding interior of PBL | |
| Physics Options | Shortwave process: Dudhia scheme Longwave process: Rapid Radiative Transfer Model scheme Cloud microphysics process: Ferrier (new Eta) scheme PBL Process: MYJ (Eta operational) scheme Surface layer process: Monin–Obukhov (Janjic Eta) scheme Land-surface process: Noah land surface model scheme Cumulus parameterization: None | |
| Case | WRF–LFM | WRF–MSM | WRF–MANAL | |
|---|---|---|---|---|
| Input Data | LFM–GPV (3 hourly) | MSM–GPV (3 hourly) | MANAL (3 hourly) | |
| Grids | Domain 1 | 1.5 km × 1.5 km (168 × 168 grids) | 2.5 km × 2.5 km (100 × 100 grids) | 2.5 km × 2.5 km (100 × 100 grids) |
| Domain 2 | 0.5 km × 0.5 km (201 × 201 grids) | 0.5 km × 0.5 km (200 × 200 grids) | 0.5 km × 0.5 km (200 × 200 grids) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Misaki, T.; Ohsawa, T.; Konagaya, M.; Shimada, S.; Takeyama, Y.; Nakamura, S. Accuracy Comparison of Coastal Wind Speeds between WRF Simulations Using Different Input Datasets in Japan. Energies 2019, 12, 2754. https://doi.org/10.3390/en12142754
Misaki T, Ohsawa T, Konagaya M, Shimada S, Takeyama Y, Nakamura S. Accuracy Comparison of Coastal Wind Speeds between WRF Simulations Using Different Input Datasets in Japan. Energies. 2019; 12(14):2754. https://doi.org/10.3390/en12142754
Chicago/Turabian StyleMisaki, Takeshi, Teruo Ohsawa, Mizuki Konagaya, Susumu Shimada, Yuko Takeyama, and Satoshi Nakamura. 2019. "Accuracy Comparison of Coastal Wind Speeds between WRF Simulations Using Different Input Datasets in Japan" Energies 12, no. 14: 2754. https://doi.org/10.3390/en12142754
APA StyleMisaki, T., Ohsawa, T., Konagaya, M., Shimada, S., Takeyama, Y., & Nakamura, S. (2019). Accuracy Comparison of Coastal Wind Speeds between WRF Simulations Using Different Input Datasets in Japan. Energies, 12(14), 2754. https://doi.org/10.3390/en12142754