Thermal Conduction Simulation Based on Reconstructed Digital Rocks with Respect to Fractures
Abstract
:1. Introduction
2. Model and Method
2.1. Thermal Conduction Model
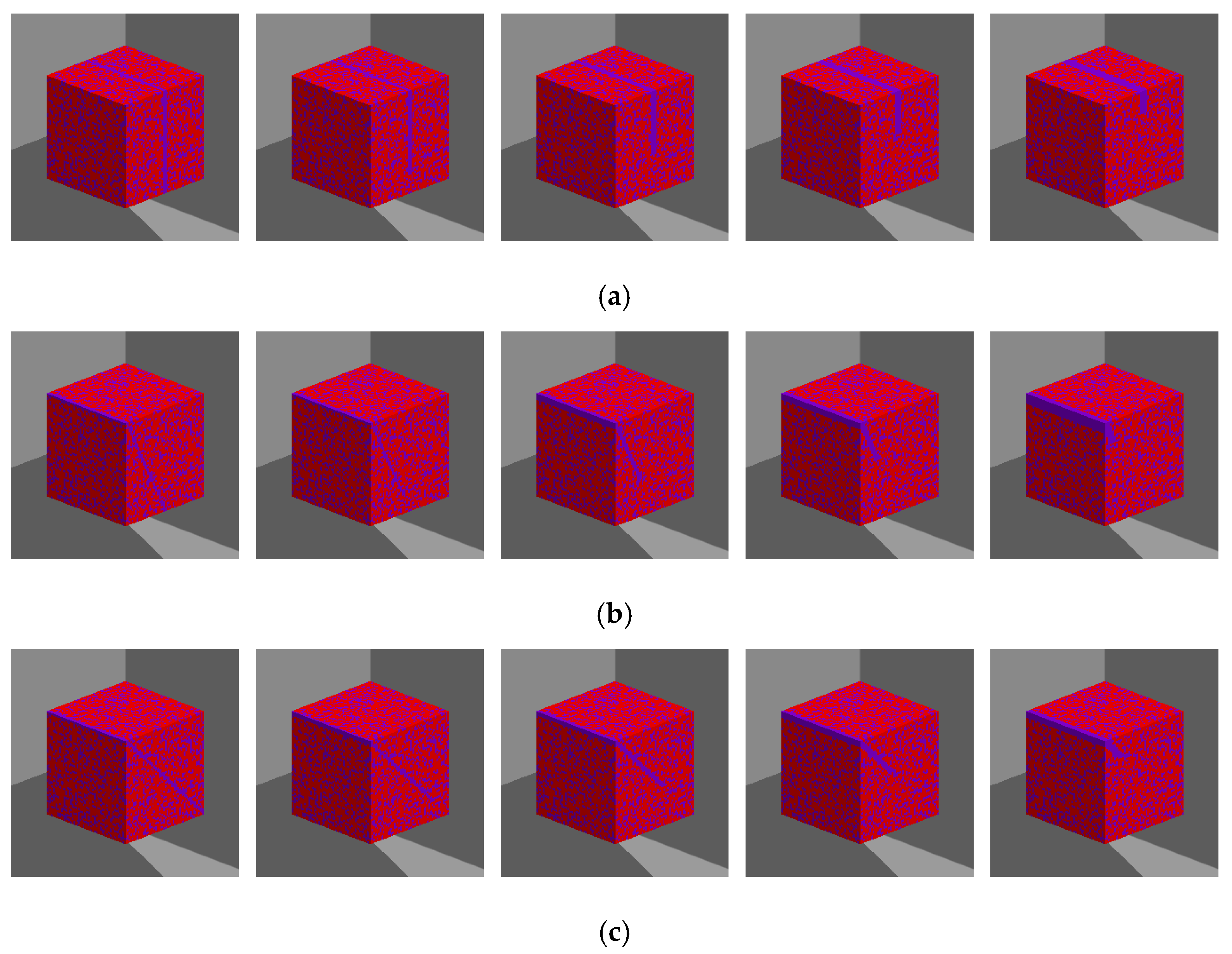
2.2. Reconstructed Digital Rocks with Different Fractures
2.3. Partial Least Squares (PLS) Regression Analysis Method
3. Thermal Conduction Simulation on Reconstructed Digital Rocks
3.1. Temperature Distribution in Digital Rocks with Different Fractures
3.2. ETC with Variable Saturated Fluid and Fracture Parameters
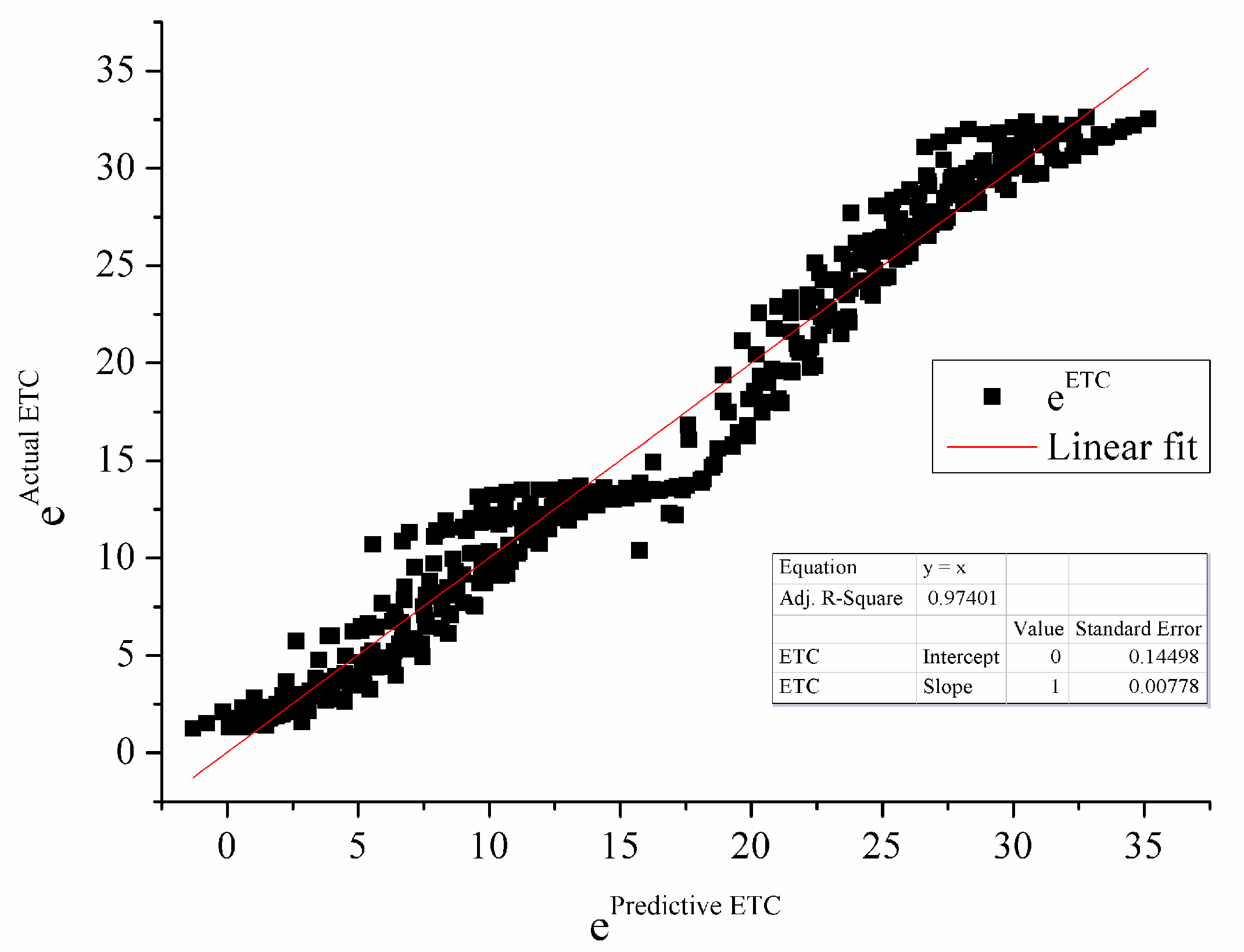
4. Partial Least Squares Regression Analysis
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Yao, J.; Zhang, X.; Sun, Z. Numerical simulation of the heat extraction in 3D-EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures mode. Geothermics 2018, 74, 19–34. [Google Scholar] [CrossRef]
- Sun, Z.X.; Zhang, X.; Xu, Y.; Yao, J.; Wang, H.X.; Lv, S.H.; Sun, Z.L.; Huang, Y.; Cai, M.Y.; Huang, X.X. Numerical simulation of the heat extraction in EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures model. Energy 2017, 120, 20–33. [Google Scholar] [CrossRef]
- Wang, T.; Sun, Z.; Zhang, K.; Jiang, C.; Xin, Y.; Mao, Q. Investigation on heat extraction performance of fractured geothermal reservoir using coupled thermal-hydraulic-mechanical model based on equivalent continuum Method. Energies 2019, 12, 127. [Google Scholar] [CrossRef]
- Sun, Z.; Xin, Y.; Yao, J.; Zhang, K.; Zhuang, L.; Zhu, X.; Wang, T.; Jiang, C. Numerical investigation on the heat extraction capacity of dual horizontal wells in enhanced geothermal systems based on the 3D THM model. Energies 2018, 11, 280. [Google Scholar] [CrossRef]
- Zuo, J.P.; Wang, J.T.; Sun, Y.J.; Chen, Y.; Jiang, G.H.; Li, Y.H. Effects of thermal treatment on fracture characteristics of granite from Beishan, a possible high-level radioactive waste disposal site in China. Eng. Fract. Mech. 2017, 182, 425–437. [Google Scholar] [CrossRef]
- Chen, S.; Yang, C.; Wang, G. Evolution of thermal damage and permeability of Beishan granite. Appl. Therm. Eng. 2017, 110, 1533–1542. [Google Scholar] [CrossRef]
- Zhu, G.P.; Yao, J.; Sun, H.; Zhang, M.; Xie, M.J.; Sun, Z.X.; Lu, T. The numerical simulation of thermal recovery based on hydraulic fracture heating technology in shale gas reservoir. J. Nat. Gas Sci. Eng. 2016, 28, 305–316. [Google Scholar] [CrossRef] [Green Version]
- Ezeuko, C.C.; Gates, I.D. Thermal oil recovery from fractured reservoirs: Energy and emissions intensities. Energy 2018, 155, 29–34. [Google Scholar] [CrossRef]
- Huai, X.L.; Wang, W.W.; Li, Z.G. Analysis of the effective thermal conductivity of fractal porous media. Appl. Therm. Eng. 2007, 27, 2815–2821. [Google Scholar] [CrossRef]
- Pia, G.; Sanna, U. Case studies on the influence of microstructure voids on thermal conductivity in fractal porous media. Case Stud. Therm. Eng. 2014, 2, 8–13. [Google Scholar] [CrossRef] [Green Version]
- Miao, T.J.; Cheng, S.J.; Chen, A.M.; Yu, B.M. Analysis of axial thermal conductivity of dual-porosity fractal porous media with random fractures. Int. J. Heat Mass Transf. 2016, 102, 884–890. [Google Scholar] [CrossRef]
- Ramazanova, A.E.; Emirov, S.N. Baric and temperature dependences for the thermal conductivity of sedimentary rocks. Bull. Russ. Acad. Sci. Phys. 2012, 76, 1152–1156. [Google Scholar] [CrossRef]
- Sun, Q.; Lv, C.; Cao, L.W.; Li, W.C.; Geng, J.S.; Zhang, W.Q. Thermal properties of sandstone after treatment at high temperature. Int. J. Rock Mech. Min. Sci. 2016, 85, 60–66. [Google Scholar] [CrossRef]
- Abdulagatova, Z.; Abdulagatov, I.M.; Emirov, V.N. Effect of temperature and pressure on the thermal conductivity of sandstone. Int. J. Rock Mech. Min. Sci. 2009, 46, 1055–1071. [Google Scholar] [CrossRef]
- Askari, R.; Hejazi, S.H.; Sahimi, M. Effect of deformation on the thermal conductivity of granular porous media with rough grain surface. Geophys. Res. Lett. 2017, 44, 8285–8293. [Google Scholar] [CrossRef]
- Alishaev, M.G.; Abdulagatov, I.M.; Abdulagatova, Z.Z. Effective thermal conductivity of fluid-saturated rocks Experiment and modeling. Eng. Geol. 2012, 135, 24–39. [Google Scholar] [CrossRef]
- Qin, X.; Cai, J.C.; Xu, P.; Dai, S.; Gan, Q. A fractal model of effective thermal conductivity for porous media with various liquid saturation. Int. J. Heat Mass Transf. 2019, 128, 1149–1156. [Google Scholar] [CrossRef]
- Chen, Y.F.; Li, D.Q.; Jiang, Q.H.; Zhou, C.B. Micromechanical analysis of anisotropic damage and its influence on effective thermal conductivity in brittle rocks. Int. J. Rock Mech. Min. Sci. 2012, 50, 102–116. [Google Scholar] [CrossRef]
- Ferone, C.; Colangelo, F.; Frattini, D.; Roviello, G.; Cioffi, R.; Maggio, R. Finite element method modeling of sensible heat thermal energy storage with innovative concretes and comparative analysis with literature benchmarks. Energies 2014, 7, 5291–5316. [Google Scholar] [CrossRef]
- Hua, Y.; Zhao, T.; Guo, Z. Transient thermal conduction optimization for solid sensible heat thermal energy storage modules by the Monte Carlo method. Energy 2017, 133, 338–347. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, H.T.; Hu, D.W.; Zhang, F.; Yang, F.J.; Lu, J.J. Estimation of the effective thermal properties of cracked rocks. Eur. J. Environ. Civ. Eng. 2016, 20, 954–970. [Google Scholar] [CrossRef]
- Choo, J.; Kim, Y.J.; Lee, J.H.; Yun, T.S.; Lee, J.; Kim, Y.S. Stress-induced evolution of anisotropic thermal conductivity of dry granular materials. Acta Geotech. 2012, 8, 91–106. [Google Scholar] [CrossRef]
- Askari, R.; Hejazi, S.H.; Sahimi, M. Thermal Conduction in Deforming Isotropic and Anisotropic Granular Porous Media with Rough Grain Surface. Transp. Porous Media 2018, 124, 221–236. [Google Scholar] [CrossRef]
- Andrä, H.; Combaret, N.; Dvorkin, J.; Glatt, E.; Han, J.; Kabel, M.; Keehm, Y.; Krzikalla, F.; Lee, M.; Madonna, C. Digital rock physics benchmarks—Part I: Imaging and segmentation. Comput. Geosci. 2013, 50, 25–32. [Google Scholar] [CrossRef]
- Andrä, H.; Combaret, N.; Dvorkin, J.; Glatt, E.; Han, J.; Kabel, M.; Keehm, Y.; Krzikalla, F.; Lee, M.; Madonna, C. Digital rock physics benchmarks—Part II: Computing effective properties. Comput. Geosci. 2013, 50, 33–43. [Google Scholar] [CrossRef]
- Song, R.; Liu, J.J.; Cui, M.M. A new method to reconstruct structured mesh model from micro computed tomography images of porous media and its application. Int. J. Heat Mass Transf. 2017, 109, 705–715. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Xu, X.M.; Lebedev, M.; Sarmadivaleh, M.; Barifcani, A.; Iglauer, S. Multi-scale X-ray computed tomography analysis of coal microstructure and permeability changes as a function of effective stress. Int. J. Coal Geol. 2016, 165, 149–156. [Google Scholar] [CrossRef]
- Yang, Y.F.; Yao, J.; Wang, C.C.; Gao, Y.; Zhang, Q.; An, S.Y.; Song, W.H. New pore space characterization method of shale matrix formation by considering organic and inorganic pores. J. Nat. Gas Sci. Eng. 2015, 27, 496–503. [Google Scholar] [CrossRef]
- An, S.Y.; Yao, J.; Yang, Y.F.; Zhang, L.; Zhao, J.L.; Gao, Y. Influence of pore structure parameters on flow characteristics based on a digital rock and the pore network model. J. Nat. Gas Sci. Eng. 2016, 31, 156–163. [Google Scholar] [CrossRef]
- Song, W.H.; Yao, J.; Li, Y.; Sun, H.; Zhang, L.; Yang, Y.F.; Zhao, J.L.; Sui, H.G. Apparent gas permeability in an organic-rich shale reservoir. Fuel 2016, 181, 973–984. [Google Scholar] [CrossRef]
- Zhao, J.L.; Yao, J.; Zhang, M.; Zhang, L.; Yang, Y.F.; Sun, H.; An, S.Y.; Li, A.F. Study of gas flow characteristics in tight porous media with a microscale Lattice Boltzmann model. Sci. Rep. 2016, 6, 32393. [Google Scholar] [CrossRef]
- Sun, H.; Yao, J.; Cao, Y.C.; Fan, D.Y.; Zhang, L. Characterization of gas transport behaviors in shale gas and tight gas reservoirs by digital rock analysis. Int. J. Heat Mass Transf. 2017, 104, 227–239. [Google Scholar] [CrossRef]
- Yang, Y.F.; Liu, Z.H.; Sun, Z.X.; An, S.Y.; Zhang, W.J.; Liu, P.F.; Yao, J.; Ma, J.S. Research on stress sensitivity of fractured carbonate reservoirs based on CT technology. Energies 2017, 10, 1833. [Google Scholar] [CrossRef]
- Zhang, K.; Ma, X.P.; Li, Y.L.; Wu, H.Y.; Cui, C.Y.; Zhang, X.M.; Zhang, H.; Yao, J. Parameter prediction of hydraulic fracture for tight reservoir based on micro-seismic and history matching. Fractals 2018, 26, 1840009. [Google Scholar] [CrossRef]
- Zhang, L.; Cui, C.; Ma, X.; Sun, Z.; Liu, F.; Zhang, K. A fractal discrete fracture network model for history matching of naturally fractured reservoirs. Fractals 2019, 27, 1940008. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, M.X.; Cheng, M.; Guo, X.T.; Li, Y.W.; Ma, P.N.; Cen, K.F. High resolution X-ray microtomography for the charaterization of pore structure and effective thermal conductivity of iron ore sinter. Appl. Therm. Eng. 2017, 127, 508–516. [Google Scholar] [CrossRef]
- Fan, L.F.; Gao, J.W.; Wu, Z.J.; Yang, S.Q.; Ma, G.W. An investigation of thermal effects on micro-properties of granite by X-ray CT technique. Appl. Therm. Eng. 2018, 140, 505–519. [Google Scholar] [CrossRef]
- Zhao, J.L.; Kang, Q.J.; Yao, J.; Zhang, L.; Li, Z.; Yang, Y.F.; Sun, H. Lattice Boltzmann simulation of liquid flow in nanoporous media. Int. J. Heat Mass Transf. 2018, 125, 1131–1143. [Google Scholar] [CrossRef]
- Rostami, A.; Masoudi, M.; Ghaderi-Ardakani, A.; Arabloo, M.; Amani, M. Effective Thermal Conductivity Modeling of Sandstones: SVM Framework Analysis. Int. J. Thermophys. 2016, 37, 59. [Google Scholar] [CrossRef]
- Vaferi, B.; Gitifar, V.; Darvishi, P.; Mowla, D. Modeling and analysis of effective thermal conductivity of sandstone at high pressure and temperature using optimal artificial neural networks. J. Pet. Sci. Eng. 2014, 119, 69–78. [Google Scholar] [CrossRef]
- Oezbek, H. Thermal conductivity of multi-fluid saturated porous media. J. Pet. Technol. 1976, 29, 275. [Google Scholar]
- Büttner, H.; Mokross, F. Fourier’s law and thermal conduction. Nature 1984, 311, 217–218. [Google Scholar] [CrossRef]
- Pribnow, D.; Williams, C.F.; Sass, J.H.; Keating, R. Thermal conductivity of water-saturated rocks from the KTB Pilot Hole at temperatures of 25 to 300 °C. Geophys. Res. Lett. 1996, 23, 391–394. [Google Scholar] [CrossRef]
- Askari, R.; Taheri, S.; Hejazi, S.H. Thermal conductivity of granular porous media: A pore scale modeling approach. AIP Adv. 2015, 5, 455–460. [Google Scholar] [CrossRef]
- Wang, X.; Yao, J.; Yang, Y.; Wang, C.; Pu, D. Permeability prediction in digital core with curved fractures based on combined plate model. J. China Univ. Pet. Ed. Nat. Sci. 2013, 37, 82–86. [Google Scholar]
- Wu, K.J.; Dijke, M.I.J.V.; Couples, G.D.; Jiang, Z.Y.; Ma, J.S.; Sorbie, K.S.; Crawford, J.; Young, I.; Zhang, X.X. 3D stochastic modelling of heterogeneous porous media–applications to reservoir rocks. Transp. Porous Media 2006, 65, 443–467. [Google Scholar] [CrossRef]
- Yang, Y.F.; Wang, K.; Zhang, L.; Sun, H.; Zhang, K.; Ma, J.S. Pore-scale simulation of shale oil flow based on pore network model. Fuel 2019, 251, 683–692. [Google Scholar] [CrossRef]
- Yang, Y.F.; Yang, H.Y.; Tao, L.; Yao, J.; Wang, W.D.; Zhang, K.; Luquot, L. Microscopic determination of remaining oil distribution in sandstones with different permeability scales using computed tomography scanning. J. Energy Resour. Technol. 2019, 141, 092903. [Google Scholar] [CrossRef]
- Tobias, R.D. An Introduction to Partial Least Squares Regression. In Proceedings of the Twentieth Annual SAS Users Group International Conference, Orlando, FL, USA, 2 April 1995; SAS Institute Inc.: Cary, NC, USA, 1995; pp. 1250–1257. [Google Scholar]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in partial least squares regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Z.; Yao, J.; Zhang, L.; Ma, J.; Hejazi, S.; Luquot, L.; Ngarta, T. Flow simulation of artificially induced microfractures using digital rock and Lattice Boltzmann Methods. Energies 2018, 11, 2145. [Google Scholar] [CrossRef]
- Liu, K.Q.; Ostadhassan, M.; Kong, L.Y. Multifractal characteristics of Longmaxi Shale pore structures by N-2 adsorption: A model comparison. J. Pet. Sci. Eng. 2018, 168, 330–341. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W.J., III. The collinearity problem in linear regression. The partial least squares (PLS) approach to generalized inverses. Siam J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, X.; Huang, Y.; Zhang, C.; Chen, Y. Heat conduction in porous media characterized by fractal geometry. Energies 2017, 10, 1230. [Google Scholar] [CrossRef]
- Haffen, S.; Géraud, Y.; Rosener, M.; Diraison, M. Thermal conductivity and porosity maps for different materials: A combined case study of granite and sandstone. Geothermics 2017, 66, 143–150. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Porosity (%) | 31.43 |
| Effective porosity (%) | 31.40 |
| Average pore radius (μm) | 6.42 |
| Average throat length (μm) | 191 |
| Average coordination number | 7.23 |
| Average tortuosity | 4.24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Zhang, L.; Liu, R.; Wen, X.; Yang, Y.; Zhang, L.; Zhang, K.; Askari, R. Thermal Conduction Simulation Based on Reconstructed Digital Rocks with Respect to Fractures. Energies 2019, 12, 2768. https://doi.org/10.3390/en12142768
Yang H, Zhang L, Liu R, Wen X, Yang Y, Zhang L, Zhang K, Askari R. Thermal Conduction Simulation Based on Reconstructed Digital Rocks with Respect to Fractures. Energies. 2019; 12(14):2768. https://doi.org/10.3390/en12142768
Chicago/Turabian StyleYang, Haiyuan, Li Zhang, Ronghe Liu, Xianli Wen, Yongfei Yang, Lei Zhang, Kai Zhang, and Roohollah Askari. 2019. "Thermal Conduction Simulation Based on Reconstructed Digital Rocks with Respect to Fractures" Energies 12, no. 14: 2768. https://doi.org/10.3390/en12142768
APA StyleYang, H., Zhang, L., Liu, R., Wen, X., Yang, Y., Zhang, L., Zhang, K., & Askari, R. (2019). Thermal Conduction Simulation Based on Reconstructed Digital Rocks with Respect to Fractures. Energies, 12(14), 2768. https://doi.org/10.3390/en12142768







