Investigation on Asymmetric Instability of Cylindrical Power-Law Liquid Jets

Abstract

An investigation has been performed to reveal the breakup mechanism of three-dimensional power-law cylindrical jets with different mode disturbances. It is observed experimentally that the asymmetric mode disturbances could prevail over the counterpart of symmetric mode under special conditions. The dispersion equation characterizing the instability of three-dimensional cylindrical jets of power-law fluids is deduced. The effects of the Weber number, generalized Reynolds number, power-law exponent, and gas–liquid density ratio on the jet instability are studied in detail. It is found that the maximum growth rates of asymmetric mode disturbances are usually larger than those of symmetric mode disturbances under high Weber numbers and low generalized Reynolds numbers, which implies that the former are more likely to be responsible for the breakup of power-law fluids. Meanwhile, the large gas–liquid interaction could trigger more short, unstable waves. Interestingly, with the increase of jet velocity, the interaction between liquid and gas phases plays an increasingly leading role on the breakup of power-law cylindrical jets, whereas the viscous force and the power-law exponent have less significant impacts. Theoretical analysis results give a better comprehensive understanding for the power-law jets.

1. Introduction

The transformation of liquid into spray is important in clean energy combustion, agriculture, meteorology, and many industrial processes. As a common type of atomization, cylindrical jets are utilized in a number of devices, such as liquid fuel rocket, irrigation, meteorology, and burners in industrial furnaces, gasifiers, combustion engines, and gas turbine [1,2,3,4]. Many researchers have investigated the liquid breakup, which could ameliorate efficiency in many real applications.

The study on the liquid breakup could be traced back to Rayleigh [5,6]. The breakup of an inviscid cylindrical liquid jet in vacuum was discussed. However, later experimental results showed that only the low-speed cases were consistent with Rayleigh’s conclusion. Weber [7] obtained a complete linear solution of a viscous Newtonian liquid jet with surface tension in a non-viscous gas environment. Thereafter, Taylor [8] pointed out that the interaction between the gas medium and the liquid jet occupied the dominant position in high-speed cases based on the linear instability theory. Li [9] established a more realistic dispersion equation to characterize the instability of cylindrical Newtonian fluid jets, and proved that the maximum growth rate of the asymmetric mode could be larger than that of the symmetrical mode under some certain conditions. Later, Ruo [10] carried out a temporal linear stability analysis for cylindrical liquid jets, and showed that the conditions in the non-axisymmetric mode would dominate the instability of the liquid jets. Although these researchers have obtained many interesting results, it should be pointed out that all of the above studies are only for Newtonian fluids.

So far, there are only a few studies on the breakup of non-Newtonian fluid jets, which are more widely involved in practical applications. According to the constitutive equation, non-Newtonian fluid could be classified as different types of fluids, such as viscoelastic fluid, power-law fluid, and Bingham fluid. For viscoelastic fluid, Liu and Liu [11,12] and Brenn et al. [13] obtained the three-dimensional linearly unstable dispersion equations for cylindrical jets and planar sheets, respectively. Their results showed that elasticity would cause the viscoelastic fluids to be more unstable than Newtonian fluids. Thompson and Rothstein [14] studied the instability of annular viscoelastic fluid jet. Yang et al. [15,16] investigated the three-dimensional instability of viscoelastic liquid jets in a swirling airflow and the instability of viscoelastic liquid sheet of gas flow with unequal velocities on two sides.

The power-law fluid, which is most widely used in practice, is characterized by a strong nonlinearity constitutive relationship. Up to now, there have been limited research studies about the breakup power-law fluid. Based on Dombrowski and Johns’s [17] results of the linear instability of liquid sheets, Chojnacki and Feikema [18] obtained the dispersion equation of the power-law liquid sheet with sinuous mode. Similar conclusions were reported in experiments by Yang [19]. Yang [20] also obtained a linearly unstable dispersion equation of the power-law fluid cylindrical jet with symmetric mode. Renardy and Renardy [21] studied the problem of the low-speed cylindrical jet of power-law fluid under the ideal gas condition. Gao and Ng [22] studied the nonlinear instability of the power-law fluid capillary jet in the spatial mode under the Carreau–Yasuda model, and predicted the occurrence of satellite droplets. Taking into account the cylindrical jet into a stationary ideal gas environment, Chang [23] simplified the constitutive relation of the power-law fluid, and analyzed the instability of shear thinning and shear thickening fluids through the Taylor mode and Rayleigh mode, respectively.

It should be noted that the above studies on the mechanism of the power-law fluid jet mainly focus on the two-dimensional fluid jet mode, neglecting the three-dimensional asymmetric fluid jet properties. Also, in our previous work, Chang [23] neglected the effect of asymmetric mode disturbances on the instability, due to only focusing on two dimensions.

In this paper, the dispersion equation with both symmetric and asymmetric mode disturbances is derived according to linear instability theory to reveal the breakup mechanism of the power-law fluid. This paper further investigates the influence of various factors on the instability of a three-dimensional cylindrical jet under different mode disturbances. The effects of dimensionless parameters, e.g., Weber number, the generalized Reynolds number, power-law exponent, and the gas–liquid density ratio, on the instability of a power-law liquid jet, are studied.

2. Mathematical Formulation of Three-Dimensional Linear Instability Analysis

2.1. Assumptions

A cylindrical power-law liquid jet with consistency coefficient K, power-law exponent n, density ρ_l, and surface tension σ, is considered. The liquid, with velocity U₀ and radius a, is injected into a static non-viscous ambient gas with density ρ_g. Figure 1 shows the schematic diagram of a cylindrical liquid jet and its interface waves. η characterizes the disturbed amplitude of the surface waves. Since the liquid velocity is lower than the local speed of sound, both fluids are regarded as incompressible, neglecting the impact of temperature. For convenience, a cylindrical coordinate system (r, θ, z) is adopted to establish the control equations. In the coordinate system, the z-axis is along the moving direction of the liquid flow, the r-axis is normal to the liquid flow with its origin located at the axis of symmetry, and the θ-axis is in the azimuthal direction.

In the initial state, the velocity and pressure in both gas and liquid streams can be expressed as follows:

$${\overline{\mathit{U}}}_j=(0,0,U_{j0})$$

(1)

$${\overline{P}}_j=P_{j0}$$

(2)

where the subscript j can be g or l, denoting the gas and liquid phases. Subscript 0 stands for the initial, and the overbar stands for the basic steady flow.

Owing to the role of surface tension, the pressure at the gas–liquid interface (r = a) satisfies:

$${\overline{P}}_l={\overline{P}}_g+\frac{\sigma }{a}$$

(3)

The jet will produce a certain deformation in the gas–liquid interface by the impact of the disturbance, causing the gas–liquid interface to go away from the original balance position. Then, the disturbed flow field becomes:

$${\mathit{U}}_j={\overline{\mathit{U}}}_j+{\mathit{u}}_j,{\mathit{u}}_j=\left(u_{jr},u_{j\theta },u_{jz}\right)$$

(4)

$$P_j={\overline{P}}_j+p_j$$

(5)

where the lower case symbols u and p are disturbances of the flow velocity and pressure, respectively.

Considering that the flow is disturbed by a small disturbance, this is expressed in the normal mode is as follows:

$$\left({\mathit{u}}_j,p_j,\eta \right)=\left({\tilde{u}}_j\left(r\right),{\tilde{p}}_j\left(r\right),{\eta }_0\right)e^{i\left(kz+m\theta \right)+st},(j=g,l)$$

(6)

where η₀ is the initial amplitude of the surface wave, k is the complex wave number, s is the complex growth rate, m is the order of the surface wave, and the tildes signify the initial values of the disturbance.

2.2. Governing Equation

The mass and the momentum conservation equations in terms of the gas phases are given as:

$$\nabla {\mathit{U}}_g=0$$

(7)

$$\frac{\partial {\mathit{U}}_g}{\partial t}+({\mathit{U}}_g\cdot \nabla )U_g=-\frac{1}{\rho }\nabla {\mathit{P}}_g+\nabla {\mathit{\tau }}_g$$

(8)

The mass and the momentum conservation equations in terms of the liquid phases are given as:

$$\nabla {\mathit{U}}_l=0$$

(9)

$$\frac{\partial {\mathit{U}}_l}{\partial t}+({\mathit{U}}_l\cdot \nabla ){\mathit{U}}_l=-\frac{1}{\rho }\nabla {\mathit{P}}_l+\nabla {\mathit{\tau }}_l$$

(10)

$${\mathit{\tau }}_l=K{(\dot{\gamma })}^n$$

(11)

For an inviscid ideal gas, substituting Equations (1), (4) and (6) into Equations (7) and (8), the continuity equation is expressed as:

$$\frac{d{\tilde{u}}_{gr}}{dr}+\frac{{\tilde{u}}_{gr}}{r}+\frac{im}{r}{\tilde{u}}_{g\theta }+ik{\tilde{u}}_{gz}=0$$

(12)

Similarly, substituting Equations (1), (4) and (6) into Equations (7) and (8), and neglecting the nonlinear terms of the disturbance, the momentum equation is obtained as follows:

$${\rho }_g\left(s+ik{U}_{g0}\right){\tilde{u}}_{gr}=-\frac{d{\tilde{p}}_g}{dr}$$

(13)

$${\rho }_g\left(s+ik{U}_{g0}\right){\tilde{u}}_{g\theta }=-\frac{im}{r}{\tilde{p}}_g$$

(14)

$${\rho }_g\left(s+ik{U}_{g0}\right){\tilde{u}}_{gz}=-ik{\tilde{p}}_g$$

(15)

For the liquid, the linearized continuity equation, with the normal mode disturbance substituted, is:

$$\frac{d{\tilde{u}}_{lr}}{dr}+\frac{{\tilde{u}}_{lr}}{r}+\frac{im}{r}{\tilde{u}}_{l\theta }+ik{\tilde{u}}_{lz}=0$$

(16)

To simplify the calculations and retain the actual flowing state of the jet, the normal deviatoric stress tensor in the axial direction is kept, whereas the others are neglected in the above equations. The momentum equation is obtained as:

$${\rho }_l\left(\frac{\partial U_{lr}}{\partial t}+U_{lr}\frac{\partial U_{lr}}{\partial r}+\frac{U_{l\theta }}{r}\frac{\partial U_{lr}}{\partial \theta }+U_{lz}\frac{\partial U_{lr}}{\partial z}-\frac{U_{l\theta }^2}{r}\right)=-\frac{\partial P_l}{\partial r}$$

(17)

$${\rho }_l\left(\frac{\partial U_{l\theta }}{\partial t}+U_{lr}\frac{\partial U_{l\theta }}{\partial r}+\frac{U_{l\theta }}{r}\frac{\partial U_{l\theta }}{\partial \theta }+U_{lz}\frac{\partial U_{l\theta }}{\partial z}+\frac{U_{lr}{U}_{l\theta }}{r}\right)=-\frac{\partial P_l}{r\partial \theta }$$

(18)

$${\rho }_l\left(\frac{\partial U_{lz}}{\partial t}+U_{lr}\frac{\partial U_{lz}}{\partial r}+\frac{U_{l\theta }}{r}\frac{\partial U_{lz}}{\partial \theta }+U_{lz}\frac{\partial U_{lz}}{\partial z}\right)=-\frac{\partial P_l}{\partial z}+\frac{\partial {\tau }_{zz}}{\partial z}$$

(19)

where the variable quantity τ_zz is expressed as:

$${\tau }_{zz}=K{(2\frac{\partial U_{lz}}{\partial z})}^n$$

(20)

In order to linearize the governing Equations (16)–(19) and keep the nonlinear characteristics of the power-law fluid, a coefficient, g, with the unit of s⁻¹, is introduced [23]. It denotes the value of the velocity change, and is related to the properties of the fluid. Then, Equation (20) becomes:

$${\tau }_{zz}=K{(2\frac{\partial U_{lz}}{\partial z})}^n=K{(2\frac{\partial u_{lz}}{\partial z})}^n\approx K{\left(2\frac{\partial }{\partial z}\left(u_{lz}+gz\right)\right)}^n=K{\left(2g+2\frac{\partial u_{lz}}{\partial z}\right)}^n$$

(21)

Expanding the right-hand side of Equation (21) by binomial theorem and neglecting the high-order terms:

$${\mathit{\tau }}_{zz}\approx K\left({\left(2g\right)}^n+2n{(2g)}^{n-1}\frac{\partial u_{lz}}{\partial z}\right)$$

(22)

Finally, substituting Equations (1), (4), (6) and (22) into Equations (17)–(19), and neglecting the nonlinear terms, the following linearized momentum equations for the liquid phase are obtained as:

$${\rho }_l(s+ik{U}_{l0}){\tilde{u}}_{lr}=-\frac{d{\tilde{p}}_l}{dr}$$

(23)

$${\rho }_l(s+ik{U}_{l0}){\tilde{u}}_{l\theta }=-\frac{im}{r}{\tilde{p}}_l$$

(24)

$${\rho }_l\left(s+ik{U}_{l0}\right){\tilde{u}}_{lz}=-ik{\tilde{p}}_l-2nK{(2g)}^{n-1}{k}^2{\tilde{u}}_{lz}$$

(25)

2.3. Boundary Conditions

The boundary conditions should satisfy the kinematic and dynamic conditions at the gas–liquid interface. Since the interface is a contact surface, the kinematic boundary conditions are written as:

$$u_{jr}=\frac{\partial \eta }{\partial t}+U_{j0}\frac{\partial \eta }{\partial z},j=l or g$$

(26)

Substituting the normal mode disturbance Equations (1), (4), and (6) into Equation (26), the continuity equation becomes:

$${\tilde{u}}_{jr}=\left(s+ik{U}_{j0}\right){\eta }_0,j=l or g$$

(27)

For the inviscid gas, the shear stresses of the power-law liquid on the gas–liquid interface have to be zero, and the normal stresses on the gas–liquid interface are balanced by the surface tension effect. The detailed dynamic boundary conditions require:

$$K{\left(\frac{\partial u_{lr}}{\partial z}+\frac{\partial u_{lz}}{\partial r}\right)}^n=0$$

(28)

$$K{\left(\frac{1}{r}\frac{\partial u_{lr}}{\partial \theta }+r\frac{\partial }{\partial r}\left(\frac{u_{l\theta }}{r}\right)\right)}^n=0$$

(29)

$$-p_l+p_g-\frac{\sigma }{a^2}\left(\eta +a^2\frac{{\partial }^2\eta }{\partial z^2}+\frac{{\partial }^2\eta }{\partial {\theta }^2}\right)=0$$

(30)

Substituting Equation (6) into Equations (28)–(30), they become:

$$\frac{d{\tilde{u}}_{lz}}{dr}+ik{\tilde{u}}_{lr}=0$$

(31)

$$\frac{im}{r}{\tilde{u}}_{lr}+r\frac{d}{dr}\left(\frac{{\tilde{u}}_{l\theta }}{r}\right)=0$$

(32)

$${\tilde{p}}_l-{\tilde{p}}_g+\frac{\sigma }{a^2}\left(1-k^2{a}^2-m^2\right){\eta }_0=0$$

(33)

Furthermore, according to the power-law fluid jet model, the velocity and pressure for the liquid and gas phases must be finite at r = 0 and r = ∞, respectively.

2.4. Dispersion Equation

For the gas phase, according to the continuity equation shown in Equation (12), the momentum equations in Equations (13) to (15), the motion condition in Equation (27), and the dynamic boundary conditions in Equations (31) to (33), the mathematical expression of the initial value of the flow field pressure disturbance can be derived as:

$${\tilde{p}}_g\left(r\right)=-\frac{{\rho }_g{\left(s+ik{U}_{g0}\right)}^2}{k}\frac{K_m\left(kr\right)}{K_m^{’}\left(ka\right)}{\eta }_0$$

(34)

where K_m(x) is the mth-order Bessel correction function of the second kind.

For the liquid phase, according to the continuity equation shown in Equation (16), the momentum equations in Equations (23) to (25), the motion condition in Equation (27), and the dynamic boundary conditions in Equations (31)–(33), the mathematical expression of the initial value of the flow field pressure disturbance can be derived as:

$${\tilde{p}}_l\left(r\right)=-\frac{{\rho }_l{\left(s+ik{U}_{l0}\right)}^2}{l}\frac{I_m\left(lr\right)}{I_m^{’}\left(la\right)}{\eta }_0$$

(35)

$$l=k\sqrt{\frac{{\rho }_{l}g(s+ik{U}_{l0})}{{\rho }_{l}g\left(s+ik{U}_{l0}\right)+Kn{k}^2{\left(2g\right)}^n}}$$

(36)

where I_m(x) is the mth-order Bessel correction function of the second kind.

Substituting the disturbed solutions in Equations (34) and (35) into the boundary condition in Equation (33), the dispersion equation can be obtained as:

$$\frac{{\rho }_l{\left(s+ik{U}_{l0}\right)}^2}{l}\frac{I_m\left(la\right)}{I_m^{’}\left(la\right)}-\frac{{\rho }_g{\left(s+ik{U}_{g0}\right)}^2}{k}\frac{K_m\left(ka\right)}{K_m^{’}\left(ka\right)}+\frac{\sigma }{a^2}\left(k^2{a}^2+m^2-1\right)=0$$

(37)

Equations (37) is used to characterize the instability of the power-law fluid in an asymmetric cylindrical jet. For convenience, the dimensionless form of the dispersion relation in Equation (37) is derived to analyze the instability of power-law fluid jet as below:

$$\frac{{\left(S+i\alpha \right)}^2}{L}\frac{I_m\left(L\right)}{I_m^{’}\left(L\right)}-\frac{Q{\left(S+i\alpha \beta \right)}^2}{\alpha }\frac{K_m\left(\alpha \right)}{K_m^{’}\left(\alpha \right)}+\frac{{\alpha }^2+m^2-1}{\mathrm{We}}=0$$

(38)

where Q = ρ_g/ρ_l is the density ratio of gas to liquid, We = ρ_lU_l0²a/σ is the Weber number denoting the ratio of inertial forces to the surface tension of the liquid phase, Re_n= ρ_lU_l0²⁻ⁿaⁿ/K is the generalized Reynolds number denoting the ratio of inertia forces to the viscous forces of the liquid, β = U_g0/U_l0 is the velocity ratio of gas to liquid, α = ka is the dimensionless complex wavenumber, S = sa/U_l0 is the dimensionless complex growth rate, G = ga/U_l0, and:

$$L=la=\alpha \sqrt{\frac{{\mathrm{Re}}_n(S+i\alpha )}{{\mathrm{Re}}_n\left(S+i\alpha \right)+2n{\alpha }^2{\left(2G\right)}^{n-1}}}$$

(39)

In the present study, by adopting the temporal instability analysis, the dispersion equation in Equation (38) can be numerically solved, and the complex solutions of S can be calculated corresponding to each wavenumber m by specifying jet parameters including We, Re_n, Q, G, β, and n. The real part of S indicates the dimensionless growth rate of the disturbance, which shows the instability of the liquid jet.

Note that Equation (38) can be reduced to the other form as shown in our previous work by setting specific parameters to zero or infinity. For example, m = 0 in Equation (38) represents an axisymmetric cylindrical jet [23]. When a approaches infinity, the liquid jet becomes a plane liquid sheet, and also, Re_n going to infinity corresponds to a non-viscous ideal liquid, such that Equation (38) degenerates into the following one:

$$\frac{{\left(S+i\alpha \right)}^2}{\alpha }\frac{I_0\left(\alpha \right)}{I_1\left(\alpha \right)}+\frac{Q{S}^2}{\alpha }\frac{K_0\left(\alpha \right)}{K_1\left(\alpha \right)}+\frac{{\alpha }^2-1}{\mathrm{We}}=0$$

(40)

Equation (40) is consistent with the dispersion equation obtained by Yang [24]. Setting Q = 0, the ambient medium gas disappears, so that Equation (40) turns to the following form:

$$\frac{{\left(S+i\alpha \right)}^2}{\alpha }\frac{I_0\left(\alpha \right)}{I_1\left(\alpha \right)}+\frac{{\alpha }^2-1}{\mathrm{We}}=0$$

(41)

It is found that Equation (41) is consistent with the dispersion equation obtained by Rayleigh [5].

In this paper, the temporal instability analysis is used to obtain the complex solutions of S = S_r + iS_i from the dispersion relation in Equation (38) at any real wavenumber α, when other parameters such as We, Re_n, Q, and n are set to certain values. In fact, the dispersion equation in Equation (38) is a complex function equation with obvious nonlinear characteristics; it is impossible to obtain its explicit analytic solutions. Due to this reason, the numerical method is adopted in the study.

3. Results and Discussion

The influence of various dimensionless parameters on the asymmetric instability for the power-law fluids of a three-dimensional cylindrical jet is studied. The relationship between the dimensionless wavenumber α and wave growth rate S_r, which denotes the degree of the liquid jet instability, can be obtained by solving Equation (38) temporally. Figure 2 shows the instability curves of a liquid cylindrical jet, with Re_n = 50, Q = 0.002, We = 8000, G = 0.5 × 10⁻⁵, n = 0.8, and β = 0. For each instability curve, the endpoints represent the maximum and minimum wavenumbers of the unstable surface wave, and their middle area represents the instability range of the jet. The wave growth rate S_r reflects the degree of the liquid jet instability, which is associated with the breakup length. The larger the maximum wave growth rate, S_r,max, the more unstable the liquid jet. The dominant wavenumber, α_dom corresponding to S_r,max, is defined as the reciprocal of the wavelength, which represents the jet breakup scale.

For a cylindrical jet, the jet surface also exhibits different structures according to the surface wave morphologies, which are reflected by m in Equation (38). The values of m—0, 1, 2, 3, and 4—characterize a single-column symmetrical jet, a single-column asymmetric jet, and two-strand, three-strand, and four-strand cylindrical liquid jets, respectively. As Figure 2 shows, with the increase of m, the range of its corresponding wavenumber becomes gradually narrowed. The asymmetric mode disturbances (m > 1) are more likely to dominate the jet breakup process. When m increases, the form of the surface disturbance corresponding to its instability curve is becoming more and more complex, and the surface wave is more likely to be unstable. For the convenience of research, the four representative surface disturbances—m = 0, 1, 2, and 3—were chosen to discuss in this study.

3.1. Near-Field Characteristics of Power-Law Fluid Jets

The high-speed photographic technique was applied to capture the near-field characteristics of the the cylindrical jet at different injection pressures. Our high-speed photography system used the shadowgraph images method. A Photron SA1.1 high-speed camera was employed to obtain the morphology characteristics of the liquid jet. The frame rate was 5400 fps, and the frame resolution was 1024 × 1024 pixels.

The instability characteristics of a three-dimensional power-law liquid jet were investigated by experiments first. Figure 3 shows the near-field morphological features of the jets under different injecting pressures, using a 0.5-mm nozzle diameter and 0.15 wt.% carbopol aqueous solution. For the experimental solution, the key parameters are measured at normal temperature as follows: the surface tension coefficient is 0.073, its power-law exponent is 0.546, and the consistency coefficient is 0.551 Pa·sⁿ. It should be noted that with the increase of injection pressure from 0.01 to 1.95 MPa, the jet speed increases from 2.0 m/s to 45.2 m/s, the Weber number increases from 27.0 to 14,008.9, and the cylindrical jet becomes more unstable.

The transition process from a smooth cylinder to a twisted cylinder at 0.1 MPa can be seen very clearly in the photos. At 0.2 MPa, the jet surface is distorted to form an apparent surface wave. From the injection pressure of 0.25 MPa, the jet appears to have obvious rope-like or twist-like structures, and the surface wave amplitude increases with the increase of the injection pressure. The amplitude of the surface wave increases as the distance from the nozzle increases and the edge is no longer smooth. When the jet pressure reaches 0.3 MPa, the surface wave indicates that the asymmetric mode disturbance (m = 1) dominates the structural of the jet.

Furthermore, when the jet pressure reaches 0.35 MPa, the surface wave seems to show the structural characteristics of the asymmetric mode disturbance (m = 2). After 0.6 MPa, the shape of the jet surface is more complicated, because some surfaces become irregular, with a higher-order asymmetric mode disturbance becoming dominant. The jet is no longer a circular cylinder, while the internal structure even appears to be a part of the separation phenomenon.

In order to have a closer look at the specific characteristics of the jet surface in Figure 3, the theoretical morphological characteristics of the near-field region of the power-law fluid cylindrical jet are given in Figure 4. From left to right, they are the 0th-order symmetric mode disturbance, the first-order asymmetric mode disturbance, the second-order asymmetric mode disturbance, the third-order asymmetric mode disturbance, and the fourth-order asymmetric mode disturbance, respectively. It is seen that the increase of the injection velocity gives rise to a more unstable surface wave, and a large wave number will make the jet more fragile. The experimental results show that the asymmetric mode disturbances can dominate the breakup of the power-law liquid jets under certain conditions. This result is contrary to previous studies [16,17,19], in which it was proposed that the symmetric mode disturbance is always the most unstable, and dominates the breakup of the jets. In the next discussion, theoretical analyses are performed to characterize the symmetry mode disturbance and the asymmetric mode disturbances simultaneously.

3.2. Effect of Liquid Weber Number

It is known that the Weber number, which is a key parameter for the jet instability, denotes the ratio of inertial force to the surface tension of the liquid phase, mainly reflecting the effect of surface tension. Figure 5a,b show the effect of the Weber number on the maximum growth rate and the dominant wavenumber, respectively. The other parameters remain constant as Re_n = 50, Q = 0.002, G = 0.5 × 10⁻⁵, n = 0.8, and β = 0. It is seen that the maximum growth rate of the zero-order mode disturbance first decreases and then increases with the increase of the Weber number. The dominant wavenumber shows a similar trend. This indicates that for the symmetrical zero-order disturbance, in a low-speed case, surface tension is the positive factor for the instability of the surface wave, while in the high-speed case, it is the negative force for the instability of the surface wave.

With the increase of the Weber number, asymmetric mode disturbances are triggered, and gradually become more unstable. As Figure 5a,b shows, both the maximum growth rate and the dominant wavenumber are positively related with the Weber number for asymmetric mode disturbances in a high-speed case. The results show that surface tension has a similar effect on both asymmetric mode disturbances and the symmetric mode disturbance in a high-speed jet, preventing the power-law fluids from breakup. Furthermore, for high-speed power-law fluid jets, the maximum growth rate of asymmetric mode disturbances is usually larger than that of the symmetric mode disturbance. It means that the asymmetric mode disturbances could easily play a leading role on the breakup of the high-speed power-law fluid jet. This also illustrates why the asymmetric mode disturbances are observed easily in the above experiment with high injection pressures. Similar results were reported by Li [9], Yang et al. [16], and Ruo et al. [25]. Therefore, in high-speed jets, the gas–liquid interface will be more irregular, and the liquid breakup process will become more complex.

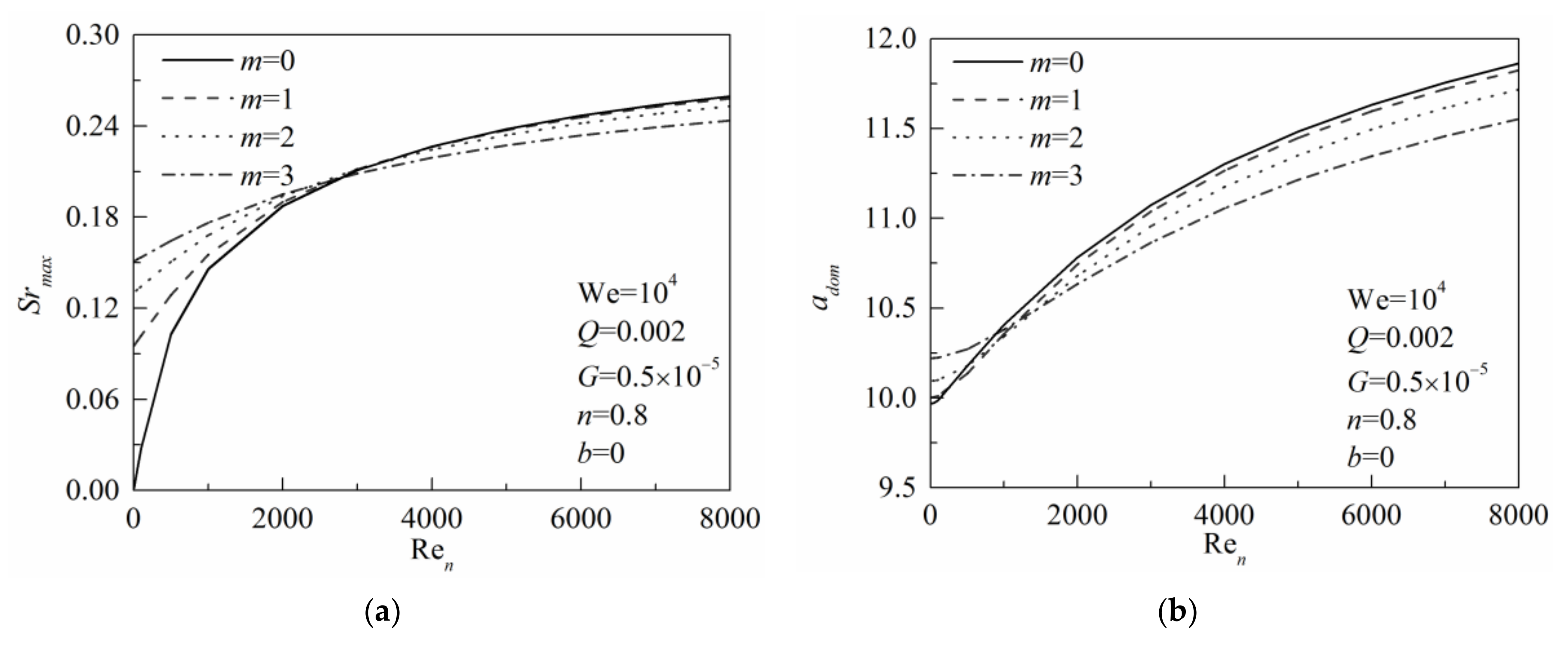
3.3. Effect of the Generalized Reynolds Number

The generalized Reynolds number reflects the effect of the viscous force of liquid phase on the jet instability. The other parameters in Figure 6a,b are We = 10000, Q = 0.002, G = 0.5 × 10⁻⁵, n = 0.8, and β = 0. Figure 6a,b shows that both the maximum growth rate and dominant wavenumber increase with the increase of Re_n in different levels, which indicates that the increase of Re_n is conducive to the jet breakup. This illustrates that the liquid viscosity will prevent the liquid jet from breakup and enlarge the breakup scale. Moreover, with the continuous increase of Re_n, the upward increasing trend of the maximum growth rate becomes weak. The reason is that when the Re_n increases continuously, the liquid viscosity is reduced constantly, so the influence of the viscous force will become smaller, compared with other factors. In Figure 6a, the slope of the maximum growth rate curve is smaller for the asymmetric mode disturbances (m > 0) of the liquid jet, whereas the dominant wavenumber curve is flatter, as shown in Figure 6b. For a large Re_n, the maximum growth rate of the symmetric mode disturbance is larger than that of the asymmetric mode disturbances. However, these asymmetric mode disturbances will prevail over the symmetric mode disturbance with a small generalized Reynolds number. The dominant wavenumber curves express the similar trend with Re_n. This shows that the liquid viscosity has a more sensitive effect on the symmetric mode disturbance than on the asymmetric mode disturbances. With a large liquid viscosity, these asymmetric mode disturbances will easily dominate the liquid breakup.

3.4. Effect of the Density Ratio of Gas to Liquid

The gas–liquid density reveals the effect of the interaction between gas and liquid on the jet instability. Figure 7a,b show the effect of the gas–liquid density ratio on the maximum growth rate and the dominant wavenumber, respectively. The others parameters are fixed at Re_n = 50, We = 4000, G = 0.5 × 10⁻⁵, n = 0.8, and β = 0. The interaction between gas and liquid plays an important role in the breakup process of power-law fluid cylindrical jets. The results also show that both the maximum growth rates and the dominant wavenumbers increase when Q increases, especially for the asymmetric mode disturbances (m >0), such as m = 2 and m = 3. This indicates that the gas–liquid interaction will effectively accelerate the breakup process of power-law liquids and reduce the breakup scale. Significantly, with the increase of Q, the maximum growth rate of asymmetric mode disturbances—i.e., m = 1, 2, and 3—prevail easily over the symmetric mode disturbance. With the increase of m, the form of the surface wave will become more and more complex. Therefore, the asymmetric mode disturbances are easier to dominate the breakup of power-law fluid jets with a high-density gas medium.

3.5. Effect of the Power-Law Exponent

It is known that the characteristic parameter of power-law fluids is the power-law exponent, n, which represents the non-Newtonian property. Given by different power-law exponents, the constitutive equation represents different fluids, such as shear-thinning fluids (n < 1), shear-thickening fluids (n > 1), and Newtonian fluids (n = 1). Figure 8a,b shows the effect of n on the maximum growth rate and the dominant wavenumber. The dimensionless parameters are We = 5000, G = 0.5 × 10⁻⁵, Q = 0.002, and β = 0. Since the power-law exponent is associated with the generalized Reynolds number, additional parameters are specified as K = 4 Pa∙sⁿ, ρ_l = 1000 kg/m³, a = 0.3mm, and U_l0 = 30 m/s.

It is found in Figure 8a that with the increase of n, the maximum growth rate decreases in symmetric mode disturbance, while it is almost independent of n at asymmetric mode disturbances. This implies that the power-law exponent has a smaller influence on asymmetric mode disturbances. Furthermore, the viscosity and generalized Reynolds number play negative roles for the breakup process; therefore, increasing them will lead to a difficulty on the power-law fluid jet breakup. The dominant wavenumber is keeping constant regardless of n, as shown in Figure 8b.

Overall, the asymmetric instability of power-law jets is mainly influenced by three major factors, i.e., surface tension on the liquid surface, the liquid viscous force, and the gas–liquid interaction. In high-speed cases, the gas–liquid interaction force has a significant effect on the liquid breakup, whereas the liquid viscous force, surface tension, and the non-Newtonian feature have less important effects.

4. Conclusions

The power-law cylindrical jet is studied theoretically with symmetric mode disturbance and asymmetric mode disturbances. According to temporal linear analysis, a dispersion relation, which included a constitutive equation that was used to describe the system, is obtained. The effects of the Weber number, the generalized Reynolds number, the gas–liquid density ratio, and the power-law exponent on the instability of power-law fluid cylindrical jets are investigated, and the main conclusions are as follows.

(1)

The symmetric mode disturbance and asymmetric mode disturbances of power-law fluid cylindrical jets are observed in experiments. The asymmetric mode (m > 0) can become the dominating mode under certain conditions.

(2)

By analyzing the instability of the dispersion relation of power-law fluid jets, it can be seen that with the increase of Weber number or the gas–liquid density ratio, the high-order modes are present, and the power-law cylindrical jet will become more fragile.

(3)

Under a low Weber number condition, only the symmetric mode is responsible for the liquid jet breakup. However, as the Weber number increases, more asymmetric mode disturbances become unstable, and the power-law jet will be controlled by shorter waves.

(4)

Both the change in the generalized Reynolds number and the power-law exponent cannot affect the number of disturbances. With a lager generalized Reynolds number, the power-law cylindrical jet is easier to disintegrate into smaller droplets. However, in the investigated flow regimes, the non-Newtonian power-law fluid behavior does not have a significant effect on the jet instability, as compared to the Newtonian fluid (n = 1).