Control of a Multiphase Buck Converter, Based on Sliding Mode and Disturbance Estimation, Capable of Linear Large Signal Operation
Abstract
:1. Introduction
- Current balancing by varying duty ratios on phases.
- A current control loop on each phase with the same reference current for all phases.
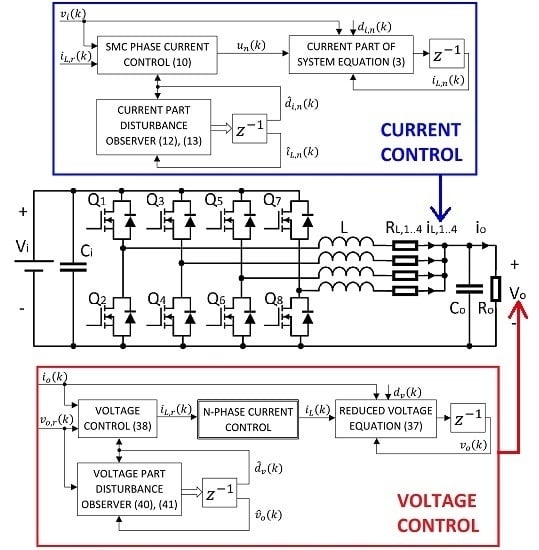
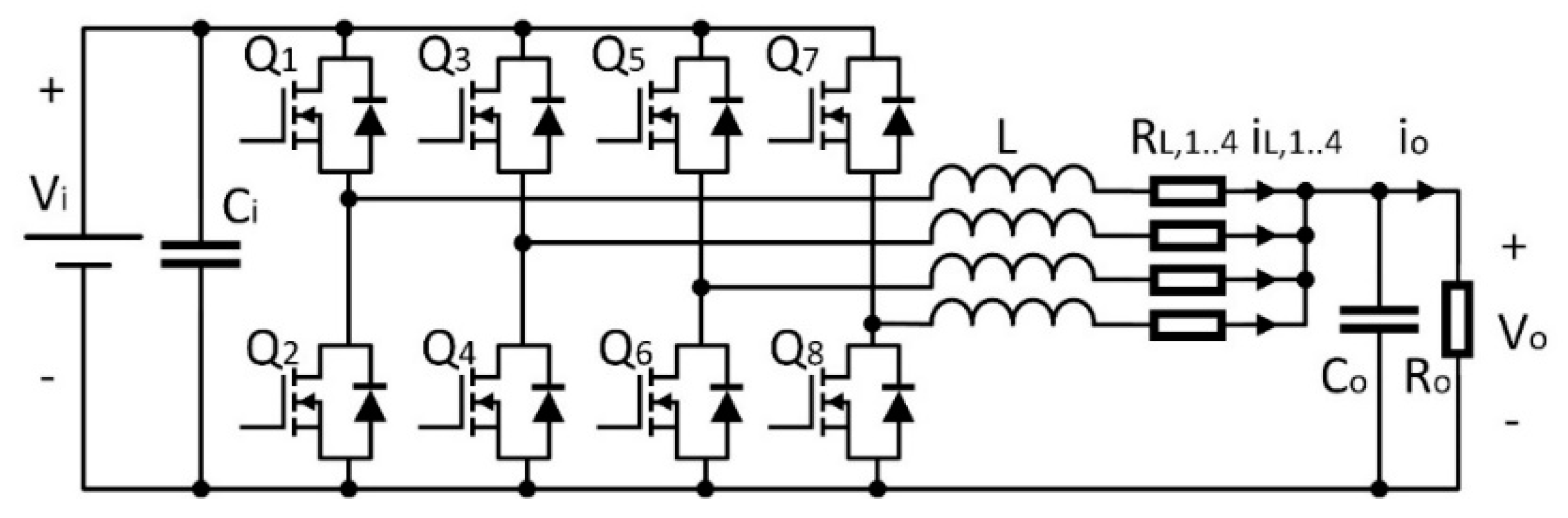
2. Multiphase Converter Modeling
3. Phase Current Control
3.1. Sliding Mode Current Control
3.2. Design of a Disturbance Observer for Current Control
3.3. Proposed Rules to Tune the Sliding Mode Current Controller and the Disturbance Observer
3.4. Current Control Model Reduction
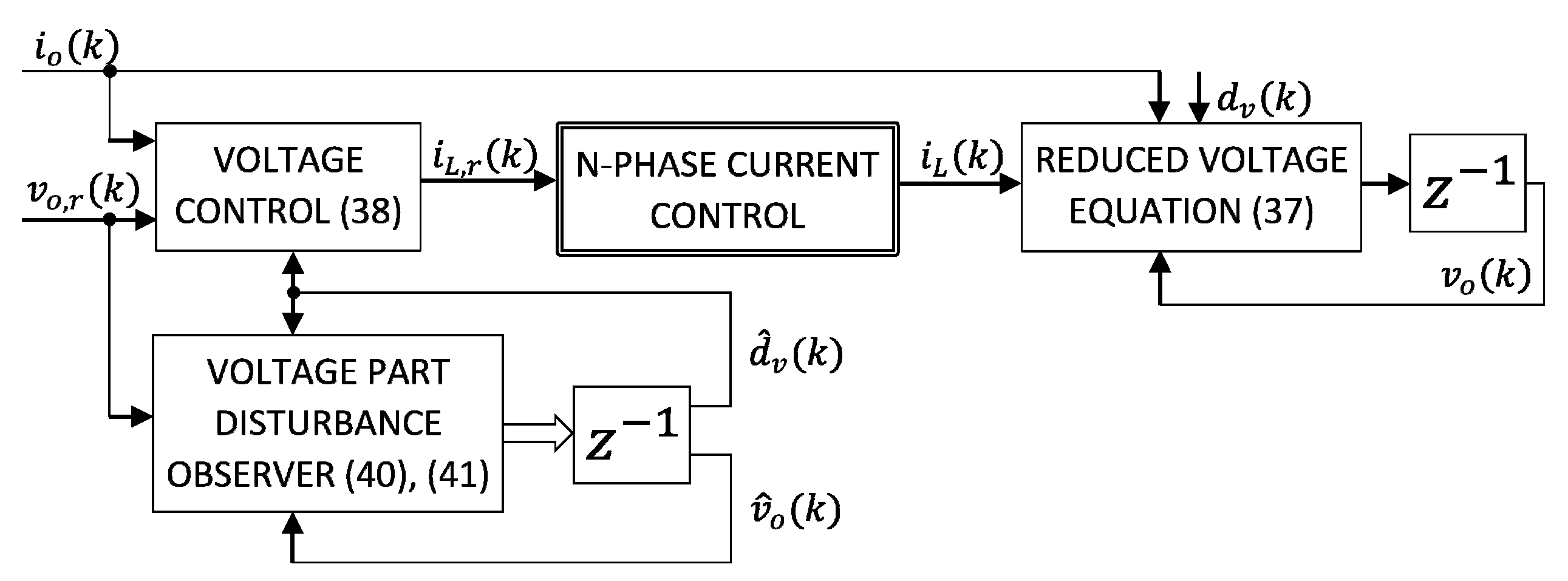
4. Output Voltage Control
4.1. Design of a Disturbance Observer for Voltage Control
4.2. Voltage Control Model Reduction
5. Results
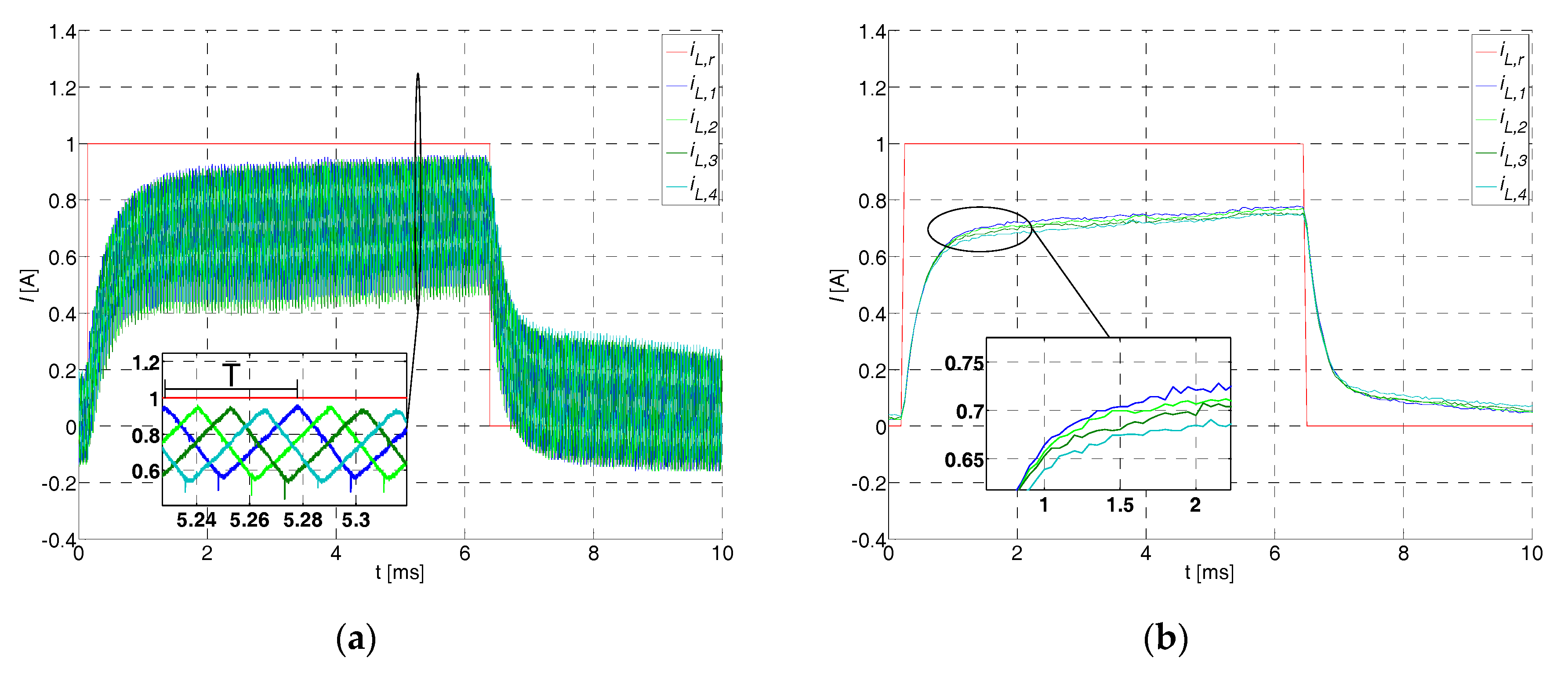
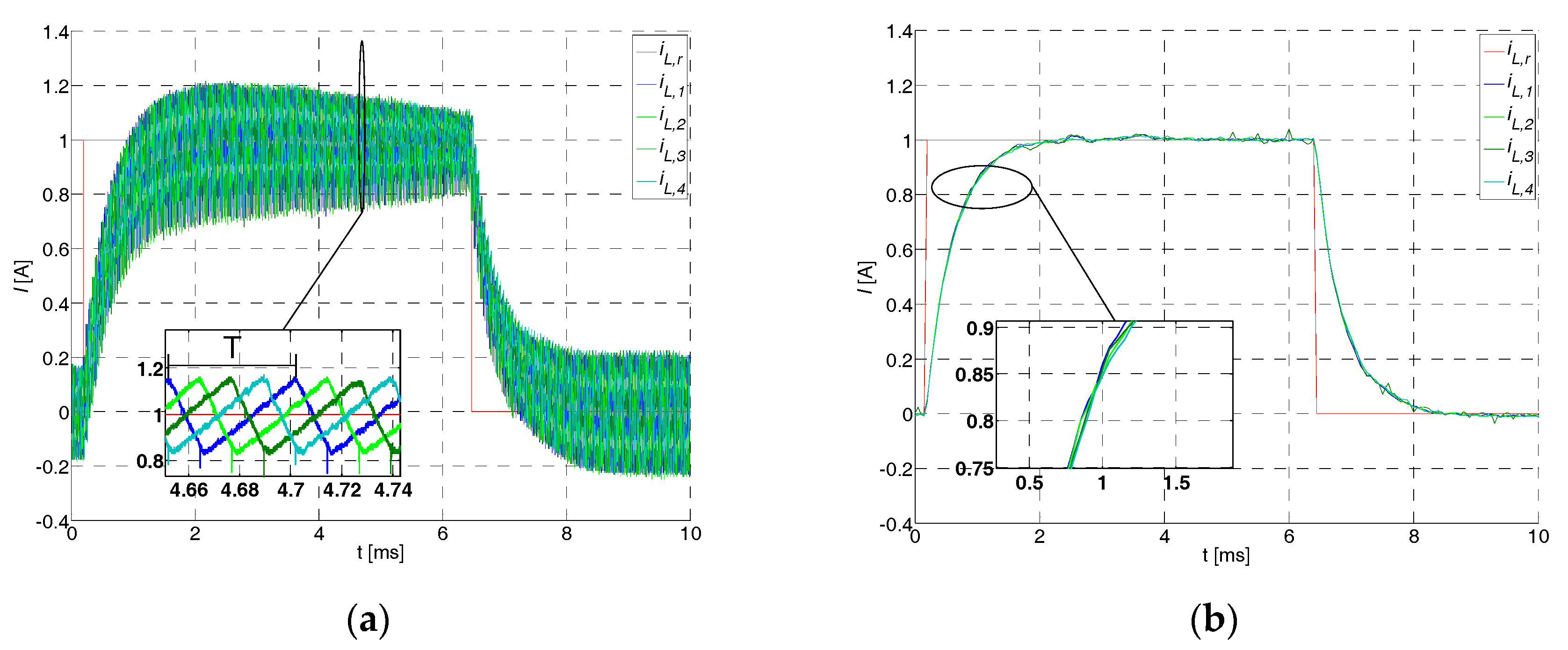
5.1. Sliding Mode Current Control with a Disturbance Observer
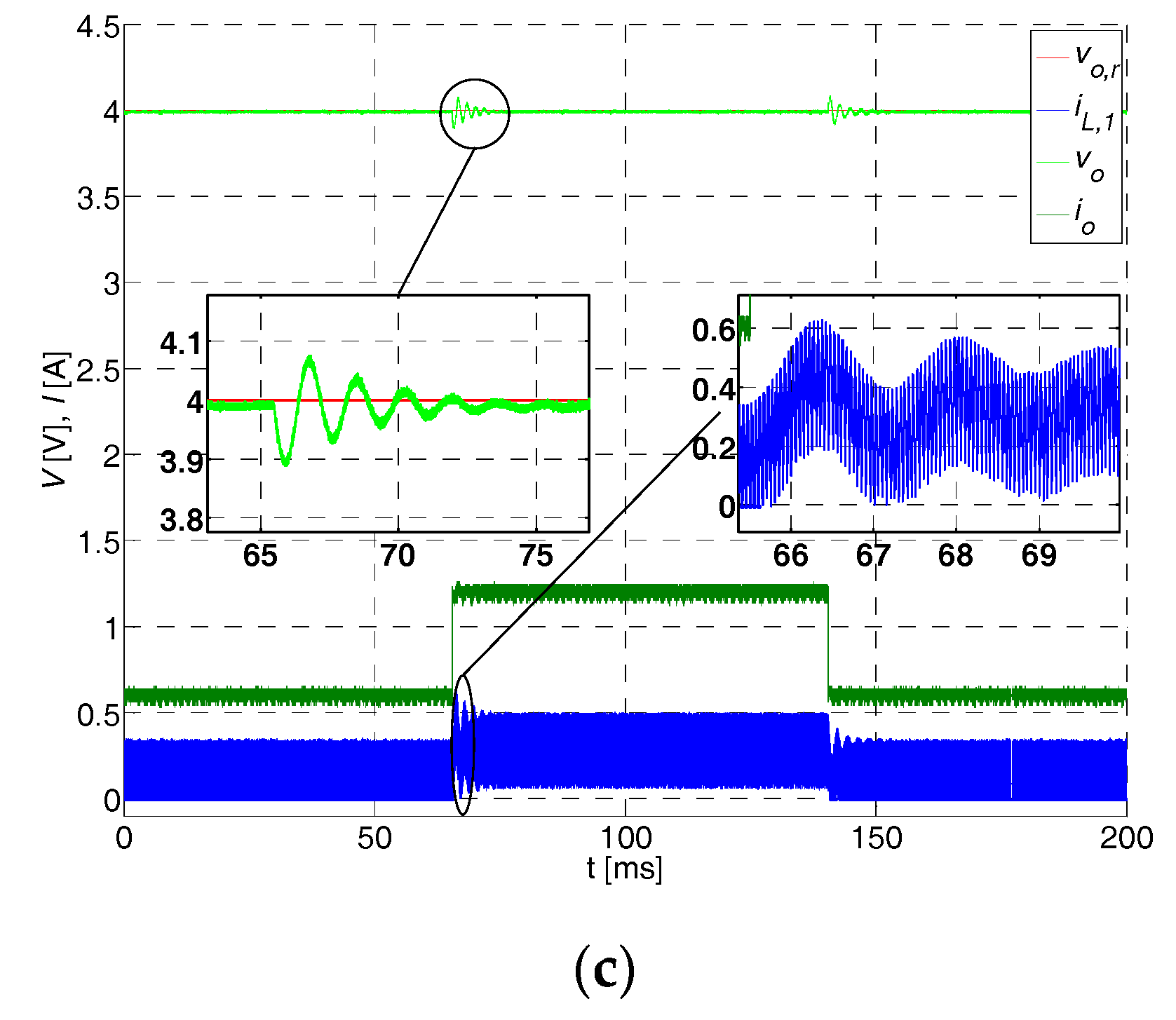
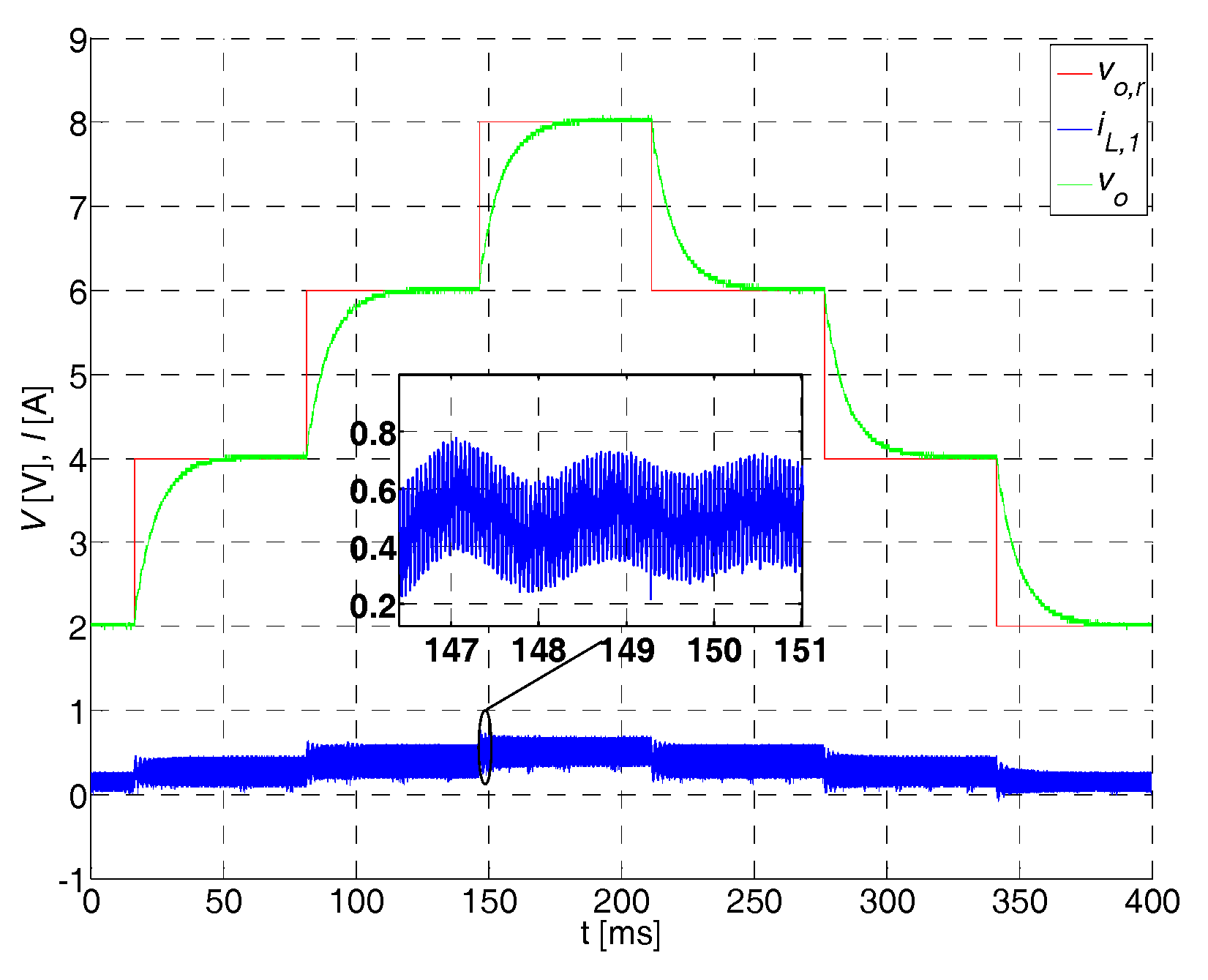
5.2. Voltage Control and Disturbance Observer
6. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mousavi, G.S.M.; Nikdel, M. Various battery models for various simulation studies and applications. Renew. Sustain. Energy Rev. 2014, 32, 477–485. [Google Scholar] [CrossRef]
- Rivetta, C.; Williamson, G.A. Large-signal analysis and control of buck converters loaded by DC-DC converters. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 3675, pp. 3675–3680. [Google Scholar]
- Qiu, W.; Mercer, S.; Liang, Z.; Miller, G. Driver deadtime control and its impact on system stability of synchronous buck voltage regulator. IEEE Trans. Power Electron. 2008, 23, 163–171. [Google Scholar] [CrossRef]
- Emadi, A.; Khaligh, A.; Rivetta, C.H.; Williamson, G.A. Constant power loads and negative impedance instability in automotive systems: definition, modeling, stability, and control of power electronic converters and motor drives. IEEE Trans. Veh. Technol. 2006, 55, 1112–1125. [Google Scholar] [CrossRef]
- El Aroudi, A.; Martínez-Treviño, B.A.; Vidal-Idiarte, E.; Cid-Pastor, A. Fixed switching frequency digital sliding-mode control of DC-DC power supplies loaded by constant power loads with inrush current limitation capability. Energies 2019, 12, 1055. [Google Scholar] [CrossRef]
- König, O.; Hametner, C.; Prochart, G.; Jakubek, S. Battery Emulation for Power-HIL Using Local Model Networks and Robust Impedance Control. IEEE Trans. Ind. Electron. 2014, 61, 943–955. [Google Scholar] [CrossRef]
- Karimi, R.; Kaczorowski, D.; Zlotnik, A.; Mertens, A. Loss optimizing control of a multiphase interleaving DC-DC converter for use in a hybrid electric vehicle drivetrain. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–8. [Google Scholar]
- König, O.; Gregorčič, G.; Jakubek, S. Model predictive control of a DC–DC converter for battery emulation. Control Eng. Pract. 2013, 21, 428–440. [Google Scholar] [CrossRef]
- König, O.; Jakubek, S.; Prochart, G. Battery impedance emulation for hybrid and electric powertrain testing. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference, Seoul, Korea, 9–12 October 2012; pp. 627–632. [Google Scholar]
- Rodič, M.; Milanovič, M.; Truntič, M. Digital control of an interleaving operated buck-boost synchronous converter used in a low-cost testing system for an automotive powertrain. Energies 2018, 11, 2290. [Google Scholar] [CrossRef]
- Eirea, G.; Sanders, S.R. Phase current unbalance estimation in multiphase buck converters. IEEE Trans. Power Electron. 2008, 23, 137–143. [Google Scholar] [CrossRef]
- Mariethoz, S.; Beccuti, A.G.; Morari, M. Model predictive control of multiphase interleaved DC-DC converters with sensorless current limitation and power balance. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 1069–1074. [Google Scholar]
- Schumacher, D.; Magne, P.; Preindl, M.; Bilgin, B.; Emadi, A. Closed loop control of a six phase interleaved bidirectional dc-dc boost converter for an EV/HEV application. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 27–29 June 2016; pp. 1–7. [Google Scholar]
- Ou, S.Y.; Liu, L.Y. Design and implementation of a four-phase converter with digital current sharing control for battery charger. In Proceedings of the 2015 IEEE International Telecommunications Energy Conference (INTELEC), Osaka, Japan, 18–22 October 2015; pp. 1–6. [Google Scholar]
- Yang, Q.; Juanjuan, S.; Ming, X.; Kisun, L.; Lee, F.C. High-bandwidth designs for voltage regulators with peak-current control. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, APEC ‘06, Dallas, TX, USA, 19–23 March 2006; p. 7. [Google Scholar]
- Ridley, R.B. A New Small-Signal Model for Current-Mode Control; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 1999. [Google Scholar]
- Truntič, M.; Milanovič, M. Voltage and current-mode control for a buck-converter based on measured integral values of voltage and current implemented in FPGA. IEEE Trans. Power Electron. 2014, 29, 6686–6699. [Google Scholar] [CrossRef]
- Cooke, P. Modeling average current mode control. In Proceedings of the APEC 2000—Fifteenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No.00CH37058), New Orleans, LA, USA, 6–10 February 2000; Volume 251, pp. 256–262. [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Szeifert, F.; Nagy, L.; Chován, T.; Abonyi, J. Constrained PI(D) algorithms (C-PID). Hungarian J. Ind. Chem. 2005, 33, 81–88. [Google Scholar]
- Halihal, Y. State-Space Oriented Advanced Analysis And Control Mehtods of Switching Converters; Ben-Gurion University of the Negev: Beersheba, Israel, 2015. [Google Scholar]
- Repecho, V.; Biel, D.; Ramos-Lara, R.; Vega, P.G. Fixed-switching frequency interleaved sliding mode eight-phase synchronous buck converter. IEEE Trans. Power Electron. 2018, 33, 676–688. [Google Scholar] [CrossRef]
- Repecho, V.; Biel, D.; Ramos, R.; Garcia, P. Sliding mode control of a m-phase DC/DC buck converter with chattering reduction and switching frequency regulation. In Proceedings of the 2016 14th International Workshop on Variable Structure Systems (VSS), Nanjing, China, 1–4 June 2016; pp. 290–295. [Google Scholar]
- Lopez, M.; Vicuna, L.G.D.; Castilla, M.; Lopez, O.; Majo, J. Interleaving of parallel DC-DC converters using sliding mode control. In Proceedings of the IECON ‘98 24th Annual Conference of the IEEE Industrial Electronics Society (Cat. No.98CH36200), Aachen, Germany, 31 August–4 September 1998; Volume 1052, pp. 1055–1059. [Google Scholar]
- Mazumder, S.K. Nonlinear Analysis and Control of Standalone, Parallel DC-DC, and Parallel Multi-Phase PWM Converters; Faculty of the Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2001. [Google Scholar]
- Zongxiang, C.; Ya-nan, G.; Mingxing, C.; Lusheng, G. Study on PI sliding mode controller for paralleled dc-dc converter. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 3079–3083. [Google Scholar]
- Marcos-Pastor, A.; Vidal-Idiarte, E.; Cid-Pastor, A.; Martinez-Salamero, L. Interleaved digital power factor correction based on the sliding-mode approach. IEEE Trans. Power Electron. 2016, 31, 4641–4653. [Google Scholar] [CrossRef]
- Vidal-Idiarte, E.; Marcos-Pastor, A.; Giral, R.; Calvente, J.; Martinez-Salamero, L. Direct digital design of a sliding mode-based control of a PWM synchronous buck converter. IET Power Electron. 2017, 10, 1714–1720. [Google Scholar] [CrossRef]
- Weibing, G.; Yufu, W.; Homaifa, A. Discrete-time variable structure control systems. IEEE Trans. Ind. Electron. 1995, 42, 117–122. [Google Scholar] [CrossRef]
- Monses, G. Discrete-Time Sliding Mode Control; Technische Universiteit Delft: Delft, The Netherlands, 2002. [Google Scholar]
- König, O.; Jakubek, S.; Prochart, G. Model predictive control of a battery emulator for testing of hybrid and electric powertrains. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–6. [Google Scholar]
- Orosco, R.; Vazquez, N. Discrete sliding mode control for DC/DC converters. In Proceedings of the 7th IEEE International Power Electronics Congress, Technical Proceedings, CIEP 2000 (Cat. No.00TH8529), Acapulco, Mexico, 15–19 October 2000; pp. 231–236. [Google Scholar]
- Cao, J.; Chen, Q.; Zhang, L.; Quan, S. Sliding mode control of bidirectional DC/DC converter. In Proceedings of the 2018 33rd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Atlanta, GA, USA, 18–20 May 2018; pp. 717–721. [Google Scholar]
- Abidi, K.; Jian-Xin, X. A Discrete-Time Integral Sliding Mode Control Approach for Output Tracking with State Estimation. IFAC Proc. Vol. 2008, 41, 14199–14204. [Google Scholar] [CrossRef] [Green Version]
- Zheng, C.; Zhang, J. Finite-time nonlinear disturbance observer based discretized integral sliding mode control for PMSM drives. J. Power Electron. 2018, 18, 1075–1085. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Yu, X. Sliding-mode control for systems with mismatched uncertainties via a disturbance observer. IEEE Trans. Ind. Electron. 2013, 60, 160–169. [Google Scholar] [CrossRef]
- Yang, J.; Su, J.; Li, S.; Yu, X. High-order mismatched disturbance compensation for motion control systems via a continuous dynamic sliding-mode approach. IEEE Trans. Ind. Inf. 2014, 10, 604–614. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, J.; Vazquez, S.; Wu, L.; Franquelo, L.G. Disturbance observer based second order sliding mode control for DC-DC buck converters. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 7117–7122. [Google Scholar]
- Wang, J.; Li, S.; Yang, J.; Wu, B.; Li, Q. Finite-time disturbance observer based non-singular terminal sliding-mode control for pulse width modulation based DC–DC buck converters with mismatched load disturbances. IET Power Electron. 2016, 9, 1995–2002. [Google Scholar] [CrossRef]
- Sanjeev Kumar, P.; Patil, S.L.; Chaudhari, B.N. Disturbance observer based sliding mode control for DC-DC power converters. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 3366–3371. [Google Scholar]
- Pandey, S.K.; Patil, S.L.; Chaskar, U.M.; Phadke, S.B. Direct Duty Ratio Control of Buck DC-DC Converters Using Disturbance Observer Based Integral Sliding Mode Control. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 5507–5512. [Google Scholar]
- Kim, K.-S.; Rew, K.-H. Reduced order disturbance observer for discrete-time linear systems. Automatica 2013, 49, 968–975. [Google Scholar] [CrossRef]
- Maksimovic, D.; Zane, R. Small-signal Discrete-time Modeling of Digitally Controlled DC-DC Converters. In Proceedings of the 2006 IEEE Workshops on Computers in Power Electronics, Troy, NY, USA, 16–19 July 2006; pp. 231–235. [Google Scholar]
- Feng, C.; Lin, Y. Robust control design based-on integral sliding-mode for systems with norm-bounded uncertainties. In Proceedings of the 2011 11th International Conference on Control, Automation and Systems, Gyeonggi-do, Korea, 26–29 October 2011; pp. 1178–1183. [Google Scholar]
- Siew-Chong, T.; Yuk-Ming, L.; Chi Kong, T. Sliding Mode Control of Switching Power Converters; Taylor & Francis Group, LLC: New York, NY, USA, 2012. [Google Scholar]
- Xiong, L.; Li, P.; Li, H.; Wang, J. Sliding mode control of DFIG wind turbines with a fast exponential reaching law. Energies 2017, 10, 1788. [Google Scholar] [CrossRef]
- Yang, Z.; Wan, L.; Sun, X.; Li, F.; Chen, L. sliding mode variable structure control of a bearingless induction motor based on a novel reaching law. Energies 2016, 9, 452. [Google Scholar] [CrossRef]
- Bartoszewicz, A.; Leśniewski, P. Refined reaching laws for sliding mode control of discrete time systems. In Proceedings of the 2013 18th International Conference on Methods & Models in Automation & Robotics (MMAR), Miedzyzdroje, Poland, 26–29 August 2013; pp. 824–829. [Google Scholar]
- Lee, C.W.; Chung, C.C. An approach to discrete-time sliding mode control with variable convergence rate to sliding surface. In Proceedings of the 2008 SICE Annual Conference, Tokyo, Japan, 20–22 August 2008; pp. 2358–2363. [Google Scholar]
- Bartoszewicz, A.; Leśniewski, P. New Switching and Nonswitching Type Reaching Laws for SMC of Discrete Time Systems. IEEE Trans. Control Syst. Technol. 2016, 24, 670–677. [Google Scholar] [CrossRef]
- Wen-Hua, C. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Kaiwei, Y.; Yuancheng, R.; Lee, F.C. Critical bandwidth for the load transient response of voltage regulator modules. IEEE Trans. Power Electron. 2004, 19, 1454–1461. [Google Scholar] [CrossRef]
- Pit-Leong, W.; Lee, F.C.; Peng, X.; Kaiwei, Y. Critical inductance in voltage regulator modules. IEEE Trans. Power Electron. 2002, 17, 485–492. [Google Scholar] [CrossRef]
- Rydel, M.; Stanisławski, R.; Latawiec, K.J.; Gałek, M. Model order reduction of commensurate linear discrete-time fractional-order systems. IFAC-PapersOnLine 2018, 51, 536–541. [Google Scholar] [CrossRef]








| Parameter | Symbol | Value |
|---|---|---|
| Inductor inductances | 330 µH | |
| Inductor resistances | 300 mΩ | |
| Input, output capacitance | 1880 µF | |
| Input, output ESR | 20 mΩ | |
| High MOSFETs ( on-state resistance | 21.5 mΩ | |
| Low MOSFETs ( on-state resistance | 13 mΩ | |
| Current sense shunt resistances | 3 Ω |
| Variable | Value |
|---|---|
| , | −1 A |
| , | 1 A |
| 10 V | |
| 14.4 V | |
| 2 V | |
| 8.5 V | |
| 0 | |
| 1 |
| Variable | Value |
|---|---|
| , | 2 V |
| , | 8.5 V |
| −1 A | |
| 1 A | |
| , | 1 A |
| −2.5 A | |
| 2.5 A |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pajer, R.; Chowdhury, A.; Rodič, M. Control of a Multiphase Buck Converter, Based on Sliding Mode and Disturbance Estimation, Capable of Linear Large Signal Operation. Energies 2019, 12, 2790. https://doi.org/10.3390/en12142790
Pajer R, Chowdhury A, Rodič M. Control of a Multiphase Buck Converter, Based on Sliding Mode and Disturbance Estimation, Capable of Linear Large Signal Operation. Energies. 2019; 12(14):2790. https://doi.org/10.3390/en12142790
Chicago/Turabian StylePajer, Rok, Amor Chowdhury, and Miran Rodič. 2019. "Control of a Multiphase Buck Converter, Based on Sliding Mode and Disturbance Estimation, Capable of Linear Large Signal Operation" Energies 12, no. 14: 2790. https://doi.org/10.3390/en12142790
APA StylePajer, R., Chowdhury, A., & Rodič, M. (2019). Control of a Multiphase Buck Converter, Based on Sliding Mode and Disturbance Estimation, Capable of Linear Large Signal Operation. Energies, 12(14), 2790. https://doi.org/10.3390/en12142790