Better Fuel Economy by Optimizing Airflow of the Fuel Cell Hybrid Power Systems Using Fuel Flow-Based Load-Following Control

Abstract

In this paper, the results of the sensitivity analysis applied to a fuel cell hybrid power system using a fuel economy strategy is analyzed in order to select the best values of the parameters involved in fuel consumption optimization. The fuel economy strategy uses the fuel and air flow rates to efficiently operate the proton-exchange membrane (PEM) fuel cell (FC) system based on the load-following control and the global extremum seeking (GES) algorithm. The load-following control will ensure the charge-sustained mode for the batteries’ stack, improving its lifetime. The optimization function’s optimum, which is defined to improve the fuel economy, will be tracked in real-time by two GES algorithms that will generate the references for the controller of the boost DC-DC converter and air regulator. The optimization function and performance indicators (such as FC net power, FC electrical efficiency, fuel efficiency, and fuel economy) have a multimodal behavior in dithers’ frequency. Furthermore, the optimum in the considered range of frequencies depends on the load level. So, the best value could be selected as the frequency where the optimum is obtained for the most load levels. Considering a dither frequency of 100 Hz selected as the best value, the sensitivity analysis of the fuel economy is further analyzed for different values of the weighting parameter k_eff, highlighting the multimodal feature in the parameters for the optimization function and fuel economy as well. A k_eff value around of 20 lpm/W seems to give the best fuel economy in the full range of load.

1. Introduction

Instead of a diesel generator [1], the proton-exchange membrane fuel cell (PEM FC) system could be used as a backup green energy source [2] for an FC hybrid power system (FC HPS) to mitigate the load variability by the load-following (LF) control [3,4,5]. A hybrid energy storage system (ESS) using batteries and ultracapacitors is mandatory to dynamically compensate the power flow balance [6,7]. The most used ESS topologies are the active and semi-active topologies, using two and one bidirectional DC-DC converters integrated into a multiport topology, respectively [8,9,10]. An active topology with two bidirectional DC-DC converters is more flexible as a control structure compared to a semi-active topology [9]. The two control references will be generated by the energy management strategies (EMS), usually to regulate the DC voltage and mitigate the load pulses via the bidirectional DC-DC converters for the batteries and ultracapacitors stacks [5,7,11,12]. The EMS has an important role in the optimal and safe operation of the FC system [13,14]. The control objectives for PEM FC system are as follows [15,16,17]: (1) minimization of the fuel consumption; (2) supplying the dynamic loads with energy, such as FC vehicles; (3) safe operation by using appropriate control loops to mitigate the load pulses, to limit the FC current slope, and to avoid fuel starvation.

The first objective can be ensured using a real-time optimization (RTO) strategy based on different optimization functions, which integrate performance indicators related to fuel consumption such as FC net power, FC lifetime, and cost [18,19,20].

The equivalent consumption minimization strategy (ECMS) is a well-known strategy applied to FC vehicles, which converts the energy difference in battery charging (at the start and end of a load cycle) into additional fuel consumption, to compensate this loss of energy by discharging the battery [21]. In last decade, several algorithms searching for the global optimum using different optimization functions have been proposed in the literature [22,23,24]. Intelligent concepts are usually involved in these algorithms [25,26,27]. In this study, the global extremum seeking (GES) algorithm is used due to the good performance reported in the previous work for FC systems [28,29,30,31], photovoltaic (PV) systems [22,23,32], and wind turbine (WT) systems [33,34].

The objective of this paper is to use the sensitivity approach to identify the best value of the parameters used by the optimization function and control loops. Except the tuning parameters of the GES algorithm, which will be designed to ensure the imposed performance and stability of the tracking loops, the dither’s frequency f_d is the most important parameter that could dynamically affect the performance of the GES algorithm.

The GES algorithm must search the optimization function’s optimum in real-time, which is defined in this study as a weighted function of the FC net power and the fuel consumption efficiency using the weighting parameters k_net and k_eff. So, if k_net = 1, then it is important to know the value of the weighting parameter k_eff, where the best fuel economy is obtained. So, the sensitivity approach in this study will be performed using the parameters f_d and k_eff.

The structure of the paper is as follows. The FC HPS architecture and LF control and optimization loops are briefly presented in Section 2. The EMS based on LF control and optimization loops is detailed in Section 3. The obtained results are presented and discussed in Section 4. Section 5 concludes this study.

2. FC Hybrid Power System

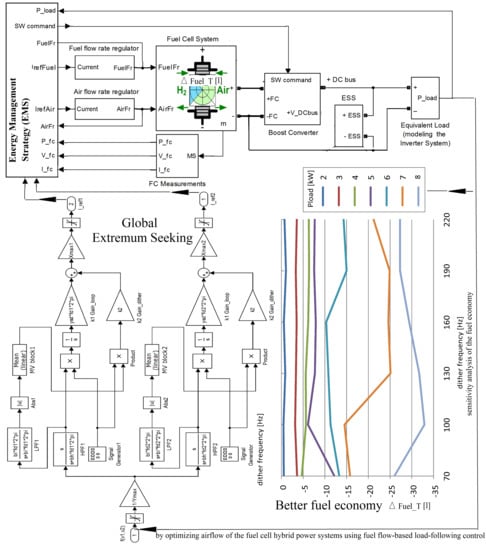
The synoptic architectures of the FC HPS and ESS are presented in Figure 1a. The FC power delivered on the DC can be controlled via the boost converter using the switching (SW) command generated by the boost controller under the EMS proposed in this paper. Also, the generated FC power depends on the fuel and air regulators controlled by the input references I_refFuel and I_refAir.

The Matlab-Simulink® diagram of the FC HPS architecture is presented in Figure 1b. The FC system is the main energy source to supply the load demand on the DC bus, which is modeled by an equivalent DC load for the inverter and an AC load in order to speed up the simulation.

The LF control will set the current reference I_refLF for the fuel flow rate (FuelFr) regulator to comply with the power flow balance on the DC bus (1), with the battery operating in charge-sustaining mode (2):

$$C_{DC}{u}_{dc}d{u}_{dc}/dt={\eta }_{boost}{p}_{FCgen}+p_{ESS}-p_{load};$$

(1)

$$P_{ESS(AV)}\cong 0.$$

(2)

So, considering (2), (1) will be rewritten in the average value (AV) during a load cycle (LC) as (3):

$$0={\eta }_{boost}{P}_{FCgen(AV)}-P_{load(AV)}\Rightarrow P_{FCgen(AV)}=P_{load(AV)}/{\eta }_{boost}.$$

(3)

Thus, the FC current generated by the FC system will be given by (4):

$$I_{FC(AV)}=P_{load(AV)}/({\eta }_{boost}{V}_{FC(AV)}).$$

(4)

Consequently, the current reference I_refLF will be estimated by the LF control using the AV filtering method, based on the mean value (MV) technique of the FC current during a dithers’ period:

$$I_{refLF}\cong I_{FC(AV)}=P_{load(AV)}/({\eta }_{boost}{V}_{FC(AV)})$$

(5)

The MV technique or another filtering technique can be used to smooth the values used in (5) for the safe operation of the FC system, thus avoiding fuel starvation due to sharp changes in load demand. The current reference I_refLF will set the fuel flow rate FuelFr value using the FuelFr regulator’s relationship (6):

$$FuelFr=\frac{60000\cdot R\cdot \left(273+\theta \right)\cdot N_C\cdot I_{LFref}}{2F\cdot (101325\cdot P_{f(H2)})\cdot (U_{f(H2)}/100)\cdot (x_{H2}/100)}.$$

(6)

Because of (5),

$$I_{FC}\cong I_{FC(AV)}\cong I_{refLF}.$$

(7)

So, the current reference I_ref2 will optimally adjust the air flow rate (AirFr) value using the AirFr regulator’s relationship (8):

$$AirFr=\frac{60000\cdot R\cdot \left(273+\theta \right)\cdot N_C\cdot \left(I_{FC}+I_{ref2}\right)}{4F\cdot (101325\cdot P_{f(O2)})\cdot (U_{f(O2)}/100)\cdot (y_{O2}/100)}.$$

(8)

Thus, the input references of the fueling regulators are set as follows: I_refFuel = I_refLF and I_refAir = I_FC + I_ref2.

The optimization function’s optimum (computed in the block called “optimization function”, in Figure 1) will be searched using the current reference I_ref1 that will set the FC current based on the 0.1 A hysteresis controller for the boost DC-DC converter.

A semi-active 100 Ah battery/100 F ultracapacitors ESS topology was chosen to dynamically compensate power in (1) and stabilize the DC voltage at 200 V (u_DC ≅ 200 V). The battery will operate in charge-sustaining mode due to the LF control applied to the fuel regulator (6), which will set the FC power close to the requested FC power on the DC bus. The FC power is $P_{FCgen(AV)}$ given by (3) if (2) is considered. Thus, the battery will compensate the minor imbalance in energy flow on the DC bus (1) due to the changes in load profile or the small difference between the FC current set by the LF control (5) $I_{FC}\cong I_{LFref}\cong I_{FC(AV)}=P_{load(AV)}/({\eta }_{boost}{V}_{FC(AV)})$ and the value $I_{FC}+I_{ref2}$ set by the GES-based optimization loop (which is applied to the air regulator (7)). So, a 100 Ah capacity of the battery has been obtained for a 1 kW imbalance in energy flow during a 12 s load cycle using the design relationships from [5,7]. This capacity is more than sufficient, considering the sizing design presented in [2]. The sharp changes in load profile, such as pulses, can produce an imbalance in power flow on the DC bus (1) due to the large response time of the FC system and the battery, which is in the order of hundreds of milliseconds and tens of minutes, respectively. During the transitory regimes of the FC system and battery, the ultracapacitors’ stack will dynamically compensate the power flow on the DC bus (1) via the bidirectional DC-DC power converter. The 100 F capacitance was obtained for a 1 kW/100 ms pulse using the design relationships from [5,7]. The DC voltage regulation was implemented on the ultracapacitors’ stack side due to the slow response of the FC system, but also because the controlled inputs AirFr and FuelFr (via the fueling regulator) of the FC system and the controller of the FC boost converter are involved in the LF and optimization loops. Thus, if the DC voltage regulation will be implemented on the FC system’s side using a proportional–integral–derivative (PID) compensation technique of one of the aforementioned loops, then a degradation of the performance indicators will be obtained compared with the cases when the DC voltage regulation is implemented on the ultracapacitors’ stack side or on the battery’s side if an active ESS topology is selected instead of a semi-active type. If an active mitigation of the pulses on the DC bus must be implemented, then an active control of the bidirectional DC-DC power converter should be implemented in order to generate an anti-pulse from the ultracapacitors’ stack [5,7]. In this case, the DC voltage regulation remains to be implemented on the battery side using a PID compensation technique of the control designed to compensate the minor imbalance in energy flow on the DC bus (1). The high frequency ripple on the DC voltage will be mitigated in all cases by a 100 μF capacitor (C_DC) designed using the design relationships from [5,7].

The FC parameters ($N_C,\theta ,U_{f(H2)},U_{f(O2)},P_{f(H2)},P_{f(O2)},x_{H2},y_{O2}$) were set for a 6 kW FC system, and R = 8.3145 J/(mol K) and F = 96485 As/mol are two well-known constants. The energy efficiency of the boost DC-DC converter may be considered constant in this study (η_boost = 0.9), because the boost controller operated in continuous current mode in the load range higher than 1 kW (so the case of light load was not considered), where the energy efficiency may vary in the range of 88% to 92%, but without significantly modifying the results obtained for a constant efficiency (as will be explained in the Discussion section).

The current references I_ref1 and I_ref2 were generated by the GES controller shown in Figure 2, as will be explained in next section.

3. Energy Management Strategy

Each GES control was implemented (see Figure 2) based on the relationships from [30]. The dither’s frequencies were chosen to be f_d1 = 100 Hz and f_d2 = 2f_d1 = 200 Hz in order to improve the dithers’ persistence by interference of the harmonics due to the nonlinear characteristics of the FC system. The cut off frequencies of the low-pass filter (LPF1 and LPF2 in Figure 2) and the high-pass filter (HPF1 and HPF2 in Figure 2) were set by the parameters b_l = 1.5 and b_h = 0.1. The tuning parameters were designed based on relationships presented in [30], as follows: k₁ = 1, k₂ = 2. The normalization values of the input (the optimization function $y=f(v_1,v_2)$, where v₁ and v₂ are the search variables) and the outputs (the reference currents $I_{ref1}$ and $I_{ref2}$ for the boost controller and the air regulator) were set to $k_{Nf}=1/Y_{\max }=1/1000$, $k_{Nv1}=X_{\max 1}=50$ and $k_{Nv2}=X_{\max 2}=20$. The normalization values were not strict, because the GES control was of the adaptive type, but choosing the right value would improve the searching speed. Readers interested in analyzing and designing a GES control for FC systems or PV, WT, and PV/WT FC HPSs may read [14,17] or [22,23,32], [33], and [35], respectively.

The searching speed was limited to 100 A/s by the slope limiters included in the FuelFr and AirFr regulators in order to ensure the safe operation of the PEM FC system. So, the FC current could increase up to 20 A during the FC time constant (T_FC) of 0.2 s. The GES algorithm needed about 10 periods of dither (T_d) to find the Global Maximum Power Point (GMPP) of the PV system for different steps in irradiance (because there was no limitation related to searching slope in this case, excepting the safe values given by the devices used in the boost the boost DC-DC power converter, which were very high compared to 100 A/s) [22,23]. Considering 10 dither periods to find the maximum efficiency point (MEP) of the FC system or the optimization function’s optimum (which is defined in relation to the FC system’s performance indicators), to avoid limitation due to FC response time, it was recommended to choose:

$$T_{d(\max )}\cong T_{FC}/10.$$

(9)

This means T_d(max) ≅ 20 ms, so f_d(min) ≅ 50 Hz. The maximum frequency of the dither would be considered f_d(max) = 200 Hz in order to have an acceptable increment per dithers’ period (about 0.5 A per T_d(min) = 5 ms). So, the frequency range of the dither was 70 Hz to 220 Hz, with a 30 Hz step in evaluation of the fuel economy based on the optimization function f defined by (10) [35]:

$$f(x,AirFr,FuelFr,P_{Load})=k_{net}\cdot P_{FCnet}+k_{fuel}\cdot Fue{l}_{eff};$$

(10)

$$\dot{x}=g(x,AirFr,FuelFr,P_{Load}),x\in X;$$

(11)

where (11) models the dynamic part of the FC HPS [36], x is the state vector, and P_Load is the disturbance. The weighting coefficients k_net (1/W) and k_fuel (liters per minute (lpm)/W) were defined in accordance with the chosen EMS objective. For example, the FC system energy efficiency (${\eta }_{sys}=P_{FCnet}/P_{FC}$) was maximized if k_net = 1 and k_fuel = 0 (in this case f = P_FCnet). If k_net = 1 and k_fuel ≠ 0, then the fuel consumption efficiency (Fuel_eff ≅ P_FCnet / FuelFr) was also considered in the optimization function. So, it was possible to improve the fuel economy for a value of the k_fuel weighting coefficient in range 5 lpm/W to 50 lpm/W, with 5 lpm/W step in evaluation of the fuel economy.

The LF control was implemented based on (5) in order to set the value of the FC net power requested by power flow balance (3). So,

$$P_{FCgen}=P_{FCnet}\cong P_{load} /{\eta }_{boost},$$

(12)

where,

$$P_{FCnet}\cong P_{FC}-P_{cm};$$

(13)

$$P_{cm}=I_{cm}\cdot V_{cm}=\left(a_2\cdot AirF{r}_{}^2+a_1\cdot AirFr+a_0\right)\cdot \left(b_1\cdot I_{FC}^{}+b_0\right).$$

(14)

The air compressor power (P_cm) was estimated with (14), considering the coefficients [37]:$a_0=0.6$, $a_1=0.04$, $a_2=-0.00003231$, $b_0=0.9987$, and $b_1=46.02$.

In order to not exceed the maximum FC power, the range of the load demand was considered from 2 kW to 8 kW, with a 1 kW step in the evaluation of the fuel economy.

The total fuel consumption, $Fue{l}_T={\displaystyle \int FuelFr(t)dt}$, will be estimated in the next section for different load levels in order to evaluate the fuel economy, measured in liters (L).

4. Results

The values of the performance indicators $P_{FCnet}$, ${\eta }_{sys}$, $Fue{l}_{eff}$, and $Fue{l}_T$ using different dither’s frequencies and constant load levels are recorded in

Table 1. FC net power for different dithers’ frequencies and constant load levels.

Load Level	sFF Strategy	Dithers’ Frequency fd (Hz)
Pload (kW)	PFCnet0 (kW)	70	100	130	160	190	220
2	1942	1895	1903	1889	1922	1900	1916
3	2880	2843	2848	2836	2805	2837	2817
4	3773	3723	3680	3711	3673	3710	3704
5	4638	4526	4601	4580	4566	4584	4557
6	5437	5315	5323	5337	5385	5346	5333
7	6188	6107	6130	6081	6116	6147	6125
8	6841	6813	6807	6805	6840	6827	6820

,

Table 2. FC electrical efficiency for different dithers’ frequencies and constant load levels.

Load Level	sFF Strategy	Dithers’ Frequency fd (Hz)
Pload (kW)	ηsys0 (%)	70	100	130	160	190	220
2	93.17	90.66	90.47	90.93	92.24	92.77	92.34
3	91.45	90.25	91.44	89.89	90.67	91.62	91.22
4	90.24	90.24	88.77	89.77	88.82	90.42	89.9
5	88.52	89.73	89.18	88.84	88.9	88.92	88.77
6	86.55	86.75	85.51	86.41	87.15	87.62	87.3
7	84.37	85.33	85.6	86.39	86.21	87.36	85.81
8	82	84.02	83.86	83.85	83.85	83.66	83.7

,

Table 3. Fuel efficiency for different dithers’ frequencies and constant load levels.

Load Level	sFF Strategy	Dithers’ Frequency fd (Hz)
Pload (kW)	Fueleff0 (W/lpm)	70	100	130	160	190	220
2	136.1	134.3	133.4	133.8	136.2	136.7	136.3
3	128.3	128.9	129.7	129.9	128.9	129.6	129.5
4	119.5	122	121.1	122.1	121.3	122.9	122.4
5	111.6	116.8	115.4	115.1	115.4	115.2	115.5
6	102.6	108.1	107.5	107.1	107.5	108.7	108.4
7	92.65	99.94	100	101.9	101.3	102.5	100.5
8	81	92.3	92.27	92.21	91.31	91.45	91.67

and

Table 4. Total fuel consumption for different dithers’ frequencies and constant load levels.

Load Level	sFF Strategy	Dithers’ Frequency fd (Hz)
Pload (kW)	FuelT0 (L)	70	100	130	160	190	220
2	34	33.46	33.53	33.12	33.44	32.95	33.3
3	54.75	51.15	51.6	51.41	51.25	51.46	51.21
4	76.88	72.2	71.24	71.28	70.72	70.51	70.59
5	98.57	86.4	92.47	90.87	90.67	91.05	90.91
6	125.5	112.2	114.2	114.7	115.2	110.5	111.2
7	152.5	136.7	138	127.4	127.9	127.6	131.3
8	193	167	160.1	161.3	163.6	165.7	165.7

. The values obtained by simulation using the static feed-forward (sFF) strategy [36], which is considered in this study as a reference strategy because it is the most known strategy implemented in commercial FC systems, are mentioned in the first column of these Tables. The differences in the performance indicators will be defined compared to the sFF strategy by using (15):

$$\Delta P_{FCnet}\cong P_{FCnet}-P_{FCnet0};$$

(15a)

$$\Delta {\eta }_{sys}={\eta }_{sys}-{\eta }_{sys0};$$

(15b)

$$\Delta Fue{l}_{eff}=Fue{l}_{eff}-Fue{l}_{eff0};$$

(15c)

$$\Delta Fue{l}_T=Fue{l}_T-Fue{l}_{T0}.$$

(15d)

The differences are recorded in

Table 5. Differences in FC net power compared to reference.

Load Level	Dithers’ Frequency fd (Hz)
Pload (kW)	70	100	130	160	190	220
2	−47	−39	−53	−20	−42	−26
3	−37	−32	−44	−75	−43	−63
4	−50	−93	−62	−100	−63	−69
5	−112	−37	−58	−72	−54	−81
6	−122	−114	−100	−52	−91	−104
7	−81	−58	−107	−72	−41	−63
8	−28	−34	−36	−1	−14	−21

,

Table 6. Differences in FC electrical efficiency compared to reference.

Load Level	Dithers’ Frequency fd (Hz)
Pload (kW)	70	100	130	160	190	220
2	−2.51	−2.7	−2.24	−0.93	−0.4	−0.83
3	−1.2	−0.01	−1.56	−0.78	0.17	−0.23
4	0	−1.47	−0.47	−1.42	0.18	−0.34
5	1.21	0.66	0.32	0.38	0.4	0.25
6	0.2	−1.04	−0.14	0.6	1.07	0.75
7	0.96	1.23	2.02	1.84	2.99	1.44
8	2.02	1.86	1.85	1.85	1.66	1.7

,

Table 7. Differences in fuel efficiency compared to reference.

Load Level	Dithers’ Frequency fd (Hz)
Pload (kW)	−1.8	−2.7	−2.3	0.1	0.6	0.2
2	0.6	1.4	1.6	0.6	1.3	1.2
3	2.5	1.6	2.6	1.8	3.4	2.9
4	5.2	3.8	3.5	3.8	3.6	3.9
5	5.5	4.9	4.5	4.9	6.1	5.8
6	7.29	7.35	9.25	8.65	9.85	7.85
7	11.3	11.27	11.21	10.31	10.45	10.67
8	2.02	1.86	1.85	1.85	1.66	1.7

and

Table 8. Differences in total fuel consumption compared to reference.

Load Level	Dithers’ Frequency fd (Hz)
Pload (kW)	−0.54	−0.47	−0.88	−0.56	−1.05	−0.7
2	−3.6	−3.15	−3.34	−3.5	−3.29	−3.54
3	−4.68	−5.64	−5.6	−6.16	−6.37	−6.29
4	−12.17	−6.1	−7.7	−7.9	−7.52	−7.66
5	−13.3	−11.3	−10.8	−10.3	−15	−14.3
6	−15.8	−14.5	−25.1	−24.6	−24.9	−21.2
7	−26	−32.9	−31.7	−29.4	−27.3	−27.3
8	−0.54	−0.47	−0.88	−0.56	−1.05	−0.7

and represented in Figure 3, Figure 4, Figure 5 and Figure 6. Note the multimodal behavior in dithers’ frequency for all performance indicators. Also, it is worth mentioning that the optimum’s position (maximum of $\Delta P_{FCnet}$, $\Delta {\eta }_{sys}$, $\Delta Fue{l}_{eff}$, and minimum of $\Delta Fue{l}_T$) depends on the load level. So, the best value in the frequencies’ range could be selected as the frequency where the optimum is obtained for most of load levels, and this seems to be the dither frequency of 100 Hz.

Considering a dither frequency of 100 Hz, the total fuel consumption ($Fue{l}_T$) for different values of the parameters k_eff and P_load is recorded in

Table 9. Total fuel consumption for different values of the parameters k_eff and P_load.

Load Level	Weighting Parameter keff (lpm/W)
Pload (kW)	0	5	10	15	20	25	30	35	40	45	50
2	34	33.74	33.72	33.53	33.51	33.53	33.54	33.91	33.45	33.49	33.76
3	54.75	51.68	51.67	52.55	51.61	51.6	51.69	51.56	51.56	51.54	51.76
4	76.88	71.5	71.47	71.37	71.25	71.24	71.1	71.11	70.98	71.37	71.63
5	99.7	92.39	92.38	92.65	92.13	92.47	92.71	92.7	92.5	92.59	92.42
6	125.5	113.8	114.3	114.2	114	114.2	114.6	114.7	114.8	114.6	114.8
7	152.5	132.1	136.7	137	137.5	138.1	138	138.7	138.8	139	139.4
8	193	155.8	156.6	158	158.9	160.1	160	161	161	162	163.4

. The values for k_eff = 0 (mentioned in the first column of the Table 9) are used as reference values. So, the differences in total fuel consumption ($\Delta Fue{l}_T$) are estimated in

Table 10. Differences in total fuel consumption compared to k_eff = 0.

Load Level	Weighting Parameter keff (lpm/W)
Pload (kW)	5	10	15	20	25	30	35	40	45	50
2	−0.26	−0.28	−0.47	−0.49	−0.47	−0.46	−0.09	−0.55	−0.51	−0.24
3	−3.07	−3.08	−2.2	−3.14	−3.15	−3.06	−3.19	−3.19	−3.21	−2.99
4	−5.38	−5.41	−5.51	−5.63	−5.64	−5.78	−5.77	−5.9	−5.51	−5.25
5	−7.31	−7.32	−7.05	−7.57	−7.23	−6.99	−7	−7.2	−7.11	−7.28
6	−11.7	−11.2	−11.3	−11.5	−11.3	−10.9	−10.8	−10.7	−10.9	−10.7
7	−20.4	−15.8	−15.5	−15	−14.4	−14.5	−13.8	−13.7	−13.5	−13.1
8	−37.2	−36.4	−35	−34.1	−32.9	−33	−32	−32	−31	−29.6

and represented in Figure 7.

The sensitivity analysis of the fuel economy ($\Delta Fue{l}_T$) highlights the better fuel economy with increase in load level, and this is normal. Also, note the multimodal behavior in the weighting parameter k_eff. This is better shown in Figure 8 (where the high values of fuel economy for a load of 7 kW and 8 kW are canceled). Looking to Table 10 (where the optimum, local minimums, and the minimums at k_eff = 5 and k_eff = 50 are highlighted in different colors: yellow, blue, and gray, respectively), a k_eff value in the range of 20 lpm/W to 30 lpm/W seems to give the best fuel economy in the load range of 2 kW to 5 kW. However, note the decrease in fuel economy with the increase in k_eff value. So, the recommended value for the entire load range is k_eff = 20 lpm/W.

The effect of a variable energy efficiency of the boost converter on the results obtained at constant energy efficiency will be analyzed and discussed in the next section.

5. Discussion

The dependence of the power loss (P_loss) and energy efficiency for a DC-DC power converter were analyzed for low and medium power applications in [38,39] and [40,41,42], respectively. The main findings of the aforementioned studies are as follows:

1)

The energy efficiency characteristic related to the load current (I_load) is dependent on the control mode used, the switching frequency, and coil inductance [42];

2)

For low [38] and high [39] power applications using the control mode based on the pulse width modulation technique and optimal control, respectively, the energy efficiency can be approximated by (16):

$${\eta }_{converter}={\eta }_{\max }-\frac{{\eta }_{\max }-{\eta }_{\min }}{4}\cdot {\lg }^2\left(\frac{I_{load}}{I_{load(opt)}}\right),$$

(16)

where η_max is the maximum of the energy efficiency (obtained at the optimal load current I_load(opt)) and η_min is the minimum of the energy efficiency (obtained in the considered load range).

3)

For low-power applications using the control mode based on the pulse frequency modulation technique, the energy efficiency can be approximated by (17) [38,39]:

$${\eta }_{converter}={\eta }_{\max }-\frac{{\zeta }_{\eta }}{I_{load}},$$

(17)

where η_max is the maximum energy efficiency (obtained at the maximum load current I_load(max)) and ζ_η is a parameter (that must be determined using the experimental values in the considered range of load). Relationship (17) highlights the nonlinear increase in energy efficiency in the range of light loads and the saturation that appears in the rest of the load range;

4)

For most types of control used in medium and high-power applications, the energy efficiency in the normal load range (therefore, except for light loads), where the converter operates in continuous current mode [43,44], can be considered as constant or linearly increasing (18):

$${\eta }_{converter}={\eta }_{\min }+{\chi }_{\eta }\cdot \frac{I_{load}}{I_{load(\max )}},$$

(18)

where η_min is the energy efficiency obtained at the load current I_load(min), which is the upper limit of light loads, and χ_η is a parameter to be determined using the experimental values in the considered load range (except the light loads).

The assumption that the energy efficiency linearly increases is valid for the medium-power FC HPS analyzed in this paper, because the load range was higher than 1 kW (so the case of light load was not considered). For different values of the load current, the LF control and optimization loops set the values of the FC current, I_FC0, and I_FC1, using the sFF strategy and the fuel economy strategy analyzed in this paper. So, (18) can be rewritten using as a variable the FC current as (19):

$${\eta }_{boost}={\eta }_{\min }+K_{\eta }\cdot \frac{I_{FC}}{I_{FC(\max )}},$$

(19)

where η_min ≅ 88.5% is the energy efficiency obtained at the nominal FC current, I_FC(min) ≅ 30 A, and K_η = 4 is a parameter which has been determined using the experimental values of the energy efficiency η_max ≅ 92% obtained at the maximum FC current, I_FC(max) ≅ 240 A. Note that the energy efficiency obtained at the nominal FC current, I_FC(nom) ≅ 130 A, was η_nom ≅ 90.17% (which is very close to the constant value considered in simulation).

The power loss of the boost converter (P_loss) was estimated using (20):

$$P_{loss}=P_{load}\cdot \left(\frac{1}{{\eta }_{boost}}-1\right).$$

(20)

The FC current, I_FC0, and I_FC1, using the sFF strategy and the fuel economy strategy, are registered in the second and third columns of

Table 11. Influence of variable energy efficiency on the FC net power estimated for f_d = 100 Hz.

Load Level	sFF Strategy	Fuel Economy Strategy		Dithers’ Frequency fd = 100 Hz
Pload (kW)	IFC0 (A)	IFC1 (A)	ηboost0 (%)	ηboost0 (%)	Ploss0 (kW)	Ploss1 (kW)	ΔPloss (kW)	ΔPloss/ΔPFCnet (%)
2	36.62	36.59	89.1103	89.1098	0.24441	0.24442	0.00001	0.00003
3	58.95	58.29	89.4825	89.4715	0.35261	0.35302	0.00041	0.00129
4	82.62	77.78	89.8770	89.7963	0.45053	0.45452	0.00400	0.00430
5	108.1	105.2	90.3017	90.2533	0.53700	0.53996	0.00297	0.00801
6	138.9	126	90.8150	90.6000	0.60684	0.62252	0.01568	0.01375
7	173	149.1	91.3833	90.9850	0.66004	0.69358	0.03354	0.05782
8	193	170.6	91.7167	91.3433	0.72251	0.75817	0.03565	0.10485

for different load levels and f_d =100 Hz. The energy efficiency (η_boost0 and η_boost1) and the power loss of the boost converter (P_loss0 and P_loss1) were estimated for the sFF strategy and the fuel economy strategy with (19) and (20), and are registered in Table 11. The difference in power loss of the boost converter (ΔP_loss) is registered in the eighth column of Table 11. The influence of ΔP_loss on ΔP_FCnet for f_d =100 Hz was estimated as ΔP_loss/ΔP_FCnet (%) and is registered in the last column of Table 11. As expected, the biggest error of 0.10485% was obtained at the maximum load.

It is worth mentioning that the biggest differences mentioned in Table 4, Table 6, and Table 8 were less than 0.2% for variable energy efficiency compared to the constant efficiency and also, this value was obtained at maximum load. So, the conclusions of this study are valid for both constant and variable energy efficiency.

6. Conclusion

The sensitivity analysis of the dither’s frequency f_d and weighting parameter k_eff was performed in this study in order to identify the best value of these parameters, which can be used to improve the fuel economy of an FC HPS. For this, the FC HPS was modeled, and the optimization and control loops of the considered strategy were designed.

The main findings of this study are as follows:

-

Firstly, the sensitivity analysis of the dither’s frequency f_d revealed that a value of 100 Hz is recommended to improve the performance indicators, such as $P_{FCnet}$, ${\eta }_{sys}$, $Fue{l}_{eff}$, and $Fue{l}_T$;

-

Secondly, the sensitivity analysis of the fuel economy ($\Delta Fue{l}_T$) in weighting parameter k_eff was performed for a 100 Hz dither; a k_eff value in the range of 20 lpm/W to 30 lpm/W gave the best fuel economy in the load range of 2–6 kW, but for a load of 6–8 kW, the fuel economy was better with a decrease in k_eff. So, k_eff = 20 lpm/W is recommended to improve the fuel economy in the full range of load.

-

Thirdly, a better fuel economy with an increase in load level has been highlighted.

Subsequent works will focus on comparing the performance of this strategy (using the load-following for the fuel regulator and the air optimization) with other strategies (for example, with the strategy which considers the fuel optimization and the load-following mode for the air regulator). But first, a sensitivity analysis for both f_d and k_eff parameters will be performed for the new strategies, to validate the recommended values of 100 Hz and 20 lpm/W obtained in this study.

Experimental tests have been performed for the first strategies (such as [3,4]) proposed in the research grant mentioned in the Acknowledgments section, but these will continue for recently proposed advanced strategies [14,45,46,47], including the strategy detailed in this paper.