Electromechanical Transient Modeling and Control Strategy of Decentralized Hybrid HVDC Systems
Abstract
:1. Introduction
- (1)
- An electromechanical transient model for a decentralized hybrid HVDC system is proposed. This model is necessary for the planning and dynamic analysis of a power grid with a decentralized hybrid HVDC system.
- (2)
- A parameter optimization strategy for the decentralized hybrid HVDC system is proposed to avoid DC power transmission obstruction in the receiving power system. This strategy can avoid the occurrence of a cascading failure in the receiving power grid.
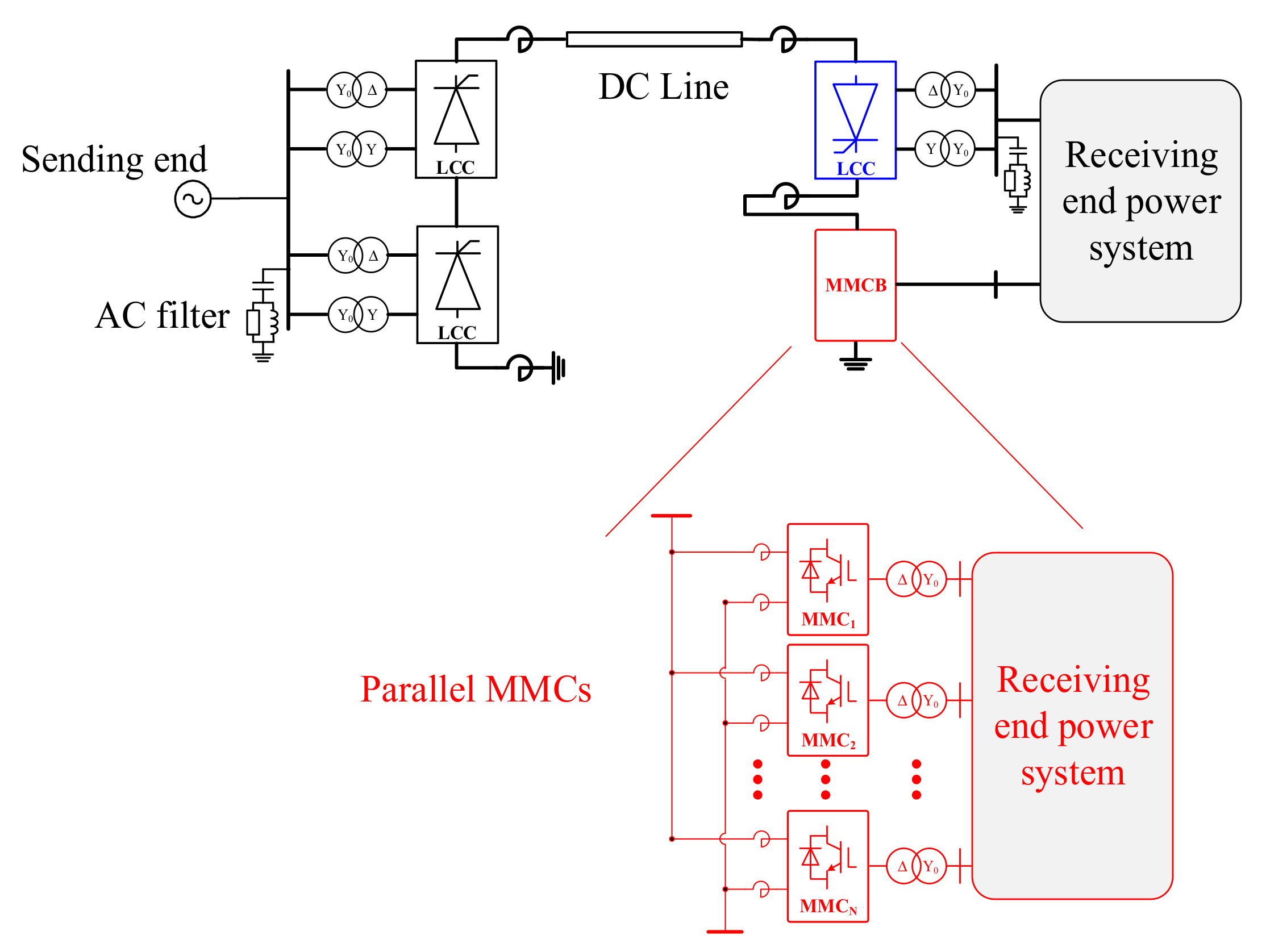
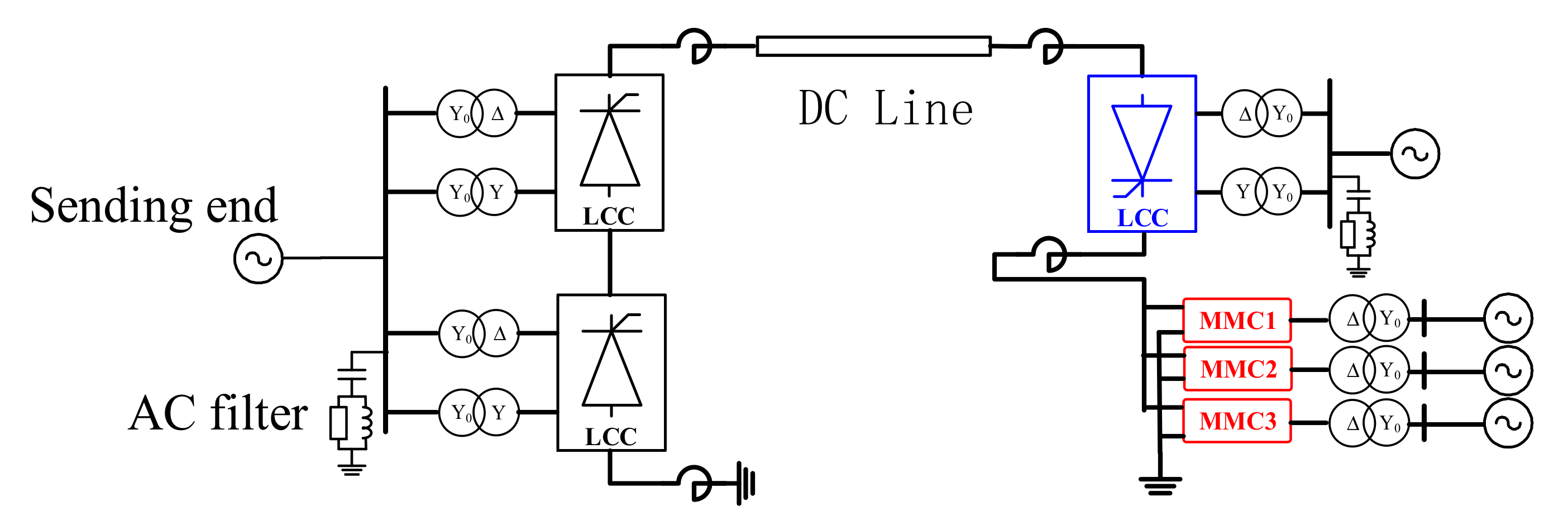
2. Topology of Decentralized Hybrid HVDC Systems
3. Electromechanical Transient Modeling of Decentralized Hybrid HVDC System
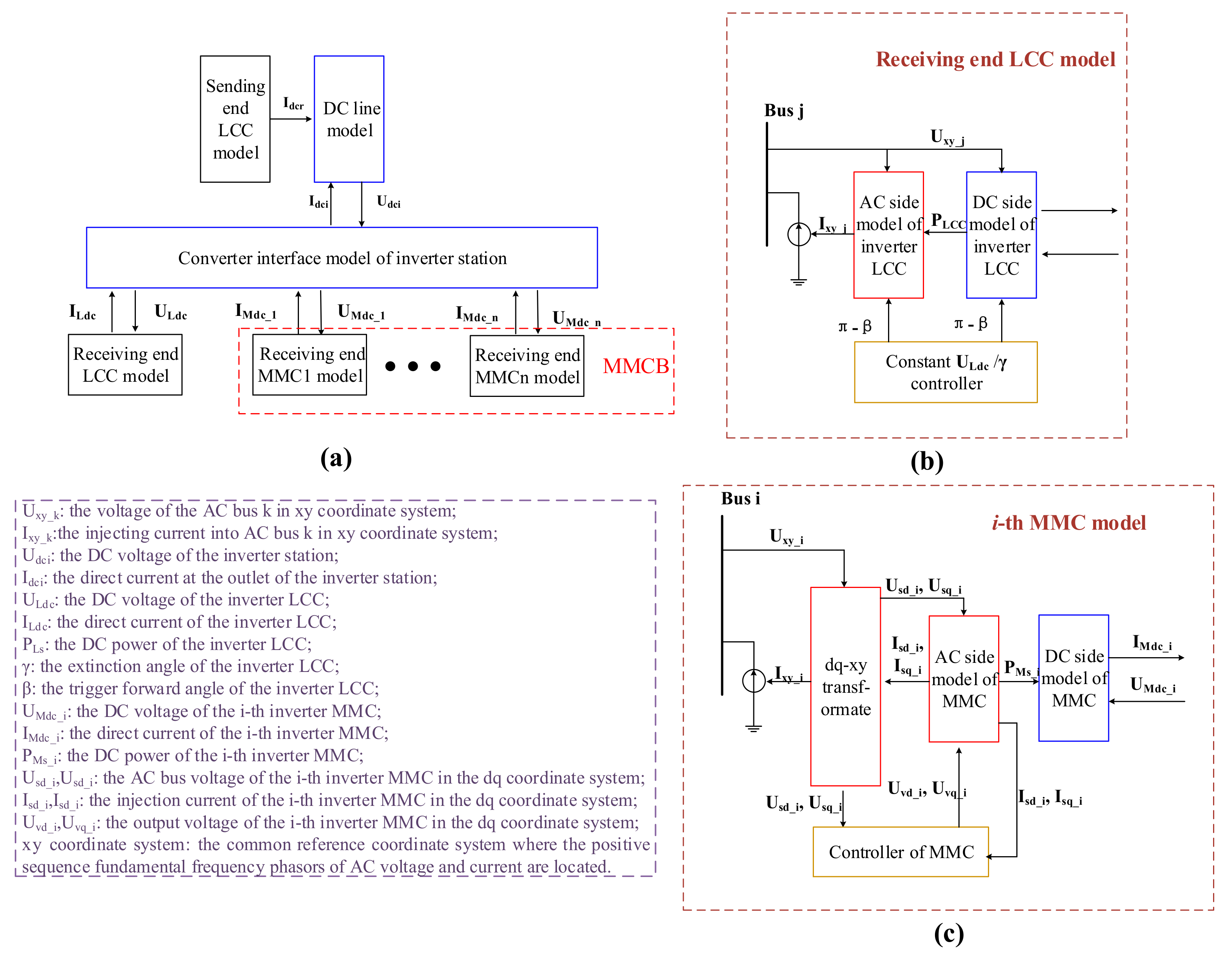
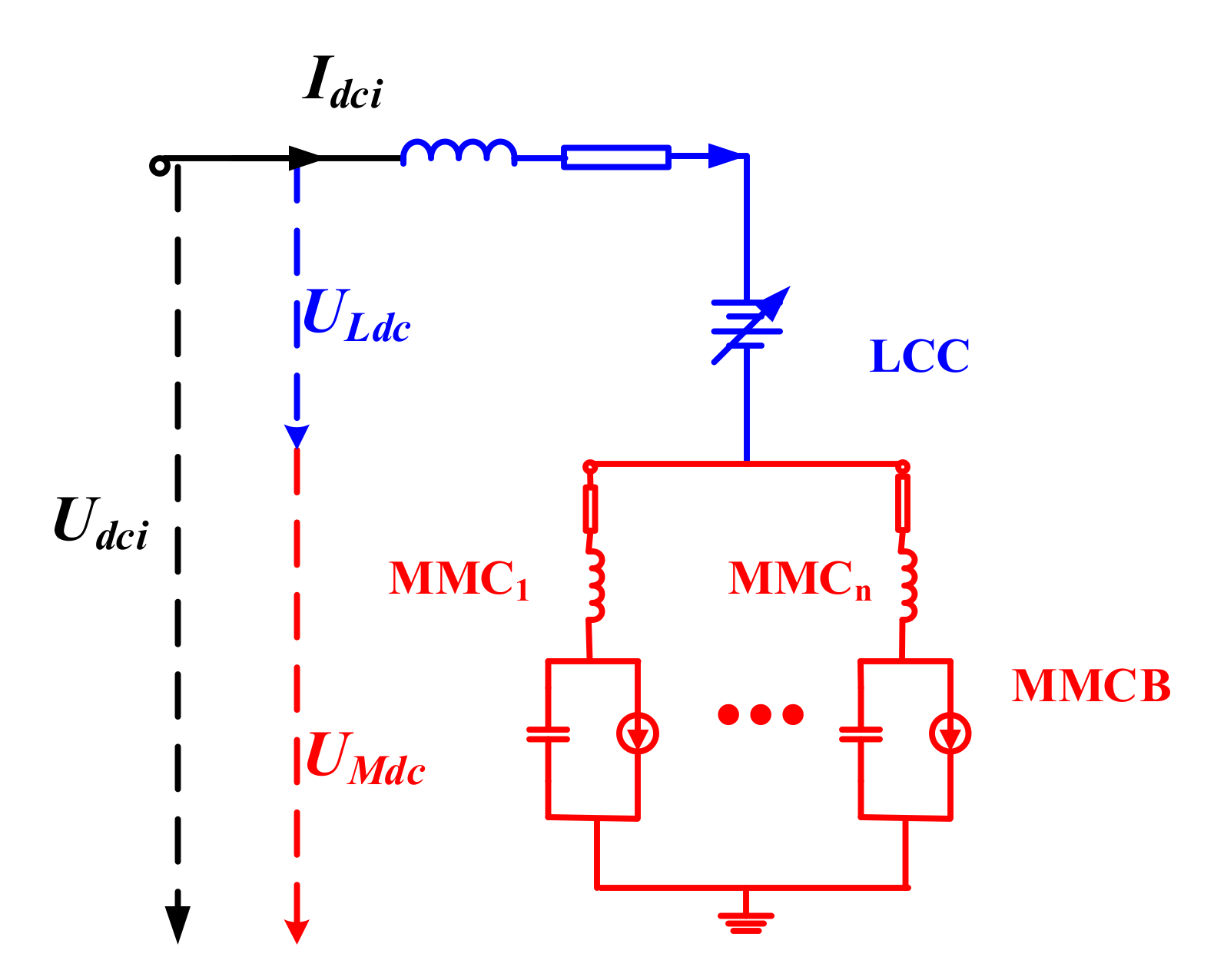
3.1. Structure of the Electromechanical Transient Model
- (1)
- The rectifier side LCC model, consisting of an AC side model and a DC side model.
- (2)
- The DC line model, with resistance, inductance, and capacitance.
- (3)
- The receiving end LCC/MMC model, consisting of an AC side model and a DC side model.
- (4)
- The interface model among the converters of the inverter station.
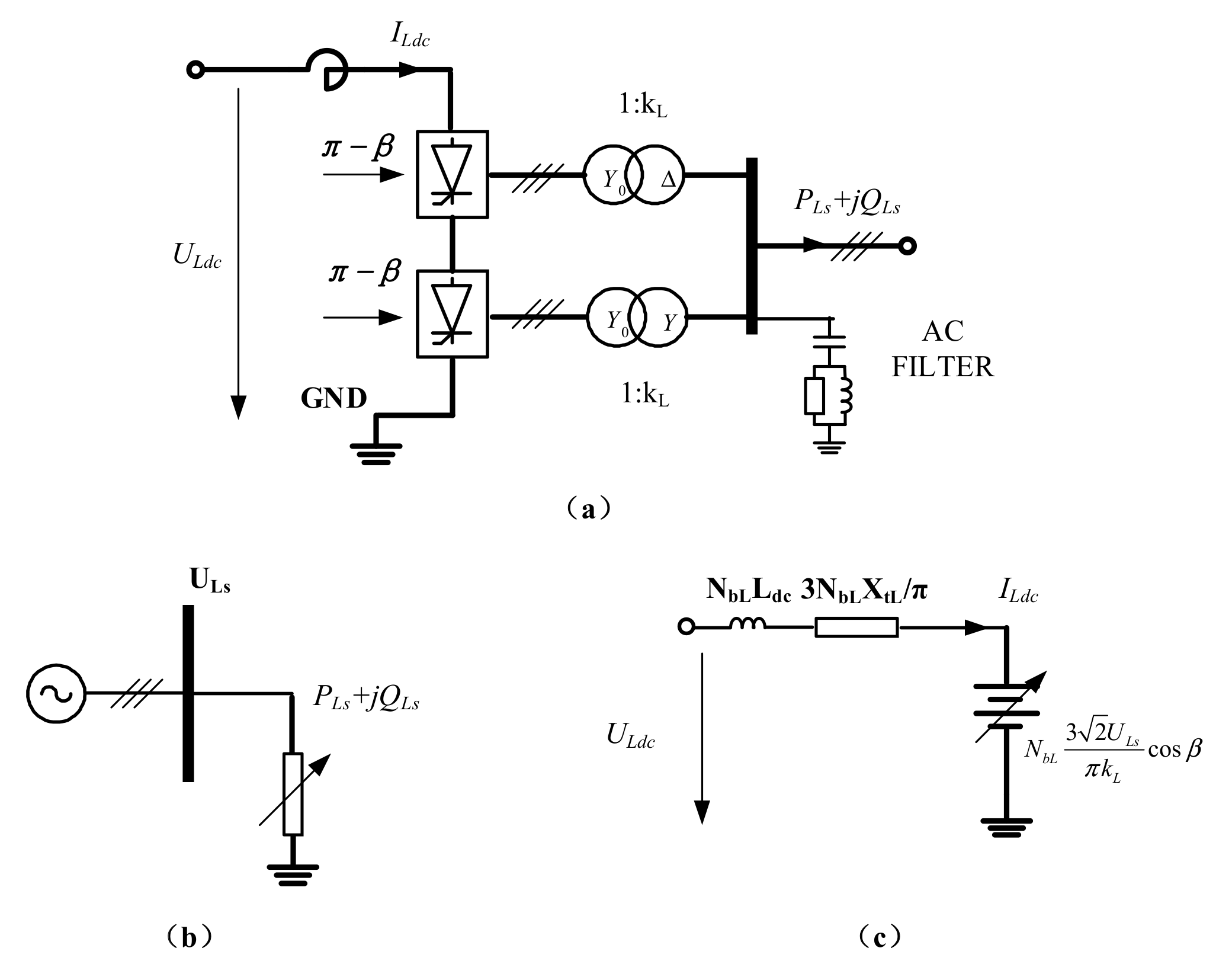
3.2. Electromechanical Transient Modeling of Receiving End LCC
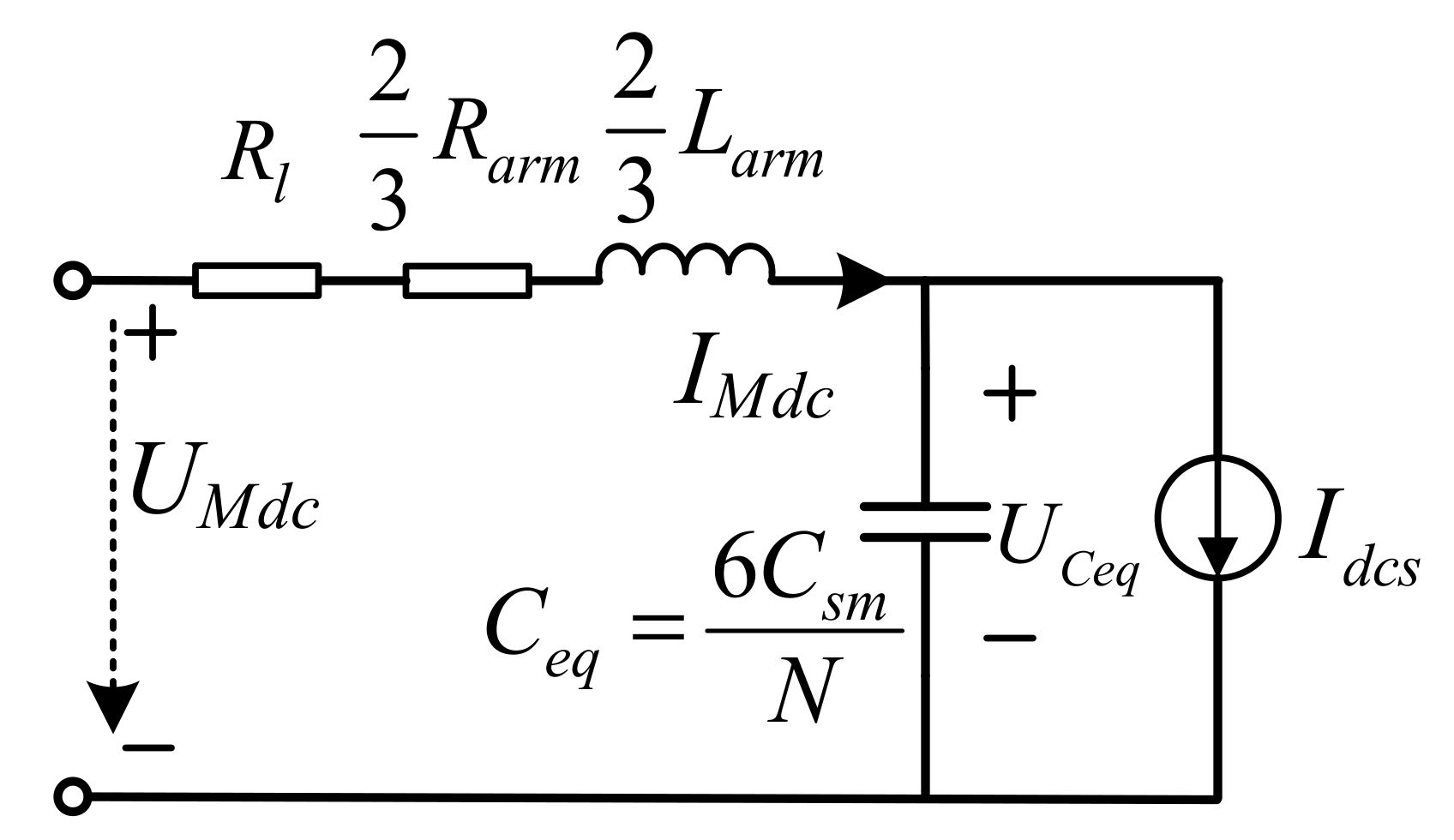
3.3. Electromechanical Transient Modeling of the MMC
3.4. Interface Model among LCC and MMCs
4. The Control Strategy of a Decentralized Hybrid HVDC System
5. Case Study
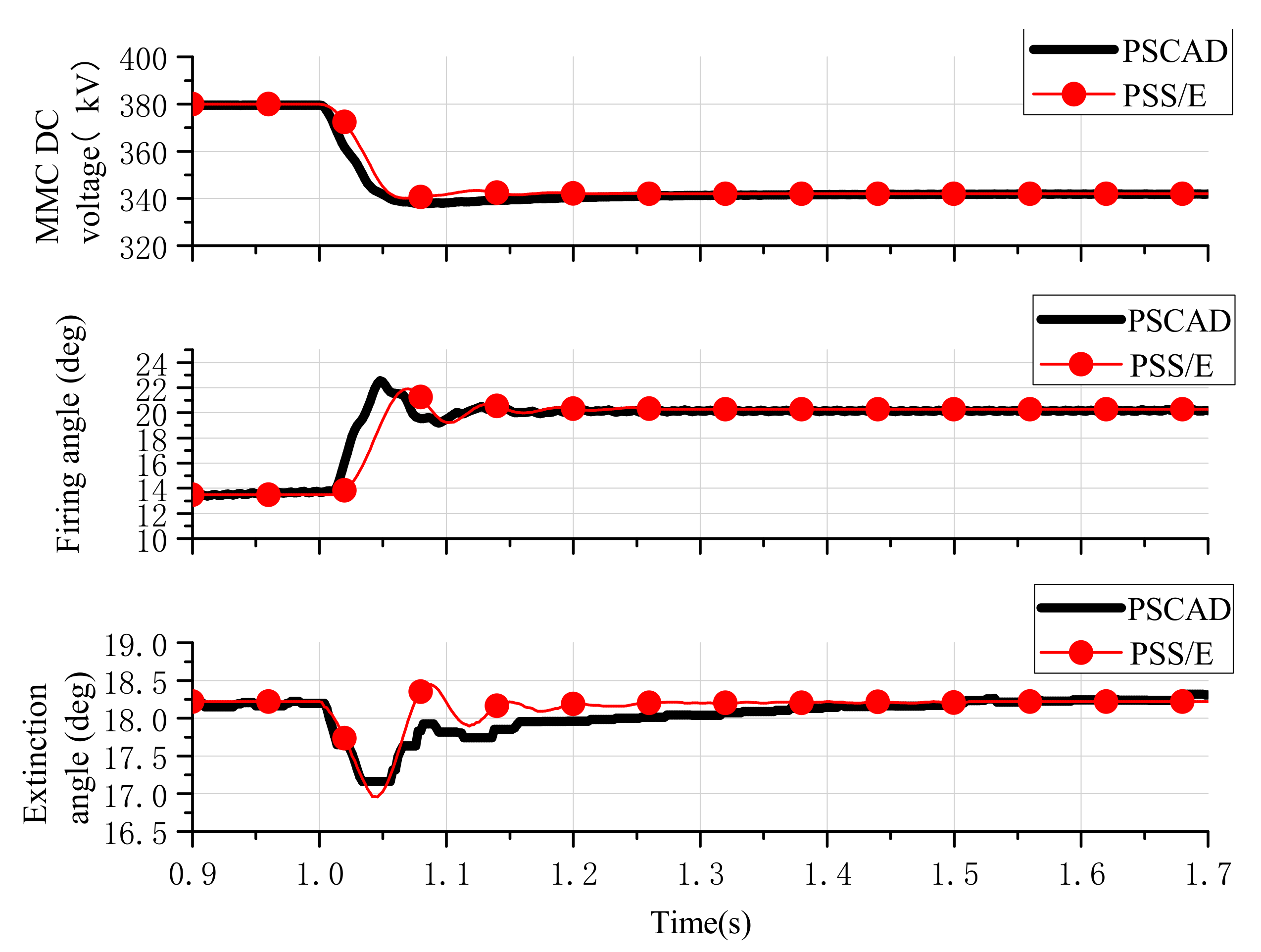
5.1. Validation of Electromechanical Transient Model of Dencentralzied Hybrid HVDC System
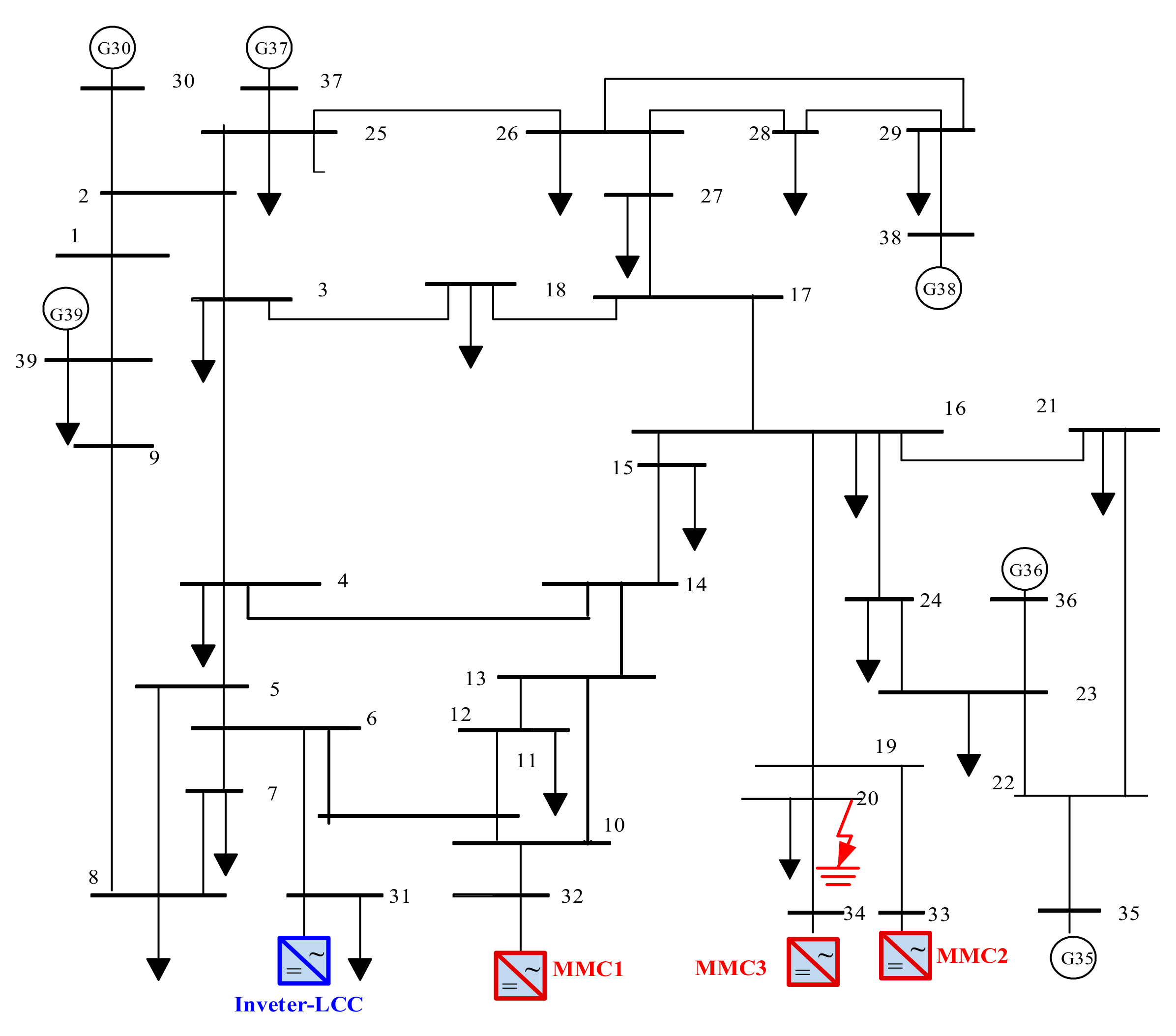
5.2. Dynamic Analysis of the 39-Bus System with a Decentralized Hybrid HVDC System
5.3. Simulation Verification of Control Strategy
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sun, Y.; Zhou, Q.; Shen, H. Analysis and Prospect on Development Patterns of China’s Power Transmission Network in Future. Power Syst. Technol. 2013, 37, 1929–1935. (In Chinese) [Google Scholar]
- Wang, C.; Zhu, L.; Chen, B.; Tang, Y.; Dai, Y. Analysis on voltage stability of hybrid system with UHVDC hierarchical connection to AC grid. In Proceedings of the 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–25 May 2016; pp. 690–695. [Google Scholar]
- Lu, S.; Xu, Z.; Xiao, L.; Jiang, W.; Bie, X. Evaluation and Enhancement of Control Strategies for VSC Stations Under Weak Grid Strengths. IEEE Trans. Power Syst. 2018, 33, 1836–1847. [Google Scholar] [CrossRef]
- Li, S.; Wu, Z.; Huang, J. Power flow modelling to UHVDC line and its hierarchical connection mode. IET Gener. Transm. Distrib. 2018, 12, 1554–1564. [Google Scholar] [CrossRef]
- Liu, Z.; Qin, X.; Zhao, L.; Zhao, Q. Study on the Application of UHVDC Hierarchical Connection Mode to Multi-infeed HVDC System. Proc. CSEE 2013, 33, 1–7. (In Chinese) [Google Scholar]
- Li, G.; Zhang, S.; Jiang, T.; Chen, H. A method of detecting commutation failure in multi-infeed HVDC systems based on critical failure impedance boundary. In Proceedings of the IEEE Power & Energy Society General Meeting (PES-2017), Chicago, IL USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Torres-Olguin, R.E.; Molinas, M.; Undeland, T. Offshore Wind Farm Grid Integration by VSC Technology With LCC-Based HVDC Transmission. IEEE Trans. Sustain. Energy 2012, 3, 899–907. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Z.; Xue, Y.; Tang, G. DC-Side Harmonic Currents Calculation and DC-Loop Resonance Analysis for an LCC–MMC Hybrid HVDC Transmission System. IEEE Trans. Power Deliv. 2015, 30, 642–651. [Google Scholar] [CrossRef]
- Xiao, L.; Li, Y.; Xiao, H.; Zhang, Z.; Xu, Z. Electromechanical Transient Modeling of Line Commutated Converter-Modular Multilevel Converter-Based Hybrid Multi-Terminal High Voltage Direct Current Transmission Systems. Energies 2018, 11, 2102. [Google Scholar] [CrossRef]
- Zi, P.; Zhao, Z.; Chen, X.; Zhou, X.; Wan, L.; Shi, H.; An, N.; Tian, F. Electromechanical transient modeling of hybrid DC grid based on LCC and VSC converter. Proc. CSEE 2015, 24, 6265–6274. (In Chinese) [Google Scholar]
- Hahn, C.; Geuß, A.; Luther, M. Modeling and control design of hybrid—LCC and VSC based—HVDC systems. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 2–5 May 2016; pp. 1–6. [Google Scholar]
- Jung, J.; Cui, S.; Lee, J.; Sul, S.K. A New Topology of Multilevel VSC Converter for a Hybrid HVDC Transmission System. IEEE Trans. Power Electron. 2017, 32, 4199–4209. [Google Scholar] [CrossRef]
- Tang, G.; Xu, Z. A LCC and MMC hybrid HVDC topology with DC line fault clearance capability. Int. J. Electr. Power Energy Syst. 2014, 62, 419–428. [Google Scholar] [CrossRef]
- Xiao, L.; Xu, Z.; Xiao, H.; Zhang, Z.; Wang, G.; Xu, Y. Electro-mechanical transient modeling of MMC based multi-terminal HVDC system with DC faults considered. Int. J. Electr. Power Energy Syst. 2019, 113, 1002–1013. [Google Scholar] [CrossRef]
- Chang, Y.; Cai, X. Hybrid Topology of a Diode-Rectifier-based HVDC System for Offshore Wind Farms. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 1. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, S.; Xiao, H. Hybrid high-voltage direct current topology with line commutated converter and modular multilevel converter in series connection suitable for bulk power overhead line transmission. IET Power Electron. 2016, 9, 2307–2317. [Google Scholar] [CrossRef]
- Guo, C.; Liu, W.; Zhao, C.; Ni, X. Small-signal dynamics and control parameters optimization of hybrid multi-infeed HVDC system. Electr. Power Energy Syst. 2018, 98, 409–418. [Google Scholar] [CrossRef]
- Lebre, J.R.; Watanabe, E.H. Fullbridge MMC control for hybrid HVDC systems. In Proceedings of the Brazilian Power Electronics Conference (COBEP), Juiz de Fora, Brazil, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Cai, Y.; Wen, M.; Chen, Y.; Shi, Y.; Qin, Y. Low DC voltage control strategy of bipolar LCC-MMC hybrid HVDC transmission system. In Proceedings of the 2nd International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 20–23 September 2017; pp. 166–171. [Google Scholar]
- Lee, Y.; Cui, S.; Kim, S.; Sul, S.-K. Control of hybrid HVDC transmission system with LCC and FB-MMC. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 475–482. [Google Scholar]
- Xue, Y.; Ge, F.; Zhao, Z.; Zhang, Z.; Xing, F. Control strategy for hybrid LCC-C-MMC HVDC system under AC fault at rectifier side. IET J. Eng. 2019, 16, 3259–3263. [Google Scholar] [CrossRef]
- Naushath, M.H.; Rajapakse, A.D.; Gole, A.M.; Fernando, I.T. Energization and regulation of a hybrid HVDC grid with LCC and VSC. In Proceedings of the IEEE Electrical Power and Energy Conference (EPEC), Saskatoon, SK, USA, 22–25 October 2017; pp. 1–6. [Google Scholar]
- Yu, Y.; Lu, Y.; Chen, Q. Internal model startup control for VSC-LCC based hybrid pseudo bipolar HVDC system. In Proceedings of the 2nd International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 20–23 September 2017; pp. 15–19. [Google Scholar]
- Sun, S.; Xiang, W.; Yao, L.; Li, Y.; Wen, J. Control and operation of a hybrid HVDC integrating wind farm based on SB-MMC and LCC. IET J. Eng. 2017, 2017, 816–821. [Google Scholar] [CrossRef]
- Prabna, K. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; ISBN 007035958X. [Google Scholar]
- Duffy, A.P.; Martin, A.J.M.; Orlandi, A.; Antonini, G.; Benson, T.M.; Woolfson, M.S. Feature selective validation (FSV) for validation of computational electromagnetics (CEM). part I—The FSV method. IEEE Trans. Electromagn. Compat. 2006, 48, 449–459. [Google Scholar] [CrossRef]
- Orlandi, A.; Duffy, A.P.; Archambeault, B.; Antonini, G.; Coleby, D.E.; Connor, S. Feature selective validation (FSV) for validation of computational electromagnetics (CEM). part II—Assessment of FSV performance. IEEE Trans. Electromagn. Compat. 2006, 48, 460–467. [Google Scholar] [CrossRef]


| Item | Rectifier | Inverter High Voltage End | Inverter Low Voltage End |
|---|---|---|---|
| Converter type | LCC | LCC | Three MMCs in parallel |
| Rated L-L RMS voltage of AC system (kV) | 525 | 525 | 525 |
| Rated capacity of converter(MVA) | 5000 | 2500 | 800 × 3 |
| Rated DC voltage (kV) | 800 | 400 | 400 |
| Smoothing reactor (mH) | 150 | 150 | 150 |
| Capacitance of sub module (μF) | / | / | 6941 |
| Number of sub module per arm | / | / | 100 |
| Control mode | Constant direct current | Constant DC voltage | Constant DC voltage/reactive power |
| Reference | 6.27 kA | 382 kV | 382 kV/0 Mvar |
| Item | Rectifier LCC | Inverter LCC | MMC |
|---|---|---|---|
| Active power output (MW) | −2450.4 | 1200.0 | 398.8 |
| Reactive power output (Mvar) | −1024.86 | −514.91 | 0.0 |
| Control mode | Constant direct current | Constant DC voltage | Constant DC voltage/reactive power |
| Reference | 3 kA | 400.0 kV | 400.0 kV/0 Mvar |
| Branch | Load Power (MVA) | Long Term Allowable Load Power (MVA) | Load Rate (%) |
|---|---|---|---|
| Bus 6–Bus 7 | 977.1 | 900 | 108.6 |
| Bus 10–Bus 13 | 577.1 | 600 | 96.2 |
| Bus 13–Bus 14 | 610.6 | 600 | 101.8 |
| Converter Type | Direct Current (kA) | DC Voltage (kV) | Output Active Power (MW) | Output Reactive Power (Mvar) |
|---|---|---|---|---|
| Sending end LCC | 3.67 | 667.68 | 2450.4 | −1445.05 |
| Receiving end LCC | 3.67 | 228.71 | 839.37 | −664.21 |
| MMC1 | 0.87 | 419.24 | 364.06 | 12.11 |
| MMC2 | 1.40 | 419.24 | 592.79 | 5.23 |
| MMC3 | 1.40 | 419.24 | 592.79 | 0.58 |
| Branch | Load Power (MVA) | Load Rate |
|---|---|---|
| Bus 6–Bus 7 | 809.0 | 89.9% |
| Bus 10–Bus 13 | 376.9 | 62.8% |
| Bus 13–Bus 14 | 393.9 | 65.6% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Xiao, H.; Xiao, L.; Zhang, Z.; Xu, Z. Electromechanical Transient Modeling and Control Strategy of Decentralized Hybrid HVDC Systems. Energies 2019, 12, 2856. https://doi.org/10.3390/en12152856
Wang G, Xiao H, Xiao L, Zhang Z, Xu Z. Electromechanical Transient Modeling and Control Strategy of Decentralized Hybrid HVDC Systems. Energies. 2019; 12(15):2856. https://doi.org/10.3390/en12152856
Chicago/Turabian StyleWang, Guoteng, Huangqing Xiao, Liang Xiao, Zheren Zhang, and Zheng Xu. 2019. "Electromechanical Transient Modeling and Control Strategy of Decentralized Hybrid HVDC Systems" Energies 12, no. 15: 2856. https://doi.org/10.3390/en12152856
APA StyleWang, G., Xiao, H., Xiao, L., Zhang, Z., & Xu, Z. (2019). Electromechanical Transient Modeling and Control Strategy of Decentralized Hybrid HVDC Systems. Energies, 12(15), 2856. https://doi.org/10.3390/en12152856









