Energy Management through Cost Forecasting for Residential Buildings in New Zealand

Abstract

Over the last two decades, the residential building sector has been one of the largest energy consumption sectors in New Zealand. The relationship between that sector and household energy consumption should be carefully studied in order to optimize the energy consumption structure and satisfy energy demands. Researchers have made efforts in this field; however, few have concentrated on the association between household energy use and the cost of residential buildings. This study examined the correlation between household energy use and residential building cost. Analysis of the data indicates that they are significantly correlated. Hence, this study proposes time series methods, including the exponential smoothing method and the autoregressive integrated moving average (ARIMA) model for forecasting residential building costs of five categories of residential buildings (one-storey house, two-storey house, townhouse, residential apartment and retirement village building) in New Zealand. Moreover, the artificial neutral networks (ANNs) model was used to forecast the future usage of three types of household energy (electricity, gas and petrol) using the residential building costs. The t-test was used to validate the effectiveness of the obtained ANN models. The results indicate that the ANN models can generate acceptable forecasts. The primary contributions of this paper are twofold: (1) Identify the close correlation between household energy use and residential building costs; (2) provide a new clue for optimizing energy management.

1. Introduction

The residential sector is one of the greatest energy consumers in New Zealand [1]. A significant amount of energy is used to provide comfortable indoor environments. Recently, the residential building sector has been increasing due to economic development, social progress, and increasing population [2]. The growth imposes great pressures on household energy consumption. If the increasing demand cannot be appropriately evaluated, it may have a negative effect on long-term energy management and economic development and structure. The decision makers desire to know the impacts of the growth on energy consumption. Hence, to establish a relationship between the residential building and energy management sector is essential. As such, examining the mechanism of the residential building sector on energy consumption has significant theoretical and practical implications for energy management. This study examines the effects of residential building costs on household energy consumption to establish a link between the residential building and energy sector. Moreover, there are many factors that may impact the future trend of energy consumption in the residential sector. To comprehensively assess every factor in detail is impossible and time-consuming. Hence, the residential building cost can be used as an indicator to forecast future household energy consumption, which enables decision makers to obtain accurate forecasts of future energy consumption in the residential building sector effectively and provides a new perspective for energy management.

To obtain a comprehensive cost indicator, the building costs of five main types of residential buildings in New Zealand including one-storey house (AR1), two-storey house (AR2), townhouse (AR3), residential apartment (AR4), and retirement village building (AR5) are considered. This study tends to use time series modelling techniques to forecast the building costs of five categories of residential building. There are two most widely used time series forecasting methods: Exponential smoothing and autoregressive integrated moving average (ARIMA). The exponential smoothing method was originally introduced by [3,4]; for short-term sales forecasting in support of supply chain management and production planning. The widespread usage of this method is mainly due to the fact that it is a relatively simple forecasting method requiring a small size sample and having a comprehensible statistical framework and model parameters. Exponential smoothing models developed are based on the trend and seasonality in time series, while ARIMA models are supposed to describe the autocorrelations in the time series. A framework for exponential smoothing methods was developed based on state-space models [5]. The autoregressive integrated moving average (ARIMA) approach is a widely used linear method [6]. It carries more flexibility by representing various components of time series including autoregressive (AR), moving average (MA), and combined AR and MA. It is the most efficient approach for short-term forecasting with rapid changes. The future predictions based on ARIMA models can be explained by previous or lagged values and the terms of the stochastic errors [7]. The performance of the two forecasting techniques was evaluated in terms of error measures.

Furthermore, an artificial intelligence (AI) method artificial neutral networks (ANNs) model is used for forecasting household energy consumption. Influence variables such as residential building costs are involved in the ANN model. The ANN technique is an intelligent method, which can learn and change its architecture when input variables are fed into it. An ANN model is developed to mimic human brain networking, which is inspired by a mathematical model of biological neutral networks [8]. In this study, multilayer perception ANN models are used to develop forecasting models for household energy consumption. Multilayer perceptron artificial neutral network (MLP ANN) models for forecasting household energy consumption are developed in this work. To improve the adequacy of the models, activation functions and a train-and-error process are used to optimize the parameters of the ANN models, including the number of hidden layers and neutrons, activation function, and training algorithm. The forecasts of household energy consumption obtained based on the proposed ANN models are compared with the actual values of the household energy consumption. The t-test is adopted to validate the effectiveness of the ANN models.

The rest of this study is organized as follows. Section 2 presents the previous studies about factors influencing residential energy use, cost forecasting methods and energy consumption methods. Section 3 introduces the correlation analysis, exponential smoothing method, ARIMA model, ANNs model, and t-test. Correlation analysis results, exponential smoothening and ARIMA models for the cost series, ANN models for household energy consumption are shown in Section 4. The results discussion is presented in Section 5. In the final section, the conclusion is presented.

2. Literature Review

2.1. Influencing Factors of Residential Energy Use

The residential sector significantly contributes to energy consumption. Recently, an increasing number of studies have been performed in this field. For example, some studies regarded that energy consumption may be influenced by factors such as climate [9], material properties and design parameters [10,11], lighting and home appliances [12], and residents’ behavior [13,14]. Other studies have been conducted considering the impacts of building features such as building shape [15,16], building orientation [15,17,18,19,20,21], thermal mass [22,23], infiltration level [18,24,25,26], floor area and volume [27], number of storeys [28], and HVAC system [29,30,31,32,33,34] on the energy efficiency of buildings. Moreover, several studies addressed that some socio-economic variables have impacts on energy consumption [35,36,37]. In addition, some studies comprehensively evaluate the life-cycle cost of an energy saving building to prompt the adoption of energy-saving building. In [38], construction costs of conventional buildings and net-zero energy buildings were compared. Construction professionals usually consider that nearly-zero energy buildings may cost more, cost is regarded as a barrier to prompt net-zero buildings. However the results indicate no significant difference between the conventional building and net-zero energy building cost. Study [39] investigated energy savings and cost effectiveness of the Italian housing stock refurbishment. Energy performance of a building before and after refurbishment, refurbishment cost of the building, and energy cost savings after refurbishment were evaluated based on building typology in order to choose an optimal package plan for the building. Study [40] provided a method to identify cost-optimal levels of minimum energy performance requirements in residential buildings. The study evaluated the cost of factors (HVAC, building envelopes, technologies used etc.) and the energy-saving cost to develop a cost-optimal residential building.

2.2. Cost Forecasting Methods

Several studies have been conducted focusing on construction cost forecasting. For example, [41] explained a way of applying neutral networks to forecast changes in the construction cost index. In [42], a dynamic regression model to forecast building cost using economic variables was addressed. Although these methods are effective in identifying the leading cost drivers and appropriate estimation at the inception of the project, they are difficult to deal with as time-varying variables and reflect the time lag effects. Since much time-related data are dependent or have an autocorrelation [43], time-related techniques can be adopted to overcome these limitations.

In an attempt to solve time-related problems in the methods, the time series techniques, which estimate future values of a certain variable according to past values of itself and random shock factors, have been adopted to forecast the building cost. For example, [44] used time-series models to provide reliable forecasts of building costs, tender prices, and the impacts of economic inflation on building projects. In [45], an integrated regression analysis and ARIMA techniques to predict a tender price index for Hong Kong building projects was introduced. Reference [46] developed a Box-Jenkins model to estimate the labor market of the Hong Kong construction industry. Reference [47] illustrated a time series method that estimates future values according to past values and corresponding random errors to produce a reliable prediction of construction cost.

2.3. Energy Consumption Forecasting

Many researchers are now working in the field of energy consumption forecasting [8,48,49]. Forecasting techniques mainly focus on three areas, including statistical, engineering, and artificial intelligence (AI) approaches [50]. Statistical approaches utilize historical data to predict important parameters. Regression models, autoregressive integrated moving average (ARIMA), Gaussian mixture techniques, and conditional demand analysis are a few examples of statistical forecasting approaches [51,52,53,54]. Engineering approaches investigate energy consumption based on architectural features and climate behavior of buildings, including building design; thermal characteristics of building materials; heating, ventilation and air conditioning (HVAC) systems; and weather conditions [12,55,56,57,58,59,60]. AI methods provide different processes for exhibiting modelled parameters based on the same historical data used by statistical forecasting methods [50]. Among all AI techniques, neutral networks have the advantage of being able to model varying, non-linear relationships between input and output variables. A few AI techniques, including genetic algorithms (GA), genetic programming (GP), fuzzy logic (FL), support vector machines (SVM), and ANNs have been employed in various studies [61,62,63].

One study [64] used statistical methods, including exponential smoothing models and Bootstrap aggregating ARIMA models, to predict electrical energy consumption in 2019 for different countries based on monthly electricity consumption data. One study [61] used three AI methods, including GP, SVM, and ANNs, to develop forecasting models of electricity consumption for five Asian counties based on long-term electricity consumption data (1971–2011). Another study [65] used both multiple regression and GP methods to predict natural gas consumption for a steel company in Slovenia; the results indicated that GP outperforms the multiple regression method. Moreover, another study [66] employed a GP method involving various social, political and economic parameters to develop a long-term forecasting model of energy consumption for a Brazilian industrial sector. An additional study [67] used the ANNs technique to develop a forecasting model of energy consumption in the residential building sector. Moreover, ANNs models have been used in the oil industry [68,69]. Study [69] employed multiple regression, ANNs, and SVM methods to forecast daily electricity consumption by oil driven pumps in China.

3. Research Methods

3.1. Data

The used data are composed of the average quarterly values of household energy usage and residential building costs observed for the period 2001:Q1-2018:Q4: (a) Household electricity usage, (b) household gas usage, (c) household petrol usage, (d) one-storey house building cost, (e) two-storey house building cost, (f) townhouse building cost, (g) apartment building cost, and (h) retirement village building cost. Household energy usage data are available from Statistics New Zealand. Electricity, gas, and petrol are the most used energy in the residential sector of New Zealand, as shown in Figure 1a [1]. The energy use in the residential sector of New Zealand are mainly in the areas such as space heating, water heating, refrigeration, and home appliances, as shown in Figure 1b [1]. The cost indices are provided by the QV cost-builder, which has been widely accepted in New Zealand. The building cost is composed of the capital construction, associated capital, and client-related cost [70]. The construction cost consists of material, labor, and equipment cost. The associated capital and client-related cost are added as the percentage of the capital construction cost.

The data (72 observations) was split into two parts: The training part for model fitting and the testing part for evaluating the forecasting performance by comparing forecasts with observations [71]. There is no clear rule for this dividing; in this study, about 72% of the data (2001:Q1–2013:Q4) were used for model fitting and the remaining 28% (2014:Q1–2018:Q4) were used for out-of-sample forecasts evaluation. The quarterly average building cost for the five categories of residential building in New Zealand from 2001:Q1-2018:Q4 are depicted in Figure 2.

3.2. Correlation Analysis

Correlation analysis is a statistical method used to evaluate the significance of correlation between two variables [72]. A significant correlation indicates that two variables have a significant relationship, while a weak correlation indicates that the variables are weakly related. In other words, the correlation analysis can be used to examine the significance of the relationship between two variables. Pearson’s correlation coefficient, also called linear correlation coefficient, assesses the linear relationship between two variables [73]. Let i and j be two random variables of the same sample n. To calculate Pearson’s correlation coefficient r, use Equation (1) as follows.

$$r=\frac{{{\displaystyle \sum }}_{k=1}^n\left(i_k-\overline{i}\right)\left(j_k-\overline{j}\right)}{\sqrt{{{\displaystyle \sum }}_{k=1}^n{\left(i_k-\overline{i}\right)}^2}\sqrt{{{\displaystyle \sum }}_{k=1}^n{\left(j_k-\overline{j}\right)}^2}},$$

(1)

where

$$\overline{i}=\frac{1}{n}{{\displaystyle \sum }}_{k=1}^n{i}_k and \overline{j}=\frac{1}{n}{{\displaystyle \sum }}_{k=1}^n{j}_k,$$

are the means of the variables i and j, respectively. The correlation coefficient r ranges between −1 and +1. If the linear correlation between i and j is positive (the increase of one variable is related to the increase of the other), then the correlation coefficient r > 0, whereas if the linear correlation between i and j is negative (the increase of one variable is related to the decrease of the other), then the correlation result r < 0. The value r = 0 indicates absence of any association between i and j. The sign of the correlation coefficient indicates the direction of the relationship. The magnitude of r indicates the significance of the correlation. For example, if r is close to 1, then the two variables are positively associated at a significant level, which also indicates that the increase of one variable is related to the increase of the other. If r is close to −1, then the two variables are negatively associated with each other at a significant level, which indicates that the increase of one variable is related to the decrease of the other. If r = 0, this usually indicates that the two variables are unrelated.

3.3. Exponential Smoothing

Exponential smoothing is one of the most effective forecasting methods when a time series has a trend that has changed over time, for example, since the 1950s [74]. It unequally weights the observed time series values. More recently observed values are weighted more heavily than more remote observations. The weights for the observed time series values decrease exponentially as one moves further into the remote. A smoothing constant can determine the rate at which the weights of older observed values decrease. Exponential smoothing techniques include simple exponential smoothing, linear trend corrected exponential smoothing, Holt-Winters methods, and damped trend exponential smoothing [74].

According to [75], exponential smoothing models have been widely used in many research fields and industry practices due to their relative simplicity and good overall forecasting performance as well as considering trends, seasonality and other features of the data. A large number of existing research and studies also indicated their extensive industrial applications [76,77]. In this study, the Holt-Winters exponential smoothing method was adopted.

3.3.1. Holt-Winters Method

Holt-Winters methods are designed for time series that exhibit linear trend and seasonal variation, which include the additive Holt-Winters method and multiplicative Holt-Winters methods [74]. An advantage of these methods is that they can model data seasonality directly instead of stationary transforming for the data. If a time series has a linear trend and additive seasonal pattern, the additive Holt-Winters method is appropriate. Then the time series can be described in Equation (2).

$$Y_t=\left({\beta }_0+{\beta }_{1}t\right)+S_t+{ϵ}_t,$$

(2)

where β₁ is the growth rate; S_t is a seasonal pattern; ${ϵ}_t$ is the error term.

For such time series, the mean, the growth rate, and the seasonal variation may be changing over time. A state space model for these changing components can be found in Equations (3)–(6).

$$l_t=l_{t-1}+b_{t-1}+\alpha \left[Y_t-\left(l_{t-1}+b_{t-1}+S_{t-L}\right)\right],$$

(3)

$$b_t=b_{t-1}+b_{t-1}+\alpha \gamma \left[Y_t-\left(l_{t-1}+b_{t-1}+S_{t-L}\right)\right],$$

(4)

$$S_t=S_{t-L}+\left(1-\alpha \right)\delta \left[Y_t-\left(l_{t-1}+b_{t-1}+S_{t-L}\right)\right],$$

(5)

$${\widehat{Y}}_t=l_{t-1}+b_{t-1}+S_{t-L},$$

(6)

To begin the estimation, the initial values for level, growth rate and seasonal variation should be estimated. Hence, first, a least squares regression model should be generated based on available data. The regression model can be expressed in Equation (7). The initial values $l_0$, $b_0$ were also obtained from the model.

$${\widehat{Y}}_t=l_0+b_{0}t,$$

(7)

Obtained estimated values for each time period are based on the above regression model. The initial seasonal factor in each of the L seasons can be calculated in Equation (8).

$$S_{Li}=\frac{\left(y_i-{\widehat{y}}_i\right)+\left(y_{i+L}-{\widehat{y}}_{i+L}\right)+\left(y_{i+2L}-{\widehat{y}}_{i+2L}\right)+\cdots +\left(y_{i+nL}-{\widehat{y}}_{i+nL}\right)}{L},$$

(8)

where $S_{Li}$ are seasonal factors; L is the number of seasons in a year; i is the number of time periods in each season.

After finding the values for the seasonal factors, the state space models are employed to obtain model parameters that minimize the sum of the squared errors. Future values of the time series are predicted by the state space model in Equation (6).

3.3.2. Multiplicative Holt-Winters Method

If a time series has a linear trend with multiplicative seasonal variations, the multiplicative Holt-Winters method is appropriate to be used. The state space models for this method can be described in Equations (9)–(12).

$$l_t=l_{t-1}+b_{t-1}+\alpha \frac{\left[Y_t-\left(l_{t-1}+b_{t-1}\right)S_{t-L}\right]}{S_{t-L}},$$

(9)

$$b_t=b_{t-1}+\alpha \gamma \frac{\left[Y_t-\left(l_{t-1}+b_{t-1}\right)S_{t-L}\right]}{S_{t-L}},$$

(10)

$$S_t=S_{t-L}+\left(1-\alpha \right)\delta \frac{\left[Y_t-\left(l_{t-1}+b_{t-1}\right)S_{t-L}\right]}{l_t},$$

(11)

$$Y_t=\left(l_{t-1}+b_{t-1}\right)S_{t-L},$$

(12)

And the seasonal factors can be computed in the following Equations (13).

$$S_{Li}=\frac{\left(y_i/{\widehat{y}}_i\right)+\left(y_{i+L}/{\widehat{y}}_{i+L}\right)+\left(y_{i+2L}/{\widehat{y}}_{i+2L}\right)+\cdots +\left(y_{i+nL}/{\widehat{y}}_{i+nL}\right)}{L},$$

(13)

3.4. Autoregressive Integrated Moving Average (ARIMA)

There are four steps to select an appropriate model for the time series data in the Box-Jenkins approach including model identification, parameters estimation, diagnosis checking and forecasting [78]. The development process of an ARIMA model is shown in Figure 3. ARIMA models are flexible and adaptive since they can forecast data values of a time series by a linear combination of its past values, and past errors (in terms of univariate analysis). Taking into account the seasonality of the time series, a seasonal ARIMA model denoted as ARIMA (p,d,q) (P,D,Q)_L is introduced, where P represents seasonal autoregressive orders, D indicates seasonal differencing orders, Q represents seasonal moving average orders, and L indicates the number of seasons. A seasonal ARIMA model can be shown in Equation (14).

$${\varnothing }_p\left(B\right){\phi }_P\left(B^L\right){\nabla }_L^D{\nabla }^d{y}_t=\mathsf{\delta }+{\theta }_q\left(B\right){\vartheta }_Q\left(B^L\right)a_t,$$

(14)

where

$${\varnothing }_p\left(B\right)=\left(1-{\varnothing }_{1}B-{\varnothing }_2{B}^2-\cdots -{\varnothing }_p{B}^p\right),$$

$${\phi }_P\left(B^L\right)=\left(1-{\phi }_{1,L}{B}^L-{\phi }_{2,L}{B}^{2L}-\cdots -{\phi }_{P,L}{B}^{PL}\right),$$

$${\nabla }_L^D{\nabla }^d{y}_t={\left(1-B^L\right)}^D{\left(1-B\right)}^d{y}_t\mathrm{z}$$

$${\theta }_q\left(B\right)=\left(1-{\theta }_{1}B-{\theta }_2{B}^2-\cdots -{\theta }_q{B}^q\right),$$

$${\vartheta }_Q\left(B^L\right)=\left(1-{\vartheta }_{1,L}{B}^L-{\vartheta }_{2,L}{B}^{2L}-\cdots -{\vartheta }_{Q,L}{B}^{PL}\right),$$

where $B$ is the backshift operator; L is the number of seasons in a year (L = 4 for quarterly data and L = 12 for monthly data); $\mathsf{\delta }$ is a constant term; $a_t, a_{t-1},\cdots$ are random shocks; ${\varnothing }_1, {\varnothing }_2,\cdots , {\varnothing }_p$ are non-seasonal autoregressive parameters; ${\phi }_{1,L}, {\phi }_{2,L},\cdots ,{\phi }_{P,L}$ are seasonal autoregressive parameters; ${\theta }_1, {\theta }_2,\cdots ,{\theta }_q$ are non-seasonal moving average parameters, ${\vartheta }_{1,L}, {\vartheta }_{2,L},\cdots , {\vartheta }_{Q,L}$ are seasonal moving average parameters.

Classical ARIMA models are usually used to describe the stationary time series. The sample auto-correlation function (SAC) can be used to determine whether the time series is stationary. For example, if the SAC of a time series values either dies down quickly or cuts off quickly at both seasonal lags and non-seasonal lags, then the time series can be considered as stationary. If the SAC of the time series values dies down extremely slowly either at seasonal lags or non-seasonal lags, it is reasonable to decide that the time series is non-stationary. In order to obtain a stationary time series, the transformation of the time series to the stationary should be undertaken. The differences of the time series values are shown in Equation (15).

$$z_t=\left(y_t-y_{t-1}\right)-\left(y_{t-L}-y_{t-L-1}\right)=y_t-y_{t-1}-y_{t-L}+y_{t-L-1},$$

(15)

where L indicate the number of seasons in a year (L = 4 for quarterly data and L = 12 for monthly data). The parameters of the ARIMA model are usually estimated by the least square method. The obtained models should be checked for whether the ARIMA assumptions are satisfied. As a more accurate test, the Ljung-Box test is usually undertaken to examine whether the autocorrelation of the residuals is statistically different from an expected white noise process. If the p-value is greater than 0.05, indicating no significant autocorrelation in residuals, in turn, the model is adequate [79].

3.5. Error Measure for Model Comparison

Although a model may well fit the historical data, it is not valid to determine that the model has a good forecasting performance. The forecasting performance of a model can only be determined by the accuracy of the out-of-sample forecasts [80]. The accuracy of the forecasts was evaluated by the mean absolute percentage error (MAPE) between the actual and predicted values of the building cost. The lower the values are, the better the forecasting performance of the proposed model.

The most widely used criterion for forecasting models is accuracy, which has many forms, including the root mean square error (RMSE) [81], mean absolute error (MAE) [82], and mean absolute percentage error (MAPE) [83]. This study evaluated the accuracy of the forecasts by the mean absolute percentage error (MAPE) between the actual and predicted values of the building cost. The lower the values are, the better the forecasting performance of the proposed model. Denote the real observations for the time series by (y_i) and the forecasting values for the same series by (${\widehat{y}}_i$). The mean absolute percentage error (MAPE) can be computed in Equation (16).

$$\mathrm{MAPE}=\frac{{{\displaystyle \sum }}_{i=1}^n\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|}{n}\times 100\%,$$

(16)

3.6. Multilayer Artificial Neutral Networks

The multilayer perceptron artificial neutral network (MLP ANN) technique has been widely used in forecasting models [84] and typically includes an input layer, an intermediate layer (hidden layer), and an output layer. The intermediate layer employs a number of neurons to optimize ANN models. All the neurons in ANNs are arranged in a layer-structure and neurons in different layers are interconnected according to the designed architecture. An architecture of the ANN model is shown in Figure 4. The ANN model is expressed as shown in Equation (17).

$$y_j=f\left({{\displaystyle \sum }}_{i=1}^m{w}_{ij}{x}_i+b_j\right),$$

(17)

The output $y_j$ is used as an input signal in the next layer, $w_{ij}$ is the weight of the connection between the i-th and j-th elements, and $b_j$ is the bias.

A training process based on the historical data is performed to decide the architecture of the networks and the weights and bias of the ANN model. During the training process, the ANN model learns the relationship between input and output variables and captures important information.

3.7. t-Test

The t-test is a statistical method that is also referred to as the Student’s t-test. The t-test includes a one-sample t-test, two independent samples t-test, and paired sample t-test [85]. Unlike some statistical methods that heavily rely on sample size for their effectiveness, the t-test can be used with small sample sizes (such as n < 30) [86]. The t-test can be used to test the difference between one sample and a set mean value (one sample t-test). The t-test can also be used to compare the difference between the mean of two samples (two sample t-test). Additionally, it can be used to test the mean difference between paired samples before and after the experiment (paired sample t-test). In this study, the paired sample t-test was used. To calculate the t-value, Equation (18) was used, as follows.

$$t=\frac{\left({{\displaystyle \sum }}_{i=1}^{n}D\right)/N}{\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{D}^2-{\left({{\displaystyle \sum }}_{i=1}^{n}D\right)}^2/n}{\left(N-1\right)N}}},$$

(18)

where D is the difference between sample x and y and n is the sample size.

Then, the t-value can be calculated. Next, the t-critical value is calculated based on the sample size n. If the t-value is smaller than the t-critical value (p > 0.05), there is no significant difference between the two samples. If the t-value is greater than the t-critical value (p < 0.05), there is a significant difference between the two samples.

4. Data Analysis

4.1. Correlation Analysis Results

The correlation analysis was performed to examine whether there is a significant correlation between household energy use and residential building costs, which indicated the reliability of using residential building costs as an indicator of the future trend of household energy use. Based on the correlation coefficient, the results of the correlation analysis show a significant correlation between the two variables. The significance level of the variables is validated by two-tailed significant correlation values at the 0.05 level.

The correlation analysis was conducted using the statistical software program SPSS (Statistical Packages for the Social Sciences, versions 23). Results of the analysis indicated that residential building costs positively correlate with household energy use. This significant correlation supports the research hypothesis. Therefore, there is a significant correlation between the energy use and residential building costs. The researcher predicts the correlation between residential building costs and household energy use. The results of the correlation analysis are essential for understanding the effectiveness of residential building costs to serve as an indicator of future trends of household energy use.

The results of the correlation analysis between household energy use variables and residential building cost are shown in

Table 1. Correlation analysis results.

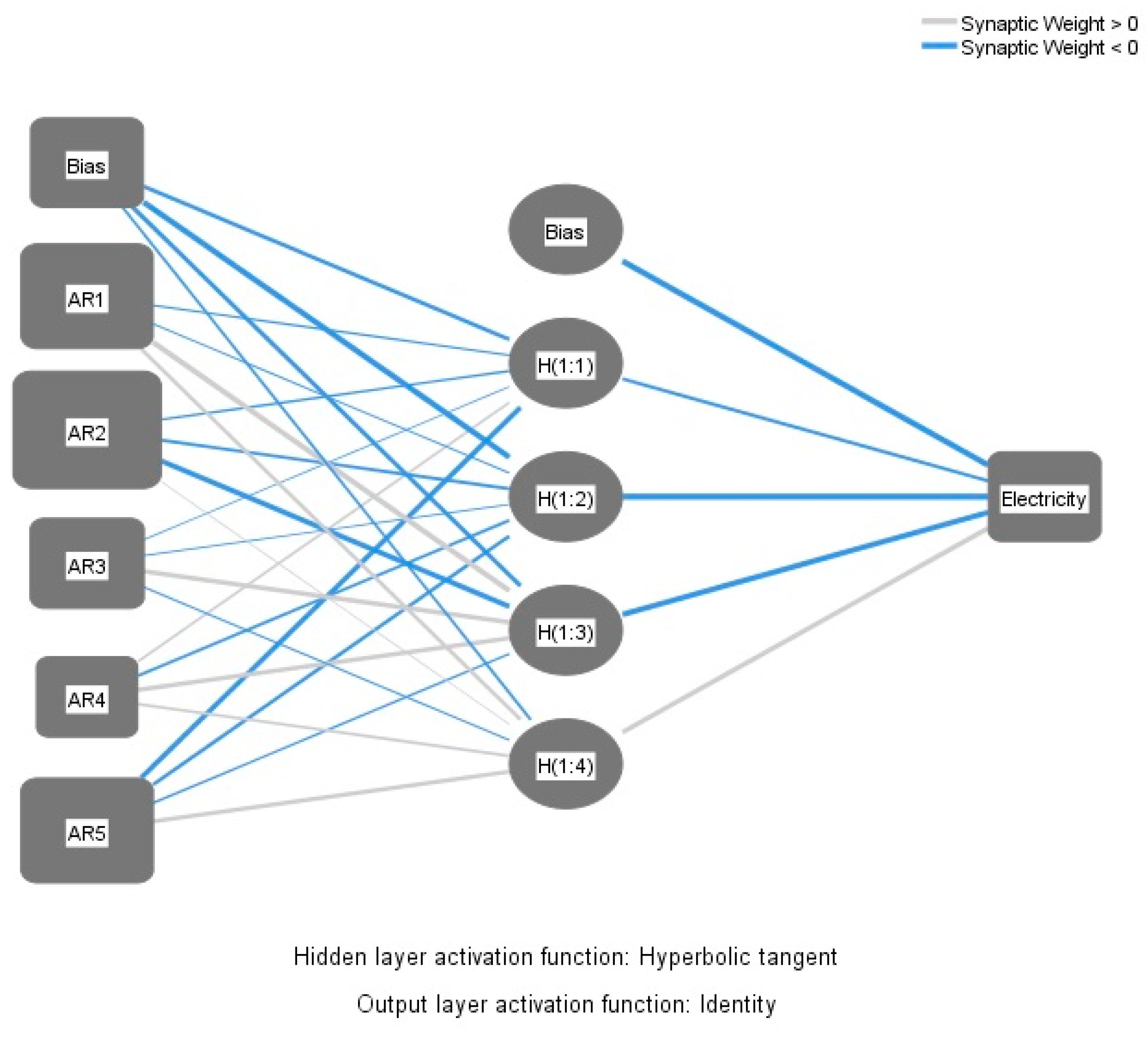
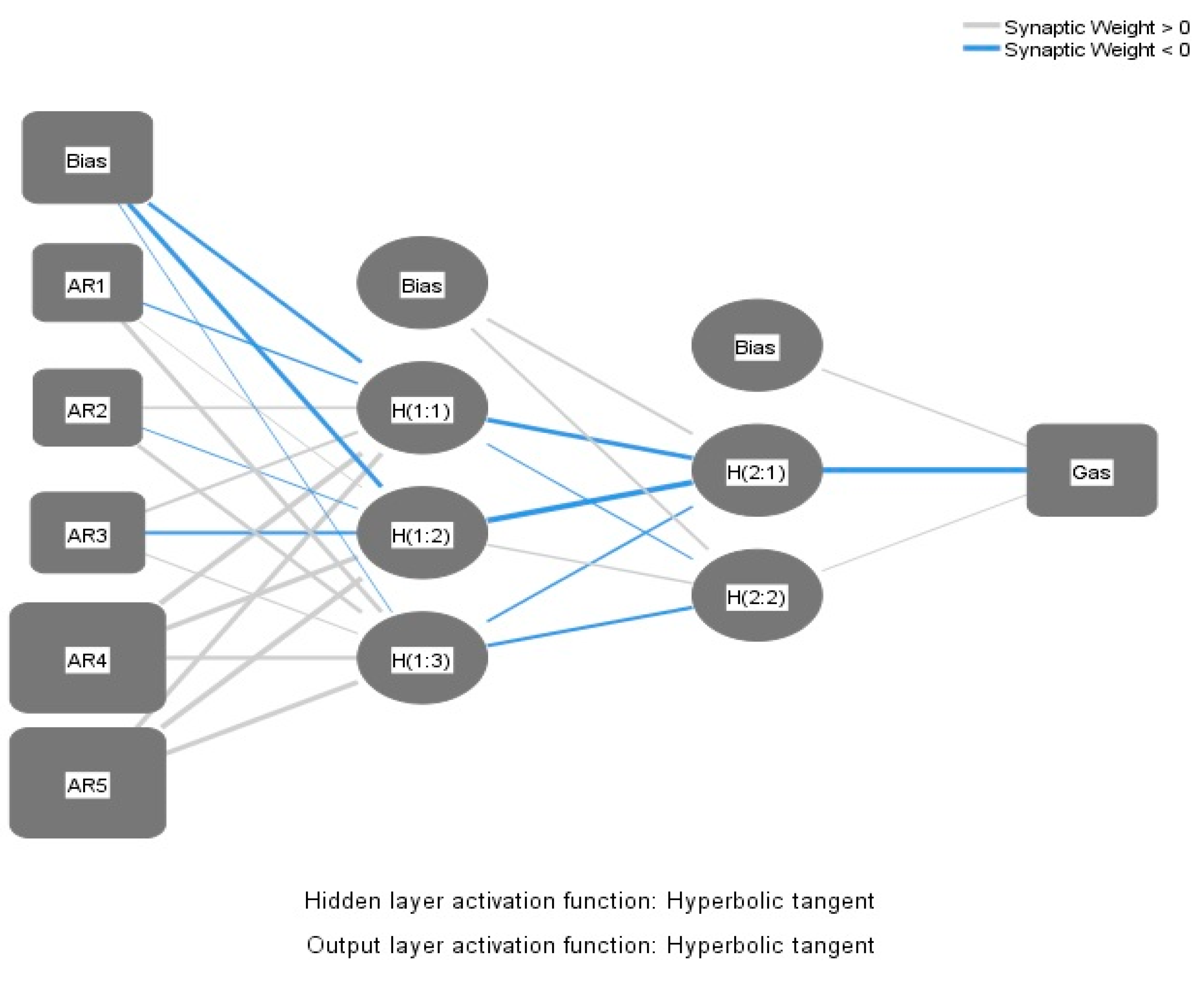
Residential Building Cost
Energies	AR1	AR2	AR3	AR4	AR5
Electricity	0.974 **	0.977 **	0.984 **	0.782 **	0.833 **
Gas	0.976 **	0.994 **	0.968 **	0.966 **	0.898 **
Petrol	0.919 **	0.916 **	0.937 **	0.884 **	0.640 **

** indicate significance at 0.05 level.

, which shows that all household energy use variables are positively correlated with residential building costs. The highest correlation coefficient was obtained from the correlation between the household gas use and residential building cost of a two-storey house (AR2), with a significant value of r = 0.994. A weakest correlation was observed between household petrol use and residential building cost of retirement village (AR5), with a coefficient of r = 0.640. Despite having a relative weak correlation, all the household energy use variables correlate with the residential building cost at a significant level.

4.2. Exponential Models for Building Cost

Both additive Holt-Winters and multiplicative Holt-Winters models were applied to the five-cost series. Following the methods outlined in [75], the model parameters were estimated. The results of the exponential smoothing models for the cost of the five categories of the residential building are displayed in

Table 2. Estimated parameter values with significant test for exponential smoothing models.

Series	Exponential Smoothing Model	Parameter	Estimate	SE	p-Value
		α	0.370	0.116	0.002
	ES(AHW)	β	0.634	0.287	0.032 **
AR1		γ	0	0.112	0.993
		α	0.379	0.112	0.001 **
	ES(MHW)	β	0.537	0.251	0.037 **
		γ	0.528	0.171	0.003 **
		α	0.899	0.150	***
	ES(AHW)	β	0	0.047	1
AR2		γ	0	0.696	1
		α	0.846	0.145	***
	ES(MHW)	β	0.001	0.045	0.983
		γ	0.028	0.298	0.925
		α	0.683	0.135	***
	ES(AHW)	β	0.218	0.113	0.059 *
AR3		γ	0.001	0.171	0.995
		α	0.578	0.128	***
	ES(MHW)	β	0.269	0.128	0.042 **
		γ	0.020	0.091	0.830
		α	0.200	0.079	0.014 **
	ES(AHW)	β	1.000	0.467	0.037 **
AR4		γ	0	0.091	1
		α	0.198	0.083	0.021 **
	ES(MHW)	β	1.000	0.503	0.052 *
		γ	0.040	0.062	0.524
		α	0.469	0.118	***
	ES(AHW)	β	0.441	0.194	0.027 **
AR5		γ	0.014	0.096	0.883
		α	0.361	0.096	***
	ES(MHW)	β	0.511	0.225	0.028 **
		γ	0.479	0.151	0.003 **

* indicate significance at 0.1 level, ** indicate significance at 0.05 level, *** indicate significance at 0.01 level.

. The p-value of the model parameters indicate that they are effective. Moreover, the model fit R-square and error measures including the root mean square error (RMSE), mean absolute percentage error (MAPE), and mean absolute error (MAE) were also generated. In addition, the model parsimony measure Bayesian Information Criterion (BIC) was also obtained. The residual tests including Ljung-Box Q test and Shapiro-Wilk test were carried out. The results are shown in

Table 3. Model fit statistics and residual statistics for exponential models.

Series	Model	R-Square	RMSE	MAPE	MAE	BIC	Ljung-Box	Shapiro-Wilk
AR1	ES(AHW)	0.976	33.205	1.655	24.52	7.233	0.238	0.203
	ES(MHW)	0.974	34.311	1.581	23.722	7.299	0.805	0.102
AR2	ES(AHW)	0.947	62.506	2.066	35.292	8.498	0.891	0.153
	ES(MHW)	0.943	64.989	2.159	37.134	8.576	0.904	0.133
AR3	ES(AHW)	0.964	52.405	1.953	36.27	8.146	0.13	0.103
	ES(MHW)	0.959	55.473	2.054	38.568	8.26	0.106	0.173
AR4	ES(AHW)	0.989	45.577	1.32	31.825	7.867	0.593	0.127
	ES(MHW)	0.988	47.836	1.385	34.24	7.964	0.333	0.104
AR5	ES(AHW)	0.991	36.083	1.312	27.824	7.4	0.477	0.393
	ES(MHW)	0.989	39.374	1.356	28.715	7.574	0.415	0.647

. They all indicate that the Holt-Winters models can fit the cost series fairly well because the models can identify the trend and seasonal variation.

4.3. Seasonal ARIMA Models

In this study, for each cost series, a total of 52 observations from 2001:Q1 to 2013:Q4 were used to obtain the proposed models. For the stationary analysis of the five cost series the autocorrelation function (ACF) and partial autocorrelation function (PACF) were used; results are shown in Figure 5. By investigating the graphs of ACF and PACF for the five building cost series; it can be observed that the ACFs decay very slowly at both non-seasonal and seasonal lags. For each cost series, the appropriate number of differencing should be determined. Hence, it is reasonable to transform to a stationary series by taking four quarter differencing of data to remove seasonality and regular differencing to remove trends for the four-cost series, except the cost series for the two-storey house in New Zealand. The cost series for the two-storey house has only made a regular differencing to transform the data into stationary. After the differencing, the results of ACFs and PACFs for the five cost series are shown in Figure 6. In order to select proper seasonal ARIMA models, different models with various combinations of regular orders (p and q) and seasonal orders (P and Q) were evaluated. The seasonal ARIMA models for the five-cost series are shown in

Table 4. Estimated parameter values for seasonal ARIMA models.

Series	Model	AR	MA	SAR	SMA
AR1	ARIMA(0,1,3)(0,1,1)4 ARIMA(0,1,1)(0,1,1)4		MA(l) = 0.34l MA(2) = −0.l0l MA(3) = −0.295 MA(l) = 0.3l7		SMA(l) = 0.447 SMA(l) = 0.290
AR2	ARIMA(0,1,0)(2,0,0)4 ARIMA(0,1,0)(0,0,2)4			SAR(1) = 0.038 SAR(2) = 0.348	SMA(l) = −0.005 SMA(2) = −0.368
AR3	ARIMA(0,1,0)(1,0,0)4 ARIMA(0,1,0)(0,1,0)4			SAR(l) = 0.562
AR4	ARIMA(1,1,0)(0,1,0)4 ARIMA(0,1,1)(0,1,0)4	AR(l) = −0.4l9	MA(l) = 0.404
AR5	ARIMA(0,1,0)(0,1,1)4 ARIMA(0,1,0)(0,1,0)4				SMA(l) = 0.554

4 means L = 4 in the ARIMA models.

. There are four seasons in a year, as L = 4 in the ARIMA models.

The Ljung-Box Q test was employed to examine the autocorrelation of model residuals. If the p-value is greater than the value of 0.05, the null hypothesis that the data are not correlated should be accepted [6]. To examine the normality of the residuals the analysis applied the Shapiro-Wilk test. If the p-value of the test is greater than the value of 0.05, it indicates that there is no evidence to reject the null hypothesis that the data follow a normal distribution [87]. As seen from

Table 5. Model fit statistics and residual statistics.

Series	Model	R-Square	RMSE	MAPE	MAE	BIC	Ljung-Box	Shapiro-Wilk
AR1	ARIMA(0,1,3)(0,1,1)4	0.959	37.234	1.716	25.866	7.644	0.873	0.461
	ARIMA(0,1,1)(0,1,1)4	0.953	38.665	1.856	27.895	7.556	0.519	0.158
AR2	ARIMA(0,1,0)(2,0,0)4	0.942	63.899	2.221	38.057	8.546	0.877	0.184
	ARIMA(0,1,0)(0,0,2)4	0.942	63.865	2.256	38.766	8.545	0.898	0.136
AR3	ARIMA(0,1,0)(0,1,0)4	0.944	54.277	1.913	35.836	8.07	0.855	0.153
	ARIMA(0,1,0)(4,1,0)4	0.95	53.423	1.823	33.945	8.366	0.956	0.122
AR4	ARIMA(1,1,0)(0,1,0)4	0.981	51.468	1.53	37.383	8.046	0.657	0.391
	ARIMA(0,1,1)(0,1,0)4	0.981	51.889	1.505	36.868	8.062	0.628	0.24
AR5	ARIMA(0,1,0)(0,1,1)4	0.986	40.162	1.325	27.306	7.55	0.489	0.127
	ARIMA(0,1,0)(0,1,0)4	0.983	43.299	1.52	31.335	7.618	0.141	0.103

4 means L = 4 in the ARIMA models.

, the residuals of all the models pass the tests, indicating that the proposed models are adequate. According to the estimation results, the model fit measures and error measures are acceptable. This suggests that the proposed models fit the data fairly well. The model fit parameters of exponential models are also shown in Table 5.

4.4. ANN Models

An adequate MLP ANN model with determined architecture, a number of hidden layers and neurons, and activation functions are obtained through a trial-and-error process, which is not a trivial effort [88]. This process aims to select a suitable number of hidden layers and neurons, an activation function, and a training algorithm to optimize the MLP ANN model. To select an optimal model in the trial-and-error process, a significant number of models are developed and examined. Three ANN models corresponding to the different types of household energy are provided in order to forecast household energy consumption. Optimal ANN models for three types of household energy consumption including electricity, gas, and petrol are shown in

Table 6. The final ANN model summary for electricity consumption in the residential sector.

Predictors		Parameter Estimates
		Hidden Layer 1				Output Layer
		H (1:1)	H (1:2)	H (1:3)	H (1:4)	Electricity
Input layer	AR1	−0.119	−0.094	1.067	0.304
	AR2	−0.151	−0.256	−0.930	0.019
	AR3	−0.039	−0.068	0.420	−0.118
	AR4	0.178	−0.219	0.414	0.245
	AR5	−0.511	−0.292	−0.132	0.409
	Bias	−0.339	−1.477	−0.409	−0.215
Hidden layer 1	H (1:1)					−0.291
	H (1:2)					−1.799
	H (1:3)					−1.209
	H (1:4)					0.458
	Bias					−1.612
Model training		SSE = 4.117
Model testing		SSE = 1.359
t-value		t = −0.841
p-value		p = 0.403

,

Table 7. The final ANN model summary for gas consumption in the residential sector.

Predictors		Parameter Estimates
		Hidden Layer 1			Hidden Layer 2		Output Layer
		H (1:1)	H (1:2)	H (1:3)	H (2:1)	H (2:2)	Gas
Input layer	AR1	−0.266	0.101	0.417
	AR2	0.301	−0.130	0.397
	AR3	0.339	−0.372	0.211
	AR4	0.662	0.626	0.406
	AR5	0.504	0.732	0.548
	Bias	−0.394	−0.456	−0.029
Hidden layer 1	H (1:1)				−0.476	−0.196
	H (1:2)				−0.916	0.282
	H (1:3)				−0.284	−0.384
	Bias				0.332	0.301
Hidden layer 2	H (2:1)						−0.852
	H (2:2)						0.135
	Bias						0.230
Model training		SSE = 2.437
Model testing		SSE = 0.831
t-value		t = −0.491
p-value		p = 0.625

and

Table 8. The final ANN model summary for petrol consumption in the residential sector.

Predictors		Parameter Estimates
		Hidden Layer 1			Output Layer
		H (1:1)	H (1:2)	H (1:3)	Petrol
Input layer	AR1	0.205	−1.019	−0.673
	AR2	0.091	0.756	−0.086
	AR3	0.085	−0.557	0.219
	AR4	0.354	−0.757	−0.773
	AR5	0.018	−0.636	−0.441
	Bias	−0.069	1.759	1.757
Hidden layer 1	H (1:1)				−0.287
	H (1:2)				−1.593
	H (1:3)				−0.338
	Bias				1.015
Model training		SSE = 1.644
Model testing		SSE = 0.422
t-value		t = 0.917
p-value		p = 0.362

, respectively. Following the training process, an ANN model for household electricity consumption containing one hidden layer and four neurons was developed, as shown in Figure 7. The ANN model for household gas consumption includes two hidden layers with three neurons in the first hidden layer and two neurons in the second hidden layer, as shown in Figure 8. An ANN model for household petrol consumption includes one hidden layer and three neurons, as shown in Figure 9. Then, the ANN models were used to generate forecasts of the household energy usage.

5. Results Discussion

The correlation analysis was performed to test the correlation between residential energy use and residential building costs. These results demonstrate that significant correlations exist between the household energy use (electricity, gas, petrol) and residential building cost. The significant positive correlations between residential building costs and household energy use indicate that an increase in residential building costs can increase household energy usage.

The forecasting performance of the cost forecasting methods was evaluated by MAPE statistics. The MAPE of the proposed models for all the five cost series are presented in

Table 9. Forecast values for building cost of one-storey house in New Zealand.

Series	Model	MAPE
AR1	ARIMA(0,1,3)(0,1,1)4	1.813
	ARIMA(0,1,1)(0,1,1)4	1.651
	ES(AHW)	1.260
	ES(MHW)	1.556
AR2	ARIMA(0,1,0)(2,0,0)4	0.922
	ARIMA(0,1,0)(0,0,2)4	0.794
	ES(AHW)	0.395
	ES(MHW)	0.650
AR3	ARIMA(0,1,0)(0,1,0)4	1.020
	ARIMA(0,1,0)(4,1,0)4	2.318
	ES(AHW)	1.211
	ES(MHW)	1.130
AR4	ARIMA(1,1,0)(0,1,0)4	0.501
	ARIMA(0,1,1)(0,1,0)4	0.446
	ES(AHW)	0.748
	ES(MHW)	0.809
AR5	ARIMA(0,1,0)(0,1,1)4	0.853
	ARIMA(0,1,0)(0,1,0)4	1.213
	ES(AHW)	0.917
	ES(MHW)	0.949

Bold numbers are smallest among the models for AR1-AR5.

. Bold type is utilized in these tables to identify the lowest values of MAPE for each proposed model. As the results show, no single forecasting method is better for all data series. In fact, for all the five-cost series of residential buildings in New Zealand to which statistical approaches were applied, the exponential smoothing models displayed excellent performance for forecasting building costs of a one-storey house and a two-storey house. Seasonal ARIMA models produced more accurate forecasts for the cost series of a townhouse, apartment, and retirement village building. The exponential smoothing (ES) approach and ARIMA technique are both effective time series forecasting methods as they both can fairly well describe trend movement in the time series, but they have both strengths and weaknesses. For example, the ARIMA approach is more readily expanded to model interventions, outliers, variations and variance changes in the time series; but it is a relatively sophisticated technique. Due to different data patterns and limited sample size, it is unjust to attempt to determine whether one time series forecasting method is better than the other. Therefore, either the exponential smoothing method or the ARIMA approach should be given a chance to demonstrate its maximum potential in any empirical case study.

ANN models for three types of household energy, including electricity, gas, and petrol, are developed. The forecasts generated by the ANN models were compared with the actual values of household energy consumption. The paired sample t-test was used to compare the mean difference between the forecasts with the actual values. The t-test was performed using SPSS. The obtained t-values are all smaller than the t-critical value (t-critical = 1.994, n = 72, p > 0.05), which indicates that no significant difference exists between the forecasts and actual values. The t-values and p-values for three ANN models are shown in Table 6, Table 7 and Table 8, respectively. The proposed ANN models for the household energy consumption are acceptable. The results indicate that the residential building cost is a good indicator that can be used in household energy management. Moreover, the ANNs model is an effective method for forecasting household energy consumption using the residential building costs. Additionally, the explored relationship between the residential building cost and household energy consumption provides a new way for better energy management.

6. Conclusions

Several methods have been used to predict future household energy use, but most of them are based on factors such as thermal envelope or HVAC systems. However, in this study, the residential building cost was used as an indicator of future trends of household energy use. In this study, quarterly household energy consumption data (electricity, gas and petroleum) and quarterly building costs data for five categories of residential building (one-storey house, two-storey house, town house, apartment, and retirement village) over an 18-year range 2001:Q1–2018:Q4 in New Zealand, were analyzed.

The correlation analysis showed a significant positive correlation between household energy usage and residential building cost. Moreover, based on the identified characteristics, the two time series forecasting techniques, exponential smoothing method and ARIMA approach, were adopted to take into account variations of residential building costs in predicting their future trends. It was concluded that both methods can produce proper forecasts. In addition, the ANN method was used to forecast future household energy use by using residential building costs as influencing factors. The ANN models generated acceptable forecasts of three different types of household energy usage (electricity, gas, and petrol).

This result not only explores the strong link between the residential building cost and household energy consumption but also establishes the relationship between the residential building sector and the energy sector. Moreover, the decision makers can easily obtain future energy consumption in the residential sector without evaluating every component of different types of buildings. The decision maker can obtain the future household energy consumption based on residential building costs, which facilitate the decision-making process and improve energy management performance and provide a new perspective for energy management. Although this study used the QV’s residential building cost index and energy variables of Statistics New Zealand, the proposed methods can be used for similar data sets in other cities as well as globally.