Determining the Optimized Hub Height of Wind Turbine Using the Wind Resource Map of South Korea
Abstract
1. Introduction
2. Data and Methods
- (1)
- Step to prepare wind profile data
- (a)
- The time-series wind profile data are fetched from the grid points in the wind resource map.
- (2)
- Steps to calculate OHH
- (a)
- AEPs are calculated by increasing HH from 40 m to 100 m with 10 m increments.
- (b)
- The COE curve is produced through regression analysis with the calculated AEPs and cost data.
- (c)
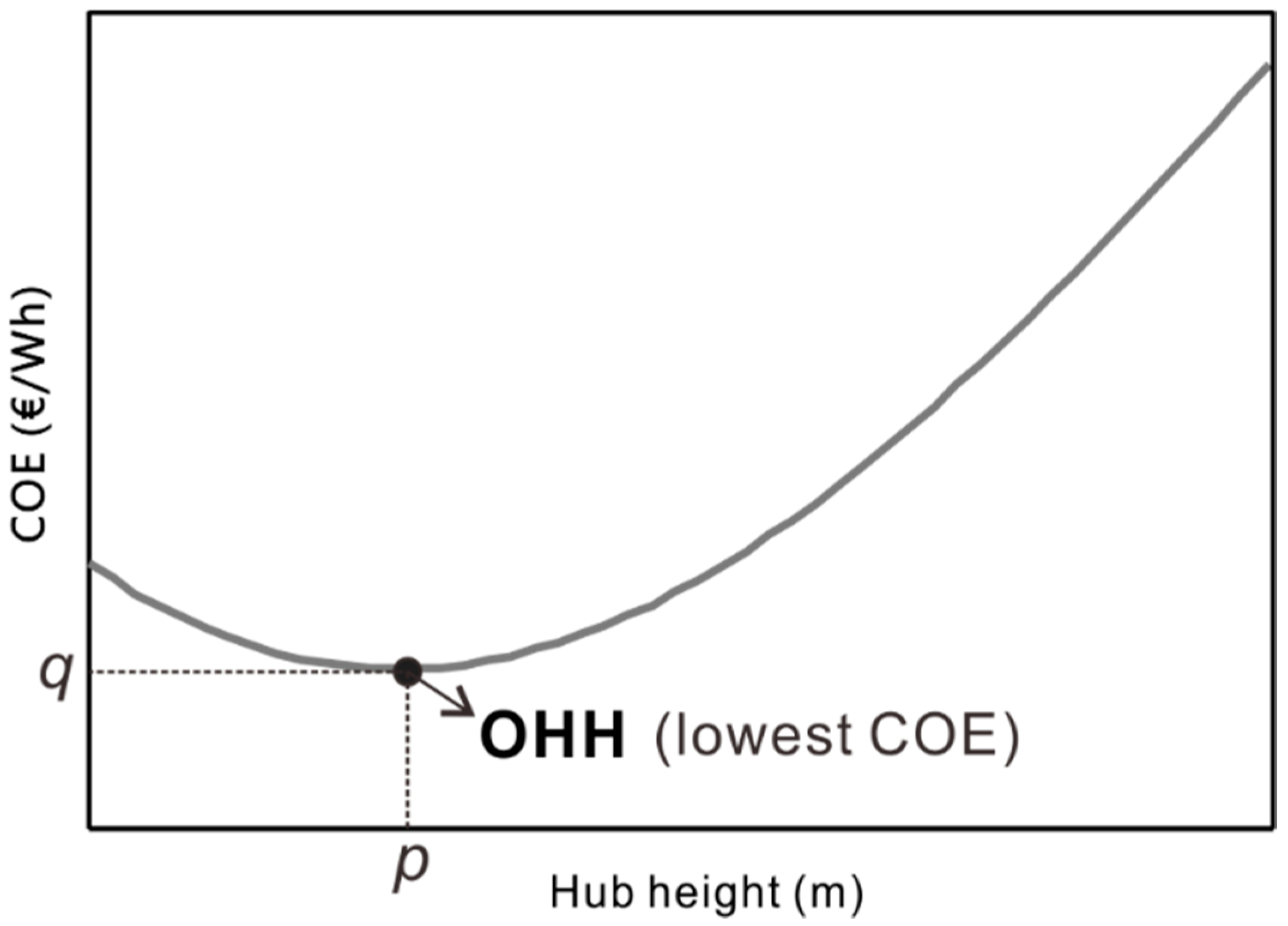
- OHH is searched when the COE curve is minimum using a numerical analysis method.
- (3)
- Steps to calculate RD
- (a)
- The AEP loss is calculated when GHH is changed to OHH.
- (b)
- The AEP increase is calculated by raising RD to 70 m, 80 m, 90 m, and 97 m.
- (c)
- The RD that can compensate for the AEP loss due to OHH is determined.
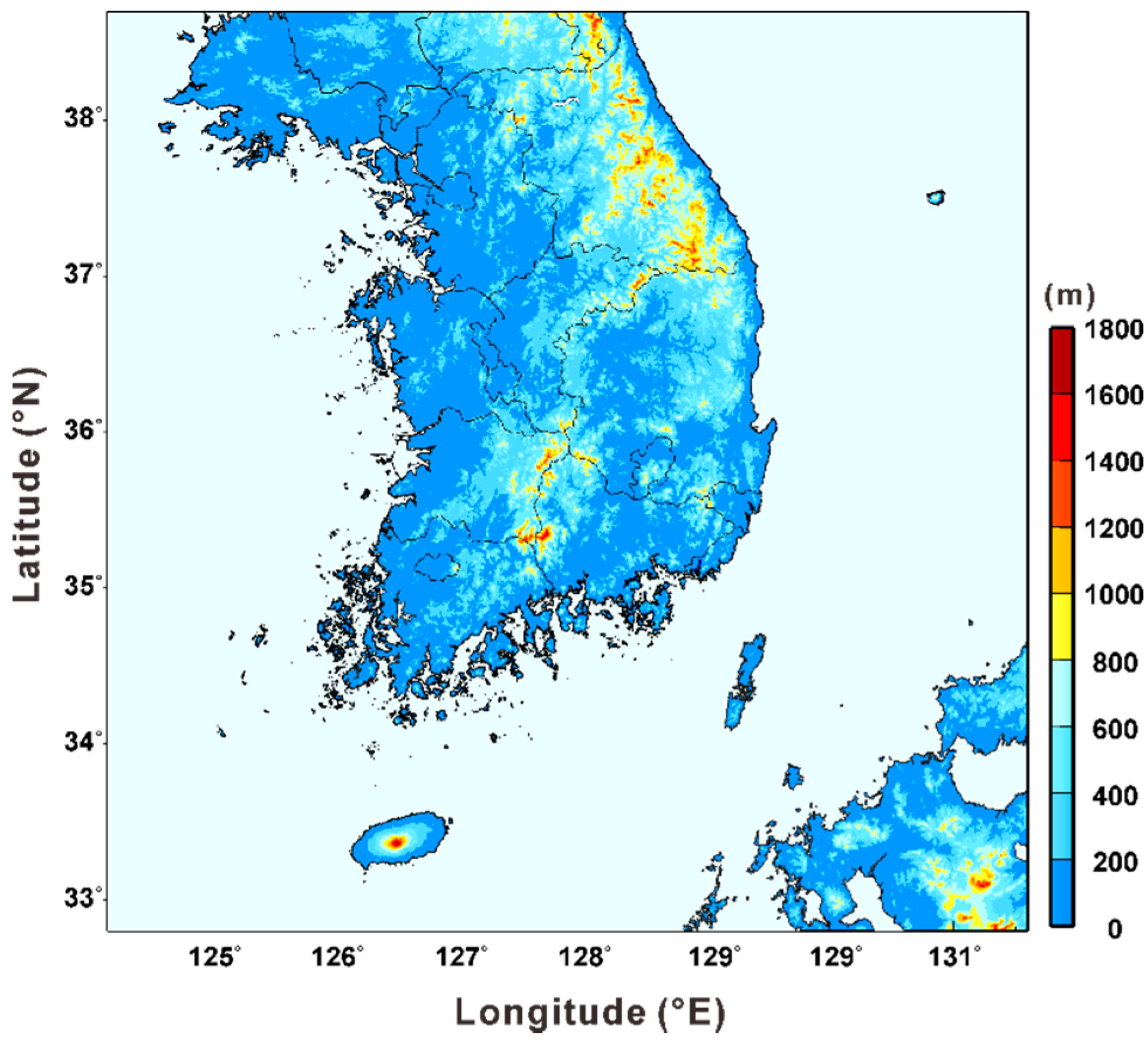
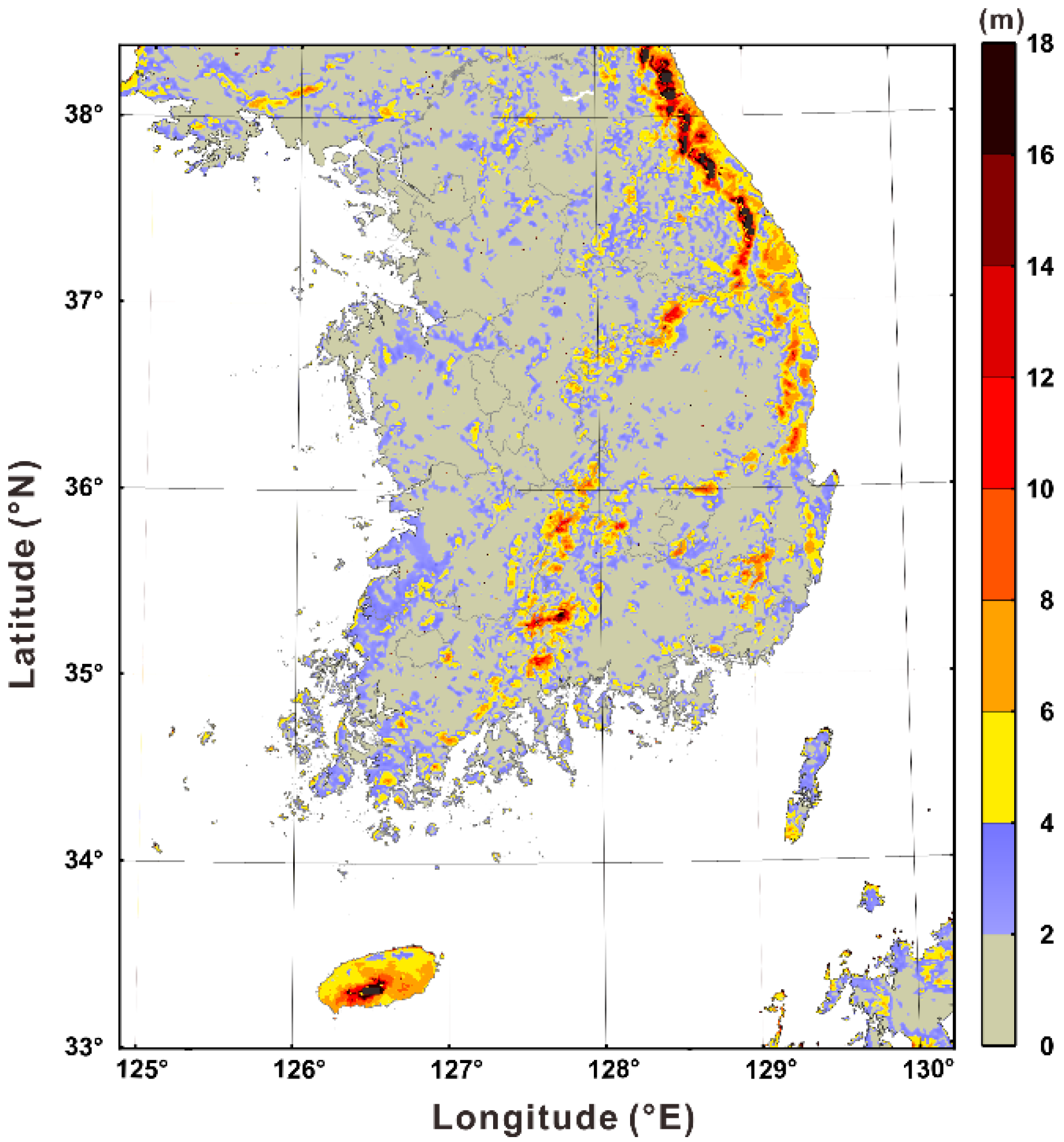
2.1. Wind Resource Map
2.2. COE Curve as a Function of HH
2.3. Calculation of RD to Compensate for AEP
2.4. Cost of Tower and Rotor
3. Results
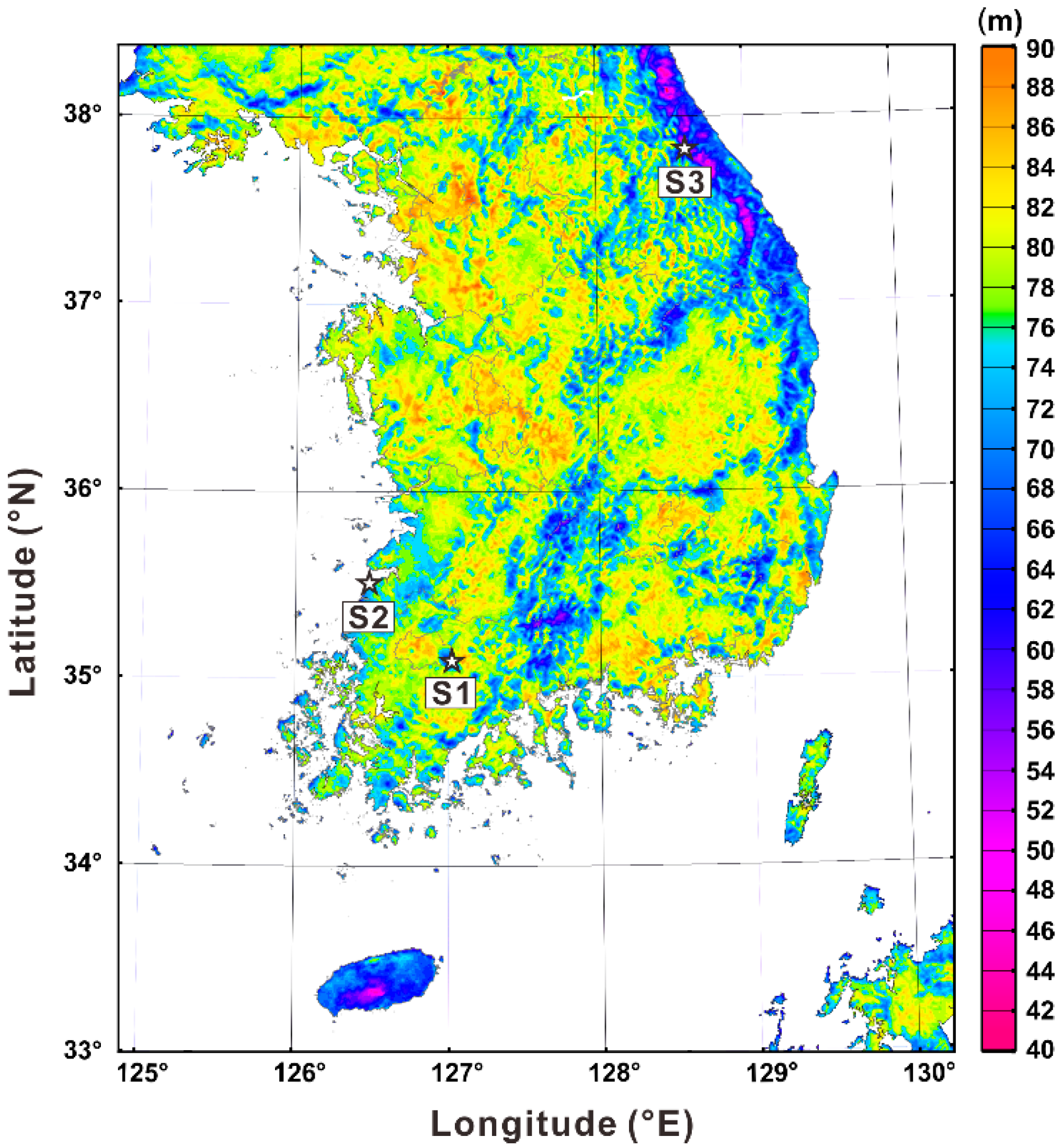
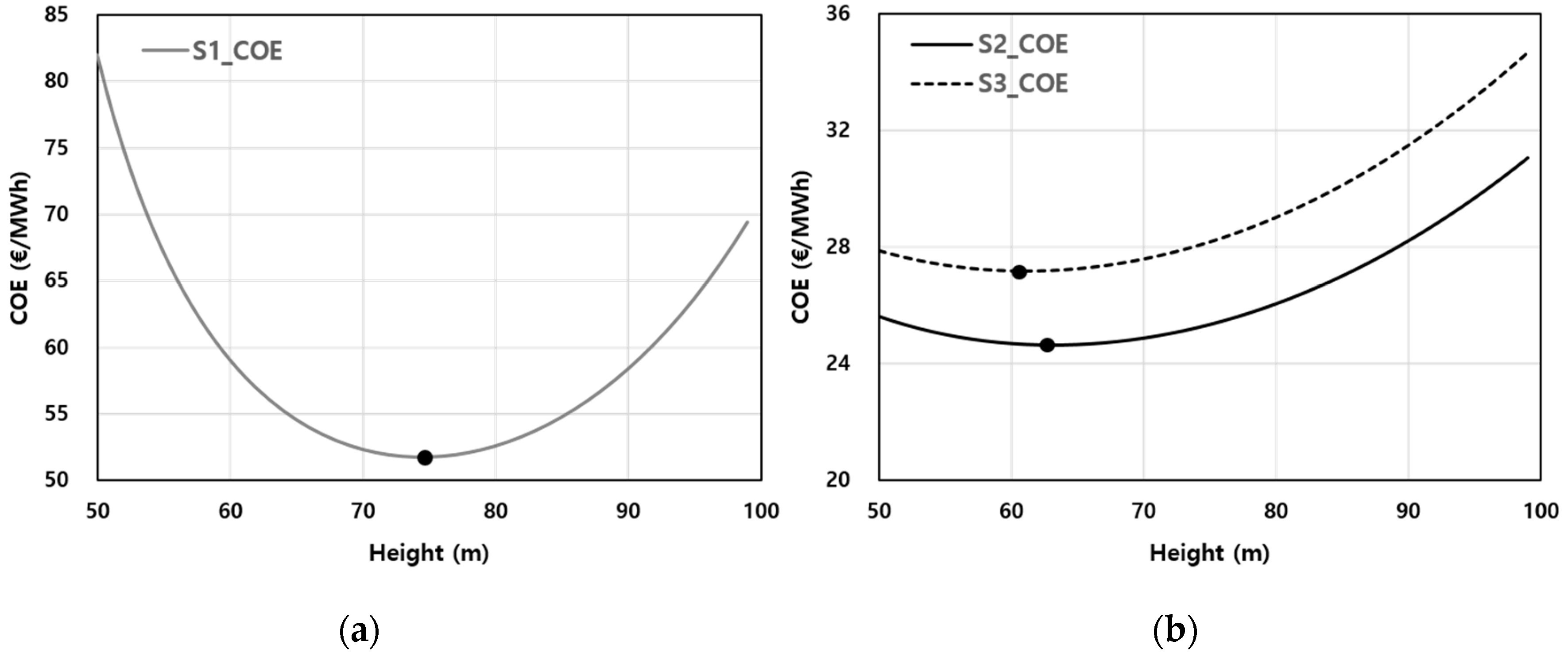
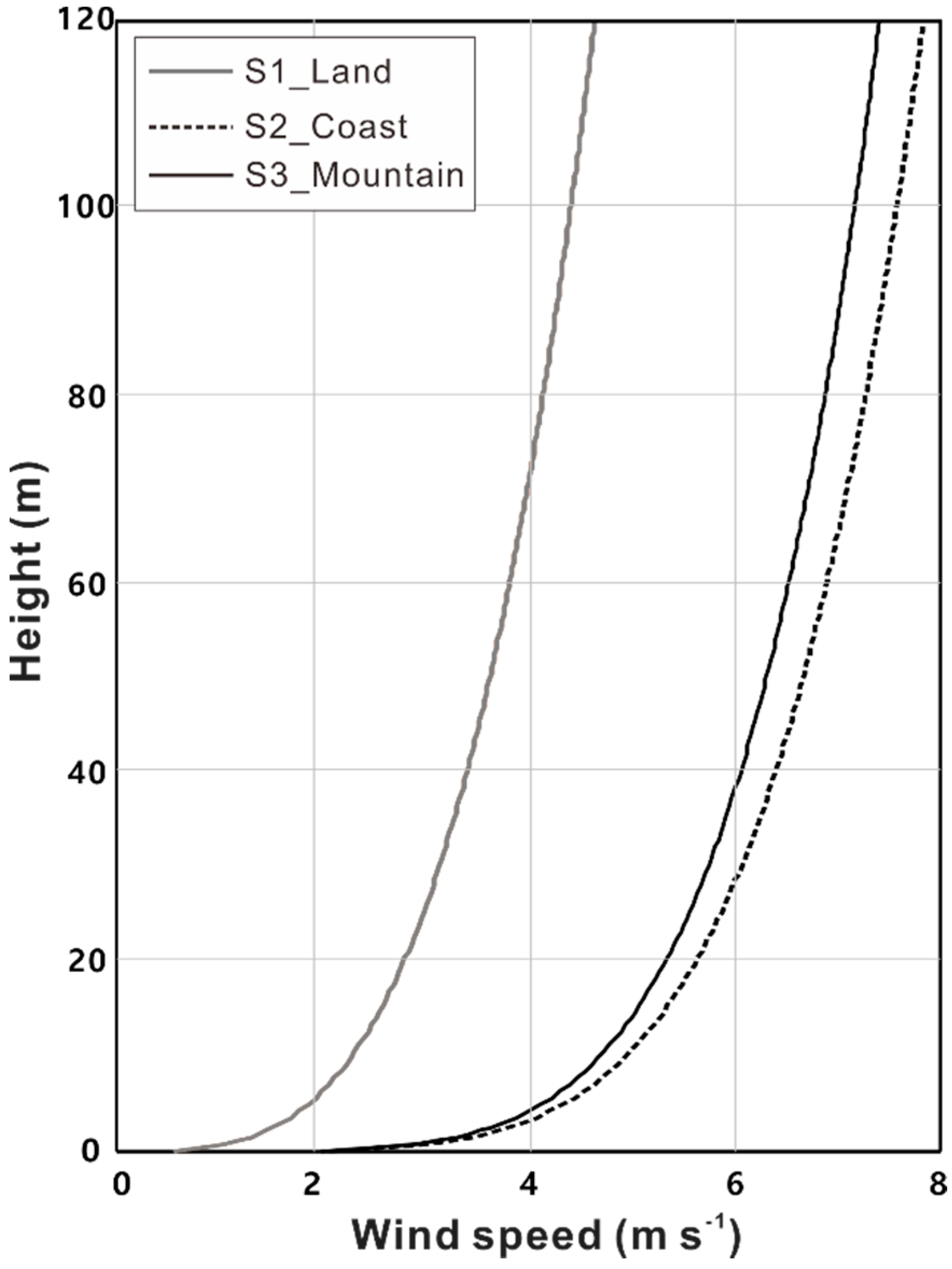
3.1. Regional Characteristics of OHH
3.2. Calculation of RD to Compensate for AEP
3.3. Discussions
4. Conclusions
- (1)
- The inland plain site in South Korea exhibited minimum COE at a height of 74 m, which was similar to GHH. Note, however, that regions with relatively high wind speed, such as onshore or mountain sites, had OHHs of 63 m and 61 m or 17 m and 19 m lower, respectively, than that of the inland site. The economic feasibility of wind farms is expected to improve by minimizing COE in the future if OHH is selected according to the wind profile characteristics.
- (2)
- Unlike the study results of Lee et al. [5], the OHH calculation algorithm in this study presented a lower OHH than GHH in most sites except inland plain sites. OHH is determined according to the regional wind profile characteristics and is characterized to be higher than GHH if the wind resource is not sufficient in the lower layer of HH.
- (3)
- This study also verified the reduction in COE when RD increased to compensate for the AEP loss due to OHH. COE was reduced if RD increased in the entire area of South Korea. This was because the increase in AEP was larger than the increase in TIC, owing to the increase in RD.
- (4)
- This study was limited to onshore wind turbines. This was because the TIC of offshore wind turbines varied much more than that of onshore wind turbines, and the relevant database was not yet available. If the TIC database for offshore wind turbines is developed in the future, the OHH that can minimize COE even offshore will be calculated. Based on the results in this study, the offshore OHH is expected to be much lower than GHH.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AEP | annual energy production |
| ASOS | automated surface observing system |
| AWS | automatic weather station |
| CAPEX | capital expenditure |
| COE | cost of energy |
| GHH | general hub height |
| HH | hub height |
| KMA | Korea Meteorological Administration |
| LC | labor cost |
| MC | material cost |
| OHH | optimal hub height |
| OPEX | operation expenditure |
| RD | rotor diameter |
| RDAPS | regional data assimilation and prediction system |
| REWS | rotor equivalent wind speed |
| RPM | revolutions per minute |
| SBL | surface boundary layer |
| TIC | total investment cost |
| WRF | weather research and forecasting |
| WT | wind turbine |
References
- Turbines, W. Part 1: Design Requirements, IEC 61400-1; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Letcher, T.M. Wind Energy Engineering: A Handbook for Onshore and Offshore Wind Turbines; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Marmidis, G.; Lazarou, S.; Pyrgioti, E. Optimal placement of wind turbines in a wind park using Monte Carlo simulation. Renew. Energy 2008, 33, 1455–1460. [Google Scholar] [CrossRef]
- Emami, A.; Noghreh, P. New approach on optimization in placement of wind turbines within wind farm by genetic algorithms. Renew. Energy 2010, 35, 1559–1564. [Google Scholar] [CrossRef]
- Meyers, J.; Meneveau, C. Optimal turbine spacing in fully developed wind farm boundary layers. Wind Energy 2012, 15, 305–317. [Google Scholar] [CrossRef]
- Stevens, R.J. Dependence of optimal wind turbine spacing on wind farm length. Wind Energy 2016, 19, 651–663. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.R.; Lee, K.-S. Optimum hub height of a wind turbine for maximizing annual net profit. Energy Convers. Manag. 2015, 100, 90–96. [Google Scholar] [CrossRef]
- Rehman, S.; Al-Hadhrami, L.M.; Alam, M.M.; Meyer, J.P. Empirical correlation between hub height and local wind shear exponent for different sizes of wind turbines. Sustain. Energy Technol. Assess. 2013, 4, 45–51. [Google Scholar] [CrossRef]
- Maki, K.; Sbragio, R.; Vlahopoulos, N. System design of a wind turbine using a multi-level optimization approach. Renew. Energy 2012, 43, 101–110. [Google Scholar] [CrossRef]
- Mirghaed, M.R.; Roshandel, R. Site specific optimization of wind turbines energy cost: Iterative approach. Energy Convers. Manag. 2013, 73, 167–175. [Google Scholar] [CrossRef]
- Stanley, A.P.; Ning, A.; Dykes, K. Optimization of turbine design in wind farms with multiple hub heights, using exact analytic gradients and structural constraints. Wind Energy 2019, 22, 605–619. [Google Scholar] [CrossRef]
- Clack, C.T.; Alexander, A.; Choukulkar, A.; MacDonald, A.E. Demonstrating the effect of vertical and directional shear for resource mapping of wind power. Wind Energy 2016, 19, 1687–1697. [Google Scholar] [CrossRef]
- Janjić, Z.I. The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Dudhia, J.; Chen, S.H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Kim, H.-G.; Kang, Y.-H. The 2010 wind resource map of the Korean Peninsular. J. Wind Eng. Inst. Korea 2012, 16, 167–172. [Google Scholar]
- Kim, H.-G.; Kang, Y.-H.; Yun, C.-Y. Comparative Analysis on Commercial Wind Resource Maps of South Korea. J. Wind Eng. Ins. Korea 2015, 19, 9–14. [Google Scholar]
- Scheurich, F.; Enevoldsen, P.B.; Paulsen, H.N.; Dickow, K.K.; Fiedel, M.; Loeven, A.; Antoniou, I. Improving the accuracy of wind turbine power curve validation by the rotor equivalent wind speed concept. J. Phys. Conf. Ser. Ger. 2016, 753, 072029. [Google Scholar] [CrossRef]
- Wagner, R.; Cañadillas, B.; Clifton, A.; Feeney, S.; Nygaard, N.; Poodt, M.; St Martin, C.; Tüxen, E.; Wagenaar, J.W. Rotor equivalent wind speed for power curve measurement–comparative exercise for IEA Wind Annex 32. J. Phys. Conf. Ser. Den. 2014, 524, 012108. [Google Scholar] [CrossRef]
- Wagner, R.; Antoniou, I.; Pedersen, S.M.; Courtney, M.S.; Jørgensen, H.E. The influence of the wind speed profile on wind turbine performance measurements. Wind Energy 2019, 12, 348–362. [Google Scholar] [CrossRef]
- Fingersh, L.; Hand, M.; Laxson, A. Wind Turbine Design Cost and Scaling Model; No. NREL/TP-500-40566; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2006.
- Wiser, R.; Hand, M.; Seel, J.; Paulos, B. Reducing Wind Energy Costs through Increased Turbine Size: Is the Sky the Limit? Lawrence Berkeley Natl. Lab. 2016. [Google Scholar]



| Model | Advanced Research WRF (v3.7.1) |
|---|---|
| Period | 2010~2012 |
| Input data | Unified Model 12 km/WRF 3 km |
| Sea-surface temperature | OSTIA Sea Surface Temperature (SST) |
| Terrain | Shuttle Radar Topography Mission (3 arc-seconds) |
| Land cover | Ministry of Environment (South Korea) |
| Grid | 933 × 1332 (1 km × 1 km) |
| Vertical levels | 37 levels |
| Data assimilation | Four-Dimensional Data Assimilation (FDDA) |
| Surface physics | Mellor-Yamada-Janjic scheme (MYJ) |
| Cloud micro physics | WRF single moment 3-class ice scheme (WSM3) |
| Cumulus physics | No cumulus physics |
| Land surface | Noah-MP land surface model |
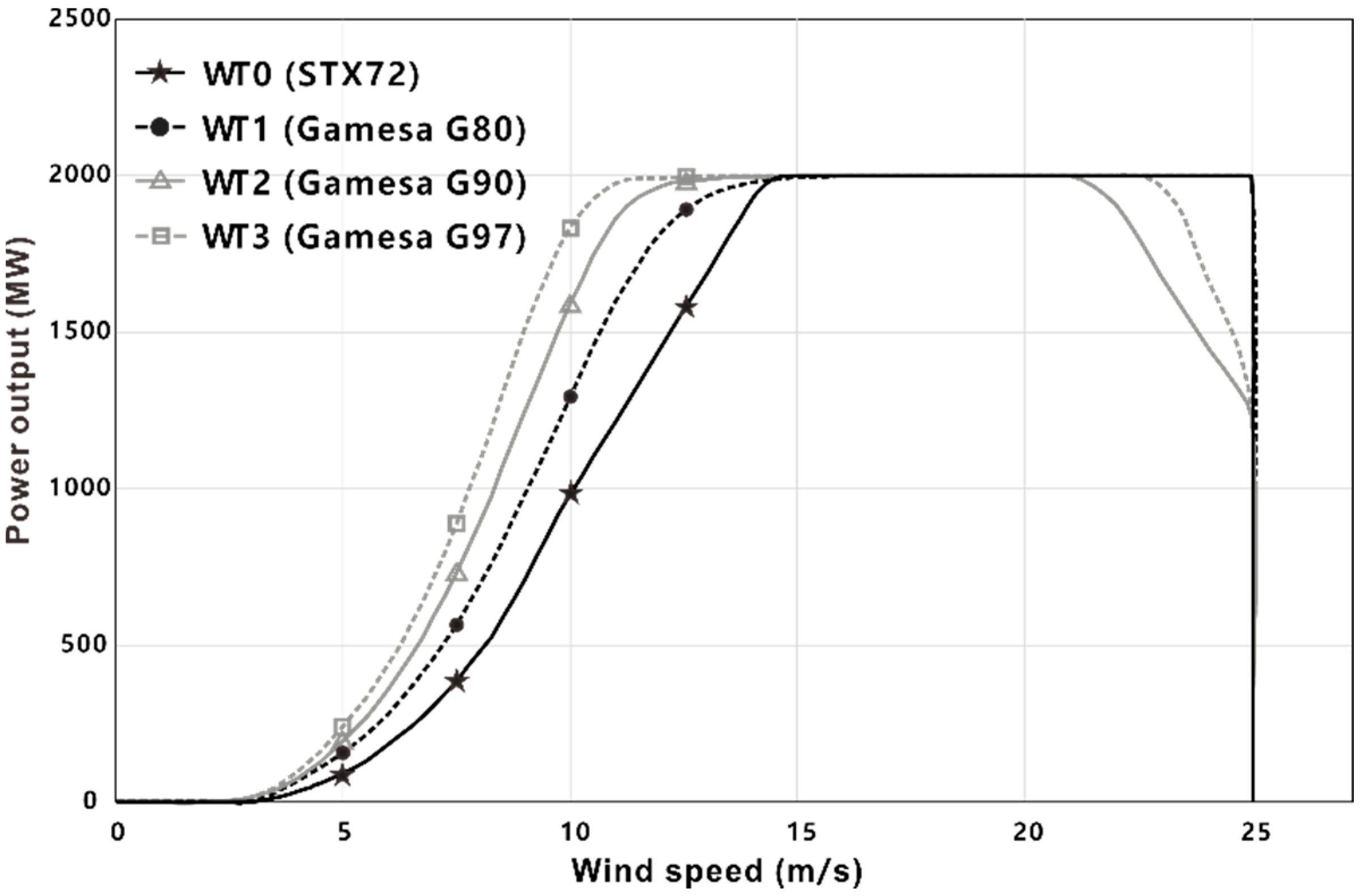
| Wind Turbine | Manufacturer | Rotor Diameter (m) |
|---|---|---|
| WT0 | STX (STX72-2.0MW) | 70.6 |
| WT1 | Gamesa (G80-2.0MW) | 80 |
| WT2 | Gamesa (G90-2.0MW) | 90 |
| WT3 | Gamesa (G97-2.0MW) | 97 |
| Hub Heights (m) | Total Capital and Installation Cost (€) |
|---|---|
| 40 | 900,000 |
| 50 | 954,000 |
| 60 | 1,020,780 |
| 70 | 1,112,650 |
| 80 | 1,235,000 |
| 90 | 1,395,500 |
| 100 | 1,618,900 |
| Rotor Diameter (m) | Material Cost (€) | Labor Cost (€) | Total Blade Cost (€) |
|---|---|---|---|
| 70 | 124,075 | 103,066 | 315,474 |
| 80 | 185,635 | 143,959 | 457,770 |
| 90 | 264,680 | 193,307 | 542,193 |
| 97 | 363,394 | 221,314 | 636,093 |
| Sites | S1 (Inland) | S2 (Onshore) | S3 (Mountain) |
|---|---|---|---|
| OHH (m) | 74 | 63 | 61 |
| COE (€ MWh−1) | 51.7 | 24.7 | 27.2 |
| Mean wind speed at GHH (m s−1) | 4.1 | 7.3 | 6.9 |
| Wind profile exponent | 0.33 | 0.12 | 0.15 |
| Sites | AEP Loss (MWh m−1) by OHH | AEP Gain (MWh m−1) by ∆RD | Increment of RD (m) |
|---|---|---|---|
| S1 | 17.2 | 39.3 | 2.1 |
| S2 | 24.7 | 77.9 | 5.8 |
| S3 | 29.5 | 91.6 | 6.6 |
| Site | COE with GHH (€ MWh−1) | COE with OHH (€ MWh−1) | COE with OHH + RD (€ MWh−1) |
|---|---|---|---|
| S1 | 66.5 | 65.9 | 63.9 |
| S2 | 26.1 | 24.7 | 22.9 |
| S3 | 29.1 | 27.2 | 25.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-T.; Kim, H.-G.; Kang, Y.-H.; Kim, J.-Y. Determining the Optimized Hub Height of Wind Turbine Using the Wind Resource Map of South Korea. Energies 2019, 12, 2949. https://doi.org/10.3390/en12152949
Lee J-T, Kim H-G, Kang Y-H, Kim J-Y. Determining the Optimized Hub Height of Wind Turbine Using the Wind Resource Map of South Korea. Energies. 2019; 12(15):2949. https://doi.org/10.3390/en12152949
Chicago/Turabian StyleLee, Jung-Tae, Hyun-Goo Kim, Yong-Heack Kang, and Jin-Young Kim. 2019. "Determining the Optimized Hub Height of Wind Turbine Using the Wind Resource Map of South Korea" Energies 12, no. 15: 2949. https://doi.org/10.3390/en12152949
APA StyleLee, J.-T., Kim, H.-G., Kang, Y.-H., & Kim, J.-Y. (2019). Determining the Optimized Hub Height of Wind Turbine Using the Wind Resource Map of South Korea. Energies, 12(15), 2949. https://doi.org/10.3390/en12152949







