Kinetics of Solid-Gas Reactions and Their Application to Carbonate Looping Systems
Abstract
:1. Introduction
2. Carbonate Looping Technologies
3. Kinetics of Solid-Gas Reactions
- Model-fitting methods, where expressions of f(α) and g(α) are approximated to defined linear or non-linear expressions dependent on α and the order of reaction n. These methods provide global values of Ea and A corresponding to kinetic mechanisms [3].
- Model-free methods assume that the dα/dt at a specific value of conversion is only a function of temperature [54] and do not fit experimental data to assumed reaction models [55]. The model-free methods often begin with Equation (12b), which is linearized to obtain Ea. This method, however, cannot obtain independent values of A without making assumptions about f(α). A posteriori application of a model fitting method of f(α) can be applied to obtain A [3].
- Generalized kinetic models allow for the reaction to consist of a simultaneous combination of multiple steps. In the case of simultaneous multi-step reactions, neither model-free nor model-fitting methods can be used to determine Ea and A. Therefore, a specific physicochemical model should be applied for the reaction in question [56]. These methods have the benefit of combining mass and heat transfer effects into a single model. However, they can be complicated to implement [57], leading to long simulation times. In addition, these methods are purely based on other empirical parameters (e.g., porosity, bulk density, void fraction) that may vary with synthesis conditions.
4. Model-Fitting Kinetic Reaction Models
4.1. Integral Approximation
4.2. Master Plots
5. Model-Free Methods of Kinetic Analysis
5.1. Differential Isoconversional Methods
5.2. Integral Isoconversional Methods
5.3. Kissinger Method
6. Combination of Model-Fitting and Model-Free Methods
7. Generalized Kinetic Models
8. Generalized Kinetic Models Applied to Carbonate Looping Systems
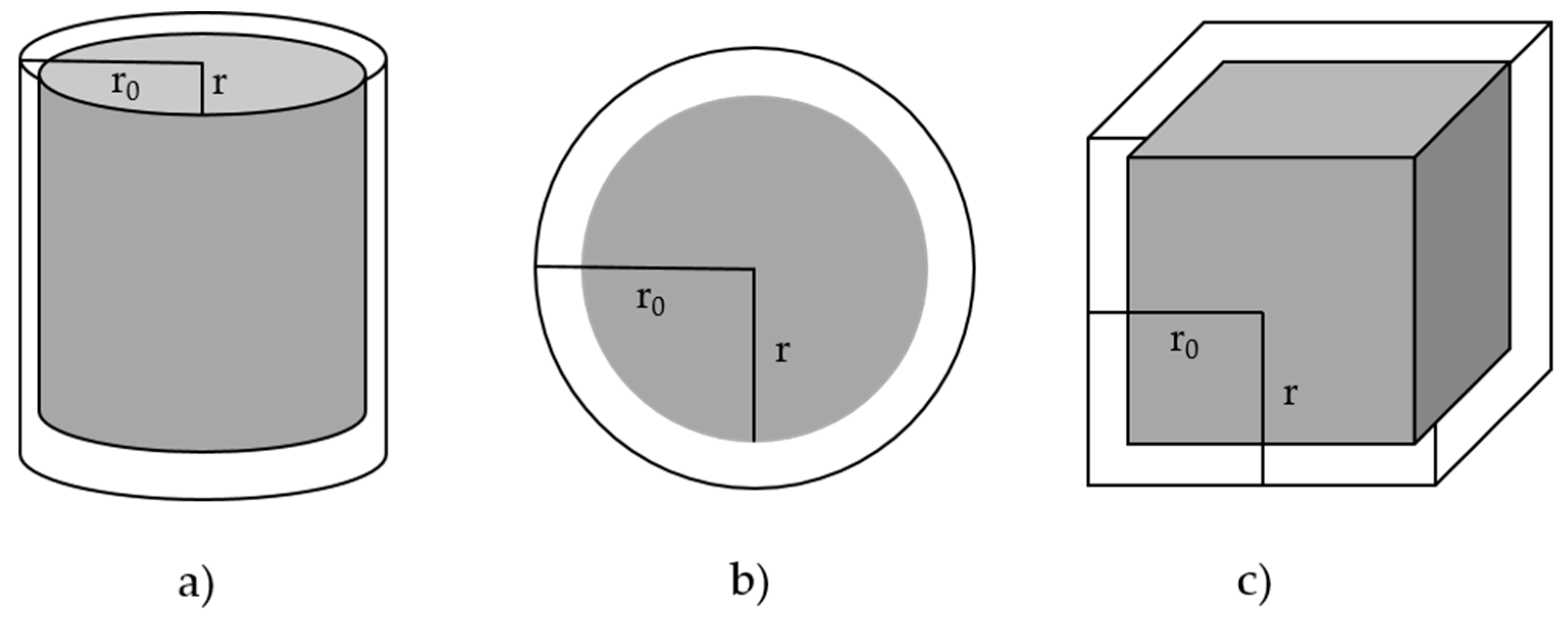
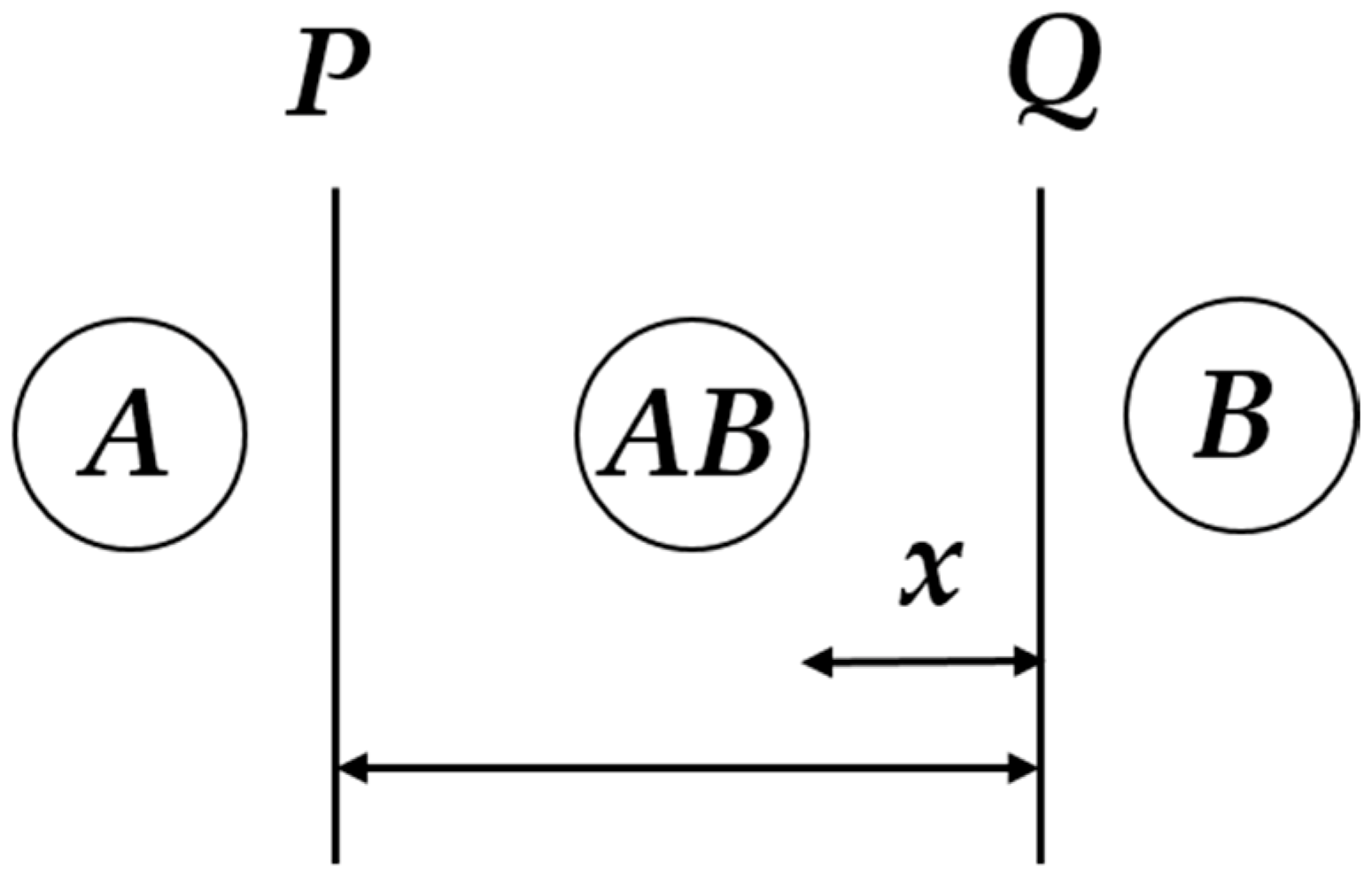
8.1. Shrinking Core Model
8.2. Pore Models
8.3. Grain Models
8.4. Nucleation Model (Rate Equation Theory)
8.5. Apparent Model
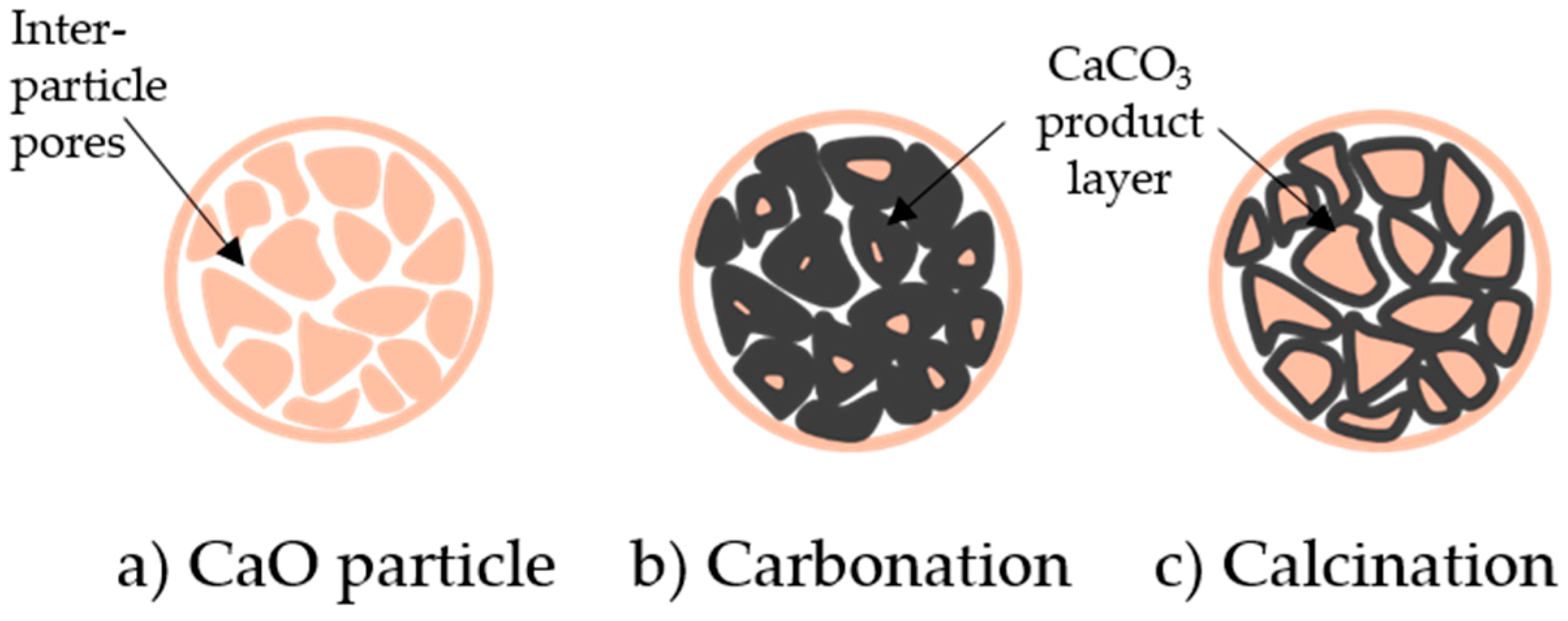
9. Calcination of Carbonate Looping Systems
- Heat transfer (thermal transport) through the particle to the reaction interface
- External mass transfer through the particle
- Mass transport of the CO2 desorbed from the reaction surface through the porous system (Internal mass transfer or CO2 diffusion inside the pore)
- CO2 diffusion through the product layer
- Chemical reaction
Comparison of Calcination Kinetic Analysis
10. Carbonation of CaO-Based Systems
10.1. Pore Models, Homogeneous Particle Models and Rate Equation Theory
10.2. Grain Models
10.3. Apparent and Isoconversional Models
10.4. Comparison of Carbonation Kinetic Analysis
11. Recommendations and Conclusions
- Quality of the measured data is critical to obtain reproducible results and lead to similar conclusions. It is important that TGA analysis is performed carefully for kinetic analysis and experimental errors should be detailed.
- Different kinetic methods should be performed in parallel and compared against each other. In particular, it has been found to be very useful to perform model-free methods (e.g., Friedman) before model-fitting methods (integral approximations or master plots). This combination should be considered for further studies of solid-gas reactions showing a single step. This recommendation is supported by the International Confederation for Thermal Analysis and Calorimetry (ICTAC) Kinetics Committee, which recommends the use of multi-heating rate experiments over single heating-rate experiments [2].
- If the previous methodology cannot reproduce the experimental results, then a generalized method should be performed. In addition, the generalized methodology should be considered when the kinetic analysis is performed on particles instead of powder form samples and where simultaneous multi-step reactions are applicable, as the previous methods will lead to the wrong conclusions.
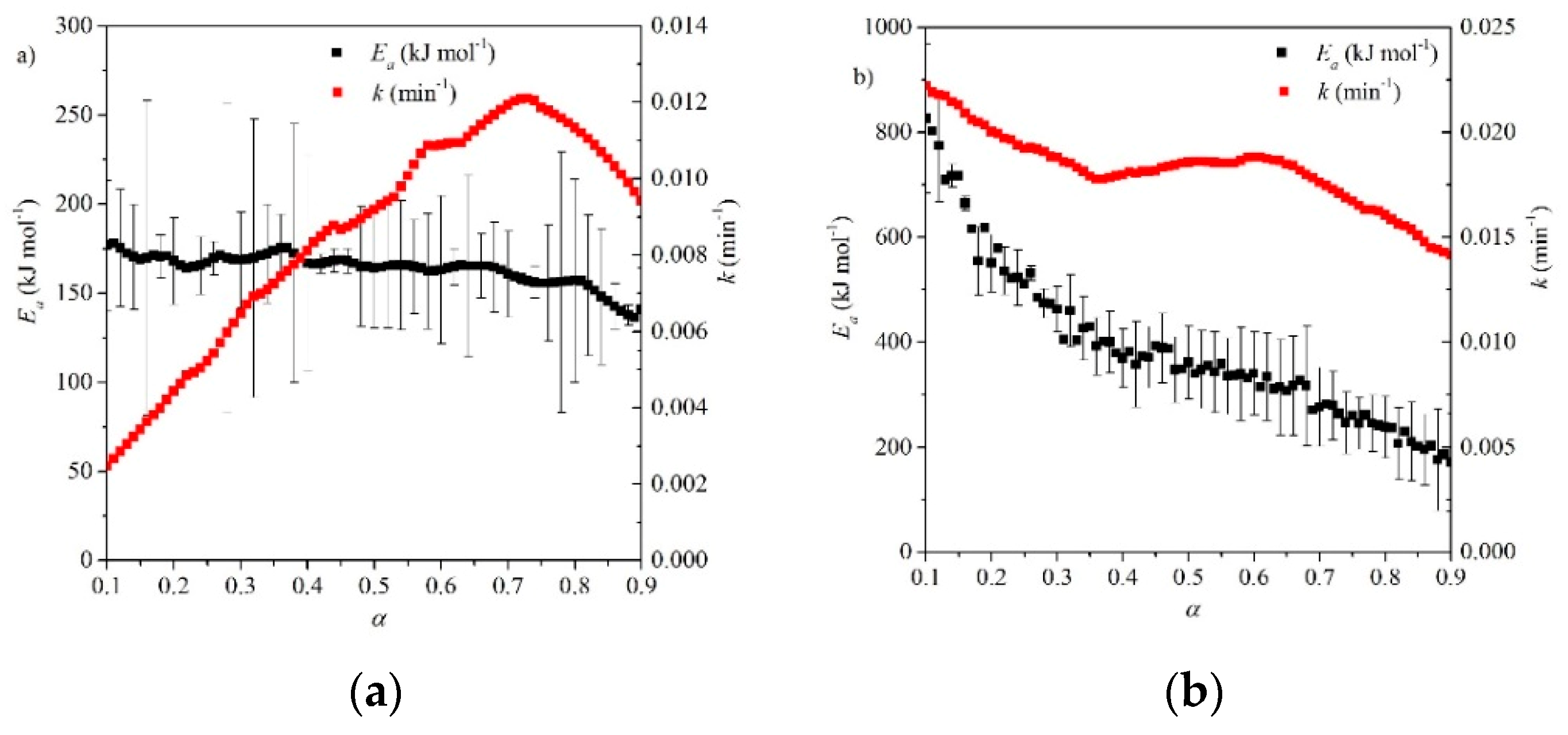
- For calcination reaction studies the disparity in results suggests that sample morphology plays an important role. Overall, the use of a multiple heating-rate isoconversional methods, such as Friedman, should be carried out to validate the model-fitting methods. This will allow comparison of the average values of Ei from model-fitting with isoconversional values of Eα, which could reveal several reaction steps. The model-free method of determining a reaction mechanism can then be employed, which could reduce the disparity in reaction mechanisms observed.
- For carbonation reaction studies, generalized models show better representation of the phenomena shown in the two reaction regions. For the kinetic control region, it is recommended that morphological methods of kinetic analysis such as pore models and grain models are recommended, as opposed to apparent or isoconversional methods. For the diffusion region, the kinetic parameters obtained are seen to vary considerably based on material properties. Therefore, material characterization such as porosimetry and scanning/transmission electron microscopy is recommended prior to the kinetic analysis. Nonporous materials evidently will not suit the use of pore models, while microporous materials may be better suited to the use of an apparent model rather than pore models.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Pre-exponential factor, min−1 |
| Ai | Model-fitting estimate of pre-exponential factor, min−1 |
| A0 | Model-free estimate of pre-exponential factor, min−1 |
| C | Concentration of diffusing gases, mol m−3 |
| Cb | Bulk concentration of diffusing gases, mol m−3 |
| Ce | Equilibrium concentration of diffusing gases, mol m−3 |
| D | Product layer diffusion constant, m2 s−1 |
| Ea | Activation energy, kJ mol−1 |
| Eα | Isoconversional activation energy (function of α), kJ mol−1 |
| Ei | Model-fitting estimate of activation energy, kJ mol−1 |
| E0 | Model-free estimate of activation energy, kJ mol−1 |
| Fn | Chemical reaction rate for nucleation, mol m3 s−1 |
| GD | Function of the particle symmetry, dimensionless |
| ΔHr | Reaction enthalpy, kJ mol−1 |
| J | Diffusion flux, mol m−2 s−1 |
| k(T) or k | Reaction rate constant, min−1 |
| kn | Chemical reaction rate constant for nucleation, m3 s−1 |
| ks | Kinetic reaction rate constant, m4 mol·s−1 |
| L0 | Pore length per unit volume (m m−3) |
| M | Molar mass, g mol−1 |
| m0 | Initial sample mass, g |
| mf | Sample mass after reaction completion, g |
| mt | Sample mass at time t, g |
| Nmolecular | Avogadro’s number |
| P | Total pressure, kPa |
| P0 | Equilibrium pressure, kPa |
| r | Particle radius, m |
| R | Universal gas constant, kJ mol−1·K−1 |
| S | Surface area of the reactional zone, m2 |
| Sm | Kinetic and morphological parameter, m2 mol−1 |
| S0 | Initial specific surface area of the reactional zone, m2 m−3 |
| ΔSr | Reaction entropy, kJ mol−1 K−1 |
| t | Time, s |
| T | Temperature, K |
| w | Mass fraction of solid contributing to reaction, dimensionless |
| X(t) | Carbonation conversion after t time, dimensionless |
| Xu | Ultimate carbonation conversion, dimensionless |
| Greek letters | |
| α | Exent of conversion, dimensionless |
| β | Heating rate, K min−1 |
| dα/dt | Reaction rate, s−1 |
| dξ/dt | Absolute speed of reaction, mol s−1 |
| ε0 | Initial sorbent porosity, dimensionless |
| ρ | Density, kg m−3 |
| ϕ | Thermodynamic parameter, mol m−2 s−1 |
| vs | Reaction rate for surface reaction, mol m−2 s−1 |
| ψ | Structural parameter, dimensionless |
References
- Brown, M.E. Reaction kinetics from thermal analysis. In Introduction to Thermal Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004. [Google Scholar]
- King, P.L.; Wheeler, V.M.; Renggli, C.J.; Palm, A.B.; Wilson, S.A.; Harrison, A.L.; Morgan, B.; Nekvasil, H.; Troitzsch, U.; Mernagh, T.; et al. Gas–solid reactions: Theory, experiments and case studies relevant to earth and planetary processes. Rev. Mineral. Geochem. 2018, 84, 1–56. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC kinetics committee recommendations for performing kinetic computations on thermal analysis data. Thermochimca Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Bayon, A.; Bader, R.; Jafarian, M.; Fedunik-Hofman, L.; Sun, Y.; Hinkley, J.; Miller, S.; Lipiński, W. Techno-economic assessment of solid–gas thermochemical energy storage systems for solar thermal power applications. Energy 2018, 149, 473–484. [Google Scholar] [CrossRef]
- Edwards, S.; Materić, V. Calcium looping in solar power generation plants. Sol. Energy 2012, 86, 2494–2503. [Google Scholar] [CrossRef]
- Sarrión, B.; Perejón, A.; Sánchez-Jiménez, P.E.; Pérez-Maqueda, L.A.; Valverde, J.M. Role of calcium looping conditions on the performance of natural and synthetic Ca-based materials for energy storage. J. CO2 Util. 2018, 28, 374–384. [Google Scholar] [CrossRef]
- Bhagiyalakshmi, M.; Hemalatha, P.; Ganesh, M.; Mei, P.M.; Jang, H.T. A direct synthesis of mesoporous carbon supported MgO sorbent for CO2 capture. Fuel 2011, 90, 1662–1667. [Google Scholar] [CrossRef]
- Ruminski, A.M.; Jeon, K.-J.; Urban, J.J. Size-dependent CO2 capture in chemically synthesized magnesium oxide nanocrystals. J. Mater. Chem. 2011, 21, 11486–11491. [Google Scholar] [CrossRef]
- Kwon, S.; Hwang, J.; Lee, H.; Lee, W.R. Interactive CO2 adsorption on the BaO (100) surface: A density functional theory (DFT) study. Bull. Korean Chem. Soc. 2010, 31, 2219–2222. [Google Scholar] [CrossRef]
- Rhodes, N.R.; Barde, A.; Randhir, K.; Li, L.; Hahn, D.W.; Mei, R.; Klausner, J.F.; AuYeung, N. Solar thermochemical energy storage through carbonation cycles of SrCO3/SrO supported on SrZrO3. ChemSusChem 2015, 8, 3793–3798. [Google Scholar] [CrossRef]
- Gunasekaran, S.; Anbalagan, G. Thermal decomposition of natural dolomite. Bull. Mater. Sci. 2007, 30, 339–344. [Google Scholar] [CrossRef] [Green Version]
- Duan, Y.; Luebke, D.; Pennline, H. Efficient theoretical screening of solid sorbents for CO2 capture applications. Int. J. Clean Coal Energy 2012, 1, 1–11. [Google Scholar] [CrossRef]
- Salaudeen, S.A.; Acharya, B.; Dutta, A. CaO-based CO2 sorbents: A review on screening, enhancement, cyclic stability, regeneration and kinetics modelling. J. CO2 Util. 2018, 23, 179–199. [Google Scholar] [CrossRef]
- André, L.; Abanades, S.; Flamant, G. Screening of thermochemical systems based on solid-gas reversible reactions for high temperature solar thermal energy storage. Renew. Sustain. Energy Rev. 2016, 64, 703–715. [Google Scholar] [CrossRef]
- Stanmore, B.R.; Gilot, P. Review: Calcination and carbonation of limestone during thermal cycling for CO2 sequestration. Fuel Process. Technol. 2005, 86, 1707–1743. [Google Scholar] [CrossRef]
- Grasa, G.; Abanades, J.C.; Alonso, M.; González, B. Reactivity of highly cycled particles of CaO in a carbonation/calcination loop. Chem. Eng. J. 2008, 137, 561–567. [Google Scholar] [CrossRef]
- Angerer, M.; Becker, M.; Härzschel, S.; Kröper, K.; Gleis, S.; Vandersickel, A.; Spliethoff, H. Design of a MW-scale thermo-chemical energy storage reactor. Energy Rep. 2018, 4, 507–519. [Google Scholar] [CrossRef]
- Ströhle, J.; Junk, M.; Kremer, J.; Galloy, A.; Epple, B. Carbonate looping experiments in a 1 MWth pilot plant and model validation. Fuel 2014, 12, 13–22. [Google Scholar] [CrossRef]
- Boot-Handford, M.E.; Abanades, J.C.; Anthony, E.J.; Blunt, M.J.; Brandani, S.; Mac Dowell, N.; Fernández, J.R.; Ferrari, M.-C.; Gross, R.; Hallett, J.P.; et al. Carbon capture and storage update. Energy Environ. Sci. 2014, 7, 130–189. [Google Scholar] [CrossRef]
- Hanak, D.P.; Anthony, E.J.; Manovic, V. A review of developments in pilot-plant testing and modelling of calcium looping process for CO2 capture from power generation systems. Energy Environ. Sci. 2015, 8, 2199–2249. [Google Scholar] [CrossRef]
- Zhou, Z.; Xu, P.; Xie, M.; Cheng, Z.; Yuan, W. Modeling of the carbonation kinetics of a synthetic CaO-based sorbent. Chem. Eng. Sci. 2013, 95, 283–290. [Google Scholar] [CrossRef]
- Fedunik-Hofman, L.; Bayon, A.; Lipinski, W.; Donne, S.W. Investigation of novel hydroxyapatite-doped CaO material for calcination-carbonation thermochemical energy storage. AIP Conf. Proc. 2018, 2033, 100004. [Google Scholar] [CrossRef]
- Erans, M.; Manovic, V.; Anthony, E.J. Calcium looping sorbents for CO2 capture. Appl. Energy 2016, 180, 722–742. [Google Scholar] [CrossRef]
- Chang, M.-H.; Chen, W.-C.; Huang, C.-M.; Liu, W.-H.; Chou, Y.-C.; Chang, W.-C.; Chen, W.; Cheng, J.-Y.; Huang, K.-E.; Hsu, H.-W. Design and experimental testing of a 1.9 MWth calcium looping pilot plant. Energy Procedia 2014, 63, 2100–2108. [Google Scholar] [CrossRef]
- Dieter, H.; Hawthorne, C.; Zieba, M.; Scheffknecht, G. Progress in calcium looping post combustion CO2 capture: Successful pilot scale demonstration. Energy Procedia 2013, 37, 48–56. [Google Scholar] [CrossRef]
- Reich, L.; Yue, L.; Bader, R.; Lipinski, W. Towards solar thermochemical carbon dioxide capture via calcium oxide looping: A review. Aerosol Air Qual. Res. 2014, 14, 500–514. [Google Scholar] [CrossRef]
- Shimizu, T.; Hirama, T.; Hosoda, H.; Kitano, K.; Inagaki, M.; Tejima, K. A twin fluid-bed reactor for removal of CO2 from combustion processes. Chem. Eng. Res. Des. 1999, 77, 62–68. [Google Scholar] [CrossRef]
- Martínez, I.; Grasa, G.; Murillo, R.; Arias, B.; Abanades, J.C. Kinetics of calcination of partially carbonated particles in a Ca-looping system for CO2 capture. Energy Fuels 2012, 26, 1432–1440. [Google Scholar] [CrossRef]
- Diego, M.; Martinez, I.; Alonso, M.; Arias, B.; Abanades, J. Calcium Looping Reactor Design for Fluidized-Bed Systems; Elsevier: Amsterdam, The Netherland, 2015; pp. 107–138. [Google Scholar]
- Alonso, M.; Rodriguez, N.; Gonzalez, B.; Arias, B.; Abanades, J.C. Capture of CO2 during low temperature biomass combustion in a fluidized bed using CaO. Process description, experimental results and economics. Energy Procedia 2011, 4, 795–802. [Google Scholar] [CrossRef] [Green Version]
- Meier, A.; Bonaldi, E.; Cella, G.M.; Lipinski, W.; Wuillemin, D.; Palumbo, R. Design and experimental investigation of a horizontal rotary reactor for the solar thermal production of lime. Energy 2004, 29, 811–821. [Google Scholar] [CrossRef]
- Nikulshina, V.; Gebald, C.; Steinfeld, A. CO2 capture from atmospheric air via consecutive CaO-carbonation and CaCO3-calcination cycles in a fluidized-bed solar reactor. Chem. Eng. J. 2009, 146, 244–248. [Google Scholar] [CrossRef]
- Bouquet, E.; Leyssens, G.; Schönnenbeck, C.; Gilot, P. The decrease of carbonation efficiency of CaO along calcination–carbonation cycles: Experiments and modelling. Chem. Eng. Sci. 2009, 64, 2136–2146. [Google Scholar] [CrossRef]
- Sun, P.; Grace, J.R.; Lim, C.J.; Anthony, E.J. A discrete-pore-size-distribution-based gas-solid model and its application to the CaO + CO2 reaction. Chem. Eng. Sci. 2008, 63, 57–70. [Google Scholar] [CrossRef]
- Grasa, G.; Murillo, R.; Alonso, M.; Abanades, J.C. Application of the random pore model to the carbonation cyclic reaction. Aiche J. 2009, 55, 1246–1255. [Google Scholar] [CrossRef]
- Yue, L.; Lipiński, W. Thermal transport model of a sorbent particle undergoing calcination–carbonation cycling. Aiche J. 2015, 61, 2647–2656. [Google Scholar] [CrossRef]
- Yue, L.; Lipiński, W. A numerical model of transient thermal transport phenomena in a high-temperature solid–gas reacting system for CO2 capture applications. Int. J. Heat Mass Transf. 2015, 85, 1058–1068. [Google Scholar] [CrossRef]
- Lasheras, A.; Ströhle, J.; Galloy, A.; Epple, B. Carbonate looping process simulation using a 1D fluidized bed model for the carbonator. Int. J. Greenh. Gas Control 2011, 5, 686–693. [Google Scholar] [CrossRef]
- Romano, M. Coal-fired power plant with calcium oxide carbonation for postcombustion CO2 capture. Energy Procedia 2009, 1, 1099–1106. [Google Scholar] [CrossRef]
- Martínez, I.; Murillo, R.; Grasa, G.; Abanades, J.C. Integration of a Ca-looping system for CO2 capture in an existing power plant. Energy Procedia 2011, 4, 1699–1706. [Google Scholar] [CrossRef]
- Hanak, D.P.; Manovic, V. Calcium looping with supercritical CO2 cycle for decarbonisation of coal-fired power plant. Energy 2016, 102, 343–353. [Google Scholar] [CrossRef]
- Carrillo, A.J.; González-Aguilar, J.; Romero, M.; Coronado, J.M. Solar energy on demand: A review on high temperature thermochemical heat storage systems and materials. Chem. Rev. 2019, 119, 4777–4816. [Google Scholar] [CrossRef]
- Norby, P. Solid-gas reactions. In Synthesis of Inorganic Materials; The University of Oslo: Oslo, Norway, 2006. [Google Scholar]
- Vyazovkin, S.; Wight, C.A. Kinetics in solids. Annu. Rev. Phys. Chem. 1997, 48, 125–149. [Google Scholar] [CrossRef]
- Khawam, A.; Flanagan, D.R. Solid-state kinetic models: Basics and mathematical fundamentals. J. Phys. Chem. B 2006, 110, 17315–17328. [Google Scholar] [CrossRef]
- Fedunik-Hofman, L.; Bayon, A.; Hinkley, J.; Lipiński, W.; Donne, S.W. Friedman method kinetic analysis of CaO-based sorbent for high-temperature thermochemical energy storage. Chem. Eng. Sci. 2019, 200, 236–247. [Google Scholar] [CrossRef]
- Koga, N.; Favergeon, L.; Kodani, S. Impact of atmospheric water vapor on the thermal decomposition of calcium hydroxide: A universal kinetic approach to a physico-geometrical consecutive reaction in solid–gas systems under different partial pressures of product gas. Phys. Chem. Chem. Phys. 2019, 21, 11615–11632. [Google Scholar] [CrossRef]
- Zawadzki, J.; Bretsznajder, S. Some remarks on the mechanism of reactions of the type: Solid = solid + gas. Trans. Faraday Soc. 1938, 34, 951–959. [Google Scholar] [CrossRef]
- Liavitskaya, T.; Vyazovkin, S. Delving into the kinetics of reversible thermal decomposition of solids measured on heating and cooling. J. Phys. Chem. C 2017, 121, 15392–15401. [Google Scholar] [CrossRef]
- Liavitskaya, T.; Vyazovkin, S. Discovering the kinetics of thermal decomposition during continuous cooling. Phys. Chem. Chem. Phys. 2016, 18, 32021–32030. [Google Scholar] [CrossRef]
- Maitra, S.; Bandyopadhyay, N.; Das, S.; Pal, A.J.; Pramanik, M.J. Non-isothermal decomposition kinetics of alkaline earth metal carbonates. J. Am. Ceram. Soc. 2007, 90, 1299–1303. [Google Scholar] [CrossRef]
- Gallagher, P.K.; Johnson, D.W. Kinetics of the thermal decomposition of CaCO3 in CO2 and some observations on the kinetic compensation effect. Thermochim. Acta 1976, 14, 255–261. [Google Scholar] [CrossRef]
- Urbanovici, E.; Popescu, C.; Segal, E. Improved iterative version of the Coats-Redfern method to evaluate non-isothermal kinetic parameters. J. Therm. Anal. Calorim. 1999, 58, 683–700. [Google Scholar] [CrossRef]
- Moukhina, E. Determination of kinetic mechanisms for reactions measured with thermoanalytical instruments. J. Therm. Anal. Calorim. 2012, 109, 1203–1214. [Google Scholar] [CrossRef] [Green Version]
- Vyazovkin, S.; Wight, C. Model free and Model-fitting approaches to kinetic analysis of isothermal and no isothermal data. Thermochimca Acta 1999, 340, 53–68. [Google Scholar] [CrossRef]
- Pijolat, M.; Favergeon, L. Kinetics and mechanisms of solid-gas reactions. In Handbook of Thermal Analysis and Calorimetry, Volume 6, 2nd ed.; Sergey, V., Nobuyoshi, K., Christoph, S., Eds.; Elsevier: Amsterdam, The Nedherlands, 2018; Volume 6, pp. 173–212. [Google Scholar]
- Lee, D.K. An apparent kinetic model for the carbonation of calcium oxide by carbon dioxide. Chem. Eng. J. 2004, 100, 71–77. [Google Scholar] [CrossRef]
- Vogel, A.I.; Mendham, J. Vogel’s Textbook of Quantitative Chemical Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Sun, P.; Grace, J.R.; Lim, C.J.; Anthony, E.J. Determination of intrinsic rate constants of the CaO-CO2 reaction. Chem. Eng. Sci. 2008, 63, 47–56. [Google Scholar] [CrossRef]
- Kierzkowska, A.M.; Pacciani, R.; Müller, C.R. CaO-based CO2 sorbents: From fundamentals to the development of new, highly effective materials. ChemSusChem 2013, 6, 1130–1148. [Google Scholar] [CrossRef]
- Ninan, K.N.; Krishnan, K.; Krishnamurthy, V.N. Kinetics and mechanism of thermal decomposition of Insitu generated calcium carbonate. J. Therm. Anal. 1991, 37, 1533–1543. [Google Scholar] [CrossRef]
- Bouineau, V.; Pijolat, M.; Soustelle, M. Characterisation of the chemical reactivity of a CaCO3 powder for its decomposition. J. Eur. Ceram. Soc. 1998, 18, 1319–1324. [Google Scholar] [CrossRef]
- Mampel, K.L. Zeitumsatzformeln für heterogene Reaktionen an Phasengrenzen fester Körper. Z. Für Phys. Chem. 1940, 187, 235–249. [Google Scholar] [CrossRef]
- McIlvried, H.G.; Massoth, F.E. Effect of particle size distribution on gas-solid reaction kinetics for spherical particles. Ind. Eng. Chem. Fundam. 1973, 12, 225–229. [Google Scholar] [CrossRef]
- Buscaglia, V.; Milanese, C. Diffusion-controlled solid-state reactions of spherical particles, a general model for multiphase binary systems. J. Phys. Chem. B 2005, 109, 18475–18482. [Google Scholar] [CrossRef]
- Maitra, S.; Chakrabarty, N.; Pramanik, J. Decomposition kinetics of alkaline earth carbonates by integral approximation method. Ceramica 2008, 54, 268–272. [Google Scholar] [CrossRef]
- Criado, J.M.; Málek, J.; Ortega, A. Applicability of the master plots in kinetic analysis of non-isothermal data. Thermochim. Acta 1989, 147, 377–385. [Google Scholar] [CrossRef]
- Vyazovkin, S. Estimating reaction models and preexponential factors. In Isoconversional Kinetics of Thermally Stimulated Processes; Springer International Publishing: New York, NY, USA, 2015; pp. 41–50. [Google Scholar]
- Yue, L.; Shui, M.; Xu, Z. The decomposition kinetics of nanocrystalline calcite. Thermochimca Acta 1999, 335, 121–126. [Google Scholar] [CrossRef]
- Málek, J. The applicability of Johnson-Mehl-Avrami model in the thermal analysis of the crystallization kinetics of glasses. Thermochim. Acta 1995, 267, 61–73. [Google Scholar] [CrossRef]
- Sanders, J.P.; Gallagher, P.K. Kinetic analyses using simultaneous TG/DSC measurements Part I: Decomposition of calcium carbonate in argon. Thermochim. Acta 2002, 388, 115–128. [Google Scholar] [CrossRef]
- Takeo, O. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Jergins, J. A Thermodynamic Approach to the Kinetics of Reversible Gas-Solid Reactions: The Calcium Carbonate System, in Department of Chemistry. Ph.D. Thesis, The University of Utah, Salt Lake City, UT, USA, 2008. [Google Scholar]
- Valverde, J.M.; Sanchez-Jimenez, P.E.; Perez-Maqueda, L.A. Limestone calcination nearby equilibrium: Kinetics, CaO crystal structure, sintering and reactivity. J. Phys. Chem. C 2015, 119, 1623–1641. [Google Scholar] [CrossRef]
- Abanades, J.C.; Alvarez, D. Conversion limits in the reaction of CO2 with lime. Energy Fuels 2003, 17, 308–315. [Google Scholar] [CrossRef]
- Arias, B.; Abanades, J.C.; Grasa, G.S. An analysis of the effect of carbonation conditions on CaO deactivation curves. Chem. Eng. J. 2011, 167, 255–261. [Google Scholar] [CrossRef]
- Grasa, G.; Abanades, J.C. CO2 capture capacity of CaO in long series of carbonation/calcination cycles. Ind. Eng. Chem. Res. 2006, 45, 8846–8851. [Google Scholar] [CrossRef]
- Rouchon, L.; Favergeon, L.; Pijolat, M. Analysis of the kinetic slowing down during carbonation of CaO by CO2. J. Therm. Anal. Calorim. 2013, 113, 1145–1155. [Google Scholar] [CrossRef]
- Mess, D.; Sarofim, A.F.; Longwell, J.P. Product layer diffusion during the reaction of calcium oxide with carbon dioxide. Energy Fuels 1999, 13, 999–1005. [Google Scholar] [CrossRef]
- Li, Z.; Sun, H.; Cai, N. Rate equation theory for the carbonation reaction of CaO with CO2. Energy Fuels 2012, 26, 4607–4616. [Google Scholar] [CrossRef]
- Yagi, S.; Kunii, D. Studies on combustion of carbon particles in flames and fluidized beds. Symp. (Int.) Combust. 1955, 5, 231–244. [Google Scholar] [CrossRef]
- Ishida, M.; Wen, C.Y. Comparison of zone-reaction model and unreacted-core shrinking model in solid—gas reactions—I isothermal analysis. Chem. Eng. Sci. 1971, 26, 1031–1041. [Google Scholar] [CrossRef]
- García-Labiano, F.; Abad, A.; de Diego, L.F.; Gayán, P.; Adánez, J. Calcination of calcium-based sorbents at pressure in a broad range of CO2 concentrations. Chem. Eng. Sci. 2002, 57, 2381–2393. [Google Scholar] [CrossRef]
- Heesink, A.B.M.; Prins, W.; van Swaaij, W.P.M. A grain size distribution model for non-catalytic gas-solid reactions. Chem. Eng. J. Biochem. Eng. J. 1993, 53, 25–37. [Google Scholar] [CrossRef]
- Chang, E.E.; Chen, C.-H.; Chen, Y.-H.; Pan, S.-Y.; Chiang, P.-C. Performance evaluation for carbonation of steel-making slags in a slurry reactor. J. Hazard. Mater. 2011, 186, 558–564. [Google Scholar] [CrossRef]
- Bhatia, S.K.; Perlmutter, D.D. Effect of the product layer on the kinetics of the CO2-lime reaction. Aiche J. 1983, 29, 79–86. [Google Scholar] [CrossRef]
- Jiang, L.; Hu, S.; Syed-Hassan, S.S.A.; Wang, Y.; Shuai, C.; Su, S.; Liu, C.; Chi, H.; Xiang, J. Performance and carbonation kinetics of modified CaO-based sorbents derived from different precursors in multiple CO2 capture cycles. Energy Fuels 2016, 30, 9563–9571. [Google Scholar] [CrossRef]
- Szekely, J.; Evans, J.W. A structural model for gas-solid reactions with a moving boundary-II. Chem. Eng. Sci. 1971, 26, 1901–1913. [Google Scholar] [CrossRef]
- Borgwardt, R.H. Calcination kinetics and surface area of dispersed limestone particles. Aiche J. 1985, 31, 103–111. [Google Scholar] [CrossRef]
- Darroudi, T.; Searcy, A. Effect of CO2 pressure on the rate of decomposition of calcite (CaCO3). J. Phys. Chem. 1981, 85, 3971–3974. [Google Scholar] [CrossRef]
- Rodriguez-Navarro, C.; Ruiz-Agudo, E.; Luque, A.; Rodriguez-Navarro, A.B.; Ortega-Huertas, M. Thermal decomposition of calcite: Mechanisms of formation and textural evolution of CaO nanocrystals. Am. Mineral. 2009, 94, 578–593. [Google Scholar] [CrossRef]
- Valverde, J.M.; Sanchez-Jimenez, P.E.; Perez-Maqueda, L.A. Ca-looping for postcombustion CO2 capture: A comparative analysis on the performances of dolomite and limestone. Appl. Energy 2015, 138, 202–215. [Google Scholar] [CrossRef]
- Ingraham, T.R.; Marier, P. Kinetic studies on the thermal decomposition of calcium carbonate. Can. J. Chem. Eng. 1963, 41, 170–173. [Google Scholar] [CrossRef]
- Khinast, J.; Krammer, G.F.; Brunner, C.; Staudinger, G. Decomposition of limestone: The influence of CO2 and particle size on the reaction rate. Chem. Eng. Sci. 1996, 51, 623–634. [Google Scholar] [CrossRef]
- Lee, J.-T.; Keener, T.; Knoderera, M.; Khang, S.-J. Thermal decomposition of limestone in a large scale thermogravimetric analyzer. Thermochimica Acta 1993, 213, 223–240. [Google Scholar] [CrossRef]
- Dai, P.; González, B.; Dennis, J.S. Using an experimentally-determined model of the evolution of pore structure for the calcination of cycled limestones. Chem. Eng. J. 2016, 304, 175–185. [Google Scholar] [CrossRef]
- Criado, J.; González, M.; Málek, J.; Ortega, A. The effect of the CO2 pressure on the thermal decomposition kinetics of calcium carbonate. Thermochimca Acta 1995, 254, 121–127. [Google Scholar] [CrossRef]
- Caldwell, K.M.; Gallagher, P.K.; Johnson, D.W. Effect of thermal transport mechanisms on the thermal decomposition of CaCO3. Thermochimca Acta 1977, 18, 15–19. [Google Scholar] [CrossRef]
- Arvanitidis, I.; Sichen, D.; Seetharaman, S.; Sohn, H.Y. The intrinsic thermal decomposition kinetics of SrCO3 by a nonisothermal technique. Metall. Mater. Trans. B 1997, 28, 1063–1068. [Google Scholar] [CrossRef]
- Ptáček, P.; Bartoníčková, E.; Švec, J.; Opravil, T.; Šoukal, F.; Frajkorová, F. The kinetics and mechanism of thermal decomposition of SrCO3 polymorphs. Ceram. Int. 2015, 41, 115–126. [Google Scholar] [CrossRef]
- Grasa, G.; Martínez, I.; Diego, M.E.; Abanades, J.C. Determination of CaO carbonation kinetics under recarbonation conditions. Energy Fuels 2014, 28, 4033–4042. [Google Scholar] [CrossRef]
- Nouri, S.M.M.; Ebrahim, H.A. Kinetic study of CO2 reaction with CaO by a modified random pore model. Pol. J. Chem. Technol. 2016, 18, 93–98. [Google Scholar] [CrossRef]
- Rouchon, L.; Favergeon, L.; Pijolat, M. New kinetic model for the rapid step of calcium oxide carbonation by carbon dioxide. J. Therm. Anal. Calorim. 2014, 116, 1181–1188. [Google Scholar] [CrossRef]
- Gupta, H.; Fan, L.S. Carbonation-calcination cycle using high reactivity calcium oxide for carbon dioxide separation from flue gas. Ind. Eng. Chem. Res. 2002, 41, 4035–4042. [Google Scholar] [CrossRef]
- Nikulshina, V.; Gálvez, M.E.; Steinfeld, A. Kinetic analysis of the carbonation reactions for the capture of CO2 from air via the Ca(OH)2–CaCO3–CaO solar thermochemical cycle. Chem. Eng. J. 2007, 129, 75–83. [Google Scholar] [CrossRef]
- Hamdi, S.; Vieille, L.; Nahdi, K.; Favergeon, L. Synthesis, characterization and low-temperature carbonation of mesoporous magnesium oxide. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Symonds, R.T.; Lu, D.Y.; Macchi, A.; Hughes, R.W.; Anthony, E.J. CO2 capture from syngas via cyclic carbonation/calcination for a naturally occurring limestone: Modelling and bench-scale testing. Chem. Eng. Sci. 2009, 64, 3536–3543. [Google Scholar] [CrossRef]
- Baker, E.H. 87. The calcium oxide–carbon dioxide system in the pressure range 1–300 atmospheres. J. Chem. Soc.(Resumed) 1962, 464–470. [Google Scholar] [CrossRef]
- Butler, J.W.; Jim Lim, C.; Grace, J.R. Kinetics of CO2 absorption by CaO through pressure swing cycling. Fuel 2014, 127, 78–87. [Google Scholar] [CrossRef]
- Yu, Y.S.; Liu, W.Q.; An, H.; Yang, F.S.; Wang, G.X.; Feng, B.; Zhang, Z.X.; Rudolph, V. Modeling of the carbonation behavior of a calcium based sorbent for CO2 capture. Int. J. Greenh. Gas. Control. 2012, 10, 510–519. [Google Scholar] [CrossRef]
- Liu, W.; Dennis, J.S.; Sultan, D.S.; Redfern, S.A.T.; Scott, S.A. An investigation of the kinetics of CO2 uptake by a synthetic calcium based sorbent. Chem. Eng. Sci. 2012, 69, 644–658. [Google Scholar] [CrossRef]
- Koga, N.; Tanaka, H. Effect of sample mass on the kinetics of thermal decomposition of a solid-II. Isothermal dehydration of Li2SO4·H2O. J. Therm. Anal. 1993, 40, 1173–1179. [Google Scholar] [CrossRef]
- Favergeon, L.; Morandini, J.; Pijolat, M.; Soustelle, M. A general approach for kinetic modeling of solid-gas. Reactions at reactor scale: Application to kaolinite dehydroxylation. Oil Gas Sci. Tech. 2013, 68, 1039–1048. [Google Scholar] [CrossRef]
- Koga, N.; Criado, J.M. The influence of mass transfer phenomena on the kinetic analysis for the thermal decomposition of calcium carbonate by constant rate thermal analysis (CRTA) under vacuum. Int. J. Chem. Kinet. 1998, 30, 737–744. [Google Scholar] [CrossRef]
- Liu, W.; An, H.; Qin, C.; Yin, J.; Wang, G.; Feng, B.; Xu, M. Performance enhancement of calcium oxide sorbents for cyclic CO2 capture: A review. Energy Fuels 2012, 26, 2751–2767. [Google Scholar] [CrossRef]


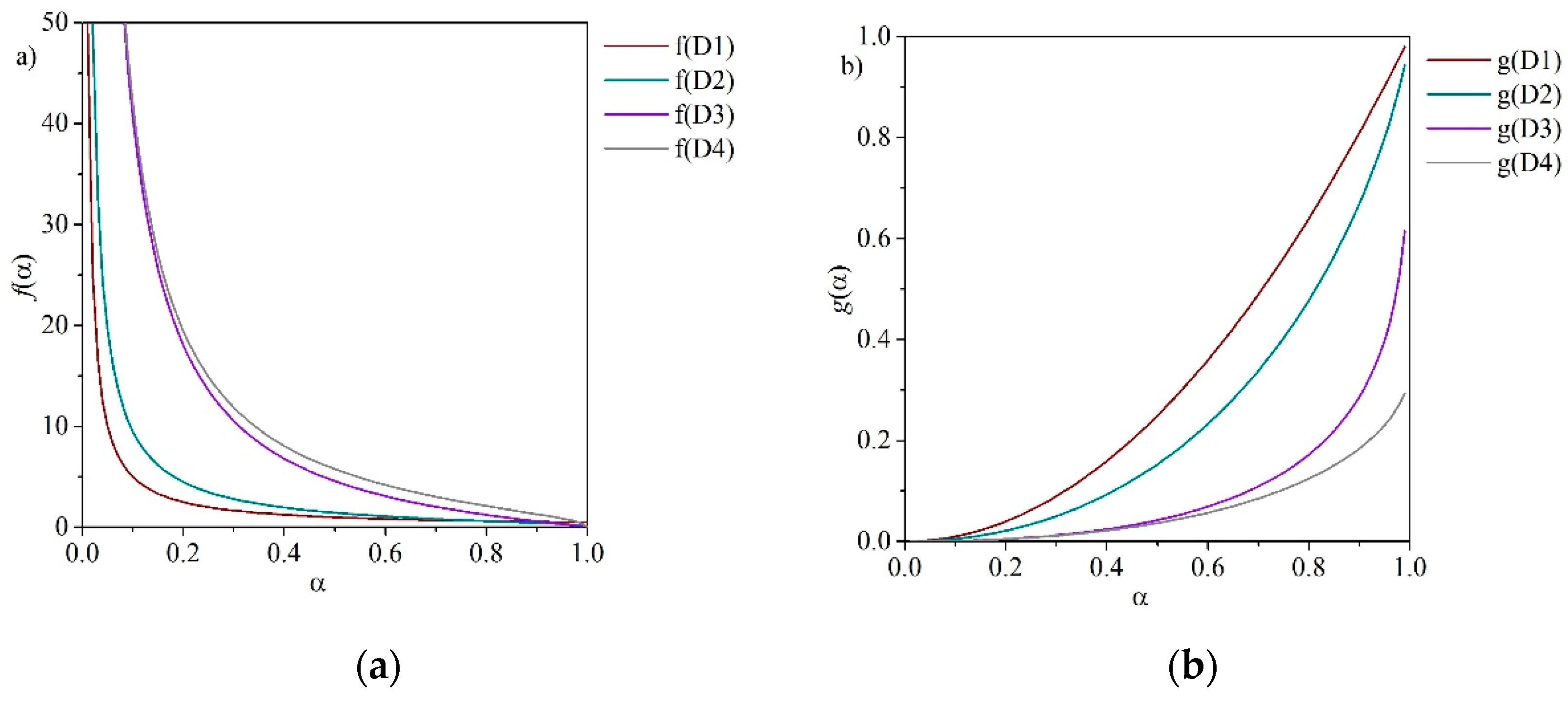
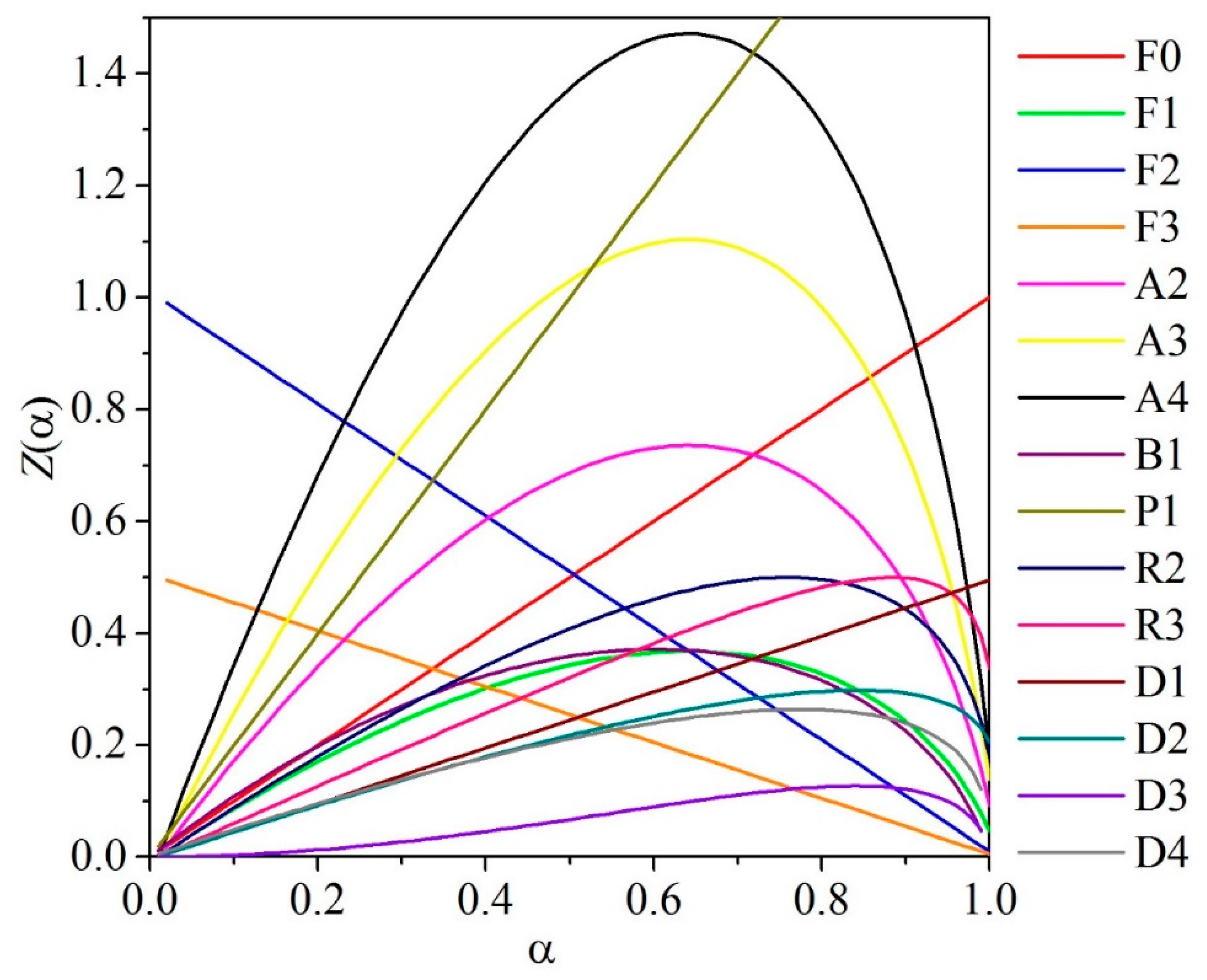


| Reaction Model | Code | f(α) | g(α) |
|---|---|---|---|
| Zero-order | F0 | 1 | |
| First-order | F1 | ||
| Second-order | F2 | ||
| Third-order | F3 | ||
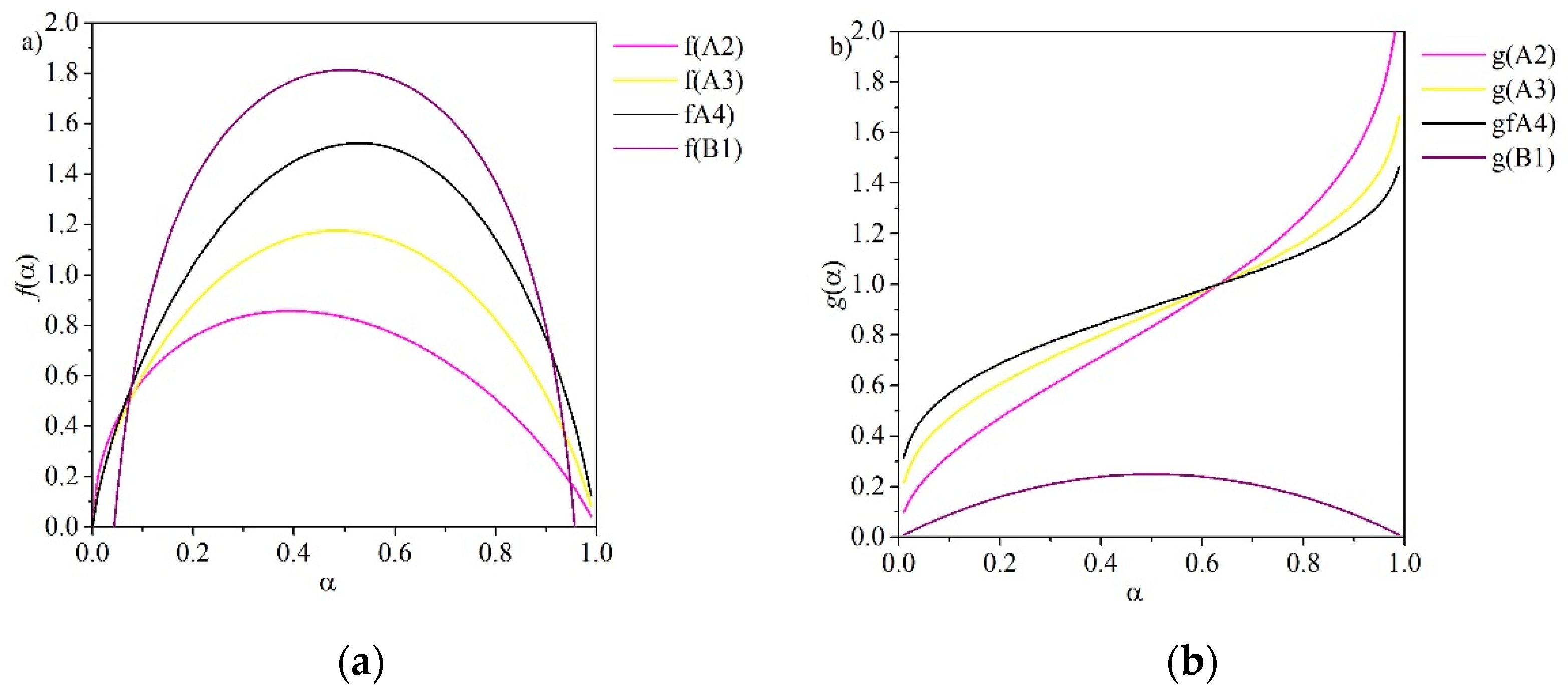
| Avrami-Erofeyev | A2 | ||
| Avrami-Erofeyev | A3 | ||
| Avrami-Erofeyev | A4 | ||
| Prout-Tompkins | B1 | ||
| Power law | P2 | ||
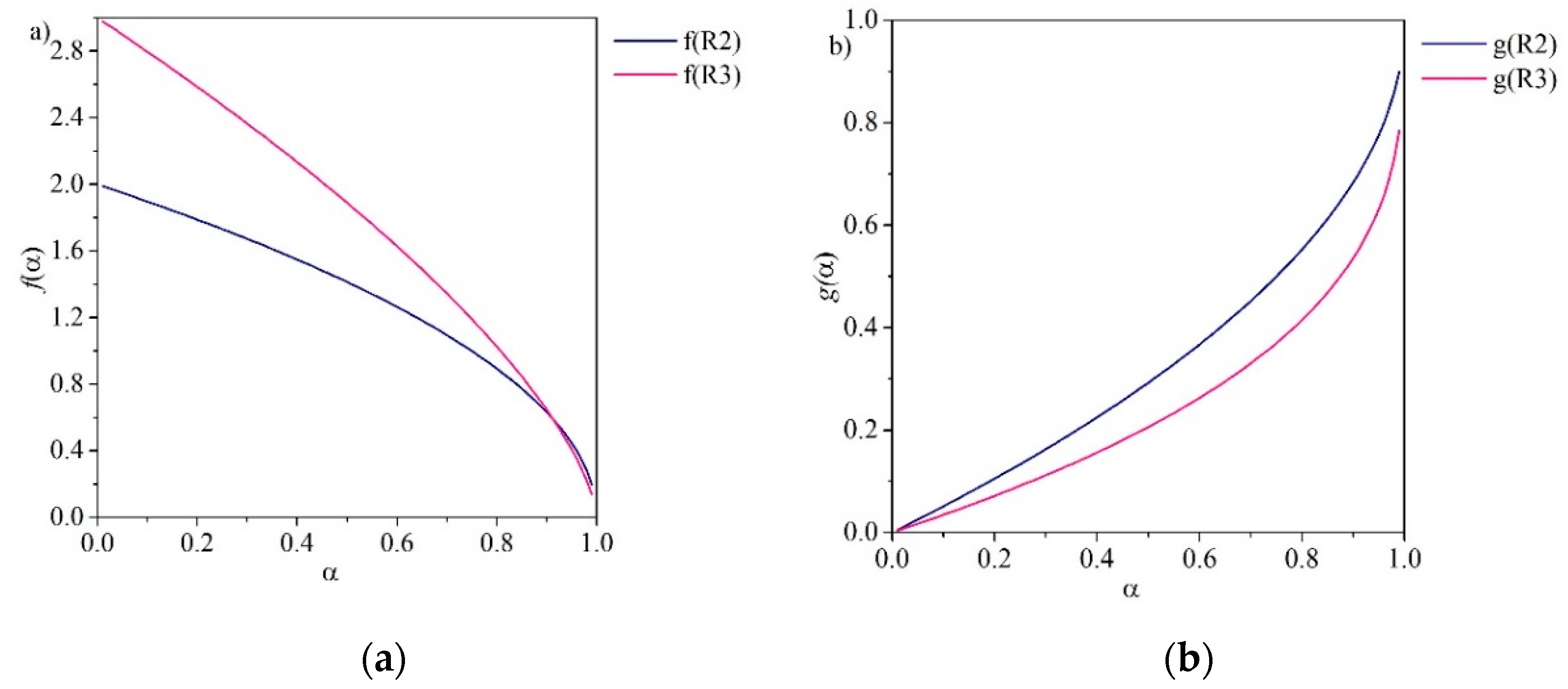
| Contracting area | R2 | ||
| Contracting volume | R3 | ||
| 1-D diffusion | D1 | ||
| 2-D diffusion | D2 | ||
| 3-D diffusion | D3 | ||
| Ginstling-Brounshtein | D4 |
| Material & Ref. | Atmosphere | Initial Sample Size (mg) Particle Sizes | Decomposition Range (°C) | Method | Ea (kJ mol−1) | A (s−1) | Reaction Order or Model |
|---|---|---|---|---|---|---|---|
| CaCO3 [61] | N2 | NS | NS | CR | 180.1212 | 1.18 × 107 | R2 |
| CaCO3 [69] | NS | NS | ~640–900 | CR | 187.1 | NS | R3 |
| CaCO3 [66] | N2 | NS | 400–960 | CR | 190.46 | 3.4 × 107 | F1 |
| CaCO3 [51] | N2 | NS | 400–960 | A&S | 224.46 | 3 × 104 | D2 |
| CaCO3 [46] | N2 | 17 | ~550–800 | Friedman | 171–147 Average: 164 | 2.5 × 105–2.9 × 105 | NS |
| CaCO3 [91] | Air | NS | ~600–810 | FWO & model-fitting (method NS) | FWO: 205 (for α < 0.2) 176 (for α > 0.2) Model-fitting: D1: 203 F1: 180 | D1: 8.02 × 107 F1: 3.98 × 107 | α < 0.2 D1 α > 0.2 F1 |
| CaCO3 [92] | N2/CO2 mixture (5–90% CO2) | NS | 830–900 isothermal | Data fitting of α vs. t curves from XRD CaCO3/CaO wt% | 150 | NS | B1/A2–A4 |
| CaCO3 (pellets) [93] | Air/ CO2 (0–100% CO2) | 455 Particle diameters <56 μm | 790–850 | General rate equation: r0ρ0f = kt where f = fractional thickness of reacted material | 169.9 | NS | R3 Double interface decomposition mechanism |
| L (type A and B) [28] | Air/ CO2 (0–10% CO2) | NS Particle diameters < 300 μm | 820–910 | RPM | A (CaCO3 ε = 0.044): 112.4 B (CaCO3 ε = 0.02): 91.7 | NS | Chemical reaction |
| L [94] | 0.4–1.3 Mean particle diameters: 7.5, 57 & 90 μm | 780 isothermal | Modified RPM | NS | NS | Chemical reaction and mass transport | |
| CaCO3 (spheres) [95] | N2/CO2 (0–21% CO2 | NSParticle diameters: 2, 5 & 7mm | 700, 800, 900 isothermal | SCM | 152.5–163.7 | 179–529 kg m−1 s−1 | Chemical reaction (assumed first order) |
| ML, SAD & BL [83] | N2/CO2 (0–80% CO2) | 2 Particle diameters: 50–75 μm | 775–960 isothermal | CGSM for ML & SAD SCM for BL | ML: 131 SAD: 114 BL: 166 | NS | Chemical reaction and mass transport |
| CaCO3 4 types of L [62] | CO2 | 5 | 700isothermal | Modified Mampel model | NS | NS | Nucleation & growth |
| CL PL (spheres) [96] | N2 | 0.1–0.5 g (Fluidized bed experiments) Particle diameters: CL: 1.4–1.7 mm PL: 0.7–0.81 & 1.4–1.7 mm | 750, 850, 875, 900 isothermal | Pore model/experimentally determined function | CL: 175 PL: 186 | NS | CL: Chemical reaction PL: <825°C: Chemical reaction >825 °C: Mass transport |
| CaCO3 [97] | Air/CO2 (pp. CO2 1.3–20 kPa) | 25 | ~700–900 | Model fitting | 187 | 4.43 × 107 | Assumed R3 |
| CaCO3 [98] | CO2 | 4 | 906 isothermal | CR | 2104.6 | 1090 | n = 2 |
| CaCO3 [52] | CO2 | 16 | ~700–977 | CR | 1037.6 | 3.98 × 1040 | n = 2/3 R3 |
| CaCO3 [46] | CO2 | 17 | ~900–980 | Friedman | 530–171 Average: 307 | 6.63 × 1032–6.2 × 102 | NS |
| D [11] | N2 | NS | ~687–840 | CR | 123.684 | 5.53 × 105 | n = 0.15 |
| SrCO3 [66] | N2 | NS | 810–1000 | CR | 238.32 | 7.3 × 107 | F1 |
| SrCO3 [51] | N2 | NS | 810–1000 | A&S | 238.32 | 5.9 × 104 | D4 |
| SrCO3 [99] | Ar | 10 | 727–1077 | Non-mechanistic integral approx. | 210 | 2.17 × 106 | n = 0.42 |
| SrCO3 [100] | Air | 30 | 875–1250 | Kissinger | α-phase: 255 β-phase: 227 | α: 15.8 × 107 β: 8.4 × 107 | α: R3 β: chemical reaction, n = 1/3 |
| BaCO3 [66] | N2 | NS | 930–1155 | CR | 292.98 | 1.4 × 108 | F1 |
| BaCO3 [51] | N2 | NS | 930–1155 | A&S | 292.98 | 1.4 × 105 | D2 |
| MgCO3 [66] | N2 | NS | 510–750 | CR | 140.16 | 2.0 × 106 | F1 |
| MgCO3 [51] | N2 | NS | 510–750 | A&S | 181.16 | 2.1 × 103 | D2 |
| Material & Ref. | Atmosphere | Initial Sample Mass (mg) Particle Sizes | Carbonation Temperatures (°C) | Method | Kinetic Region Ea (kJ mol−1) | ks, (m4 mol−1 s−1)/Reaction Order/Kinetic Reaction Rate (min−1) | Diffusion Region Ea (kJ mol−1) | D (m2 s−1)/Reaction Order/Diffusion Rate (min−1) |
|---|---|---|---|---|---|---|---|---|
| CaO [86] | N2/CO2 (0.2–0.4 atm) | 1.3 Particle sizes: 81 & 137 μm | 500–725 | RPM | 0 | 5.95 × 10−10 m4 mol−1 s−1 CO2 < 10%: F1 | <961°C: 89 >961°C: 180 | 0.0595 cm4 gmol−1 s−1 |
| IL KL [35] | Air/CO2 (0.01–0.1 MPa CO2) | 5–20 | 550–750 | RPM | IL: 21.3 KL: 19.2 | IL:5.559 × 10−10 m4 mol−1 s−1 KL: 5.293 × 10−10 m4 mol−1 s−1 F1 (pCO2 < 100 kPa) F0 (pCO2 > 100 kPa) | IL: 163 KL: 163 | I: 3.37 × 10−6 m2 s−1 K: 4.32 × 10−6 m2 s−1 |
| L [101] | CO2 & O2/air mixture (5–85 kPa CO2) | 3 | 650, 700 & 800 | RPM | 21.3 | 3.335 × 10−9 m4 mol−1 s−1 | 140 | 3.37 × 10−5 m2 s−1 |
| Com. CaO [102] | N2/CO2 (7–50% v/v CO2) | NS | 550–700 | RPM | 46.42 | CO2 < 10%: F1 CO2 > 10%: F0 | 137.7 | 10−16 cms−1 |
| L D [34] | N2/CO2 mixture (25–80% v/v CO2) | 2.9 Particle size: 38–45 μm | 550–850 | Pore model | - | - | L: 215 D: 187 | F1 (pCO2 < 10kPa) F0 (pCO2 > 10kPa) |
| CaO/MY [21] | N2/CO, (0.005–0.015 MPa CO2) | 10 Particle size: 50–75 μm | 500–700 | RPM | 28.4 | 5.44 × 10−6 m s−1 | 88.7 | 1.03 × 10−14 m2 s−1 |
| CaO/CA [87] | N2/CO2 (25%v/v CO2) | 25 | 550–650 | Simplified RPM | - | - | 96.01 | NS |
| L [16] | N2/CO2 (0.002–0.01 MPa) | 15 | NS | Homogeneous particle model | NS | 3.2–8.9 × 10−10 m4 mol−1 s−1 | - | - |
| CaO [80] | N2/CO2, (14%v/v CO2) | 8–10 Particle size: 20 μm | 515–743 | Rate (nucleation) model | NS | 1.33 × 10−5 m3 s−1 (515 °C) | - | - |
| CaO [103] | He/ CO2, (2–30 kPa CO2) | 10 | 650 | Surface nucleation & isotropic growth model | Temperature coefficient: 23.15 | 5.9 × 10−5 m3 s−1 | - | - |
| CaO [79] | N2/CO2 (1–11.7 atm) | 3 Particle size: 15–20 μm | 550–1100 | Grain model | - | - | 238 | 6.5 × 10−5 m2 s−1 (1000 °C) |
| L D [59] | N2/CO2 mixture (25–80% v/v CO2) | 2.9 Particle size: 38–45 μm | 550–850 | Grain model (intrinsic rate constants) | L: 29 D: 24 | F1 (pCO2 < 10 kPa) F0 (pCO2 > 10 kPa) | - | - |
| CaO/MY [21] | N2/CO, (0.005–0.015 MPa CO2) | 10 Particle size: 50–75 μm | 500–700 | OGM | 32.3 | 1.67 × 10−5 m/s | 113.1 | 2.74 × 10−13 m2 s−1 |
| CaO [57] Data from [86] & [104] | N2/CO2 (0.2–0.4 atm) | 1.3 5–20 | 500–725 | Apparent model | [86] 72 A (s−1): 1.03 × 104 [104] 72 A (s−1): 1.16 × 104 | 0.858 min−1 (650°C) | [86] 102.5 A (s−1): 2.33 × 105[104] 189.3 A (s−1): 1.57 × 1010 | 0.375 min−1 (650 °C) |
| CaO [46] | CO2 | 17 | ~890–720 (850 isotherm) | Friedman | 573–414 Average: 350 | 1 × 10−2 min−1 | 1237 | 4 × 10−3 min−1 |
| CaO [46] | N2/CO2 (25 %v/v CO2) | 17 | ~775–500 (650 isotherm) | Friedman | 262–149 Average: 205 | 8 × 10−3 min−1 | 269 | 2 × 10−3 min−1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fedunik-Hofman, L.; Bayon, A.; Donne, S.W. Kinetics of Solid-Gas Reactions and Their Application to Carbonate Looping Systems. Energies 2019, 12, 2981. https://doi.org/10.3390/en12152981
Fedunik-Hofman L, Bayon A, Donne SW. Kinetics of Solid-Gas Reactions and Their Application to Carbonate Looping Systems. Energies. 2019; 12(15):2981. https://doi.org/10.3390/en12152981
Chicago/Turabian StyleFedunik-Hofman, Larissa, Alicia Bayon, and Scott W. Donne. 2019. "Kinetics of Solid-Gas Reactions and Their Application to Carbonate Looping Systems" Energies 12, no. 15: 2981. https://doi.org/10.3390/en12152981
APA StyleFedunik-Hofman, L., Bayon, A., & Donne, S. W. (2019). Kinetics of Solid-Gas Reactions and Their Application to Carbonate Looping Systems. Energies, 12(15), 2981. https://doi.org/10.3390/en12152981







