The Hierarchical Control Algorithm for DC Microgrid Based on the Improved Droop Control of Fuzzy Logic
Abstract
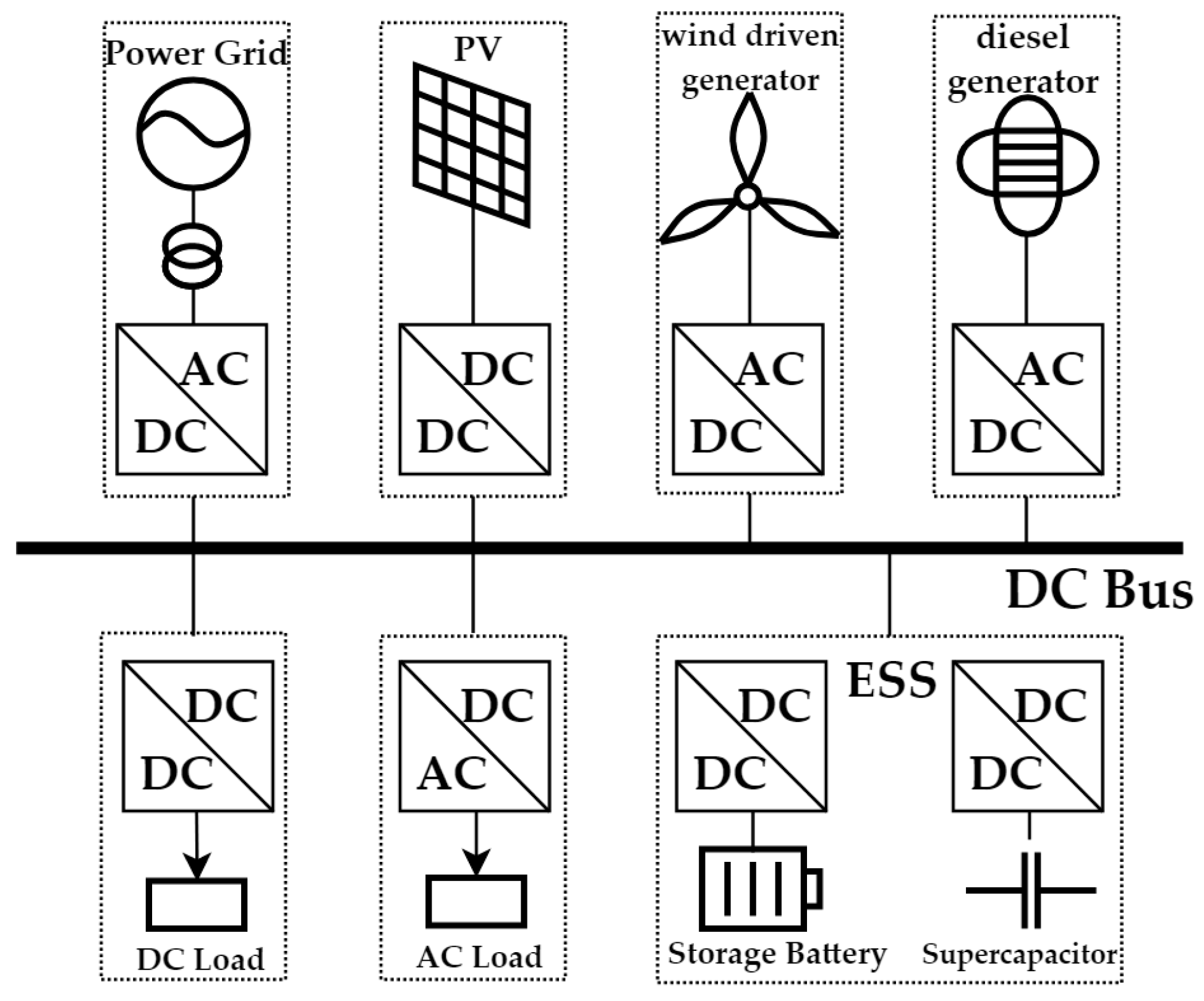
:1. Introduction
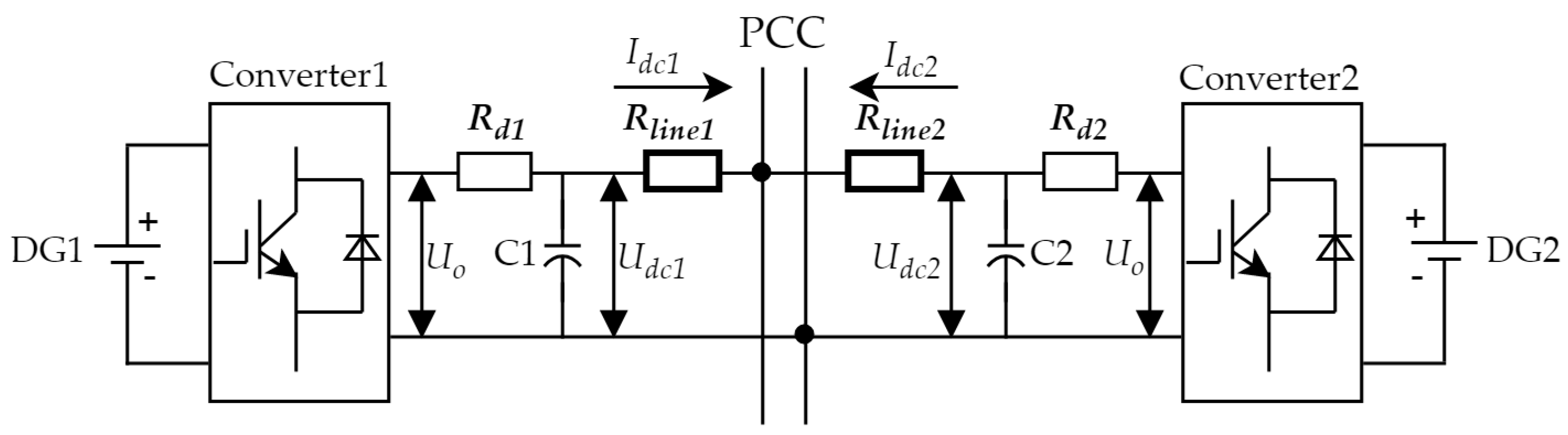
2. DC Droop Control
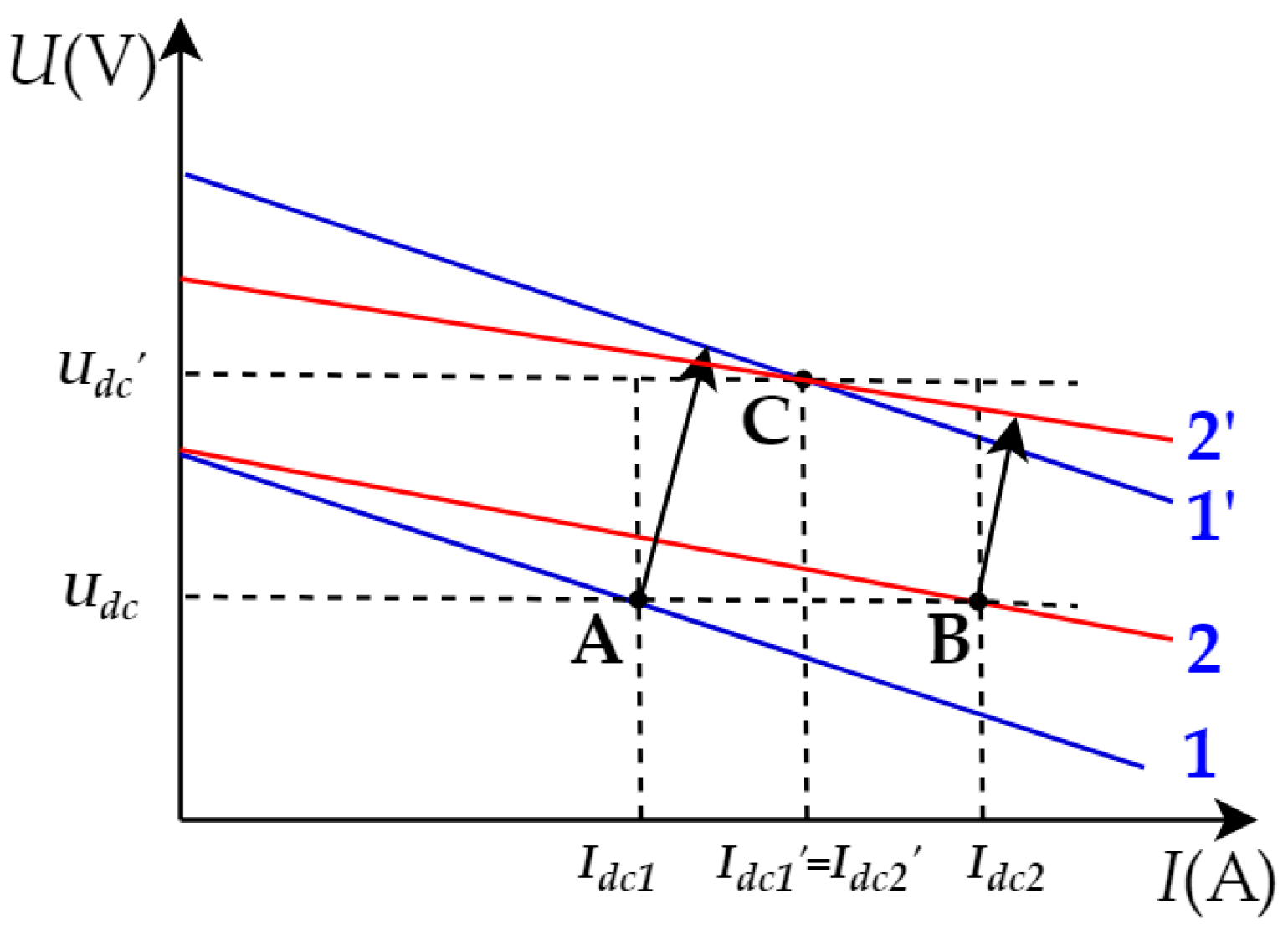
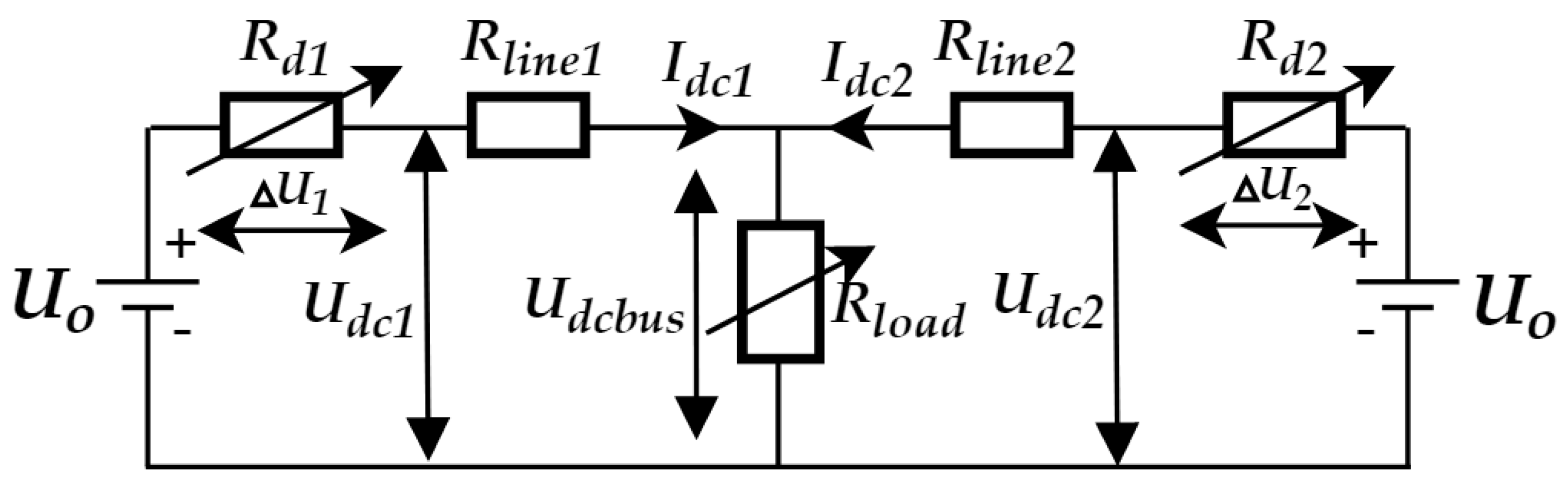
2.1. Principle of DC Droop Control
2.2. Limitations of DC Droop Control
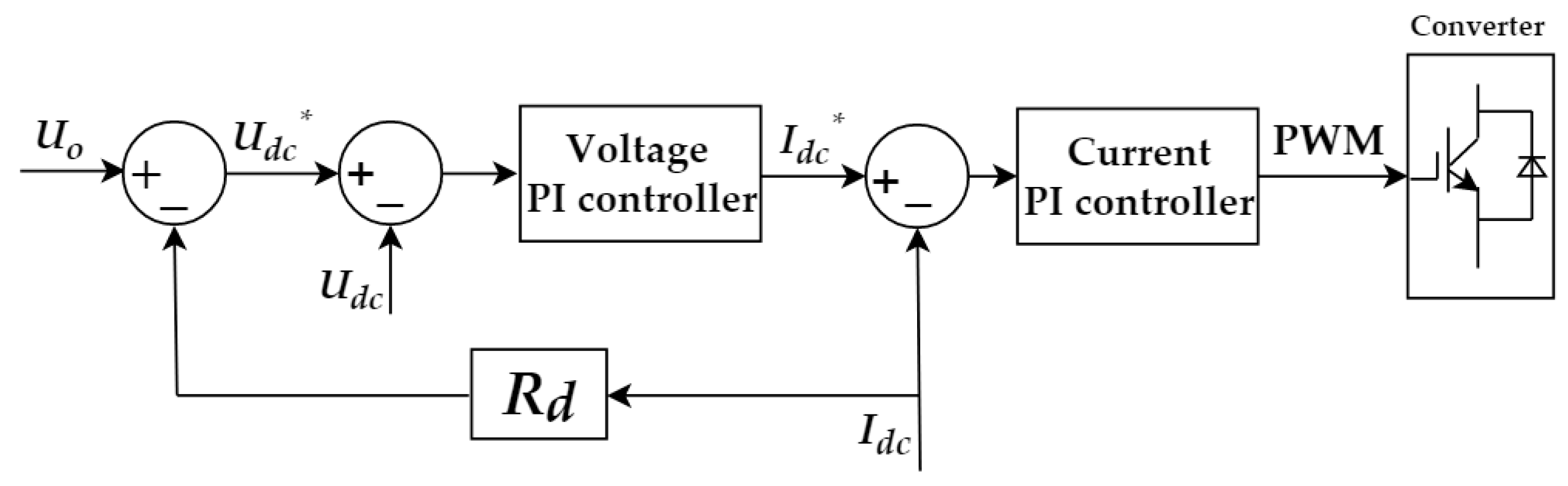
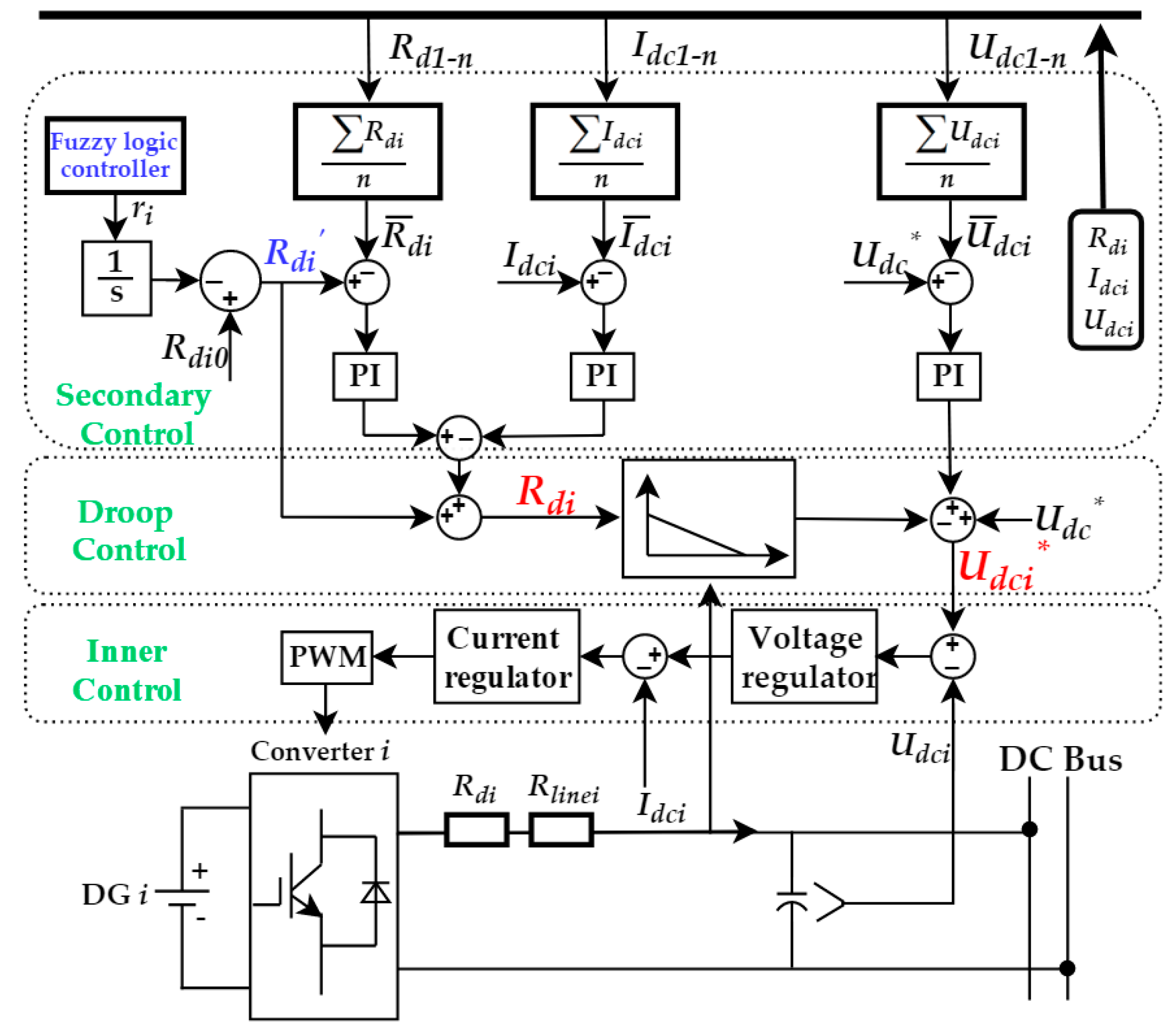
3. The Hierarchical Control Algorithm Based on the Improved Droop Control of Fuzzy Logic
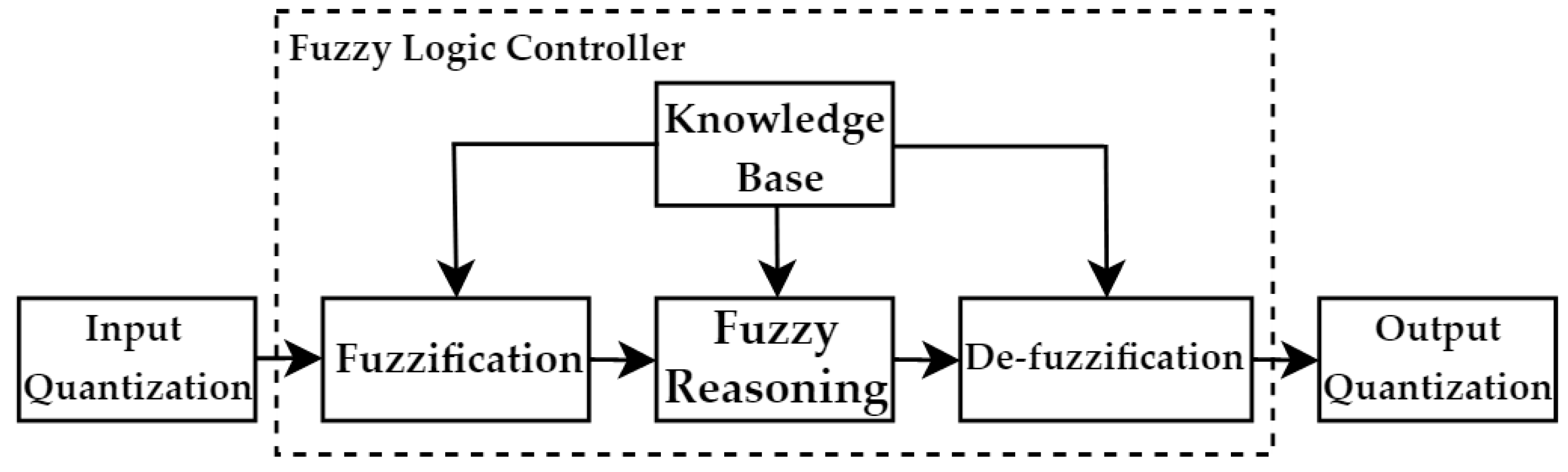
3.1. The Design of Fuzzy Logic Controller
3.1.1. The Fuzzy Logic Controller
3.1.2. Determination of Fuzzy Logic Rules
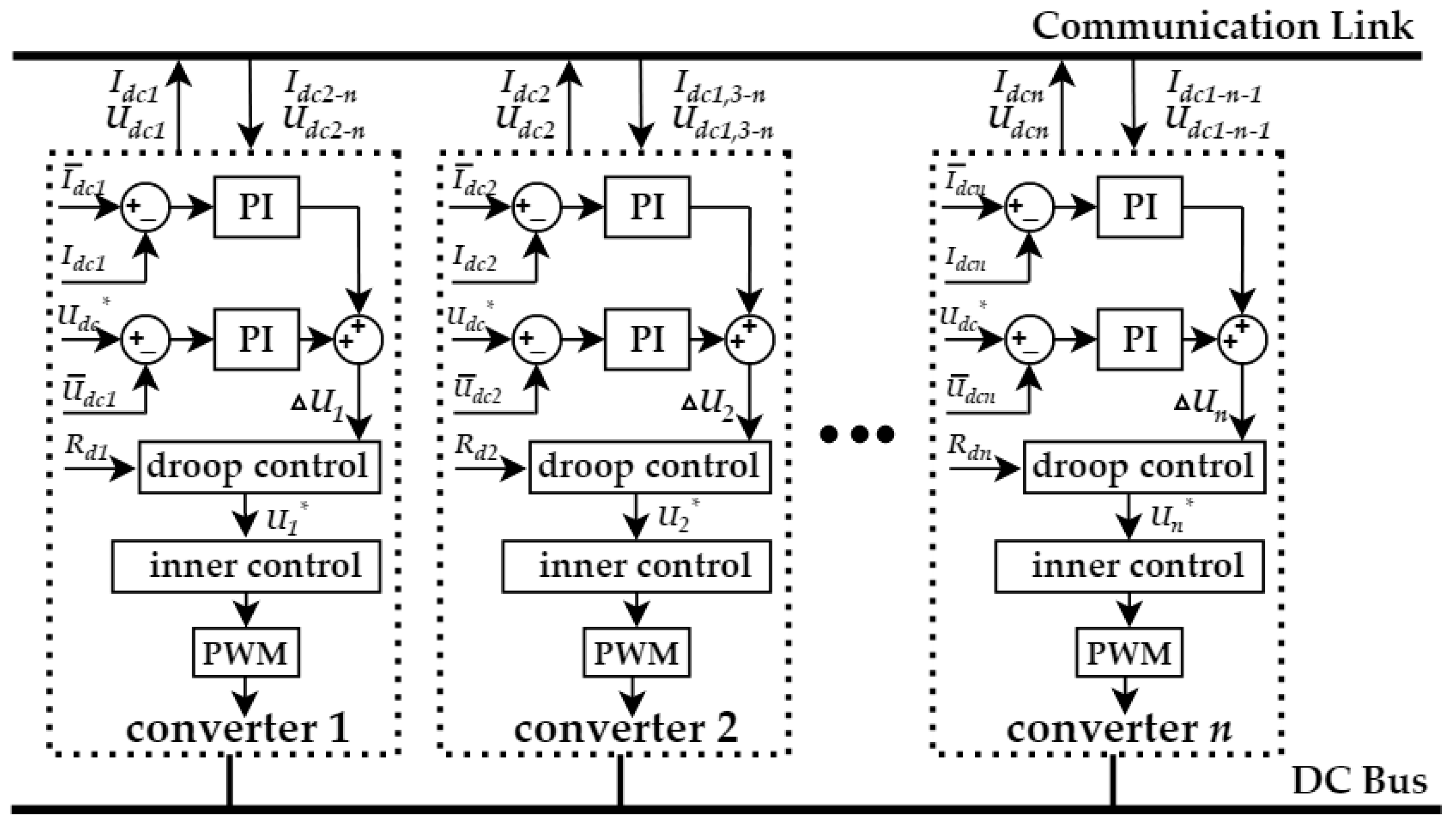
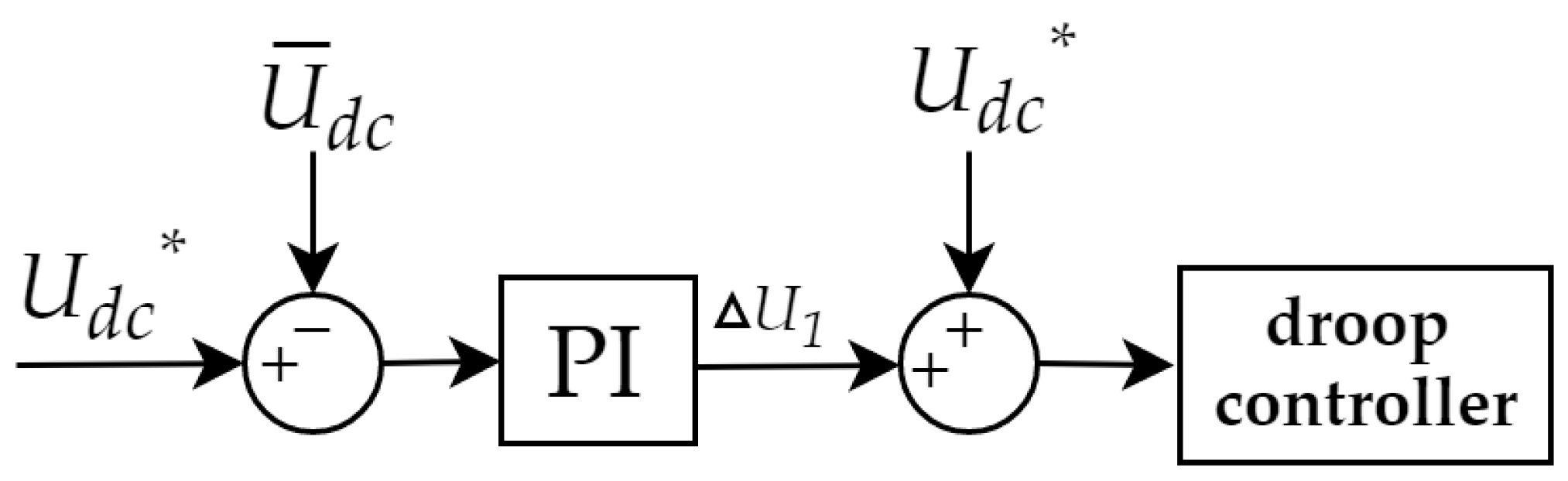
3.2. The Improved Hierarchical Control Algorithm
3.3. Modeling and Analysis of Improved Hierarchical Control Algorithm
4. Simulation Analysis
4.1. Design of Control System Parameters
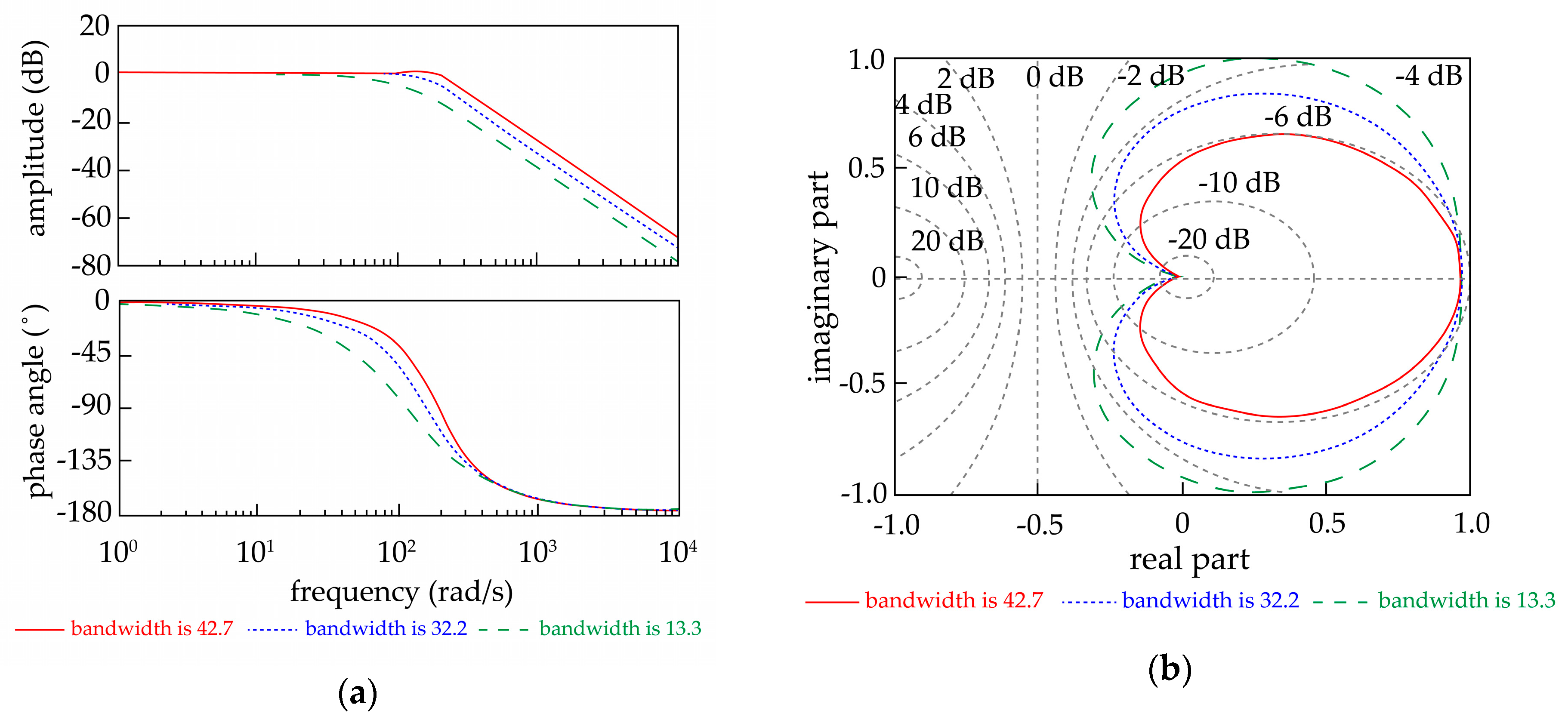
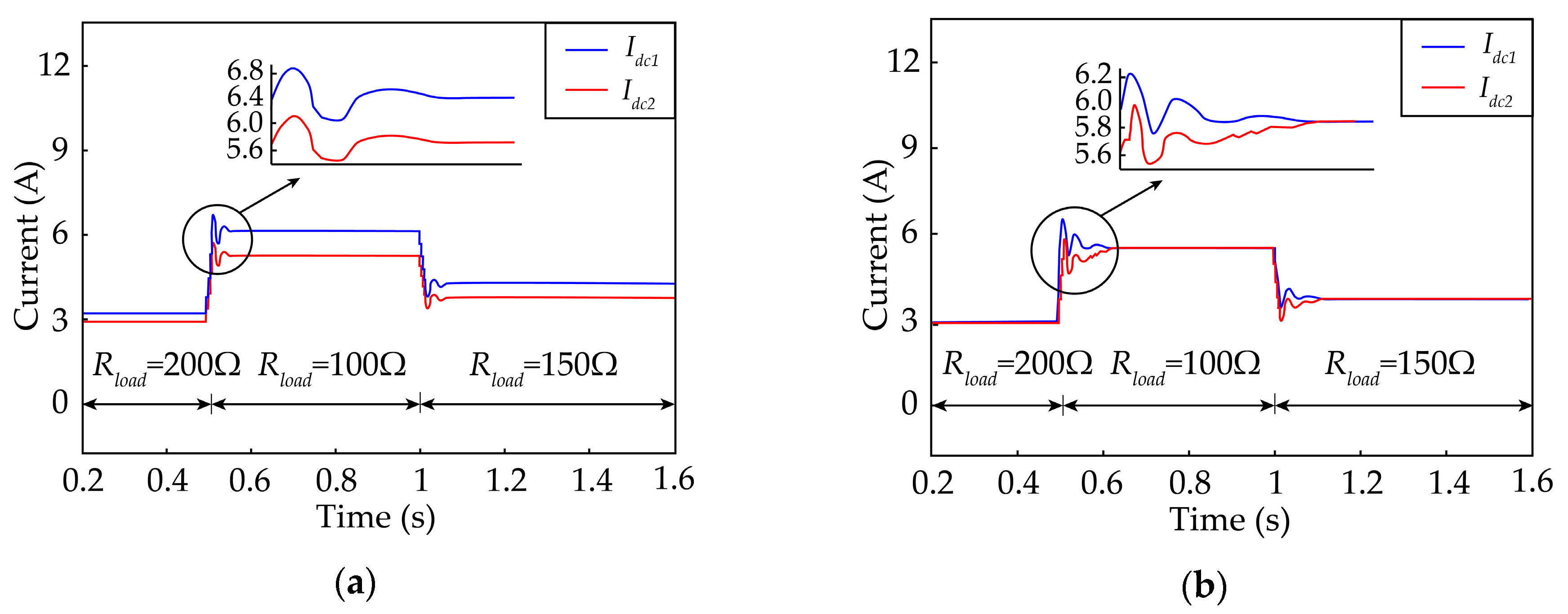
4.2. Simulation Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DC | direct current | |
| DG | distributed generation | |
| SOC | state of charge | |
| Udc/Idc | bus voltage/current | V/A |
| Udc*/Idc* | reference bus voltage/current | V/A |
| U0 | open circuit voltage | V |
| Rd | droop resistance (droop gain) | Ω |
| PCC | point of common coupling | |
| Rline | line resistance | Ω |
| ΔUi | voltage drop through the droop resistance | V |
| Idcf | full load current | A |
| ΔPi | power difference | kW |
| ΔRdi | adjustment of the droop coefficient | Ω |
| Rload | load resistance | Ω |
| // | average voltage/current/droop resistance | V/A/Ω |
| PI | proportion-integral | |
| kpv/kiv | proportional and integral coefficients of voltage regulator | |
| kpc/kic | proportional and integral coefficients of current regulator | |
| kpd/kid | proportional and integral coefficients of droop coefficient regulator | |
| PWM | pulse width modulation |
References
- Mi, Y.; Wu, Y.W.; Zhu, Y.Z.; Fu, Y.; Wang, C.S. Coordinated Control for Autonomous DC Microgrid with Dynamic Load Power Sharing. Power Syst. Technol. 2017, 41, 440–447. [Google Scholar]
- Yang, J.; Jin, X.M.; Yang, X.L.; Wu, X.Z. Overview on power control technologies in hybrid AC-DC microgrid. Power Syst. Technol. 2017, 41, 29–39. [Google Scholar]
- Nasirian, V.; Davoudi, A.; Lewis, F.L.; Guerrero, J.M. Distributed Adaptive Droop Control for DC Distribution Systems. IEEE Trans. Energy Convers. 2014, 29, 944–956. [Google Scholar] [CrossRef] [Green Version]
- Tahim, A.P.N.; Pagano, D.J.; Lenz, E.; Stramosk, V. Modeling and Stability Analysis of Islanded DC Microgrids Under Droop Control. IEEE Trans. Power Electron. 2015, 30, 4597–4607. [Google Scholar] [CrossRef]
- Zhu, S.S.; Wang, F.; Guo, H.; Wang, Q.F.; Gao, Y.X. Overview of Droop Control in DC Microgrid. Proc. CSEE 2018, 38, 72–84. [Google Scholar]
- Du, W.J.; Zhang, J.M.; Zhang, Y.; Qian, Z.M. Stability Criterion for Cascaded System with Constant Power Load. IEEE Trans. Power Electron. 2013, 28, 1843–1851. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.R.; Li, H.M.; Liu, J.P. Hierarchical coordinated control of wind turbine-based DC microgrid. Proc. CSEE 2013, 33, 16–24. [Google Scholar]
- Liu, J.Y.; Han, X.Q.; Wang, L.; Zhang, P.; Wang, J. Operation and Control Strategy of DC Microgrid. Power Syst. Technol. 2014, 38, 886–896. [Google Scholar]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; Vicuna, L.G.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids-A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Xu, Q.W.; Xiao, J.F.; Hu, X.L.; Wang, P.; Lee, M.Y. A Decentralized Power Management Strategy for Hybrid Energy Storage System with Autonomous Bus Voltage Restoration and State-of-Charge Recovery. IEEE Trans. Ind. Electron. 2017, 64, 7098–7108. [Google Scholar] [CrossRef]
- Xu, Q.W.; Hu, X.L.; Wang, P.; Xiao, J.F.; Tu, P.F.; Wen, C.Y.; Yeong, M. A Decentralized Dynamic Power Sharing Strategy for Hybrid Energy Storage System in Autonomous DC Microgrid. IEEE Trans. Ind. Electron. 2017, 64, 5930–5941. [Google Scholar] [CrossRef]
- Dragičević, T.; Guerrero, J.M.; Vasquez, J.C.; Škrlec, D. Supervisory Control of an Adaptive-Droop Regulated DC Microgrid with Battery Management Capability. IEEE Trans. Power Electron. 2014, 29, 695–706. [Google Scholar] [CrossRef]
- Anand, S.; Fernandes, B.G.; Guerrero, J. Distributed control to ensure proportional load sharing and improve voltage regulation in low-voltage DC microgrids. IEEE Trans. Power Electron. 2013, 28, 1900–1913. [Google Scholar] [CrossRef]
- LÜ, Z.Y.; Wu, Z.J.; Dou, X.B.; Hu, M.Q.; Zhao, B. An Adaptive Droop Control for the Islanded DC Microgrid Based on Discrete Consensus Algorithm. Proc. CSEE 2015, 35, 4397–4407. [Google Scholar]
- Xie, W.Q.; Han, M.X.; Wang, H.J.; Li, R.; Wu, M. Multi-source coordinated control strategy of DC micro-grid based on virtual voltage. Proc. CSEE 2018, 38, 1408–1418. [Google Scholar]
- Ding, L.; Han, Q.L.; Wang, L.Y.; Sindi, E. Distributed Cooperative Optimal Control of DC Microgrids with Communication Delays. IEEE Trans. Ind. Inform. 2018, 14, 3924–3935. [Google Scholar] [CrossRef]
- Hu, J.; Duan, J.; Ma, H.; Chow, M.Y. Distributed Adaptive Droop Control for Optimal Power Dispatch in DC Microgrid. IEEE Trans. Ind. Electron. 2018, 65, 778–789. [Google Scholar] [CrossRef]
- Wang, H.J.; Han, M.X.; Guerrero, J.M.; Vasquez, J.C.; Teshager, B.G. Distributed secondary and tertiary controls for I-V droop-controlled-paralleled DC-DC converters. IET Gener. Transm. Distrib. 2018, 12, 1538–1546. [Google Scholar] [CrossRef]
- Lu, X.N.; Sun, K.; Huang, L.P.; Xiao, X.; Guerrero, J.M. Dynamic Load Power Sharing Method with Elimination of Bus Voltage Deviation for Energy Storage Systems in DC Micro-grids. Proc. CSEE 2013, 33, 37–46. [Google Scholar]
- Du, W.J.; Fu, Q.; Wang, H.F. Comparing AC Dynamic Transients Propagated Through VSC HVDC Connection with Master-Slave Control Versus DC Voltage Droop Control. IEEE Trans. Sustain. Energy 2018, 9, 1285–1297. [Google Scholar] [CrossRef]
- Shi, M.X.; Chen, X.; Zhou, J.Y.; Chen, Y.; Wen, J.Y.; He, H.B. Advanced Secondary Voltage Recovery Control for Multiple HESSs in a Droop-Controlled DC Microgrid. IEEE Trans. Smart Grid 2019, 10, 3828–3839. [Google Scholar] [CrossRef]
- He, J.W.; Pan, Y.W.; Liang, B.H.; Wang, C.S. A Simple Decentralized Islanding Microgrid Power Sharing Method Without Using Droop Control. IEEE Tran. Smart Grid 2018, 9, 6128–6139. [Google Scholar] [CrossRef]
- Aderibole, A.; Zeineldin, H.H.; Al Hosani, M.; El-Saadany, E.F. Demand Side Management Strategy for Droop-Based Autonomous Microgrids Through Voltage Reduction. IEEE Trans. Energy Convers. 2019, 34, 878–888. [Google Scholar] [CrossRef]
- Yang, J.; Jin, X.M.; Wu, X.Z.; Jiang, C. An Improved Load Current Sharing Control Method in DC Microgrids. Proc. CSEE 2016, 36, 59–67. [Google Scholar]
- Khorsandi, A.; Ashourloo, M.; Mokhtari, H. A decentralized control method for a low-voltage DC microgrid. IEEE Trans. Energy Convers. 2014, 29, 793–801. [Google Scholar] [CrossRef]
- Lu, X.N.; Guerrero, J.M.; Sun, K.; Vasquez, J.C. An Improved Droop Control Method for DC Microgrids Based on Low Bandwidth Communication with DC Bus Voltage Restoration and Enhanced Current Sharing Accuracy. IEEE Trans. Power Electron. 2014, 29, 1800–1812. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, J.D.; Mao, C.X.; Lu, J.M.; Wang, D.; Huang, H. Optimal Control of Energy Storage System for Wind Power Generation Based on Fuzzy Algorithm. Trans. China Electrotech. Soc. 2012, 27, 235–241. [Google Scholar]
- Ahmadi, S.; Shokoohi, S.; Bevrani, H. A fuzzy logic-based droop control for simultaneous voltage and frequency regulation in an AC microgrid. Electr. Power Energy Syst. 2015, 64, 148–155. [Google Scholar] [CrossRef]
- Yan, L.F.; Liu, J.; Shi, M.X.; Chen, X.; Wen, J.Y. Adaptive Power Allocation Strategy Based on Fuzzy Logic Algorithm for Hybrid Energy Storage System in DC Microgrid. Proc. CSEE 2019, 39, 2658–2669. [Google Scholar]
- Yu, X.W.; She, X.; Ni, X.J.; Huang, A.Q. System Integration and Hierarchical Power Management Strategy for a Solid-State Transformer Interfaced Microgrid System. IEEE Trans. Power Electron. 2014, 29, 4414–4425. [Google Scholar] [CrossRef]
- Guo, Q.L.; Fan, S.; Zhou, C.Y.; Wang, H.; Wang, X.J. Research on Control Strategy of Smooth Switching Between Microgrid and Distribution Network Based on Fuzzy Principle. High Volt. Eng. 2015, 41, 3281–3287. [Google Scholar]
- Li, X.L.; Wang, C.S.; Guo, L.; Zhou, L.H.; Feng, T.B. Key technologies of DC microgrids: An overview. Proc. CSEE 2016, 36, 2–17. [Google Scholar]
- Mi, Y.; Wu, Y.W.; Fu, Y.; Wang, C.S. Hierarchical coordinated control of island DC microgrid with photovoltaic and storage system. Power Syst. Prot. Control 2017, 45, 37–45. [Google Scholar]
- Wang, P.B.; Lu, X.N.; Yang, X.; Wang, W.; Xu, D.G. An Improved Distributed Secondary Control Method for DC Microgrids with Enhanced Dynamic Current Sharing Performance. IEEE Trans. Power Electron. 2016, 31, 6658–6673. [Google Scholar] [CrossRef]
- Zhi, N.; Zhang, H.; Xiao, X. Research on Improved Drop Control Strategy for Improving Dynamic Characteristics of DC Microgrid. Trans. China Electrotech. Soc. 2016, 31, 31–39. [Google Scholar]
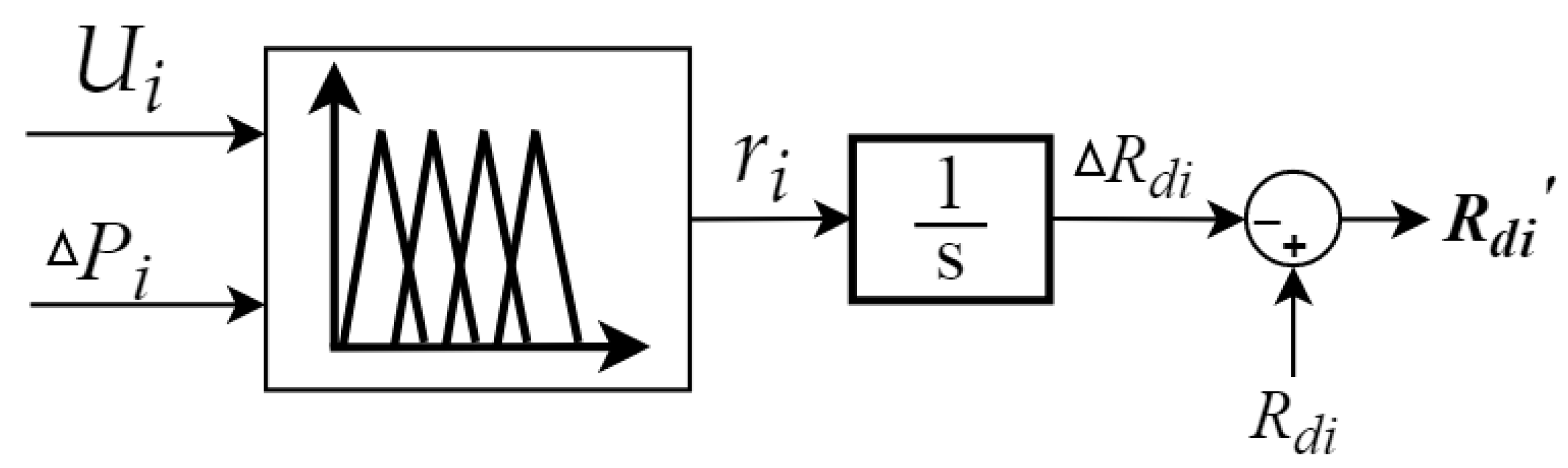
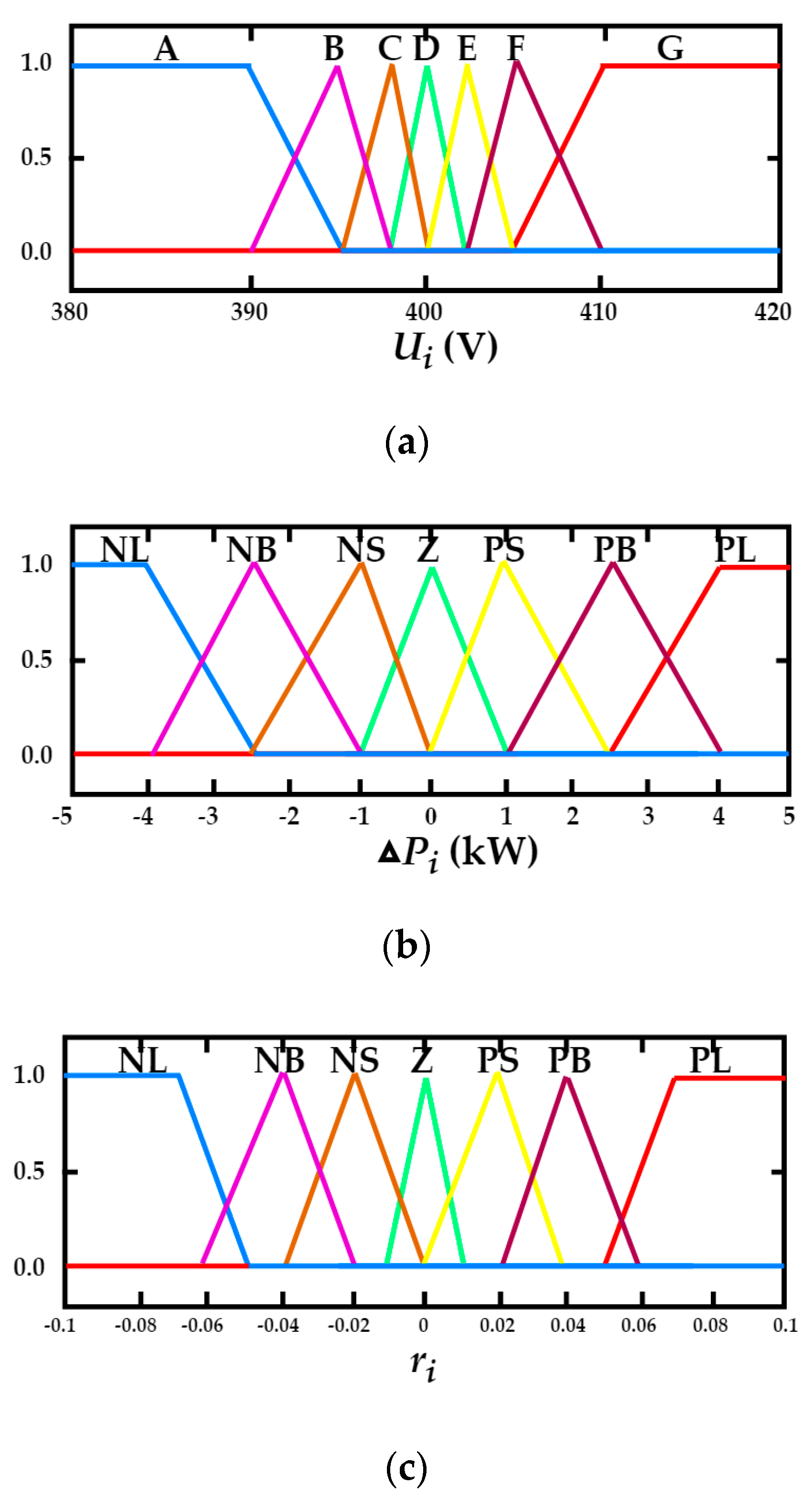




| ri Is NL | ri Is NB | ri Is NS | ri Is Z | ri Is PS | ri Is PB | ri Is PL | |
|---|---|---|---|---|---|---|---|
| Ui | ΔPi | ||||||
| A | PL | PL | PB | Z | Z | Z | NB |
| B | PL | PL | PB | Z | Z | NS | NB |
| C | PL | PB | PS | Z | NS | NB | NL |
| D | PL | PB | PS | Z | NS | NB | NL |
| E | PL | PB | PS | Z | NS | NB | NL |
| F | PB | PS | Z | Z | NB | NL | NL |
| G | PB | Z | Z | Z | NB | NL | NL |
| Symbol | Parameters | Values |
|---|---|---|
| Udc | DC bus voltage (V) | 400 |
| L | converter filters inductance (mH) | 1.5 |
| rL | filter inductance parasitic resistance (Ω) | 0.03 |
| C | DC bus capacitance (mF) | 0.6 |
| Rline1 | line resistance (Ω) | 0.3 |
| Rline2 | line resistance (Ω) | 0.3, 0.4, 0.6 |
| Rload | load resistance (Ω) | 200, 100, 150 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Chen, K.; Chi, S.; Lyu, L.; Cai, G. The Hierarchical Control Algorithm for DC Microgrid Based on the Improved Droop Control of Fuzzy Logic. Energies 2019, 12, 2995. https://doi.org/10.3390/en12152995
Zhang L, Chen K, Chi S, Lyu L, Cai G. The Hierarchical Control Algorithm for DC Microgrid Based on the Improved Droop Control of Fuzzy Logic. Energies. 2019; 12(15):2995. https://doi.org/10.3390/en12152995
Chicago/Turabian StyleZhang, Liang, Kang Chen, Shengbin Chi, Ling Lyu, and Guowei Cai. 2019. "The Hierarchical Control Algorithm for DC Microgrid Based on the Improved Droop Control of Fuzzy Logic" Energies 12, no. 15: 2995. https://doi.org/10.3390/en12152995




