Optimal Sizing of Hydro-PV-Pumped Storage Integrated Generation System Considering Uncertainty of PV, Load and Price
Abstract
1. Introduction
- (1)
- The nonlinear characteristics of the output, reservoir, water level, flow and other variables of cascade hydropower stations are analyzed, and the nonlinear model of ladder water is established, considering the uncertainty of PV’s output, based on the normal probability distribution model the uncertainty model of PV is established. The model of the pumped storage power station is established with consideration of the conversion constraints of units.
- (2)
- On the basis of the complementary characteristics of the hydropower station, PV and pumped storage, the output characteristic model of hydro-PV-pumped storage integrated generation system is established. The volatility ration of the transaction’s curve and coefficient of load tracking are constructed as the index of complementary effect.
- (3)
- The uncertainty model of load and spot price are established. The Pearson correlation coefficient is used to define the correlation between the transaction’s curve and the spot price. All of them would affect the economy of the system.
- (4)
- Considering the above factors, the sizing model of integrated generation system with meeting the complementary and maximum annual revenue is proposed, the economy of the system could be improved while ensuring the complementary index.
- (5)
- The rest of this paper is organized as followed. In Section 2, the output characteristic model of hydro-PV-pumped storage integrated generation system and performance indices of the system are established. Section 3 represents the sizing model of integrated generation system in the electricity market with considering uncertainty of PV and load. In Section 4, the sizing method of the hydro-PV-pumped storage integrated generation system is proposed. In Section 5, case studies verify the effectiveness of the proposed model. The conclusion is given in Section 6.
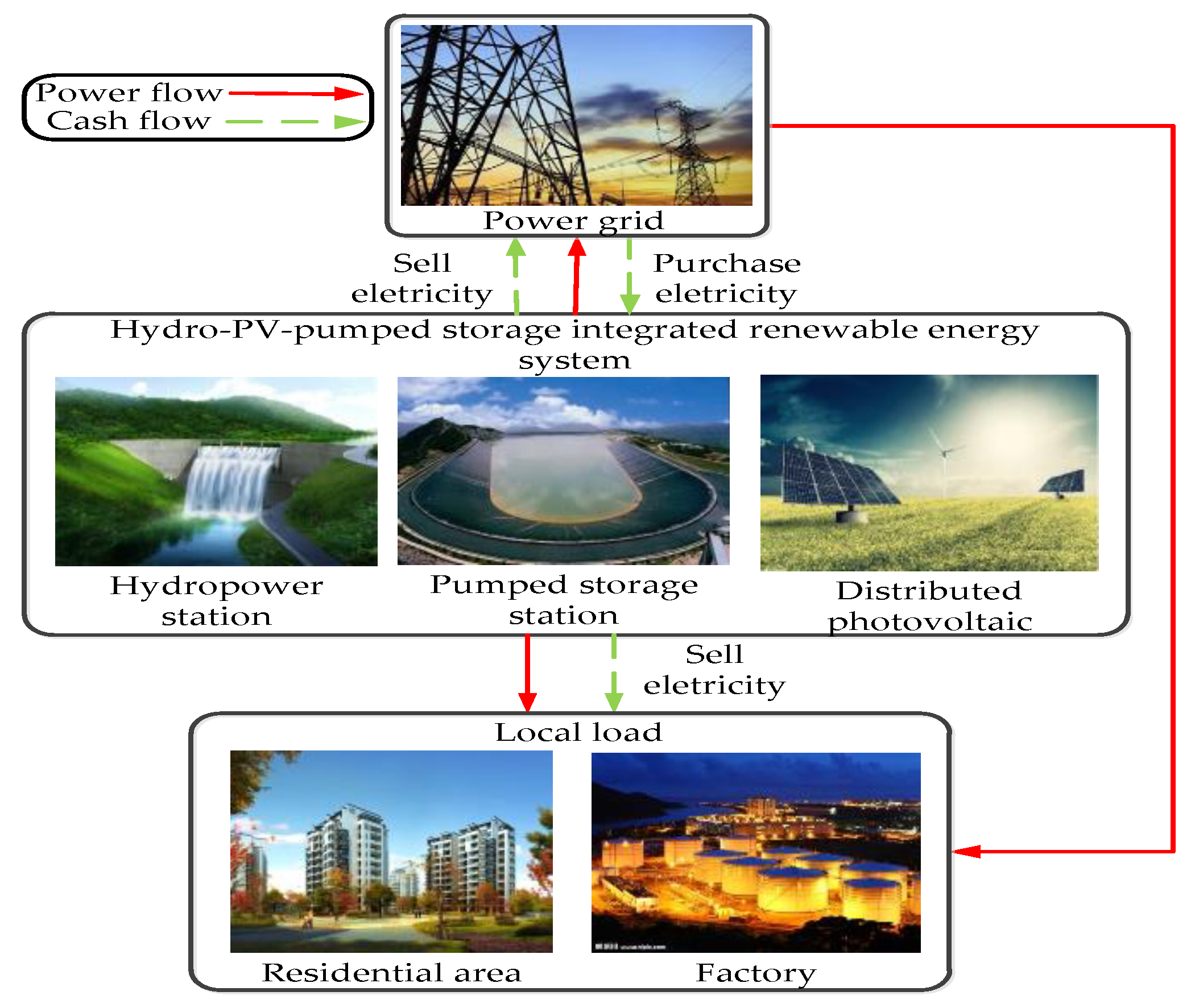
2. Hydro-PV-Pumped Storage Integrated Generation System
2.1. Modeling of the Hydro-PV-Pumped Storage Integrated Generation System
2.1.1. Modeling of the Hydropower Station
2.1.2. Modeling of the Pumped Storage Station
2.1.3. Modeling of Distributed PV’s
2.2. Complementary Index of the Integrated Generation System
3. Sizing Model of the Integrated Generation System Combined Market Operation
3.1. Uncertainty Model of the Spot Price
3.2. Degree of Matching between Transaction‘s Curve and Spot Price
3.3. Uncertainty Analysis of the Load
3.4. Sizing of the Hydro-PV-Pumped Storage Integrated Generation System in the Electricity Market
3.4.1. Profit from the Local Load
3.4.2. Cost of Purchasing Electricity or Profit from Selling Electricity in the Day-Ahead Market
3.4.3. Cost of Purchasing Electricity or Profit from Selling Electricity in the Real-Time Market
3.4.4. Abandoned Water Cost of the Hydropower Station
3.4.5. Generation and Pumping Cost of the Pumped Storage Unit
3.4.6. Costs of Investment and Maintenance of the Integrated Generation System
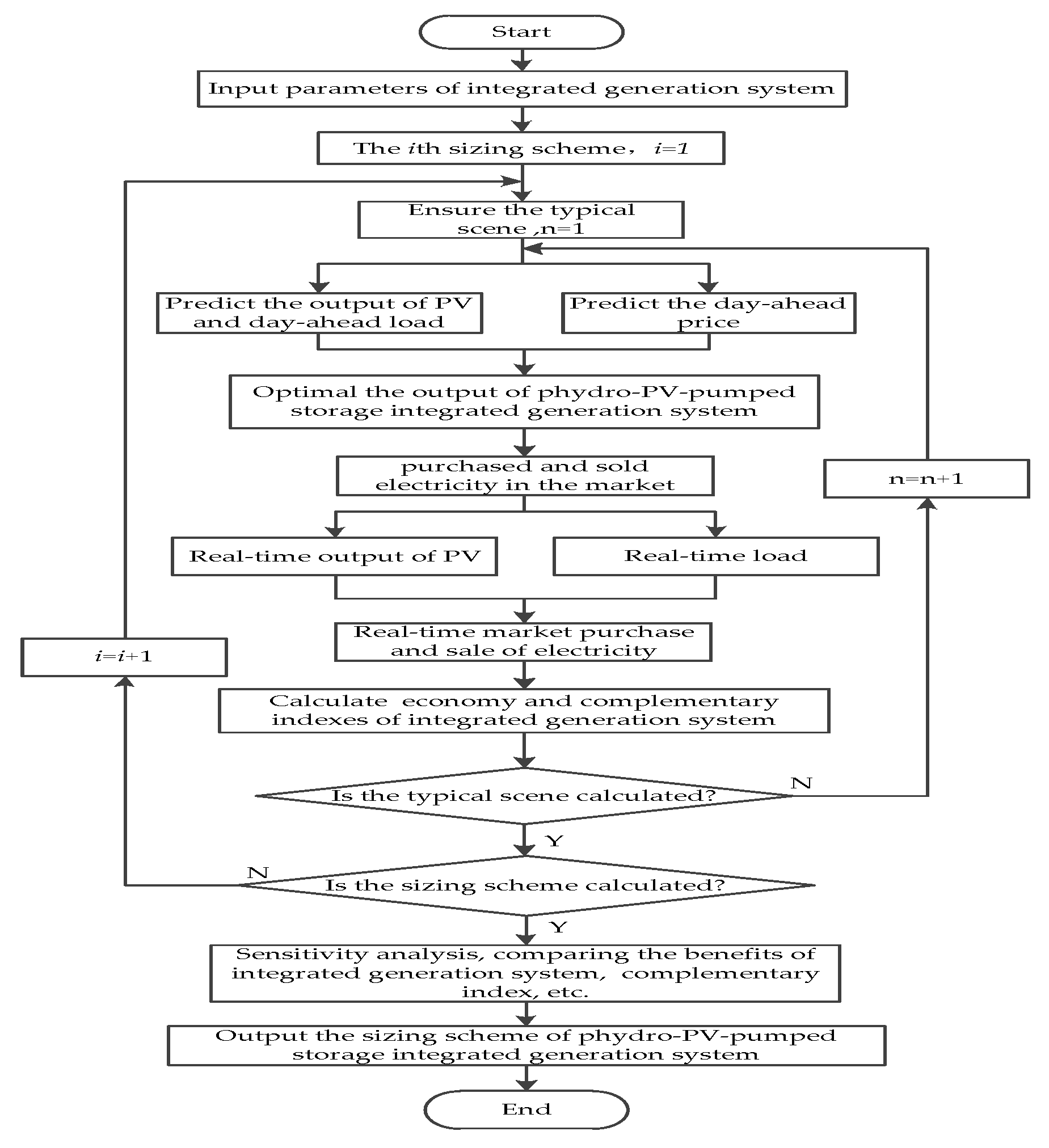
4. The Steps of Sizing of the Hydro-PV-Pumped Storage Generation System
- (1)
- Input the raw data including parameters of hydropower stations, PV’s and the pumped storage unit, local load data and historical electricity price data.
- (2)
- Plan the sizing of the hydro-PV-pump storage integrated generation system. The sizing set of the power generation system is determined. The determined sizing scheme is selected, the corresponding equivalent annual cost and annual maintenance cost of the complementary power generation system are obtained, and the determined typical scenario is selected for analysis.
- (3)
- Local load, output of PV and spot price are predicted, on the basis of the above data, the output of the integrated generation system is optimized and the transaction’s curve is obtained. Based on real-time load’s curve and real-time output’s curve of PV, the predicted deviation between day-ahead and real-time is received, the purchase and sale of electricity is determined. The revenue from selling electricity and cost from purchasing electricity in a typical scenario is calculated. All the typical scenarios are calculated, the system benefits of the scheme can be obtained.
- (4)
- All the planning have been calculated, sensitivity analysis of the influence for some sensitive parameters is carried out, such as different complementary indices, sizing schemes and spot price uncertainty on the economy of power generation system.
- (5)
- The indices of the system of all schemes are compared, the sizing scheme of hydro-PV-pumped storage integrated generation system is proposed based on trade-off consideration of economics and complementary characteristics.
5. Case Study and Discussion
5.1. Case Description
5.2. Case Simulation
5.3. Discussion
- Considering the nonlinear characteristics of cascade hydropower, the operating conditions of pumped storage and uncertainty of PV, the output characteristic model hydro-PV-pumped storage integrated generation system was proposed.
- The optimization of complementarity of hydropower and PV at the minute time scale was achieved, which ensured the smooth and stable total output. Full consumption of PV’s was achieved by using the energy storage characteristics of pumped storage.
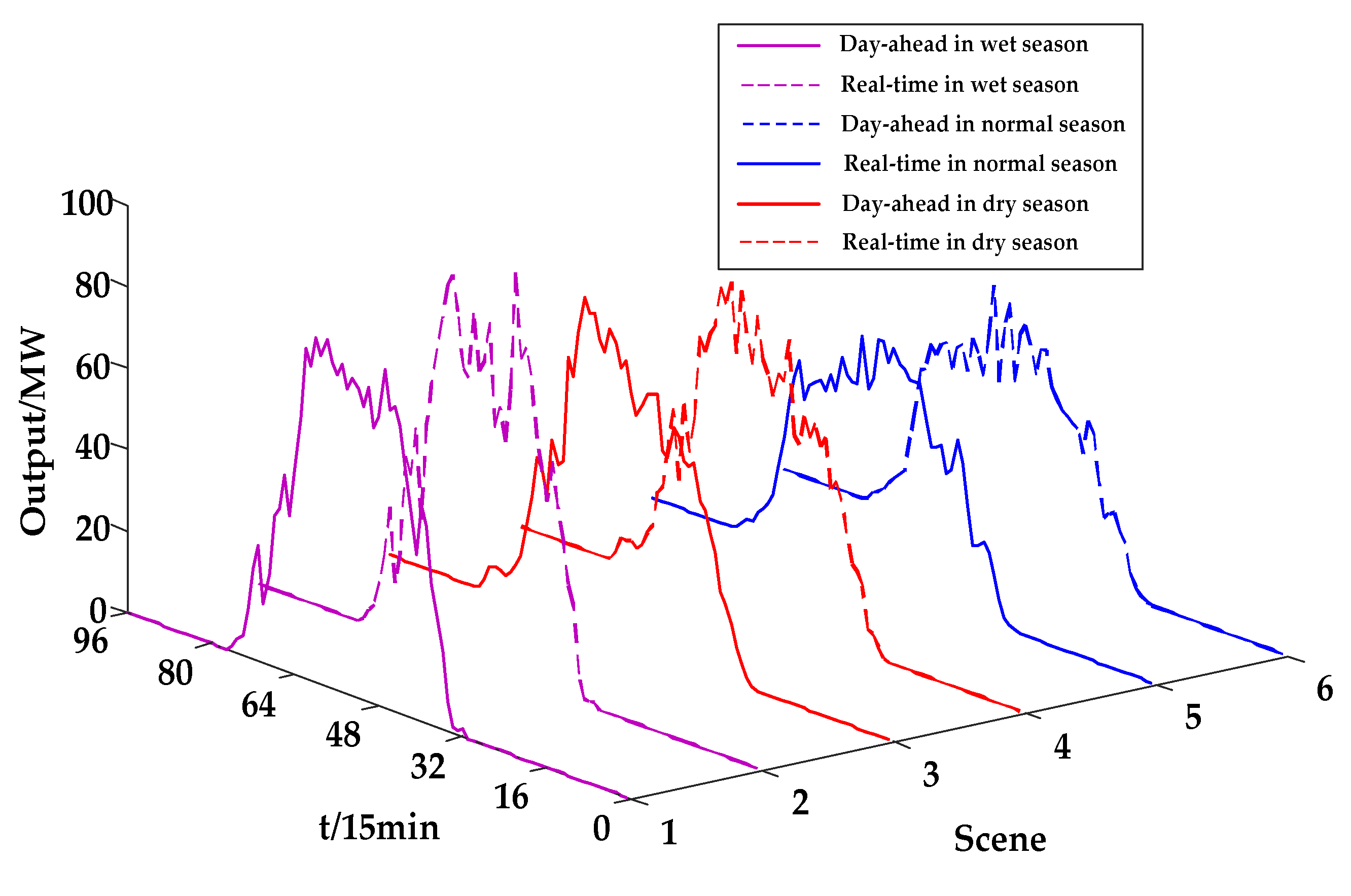
- In the electricity market, the output of hydro-PV-pumped storage integrated generation system was optimized in the day-ahead market, the power deviation was balanced in the real-time market.
- Complementary indices of the system were constructed, complementary indices and economy were mutually restrictive by the sensitivity analysis, this sizing method could maximize profits with meeting complementary indices.
6. Conclusions
- With utilizing the output characteristics of various energy source, hydro-PV-pumped storage integrated generation system could improve the complementary performance and schedulability of the system, the fluctuation of output could suppress on a smaller time scale, and full consumption of PV’s was achieved by using the energy storage characteristics of pumped storage.
- The complementary ability of the hydro-PV-pumped storage integrated generation system in different typical scenarios was an obvious difference. The complementary index in the flood season was obviously better than that in the normal and dry season, but the cost of abandoned water in the wet season was higher than that in the normal and dry season.
- In different complementary modes, the complementary index, spot price correlation coefficient and system benefits of the system had certain regularity changes. There was a mutual constraint between the both, as the complementary index decreased, the volatility of the day-ahead transaction’s curve would be smaller, which would reduce the annual revenue and influence the economy of sizing of the system.
- Considering the uncertainty of PV, spot price and load, the reasonable sizing scheme of the integrated generation system combined market operation mode proposed could improve the economy with meeting actual complementary indices in different typical scenes.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Parameters of relational function of head loss—discharge volume of reservoir | |
| Parameters of relational function of downstream water level—discharge volume | |
| Parameters of relational function of reservoir storage—upstream water level | |
| Abandoned water cost of hydropower station in the day in the typical scene | |
| Generation cost of pumped storage in the day in the typical scene | |
| Sum of the equivalent annual cost of investment and annual maintenance cost | |
| The start-up cost of the generation and pumping of pumped storage station | |
| Start-up cost of pumping of the pumped storage station at the period of | |
| Start-up cost power generation of the pumped storage station at the period of | |
| Annual total cost of the hydropower station | |
| Equivalent annual cost of the hydropower station | |
| Maintenance cost of the hydropower station | |
| Annual total cost of the pumped storage station | |
| Equivalent annual cost of the pumped storage station | |
| Maintenance cost of the pumped storage station | |
| Annual total cost of the PV station | |
| Equivalent annual cost of the PV station | |
| Maintenance cost of the PV station | |
| Equivalent annual cost of equipment | |
| Total cost of investment of equipment | |
| The number of days for a typical scene | |
| Average value of net head of hydropower stations in a day | |
| Net power generation head of hydropower station at the period of | |
| Head loss of reservoir at the period of | |
| Natural water of hydropower station at the period of | |
| Coefficient of load tracking | |
| Maximum volatility ratio of power exchange to power grid | |
| Power–temperature coefficient of PV | |
| Life-cycle of equipment | |
| Light intensity at the period of | |
| Test light intensity | |
| Number of hydropower stations, distributed PV and pumped storage station. | |
| Number of distributed PV stations | |
| Number of pumped storage stations | |
| Number of typical scenes | |
| Value of power exchange to power grid at the period of | |
| The most power exchange | |
| Average value of exchange power in a day | |
| Output of hydroelectric hydropower station at the period of | |
| Minimum output of the hydropower station | |
| Maximum output of the hydropower station | |
| Maximum output of the integrated generation system | |
| Pumping power of the pumped storage station at the period of | |
| Power generation of the pumped storage station at the period of | |
| Minimum pumping power of the pumped storage station | |
| Maximum pumping power of the pumped storage station | |
| Minimum power generation of the pumped storage station | |
| Maximum power generation of the pumped storage station | |
| Predictive output of PV at the period of | |
| Actual output of PV at the period of | |
| Maximum output of distributed PV in a standard test environment | |
| Prediction deviation of PV at the period of | |
| Load value at the period of | |
| Load value at the period of | |
| Day-ahead predicted load and at the period of | |
| Real-time load at the period of | |
| Transacted electricity in the day-ahead market at the period of | |
| Transacted electricity in the real-time market at the period of | |
| Discharge volume of reservoir at the period of | |
| Abandoned water hydropower station at the period of | |
| Abandoned water hydropower station at the period of | |
| Average power generation flow of hydropower station at the period of | |
| Average power generation flow of hydropower station at the period of | |
| Minimum power generation flow of the hydropower station | |
| Maximum power generation flow of the hydropower station | |
| Interval water of hydropower station at the period of | |
| Pearson correlation coefficient | |
| Profit from local load in the day in the typical scene | |
| Profit from the day-ahead market in the day in the typical scene | |
| Profit from the real-time market in the day in the typical scene | |
| Annual income of the integrated generation system | |
| Profit from the local load | |
| Cost of purchasing electricity or profit from selling electricity in the day-ahead market | |
| Cost of purchasing electricity or profit from selling electricity in the real-time market | |
| Optimized scheduling time period | |
| Total number of time period | |
| Ambient temperature at the location of distributed PV at the period of | |
| Reference temperature | |
| Water volume of the reservoir at the period of | |
| Water volume of the reservoir at the period of | |
| Minimum water quantity of the reservoir of the hydropower station | |
| Maximum water quantity of the reservoir of the hydropower station | |
| Initial water volume of the reservoir during the scheduling period | |
| Final water volume of the reservoir during the scheduling period | |
| Amount of change of water volume of the reservoir i in a day, | |
| Water volume of the pumped storage station at the period of | |
| Water volume of the pumped storage station at the period of , | |
| Minimum water volume of the pumped storage station | |
| Maximum water volume of the pumped storage station | |
| Initial the water volume of the pumped storage during the scheduling period. | |
| Final the water volume of the pumped storage during the scheduling period | |
| Pumping condition state variable of the pumped storage station at the period of | |
| Generation condition state variable of the pumped storage station at the period of | |
| Upstream water level of the reservoir at the period of | |
| Downstream water level of the reservoir at the period of | |
| Upstream water level of the reservoir at the period of | |
| Change rate (p.u.) of total output | |
| Proportional coefficient | |
| Change rate (p.u.) of total output | |
| Standard deviation | |
| Discount rate | |
| Generation efficiency of the hydropower station | |
| Electricity/water conversion coefficient at pumping condition | |
| Electricity/water conversion coefficient at generation condition | |
| Error factor between day-ahead load and real-time load at the period of | |
| Average value of spot price in a day | |
| Fixed electricity price | |
| Real-time price at the period of | |
| Penalty factor of abandoned water at the period of | |
| Day-ahead price at the period of | |
| Difference price between real-time price and day-ahead price at the period of | |
| Predicted day-ahead price at the period of | |
| Maximum predicted price | |
| Prediction error factor of day-ahead price at the period of | |
| Conservative degree of robust optimization of spot price |
References
- Nehrir, M.H.; Wang, C.; Strunz, K. A Review of Hybrid Renewable/Alternative Energy Systems for Electric Power Generation: Configurations, Control, and Applications. IEEE Trans. Sustain. Energy 2011, 2, 392–403. [Google Scholar] [CrossRef]
- Garcia, P.; Garcia, C.; Fernandez, L.M. ANFIS-Based Control of a Grid-Connected Hybrid System Integrating Renewable Energies, Hydrogen and Batteries. IEEE Trans. Ind. Inform. 2014, 10, 1107–1117. [Google Scholar] [CrossRef]
- Yang, H.T.; Huang, C.M.; Huang, Y.C.; Pai, Y.S. A Weather-Based Hybrid Method for 1-Day Ahead Hourly Forecasting of PV Power Output. IEEE Trans. Sustain. Energy 2014, 5, 917–926. [Google Scholar] [CrossRef]
- Gao, Y.J.; Xue, F.S.; Yang, W.H.; Yang, Q.; Sun, Y.J.; Sun, Y.P.; Liang, H.F.; Li, P. Optimal operation modes of photovoltaic battery energy storage system based power plants considering typical scenarios. Prot. Control Mod. Power Syst. 2017, 2, 36. [Google Scholar] [CrossRef]
- Li, J.H.; Wang, S.; Ye, L.; Fang, J. A coordinated dispatch method with pumped-storage and battery-storage for compensating the variation of wind power. Prot. Control Mod. Power Syst. 2018, 3, 2. [Google Scholar] [CrossRef]
- Ming, B.; Huang, Q.; Wang, Y.M.; Fang, W.; Xie, X.P. The feasibility analysis of short-term scheduling for joint operation of hydropower and photoelectric. Acta Energiae Solaris Sinica 2015, 36, 2731–2737. (In Chinese) [Google Scholar] [CrossRef]
- Shang, Y.Z.; Xu, Y.; Shang, L.; Fan, Q.X.; Wang, Y.Y.; Liu, Z.W. A method of direct, real-time forecasting of downstream water levels via hydropower station reregulation: A case study from Ge zhou ba Hydropower Plant, China. J. Hydrol. 2019, 573, 895–907. [Google Scholar] [CrossRef]
- Guan, X.; Wu, J.; Gao, F.; Sun, G.J. Optimization-Based Generation Asset Allocation for Forward and Spot Markets. IEEE Trans. Power Syst. 2008, 23, 1796–1808. [Google Scholar] [CrossRef]
- Baillo, A.; Ventosa, M.; Rivier, M.; Ramos, A. Optimal offering strategies for generation companies operating in electricity spot markets. IEEE Trans. Power Syst. 2004, 19, 745–753. [Google Scholar] [CrossRef]
- Ming, B.; Liu, P.; Guo, S.L.; Zhang, X.Q.; Feng, M.Y.; Wang, X.X. Optimizing utility-scale photovoltaic power generation for integration into a hydropower reservoir by incorporating long-and short-term operational decisions. Appl. Energy 2017, 204, 432–445. [Google Scholar] [CrossRef]
- Sun, K.Q.; Li, K.J.; Pan, J.P.; Liu, Y.; Liu, Y.L. An optimal combined operation scheme for pumped storage and hybrid wind-photovoltaic complementary power generation system. Appl. Energy 2019, 242, 155–1163. [Google Scholar] [CrossRef]
- Zhang, H.X.; Lu, Z.X.; Hu, W.; Wang, Y.T.; Dong, L.; Zhang, J.T. Coordinated optimal operation of hydro–wind–solar integrated systems. Appl. Energy 2019, 242, 883–896. [Google Scholar] [CrossRef]
- Jurasz, J.; Ciapała, B. Solar–hydro hybrid power station as a way to smooth power output and increase water retention. Sol. Energy 2018, 173, 675–690. [Google Scholar] [CrossRef]
- Ioannis, K.; Sándor, S.; Fabio, M.F.; Thomas, H.; Katalin, B. A methodology for optimization of the complementarity between small-hydropower plants and solar PV systems. Renew. Energy 2016, 87, 1023–1030. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, J.; Li, G.; Zhang, B. Cost reduction of a hybrid energy storage system considering correlation between wind and PV power. Prot. Control Mod. Power Syst. 2016, 1, 11. [Google Scholar] [CrossRef]
- Xu, B.; Chen, D.Y.; Kumar, M.V.; Xiao, Y.; Yue, Y.; Xing, Y.Q.; Li, P.Q. Modeling a pumped storage hydropower integrated to a hybrid power system with solar-wind power and its stability analysis. Appl. Energy 2019, 248, 446–462. [Google Scholar] [CrossRef]
- Xu, Y.; Singh, C. Adequacy and Economy Analysis of Distribution Systems Integrated with Electric Energy Storage and Renewable Energy Resources. IEEE Trans. Power Syst. 2012, 27, 2332–2341. [Google Scholar] [CrossRef]
- He, G.; Chen, Q.; Kang, C.; Xia, Q.; Poolla, K. Cooperation of Wind Power and Battery Storage to Provide Frequency Regulation in Power Markets. IEEE Trans. Power Syst. 2017, 32, 3559–3568. [Google Scholar] [CrossRef]
- Pérez-Díaz, J.I.; Wilhelmi, J.R.; Arévalo, L.A. Optimal short-term operation schedule of a hydropower plant in a competitive electricity marke. Energy Convers. Manag. 2010, 51, 2955–2966. [Google Scholar] [CrossRef]
- Koraki, D.; Strunz, K. Wind and Solar Power Integration in Electricity Markets and Distribution Networks Through Service-centric Virtual Power Plants. IEEE Trans. Power Syst. 2018, 33, 473–485. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, L.Z. Long Term Optimal Operation of Cascade Hydropower Based on Multicore Cluster Parallel Computing and Large System Decomposition-coordination. Proc. CSEE 2017, 37, 2479–2490. (In Chinese) [Google Scholar] [CrossRef]
- Xia, P.; Deng, C.H.; Long, Z.J.; Yao, W.W.; Zhang, K.; Wang, W.Z. Robust Unit Commitment with Pumped Storage Units for Wind Power Accommodation. Autom. Electr. Power Syst. 2018, 42, 47–55. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Y.F.; Fu, Y.C.; Sun, L.; Xue, H. Ultra-Short Term Prediction Model of Photovoltaic Output Power Based on Chaos-RBF Neural Network. Power Syst. Technol. 2018, 42, 1110–1116. (In Chinese) [Google Scholar] [CrossRef]
- Conejo, A.J.; Contreras, J.; Espínola, R.; Plazas, M.A. Forecasting electricity prices for a day-ahead pool-based electric energy market. Int. J. Forecast. 2005, 21, 435–462. [Google Scholar] [CrossRef]
- Zhang, X.D.; Wang, H.J.; Geng, W.; Zeng, M.; Zhou, X. Robust power-loss cost optimization model considering price uncertainty for active distribution network. Electr. Power Autom. Equip. 2017, 37, 131–138. (In Chinese) [Google Scholar] [CrossRef]
- Xu, W.; Chang, C.; Hung, Y.S.; Fung, P.C.W. Asymptotic Properties of Order Statistics Correlation Coefficient in the Normal Cases. IEEE Trans. Signal Process. 2008, 56, 2239–2248. [Google Scholar] [CrossRef]
- Ke, B.R.; Ku, T.T.; Ke, Y.L.; Chuang, C.Y.; Chen, H.Z. Sizing the Battery Energy Storage System on a University Campus with Prediction of Load and Photovoltaic Generation. IEEE Trans. Ind. Appl. 2016, 52, 1136–1147. [Google Scholar] [CrossRef]


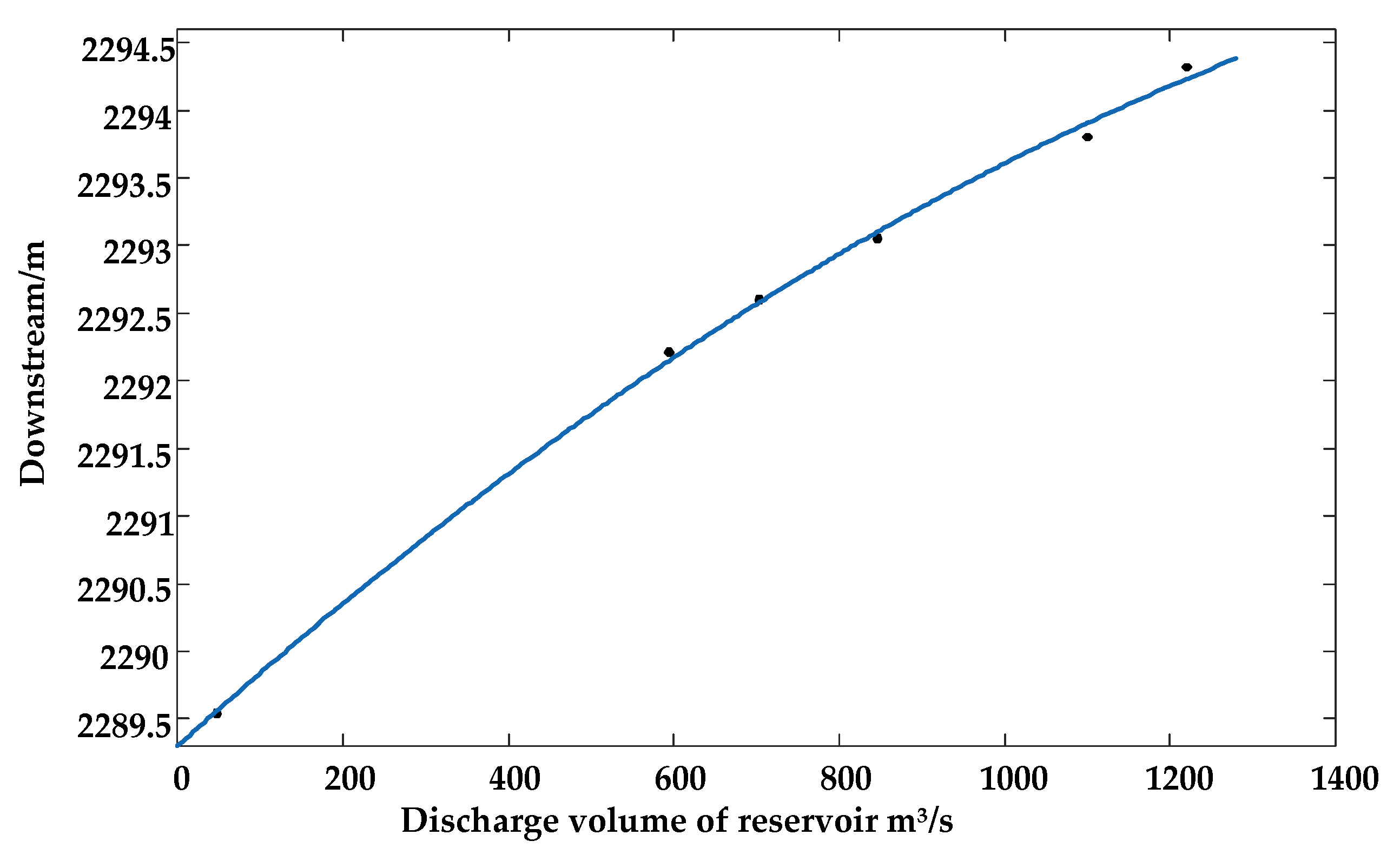

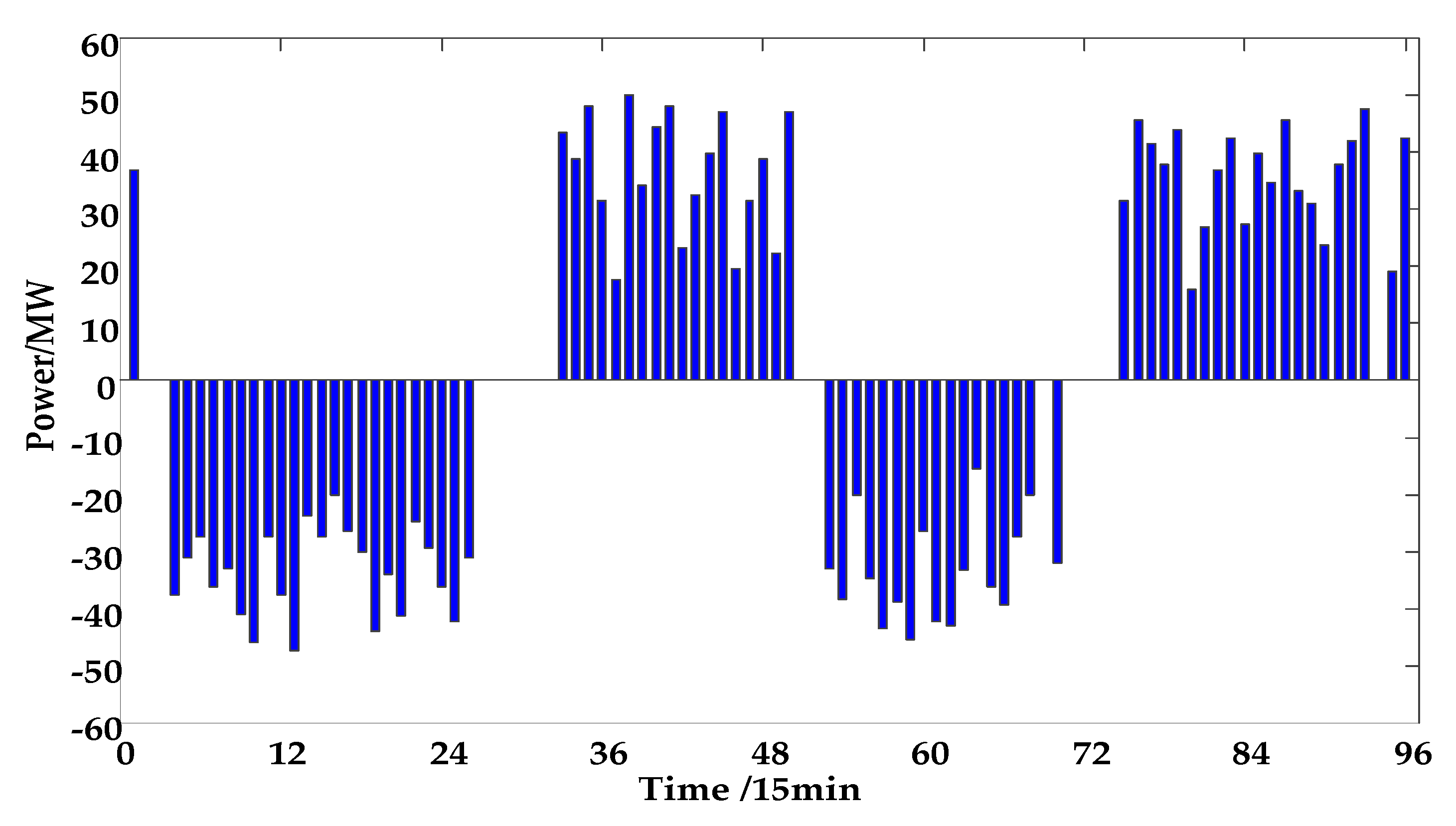
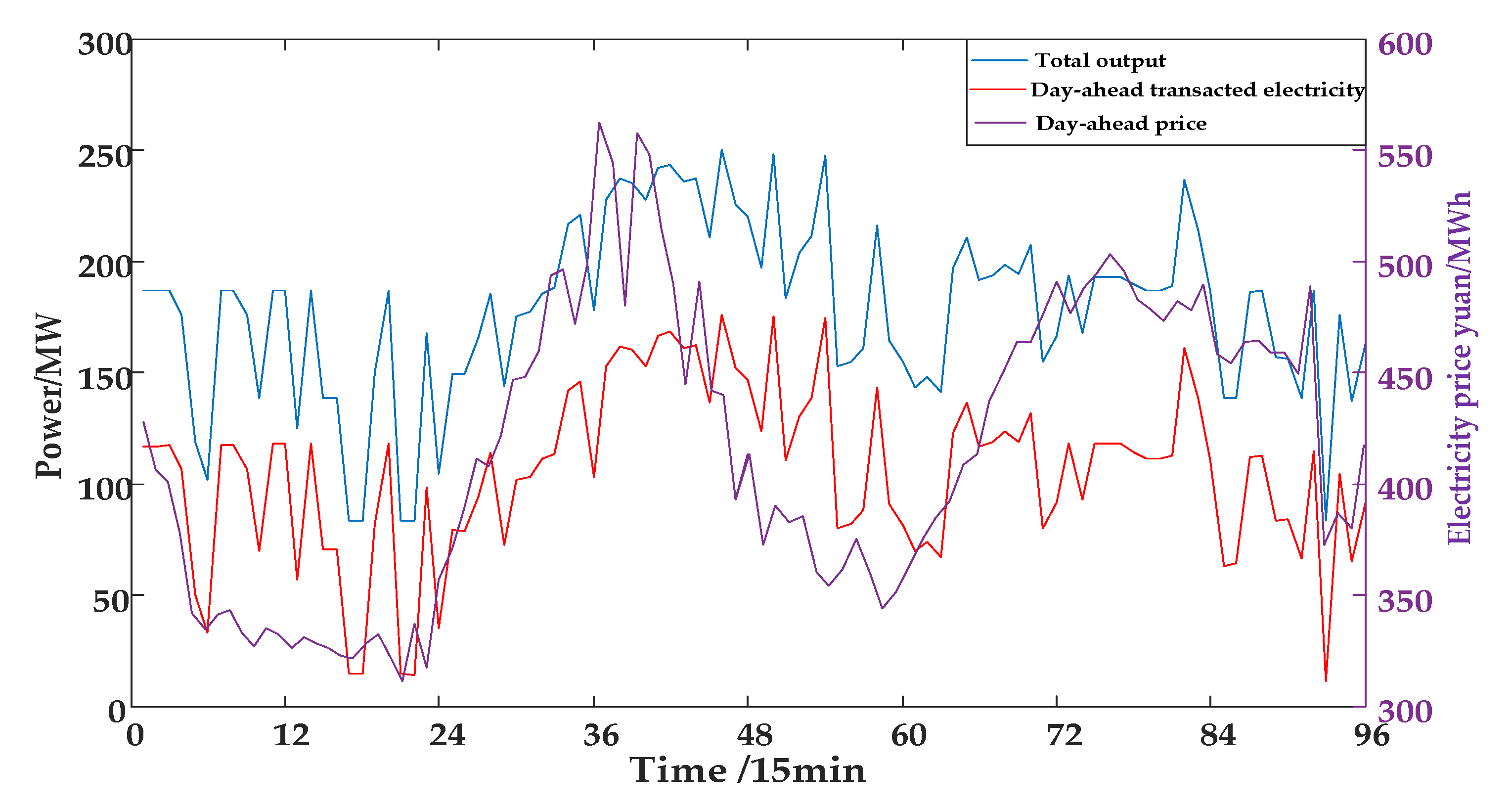
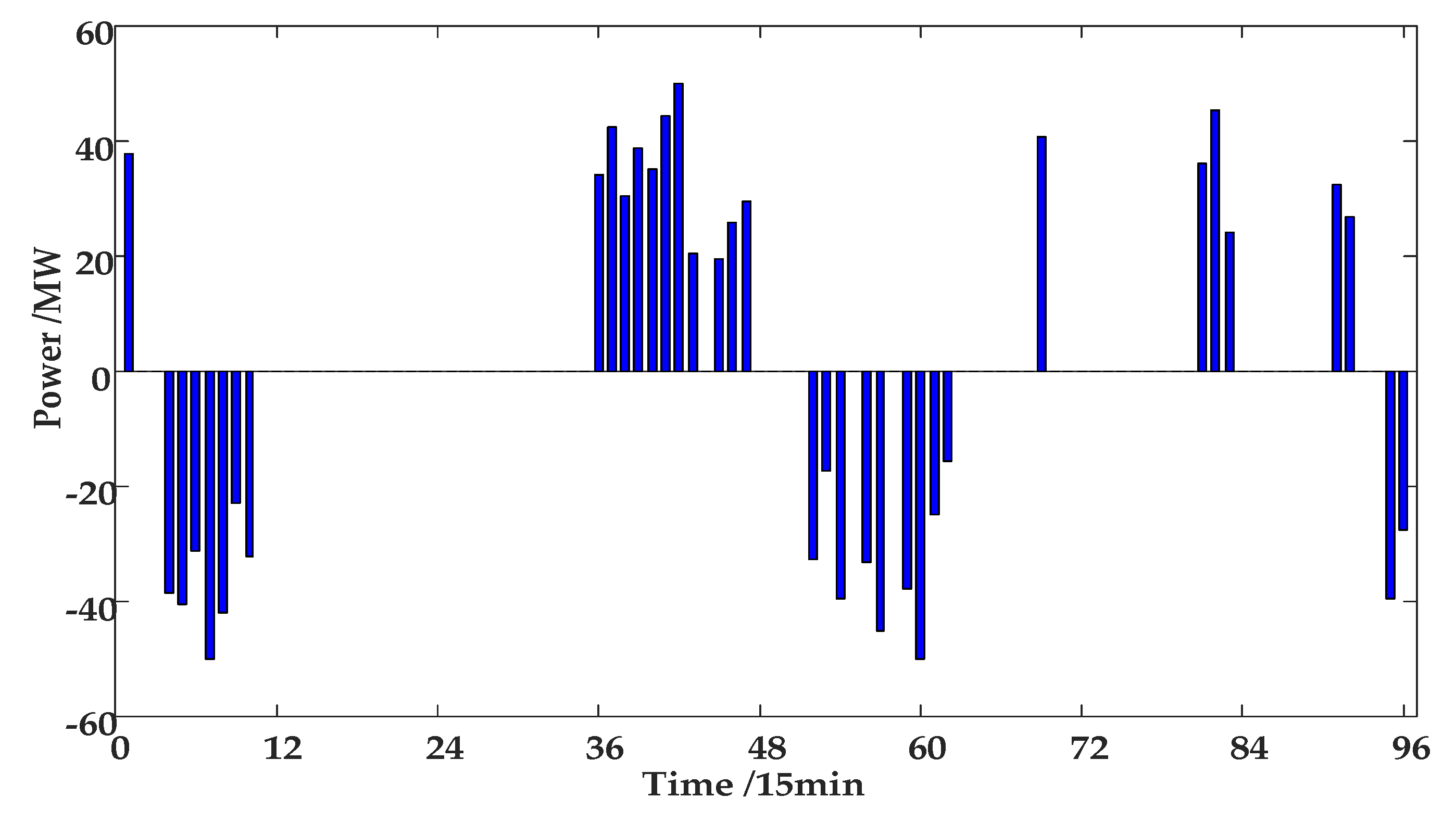
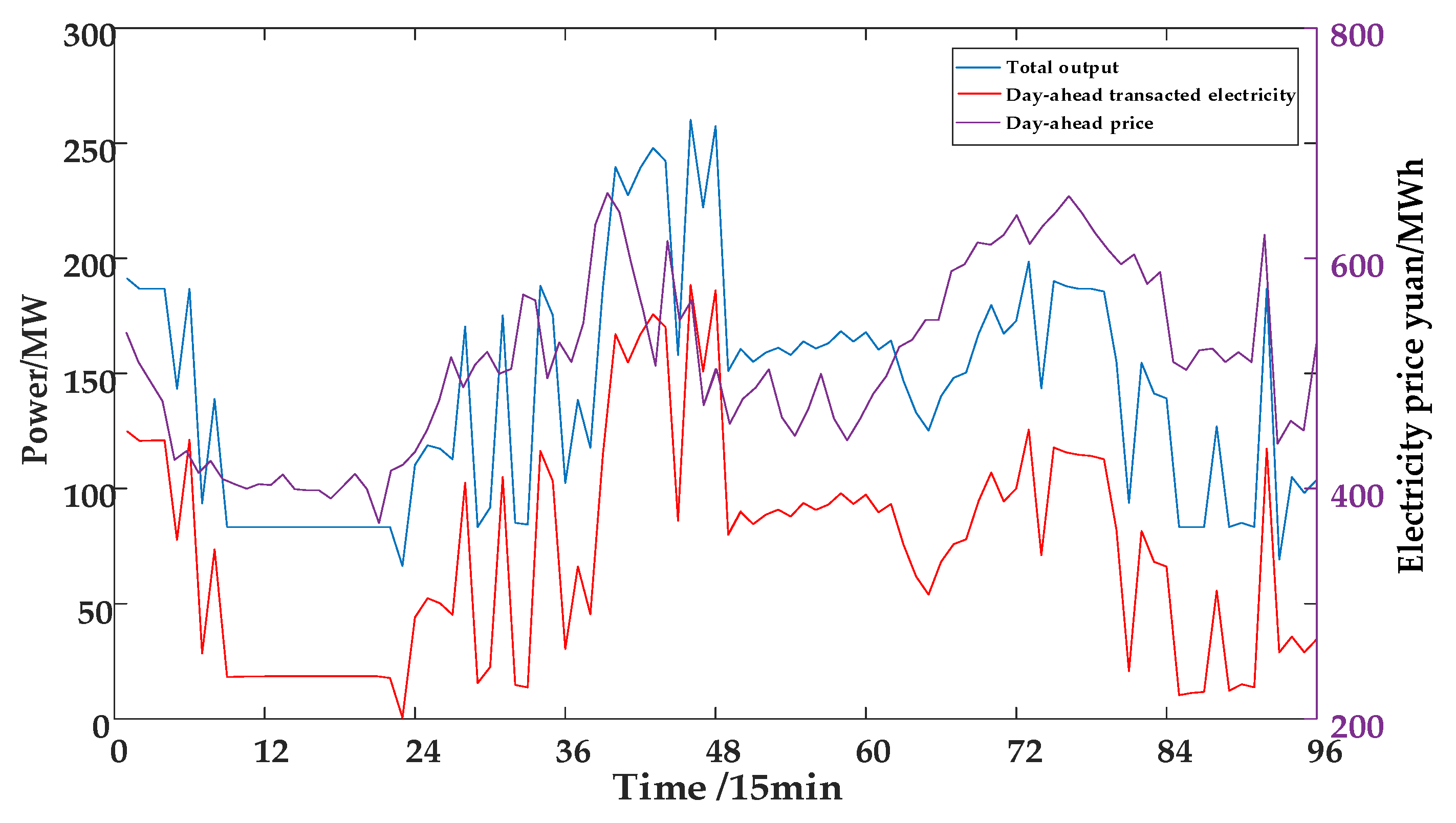
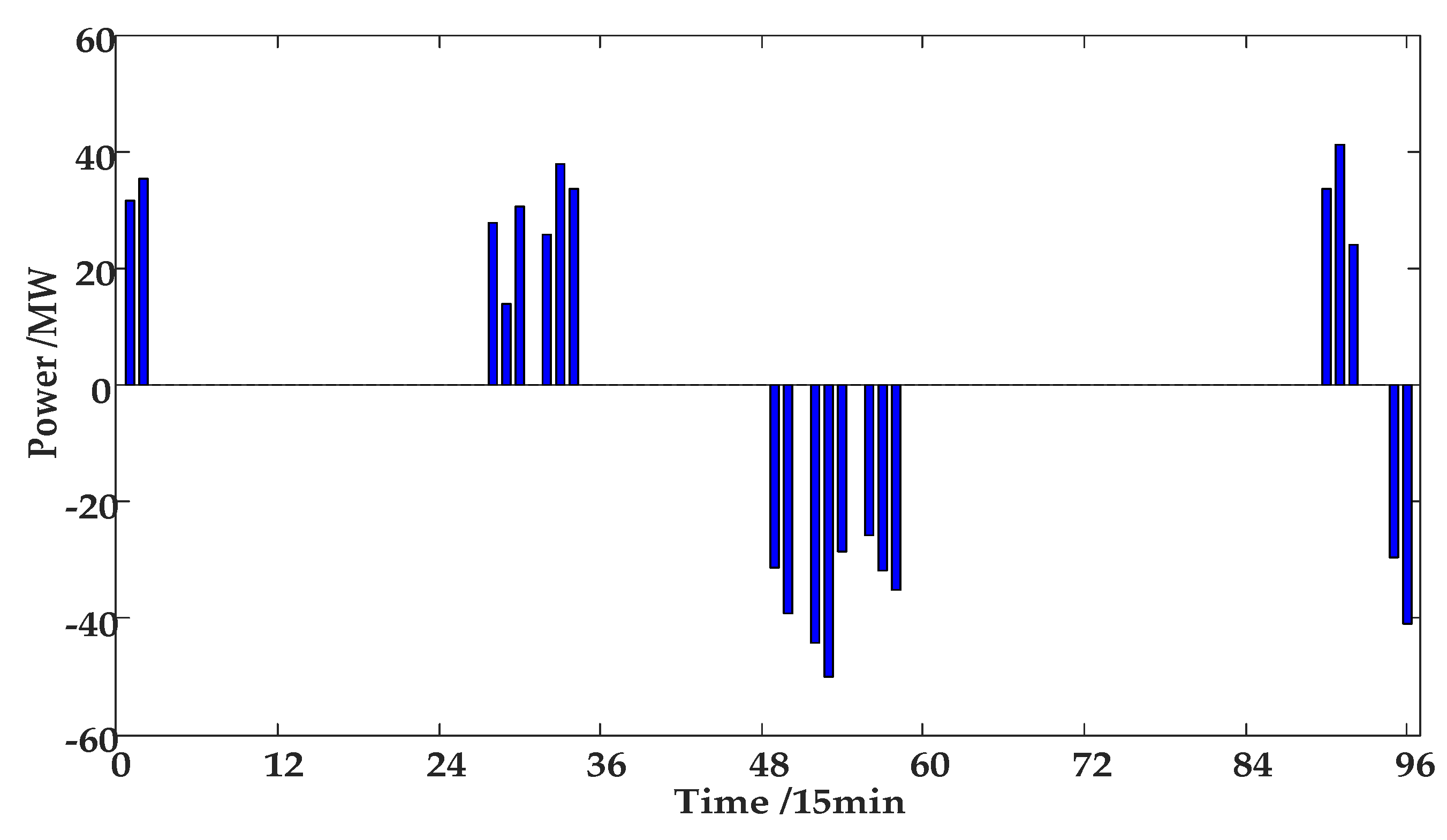


| Number | Normal Upstream Water Level | Lowest Water Level | Normal Downstream Water Level | Max Storage Capacity (104 m3) | Min Storage Capacity (104 m3) | Max Flow (m3/s) | Min Flow (m3/s) | Power Generation Efficiency |
|---|---|---|---|---|---|---|---|---|
| 1 | 2756 | 2752 | 2621.3 | 30.1 | 14.0 | 43.32 | 11.3 | 0.80 |
| 2 | 2608.7 | 2606.7 | 2451.4 | 96.1 | 75.2 | 53.4 | 13.2 | 0.85 |
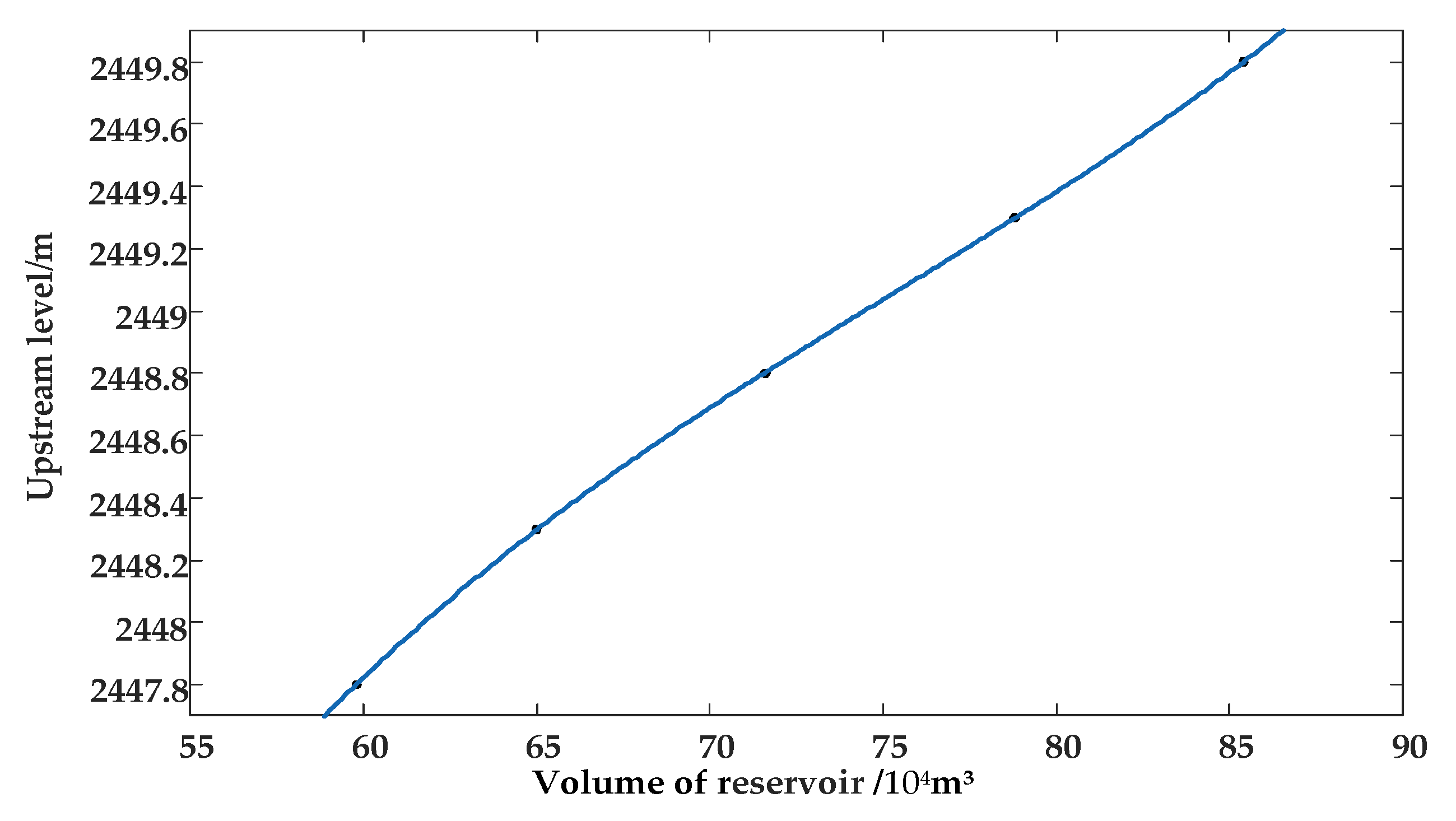
| 3 | 2449.8 | 2447.8 | 2294.3 | 85.4 | 59.8 | 47.1 | 12.6 | 0.85 |
| Initial Storage Capacity (104m3) | Max Storage Capacity (104m3) | Min Storage Capacity (104m3) | Max Pumping/Generation Power (MW) | Min Pumping/Generation Power (MW) | Water/Electricity Conversion Coefficient in Generation State m3/(MWh) | Water/Electricity Conversion Coefficient in Pumping State m3/(MWh) |
|---|---|---|---|---|---|---|
| 130 | 210 | 25 | 50 | 5 | 108 | 85 |
| Reference Temperature (°C) | Temperature Coefficient | Test Light Intensity (W/m2) |
|---|---|---|
| 25 | −0.5% | 1000 |
| Scene | Load Tracking Coefficient | Complementary Index | Revenue in Typical Days | Pearson Correlation Coefficient | Cost of Abandoned Water |
|---|---|---|---|---|---|
| Wet | 0.0687 | 0.44 | 6,813,027 | 1.0259 | 135,011 |
| Normal | 0.0935 | 0.59 | 6,465,077 | 1.0384 | 51,468 |
| Dry | 0.1052 | 0.62 | 6,136,612 | 0.9946 | 48,456 |
| Mode | Complementary Index | Load Tracking Coefficient | Pearson Correlation Coefficient | Cost of Annual Investment and Maintenance | Annual Revenue/Yuan | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Wet | Normal | Dry | Wet | Normal | Dry | Wet | Normal | Dry | |||
| 1 | 0.43 | 0.67 | 0.83 | 0.0686 | 0.0935 | 0.1052 | 1.02 | 1.03 | 0.99 | 485321300 | 1845029176 |
| 2 | 0.40 | 0.58 | 0.72 | 0.0631 | 0.0874 | 0.0976 | 0.85 | 0.89 | 0.91 | 1741148292 | |
| 3 | 0.38 | 0.55 | 0.66 | 0.0563 | 0.0816 | 0.0845 | 0.75 | 0.75 | 0.82 | 1632119713 | |
| 4 | 0.35 | 0.50 | 0.59 | 0.0492 | 0.0735 | 0.0787 | 0.71 | 0.62 | 0.71 | 1498362824 | |
| 5 | 0.32 | 0.45 | 0.52 | 0.0443 | 0.0652 | 0.0676 | 0.65 | 0.53 | 0.59 | 1359375705 | |
| 6 | 0.28 | 0.42 | 0.46 | 0.0386 | 0.0575 | 0.0592 | 0.58 | 0.46 | 0.48 | 1243605618 | |
| 7 | 0.25 | 0.38 | 0.39 | 0.0323 | 0.0473 | 0.0482 | 0.49 | 0.37 | 0.36 | 1124590215 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, J.; Xiang, Y.; Hu, S. Optimal Sizing of Hydro-PV-Pumped Storage Integrated Generation System Considering Uncertainty of PV, Load and Price. Energies 2019, 12, 3001. https://doi.org/10.3390/en12153001
Liu J, Li J, Xiang Y, Hu S. Optimal Sizing of Hydro-PV-Pumped Storage Integrated Generation System Considering Uncertainty of PV, Load and Price. Energies. 2019; 12(15):3001. https://doi.org/10.3390/en12153001
Chicago/Turabian StyleLiu, Jichun, Jianhua Li, Yue Xiang, and Shuai Hu. 2019. "Optimal Sizing of Hydro-PV-Pumped Storage Integrated Generation System Considering Uncertainty of PV, Load and Price" Energies 12, no. 15: 3001. https://doi.org/10.3390/en12153001
APA StyleLiu, J., Li, J., Xiang, Y., & Hu, S. (2019). Optimal Sizing of Hydro-PV-Pumped Storage Integrated Generation System Considering Uncertainty of PV, Load and Price. Energies, 12(15), 3001. https://doi.org/10.3390/en12153001




