Risk Assessment Method for Integrated Transmission–Distribution System Considering the Reactive Power Regulation Capability of DGs
Abstract
:1. Introduction
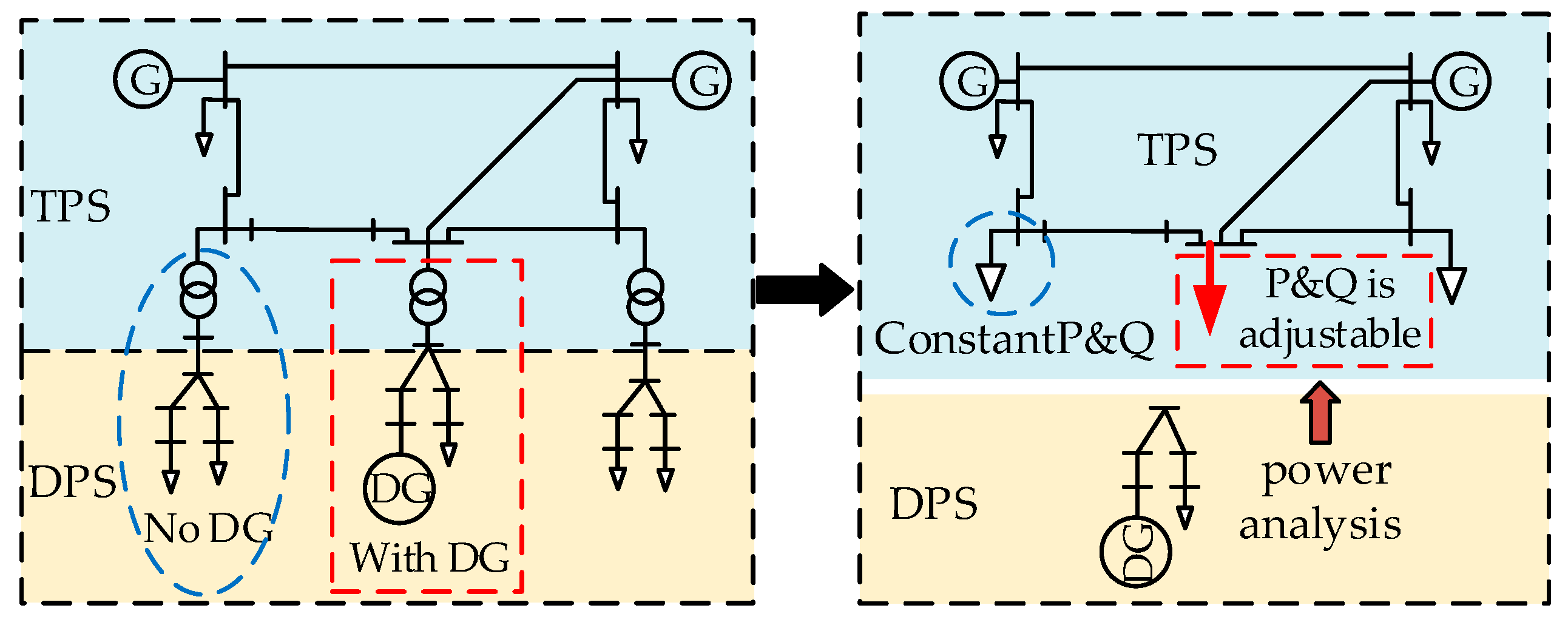
2. Influence of DPS’s Reactive Power on TPS
3. Analysis of Reactive Power Regulation Capability of DPS with DG Integrated
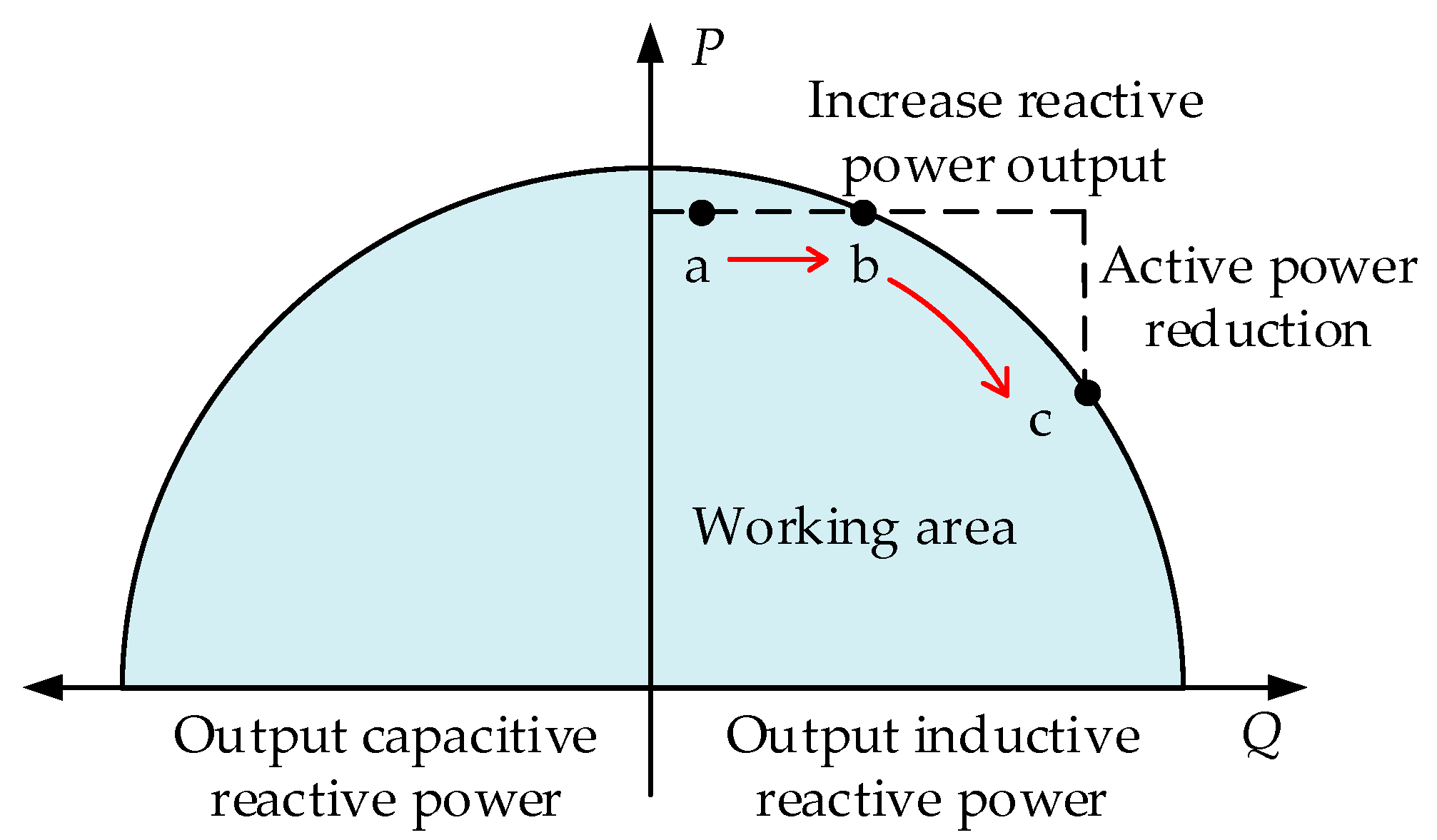
3.1. The Reactive Power Output Capacity of Distributed PV
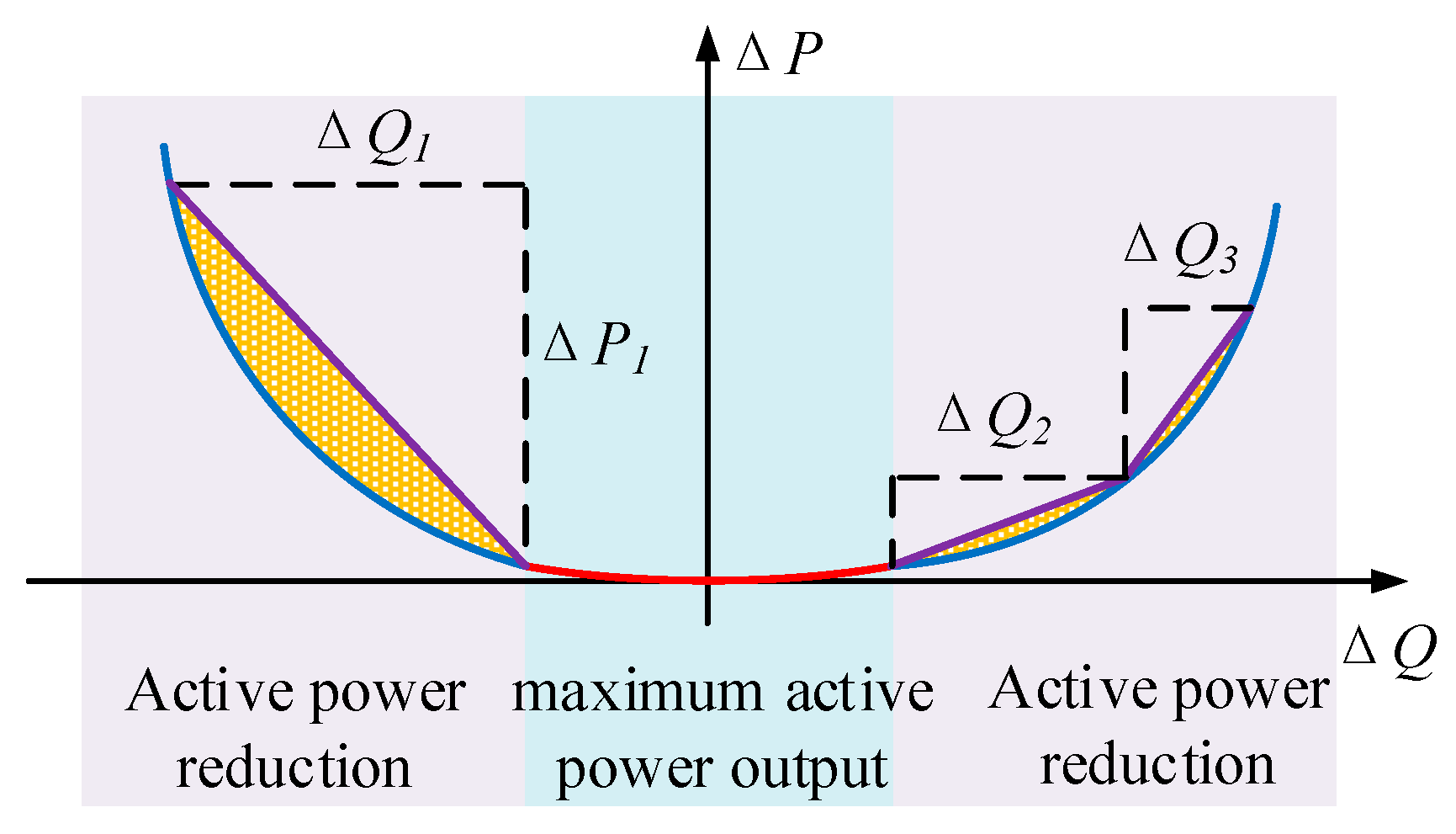
3.2. Calculation of Reactive Power Regulation Capability of DPS
3.2.1. Maximum Active Power Output State
3.2.2. Active Power Reduction State
4. Risk Assessment Method of TPS Considering the Reactive Power Support of DPS
4.1. System State Analysis
4.2. Risk Indicator
4.2.1. Loss of Load Probability
4.2.2. Expected Power Not Served
4.3. Steps of Risk Assessment
- (1)
- The power flow analysis is utilized in the DPS to obtain the relationship between and of the DPS;
- (2)
- Monte Carlo simulation method is used to simulate the system status. For all generators and power transmission and transformation components in the system, two states model are used for simulation;
- (3)
- The fault analysis of the TPS is carried out, and the power generation is rescheduled to eliminate the off-limit of the system. If the load shedding cannot be avoided, the reactive power support of the DPS needs to be considered to calculate the load shedding;
- (4)
- According to the load shedding and the reactive power provided by the DPS, calculate the active and reactive power of the boundary bus. Determine whether the DPS can meet the active and reactive power state requirements of the boundary bus. If the error of reactive power exceeds the limit, send the error to the TPS to further optimize the load reduction;
- (5)
- If the number of samples reaches the given maximum number, the calculation is terminated; otherwise, return to step (2) for the next sampling;
- (6)
- Calculate risk indicators LOLP and EPNS.
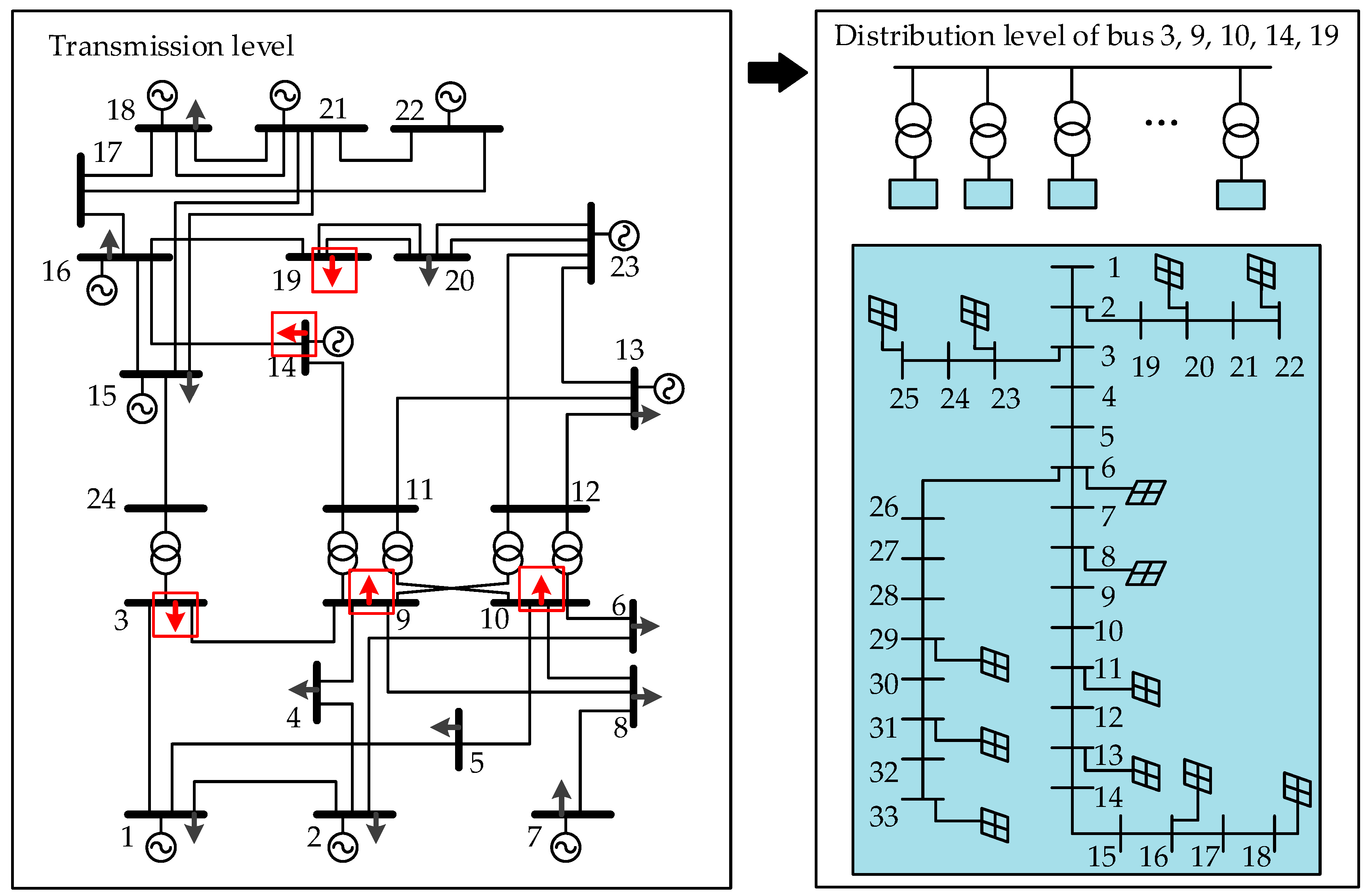
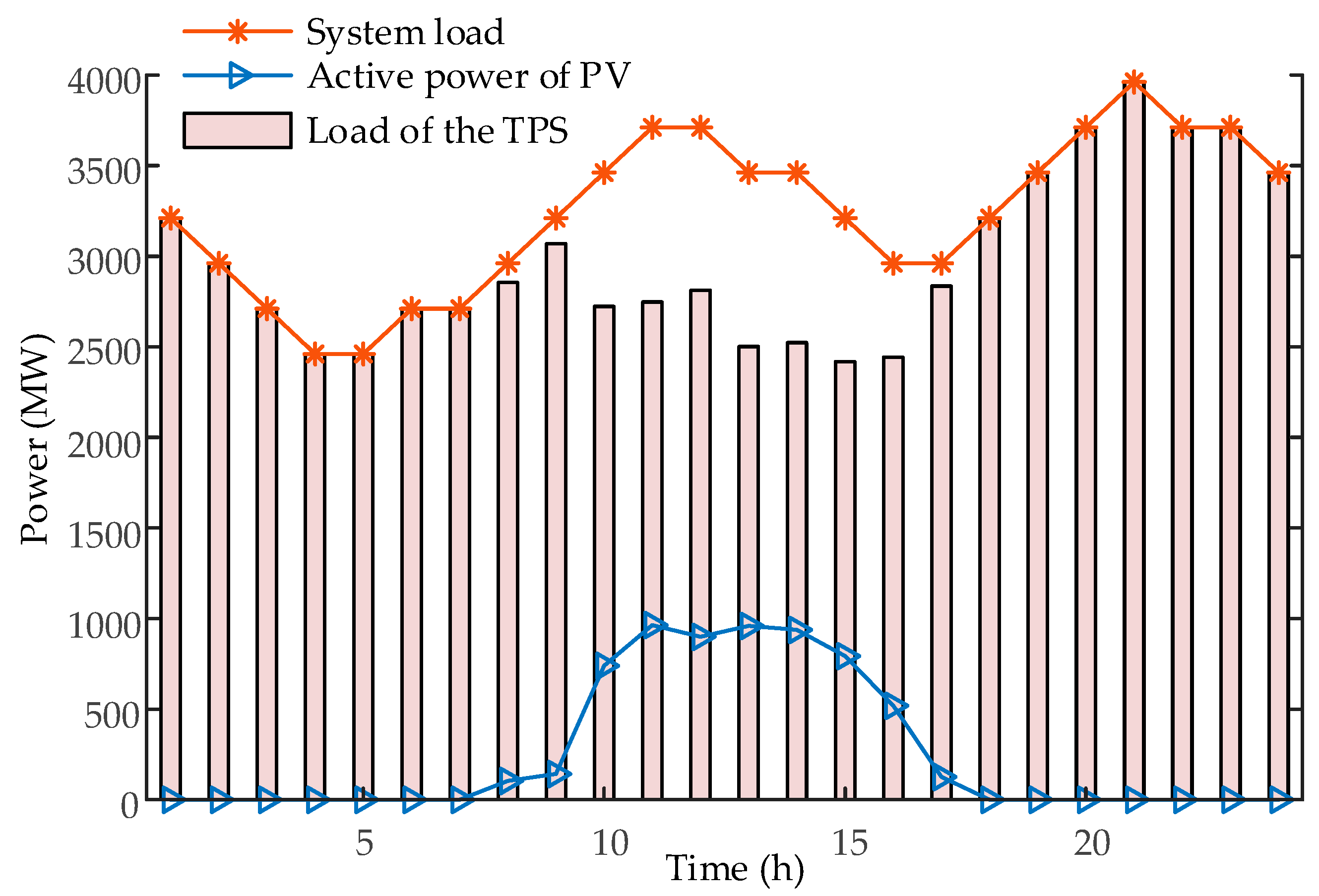
5. Case Study
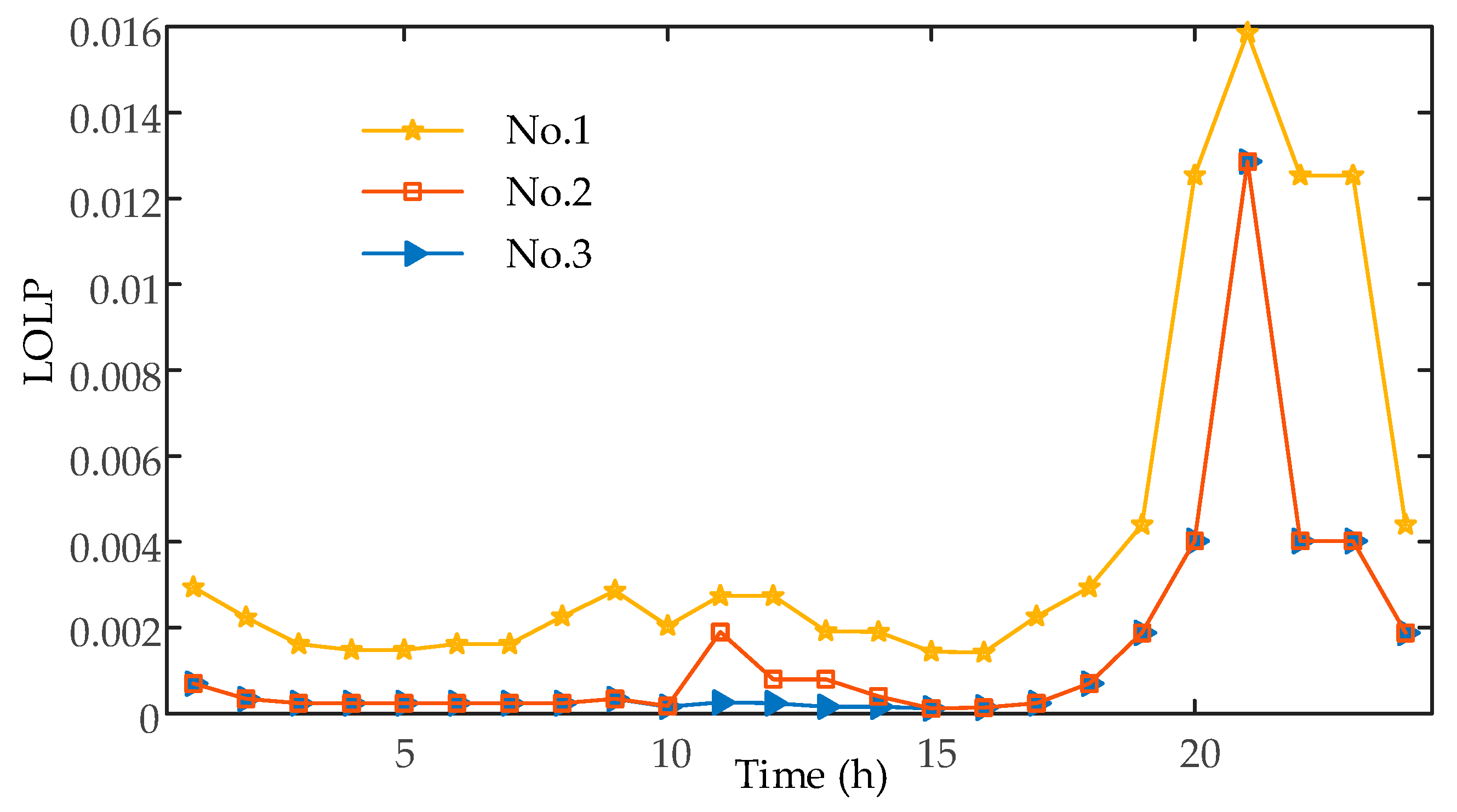
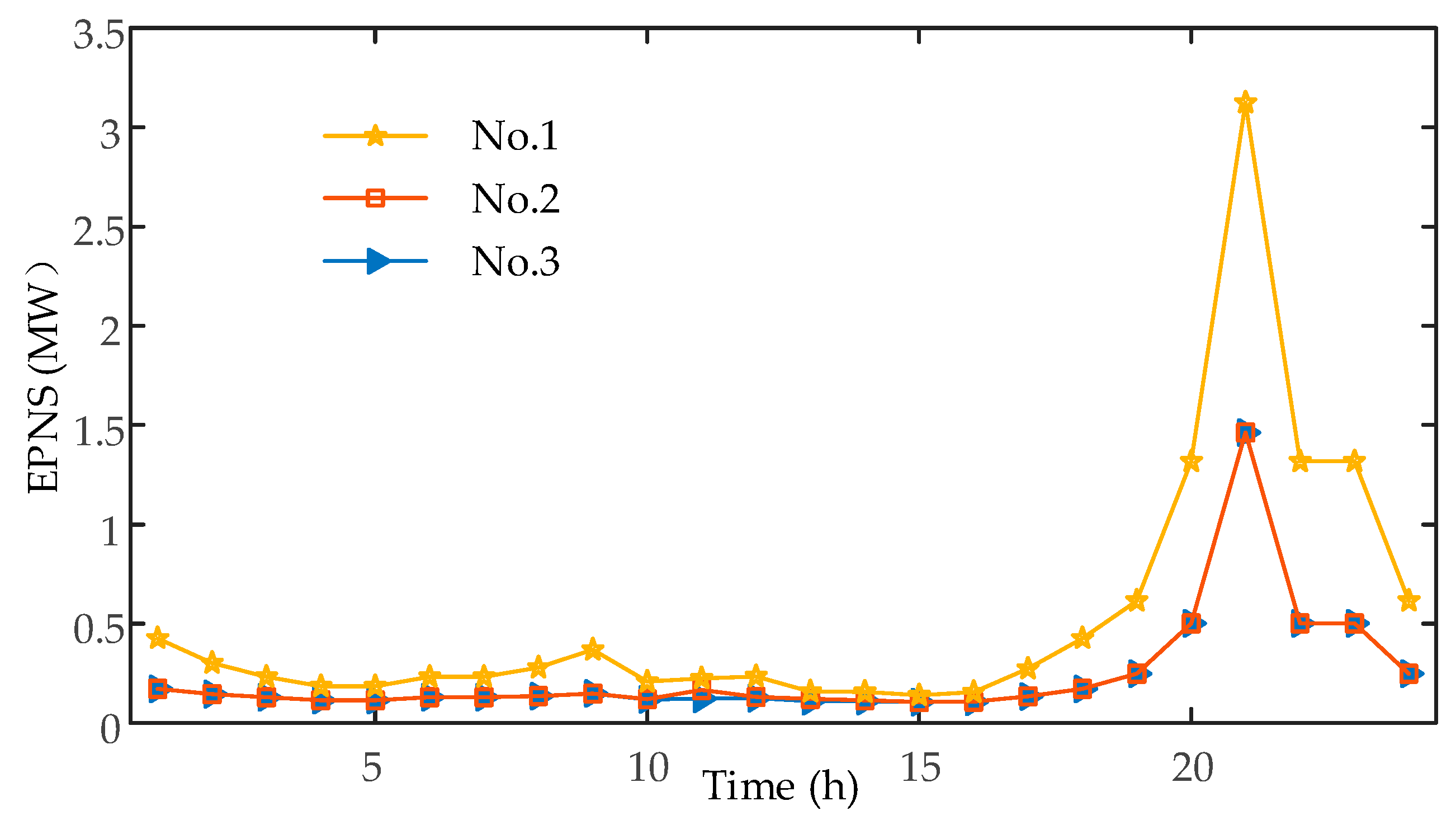
5.1. Risk Assessment of TPS
- (1)
- The reactive power regulation capacity of the DPS is not considered;
- (2)
- Consider the reactive power regulation capacity of the DPS, but do not consider the active power reduction of DGs;
- (3)
- Consider the reactive power regulation capacity of the DPS, and consider the active power reduction of DGs.
5.2. Analysis of Factors Affecting PV Active Power Reduction
5.3. Influence of DGs’ Location on TPS Risk
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lin, C.; Wu, W.; Zhang, B.; Wang, B.; Zheng, W.; Li, Z. Decentralized Reactive Power Optimization Method for Transmission and Distribution Networks Accommodating Large-Scale DG Integration. IEEE Trans. Sustain. Energy 2017, 8, 363–373. [Google Scholar] [CrossRef]
- Jain, H.; Rahimi, K.; Tbaileh, A.; Broadwater, R.P.; Jain, A.K.; Dilek, M. Integrated transmission & distribution system modeling and analysis: Need & advantages. In Proceedings of the IEEE Power and Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Jia, H.; Qi, W.; Liu, Z.; Wang, B.; Zeng, Y.; Xu, T. Hierarchical risk assessment of transmission system considering the influence of active distribution network. IEEE Trans. Power Syst. 2015, 30, 1084–1093. [Google Scholar] [CrossRef]
- Liang, C.; Wang, P.; Han, X.; Qin, W.; Billinton, R.; Li, W. Operational Reliability and Economics of Power Systems with Considering Frequency Control Processes. IEEE Trans. Power Syst. 2017, 32, 2570–2580. [Google Scholar] [CrossRef]
- Ansari, O.A.; Chung, C.Y. A hybrid framework for short-term risk assessment of wind-integrated composite power systems. IEEE Trans. Power Syst. 2019, 34, 2334–2344. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, B.; Ding, H.; Li, H. Risk-based probabilistic voltage stability assessment in uncertain power system. Energies 2017, 10, 180. [Google Scholar] [CrossRef]
- Lin, W.M.; Yang, C.Y.; Tu, C.S.; Tsai, M.T. An optimal scheduling dispatch of a microgrid under risk assessment. Energies 2018, 11, 1423. [Google Scholar] [CrossRef]
- Shahidehpour, M.; Li, Z.; Liu, X.; Li, Z.; Cao, Y.; Liu, X. Power System Risk Assessment in Cyber Attacks Considering the Role of Protection Systems. IEEE Trans. Smart Grid 2016, 8, 572–580. [Google Scholar]
- Yong, P.; Zhang, N.; Kang, C.; Xia, Q.; Lu, D. MPLP-Based Fast Power System Reliability Evaluation Using Transmission Line Status Dictionary. IEEE Trans. Power Syst. 2019, 34, 1630–1640. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, W.; Liang, J.; Cong, P.; Cai, Y. Coordinated Day-Ahead Reactive Power Dispatch in Distribution Network Based on Real Power Forecast Errors. IEEE Trans. Power Syst. 2016, 31, 2472–2480. [Google Scholar] [CrossRef]
- Onlam, A.; Yodphet, D.; Chatthaworn, R.; Surawanitkun, C.; Siritaratiwat, A.; Khunkitti, P. Power Loss Minimization and Voltage Stability Improvement in Electrical Distribution System via Network Reconfiguration and Distributed Generation Placement Using Novel Adaptive Shuffled Frogs Leaping Algorithm. Energies 2019, 12, 553. [Google Scholar] [CrossRef]
- Chen, Q.; Zhao, X.; Gan, D. Active-reactive scheduling of active distribution system considering interactive load and battery storage. Prot. Control Mod. Power Syst. 2017, 2, 29. [Google Scholar] [CrossRef] [Green Version]
- Ustun, T.S.; Aoto, Y. Analysis of smart inverter’s impact on the distribution network operation. IEEE Access 2019, 7, 9790–9804. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Sun, H.; Qiu, F.; Guo, Q. Robust Estimation of Reactive Power for an Active Distribution System. IEEE Trans. Power Syst. 2019. [Google Scholar] [CrossRef]
- Goergens, P.; Potratz, F.; Godde, M.; Schnettler, A. Determination of the potential to provide reactive power from distribution grids to the transmission grid using optimal power flow. In Proceedings of the Universities Power Engineering Conference, Stoke on Trent, UK, 1–4 September 2015. [Google Scholar]
- Li, Z.; Guo, Q.; Sun, H.; Wang, J. Impact of Coupled Transmission–distribution on Static Voltage Stability Assessment. IEEE Trans. Power Syst. 2017, 32, 3311–3312. [Google Scholar] [CrossRef]
- Li, Z.; Guo, Q.; Sun, H.; Wang, J.; Xu, Y.; Fan, M. A Distributed Transmission–distribution-Coupled Static Voltage Stability Assessment Method Considering Distributed Generation. IEEE Trans. Power Syst. 2018, 33, 2621–2632. [Google Scholar] [CrossRef]
- Arnold, D.B.; Sankur, M.D.; Negrete-Pincetic, M.; Callaway, D.S. Model-free optimal coordination of distributed energy resources for provisioning transmission-level services. IEEE Trans. Power Syst. 2018, 33, 817–828. [Google Scholar] [CrossRef]
- Valverde, G.; Shchetinin, D.; Hug-Glanzmann, G. Coordination of Distributed Reactive Power Sources for Voltage Support of Transmission Networks. IEEE Trans. Sustain. Energy 2019, 10, 1544–1553. [Google Scholar] [CrossRef]
- Xu, C.; Sun, D.; Tang, Y.; Yu, J.; Wu, H. Risk Assessment Method for Transmission–distribution Integrated System with Distributed PV. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration, Beijing, China, 20–22 October 2018; pp. 1–6. [Google Scholar]
- Li, W.; Zhou, J.; Xie, K.; Xiong, X. Power system risk assessment using a hybrid method of fuzzy set and Monte Carlo simulation. IEEE Trans. Power Syst. 2008, 23, 336–343. [Google Scholar]
- Subcommittee, P.M. IEEE reliability test system. IEEE Trans. Power Appar. Syst. 1979, 6, 2047–2054. [Google Scholar] [CrossRef]


| Branch | r | x | Branch | r | x | Branch | r | x | Branch | r | x |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-2 | 0.019 | 0.020 | 9-10 | 0.217 | 0.308 | 17-18 | 0.152 | 0.239 | 6-26 | 0.042 | 0.043 |
| 2-3 | 0.103 | 0.104 | 10-11 | 0.041 | 0.027 | 2-19 | 0.034 | 0.065 | 26-27 | 0.059 | 0.060 |
| 3-4 | 0.076 | 0.078 | 11-12 | 0.078 | 0.051 | 19-20 | 0.313 | 0.564 | 27-28 | 0.220 | 0.388 |
| 4-5 | 0.079 | 0.081 | 12-13 | 0.305 | 0.480 | 20-21 | 0.085 | 0.199 | 28-29 | 0.167 | 0.291 |
| 5-6 | 0.170 | 0.294 | 13-14 | 0.113 | 0.297 | 21-22 | 0.147 | 0.390 | 29-30 | 0.106 | 0.108 |
| 6-7 | 0.039 | 0.257 | 14-15 | 0.123 | 0.219 | 3-23 | 0.094 | 0.128 | 30-31 | 0.203 | 0.401 |
| 7-8 | 0.148 | 0.098 | 15-16 | 0.155 | 0.227 | 23-24 | 0.187 | 0.295 | 31-32 | 0.065 | 0.151 |
| 8-9 | 0.214 | 0.308 | 16-17 | 0.268 | 0.716 | 24-25 | 0.186 | 0.292 | 32-33 | 0.071 | 0.221 |
| Bus | P | Q | Bus | P | Q | Bus | P | Q | Bus | P | Q |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.027 | 0.032 | 10 | 0.016 | 0.008 | 18 | 0.024 | 0.015 | 26 | 0.016 | 0.009 |
| 3 | 0.024 | 0.015 | 11 | 0.012 | 0.011 | 19 | 0.024 | 0.015 | 27 | 0.016 | 0.009 |
| 4 | 0.032 | 0.030 | 12 | 0.016 | 0.013 | 20 | 0.024 | 0.015 | 28 | 0.016 | 0.008 |
| 5 | 0.016 | 0.011 | 13 | 0.016 | 0.013 | 21 | 0.024 | 0.226 | 29 | 0.032 | 0.026 |
| 6 | 0.016 | 0.008 | 14 | 0.032 | 0.030 | 22 | 0.024 | 0.015 | 30 | 0.054 | 0.023 |
| 7 | 0.054 | 0.038 | 15 | 0.016 | 0.004 | 23 | 0.024 | 0.019 | 31 | 0.040 | 0.026 |
| 8 | 0.054 | 0.038 | 16 | 0.016 | 0.008 | 24 | 0.113 | 0.226 | 32 | 0.057 | 0.004 |
| 9 | 0.016 | 0.008 | 17 | 0.016 | 0.008 | 25 | 0.113 | 0.075 | 33 | 0.016 | 0.015 |
| α | LOLP | EPNS | DGAPRP | DGAPRE |
|---|---|---|---|---|
| 0.8 | 0.01132 | 0.28960 | 0.03873 | 0.38251 |
| 0.9 | 0.00532 | 0.17850 | 0.02316 | 0.12184 |
| 1.0 | 0.00028 | 0.12326 | 0.01480 | 0.05507 |
| β | LOLP | EPNS | DGAPRP | DGAPRE |
|---|---|---|---|---|
| 0.85 | 0.00513 | 0.17331 | 0.00047 | 0.00628 |
| 0.9 | 0.00523 | 0.17717 | 0.00840 | 0.03552 |
| 0.95 | 0.00532 | 0.17850 | 0.02316 | 0.12184 |
| Cases | Bus in the DPS with PVs Connected |
|---|---|
| Case 1 | 6, 8, 11, 13, 16, 18, 20, 22, 23, 25, 29, 31, 33 |
| Case 2 | 11(3) 1, 18(3), 22(2), 25(2), 33(3) |
| Case 3 | 18(5), 25(3), 33(5) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Sun, D.; Hu, J.; Wu, Y.; Zhou, J.; Tang, Y. Risk Assessment Method for Integrated Transmission–Distribution System Considering the Reactive Power Regulation Capability of DGs. Energies 2019, 12, 3040. https://doi.org/10.3390/en12163040
Wang Q, Sun D, Hu J, Wu Y, Zhou J, Tang Y. Risk Assessment Method for Integrated Transmission–Distribution System Considering the Reactive Power Regulation Capability of DGs. Energies. 2019; 12(16):3040. https://doi.org/10.3390/en12163040
Chicago/Turabian StyleWang, Qi, Dasong Sun, Jianxiong Hu, Yi Wu, Ji Zhou, and Yi Tang. 2019. "Risk Assessment Method for Integrated Transmission–Distribution System Considering the Reactive Power Regulation Capability of DGs" Energies 12, no. 16: 3040. https://doi.org/10.3390/en12163040
APA StyleWang, Q., Sun, D., Hu, J., Wu, Y., Zhou, J., & Tang, Y. (2019). Risk Assessment Method for Integrated Transmission–Distribution System Considering the Reactive Power Regulation Capability of DGs. Energies, 12(16), 3040. https://doi.org/10.3390/en12163040




