Optimization of Radio Interference Levels for 500 and 600 kV Bipolar HVDC Transmission Lines †
Abstract
:1. Introduction
2. Transmission Line Model for Corona Propagation Analysis
- Γ is the RI excitation function in dB above ;
- gmax is the maximum bundle electric field in kV/cm;
- nc is the number of sub-conductors in the bundle;
- d is the sub-conductor diameter in cm;
- n0, g0, and d0 are reference values given by n0 = 6, d0 = 4.064 cm and g0 = 25 kV/cm.
- V is the line to ground voltage in kV;
- r is the radius of each sub-conductor in cm;
- R is the bundle radius in cm;
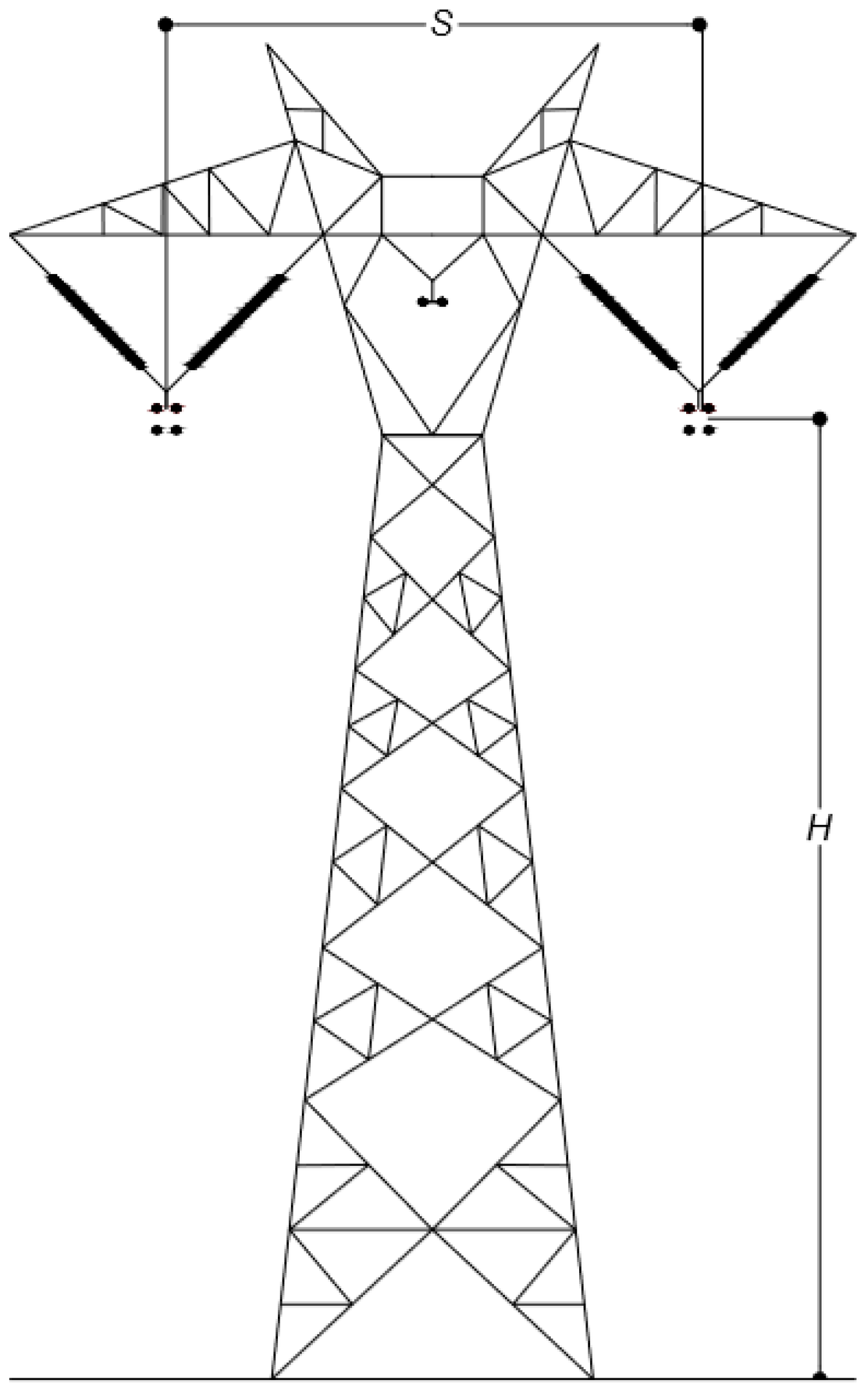
- H is the height of the poles;
- S is the distance between poles.
- n is the number of poles;
- Ii is the current of the ith conductor;
- hi is the ith conductor height;
- xi is the ith conductor lateral distance from the center of the tower;
- x is the lateral distance of the measurement point from the center of the tower;
- y is the measurement point height above the ground;
- P is the complex depth of penetration for the ground return defined as
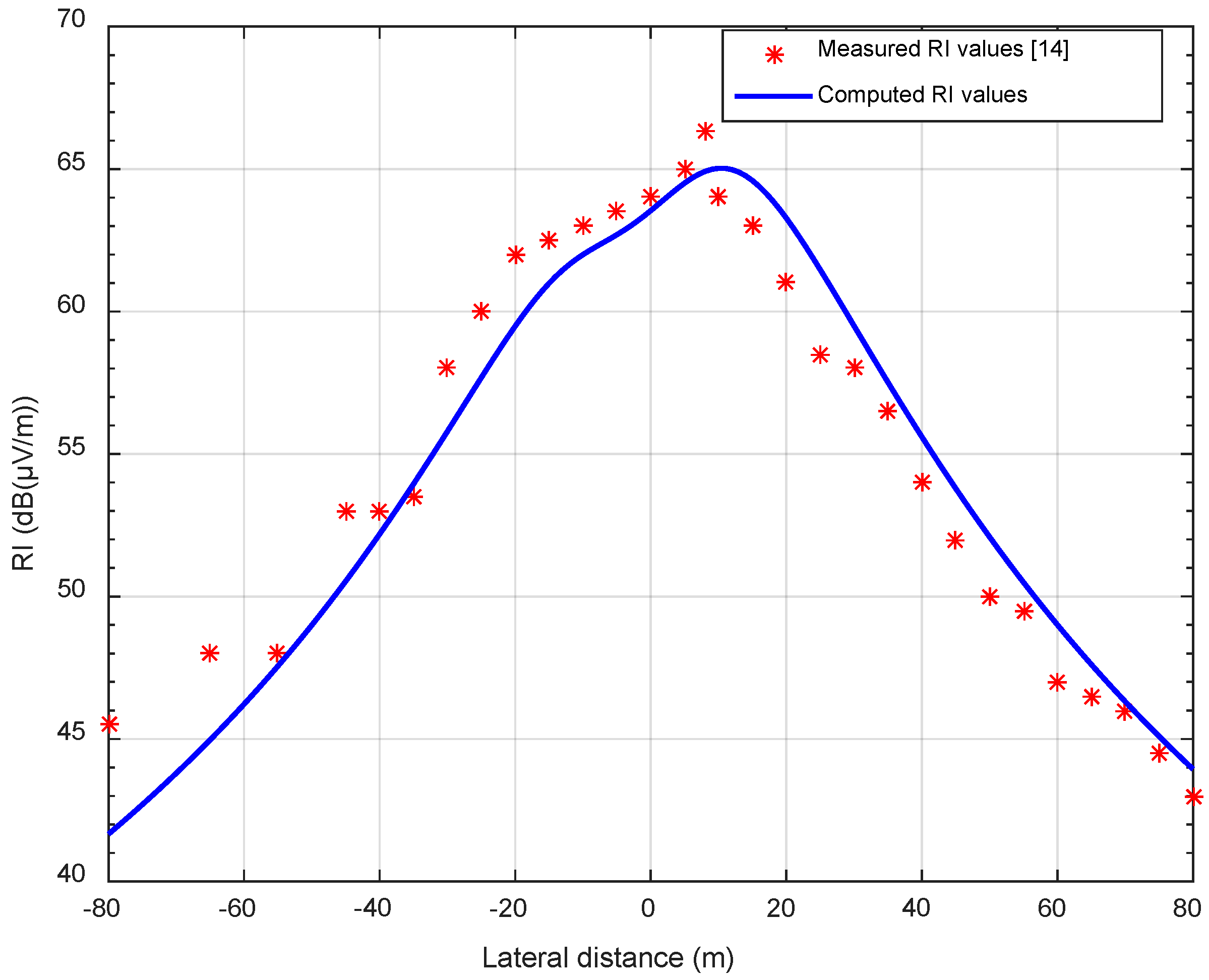
3. Comparison of Measured and Computed RI Profiles of an HVDC Test Line
4. Computation of RI Levels in ±500 and ±600 kV HVDC Transmission Lines
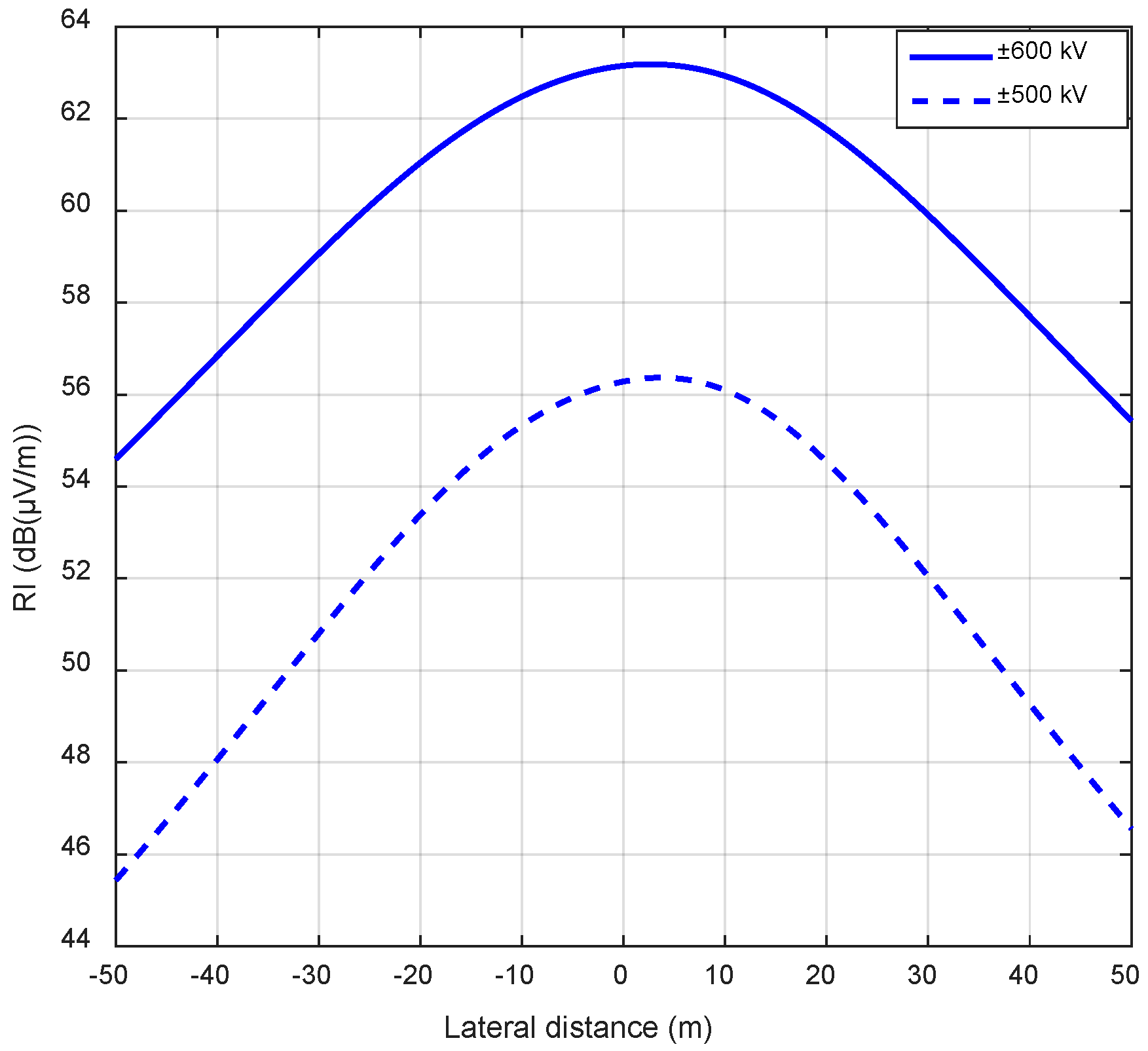
4.1. Radio Interference Lateral Profiles
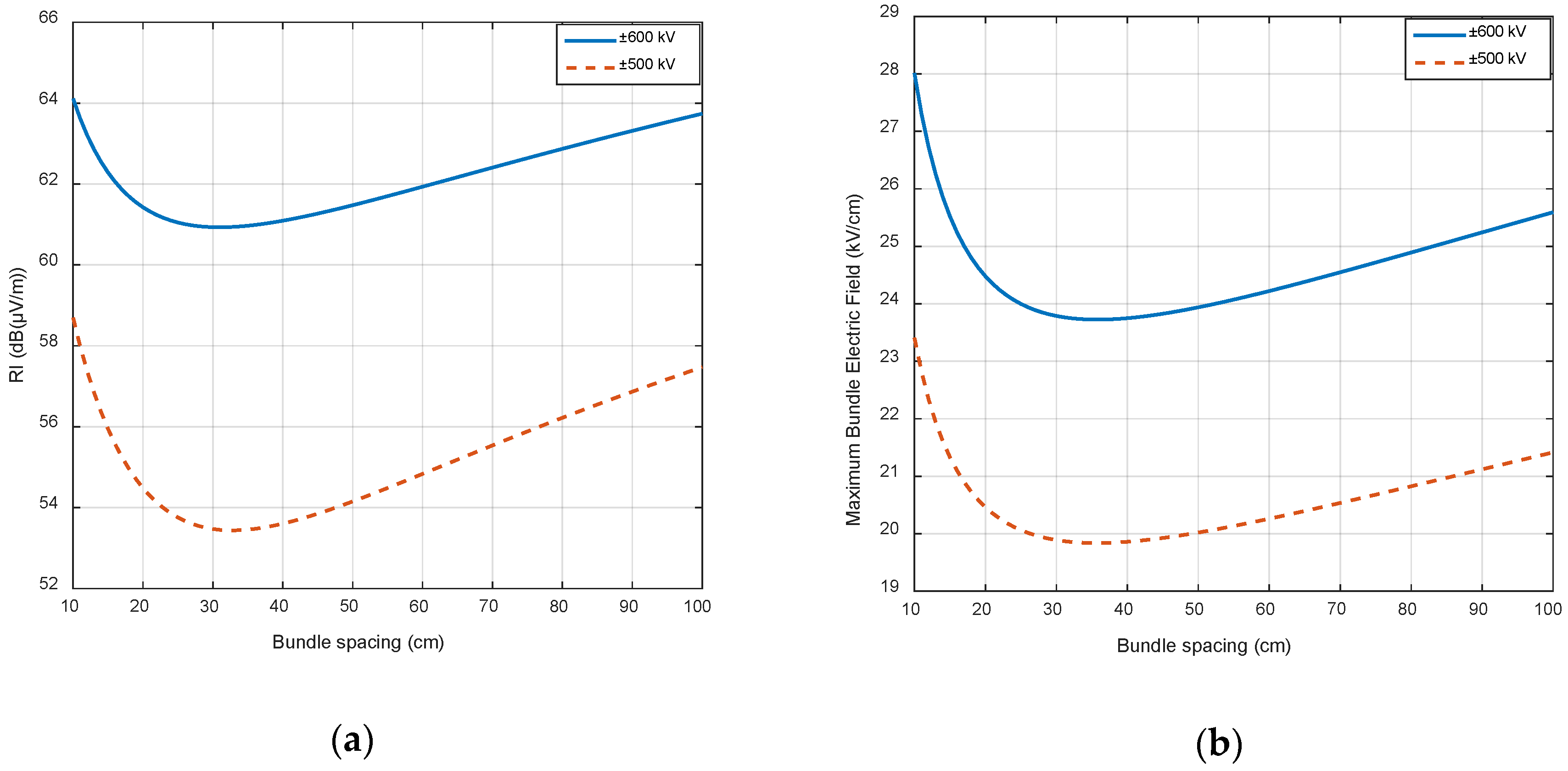
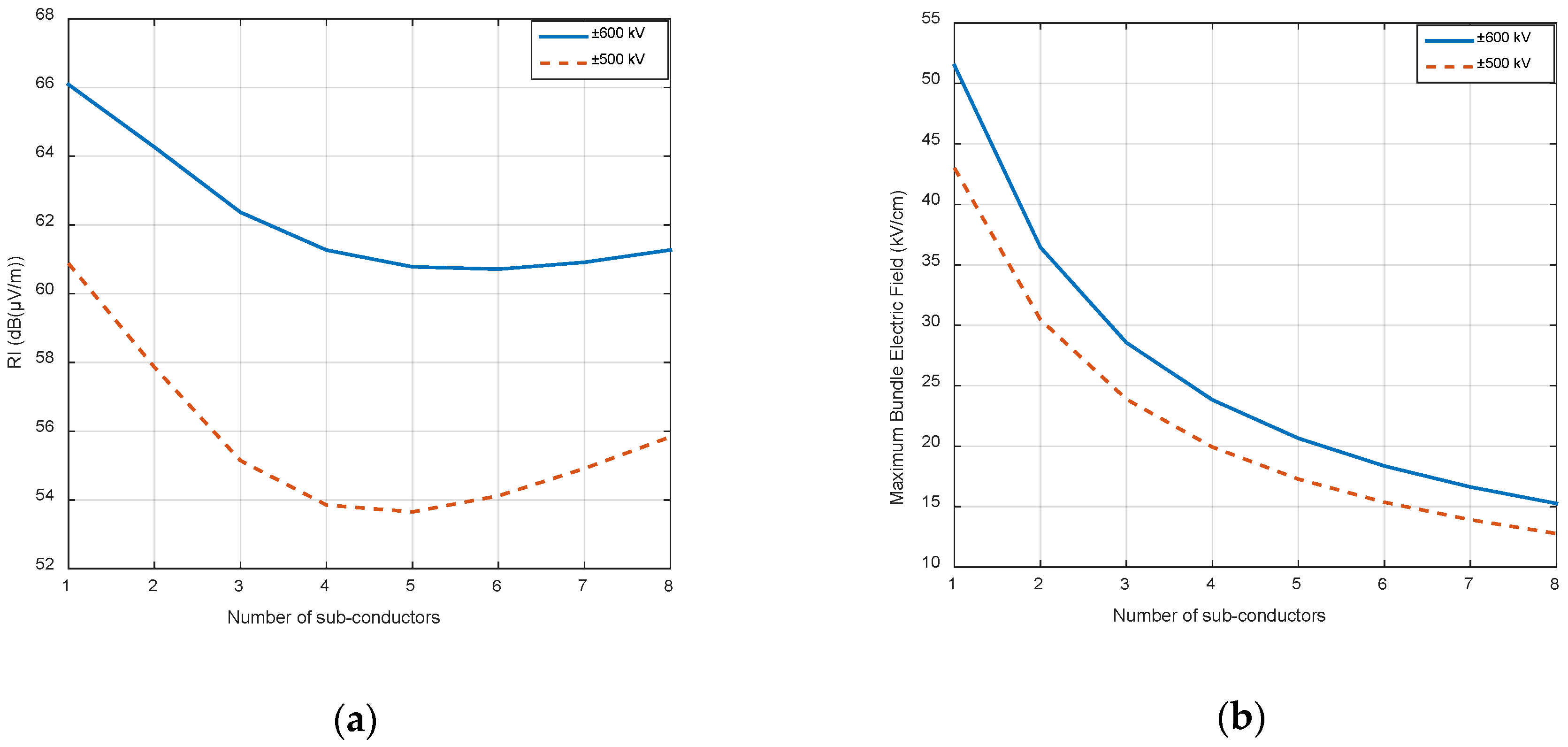
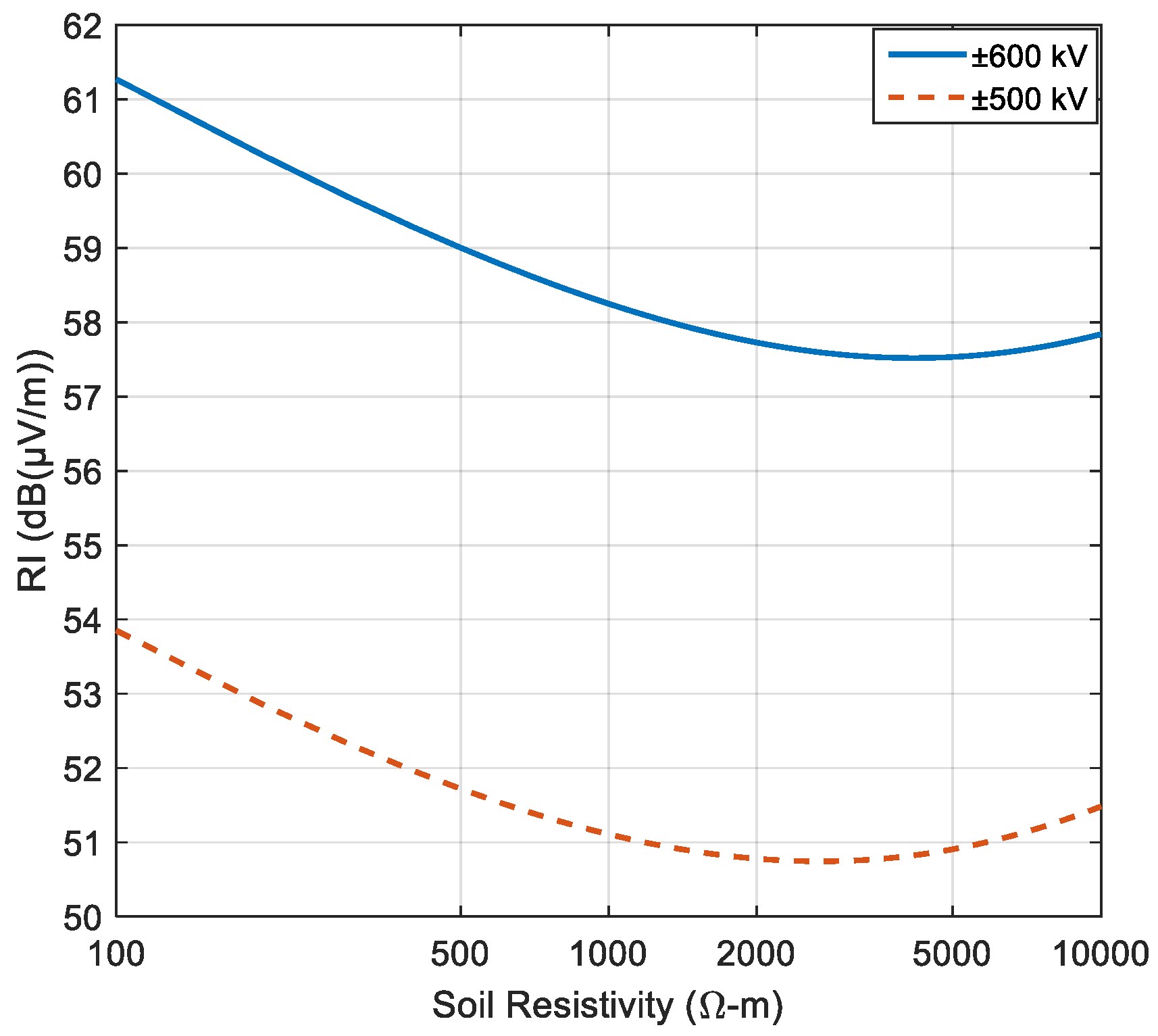
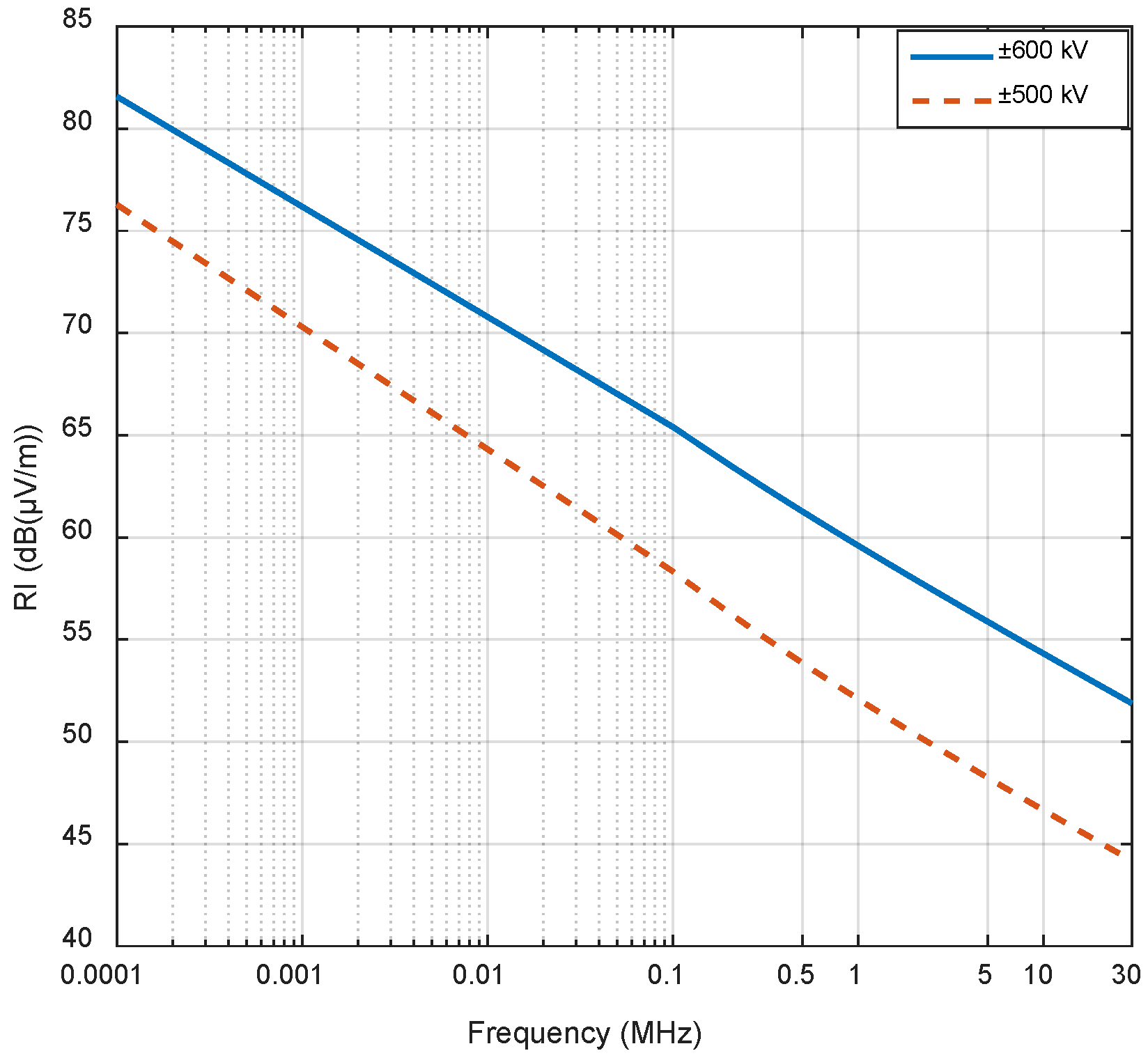
4.2. Parametric Sweeps
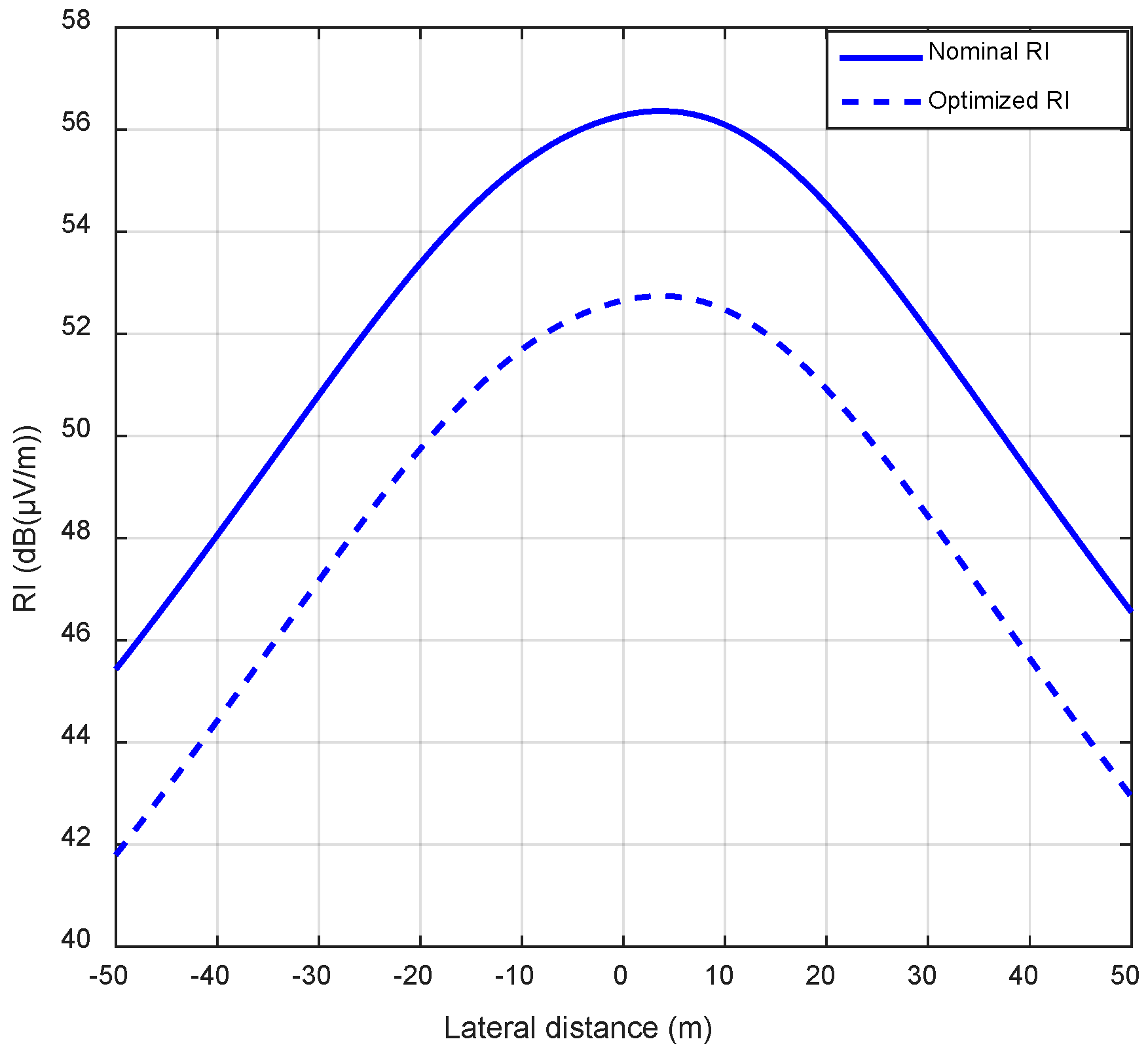
5. Optimization of Radio Interference Levels in HVDC Lines
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Font, A.; Ilhan, S.; Ismailoglu, H.; Espino-Cortes, F.P.; Ozdemir, A. Design and Technical Analysis of 500–600 kV HVDC Transmission System for Turkey. In Proceedings of the 10th International Conference on Electrical and Electronics Engineering ELECO 2017, Bursa, Turkey, 30 November–2 December 2017. [Google Scholar]
- Rodrigues, E.; Pontes, R.S.T.; Bandeira, J.; Aguiar, V.P.B. Analysis of the Incidence of Direct Lightning over a HVDC Transmission Line through EFD Model. Energies 2019, 12, 555. [Google Scholar] [CrossRef]
- Pei, X.; Tang, G.; Zhang, S. A Novel Pilot Protection Principle Based on Modulus Traveling-Wave Currents for Voltage-Sourced Converter Based High Voltage Direct Current (VSC-HVDC) Transmission Lines. Energies 2018, 11, 2395. [Google Scholar] [CrossRef]
- Naeem, R.; Cheema, M.S.; Ahmad, M.; Haider, S.A.; Shami, U.T. Impact of HVDC grid segmentation topology on transient stability of HVDC-segmented electric grid. In Proceedings of the 2015 International Conference on Open Source Systems & Technologies (ICOSST), Lahore, Pakistan, 17–19 December 2015; pp. 132–136. [Google Scholar]
- Maruvada, P.S. Corona Performance of High-Voltage Transmission Lines; Research Studies Press Ltd.: Baldock, UK, 2000. [Google Scholar]
- Electric Power Transmission and the Environment: Fields, Noise and Interference. In CIGRE Technical Brochure; No. 74; National Grid Research and Development Centre: Paris, France, 2000.
- Tejada-Martinez, C.; Espino-Cortes, F.P.; Ilhan, S.; Ozdemir, A. Computation of Corona Radio Interference Levels in HVDC Transmission Lines. In Proceedings of the 10th International Conference on Electrical and Electronics Engineering ELECO 2017, Bursa, Turkey, 30 November–2 December 2017. [Google Scholar]
- Tejada-Martinez, C.; Espino-Cortes, F.P.; Ilhan, S.; Ozdemir, A. Optimization of Corona Radio Interference Levels in HVDC Transmission Lines. In Proceedings of the 2018 International Conference on High Voltage Engineering and Application, ICHVE 2018, Athens, Greece, 10–13 September 2018. [Google Scholar]
- Interferences Produced by Corona Effect of Electric Systems. In CIGRE Technical Brochure; No. 61; CIGRE Committee Report: Paris, France, 1996.
- Impacts of HVDC Lines on the Economics of HVDC Projects. In CIGRE Technical Brochure; No. 388; Task Force: Paris, France, 2009.
- Tejada-Martinez, C.; Gómez, P.; Escamilla, J.C. Computation of Radio Interference Levels in High Voltage Transmission Lines with Corona. IEEE Lat. Am. Trans. 2009, 7, 54–61. [Google Scholar] [CrossRef]
- Paul, C.R. Analysis of Multiconductor Transmission Lines, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2008. [Google Scholar]
- Padiyar, K.R. HVDC Power Transmission Systems: Technology and System Interactions; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Tian, F.; Yu, Z.; Zeng, R. Radio Interference and Audible Noise of the UHVDC test line under high altitude condition. In Proceedings of the 2012 Asia-Pacific Symposium on Electromagnetic Compatibility, Singapore, 21–24 May 2012; pp. 449–452. [Google Scholar]
- Yu, Z.; Zeng, R.; Li, M.; Li, R.; Liu, L.; Yang, D.; Zhang, Z.; Zhang, B.; Tian, F. Radio Interference of Ultra HVDC Transmission Lines in High Altitude Region. In Proceedings of the 2010 Asia-Pacific International Symposium on Electromagnetic Compatibility, Beijing, China, 12–16 April 2010; pp. 1672–1675. [Google Scholar]
- Zhao, L.; Cui, X.; Xie, L.; Lu, J.; He, K.; Ju, Y. Altitude Correction of Radio Interference of HVdc Transmission Lines Part II: Measured Data Analysis and Altitude Correction. IEEE Trans. Electromagn. Compat. 2017, 59, 284–292. [Google Scholar] [CrossRef]
- Baoquan, W.; Dichen, L.; Xiong, W.; Yao, L. The study on the radio interference from ±800kV Yun Guang UHVDC transmission line. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–26 October 2006; pp. 1–5. [Google Scholar]
- Limits and Measurement Methods of EM Noise from AC Power Systems, 0.15–30 MHz; Standard CAN3-C108.3.1-M84; Canadian Standard Association: Toronto, ON, Canada, 2014.
- IEC TR, CISPR 18-3, Radio Interference Characteristics of Overhead Power Lines and High Voltage Equipment—Part 3: Code of Practice for Minimizing the Generation of Radio Noise; IEC: Geneva, Switzerland, 2010; pp. 30–31.
- Yang, J.; Wu, J.; Li, M.; Han, J. Structural Optimization for the China UHV Transmission Steel Tower. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–4. [Google Scholar]
- Vivek, K.S.; Nagendra, V. Optimized Design of Steel Transmission Line Tower by Limit State Methodology. Int. J. Mod. Eng. Res. IJMER 2015, 5, 81–100. [Google Scholar]


| Variable | Value |
|---|---|
| Voltage (V) | ±800 kV |
| Number of poles (n) | 2 |
| Conductor height (H) | 18 m |
| Distance between the poles (S) | 22 m |
| Number of sub-conductors in the bundle (nc) | 6 |
| Bundle spacing (a) | 45 cm |
| Sub-conductor radius (r) | 1.68 cm |
| Ground resistivity (ρe) | 100 Ωm |
| Measuring frequency (f) | 500 kHz |
| Variable | Value |
|---|---|
| Voltage (V) | ±500 or ±600 kV |
| Number of poles (n) | 2 |
| Conductor height of ±500 kV line (H) | 27 m |
| Conductor height of ±600 kV line (H) | 34 m |
| Distance between the poles (S) for both voltage levels | 16 m |
| Number of sub-conductors in the bundle (nc) | 4 |
| Bundle spacing (a) | 45 cm |
| Sub-conductor radius (r) | 1.71 cm |
| Variable | Line of ±500 kV | Line of ±600 kV |
|---|---|---|
| Maximum bundle electric field (gmax) | 19.93 kV/cm | 23.83 kV/cm |
| Excitation function (Γ) | 6.65 dB | 13.79 dB |
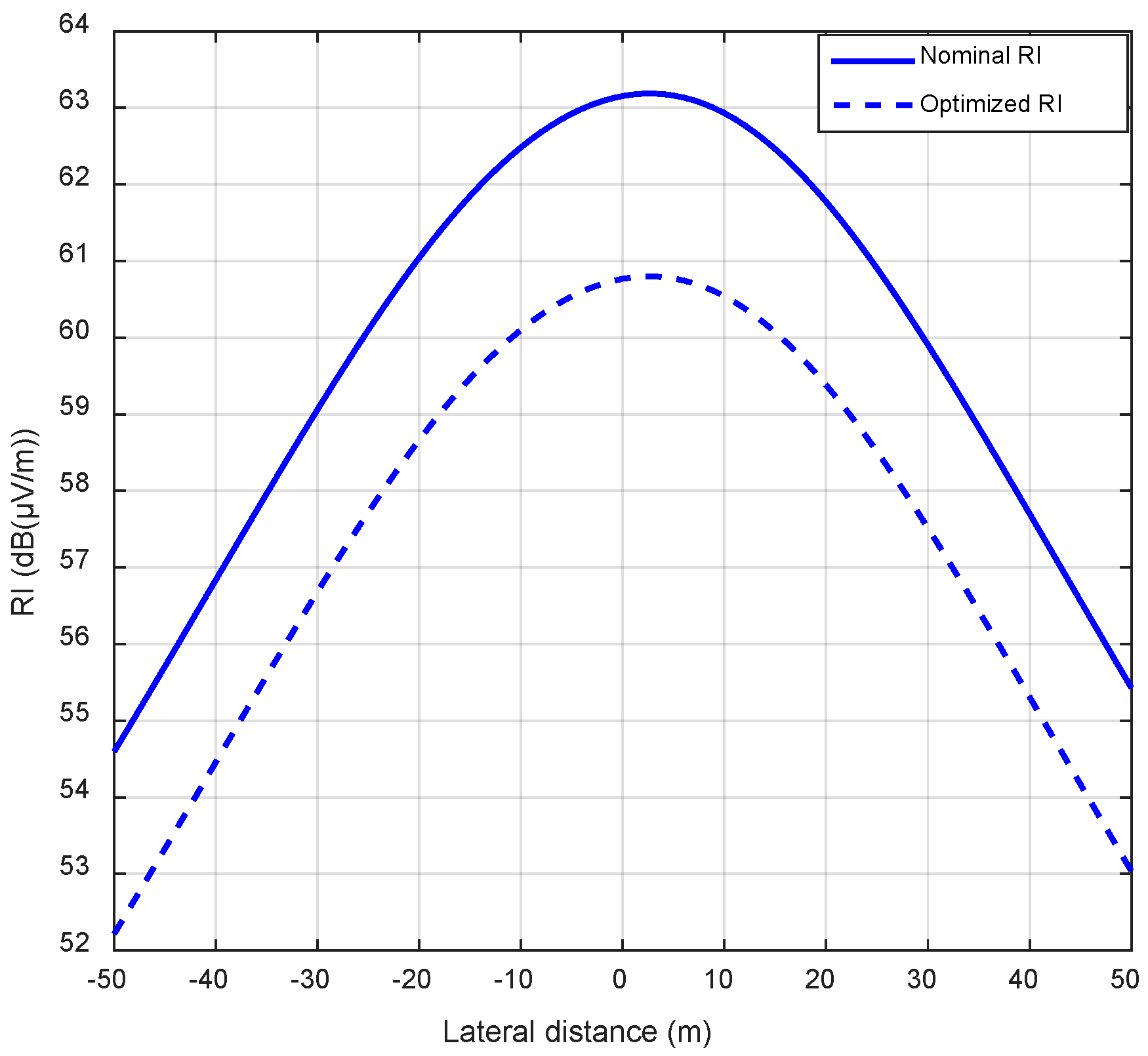
| Maximum value of RI | 56.37 dB | 63.19 dB |
| RI at point (x, y) = (23 m, 1.0 m) | 53.85 dB | 61.27 dB |
| Parameter | Value |
|---|---|
| Population type | Double vector |
| Population size | 100 |
| Scaling function | Rank |
| Selection function | Stochastic uniform |
| Elite count | 1.5 |
| Crossover fraction | 0.8 |
| Mutation function | Constraint dependent |
| Crossover function | Constraint dependent |
| Migration direction | Forward |
| Migration fraction | 0.2 |
| Migration interval | 20 |
| Constraint initial penalty | 10 |
| Constraint penalty factor | 100 |
| Variable | Lower Bound | Upper Bound | Nominal Value | Optimal Value |
|---|---|---|---|---|
| Sub-conductor radius | 1.04 cm 477 MCM | 2.21 cm 2167 MCM | 1.71 cm 1272 MCM | 2.21 cm 2167 MCM |
| Bundle spacing | 20 cm | 80 cm | 45 cm | 42 cm |
| Number of sub-conductors | 2 | 8 | 4 | 3 |
| RI at (x, y) = (23 m, 1.0 m) | 53.85 dB | 50.23 dB | ||
| Total mass of the bundle | 4 × 2135 = 8540 kg/km | 3 × 3431 = 10,293 kg/km | ||
| Variable | Lower Bounds | Upper Bounds | Nominal Values | Optimal Values |
|---|---|---|---|---|
| Sub-conductor radius | 1.04 cm 477 MCM | 2.21 cm 2167 MCM | 1.71 cm 1272 MCM | 2.21 cm 2167 MCM |
| Bundle spacing | 20 cm | 80 cm | 45 cm | 38 cm |
| Number of sub-conductors | 2 | 8 | 4 | 4 |
| RI at (x, y) = (23 m, 1.0 m) | 61.27 dB | 58.88 dB | ||
| Total mass of the bundle | 4 × 2135 = 8540 kg/km | 4 × 3431 = 13,724 kg/km | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tejada-Martinez, C.; Espino-Cortes, F.P.; Ilhan, S.; Ozdemir, A. Optimization of Radio Interference Levels for 500 and 600 kV Bipolar HVDC Transmission Lines. Energies 2019, 12, 3187. https://doi.org/10.3390/en12163187
Tejada-Martinez C, Espino-Cortes FP, Ilhan S, Ozdemir A. Optimization of Radio Interference Levels for 500 and 600 kV Bipolar HVDC Transmission Lines. Energies. 2019; 12(16):3187. https://doi.org/10.3390/en12163187
Chicago/Turabian StyleTejada-Martinez, Carlos, Fermin P. Espino-Cortes, Suat Ilhan, and Aydogan Ozdemir. 2019. "Optimization of Radio Interference Levels for 500 and 600 kV Bipolar HVDC Transmission Lines" Energies 12, no. 16: 3187. https://doi.org/10.3390/en12163187
APA StyleTejada-Martinez, C., Espino-Cortes, F. P., Ilhan, S., & Ozdemir, A. (2019). Optimization of Radio Interference Levels for 500 and 600 kV Bipolar HVDC Transmission Lines. Energies, 12(16), 3187. https://doi.org/10.3390/en12163187






