Thermal-Hydraulic Studies on the Shell-and-Tube Heat Exchanger with Minijets
Abstract
1. Introduction
- change of the heat transfer surface roughness,
- extension of the heat transfer surface through the usage of the fins,
- twisting the heat transfer surface,
- making an additions, for example in the form of solid particles constructing the nanofluids,
- reduction of hydraulic diameter of the flow channel,
- application of the impinging jets.
2. Object of the Study
2.1. Minijets Heat Exchanger (MJHE)
2.2. Reference Heat Exchanger
- -
- the heat exchange surface,
- -
- the diameters of the inlet and outlet connectors,
- -
- the diameters of the cylindrical heat transfer partition and the heat exchanger shell,
- -
- the length of the heat exchanger.
3. Experimental System
4. Results
4.1. Thermal Characteristics
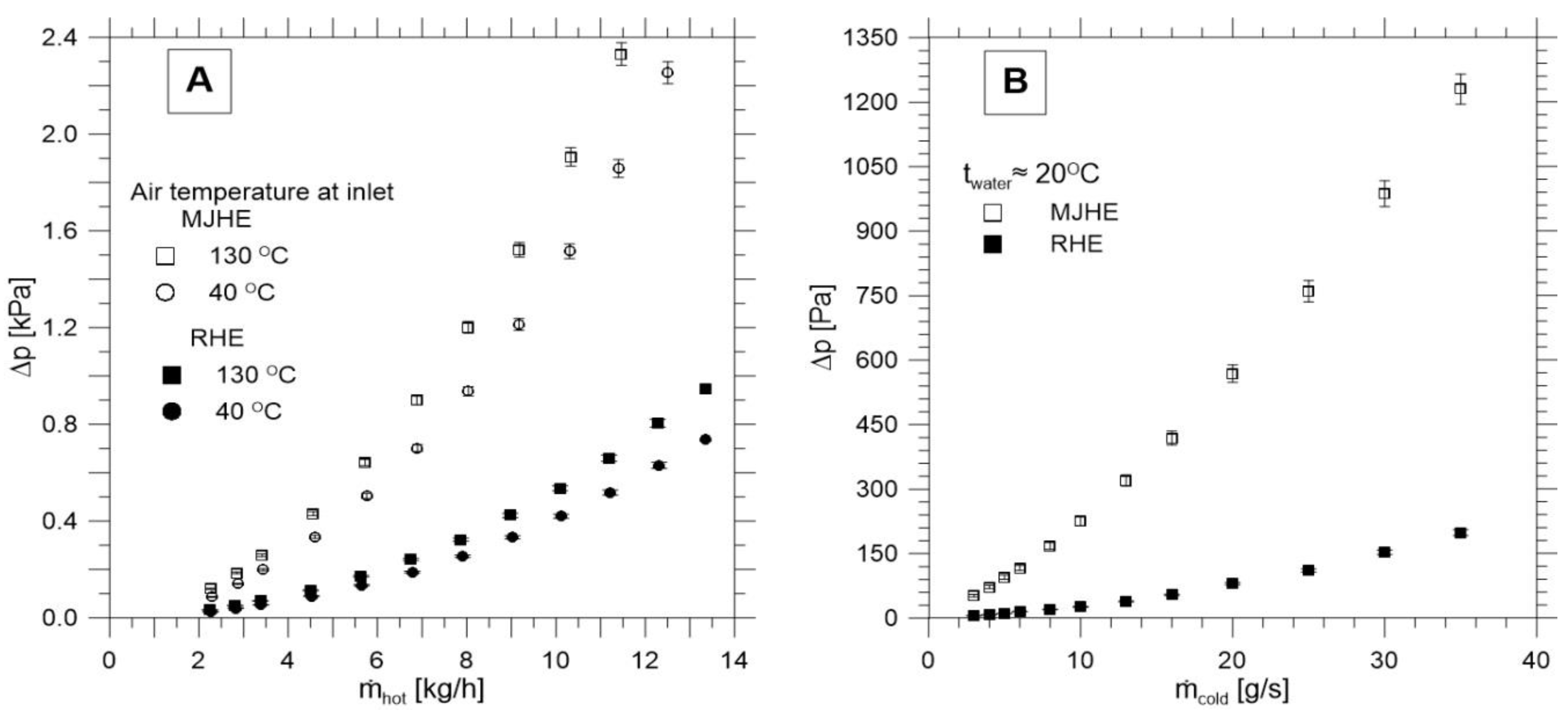
4.2. Hydraulic Characteristics
4.3. Analysis of the Measurements Uncertainies
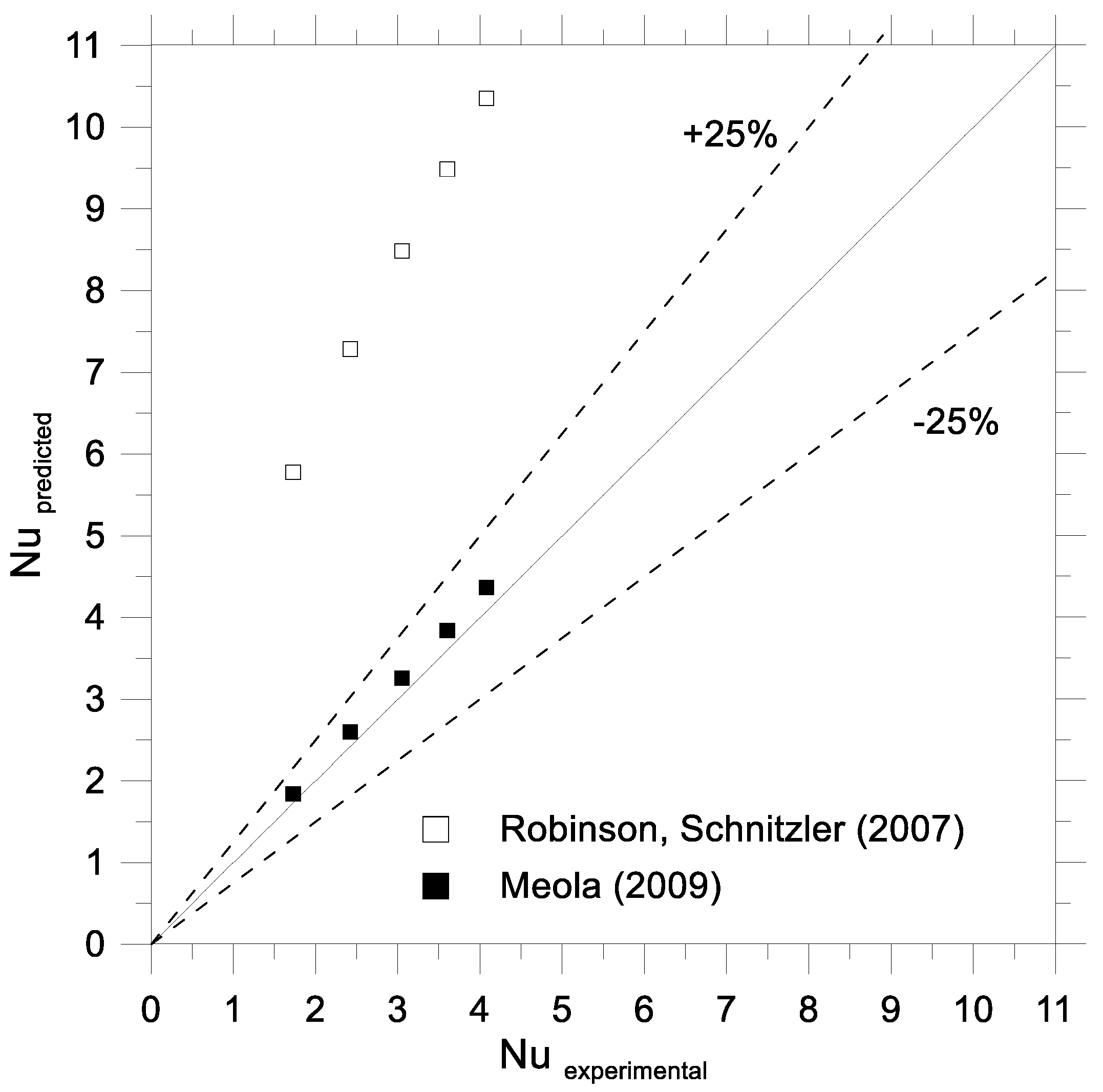
5. Validation of the Exemplary Nusselt Number Correlations
6. Future Works
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | heat transfer area, m2 |
| An | total nozzle area, m2 |
| cp | specific heat, J/(kg·K) |
| Cf | flow coefficient, |
| d | orifice diameter, m |
| f | relative nozzle area, |
| G | mass flux, kg/(m2·s) |
| H | distance between nozzle and impingement surface, m |
| mass flow rates, kg/h, g/s | |
| n | number of orifices forming the jets, |
| Nu | Nusselt number, |
| p | pressure, Pa |
| Pr | Prandtl number, |
| S | jet-to-jet spacing, m |
| Re | Reynolds number, |
| t | temperature, °C |
| volume flow rates, m3/h | |
| u(y) | uncertainty of determined quantity |
| u(xk) | maximal uncertainty of measured/calculated component |
| Greek letters | |
| α | heat transfer coefficient, W/(m2·K) |
| Δ | difference value, |
| δy | relative uncertainty of determined quantity, % |
| λ | thermal conductivity of fluid, W/(m·K) |
| μ | dynamic viscosity of fluid, Pa·s |
| Subscripts | |
| cold | in regard to heated medium |
| exp | experiment |
| hot | in regard to heating medium |
| in | inlet |
| out | outlet |
References
- Kreith, F.; Goswami, D.Y. The CRC Handbook of Mechanical Engineering, 2nd ed.; CRC Press LLC: Boca Raton, FL, USA, 2005. [Google Scholar]
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y.I. Handbook of Heat Transfer; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Bergles, A.E. The implications and challenges of enhanced heat transfer for the chemical process industries. Chem. Eng. Res. Des. 2001, 79, 437–444. [Google Scholar] [CrossRef]
- Błasiak, P.; Pietrowicz, S. Towards a better understanding of 2D thermal-flow processes in a scraped surface heat exchanger. Int. J. Heat Mass Transf. 2016, 98, 240–256. [Google Scholar] [CrossRef]
- Gondrexon, N.; Rousselet, Y.; Legay, M.; Boldo, P.; Le Person, S.; Bontemps, A. Intensification of heat transfer process: Improvement of shell-and-tube heat exchanger performances by means of ultrasound. Chem. Eng. Process. 2010, 49, 936–942. [Google Scholar] [CrossRef]
- Legay, M.; Simony, B.; Boldo, P.; Gondrexon, N.; Le Person, S.; Bontemps, A. Improvement of heat transfer by means of ultrasound: Application to a double-tube heat exchanger. Ultrason. Sonochem. 2012, 19, 1194–1200. [Google Scholar] [CrossRef] [PubMed]
- Wajs, J.; Mikielewicz, D. Effect of surface roughness on thermal-hydraulic characteristics of plate heat exchanger. Key Eng. Mater. 2014, 597, 63–74. [Google Scholar] [CrossRef]
- Kalawa, W.; Wójcik, T.M.; Piasecka, M. Heat transfer research on enhanced heating surfaces in pool boiling. EPJ Web Conf. 2017, 143, 02048. [Google Scholar] [CrossRef]
- Jafari, R.; Okutucu-Özyurt, T.; Ünver, H.Ö.; Bayer, Ö. Experimental investigation of surface roughness effects on the flow boiling of R134a in microchannels. Exp. Therm. Fluid Sci. 2016, 79, 222–230. [Google Scholar] [CrossRef]
- Strąk, K.; Piasecka, M.; Maciejewska, B. Spatial orientation as a factor in flow boiling heat transfer of cooling liquids in enhanced surface minichannels. Int. J. Heat Mass Transf. 2018, 117, 375–387. [Google Scholar] [CrossRef]
- Akpinar, E.K.; Bicer, Y.; Yildiz, C.; Pehli̧van, D. Heat transfer enhancements in a concentric double pipe exchanger equipped with swirl elements. Int. Commun. Heat Mass 2004, 31, 857–868. [Google Scholar] [CrossRef]
- Akpinar, E.K. Evaluation of heat transfer and exergy loss in a concentric double pipe exchanger equipped with helical wires. Energy Convers. Manag. 2006, 47, 3473–3486. [Google Scholar] [CrossRef]
- Cieśliński, J.T.; Fiuk, A.; Miciak, W.; Siemieńczuk, B. Performance of a plate heat exchanger operated with water-Al2O3 nanofluid. Appl. Mech. Mater. 2016, 831, 188–197. [Google Scholar] [CrossRef]
- Huang, D.; Wu, Z.; Sunden, B. Effects of hybrid nanofluid mixture in plate heat exchangers. Exp. Therm. Fluid Sci. 2016, 72, 190–196. [Google Scholar] [CrossRef]
- Wajs, J.; Mikielewicz, D.; Jakubowska, B. Performance of the domestic micro ORC equipped with the shell-and-tube condenser with minichannels. Energy 2018, 157, 853–861. [Google Scholar] [CrossRef]
- Ma, T.; Li, L.; Xu, X.-Y.; Chen, Y.-T.; Wang, Q.-W. Study on local thermal–hydraulic performance and optimization of zigzag-type printed circuit heat exchanger at high temperature. Energy Convers. Manag. 2015, 104, 55–66. [Google Scholar] [CrossRef]
- Aneesh, A.M.; Sharma, A.; Srivastava, A.; Vyas, K.N.; Chaudhuri, P. Thermal-hydraulic characteristics and performance of 3D straight channel based printed circuit heat exchanger. Appl. Therm. Eng. 2016, 98, 474–482. [Google Scholar] [CrossRef]
- Dąbrowski, P.; Klugmann, M.; Mikielewicz, D. Channel blockage and flow maldistribution during unsteady flow in a model microchannel plate heat exchanger. J. Appl. Fluid Mech. 2019, 12, 1023–1035. [Google Scholar] [CrossRef]
- Klugmann, M.; Dabrowski, P.; Mikielewicz, D. Pressure drop related to flow maldistribution in a model minichannel plate heat exchanger. Arch. Thermodyn. 2018, 39, 123–146. [Google Scholar]
- Kumar, R.; Singh, G.; Mikielewicz, D. New approach for the mitigating of flow maldistribution in parallel microchannel heat sink. J. Heat Transf. 2018. [Google Scholar] [CrossRef]
- Chauhan, R.; Singh, T.; Thakur, N.S.; Kumar, N.; Kumar, R.; Kumar, A. Heat transfer augmentation in solar thermal collectors using impinging air jets: A comprehensive review. Renew. Sustain. Energy Rev. 2018, 82, 3179–3190. [Google Scholar] [CrossRef]
- Zukowski, M. Heat transfer performance of a confined single slot jet of air impinging on a flat surface. Int. J. Heat Mass Transf. 2013, 57, 484–490. [Google Scholar] [CrossRef]
- Zukowski, M. Experimental investigations of thermal and flow characteristics of a novel microjet air solar heater. Appl. Energy 2015, 142, 10–20. [Google Scholar] [CrossRef]
- Wajs, J.; Mikielewicz, D.; Fornalik-Wajs, E. Microjet Heat Exchanger with a Cylindrical Geometry, Especially for Heat Recovery from Low-Temperature Waste Energy Sources. Polish Patent PL224494, 8 July 2013. (In Polish). [Google Scholar]
- Kura, T.; Fornalik-Wajs, E.; Wajs, J. Thermal and hydraulic phenomena in boundary layer of minijets. Arch. Thermodyn. 2018, 39, 147–166. [Google Scholar]
- Nakabe, K.; Fornalik, E.; Eschenbacher, J.F.; Yamamoto, Y.; Ohta, T.; Suzuki, K. Interactions of longitudinal vortices generated by twin inclined jets and enhancement of impingement heat transfer. Int. J. Heat Fluid Flow 2001, 22, 287–292. [Google Scholar] [CrossRef]
- Wajs, J.; Mikielewicz, D.; Fornalik-Wajs, E.; Bajor, M. Recuperator with microjet technology as a proposal for heat recovery from low-temperature sources. Arch. Thermodyn. 2015, 36, 48–63. [Google Scholar] [CrossRef][Green Version]
- Wajs, J.; Mikielewicz, D.; Fornalik-Wajs, E.; Bajor, M. High performance tubular heat exchanger with minijet heat transfer enhancement. Heat Transf. Eng. 2019, 40, 772–783. [Google Scholar] [CrossRef]
- Shah, R.K. Assessment of Modified Wilson Plot Techniques for Obtaining Heat Exchanger Design Data. In Proceedings of the 9th International Heat Transfer Conference, Jerusalem, Israel, 19–24 August 1990. [Google Scholar]
- Working Group 1 of the Joint Committee for Guides in Metrology. Evaluation of Measurement Data–Guide to the Expression of Uncertainty in Measurement; JCGM, 2008; Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 9 August 2019).
- Zieba, A. Analysis of the Data in Science and Technology; PWN: Warszawa, Poland, 2013. (In Polish) [Google Scholar]
- Robinson, A.J.; Schnitzler, E. An experimental investigation of free and submerged miniature liquid jet array impingement heat transfer. Exp. Therm. Fluid Sci. 2007, 32, 1–13. [Google Scholar] [CrossRef]
- Meola, C. A new correlation of Nusselt number for impinging jets. Heat Transf. Eng. 2009, 30, 221–228. [Google Scholar] [CrossRef]
- Kosowski, K.; Tucki, K.; Piwowarski, M.; Stępień, R.; Orynycz, O.; Włodarski, W.; Bączyk, A. Thermodynamic cycle concepts for high-efficiency power plans. Part A: Public power plants 60+. Sustainability 2019, 11, 554. [Google Scholar] [CrossRef]
- Kosowski, K.; Tucki, K.; Piwowarski, M.; Stępień, R.; Orynycz, O.; Włodarski, W. Thermodynamic cycle concepts for high-efficiency power plants. Part B: Prosumer and distributed power industry. Sustainability 2019, 11, 2647. [Google Scholar] [CrossRef]
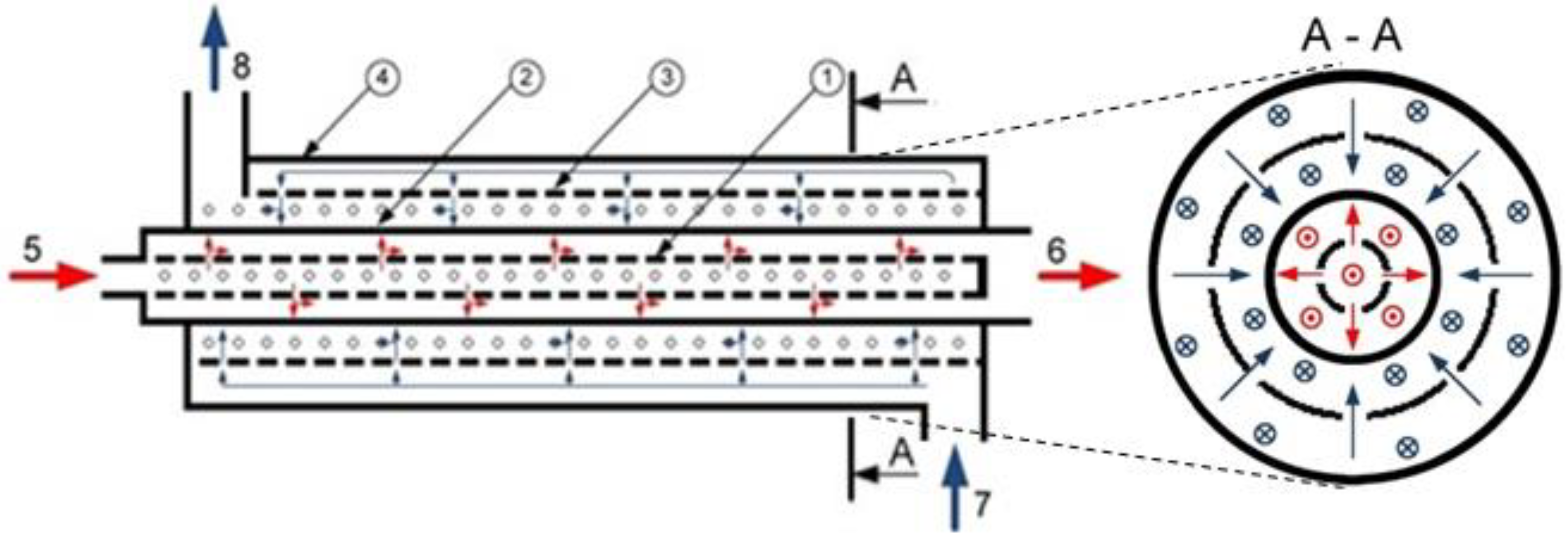
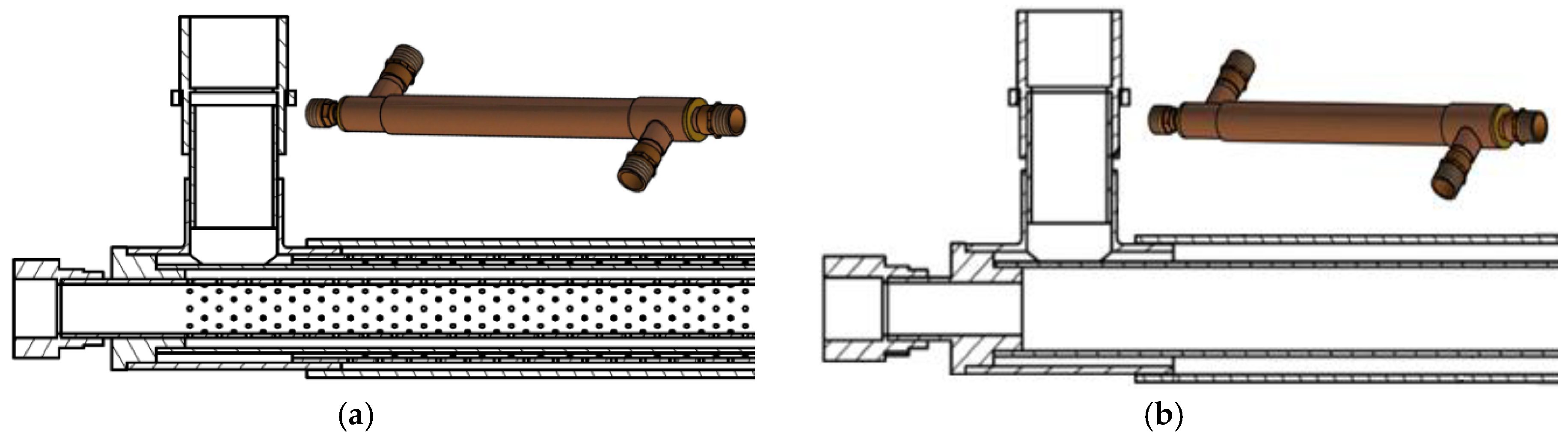


| Parameter | Size |
|---|---|
| Length of the heat transfer wall (m) | 0.281 |
| Outer diameter of the heat transfer wall (m) | 0.018 |
| Thickness of the heat transfer wall, t (m) | 0.001 |
| Heat transfer area, A (m2) | 0.015 |
| Inner diameter of the connection—heating side (m) | 0.012 |
| Inner diameter of the connection—heated side (m) | 0.015 |
| Orifice diameter, d (m) | 0.001 |
| Number of orifices (heating/heated side), n | 752/820 |
| Distance between the orifice and the heat transfer wall—heating side, h (m) | 0.002 |
| Distance between the orifice and the heat transfer wall—heated side, h (m) | 0.001 |
| Nozzle-to-nozzle spacing, S (m) | 0.004 |
| Name | Measured Parameter | Producer, Type/Model | Measurement Range | Maximal Mesurement Uncertainty |
|---|---|---|---|---|
| Rotameter | air volume flow rate | Metalchem, ROL-253 | 1.2 ÷ 18.8 m3/h | ±2.5% ZP |
| Pressure transducer | air pressure: (1) behind the rotameter (2) at the inlet to hx | Peltron, NPXA 2 | 0 ÷ 200 kPa abs. | ±0.1% ZP (±0.2 kPa) |
| T type thermocouple | temperature | Czach, TTP-1-100–0,5 | –100 ÷ 400 °C | ±0.5 °C |
| Mass flowmeter with the signal converter | water mass flow rate | Siemens /Massflo, MASS 2100, DI 3 | 0 ÷ 250 kg/h (0 ÷ 69.4 g/s) | ±0.15% of instantaneous flow rate |
| Pressure transducer | water pressure at the inlet to hx | Peltron, NPXA 2 | 0 ÷ 200 kPa abs. | ±0.25% ZP (±0.5 kPa) |
| Askania micromanometer | hydraulic resistance on the air (heating medium) side | Zakłady “Szopienice”, MK-2 | 0 ÷ 250 mm H2O | ±0.13 mm H2O |
| Electronic micromanometer | hydraulic resistance on the water (heated medium) side | Furness Controls, FCO12 | ZI: ±19 mm H2O ZII: ±99 mm H2O | ±0.5% ZP (ZI: ±0.1 mm H2O; ZII: ±1.0 mm H2O) |
| Quantity | Relative Value [%] |
|---|---|
| Air volumetric flow rate | 8.78 |
| Water mass flow rate | 1.16 |
| Temperature | 0.76 |
| Pressure drop | 1.10 |
| Heat rate | 13.14 |
| Heat transfer coefficients (heating side) | 1.66 |
| Heat transfer coefficients (heated side) | 6.91 |
| Mass flux (heating side) | 9.68 |
| Mass flux (heated side) | 1.15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wajs, J.; Bajor, M.; Mikielewicz, D. Thermal-Hydraulic Studies on the Shell-and-Tube Heat Exchanger with Minijets. Energies 2019, 12, 3276. https://doi.org/10.3390/en12173276
Wajs J, Bajor M, Mikielewicz D. Thermal-Hydraulic Studies on the Shell-and-Tube Heat Exchanger with Minijets. Energies. 2019; 12(17):3276. https://doi.org/10.3390/en12173276
Chicago/Turabian StyleWajs, Jan, Michał Bajor, and Dariusz Mikielewicz. 2019. "Thermal-Hydraulic Studies on the Shell-and-Tube Heat Exchanger with Minijets" Energies 12, no. 17: 3276. https://doi.org/10.3390/en12173276
APA StyleWajs, J., Bajor, M., & Mikielewicz, D. (2019). Thermal-Hydraulic Studies on the Shell-and-Tube Heat Exchanger with Minijets. Energies, 12(17), 3276. https://doi.org/10.3390/en12173276





