Study on Flow and Heat Transfer Characteristics of Porous Media in Engine Particulate Filters Based on Lattice Boltzmann Method
Abstract
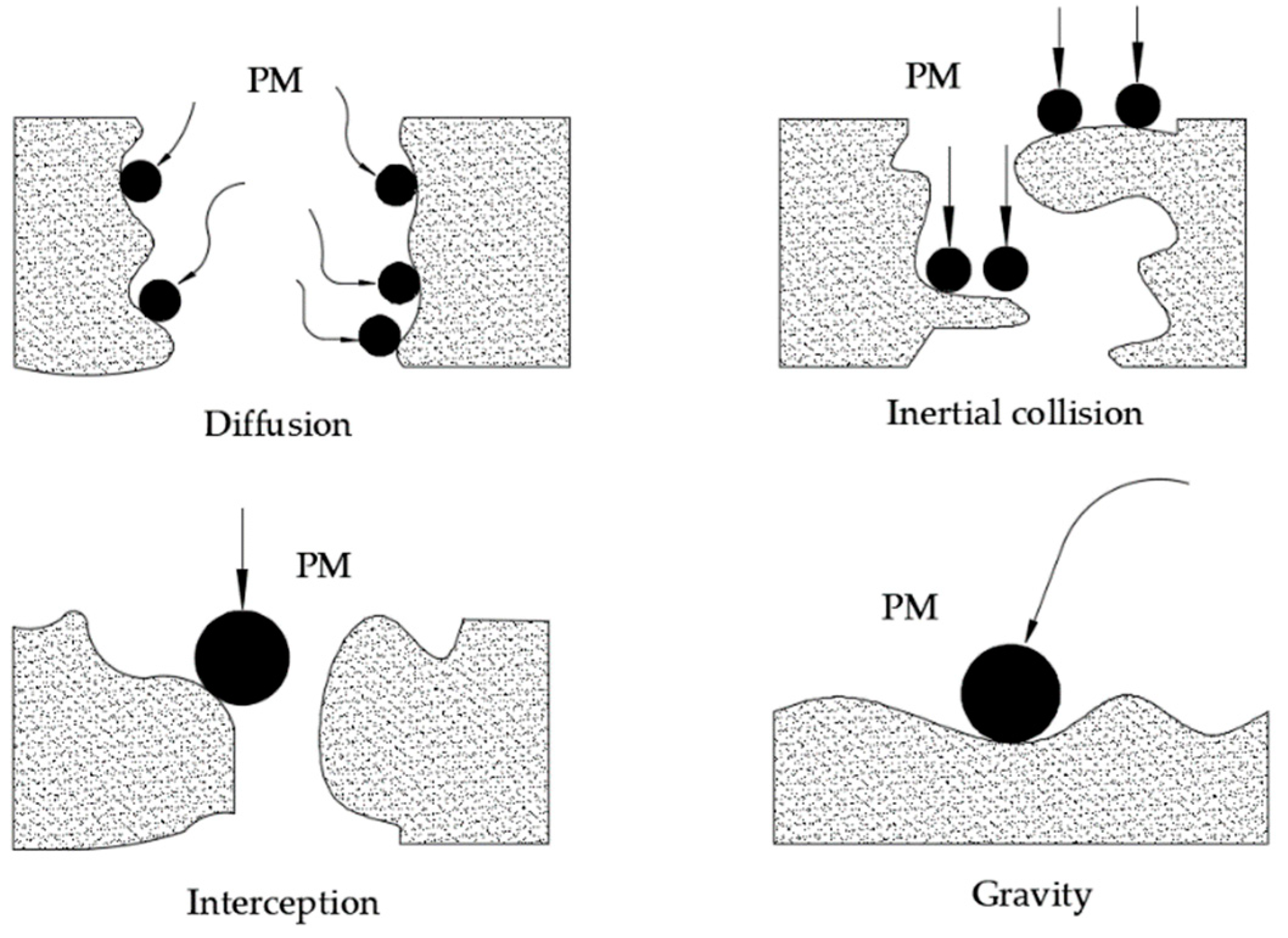
1. Introduction
2. LBM Theoretical Model
2.1. Two-Dimensional LBM Model
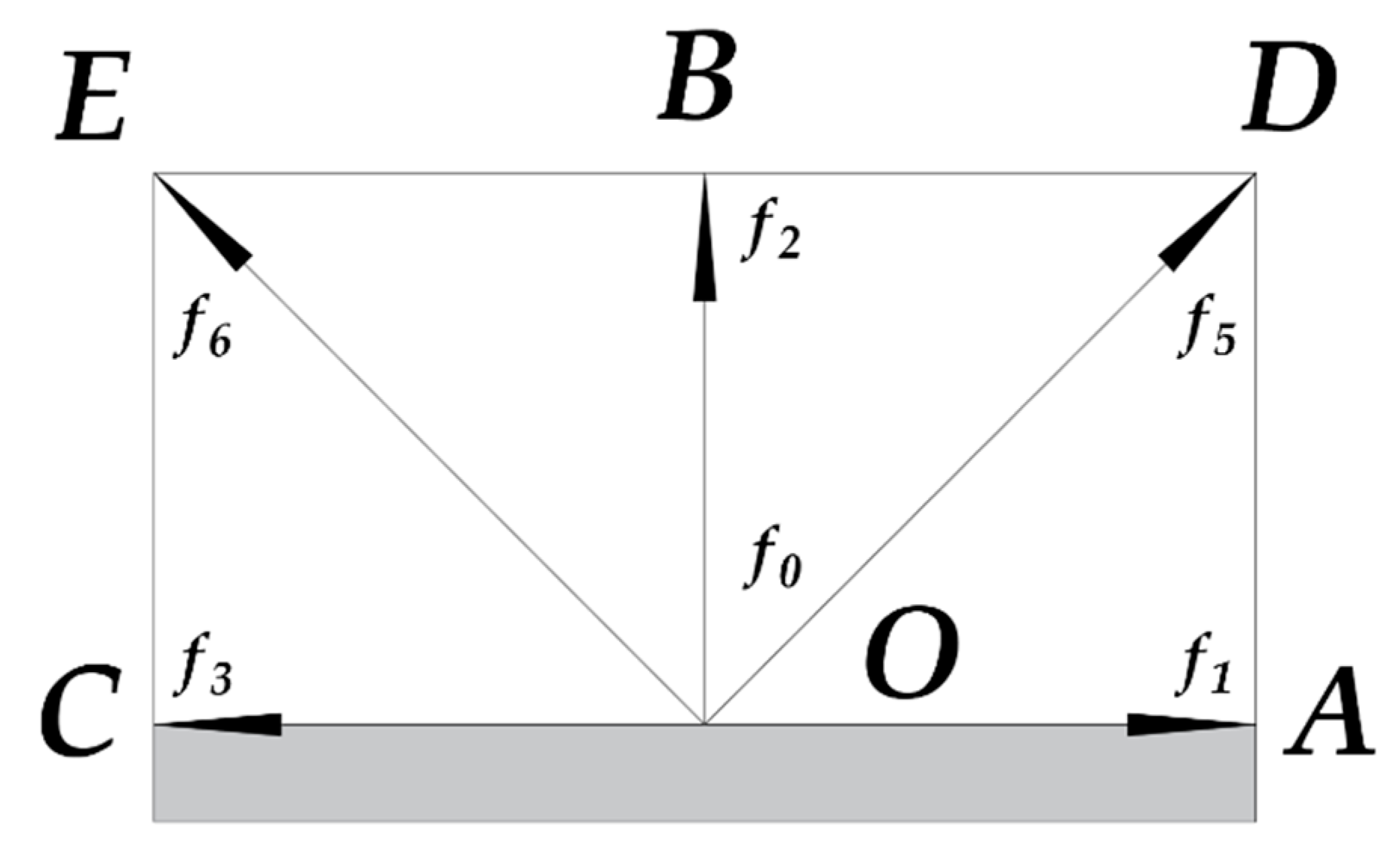
2.2. Boundary Conditions
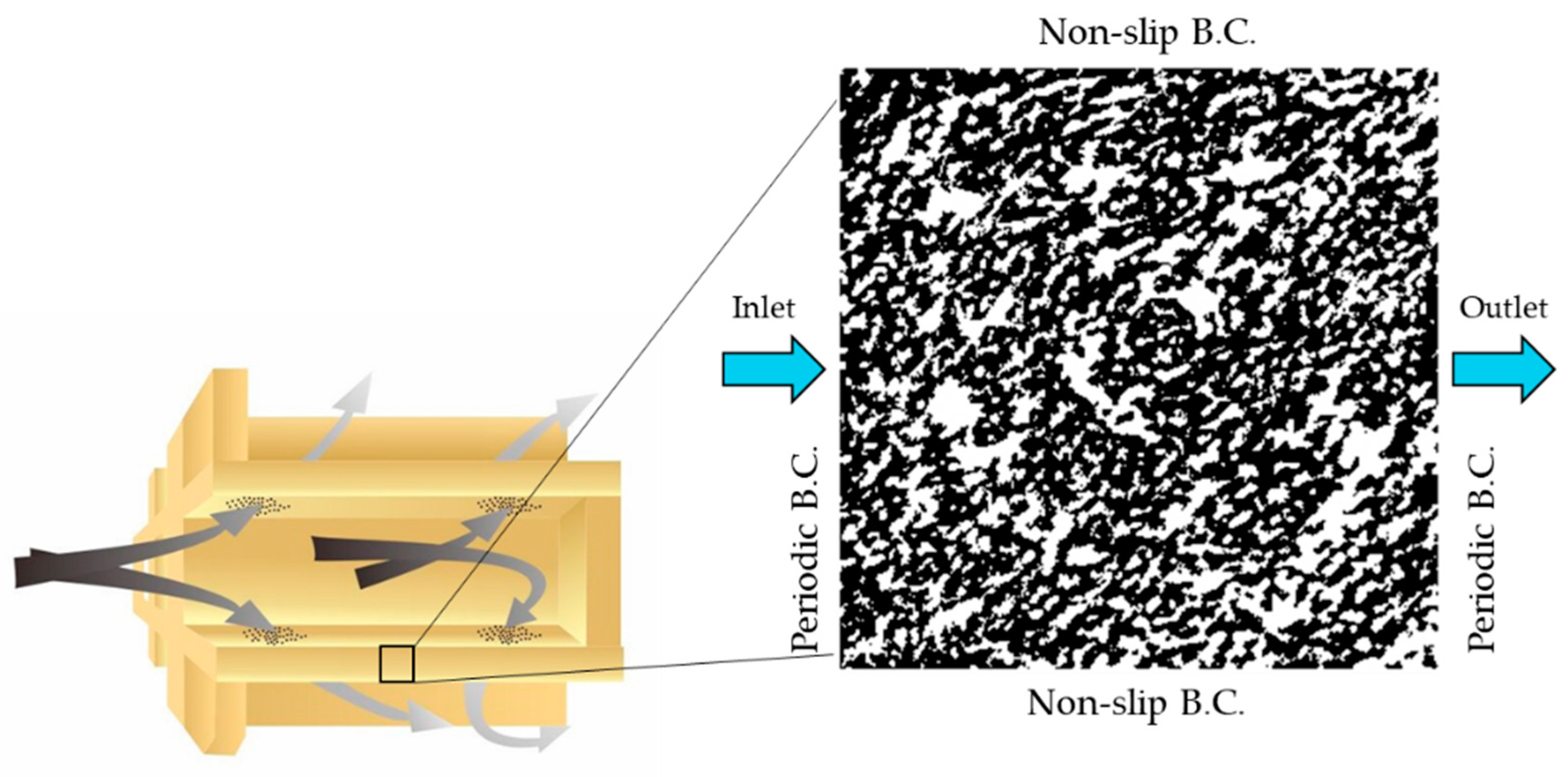
2.3. Construction of Porous Media by Quartet Structure Generation Set
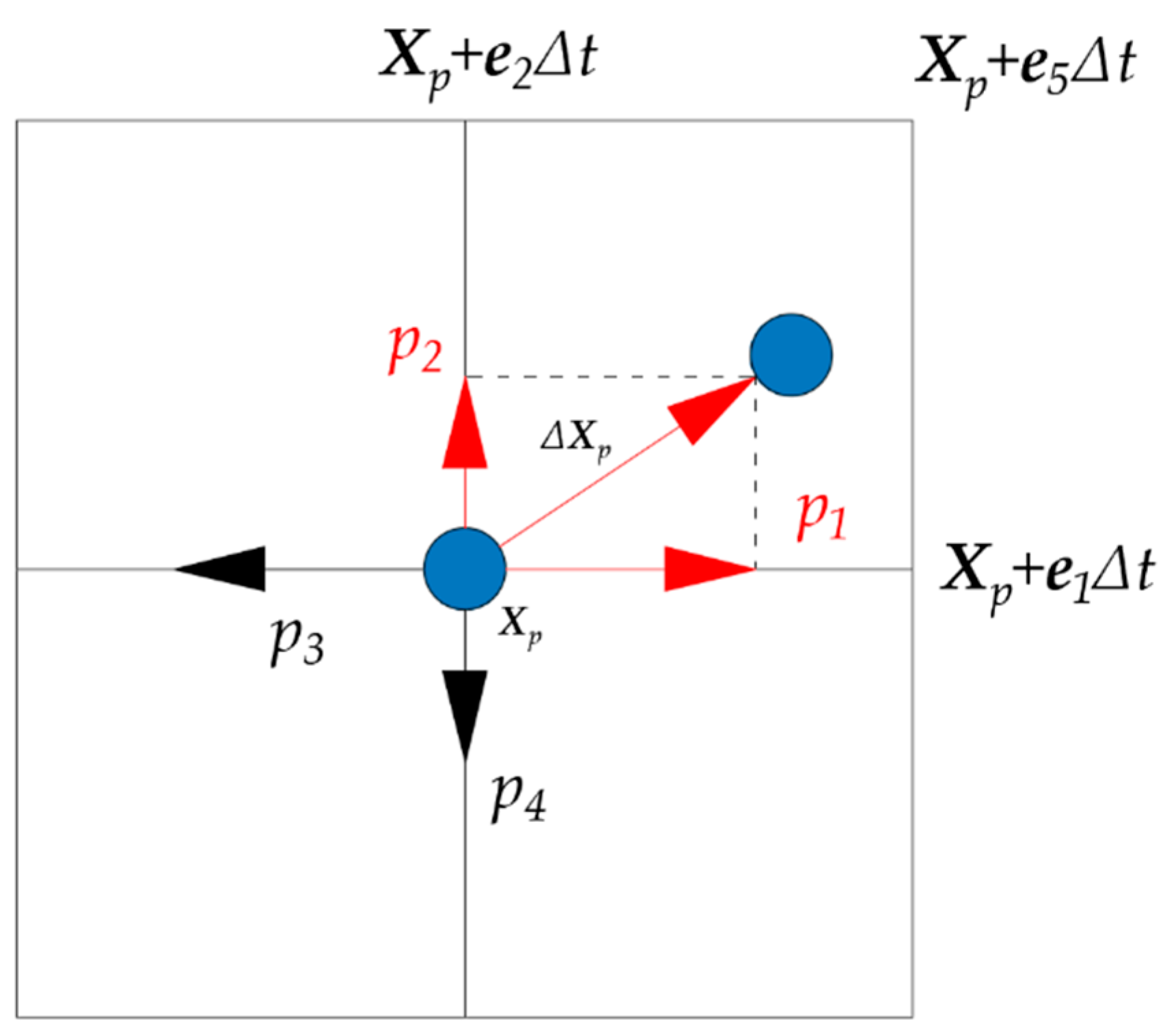
2.4. Cellular Automata Model
2.5. Program Validation
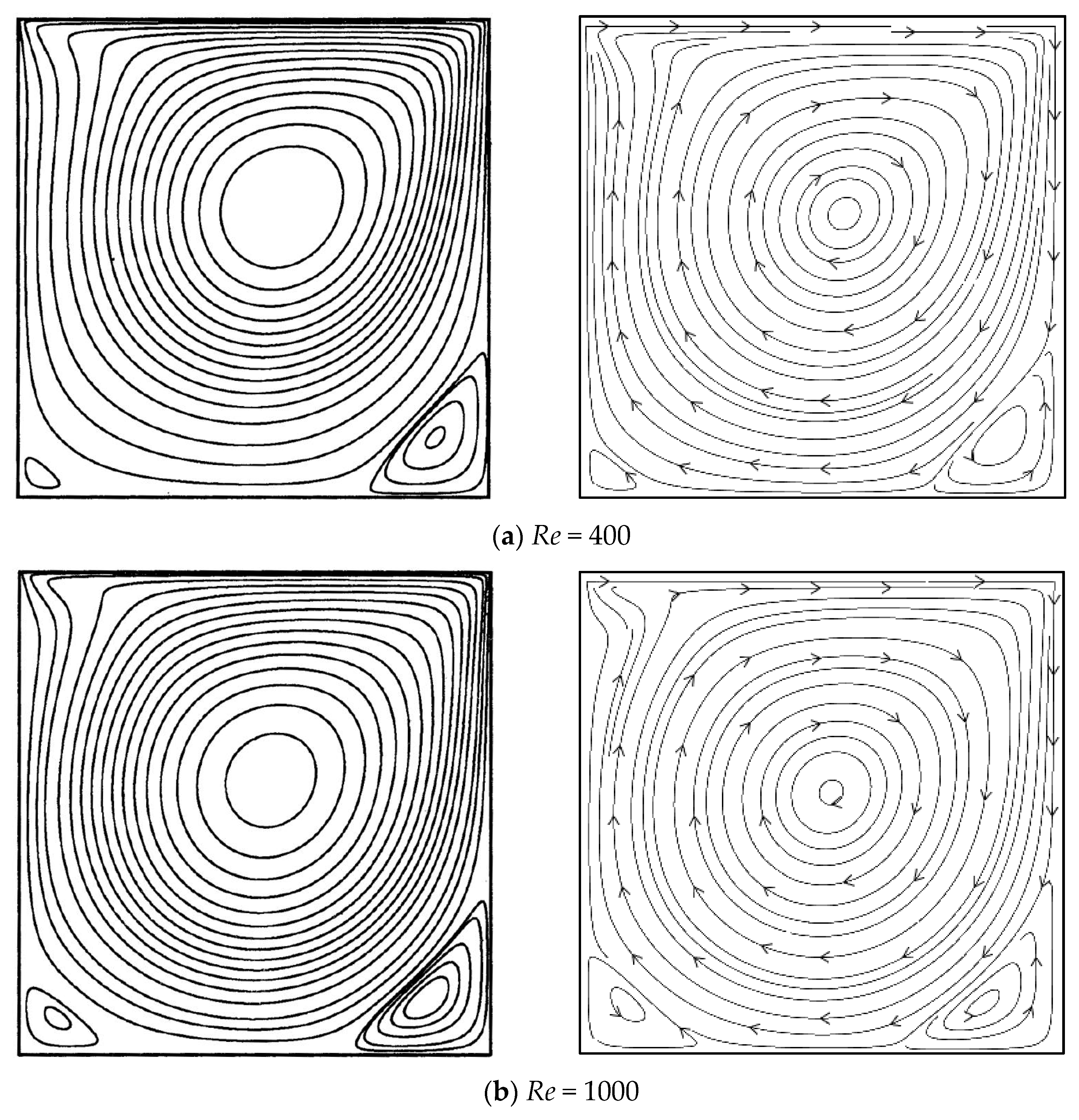
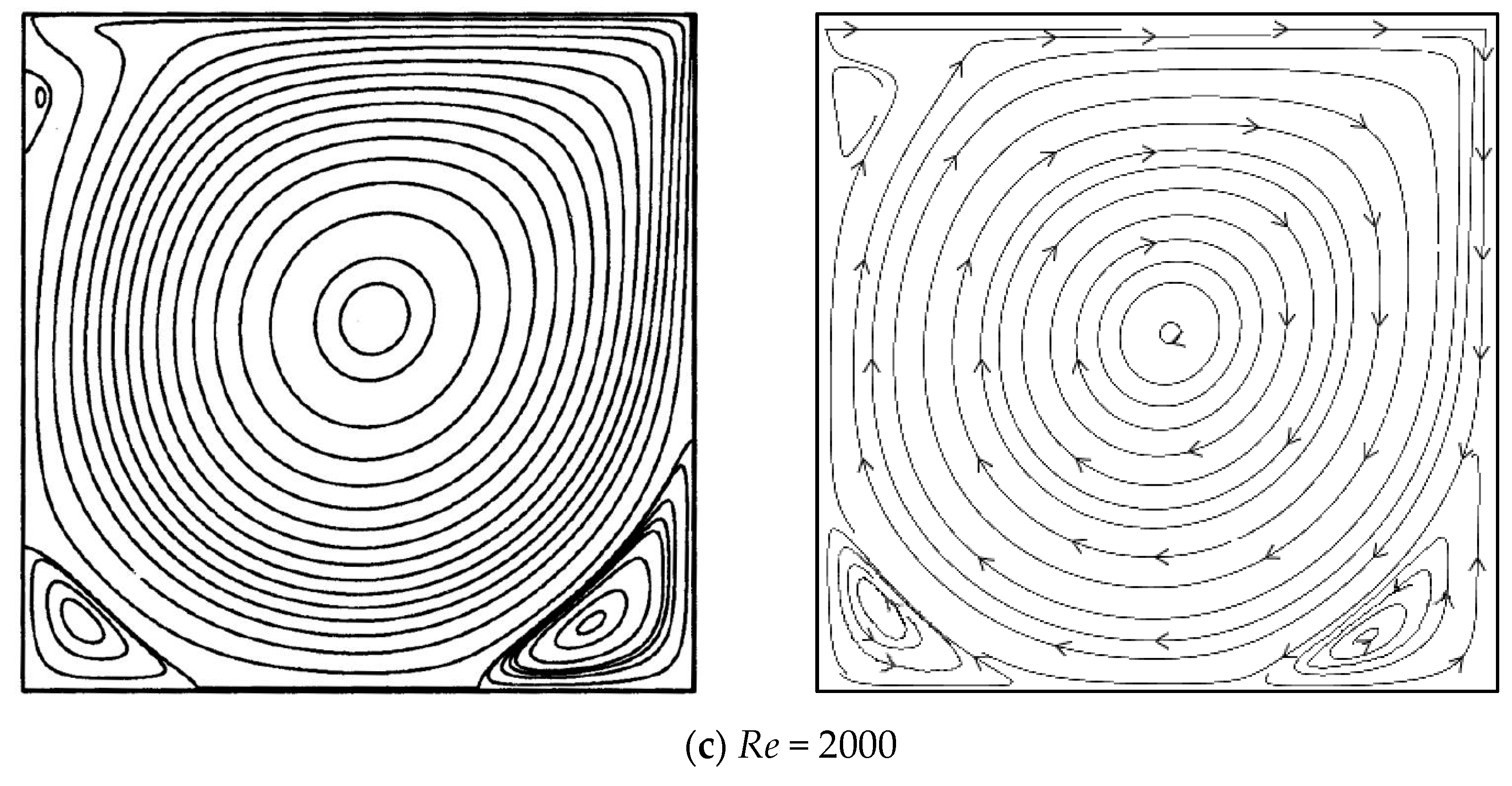
2.5.1. Lid Driven Cavity Flow
2.5.2. Natural Convection in a Square Cavity
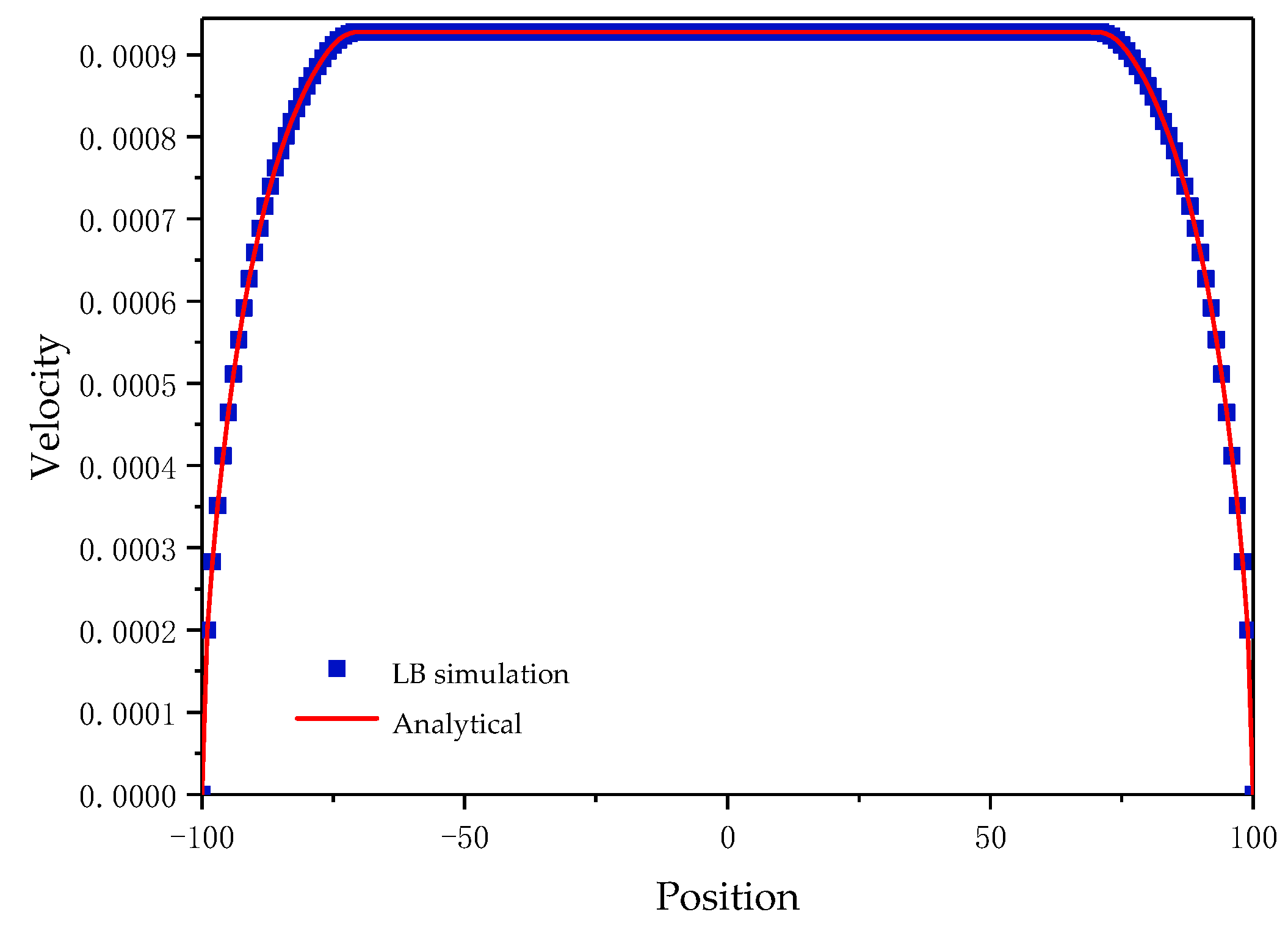
2.5.3. Poiseuille Flow in 2D Porous Media
2.5.4. CA Model Validation
2.5.5. Mesh Sensitivity Analysis
3. Results and Discussion
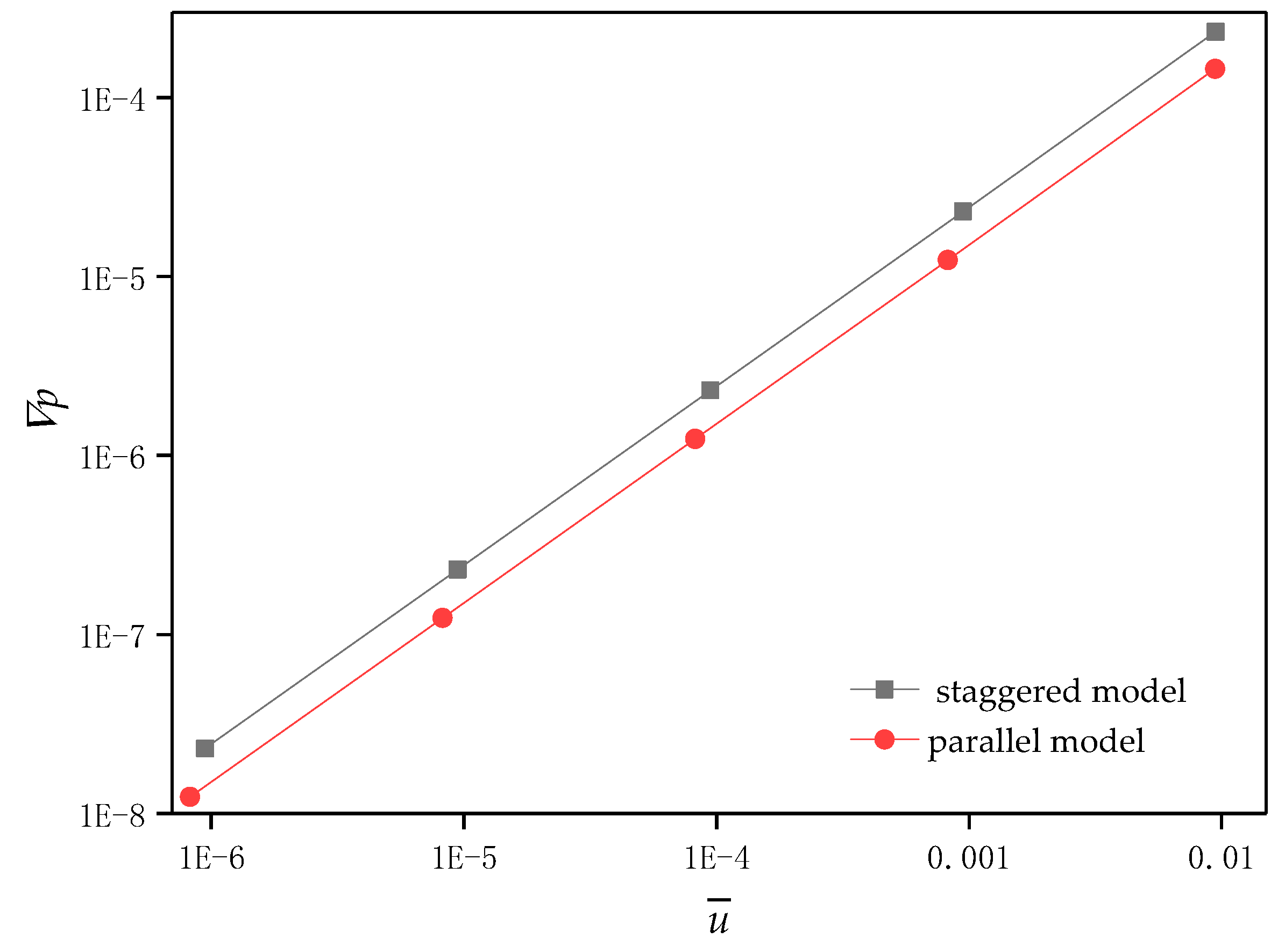
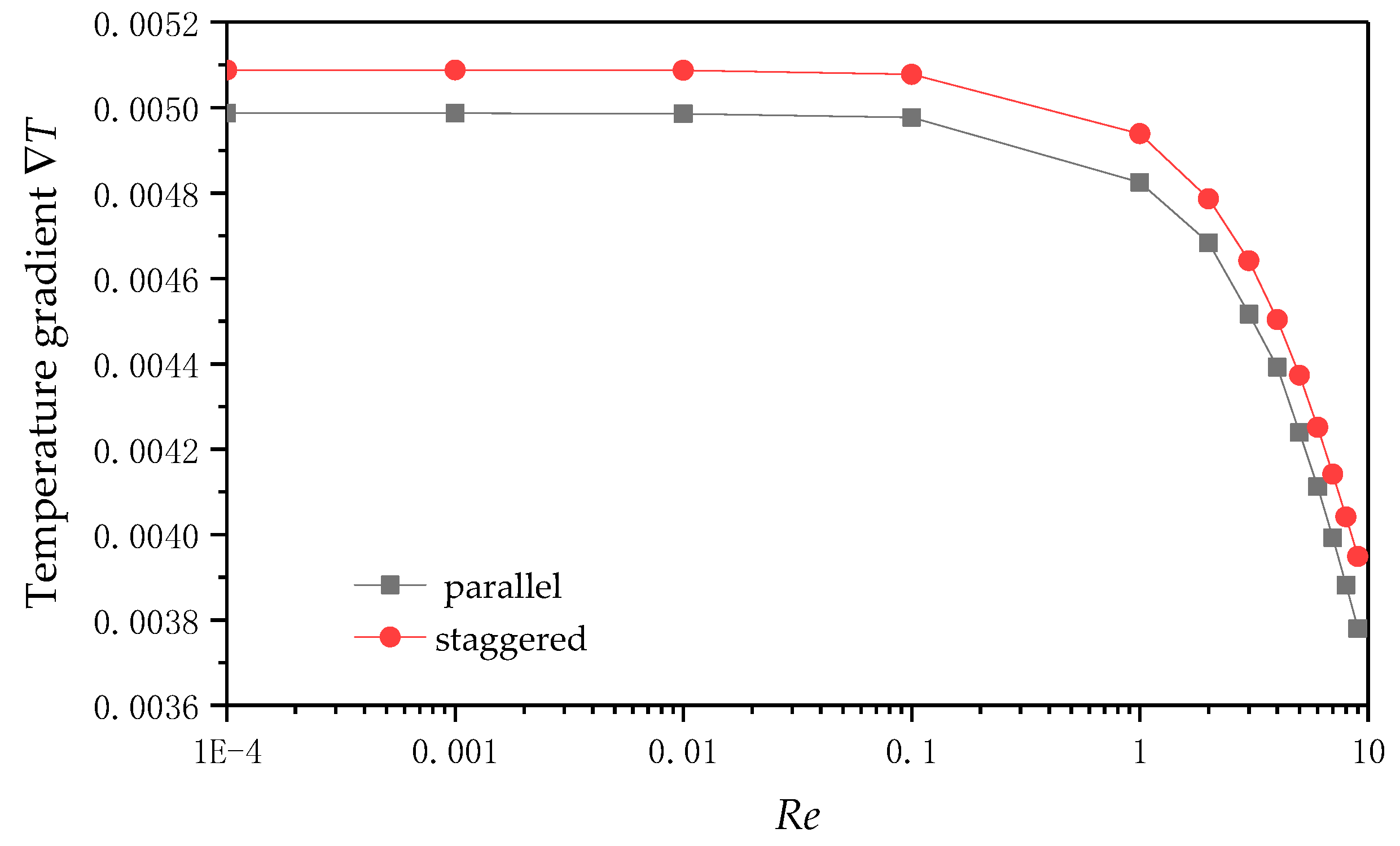
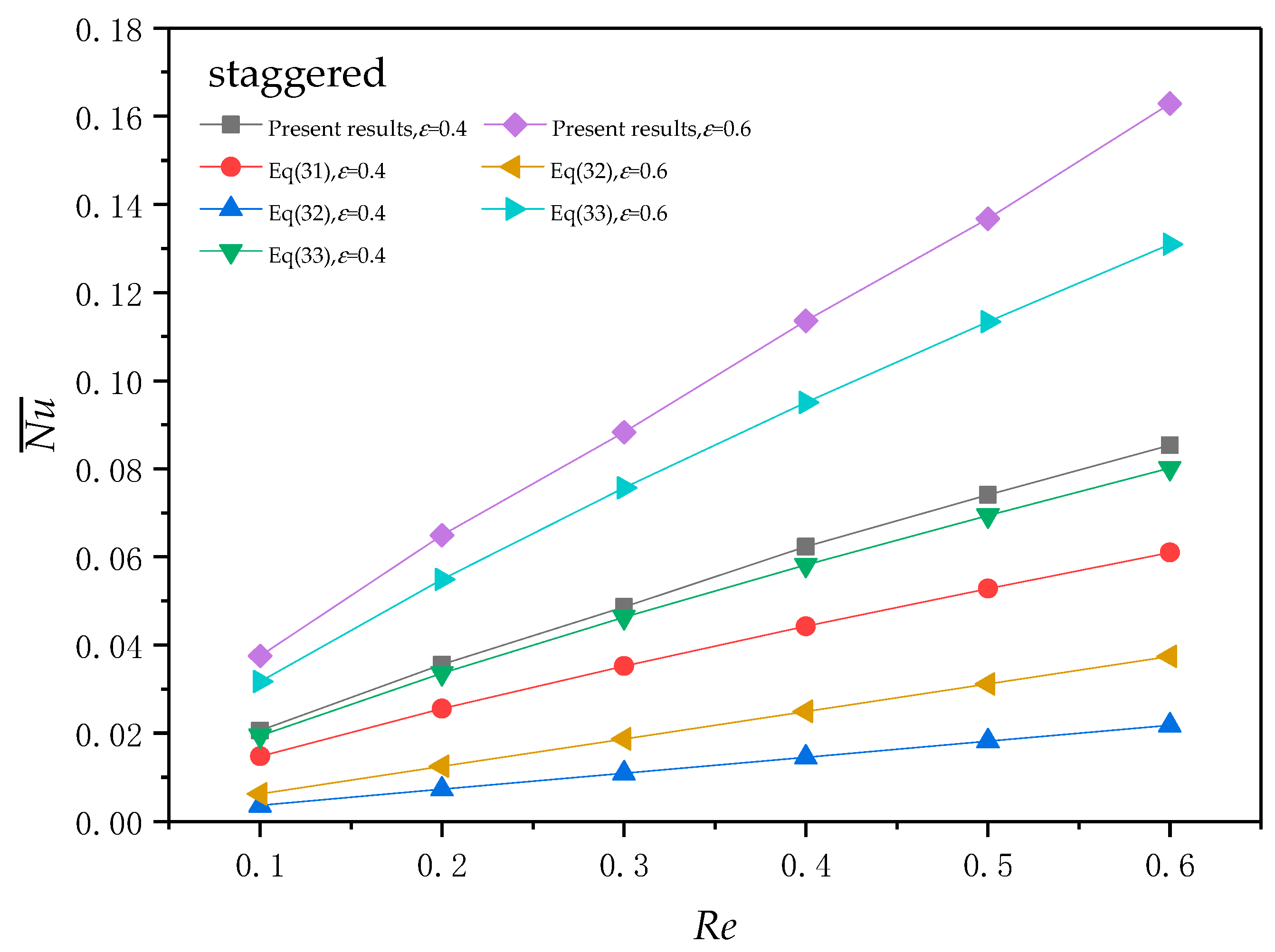
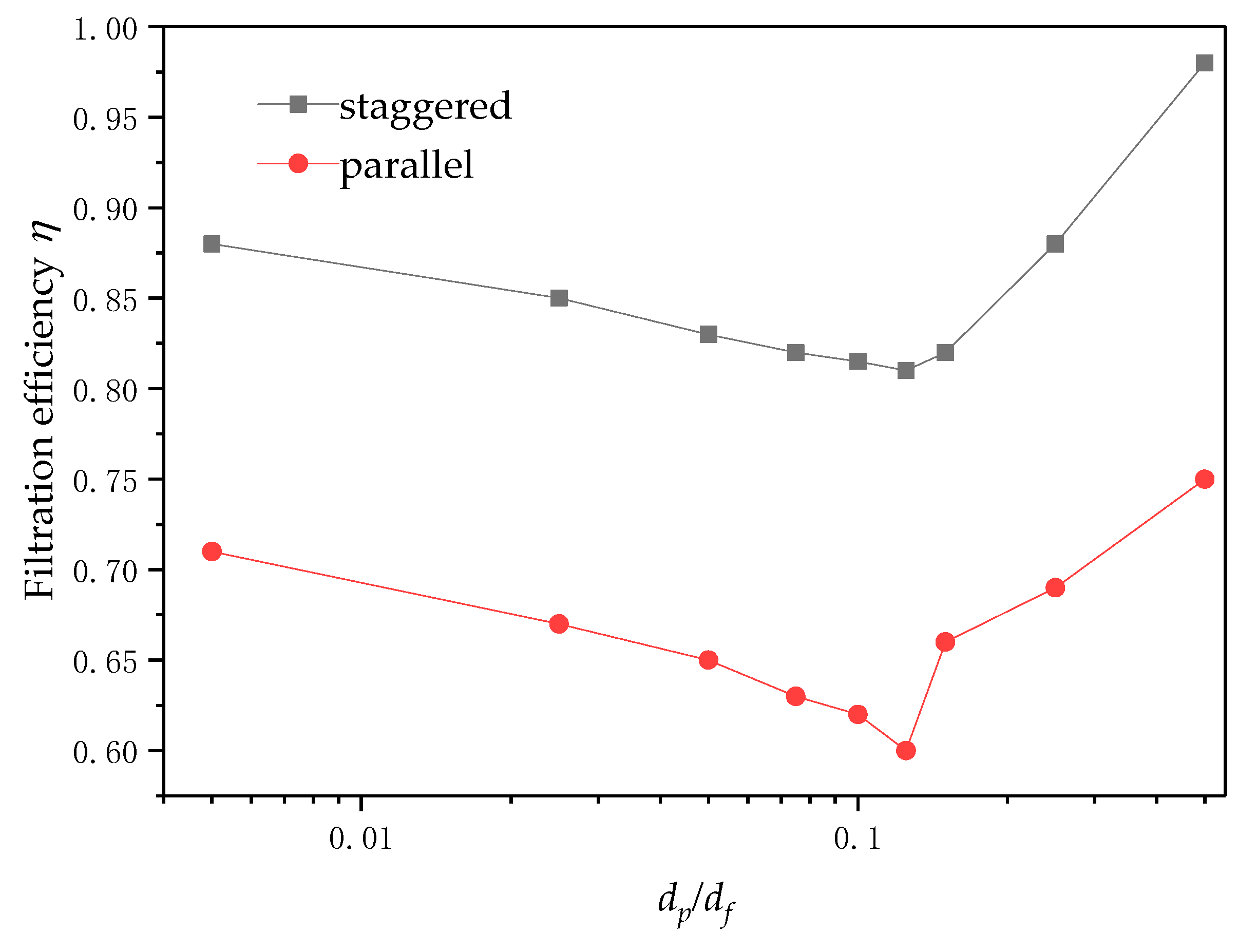
3.1. Flow and Heat Transfer Analysis of Parallel and Staggered Structures
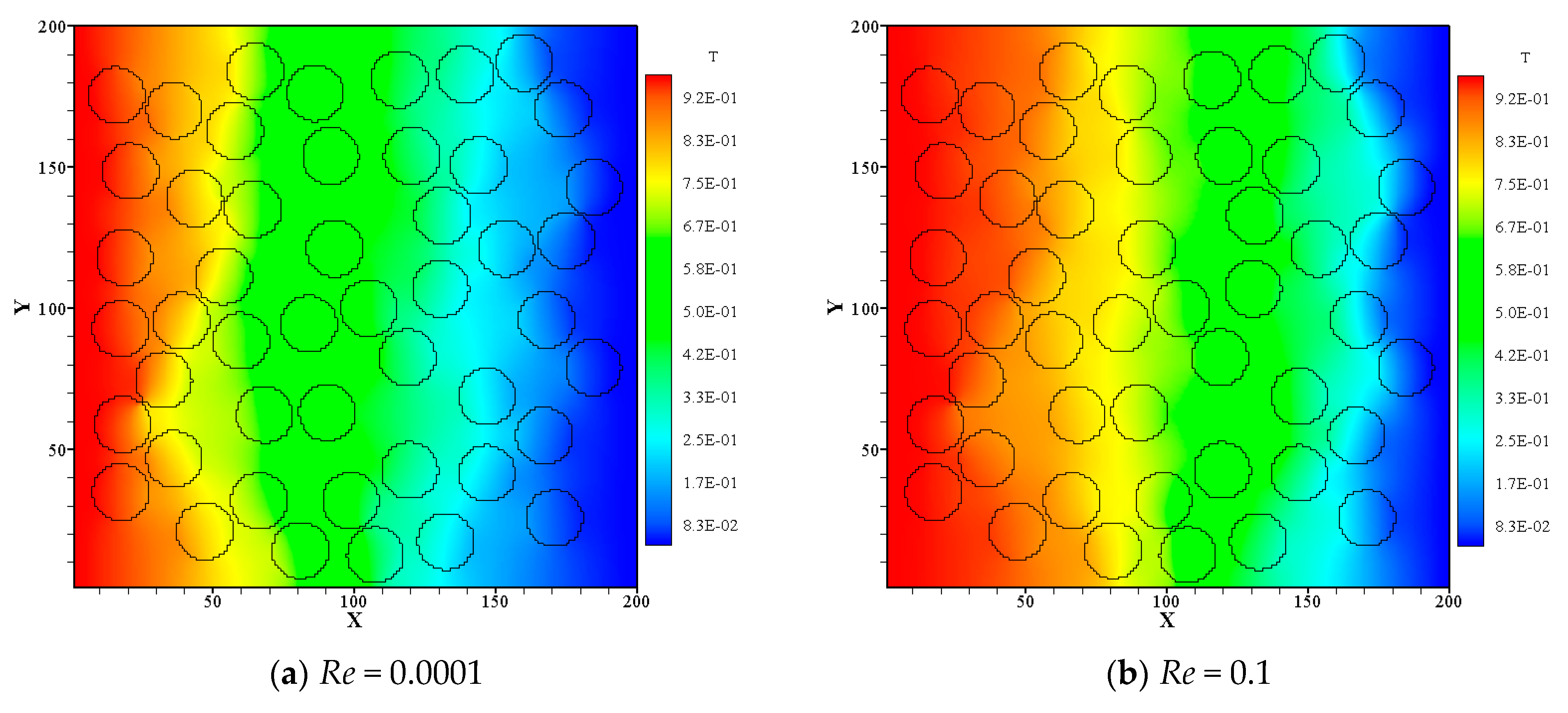
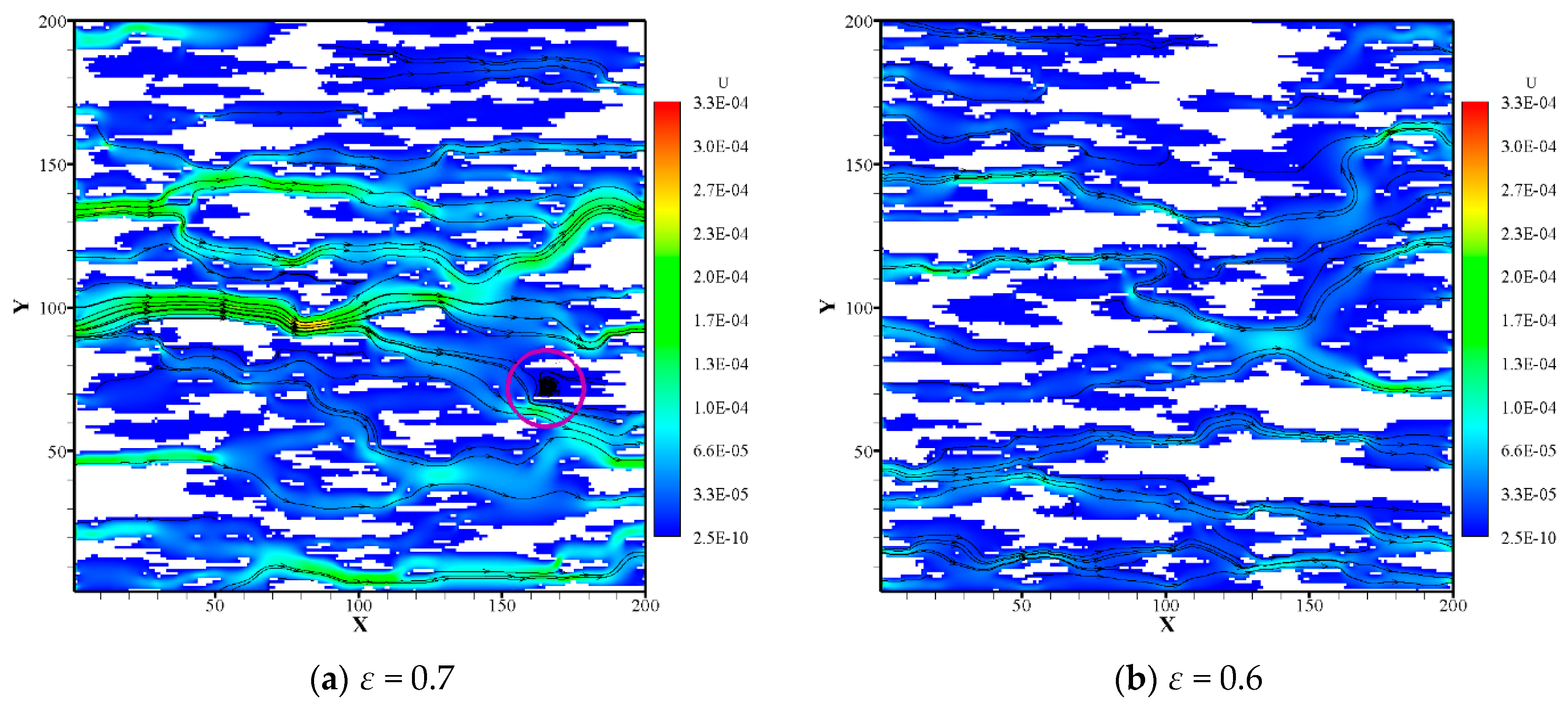
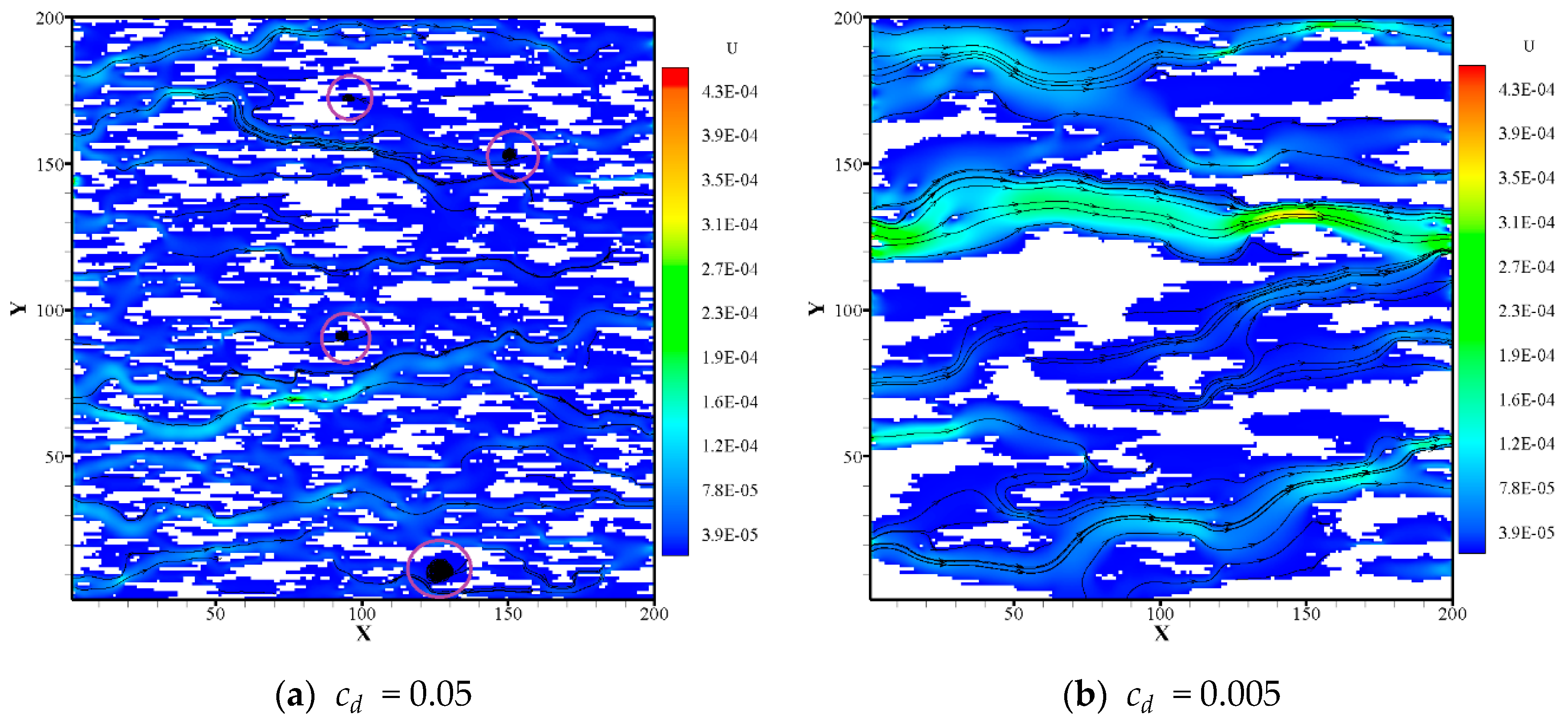
3.2. Flow and Heat Transfer Analysis of Random Structure
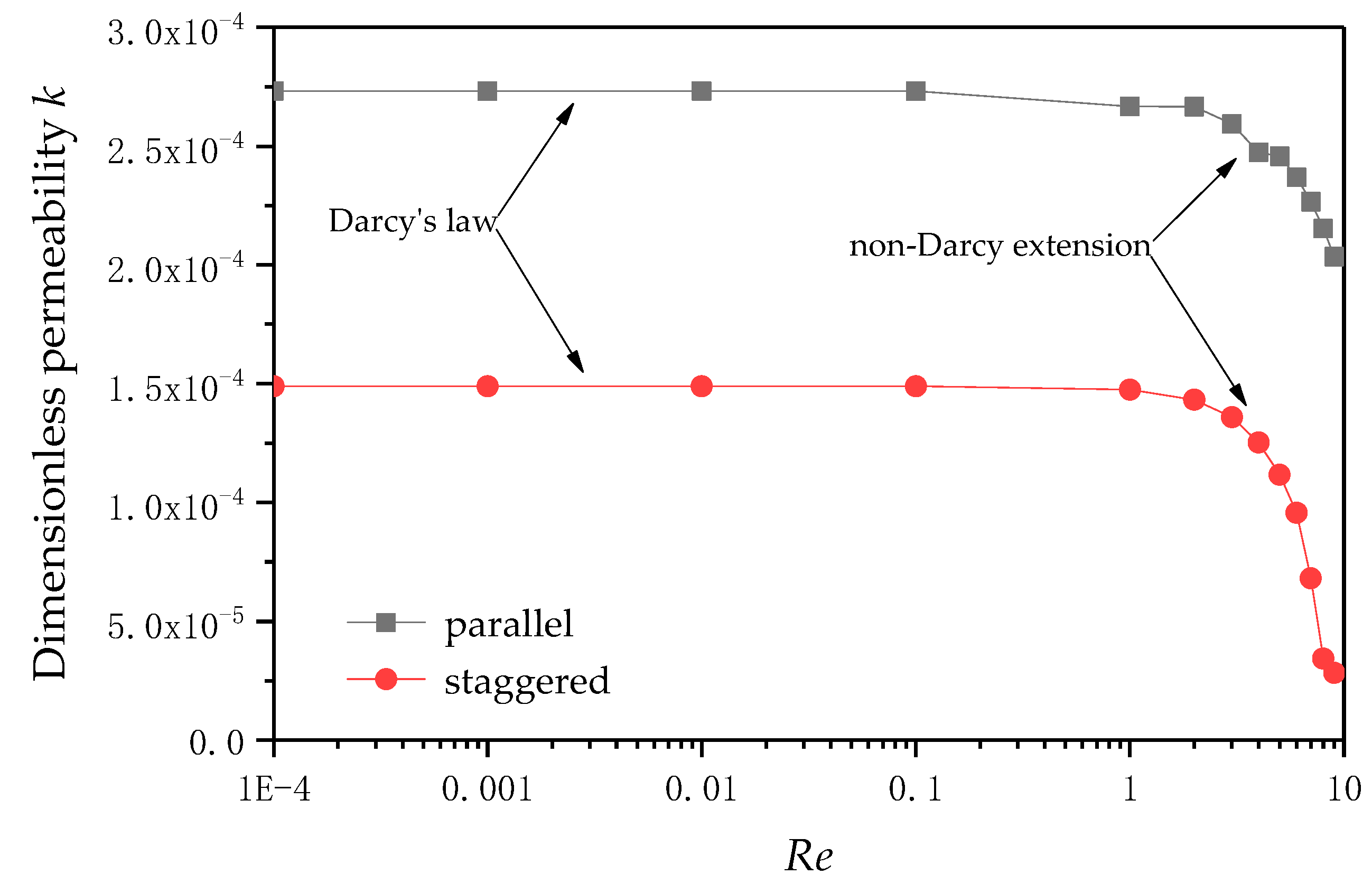
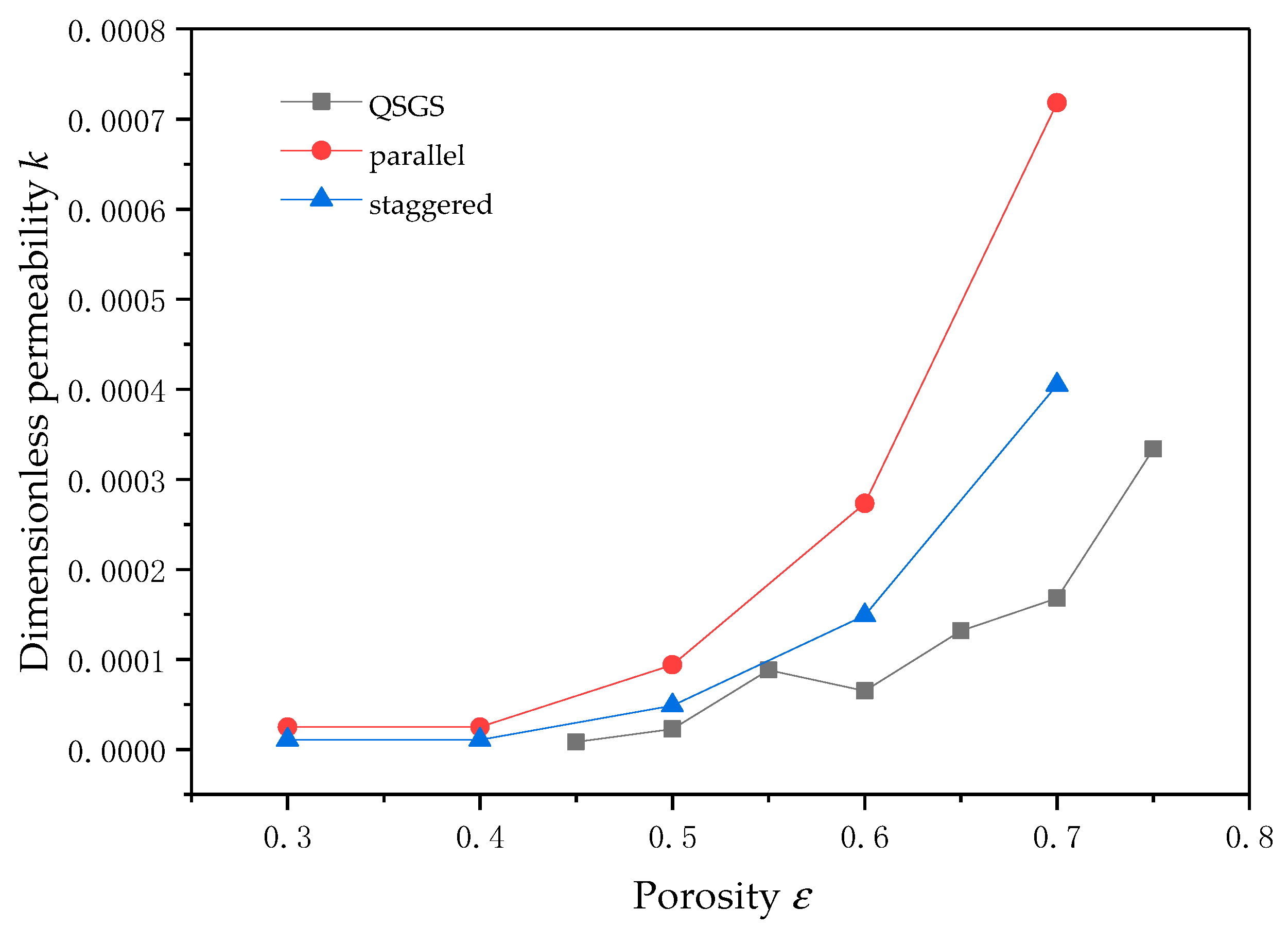
3.3. Flow Analysis of Quartet Structure Generation Set
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbols | |
| probability of growth core (QSGS) | |
| constant pressure heat capacity | |
| lattice sound speed | |
| df | fiber diameter |
| probability of growth in the direction i (QSGS) | |
| probability of along the horizontal direction (QSGS) | |
| probability of along the quadrangle direction (QSGS) | |
| particle diameter | |
| probability of along the vertical direction (QSGS) | |
| lattice velocity in a direction | |
| density distribution function | |
| equilibrium distribution function for | |
| drag force | |
| Brownian force | |
| gravity | |
| structure function related to | |
| gravitational acceleration | |
| energy distribution function | |
| equilibrium distribution function for | |
| volume force | |
| average convective heat transfer coefficient | |
| Boltzmann constant | |
| dimensionless permeability | |
| mass flow rate | |
| Nu | Nusselt number |
| average Nusselt number | |
| Nx, Ny | numbers of discretization nodes in the x and y direction |
| pressure of gas | |
| discrete motion probabilities | |
| pressure gradient | |
| Pr | Prandtl number |
| average heat flow | |
| volume flow rate | |
| r | position vector |
| Ra | Rayleigh number |
| Re | Reynolds number |
| gas temperature | |
| velocity vector of the gas | |
| velocity vector of the particle | |
| displacement vector | |
| displacement vector of the particle | |
| # | number |
| Greek Letters | |
| lattice spacing | |
| time step in lattice unit | |
| porosity | |
| zero-mean, unit-variance independent Gaussian random number | |
| a Boolean variable | |
| thermal conductivity of fluid | |
| gas dynamic viscosity | |
| gas kinematic viscosity | |
| density of gas | |
| density of the particle | |
| dimensionless relaxation time | |
| dimensionless relaxation time for | |
| relaxation time of the particle | |
| weight coefficient | |
| Abbreviations | |
| D2Q4 | the two-dimensional four-velocity lattice model |
| D2Q9 | the two-dimensional nine-velocity lattice model |
| LBM | Lattice Boltzmann Method |
| LB–CA | Lattice Boltzmann–Cellular Automata |
| QSGS | quartet structure generation set |
References
- Price, P.; Stone, R.; OudeNijeweme, D.; Chen, X. Cold Start Particulate Emissions from a Second Generation DI Gasoline Engine. SAE Int. 2007. [Google Scholar] [CrossRef]
- Viswanathan, S.; Rothamer, D.; Zelenyuk, A.; Stewart, M.; Bell, D. Experimental investigation of the effect of inlet particle properties on the capture efficiency in an exhaust particulate filter. J. Aerosol Sci. 2017, 113, 250–264. [Google Scholar] [CrossRef]
- Limits and Measurement Methods for Emissions from Light-Duty Vehicles. GB: 18352.6-2016. 2016. Available online: http://www.vecc-mep.org.cn/info/one/889.html (accessed on 28 August 2019).
- Ohara, E.; Mizuno, Y.; Miyairi, Y.; Mizutani, T.; Yuuki, K.; Noguchi, Y.; Hiramatsu, T.; Makino, M.; Takahashi, A.; Sakai, H.; et al. Filtration Behavior of Diesel Particulate Filters (1). SAE Int. 2007. [Google Scholar] [CrossRef]
- Somiya, S. Handbook of Advanced Ceramics: Materials, Applications, Processing, and Properties; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Bao, H.; Chen, J.; Gu, X.; Cao, B. A review of Simulation Methods in Micro/Nanoscale Heat Conduction. ES Energy Environ. 2018, 1, 16–55. [Google Scholar] [CrossRef]
- Bensaid, S.; Marchisio, D.L.; Fino, D.; Saracco, G.; Specchia, V. Modelling of diesel particulate filtration in wall-flow traps. Chem. Eng. J. 2009, 154, 211–218. [Google Scholar] [CrossRef]
- Serrano, J.R.; Climent, H.; Piqueras, P.; Angiolini, E. Filtration modelling in wall-flow particulate filters of low soot penetration thickness. Energy 2016, 112, 883–898. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, J.; Fu, J.; Cai, H.; Long, G. Nanoparticle motion trajectories and deposition in an inlet channel of wall-flow diesel particulate filter. J. Aerosol Sci. 2009, 40, 307–323. [Google Scholar] [CrossRef]
- Lee, D.Y.; Lee, G.W.; Yoon, K.; Chun, B.; Jung, H.W. Lattice Boltzmann simulations for wall-flow dynamics in porous ceramic diesel particulate filters. Appl. Surf. Sci. 2018, 429, 72–80. [Google Scholar] [CrossRef]
- Kong, X.; Li, Z.; Shen, B.; Wu, Y.; Zhang, Y.; Cai, D. Simulation of flow and soot particle distribution in wall-flow DPF based on lattice Boltzmann method. Chem. Eng. Sci. 2019, 202, 169–185. [Google Scholar] [CrossRef]
- Abchouyeh, M.A.; Fard, O.S.; Mohebbi, R.; Sheremet, M.A. Enhancement of heat transfer of nanofluids in the presence of sinusoidal side obstacles between two parallel plates through the lattice Boltzmann method. Int. J. Mech. Sci. 2019, 156, 159–169. [Google Scholar] [CrossRef]
- Mohebbi, R.; Izadi, M.; Sajjadi, H.; Delouei, A.A.; Sheremet, M.A. Examining of nanofluid natural convection heat transfer in a Γ-shaped enclosure including a rectangular hot obstacle using the lattice Boltzmann method. Phys. A Stat. Mech. Its Appl. 2019, 526, 120831. [Google Scholar] [CrossRef]
- Lupše, J.; Campolo, M.; Soldati, A. Modelling soot deposition and monolith regeneration for optimal design of automotive DPFs. Chem. Eng. Sci. 2016, 151, 36–50. [Google Scholar] [CrossRef]
- Galindo, J.; Serrano, J.R.; Piqueras, P.; García-Afonso, Ó. Heat transfer modelling in honeycomb wall-flow diesel particulate filters. Energy 2012, 43, 201–213. [Google Scholar] [CrossRef]
- Yamamoto, K.; Nakamura, M. Simulation of heat conduction and soot combustion in diesel particulate filter. Prog. Comput. Fluid Dyn. Int. J. 2012, 12, 286–292. [Google Scholar] [CrossRef]
- Eshghinejadfard, A.; Thévenin, D. Numerical simulation of heat transfer in particulate flows using a thermal immersed boundary lattice Boltzmann method. Int. J. Heat Fluid Flow 2016, 60, 31–46. [Google Scholar] [CrossRef]
- Zhang, P.; Galindo-Torres, S.A.; Tang, H.; Jin, G.; Scheuermann, A.; Li, L. An efficient Discrete Element Lattice Boltzmann model for simulation of particle-fluid, particle-particle interactions. Comput. Fluids 2017, 147, 63–71. [Google Scholar] [CrossRef]
- Qian, Y.-H.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. EPL 1992, 17, 479. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, B.; Wang, N. Lattice BGK Model for Incompressible Navier–Stokes Equation. J. Comput. Phys. 2000, 165, 288–306. [Google Scholar] [CrossRef]
- Delouei, A.A.; Nazari, M.; Kayhani, M.H.; Ahmadi, G. A non-Newtonian direct numerical study for stationary and moving objects with various shapes: An immersed boundary—Lattice Boltzmann approach. J. Aerosol Sci. 2016, 93, 45–62. [Google Scholar] [CrossRef]
- Chang, C.-C.; Yang, Y.-T.; Yen, T.-H.; Chen, C.O.-K. Numerical investigation into thermal mixing efficiency in Y-shaped channel using Lattice Boltzmann method and field synergy principle. Int. J. Therm. Sci. 2009, 48, 2092–2099. [Google Scholar] [CrossRef]
- Bohn, C.D.; Scott, S.A.; Dennis, J.S.; Müller, C.R. Validation of a lattice Boltzmann model for gas–solid reactions with experiments. J. Comput. Phys. 2012, 231, 5334–5350. [Google Scholar] [CrossRef]
- Wang, J.; Wang, M.; Li, Z. A lattice Boltzmann algorithm for fluid–solid conjugate heat transfer. Int. J. Therm. Sci. 2007, 46, 228–234. [Google Scholar] [CrossRef]
- Mohamad, A.A. Applied lattice Boltzmann method for transport phenomena, momentum, heat and mass transfer. Can. J. Chem. Eng. 2007, 85, 946. [Google Scholar]
- Succi, S. The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Guo, Z.; Zheng, C.; Shi, B. Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method. Chin. Phys. 2002, 11, 366. [Google Scholar] [CrossRef]
- Wang, M.; Pan, N.; Wang, J.; Chen, S. Mesoscopic simulations of phase distribution effects on the effective thermal conductivity of microgranular porous media. J. Colloid Interface Sci. 2007, 311, 562–570. [Google Scholar] [CrossRef]
- Chopard, B.; Masselot, A. Cellular automata and lattice Boltzmann methods: A new approach to computational fluid dynamics and particle transport. Future Gener. Comput. Syst. 1999, 16, 249–257. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, H.; Guo, Z.; Zheng, C. Numerical simulation of particle capture process of fibrous filters using Lattice Boltzmann two-phase flow model. Powder Technol. 2012, 227, 111–122. [Google Scholar] [CrossRef]
- He, Y.; Wang, Y.; Li, Q. Lattice Boltzmann Method: Theory and Applications; Science: Beijing, China, 2009. [Google Scholar]
- Guo, Z.; Shi, B.; Zheng, C. A coupled lattice BGK model for the Boussinesq equations. Int. J. Numer. Methods Fluids 2002, 39, 325–342. [Google Scholar] [CrossRef]
- De Vahl Davis, G. Natural convection of air in a square cavity: A bench mark numerical solution. Int. J. Numer. Methods Fluids 1983, 3, 249–264. [Google Scholar] [CrossRef]
- Hortmann, M.; Perić, M.; Scheuerer, G. Finite volume multigrid prediction of laminar natural convection: Bench-mark solutions. Int. J. Numer. Methods Fluids 1990, 11, 189–207. [Google Scholar] [CrossRef]
- Hu, Y. Numerical Methods of Flow and Heat Transfer in Complex Geometries and Porous Media Based on Lattice Boltzmann Method; Beijing Jiaotong Univercity: Beijing, China, 2017. [Google Scholar]
- Wang, H.; Zhao, H.; Guo, Z.; He, Y.; Zheng, C. Lattice Boltzmann method for simulations of gas-particle flows over a backward-facing step. J. Comput. Phys. 2013, 239, 57–71. [Google Scholar] [CrossRef]
- Liu, Z.G.; Wang, P.K. Pressure Drop and Interception Efficiency of Multifiber Filters. Aerosol Sci. Technol. 1997, 26, 313–325. [Google Scholar] [CrossRef]
- Yazdchi, K.; Srivastava, S.; Luding, S. Micro–macro relations for flow through random arrays of cylinders. Compos. Part A Appl. Sci. Manuf. 2012, 43, 2007–2020. [Google Scholar] [CrossRef]
- Yazdchi, K.; Luding, S. Towards unified drag laws for inertial flow through fibrous materials. Chem. Eng. J. 2012, 207, 35–48. [Google Scholar] [CrossRef]
- Wen, J.; Teng, Q. A Research Review on Gasoline Particulate Filter Technology for Gasoline Direct Injection Engine. Small Intern. Combust. Engine Veh. Tech. 2016, 45, 77–83. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Zhang, M.; Ye, G.; Breugel, K. Microstructure-based modeling of permeability of cementitious materials using multiple-relaxation-time lattice Boltzmann method. Comput. Mater. Sci. 2013, 68, 142–151. [Google Scholar] [CrossRef]
- Firdaouss, M.; Guermond, J.-L.; Le Quéré, P. Nonlinear corrections to Darcy’s law at low Reynolds numbers. J. Fluid Mech. 1997, 343, 331–350. [Google Scholar] [CrossRef]
- Marusic-Paloka, E.; Mikelic, A. The derivation of a nonlinear filtration law including the inertia effects via homogenization. Nonlinear Anal. 2000, 42, 97. [Google Scholar] [CrossRef]
- Mei, C.; Auriault, J.-L. The effect of weak inertia on flow through a porous medium. J. Fluid Mech. 1991, 222, 647–663. [Google Scholar] [CrossRef]
- Newman, M.S.; Yin, X. Lattice Boltzmann Simulation of Non-Darcy Flow In Stochastically Generated 2D Porous Media Geometries. SPE J. 2013, 18, 12–26. [Google Scholar] [CrossRef]
- Lin, T. Numerical Study on Single Phase Flow and Heat Transfer in Porous Media with Lattice Boltzmann Method; China University of Petroleum: Beijing, China, 2016. [Google Scholar]
- Tang, W.; Kang, X. Lattice Boltzmann method simulating flow in porous media. J. Beijing Norm. Univ. 2016, 52, 12–16. [Google Scholar] [CrossRef]
- Kamiuto, K.; Yee, S.S. Heat transfer correlations for open-cellular porous materials. Int. Commun. Heat Mass Transf. 2005, 32, 947–953. [Google Scholar] [CrossRef]
- Nakayama, A.; Ando, K.; Yang, C.; Sano, Y.; Kuwahara, F.; Liu, J. A study on interstitial heat transfer in consolidated and unconsolidated porous media. Heat Mass Transf. 2009, 45, 1365–1372. [Google Scholar] [CrossRef]
- Kuwahara, F.; Shirota, M.; Nakayama, A. A numerical study of interfacial convective heat transfer coefficient in two-energy equation model for convection in porous media. Int. J. Heat Mass Transf. 2001, 44, 1153–1159. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, H.; Wang, K.; He, Y.; Zheng, C. Simulation of filtration process for multi-fiber filter using the Lattice-Boltzmann two-phase flow model. J. Aerosol Sci. 2013, 66, 164–178. [Google Scholar] [CrossRef]










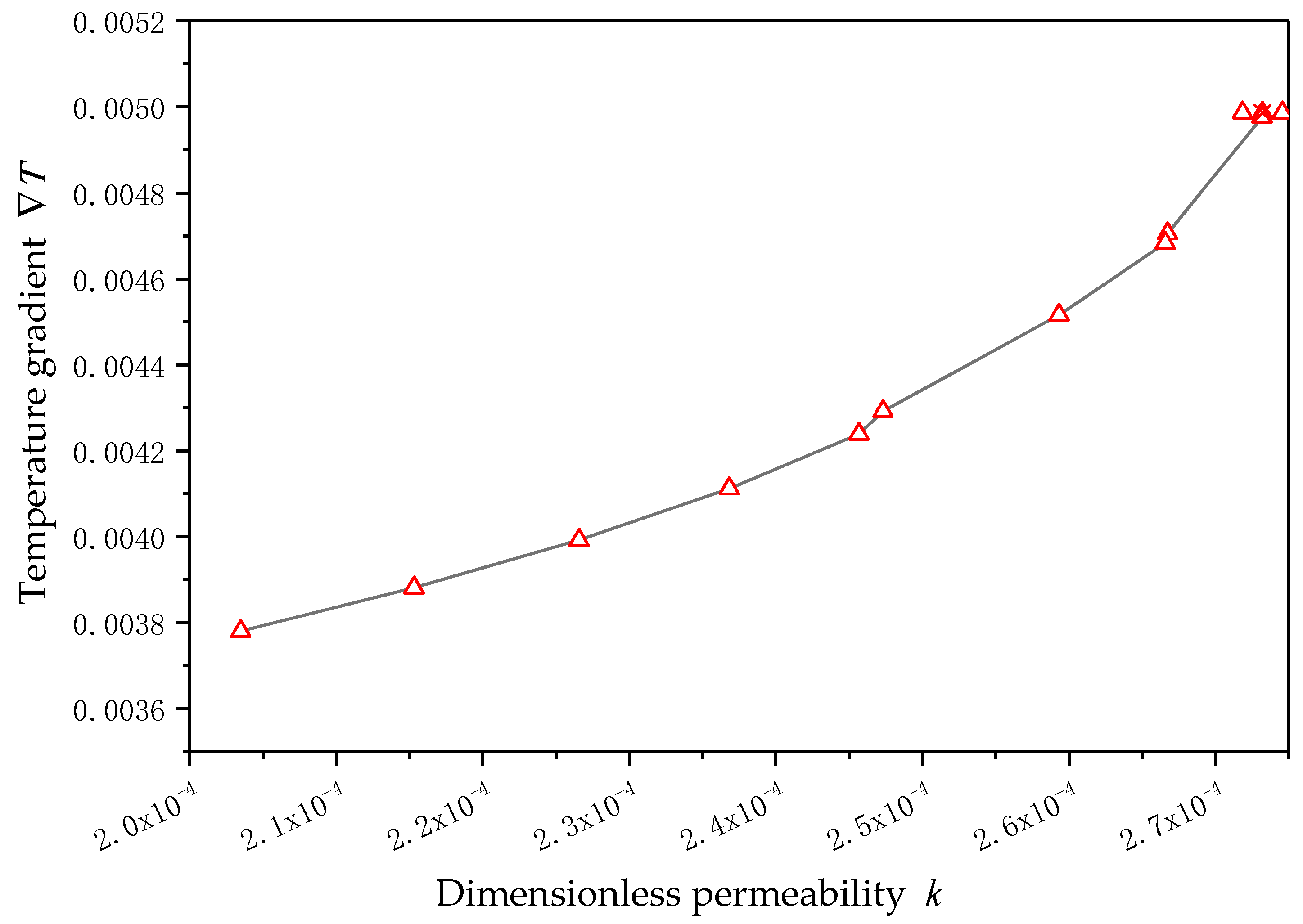





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, J.; Zhang, T.; Li, M.; Li, S.; Zhong, X.; Liu, X. Study on Flow and Heat Transfer Characteristics of Porous Media in Engine Particulate Filters Based on Lattice Boltzmann Method. Energies 2019, 12, 3319. https://doi.org/10.3390/en12173319
Fu J, Zhang T, Li M, Li S, Zhong X, Liu X. Study on Flow and Heat Transfer Characteristics of Porous Media in Engine Particulate Filters Based on Lattice Boltzmann Method. Energies. 2019; 12(17):3319. https://doi.org/10.3390/en12173319
Chicago/Turabian StyleFu, Jiale, Tiechen Zhang, Menghan Li, Su Li, Xianglin Zhong, and Xiaori Liu. 2019. "Study on Flow and Heat Transfer Characteristics of Porous Media in Engine Particulate Filters Based on Lattice Boltzmann Method" Energies 12, no. 17: 3319. https://doi.org/10.3390/en12173319
APA StyleFu, J., Zhang, T., Li, M., Li, S., Zhong, X., & Liu, X. (2019). Study on Flow and Heat Transfer Characteristics of Porous Media in Engine Particulate Filters Based on Lattice Boltzmann Method. Energies, 12(17), 3319. https://doi.org/10.3390/en12173319




