Modeling and Validation of an Electrohydraulic Power Take-Off System for a Portable Wave Energy Convertor with Compressed Energy Storage
Abstract
:1. Introduction
2. Mathematical Models
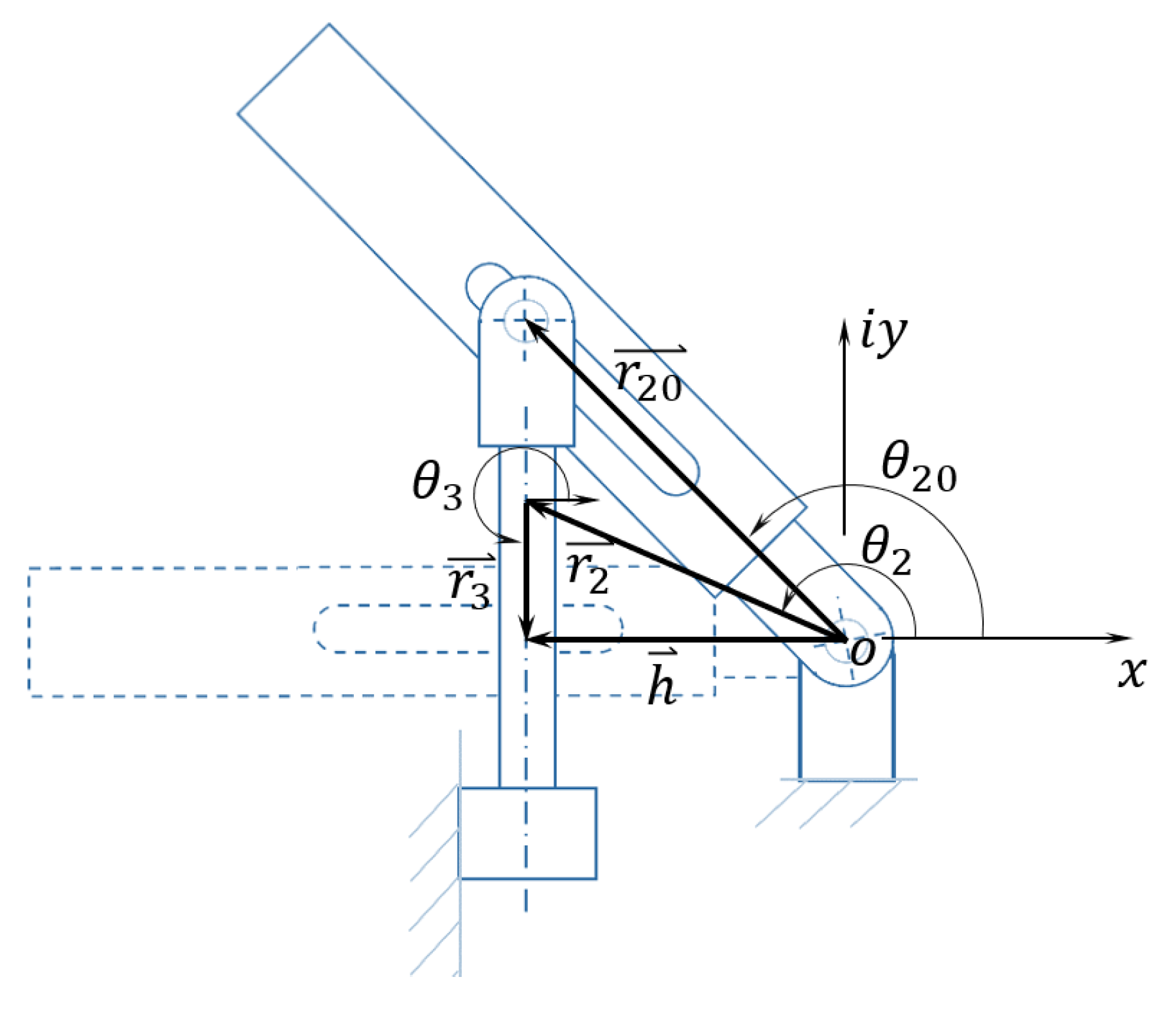
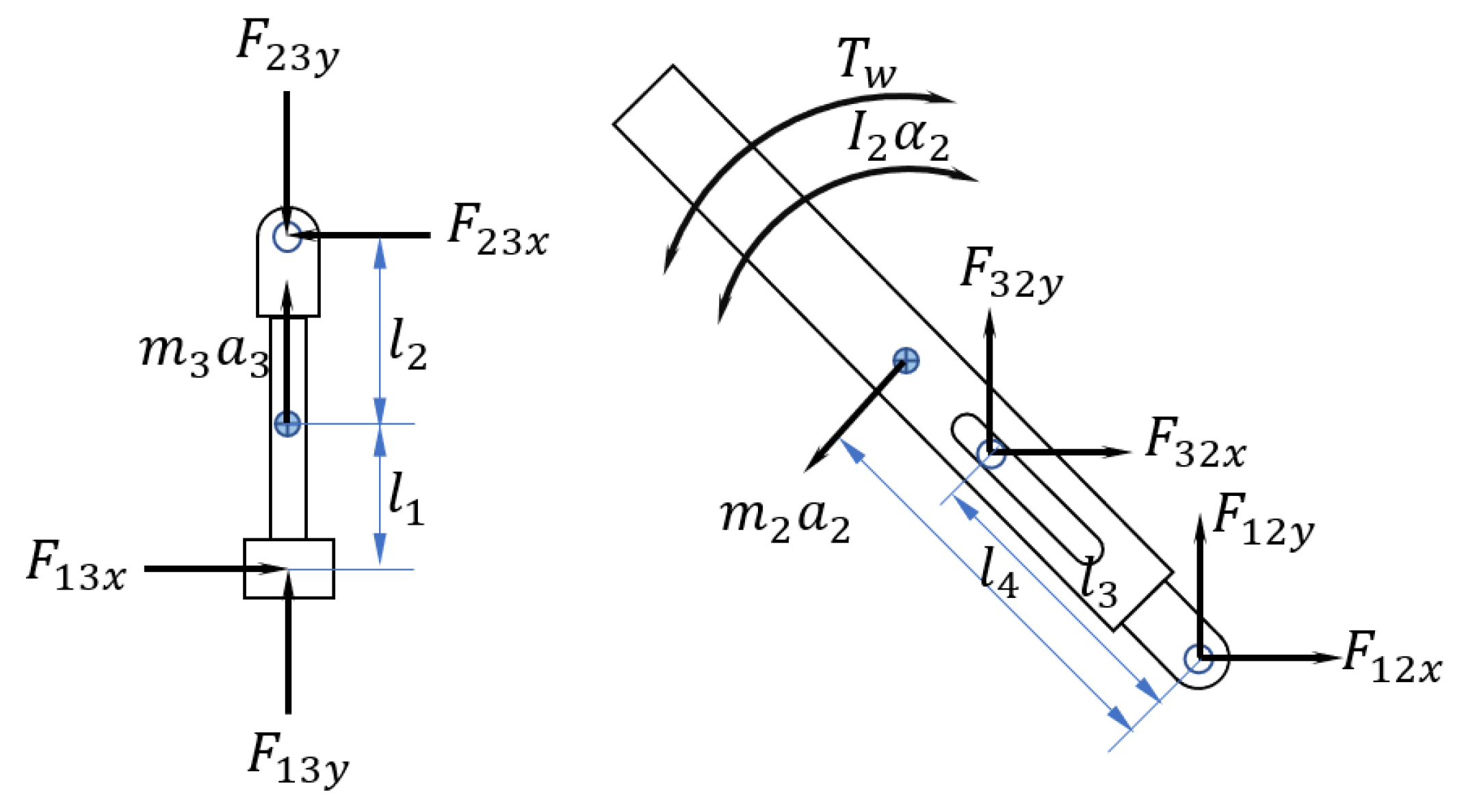
2.1. Dynamics of the Linkage Wave Follower
2.2. Dynamics of the Electrohydraulic PTO System
2.3. Energy Storage and Power Output
3. Experimental System
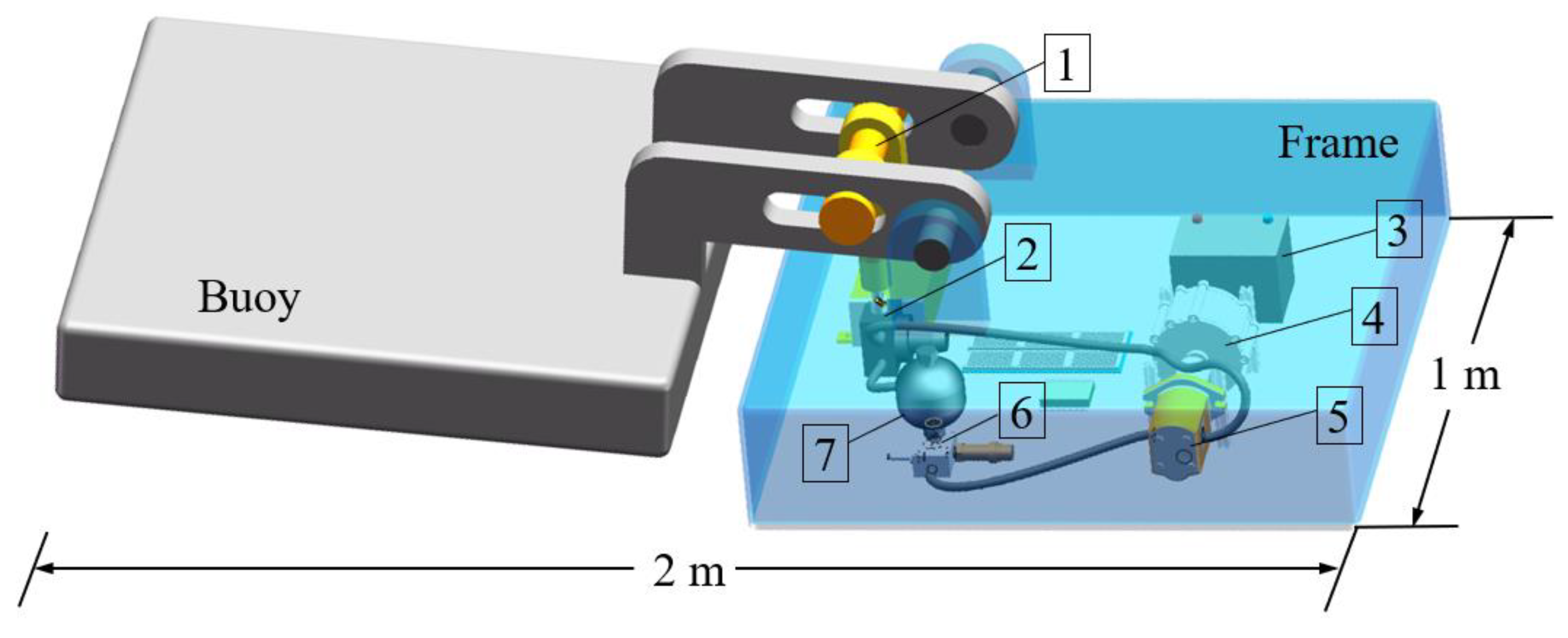
3.1. Testbed
3.2. Test Procedures
4. Results and Discussion
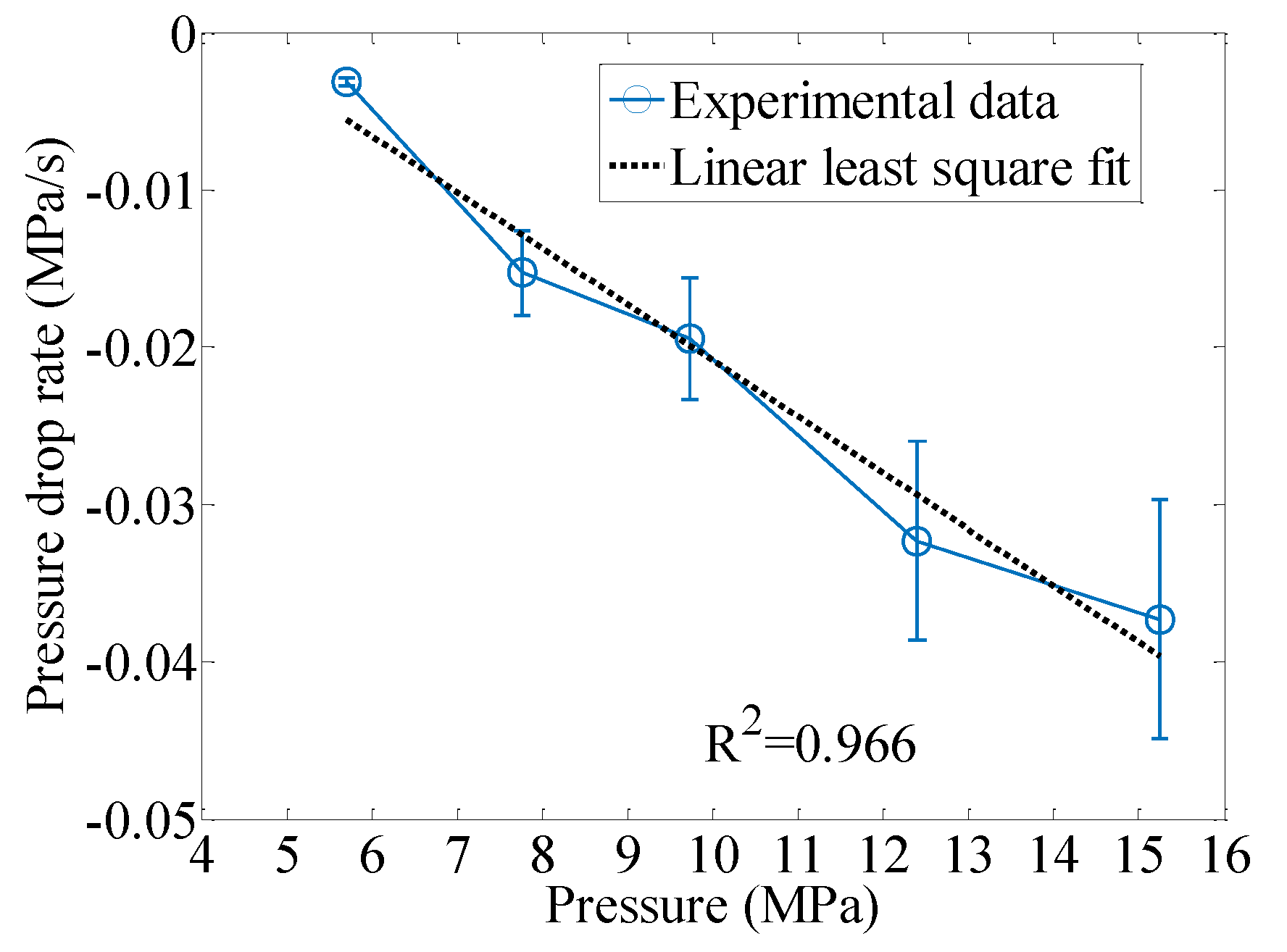
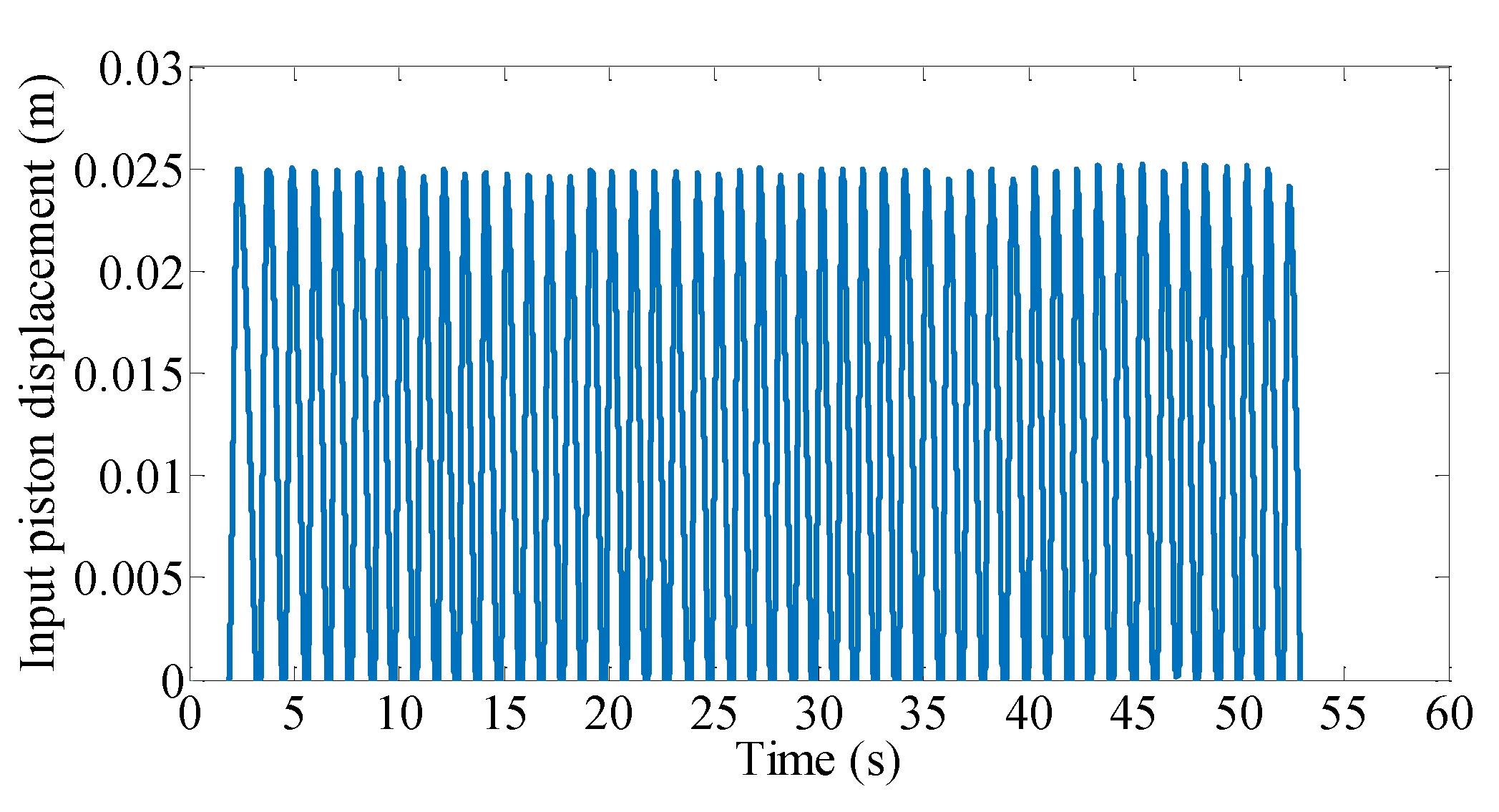
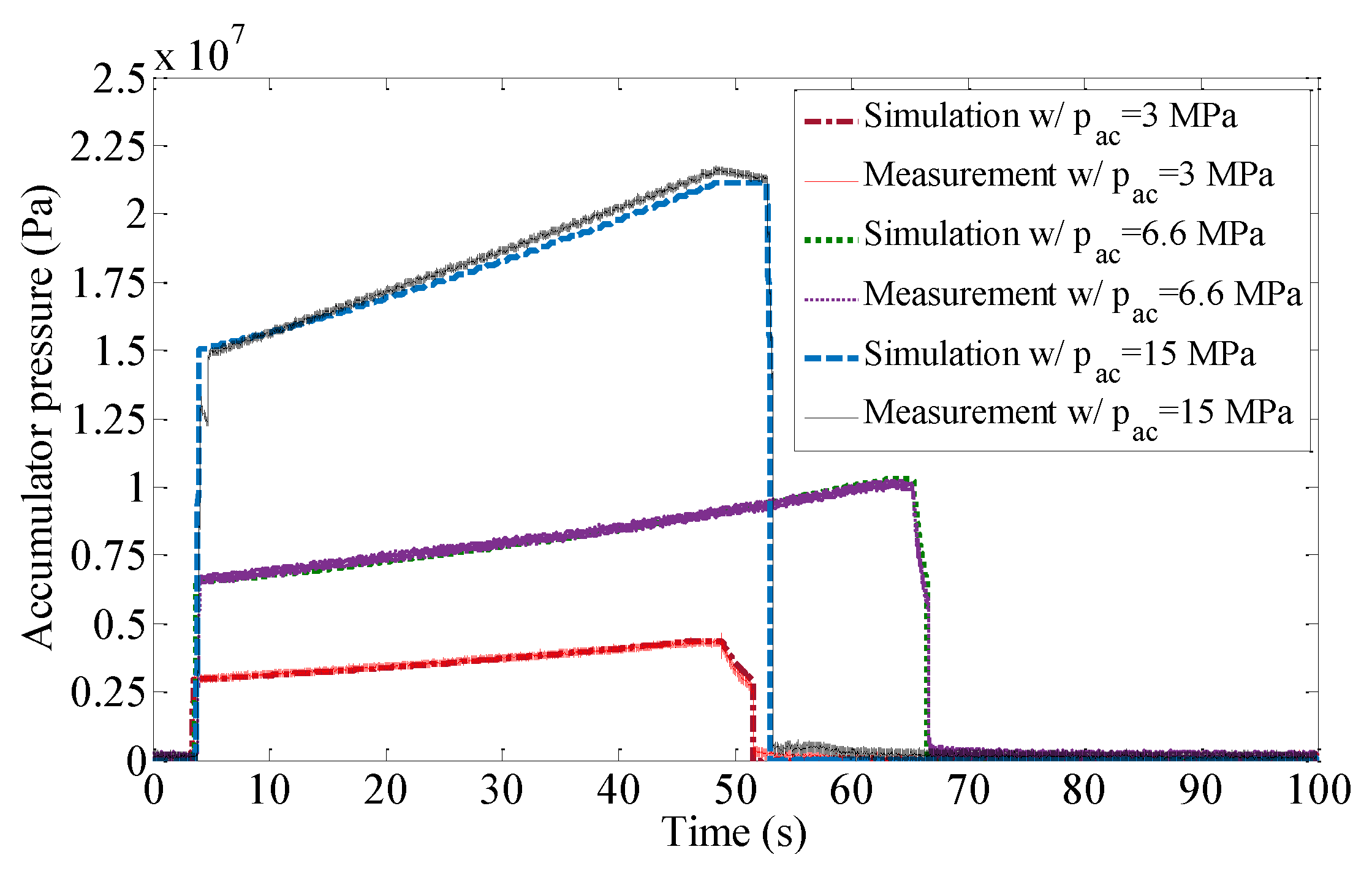
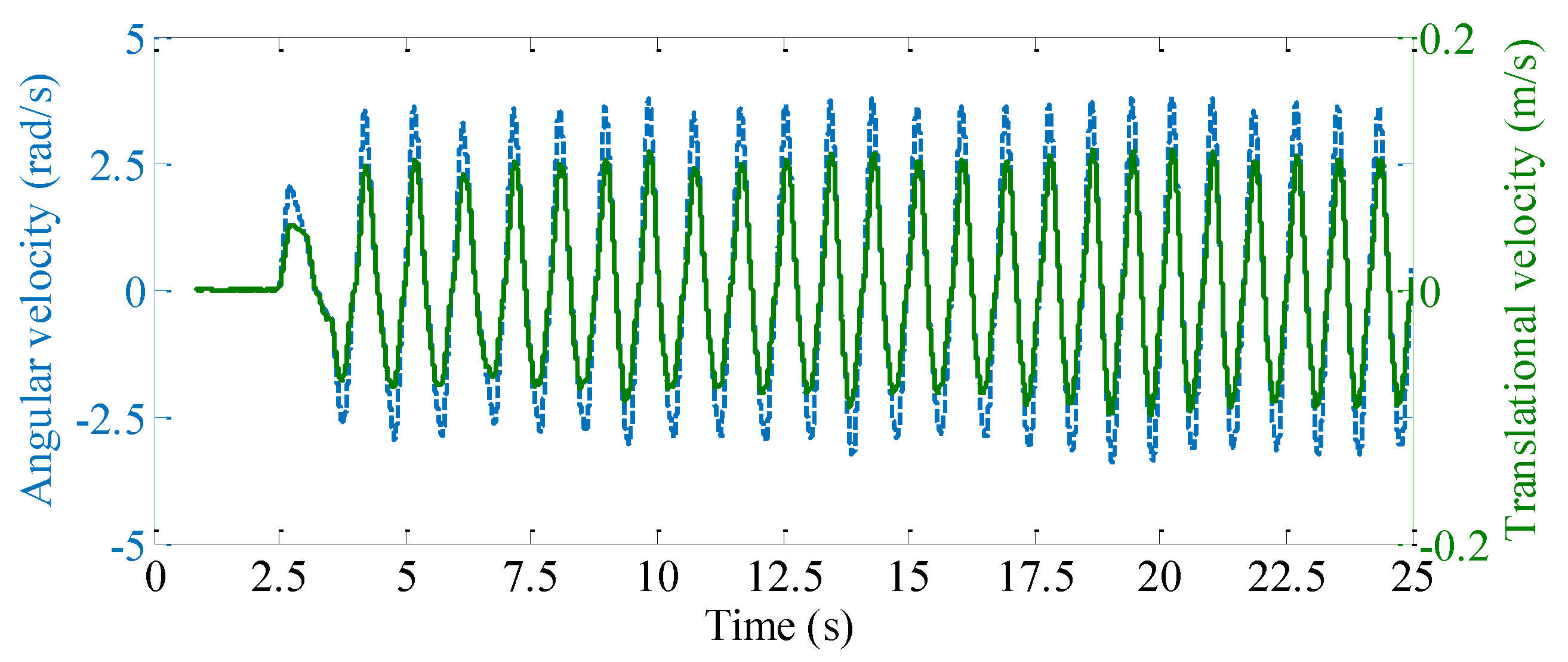
4.1. Model Validation
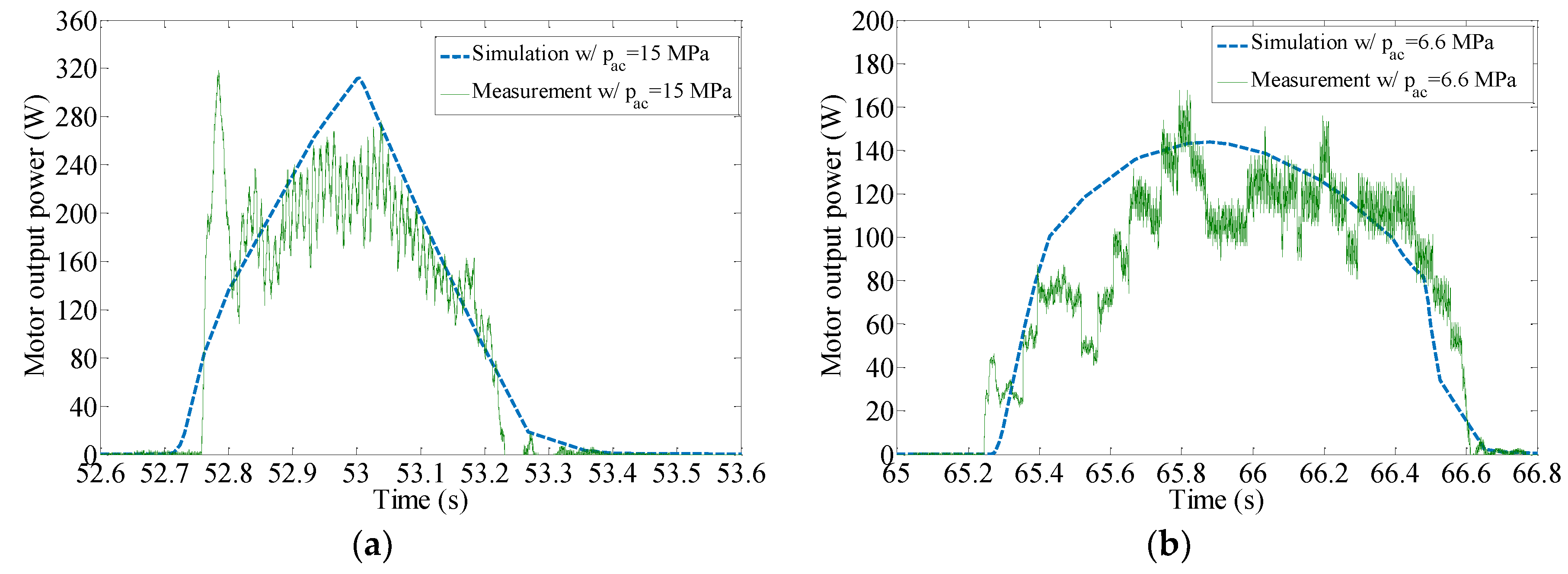
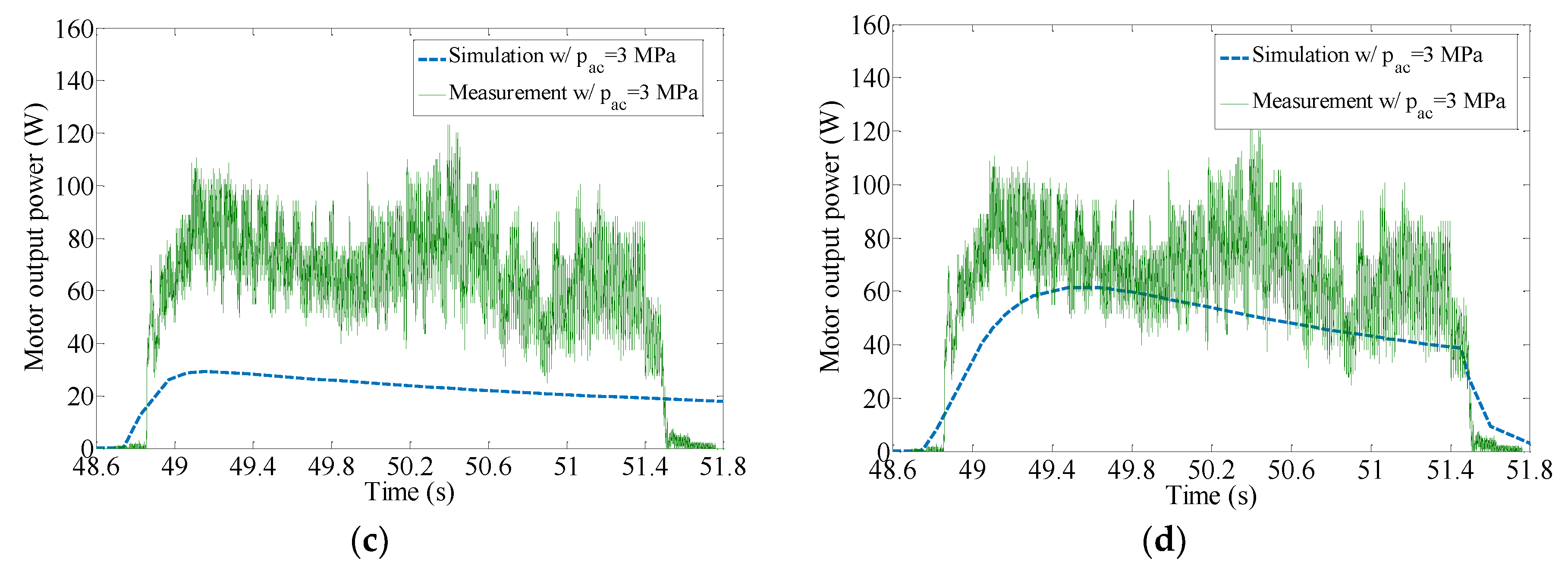
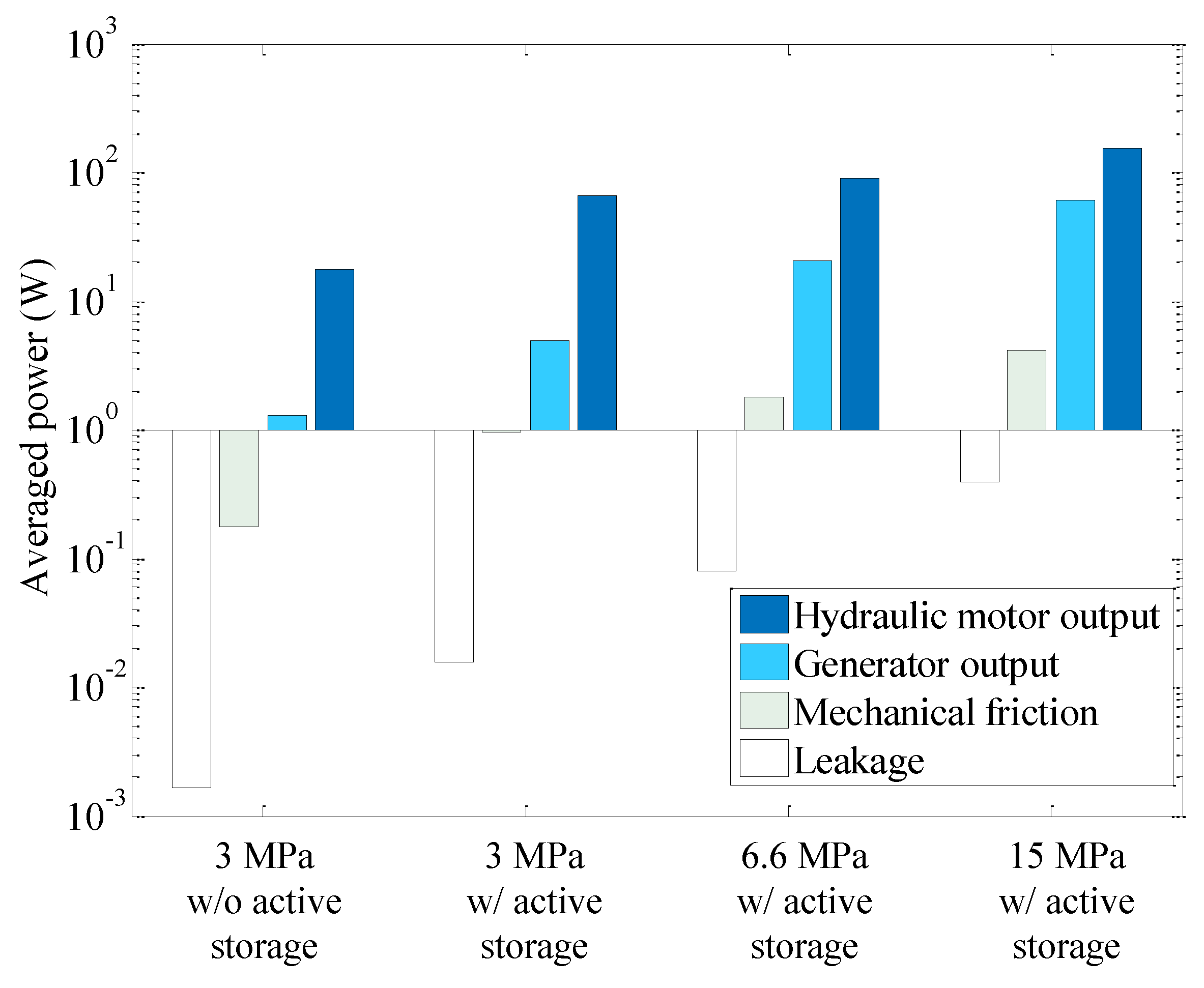
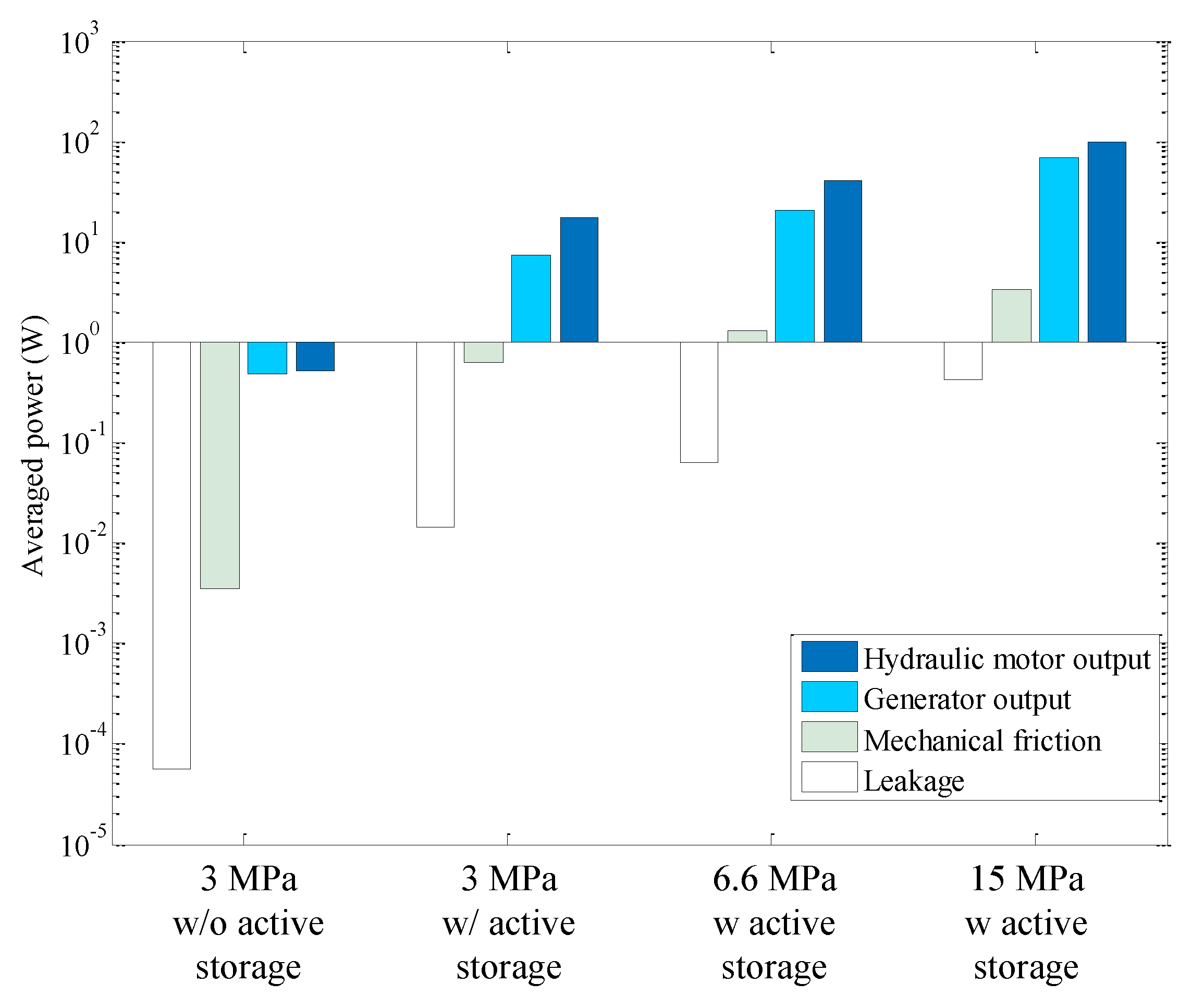
4.2. Power Output and Losses
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Derivation of the Power Loss on Leakage
References
- Wang, S.; Yuan, P.; Li, D.; Jiao, Y. An overview of ocean renewable energy in China. Renew. Sustain. Energy Rev. 2011, 15, 91–111. [Google Scholar] [CrossRef]
- Sheng, W. Wave energy conversion and hydrodynamics modelling technologies: A review. Renew. Sustain. Energy Rev. 2019, 109, 482–498. [Google Scholar] [CrossRef]
- Zhao, X.; Ning, D.; Zou, Q.; Qiao, D.; Cai, S. Hybrid floating breakwater-WEC system: A review. Ocean Eng. 2019, 186, 106126. [Google Scholar] [CrossRef]
- Rodríguez, C.A.; Rosa-Santos, P.; Taveira-Pinto, F. Assessment of damping coefficients of power take-off systems of wave energy converters: A hybrid approach. Energy 2019, 169, 1022–1038. [Google Scholar] [CrossRef]
- Jiang, X.; Day, S.; Clelland, D. Hydrodynamic responses and power efficiency analyses of an oscillating wave surge converter under different simulated PTO strategies. Ocean Eng. 2018, 170, 286–297. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez, C.A.; Rosa-Santos, P.; Taveira-Pinto, F. Assessment of the power conversion of wave energy converters based on experimental tests. Energy Convers. Manag. 2018, 173, 692–703. [Google Scholar] [CrossRef]
- Reabroy, R.; Zheng, X.B.; Zhang, L.; Zang, J.; Yuan, Z.; Liu, M.Y.; Sun, K.; Tiaple, Y. Hydrodynamic response and power efficiency analysis of heaving wave energy converter integrated with breakwater. Energy Convers. Manag. 2019, 195, 1174–1186. [Google Scholar] [CrossRef]
- Zou, H.; Wang, M.; Tang, M.; Li, C.; Tian, C. Experimental investigation and performance analysis of a direct-driven linear generator. Energy Procedia 2017, 142, 284–290. [Google Scholar] [CrossRef]
- Dai, Y.; Chen, Y.; Xie, L. A study on a novel two-body floating wave energy converter. Ocean Eng. 2017, 130, 407–416. [Google Scholar] [CrossRef]
- Martinelli, L.; Zanuttigh, B.; Kofoed, J.P. Selection of design power of wave energy converters based on wave basin experiments. Renew. Energy 2011, 36, 3124–3132. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, Y. Dynamics of a mechanical frequency up-converted device for wave energy harvesting. J. Sound Vib. 2017, 367, 170–184. [Google Scholar] [CrossRef]
- Liermann, M.; Samhoury, O.; Atshan, S. Energy efficiency of pneumatic power take-off for wave energy converter. Int. J. Mar. Energy 2016, 13, 62–79. [Google Scholar] [CrossRef]
- Do, H.-T.; Dinh, Q.-T.; Nguyen, M.-T.; Phan, C.-B.; Dang, T.-D.; Lee, S.; Park, H.-G.; Ahn, K.K. Proposition and experiment of a sliding angle self-tuning wave energy converter. Ocean Eng. 2017, 132, 1–10. [Google Scholar] [CrossRef]
- Truong, D.Q.; Ahn, K.K. Development of a novel point absorber in heave for wave energy conversion. Renew. Energy 2014, 65, 183–191. [Google Scholar] [CrossRef]
- Crowley, S.; Porter, R.; Taunton, D.; Wilson, P.; Taunton, D.; Wilson, P. Modelling of the WITT wave energy converter. Renew. Energy 2018, 115, 159–174. [Google Scholar] [CrossRef]
- Yu, H.-F.; Zhang, Y.-L.; Zheng, S.-M. Numerical study on the performance of a wave energy converter with three hinged bodies. Renew. Energy 2016, 99, 1276–1286. [Google Scholar] [CrossRef]
- Sheng, L.; Zhou, Z.; Charpentier, J.; Benbouzid, M. Stand-alone island daily power management using a tidal turbine farm and an ocean compressed air energy storage system. Renew. Energy 2017, 103, 286–294. [Google Scholar] [CrossRef] [Green Version]
- Wilkinson, L.; Whittaker, T.J.T.; Thies, P.R.; Day, A.; Ingram, D. The power-capture of a nearshore, modular, flap-type wave energy converter in regular waves. Ocean Eng. 2017, 137, 394–403. [Google Scholar] [CrossRef]
- Thorburn, K.; Bernhoff, H.; Leijon, M. Wave energy transmission system concepts for linear generator arrays. Ocean Eng. 2004, 31, 1339–1349. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L. Towards realistically predicting the power outputs of wave energy converters: Nonlinear simulation. Energy 2018, 144, 120–128. [Google Scholar] [CrossRef]
- Li, P.Y.; Loth, E.; Qin, C.; Simon, T.W.; Van de Ven, J.D. Open Accumulator Isothermal Compressed Air Energy Storage (OA-ICAES) System. In Energy Storage Handbook; Wiley Publishing: Hoboken, NJ, USA, 2018. [Google Scholar]
- Erdman, A.G.; Sandor, G.N.; Kota, S. Introduction to Dynamics of Mechanisms. In Mechanism Design: Analysis and Synthesis, 4th ed.; Pearson: Boston, MA, USA, 2001; pp. 279–329. [Google Scholar]
- Cho, B.B.H.; Lee, H.H.W.; Oh, J.S.J. Estimation technique of air content in automatic transmission fluid by measuring effective bulk modulus. Int. J. Automot. Technol. 2002, 3, 57–61. [Google Scholar]
- Tian, H. Study of Active Valve Timing on Efficient Hydraulic Piston Motor Operations. Ph.D. Thesis, Department of Mechanical Engineering, University of Minnesota, Twin Cities, Minneapolis, MN, USA, 2016. [Google Scholar]
- Cengel, Y.A.; Turner, R.H.; Cimbala, J.M. External flow: Drag and lift. In Fundamentals of Thermal-Fluid Sciences, 3rd ed.; McGraw-Hill: New York, NY, USA, 2008; pp. 581–584. [Google Scholar]
- Ashtonn, I.G.C.; Johanning, L. On errors in low frequency wave measurements from wave buoy. Ocean Eng. 2015, 95, 11–22. [Google Scholar] [CrossRef]




| Symbol | Parameter Definition | Value | Unit |
|---|---|---|---|
| mass of link 2 | 33.6 | kg | |
| mass of link 3 | 0.2 | kg | |
| moment of inertia of link 2 | 0.14 | kgm2 | |
| moment of inertia of link 3 | 0.10 | kgm2 | |
| length of ground link | 23 | mm | |
| maximum length of link 2 | 34 | mm |
| Simulation Parameters | Value | Unit |
|---|---|---|
| Simulation duration | 100 | s |
| Solver | ODE15s | − |
| Piston area | 110−4 | m2 |
| Piston stroke (nominal) | 0.025 | m |
| Bulk modulus | 1.4 | GPa |
| Entrained air vol. fraction | 0.02 | − |
| Moment of inertia of motor | 0.05 | kgm2 |
| Rotary damping coefficient | 0.5 | Nm/rad/s |
| Crack pressure (check valve) | 7 | kPa |
| Accumulator volume | 0.5 | L |
| Description | Equation | Unit |
|---|---|---|
| Heaving input | W | |
| Hydraulic motor output | W | |
| Electric output | W |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, H.; Zhou, Z.; Sui, Y. Modeling and Validation of an Electrohydraulic Power Take-Off System for a Portable Wave Energy Convertor with Compressed Energy Storage. Energies 2019, 12, 3378. https://doi.org/10.3390/en12173378
Tian H, Zhou Z, Sui Y. Modeling and Validation of an Electrohydraulic Power Take-Off System for a Portable Wave Energy Convertor with Compressed Energy Storage. Energies. 2019; 12(17):3378. https://doi.org/10.3390/en12173378
Chicago/Turabian StyleTian, Hao, Zijian Zhou, and Yu Sui. 2019. "Modeling and Validation of an Electrohydraulic Power Take-Off System for a Portable Wave Energy Convertor with Compressed Energy Storage" Energies 12, no. 17: 3378. https://doi.org/10.3390/en12173378
APA StyleTian, H., Zhou, Z., & Sui, Y. (2019). Modeling and Validation of an Electrohydraulic Power Take-Off System for a Portable Wave Energy Convertor with Compressed Energy Storage. Energies, 12(17), 3378. https://doi.org/10.3390/en12173378





