Experimental and Numerical Analysis on Flow Characteristics in a Double Helix Screw Pump

Abstract

Experimental overall performances on a double helix screw pump are presented and discussed, focusing on the leakage flow for two different rotational speeds. A comparison between experimental and URANS CFD approaches is performed in order to check the CFD closure models’ validity. Some specific local flow characteristics are extracted from the numerical results which give explanations about leakage backflows inside the screws and local distortion at the pump inlet section.

1. Introduction

Screw pumps are specific types of axial flow rotary positive displacement devices that are mainly used when flow delivery is relatively low with high pressure differences. They are characterized by specific speed values in Ω around 0.1, between gear and centrifugal types of rotating machines. Double helix screw pumps are widely used in petroleum, environmental protection and other major industries because they operate in a stable and reliable way, using a wide range of transmission media, fluid viscosities and multiphase flow types. Basic understanding and an analytical prediction on screw pump performances were initiated in 1993 by Vetter, G. and Wincek, M. [1]. Prang and Cooper [2] proposed an extensive analysis with slip leakage modelling, including an experimental validation for different fluid viscosities and various multiphase mixtures. Liu et al. [3] proposed a validation of an equivalent model for a variety of operating conditions. Researchers also focus on design parameter influences such as rotor profile, helical groove shape, helix angle, groove depth, gap and helix length [4,5]. Compared with a classical “screw pump”, the shape parameter of a double helix pump rotor can be controlled more, as pointed out by Li Fu-tian [5]. Mao Hua-Yong [6] analyzed the effect of the trochoidal rotor pump rotor tooth profile. The effects of different profile shapes are also tested by Ryazatsev [7]. Zhang Yuan-Xun [8] and others performed screw meshing gap analysis to study the leakage mechanism.

In recent years, with the development of computers and the rise of numerical simulation, Tian Guo-wen [9] and others have used commercial CFD software to characterize flow behavior in the labyrinth spiral pump, using a laminar flow model. Wang Chun-lin [10] and Tang Qian [11] simulated the three-dimensional turbulent flow field inside the trapezoidal labyrinth screw pump, for the first time, with clear water conditions and obtained the main performance characteristics and some local internal flow characteristics. More recently Yan et al. performed numerical studies using the moving mash technique [12], and applied it to the cavitation problem in the screw pump type [13].

However, due to the relative complexity of the double helix pump geometry, only a few publications are devoted to CFD results on both local flow features including inlet and outlet end cap regions. The first section of the present paper is devoted to presenting the experimental results obtained for two different rotational speeds completed by a leakage model analysis for several flow rates. In the second section, a numerical approach, based on the immersion solid method, is used to calculate the internal flow field in the fixed and rotating parts of the pump. CFD overall performances are obtained and compared with experimental results. In addition, some local analyses on the velocity field and the pressure distribution in specific areas of the double helix pump are performed. The numerical approach’s capability to predict the overall pump performance of this double helix pump is discussed, the results of which can be considered as a starting point to enhance future numerical and experimental orientations.

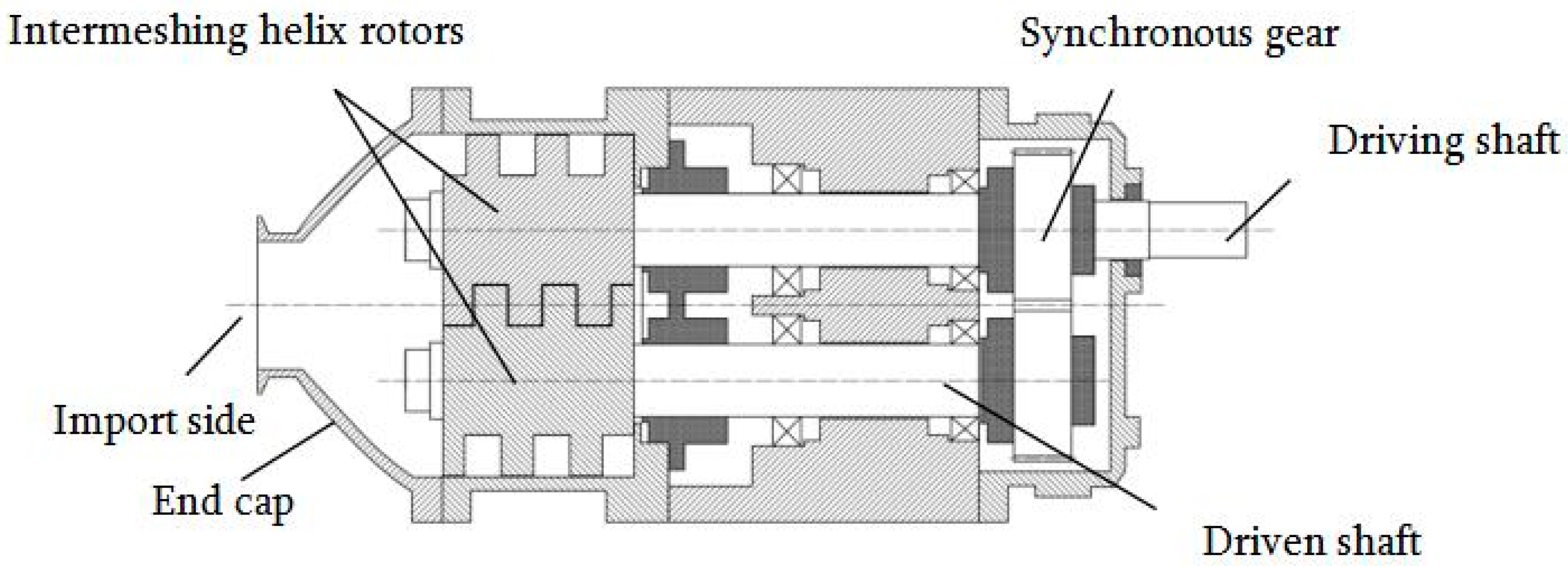
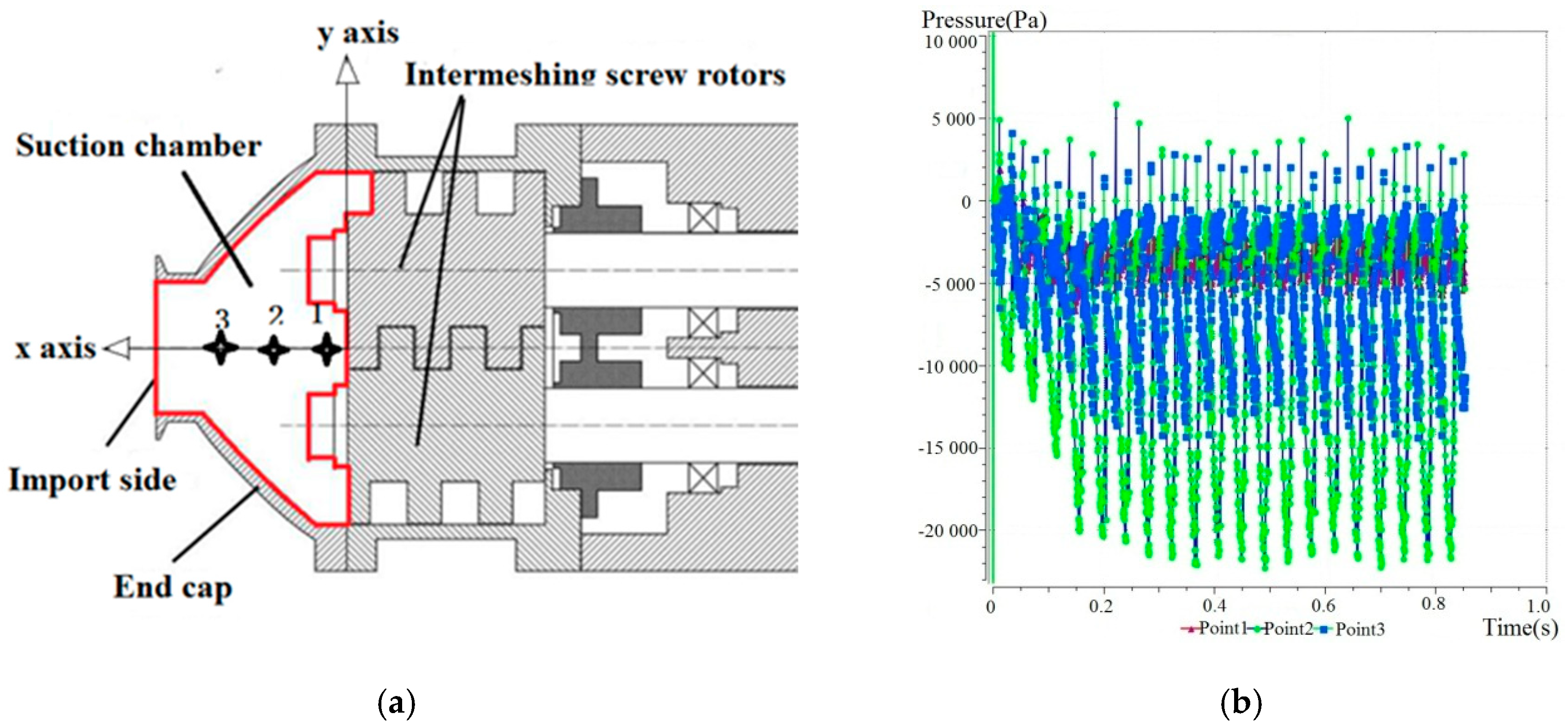
2. The Pump’s Main Characteristics and Working Principle

The double helix pump is represented in Figure 1. The first screw rotor is the active one and is driven by an electric motor. The second one is the driven screw, which is driven by the active screw through a pair of synchronous gears that ensure the same rotational speed with an opposite direction of rotation. Because of the helical rotation and intermeshing of the two rotors, chambers are intermittently formed at the inlet edge of the rotating screw, the liquid being continuously axially displaced from the suction chamber to the discharge ends. Both helical rotors are designed and manufactured with the contactless and wear-free operation of the system, ensuring the equipment system is trouble-free and long-lasting. As the direction of movement of the pump and the material are in the same direction, mechanical shear stress is quite low so that material is not damaged, stirred or squeezed. In order to avoid metal-to-metal contact, several gaps exist between the stationary and the moving parts. For a given fluid (single or multiphase), these gaps and the related overall dimensions play a major role in pump performance-governing parameters with rotational speed as well.

The geometric parameters of the helix screw pump are given in

Table 1. The pump’s main dimensions.

Name	Value	Units
chamber’s depth	24	mm
chamber’s width	18.2	mm
tip radial gap between the screw land and pump housing	1.15	mm
screw tooth width	16.4	mm
flank clearance gap between active and passive screw teeth	0.9	mm
screw rotor length (axial extend)	88	mm
screw revolution number	2.54	circle
pitch of the screw	34.6	mm
screw tip diameter	99	mm
screw hub diameter	51	mm
pipe diameter at pump inlet section	63	mm
pipe diameter at pump outlet section	63	mm
distance between two rotors axis	75.9	mm

. The rotor main parameters and the view of both screws are shown in Figure 2.

3. Numerical Simulation Method

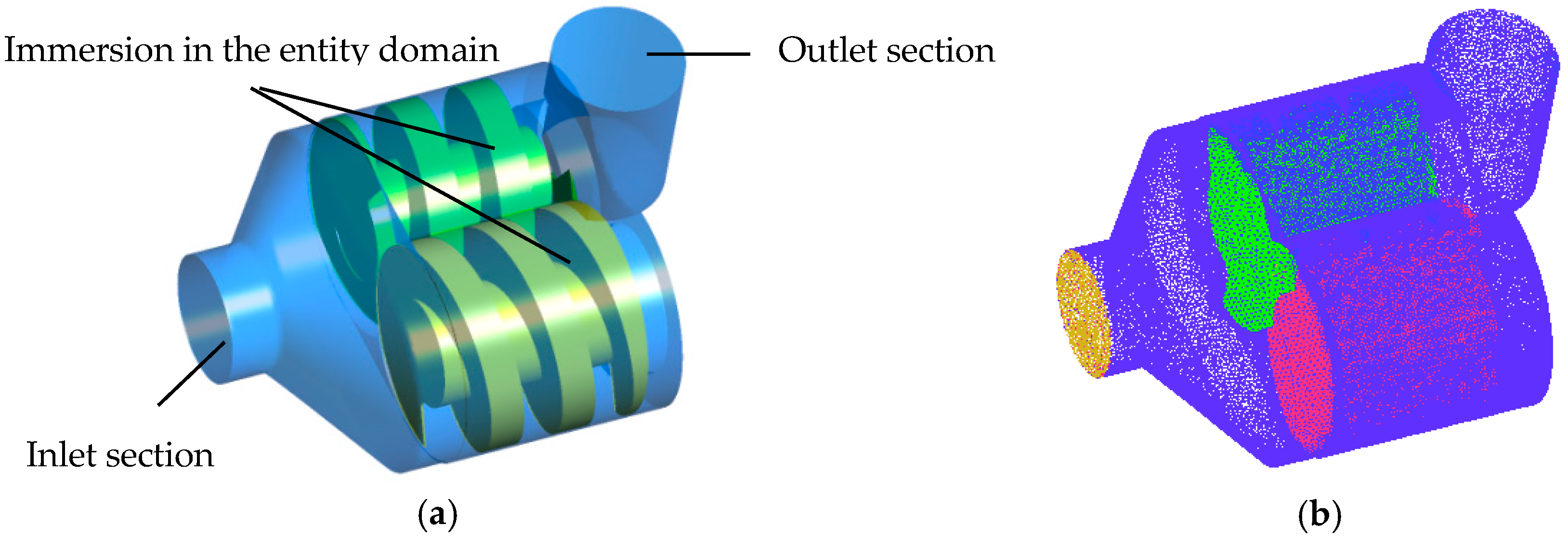
3.1. Immersed Solid Method

Since the working chamber volume domain is continuously modified according to each step rotor position, numerical calculation uses an immersed solid technique. An immersed solid method is a dynamic mesh method, proposed in the ANSYS CFX software, which can perform steady state or unsteady simulation with rigid solid objects immersed in the fluid field. The simulation method is mainly applied to the simulation of moving boundary problems that are difficult to solve by other methods (such as for gear pumps, screw pumps and other grids with minimal mesh movement problems). During the simulation, the CFX solver applies a momentum source to the fluid in the immersed solids area to force the fluid to move with the solids. Immersed solids are considered as source terms in the flow equation that drives fluid motion to match solid motion. In order to solve the shape of the interface immersed in solid, immersed solid surface mesh quality requirements should be relatively high, as shown by Song et al. [14,15].

3.2. Control Equations and Turbulence Model

The flow inside the double helix pump depends on the mean flow rate, the screws’ relative positions versus time and the interaction between screw rotation and the pump boundary walls. In this paper, the Reynolds time-averaged method is used to simulate the control equations of pump internal flow with a continuous equation, a three-dimensional Reynolds averaged N-S equation and a standard k-ε double equation assuming turbulent flow as performed by Song et al. [15]. For some specific working points, the k-omega SST model is also used for comparison purposes. The laminar model is also used for some working points when a low-pressure difference governs specific low values of the leakage backflows.

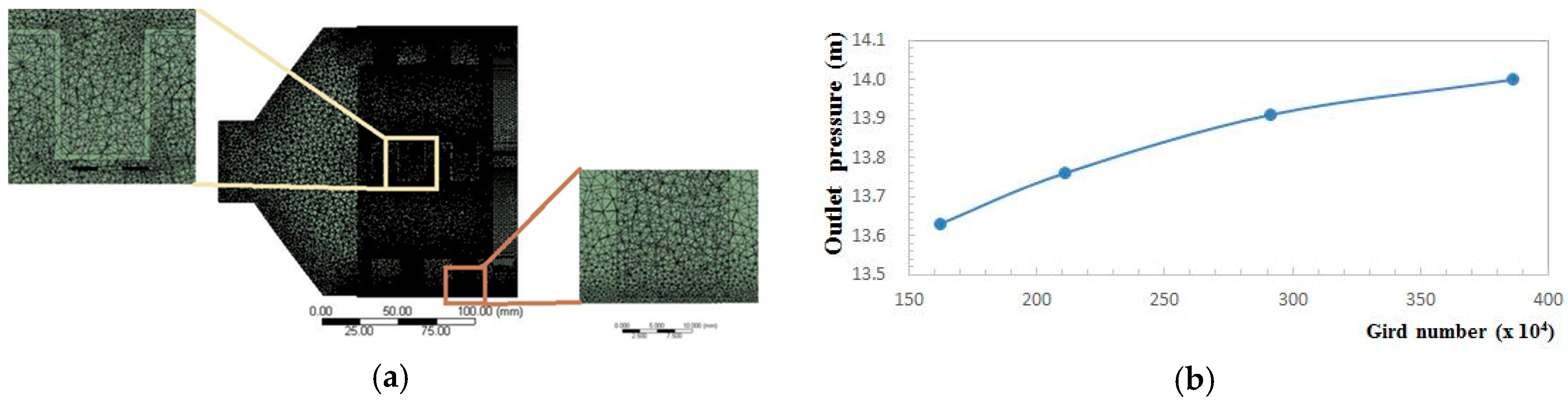
3.3. Meshing

UG software is used for modelling the three-dimensional calculation area of the helix pump runner and casing. Meshing in the ICEM CFD software is uesd to slove the physical method in the numerical simulation process without the fluid domain and the solid domain grid deformed, and an unstructured grid division is used. The unstructured grid of the calculation is shown in Figure 3 and Figure 4a, the total grid number is 3,862,159 and the total node number is 632,906. This number is quite comparable with what has been chosen by Yan. et al. [12,13,16], using a polyhedral mesh set-up. However, the present grid number is probably not sufficient inside the flank gaps (see the enlarged region on the left side of Figure 4a) in between the two screws. A much denser mesh is chosen inside the tip gaps (see the enlarged region on the right side of Figure 4) because about 80% of all leakage occurs in this region, as suggested by Vetter and Wincek [1].

A mesh sensitivity analysis was performed for one flow rate value (3.6 m³/h), N = 1430 rpm, with a given time step of 0.0004 s. The corresponding results are given in

Table 2. Mesh sensitivity analysis.

Grid Number	Outlet Pressure (m)
1,621,784	13.63
2,109,872	13.76
2,915,482	13.91
3,862,159	14.00

and in Figure 4b for the outlet pressure value. There is a slight modification of 0.64% on the outlet pressure result in between the last two mesh numbers. It has been considered that an asymptotic value is reached for a mesh number of 3,862,159.

The boundary conditions are defined as follows:

• The rotor is considered as an immersed solid, keeping the momentum scaling factor at 10.0.
• The total pressure value is given at the inlet plane of the calculation domain. The pressure value levels are given relative to a standard atmospheric pressure of 101,325 Pascals.
• A volume flow rate is imposed as the outlet boundary condition; the flow direction is perpendicular to the exit boundary.
• The flow (water) is incompressible and at normal temperature. No heat exchange is taken into account.
• Calculations are performed for five different flow rates with different time steps. The inlet section location is closed to the experimental pressure tap. However, for simulation, another section is also tested, much further upstream, in order to check how initial conditions may influence the local numerical results.

4. Experimental Set-Up and Results

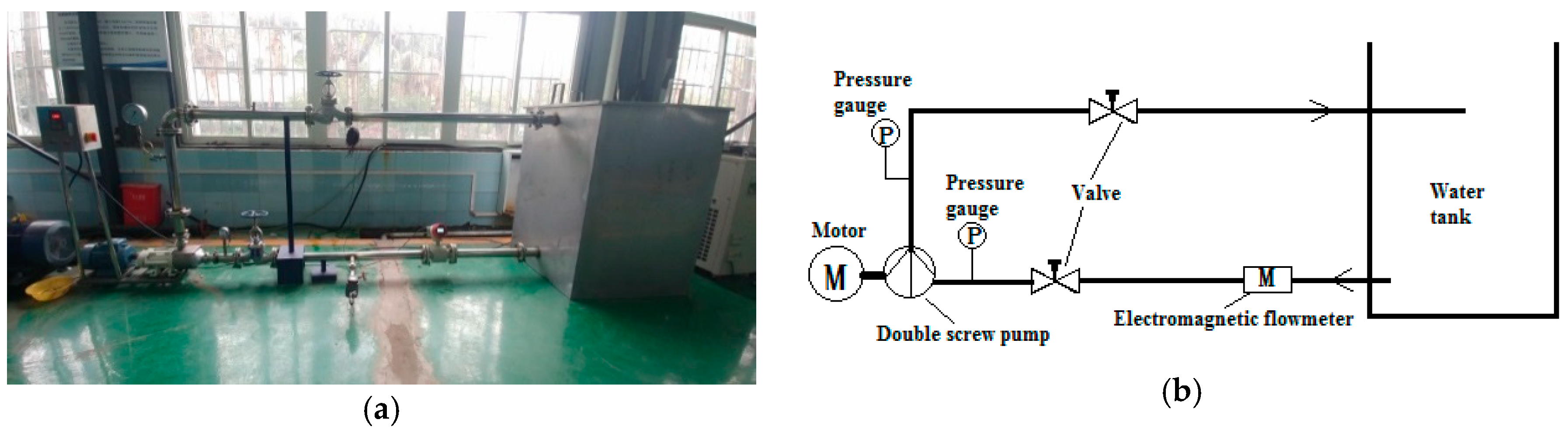
4.1. Experimental Set-Up

The experiments were carried out at the Key Laboratory of Fluid and Power Machinery of the Ministry of Education, Xihua University. Normal-temperature water was used as the test medium. The flow rate is measured by an LDG-MIK electromagnetic flowmeter. Inlet and outlet pressures are measured by an MIK-Y109 digital pressure gauge. Rotational speed can be continuously controlled and modified. The test loop is shown in Figure 5. An electromagnetic flow meter is placed further upstream from the pump inlet. Its accuracy is ±0.5% (full scale 3.58–83.62 m³/h), the accuracy of the outlet pressure gauge is ±0.25% (full scale 0–0.6 MPa) and the accuracy of inlet pressure gauge is ±0.5% (full scale −0.1–0.1 MPa).

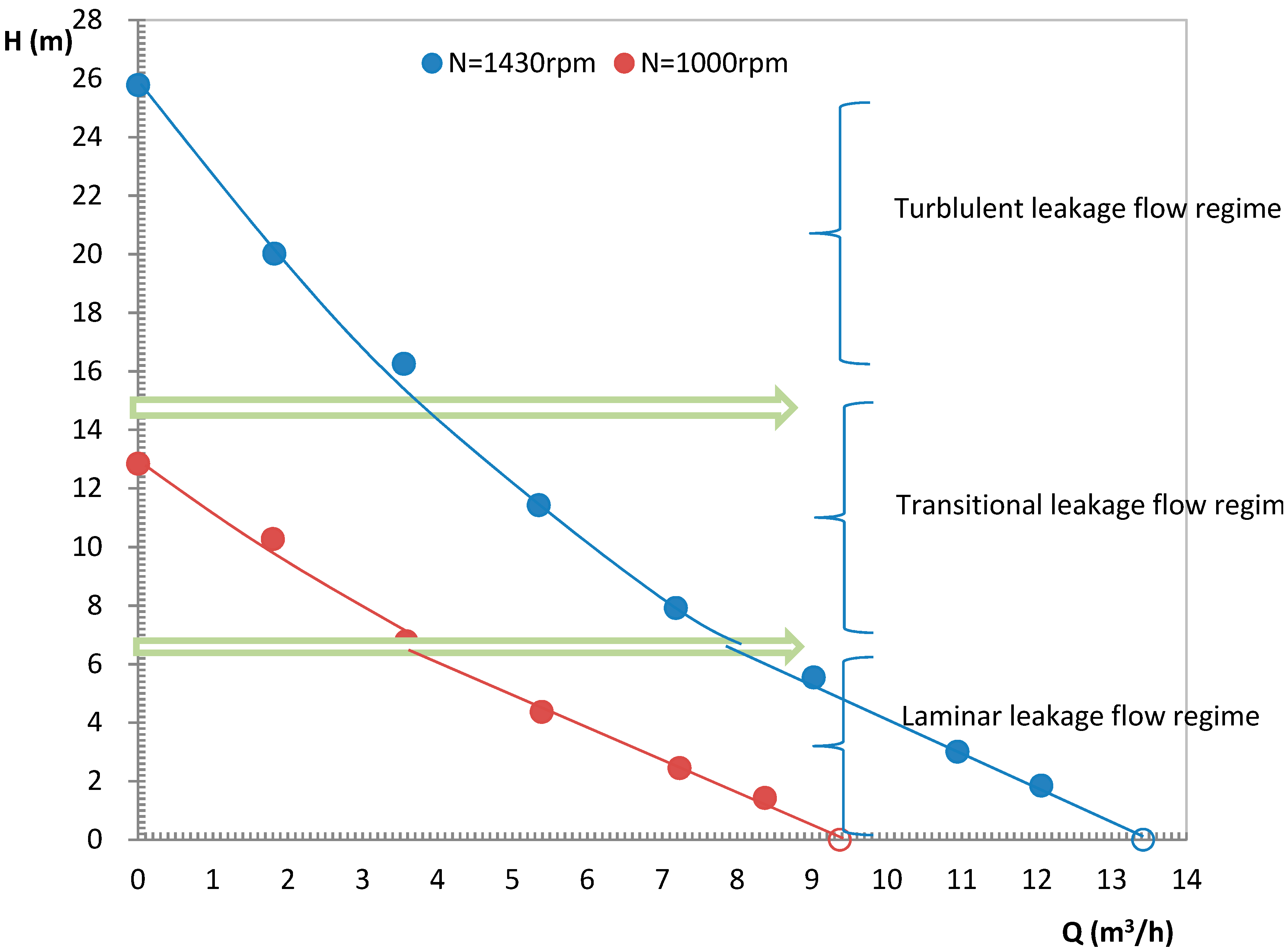
4.2. Experimental Results

The experimental tests were carried out for several water flow rates operated with two different rotational speeds equal, respectively, to N = 1430 rpm (rated value) and N = 1000 rpm. The corresponding results are given in Figure 6. The maximum volume flow rate value can be theoretically evaluated when the pressure change between the inlet and outlet sections is equal to 0. It corresponds to the displacement volume (or swept volume), which is conveyed by the helix pump. The corresponding values, according to the relation proposed by Prang and Cooper [2], are 13.42 m³/h and 9.34 m³/h, respectively, for 1430 and 1000 rpm. These values are determined assuming no leakage between each chamber; so, they are slightly overestimated. However, they correspond well to the extrapolation from the experimental curves in Figure 6, taking experimental uncertainties into account. Compared with roto-dynamic pumps (centrifugal, mixed and axial ones), screw pump performance curves exhibit an opposite curvature. The more the pressure difference increases, the more the slip across each land increases, affecting the pump volumetric efficiency. The volumetric efficiency variation is strongly related to the leakage velocity and the local friction factor, which also depends on the local Reynolds number value. An approximate evaluation of the Reynolds number value can be done using the present experimental results. For the maximum head value, which is reached with a zero measured flow rate (when the circuit vane is closed), leaks are strongly present inside the pump land and chambers. Anticipating a turbulent flow regime, the evaluation of the maximum slip velocities gives 10 m/s and 7.25 m/s, respectively, for 1430 and 1000 rpm. These values are about 10 times larger compared with the axial screw land velocities, which are in the opposite direction to the slip (leakage) velocities. The corresponding axial slip Reynolds number values are, respectively, 1.4 × 10⁴ and 0.9 × 10⁴. These values correspond to the region from which a turbulent flow regime may occur according to the well-known Moody chart. This means that the axial Reynolds number range will probably tend to a transitional or laminal region for a decreasing pump operating head and low rotational speeds. Looking at the experimental results given in Figure 6, it can be observed that the slopes of the two performance curves are modified when the head approximately reaches a value of 8 m. For low H values, each slope value remains constant, indicating a laminar leakage flow regime. On the opposite side, for high H values and N = 1450 rpm, the curves exhibit a concave downward shape typically related to a turbulent leakage flow regime. This has already been suggested by Prang and Cooper [2]. When H is between 7 m and 14 m, a transitional zone can be detected for both rotational speeds; a rapid estimation of the leakage Reynolds number gives a value of 4 × 10³, which corresponds to a transitional regime. A rough evaluation of the three regime zones that are shown in Figure 6 also corresponds to the leakage Reynolds number values obtained using the one-dimensional relations given in Section 4.4.2.

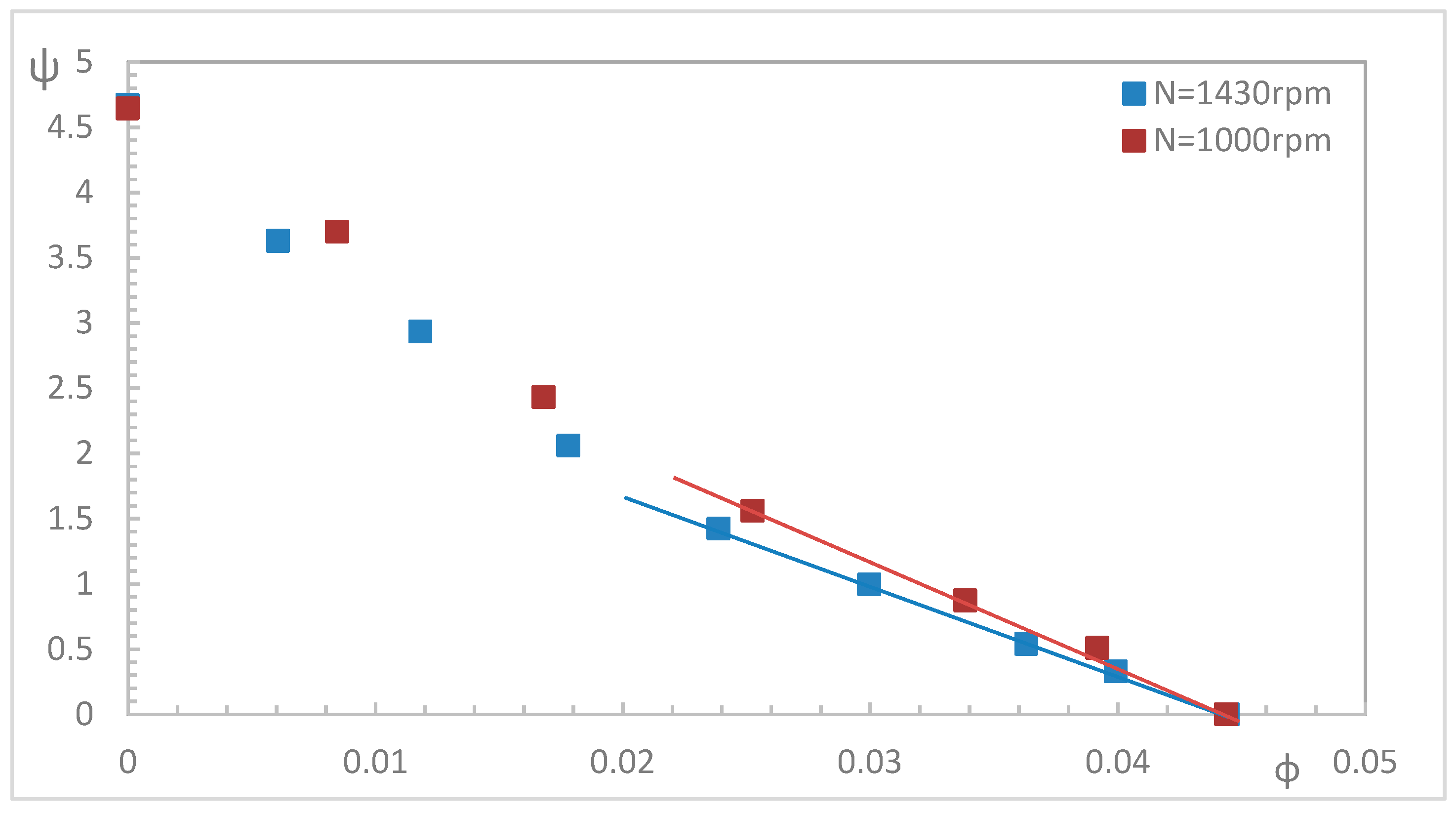
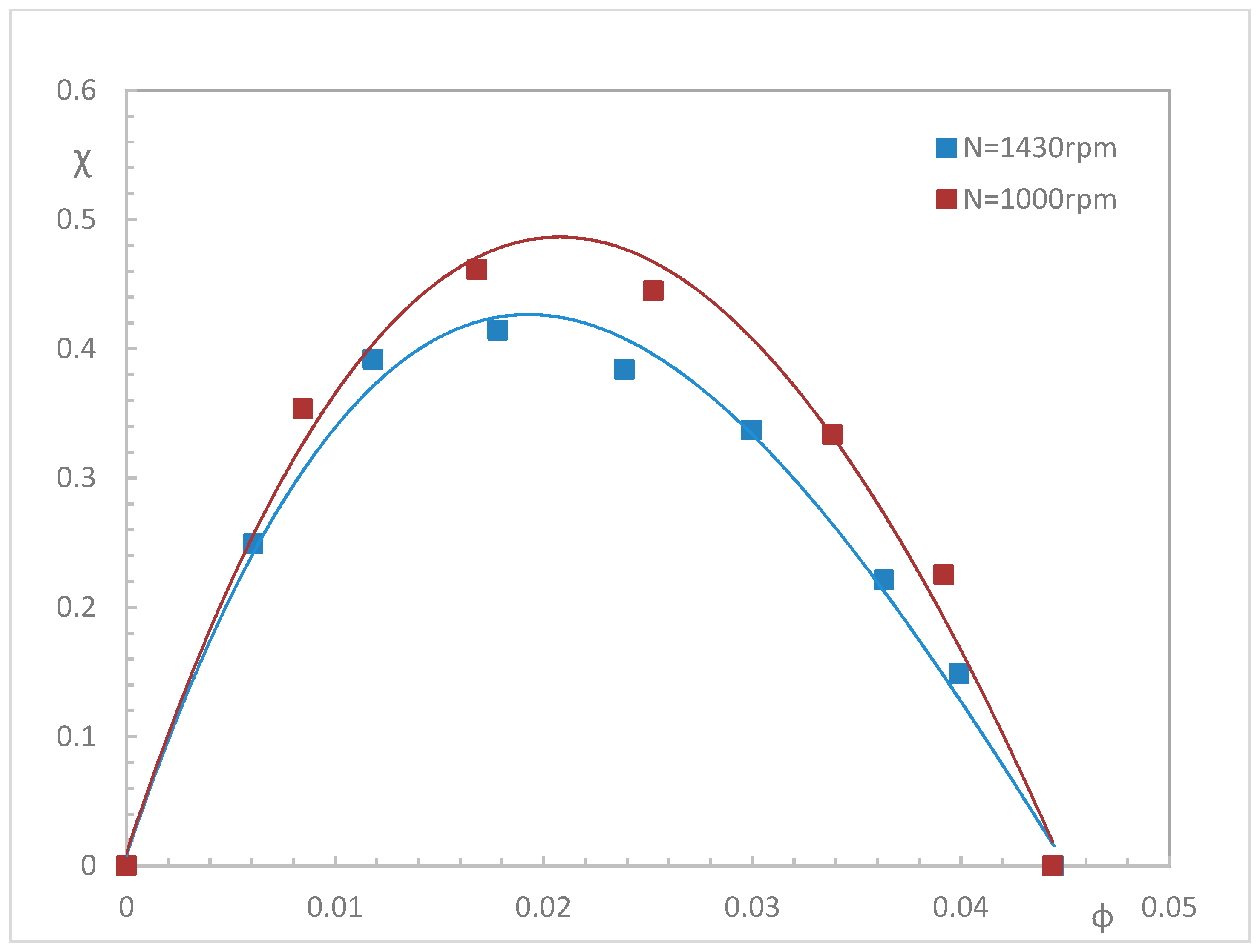
4.3. Non-Dimensional Performance Coefficients

The maximum screw pump volume flow rate is directly proportional to the rotational speed. The experimental maximum head value was found to be related to the squared of the rotational speed. Consequently, non-dimensional coefficients are used, the definitions of which are given below [17,18,19,20]:

Flow coefficient: $\mathsf{\Phi }=\mathrm{Q}/\left(2\mathrm{S}\times {\mathrm{U}}_{\mathrm{t}}\right)$,

Head coefficient: $\mathsf{\psi }=\mathrm{gH}/{\mathrm{U}}_{\mathrm{t}}^2$,

Fluid power coefficient: $\mathsf{\chi }=\mathsf{\rho }\mathrm{gHQ}/{\mathrm{U}}_{\mathrm{t}}^3$

Results are shown in Figure 7 and Figure 8, respectively, for the flow head coefficient ψ and the flow power coefficient χ. Each curve depends on the rotational speed. In Figure 7, and for low head coefficient values, ψ evolutions are quasi-linear when the flow coefficient is high, as pointed out in the previous section related to a laminar leakage flow regime (see Figure 6). Figure 8 shows that χ reaches a maximum value for a specific flow coefficient value that depends on the rotational speed. The maximum value of the flow power corresponds well to the manufacturer’s instructions when low viscosity fluid is used. Finally, both non-dimensional coefficient values are higher when the rotational speed is small. This could be related to the driven main flow friction losses is low when the rotational speed is small (except for leakage flow areas).

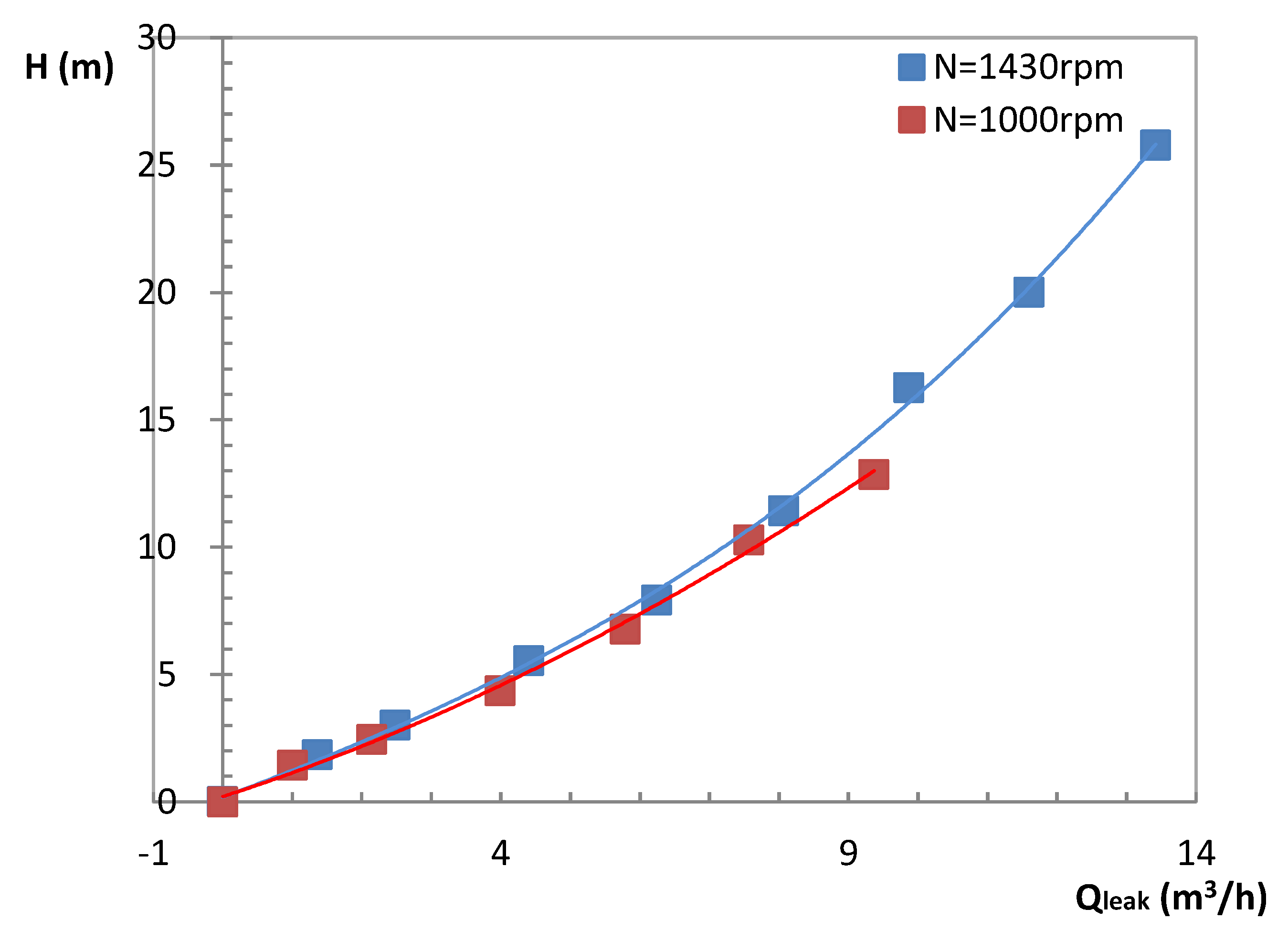
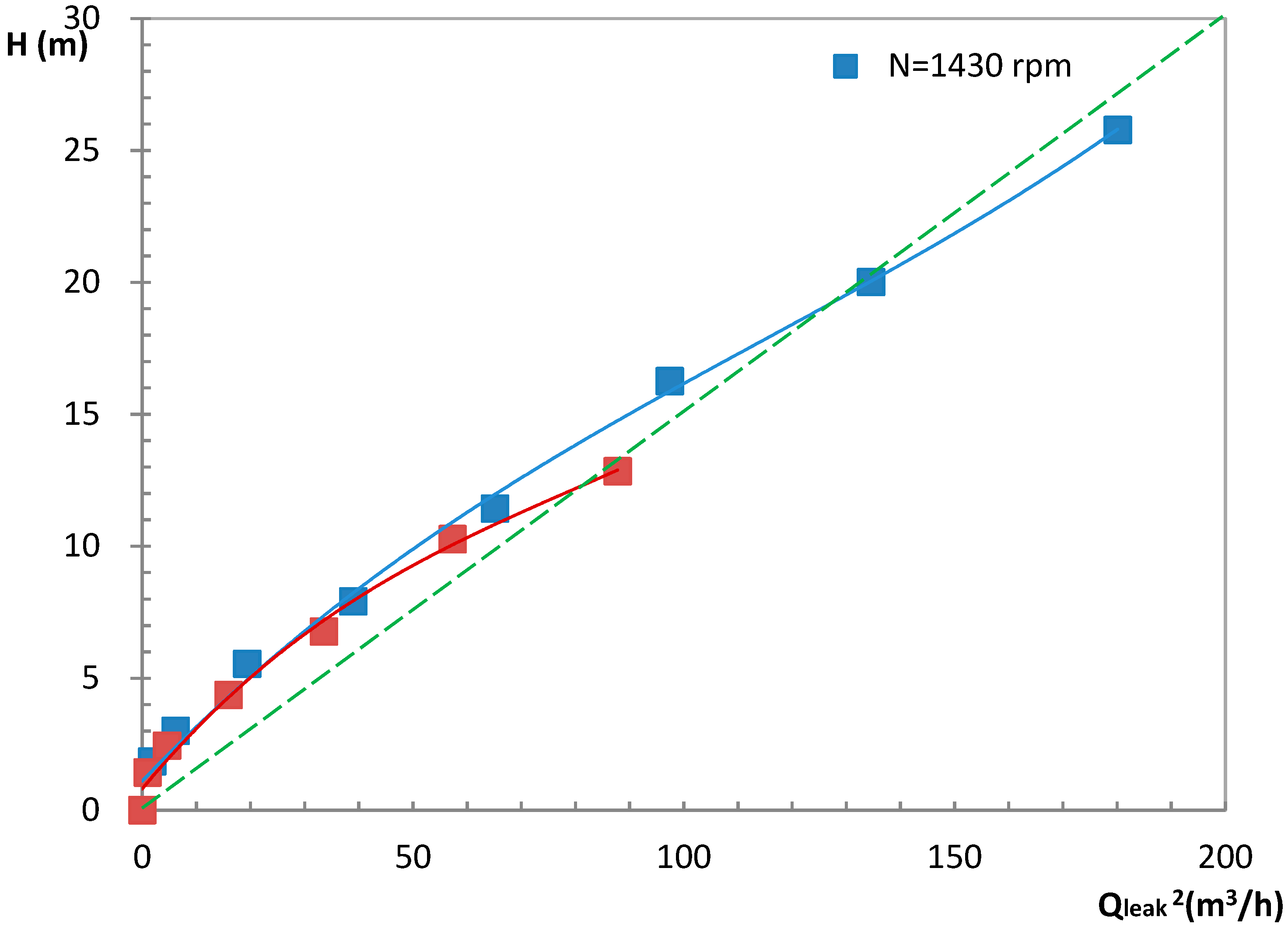
4.4. Leakage Volume Flow Rate Evaluation

4.4.1. Experimental Leakage Calculation

Starting from the experimental results obtained in Figure 6, it is possible to deduce the leakage flow rate amount Q_leak versus head as shown in Figure 9. One single curve is then obtained. Thus the leakage amount mainly depends on the difference of pressure. Since the leakage velocity amount should be proportional to the root mean squared of the pressure difference for turbulent flow leak regime, H versus Q_leak² is plotted in Figure 10. One can observe that, for high H values (more than 13–14 m), the experimental leakage results are on a straight line, corresponding to a turbulent assumption concerning the loss coefficient that governs the leakage flow between each land. Below H = 14 m, the experimental leakage flow rate is lower than the estimated turbulent region and the friction coefficient is larger and tends to reduce the leak. The observed limiting value around H = 14 m for a turbulent regime also corresponds to the estimated one already proposed in the previous section (see Figure 6)

4.4.2. Analytical Leakage Evaluation

According to several authors [1,2,21,22,23,24,25,26], an evaluation of the flow rate leakage can be done using the following relationship:

Q_leak = V_leak × A_leak = A_leak × (2 × g × Δh /(k + λ l/ d_h ))^0.5

• where Δh is the difference of head in each land. Neglecting the losses at inlet and outlet pump end caps, the head difference of each land is obtained assuming the same head step value in each screw land. This is confirmed by the numerical results given in Section 6.
• k = 1.5 (k = k1 + k2; k1 = 0.5 for a sudden acceleration and k2 = 1.0 for a sudden expansion)
• λ = 64/Re_leak for a laminar flow regime
• λ = 0.3322 × Re_leak^−0.25 for a turbulent flow regime; Re_leak = V_leak × δ/υ

The related leak velocity and leakage flow rate are calculated using an iterative procedure since λ depends on the local leak velocity. Convergence is obtained within a maximum of 4 to 5 iteration steps. The results are found to be always 20% overestimated compared with the experimental leakage amount. This evaluation can be probably altered by viscous and rotational effects inside the screw main flow that have been neglected in the present approach. The evaluation of Δh is also difficult to perform because losses at the inlet and outlet pump end caps are difficult to evaluate.

5. Comparisons between Experimental Performances and CFD Results

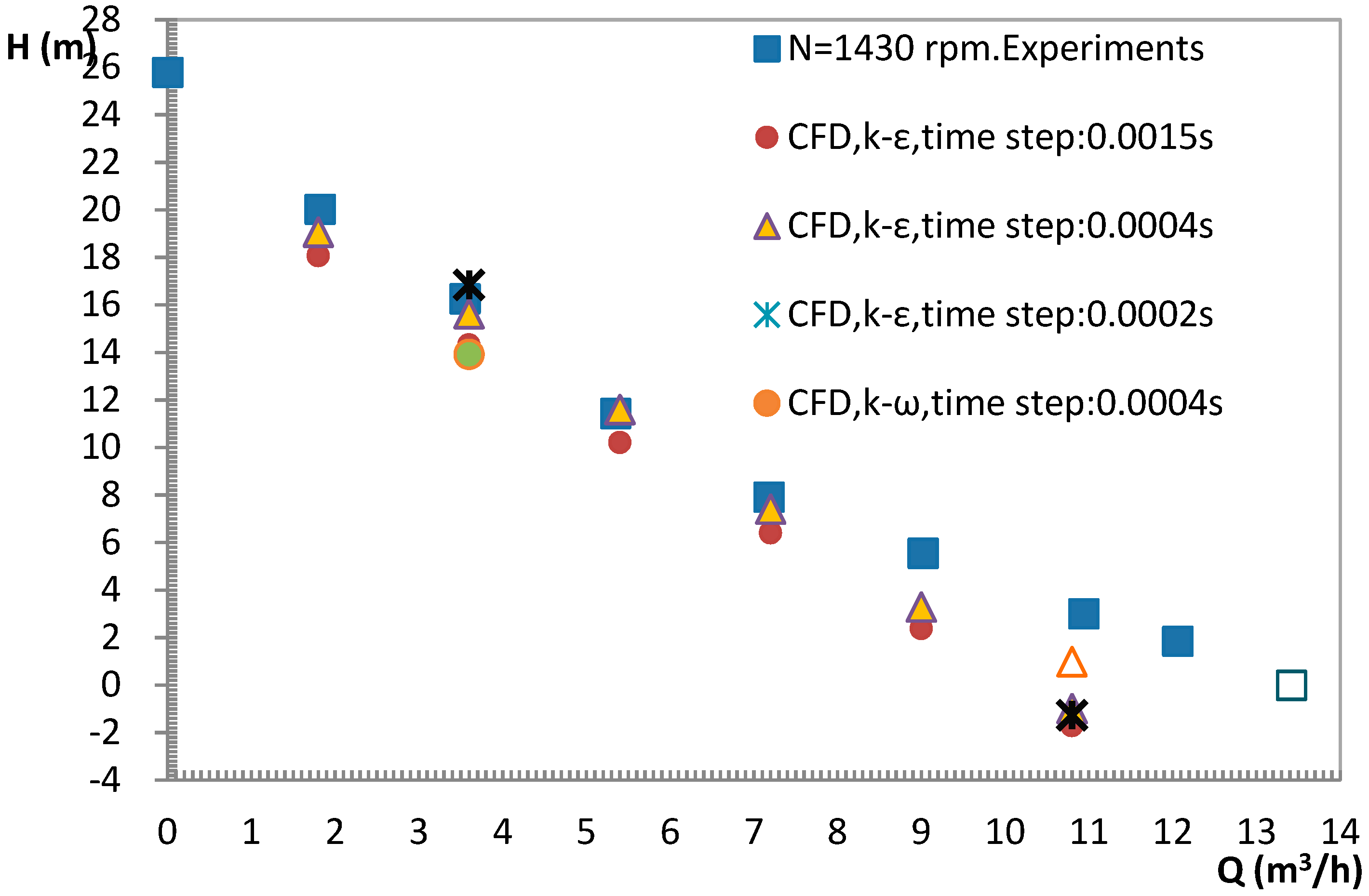
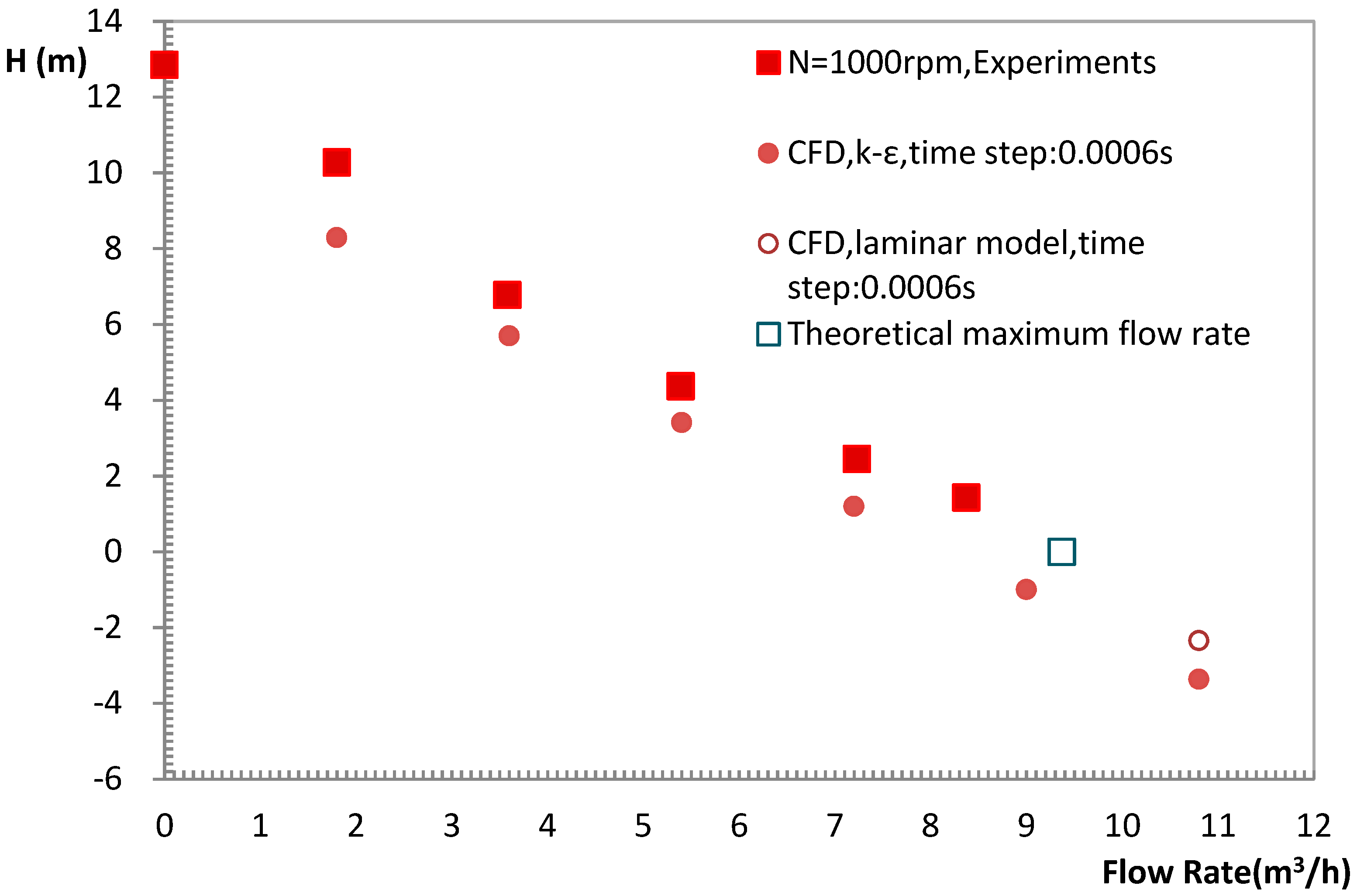
5.1. Numerical Set-Up Conditions

(a) Three selected points, located at the inlet section of the twin screws (see Figure 11a), are used to record local calculated wall static pressure with time. The results are given in Figure 11b for points 1,2 and 3, which are aligned with the pump inlet axis. Periodic and stable results are obtained after eight complete screw revolutions, corresponding to 0.3356 s. Wall static pressure negative values correspond to relative pressure values compared to a reference pressure set at zero. The corresponding lowest absolute pressure values are close to 101,325 − 22,000 = 79,325 Pascals.

(b) Upstream boundary location effects on numerical results.

In order to evaluate the influence of the inlet condition location, two different inlet tube lengths are modelled at 0.5 d (which corresponds to the actual size) and a longer one of 6.5 d, which is a fictitious one. All results (not presented here, for simplification) do not depend on the location of the inlet plane and specifically the instantaneous variation of local pressure and velocity that are discussed in the next section. In addition, no damping phenomena have been detected because of a longer inlet tube. This is probably due to the inlet boundary condition being only pressure combined with an outlet condition for which flow rate is imposed.

5.2. Overall Pump Performances

As shown in Figure 11 for N = 1430 rpm, CFD results are always lower compared with experimental ones when the time step between two successive screw rotary positions is too big (initially set at 0.0045 s). The difference between experimental and calculation results is, however, less than 5% for flow rate values between 0 and 6 m³/h, for which a turbulent leakage flow regime is supposed. This can be considered to meet the engineering purpose which indicates that such numerical simulation results may be considered for relative comparisons. CFD results assuming a laminar regime were also performed for a large flow rate value of 10.8 m³/h. Much better results are obtained closer to the experimental ones (see Figure 12).

In order to evaluate the influence of time step on the CFD results, two additional values are tested, 0.0004 s and 0.0002 s, corresponding, respectively, to four times and eight times lower than the initial one. The results are given in Figure 12. The smaller the time step, the closer the calculated pressures compared with the experimental ones inside the turbulent flow regime zone. This is typically the case when a time step of 0.0002 s is applied, for example, at N = 1430 rpm (this time step of 0.0002 s is set for only two different flow rates for comparison). Note that a time step of 0.0004 s corresponds to a rotor angular rotation of 3.43 degrees for 1430 rpm.

For N = 1000 rpm, a time step of 0.0006 s is chosen in order to keep the same angular rotation of 3.43 degrees. The corresponding comparison is given in Figure 13. The same kind of results are observed: CFD results always underestimated the delivered pump flow rate for a given head coefficient value when a turbulent model is used. Thus, in the specific zone of a laminar regime (most of the experimental results obtained for N = 1000 rpm are inside this zone), CFD results at a high flow rate, using a laminar flow model, give quite better results, as shown in Figure 13. It is believed that a laminar model will be suitable for the whole performance prediction for this rotational speed.

6. Local Results from CFD and Analysis

Since the solid boundary varies with time as the helix pump rotates, the instantaneous flow field over a series of phases is used to represent flow features for an entire time period. The following analysis is based on the result for a mass flow value of 3.6 m³/h.

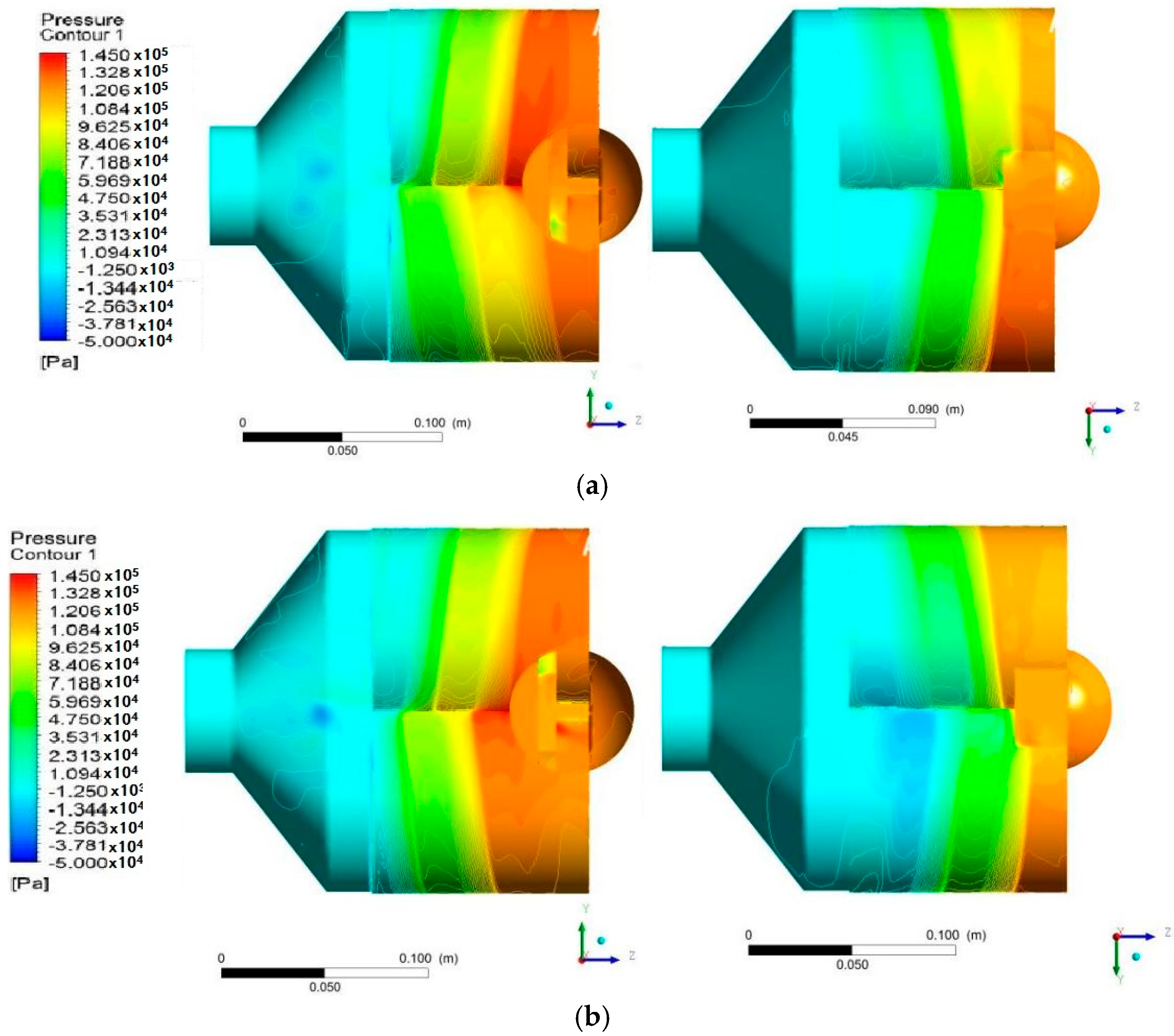
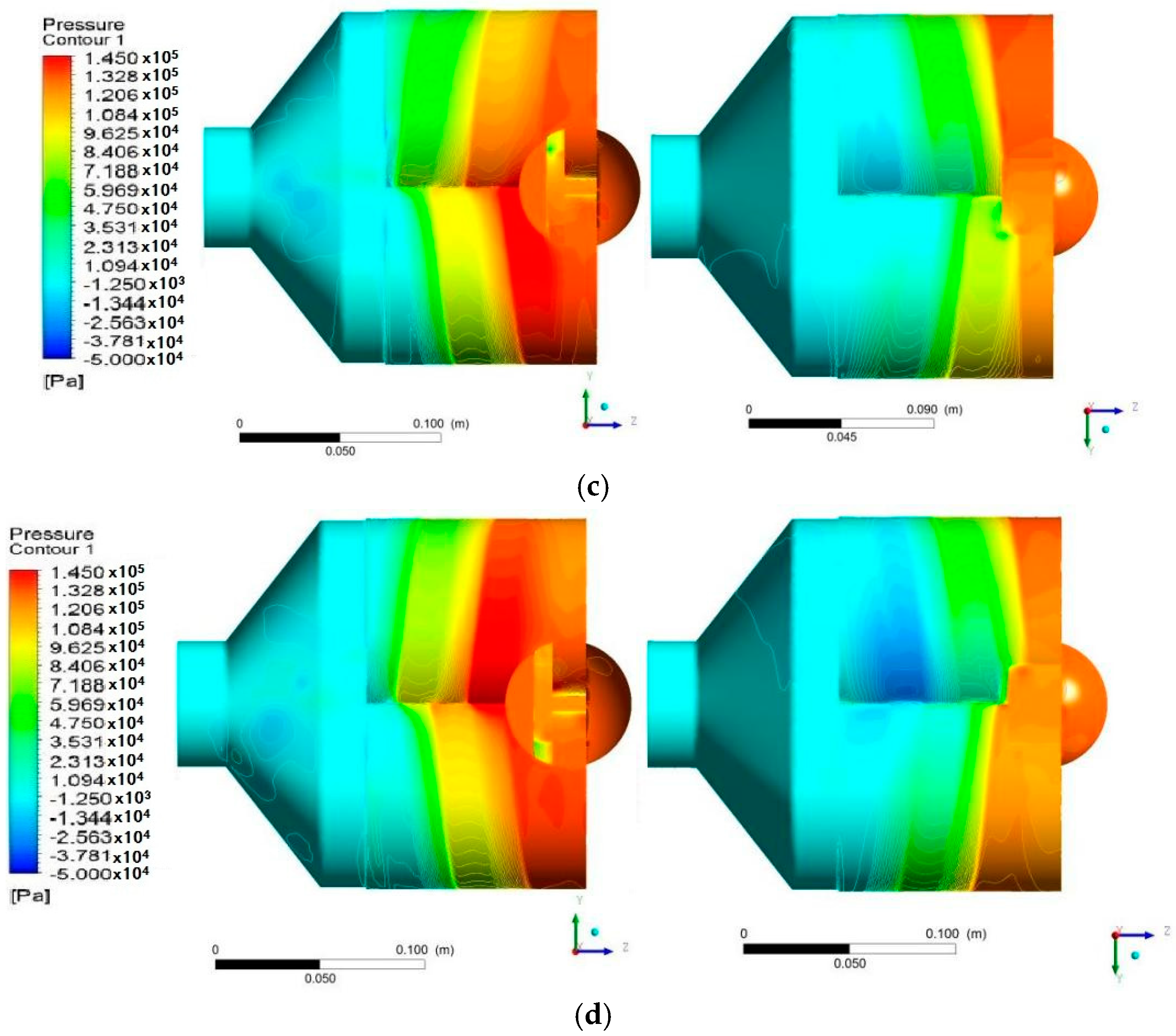
6.1. Pressure Distribution

Four instantaneous instants corresponding to equal intervals of 90° steps are chosen to represent parts of the entire time period change in the flow boundary at 1/4T, 2/4T, 3/4T, 1T, where T is the time for one rotation cycle. The pressure distributions are shown in Figure 14. The right and left parts of Figure 14 correspond, respectively, to the top view and the upward view. Velocity fields are also shown in Figure 15 for the four different time steps previously defined.

It can be seen in Figure 14a–d that the mean pressure gradually increases step by step along the axial direction from the inlet to the outlet, indicating that the helical rotor is the main pressurizing part with the supercharging effect and the maximum pressure at 195,300 Pa. Negative relative pressure can be observed upstream from the rotor inlet with an instantaneous value of approximatively −22,000 Pa, which is mainly due to the reverse leakage velocity of the helix pump close to the inlet land section; this value corresponds the dynamic pressure related to a local leak velocity value around 7 m/s. During one rotation, there are alternating low pressure zones between the two rotor intermeshing zones. The high-pressure zone at the exit side also simultaneously alternates between the two rotors. It can be seen from Figure 9 that the overall pressure varies with time, indicating that the pressure variation is well related to the process of transporting liquid from inlet to outlet. The main of the high-pressure and low-pressure zones is so related to the rotor area modification that it allows flow transfer.

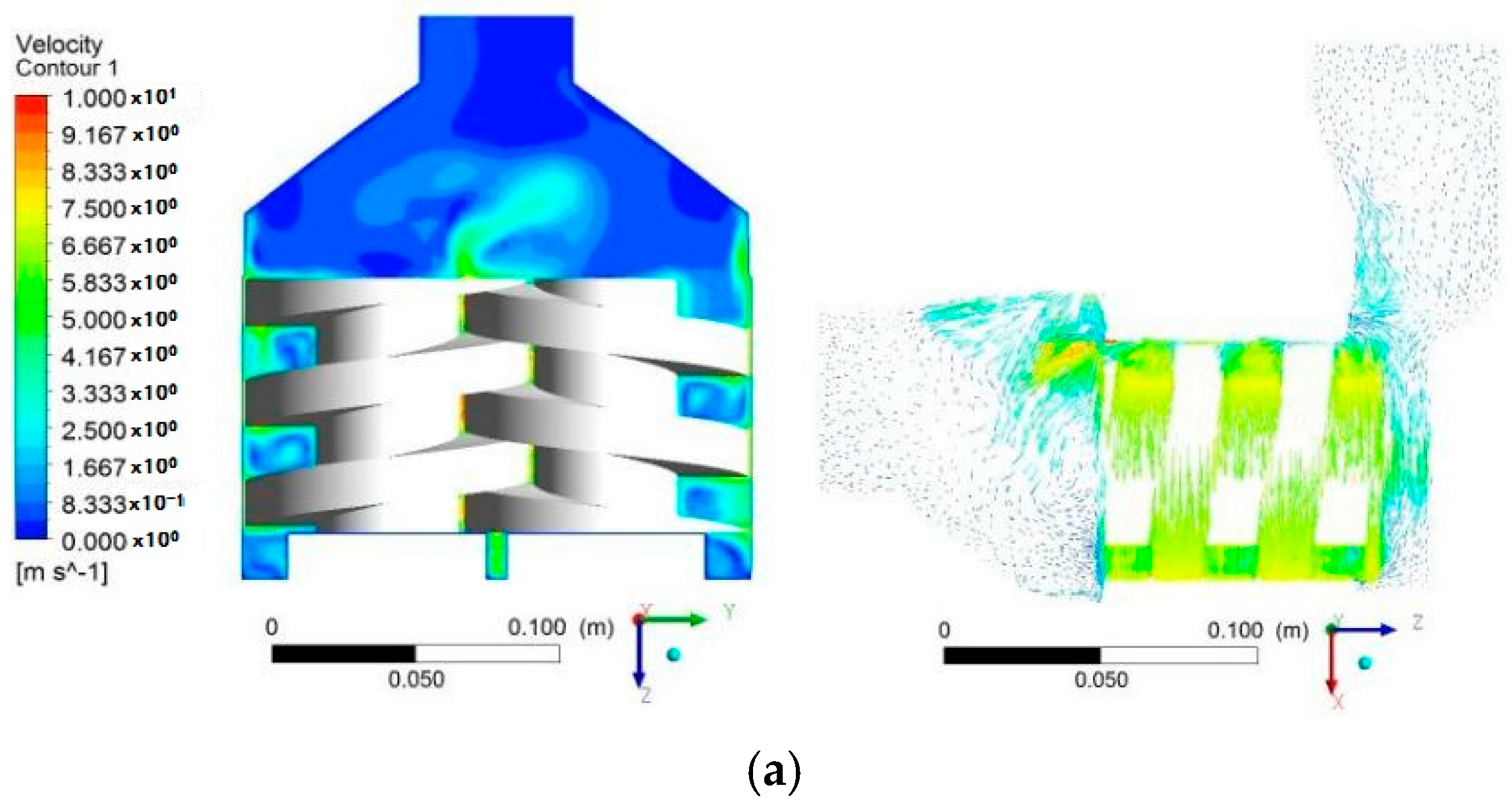
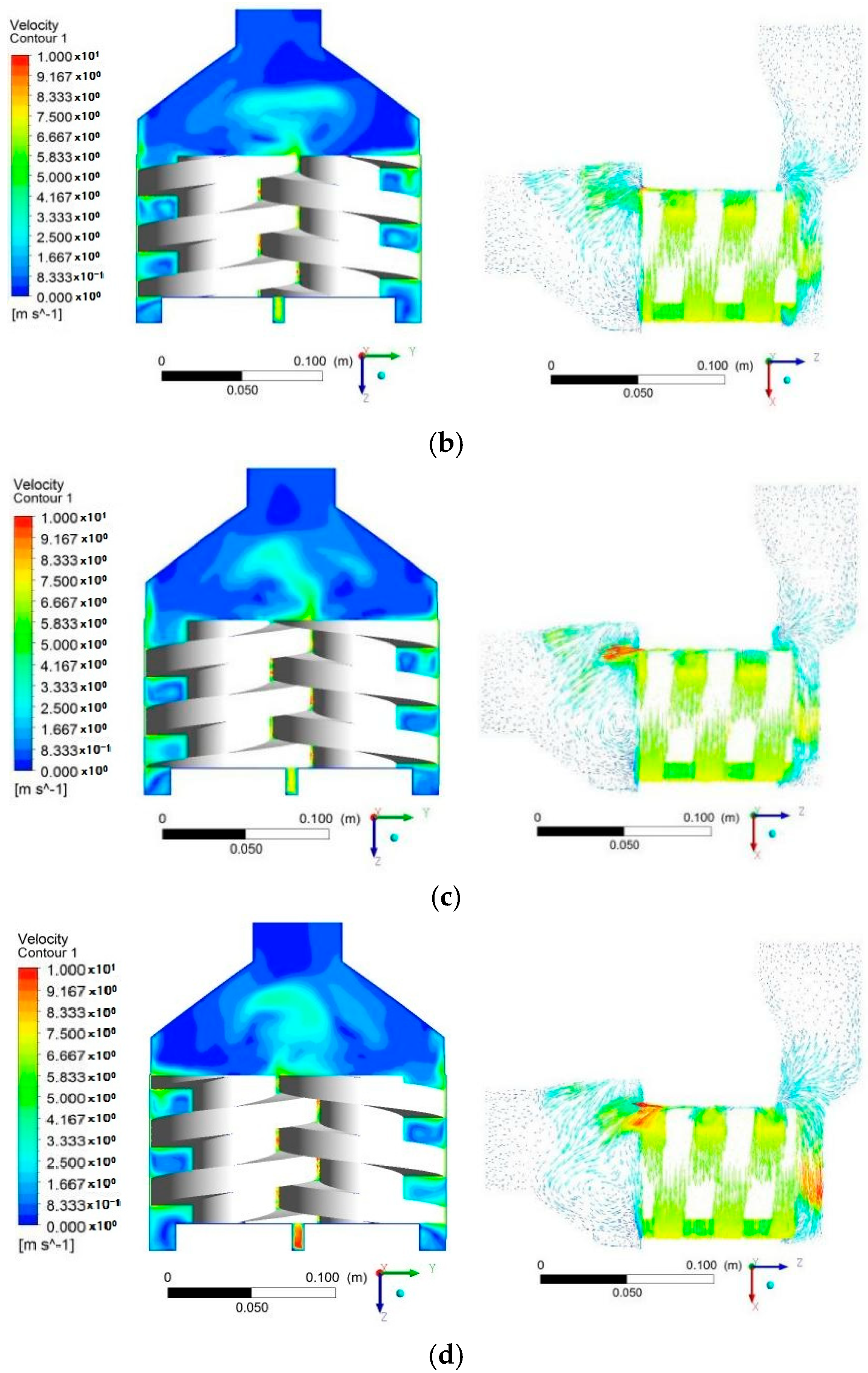
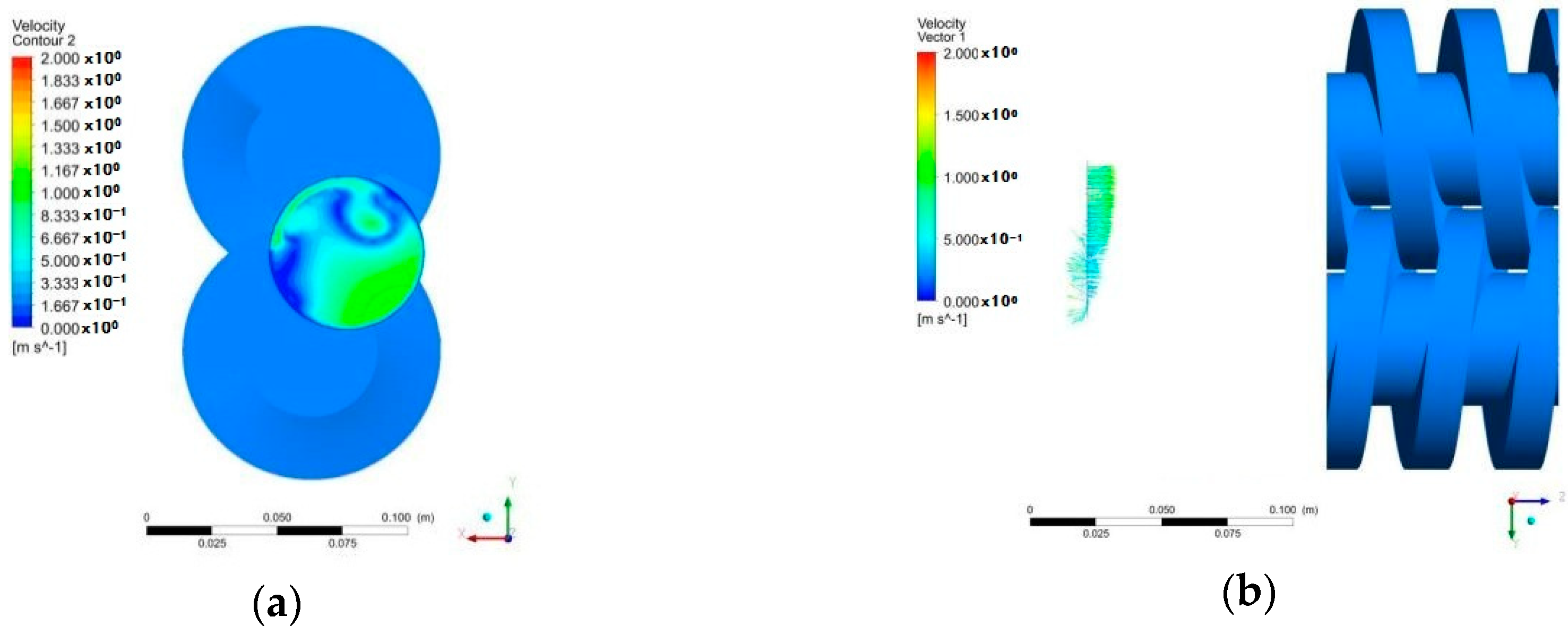
6.2. Velocity Distribution

Figure 15a–d shows the velocity contours and vectors in a specific radial cross-section of the pump. After entering the rotor intermeshing region, local velocities can reach high values related to high rotational speed. Some negative axial velocity regions can be observed (reaching 10 m/s), directing towards the inlet pipe section, located close to the gap between the helix addendum circle and the lining inner bores, that corresponds to the main leakage areas. High velocity distortions also exist at the exit end of the pump. A local specific analysis on velocity fields in some additional locations is given in the following section.

6.3. Particular Velocity Fields

This section focuses on the instantaneous velocity and pressure fields in the inlet pump plane (Figure 16), the intermediate plane located just in front of the rotating parts (Figure 17) and the outlet plane (Figure 18). In Figure 16, one can observe that the inlet section center’s diameter is not located in the mid plane corresponding to the rotor’s rotation axis. This position faces the inlet location for which the two screws capture the flow in the entering meshing system. This asymmetry is responsible for high velocity gradients with some negative leakage velocities that have already been seen in Figure 15. The combination of the inlet chamber size creates strong flow distortions that are transported upstream in the inlet plane. These velocity distortions also depend on time due to the screw combined rotation.

In Figure 18, pressure and velocity gradients still exist at the outlet pump plane, but with lower values compared with the two previous inlet sections. A symmetry plane can be detected, corresponding to y = 0, that is the symmetry plane of the whole pump.

These numerical results will be used to establish more suitable loss coefficients in order to calibrate and upgrade the analytical model presented in Section 4.4.

7. Conclusions

In this paper, an immersed solid method coupled with CFD simulations was used to simulate the internal flow field of a double helix pump. The analysis between numerical calculation and experimental results comes to the following conclusions:

(1)

Overall performance measurements were performed in a twin screw pump for two rotational speeds, using water as the working fluid. As expected, the leakage amount was found to be independent of the rotational speed and only depends on the pressure difference.

(2)

Physical analysis allows the determination of laminar, transitional and turbulent leakage flow regimes that govern the leakage amount in such pump geometry.

(3)

Analytical evaluation based on loss friction models always overestimated leakage values compared with experimental ones. The empirical loss coefficient must be re-evaluated according to rotational effects and viscous forces that have been neglected in the present study.

(4)

CFD simulation results generally show better results compared with analytical ones. The pressure gradient in the rotor meshing area is related to the displaced volume with time.

(5)

In order to obtain suitable numerical outlet pressure delivery values, three rotating time steps were tested. A time step value corresponding to an angular rotor variation of at least three degrees was sufficient enough to reach experimental results within an error of less than 2%. In the same respect, stable periodic results were obtained for a minimum of six complete screw revolutions.

(6)

The main leakage areas correspond to the casing gap between the rotor and the pump casing. The results on leakage values strongly depend on a correct evaluation of the laminar and turbulent flow regime that depends on the local pressure differences.

(7)

The inlet flow before the screw inlet plane is highly non-uniform. This is related to the squeezing effect of the two rotors and the large local amount of leakage flows from the casing gap.