Fault-Tolerant Control Strategy for 12-Phase Permanent Magnet Synchronous Motor
Abstract
:1. Introduction
2. Mathematical Model of 12-Phase Permanent Magnet Synchronous Motor (PMSM)
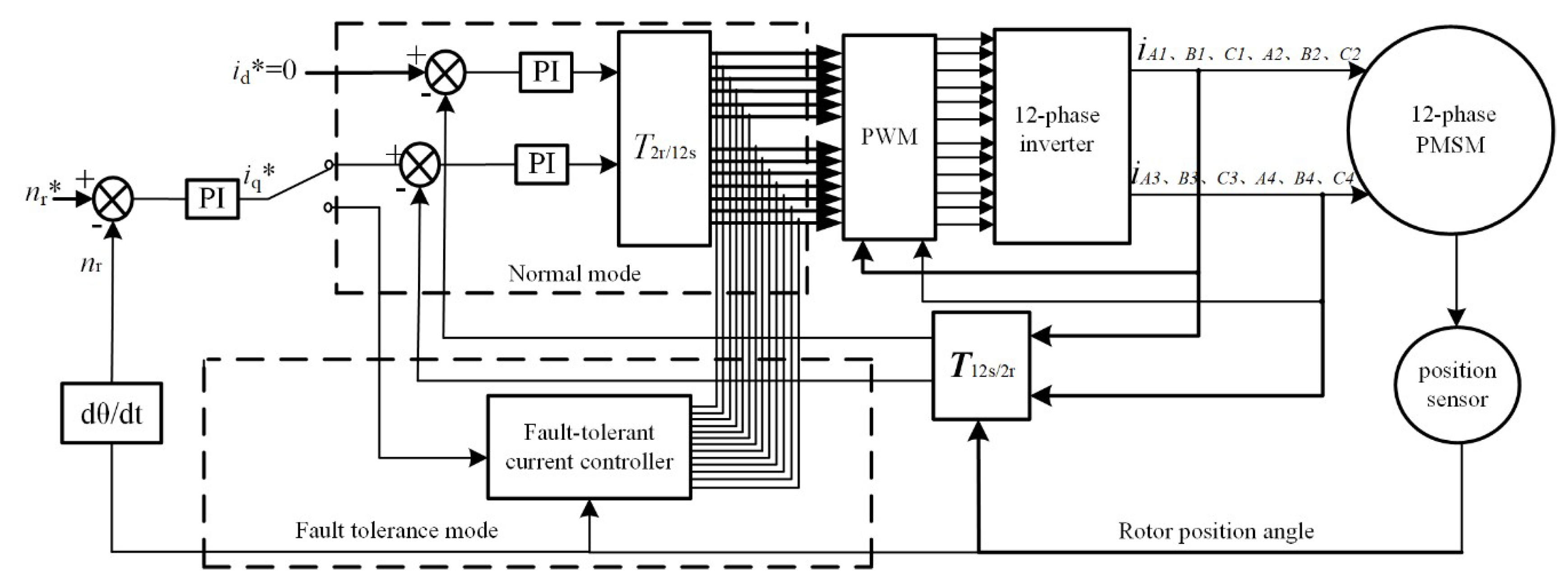
3. Fault-Tolerant Control Strategy of 12-Phase PMSM
3.1. Minimum Copper Consumption (MCC) Fault-Tolerant Mode of 12-Phase PMSM
3.2. Maximum Torque Output (MTO) Fault-Tolerant Mode of 12-Phase PMSM
4. Simulation of 12-Phase Fault-Tolerant System
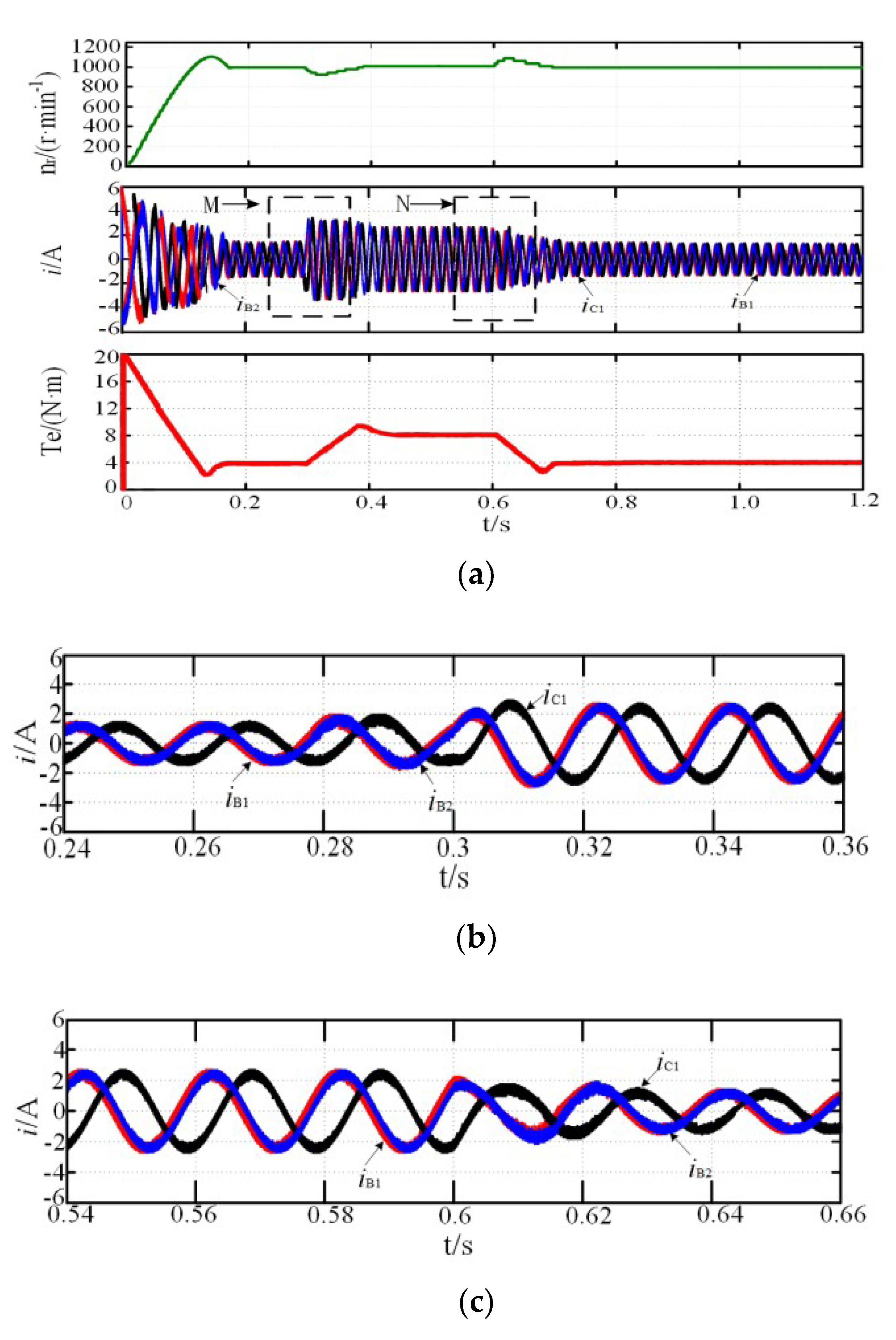
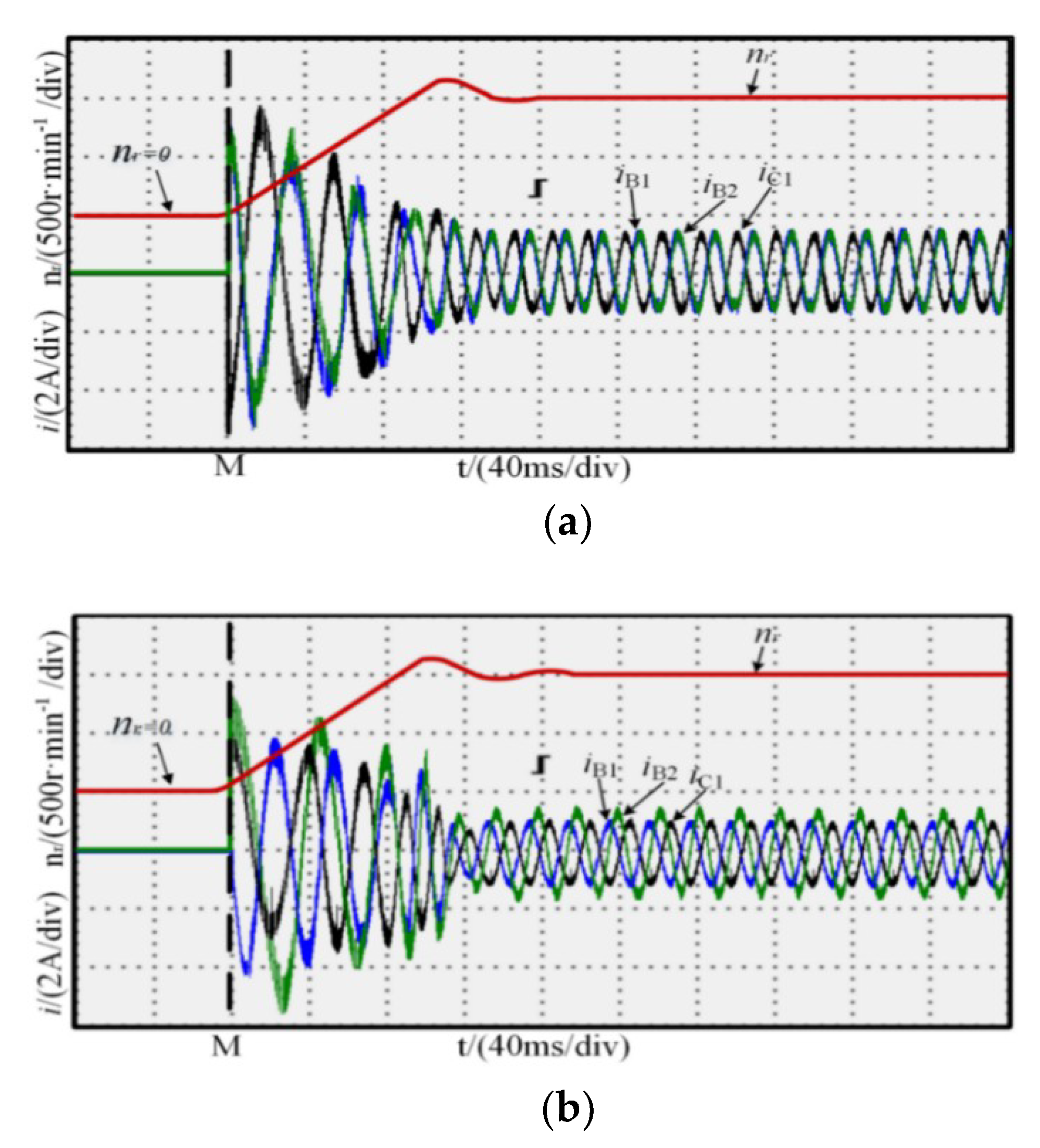
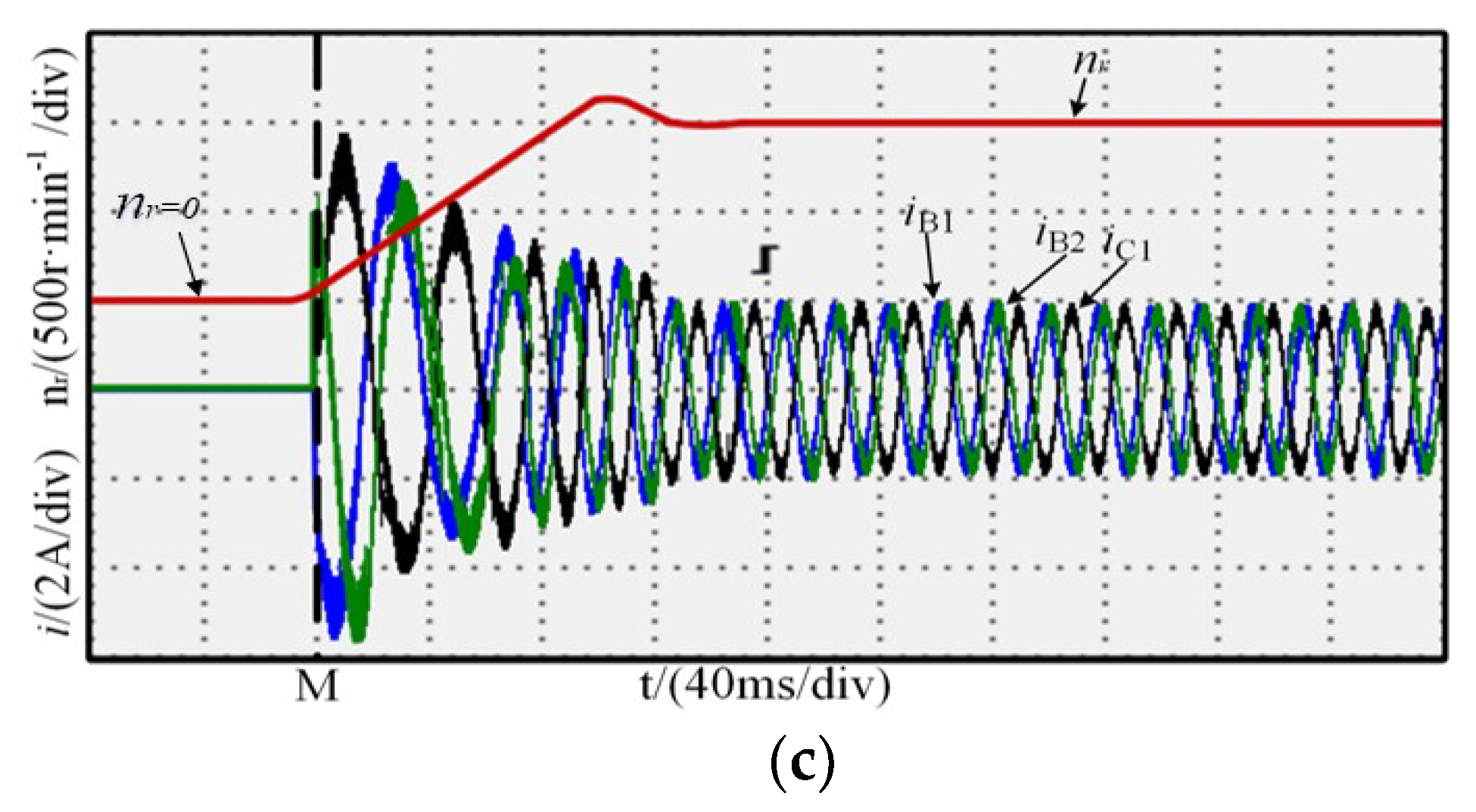
4.1. Simulation of the Start-Up Process
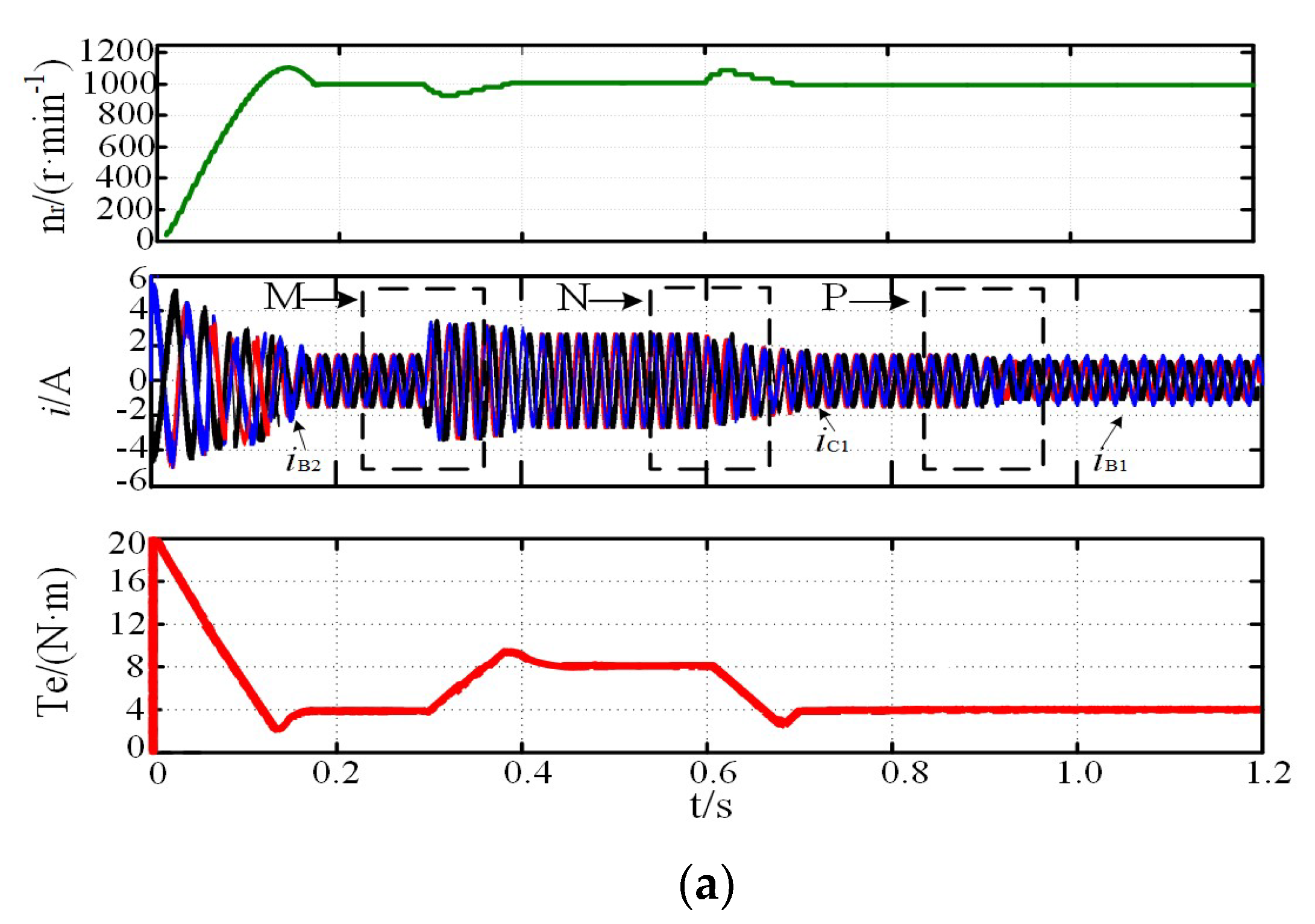
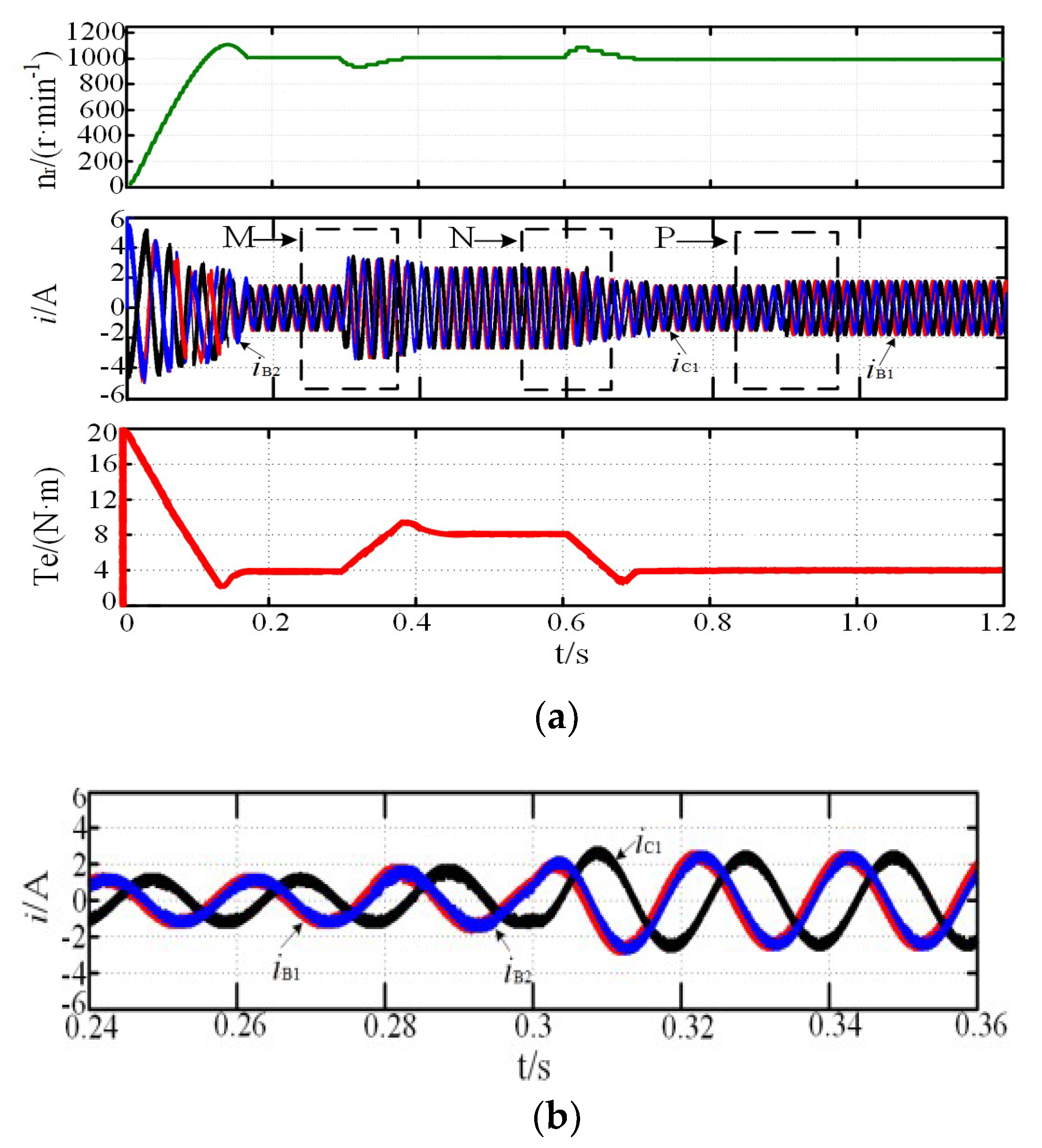
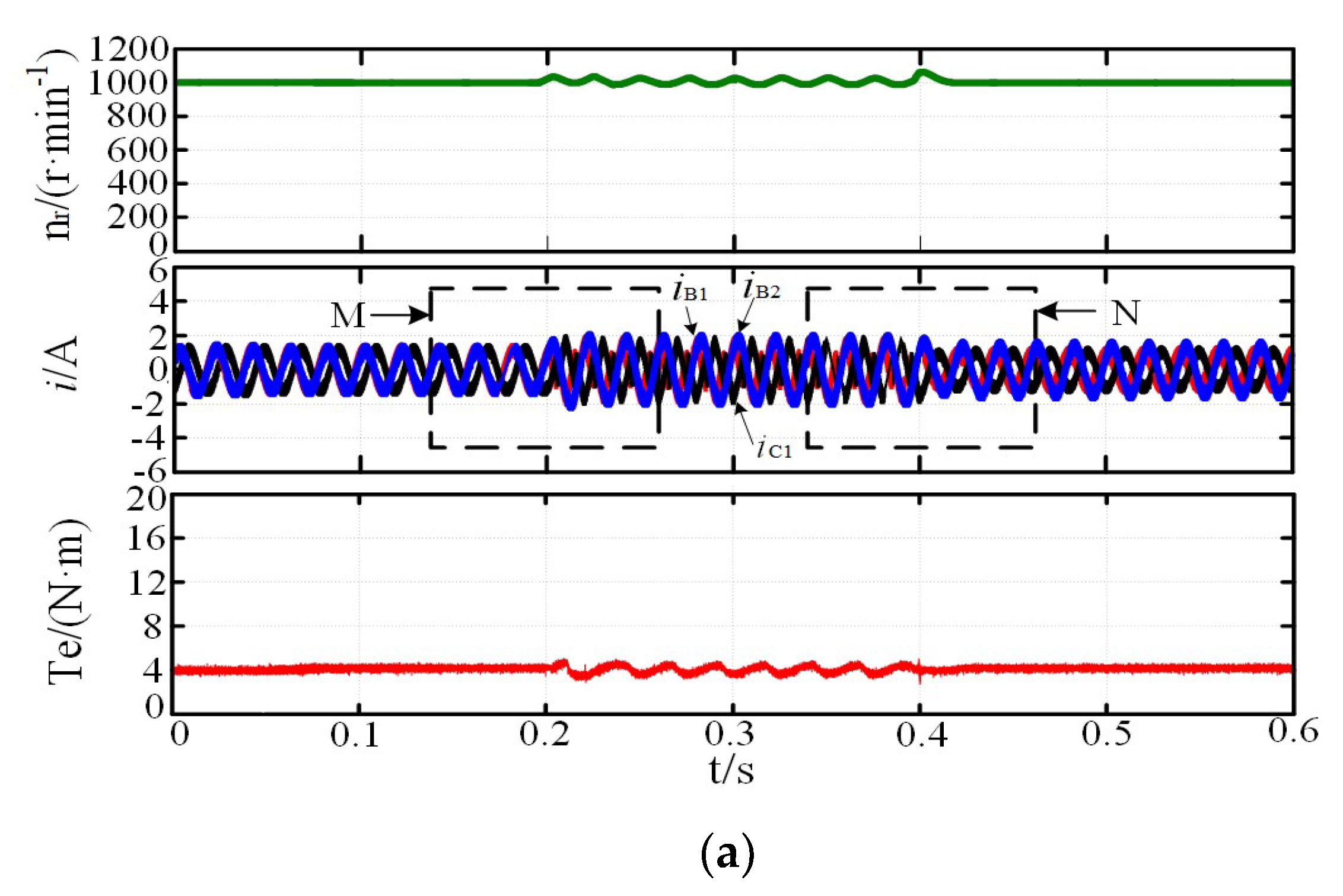
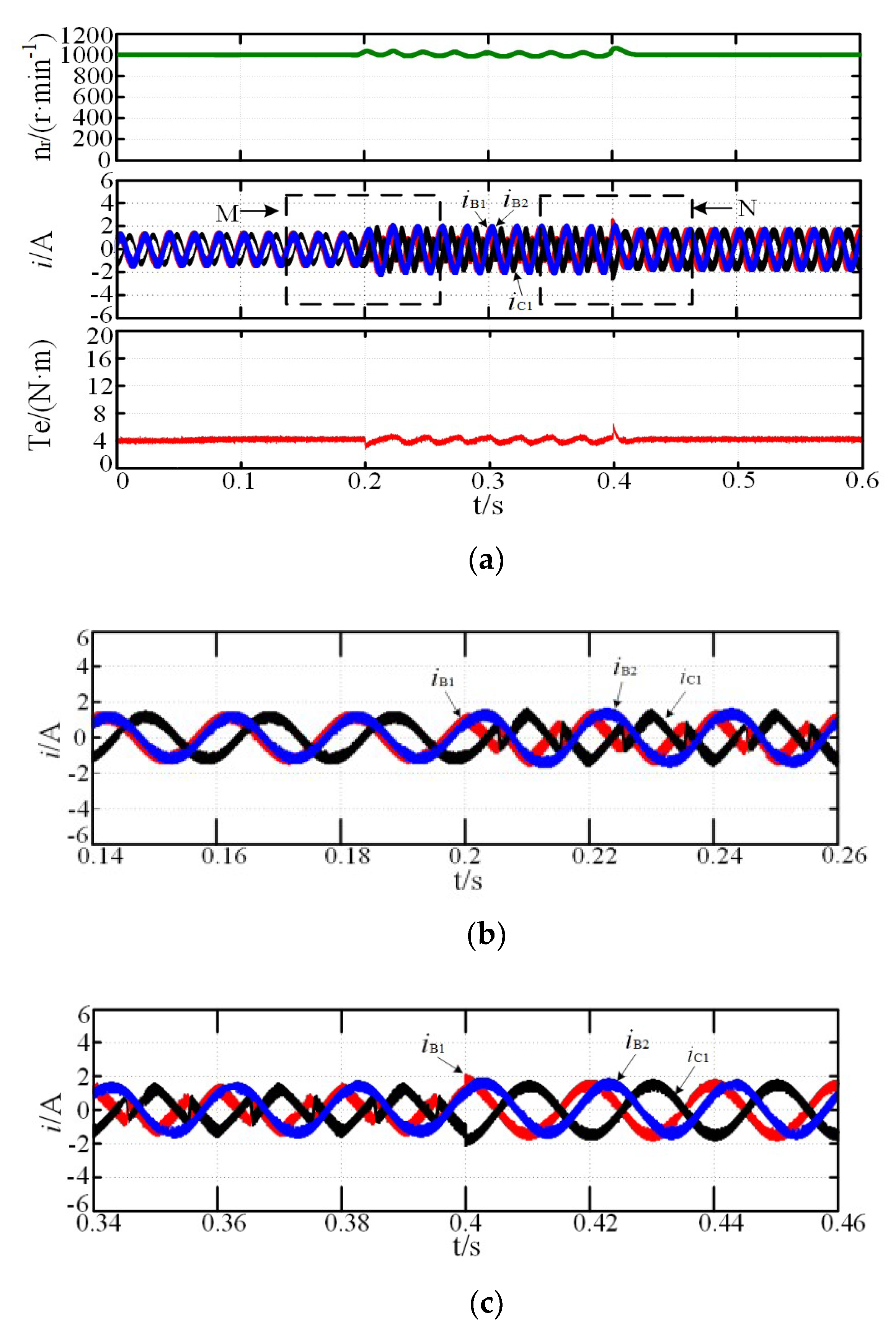
4.2. System Simulation of Fault-Tolerant Operation
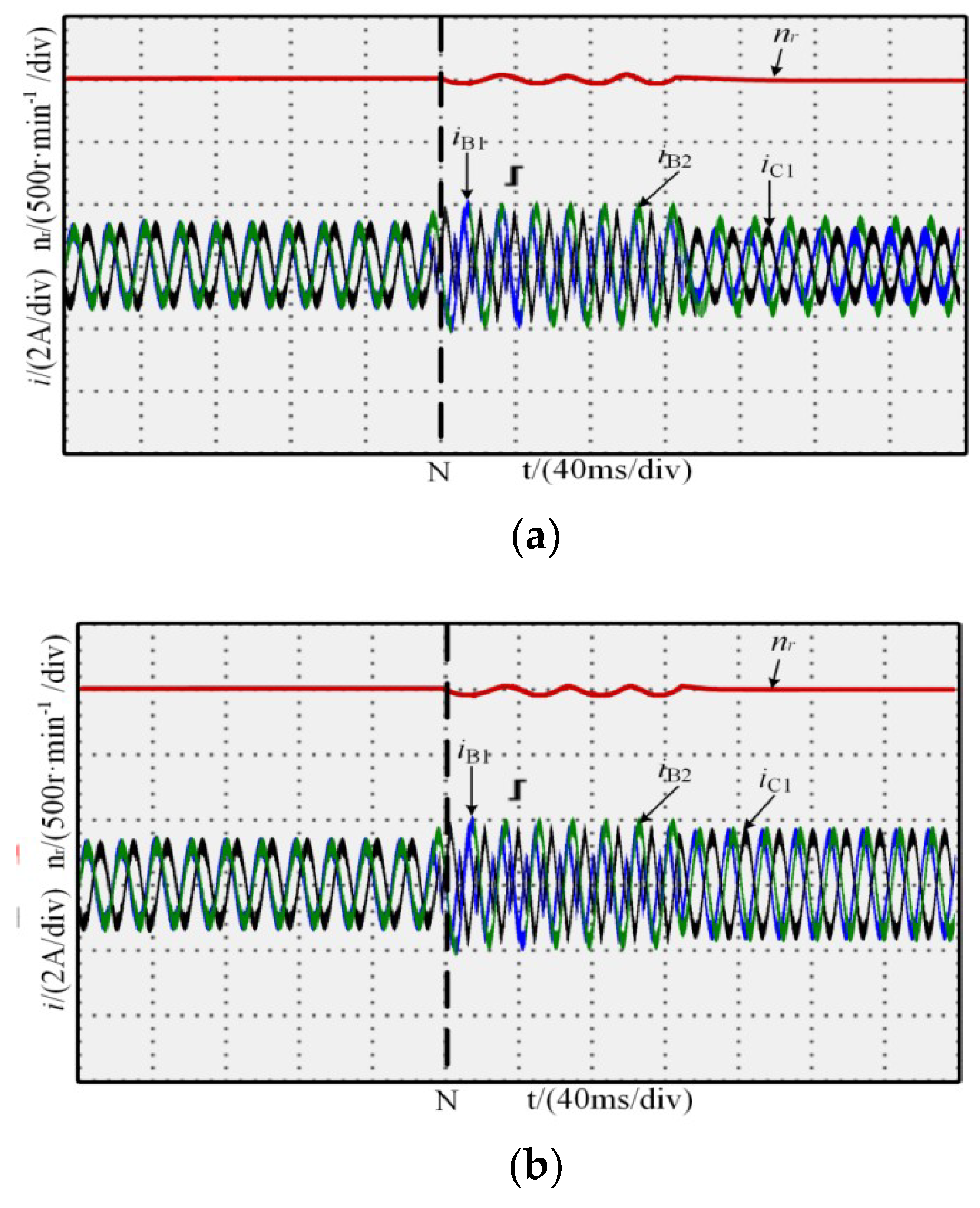
5. Experiment and Result Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guo, Q.; Yan, J.; Xu, W. Localized Fault Tolerant Algorithm Based on Node Movement Freedom Degree in Flying Ad Hoc Networks. Symmetry 2019, 11, 106. [Google Scholar] [CrossRef]
- Baek, H.; Lee, J. Task-Level Re-Execution Framework for Improving Fault Tolerance on Symmetry Multiprocessors. Symmetry 2019, 11, 651. [Google Scholar] [CrossRef]
- Wu, N.; Zuo, D.; Zhang, Z. Dynamic Fault-Tolerant Workflow Scheduling with Hybrid Spatial-Temporal Re-Execution in Clouds. Information 2019, 10, 169. [Google Scholar] [CrossRef]
- Peng, N.; Zhang, W.; Ling, H.; Zhang, Y.; Zheng, L. Fault-Tolerant Anomaly Detection Method in Wireless Sensor Networks. Information 2018, 9, 236. [Google Scholar] [CrossRef]
- Lin, B.; Zhang, P.; Ding, S.; Hang, J.; Hu, C.; Wang, Q. Investigation of the modulation method of a five-phase permanent magnet synchronous motor drive system. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 2435–2438. [Google Scholar]
- Kumar, P.A.; Kumar, K.V. Modelling, fault-analysis and vector-control implementation of a multi-phase induction motor. In Proceedings of the 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES), Paralakhemundi, India, 3–5 October 2016; pp. 870–876. [Google Scholar]
- Lin, X.; Huang, W.; Jiang, W.; Zhao, Y. Robust Direct Torque Control for Six-Phase Symmetrical Winding Permanent Magnet Synchronous Motor. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 6537–6541. [Google Scholar]
- Wang, P.; Zheng, P.; Wu, F.; Zhang, J.; Li, T. Research on dual-plane vector control of five-phase fault-tolerant permanent magnet machine. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar]
- Munim, W.N.W.A.; Che, H.S.; Hew, W.P. Fault tolerant capability of symmetrical multi-phase machines under one open-circuit fault. In Proceedings of the 4th IET Clean Energy and Technology Conference (CEAT 2016), Kuala Lumpur, Malaysia, 14–15 November 2016; pp. 1–6. [Google Scholar]
- Zhou, H.; Zhao, W.; Liu, G.; Cheng, R.; Xie, Y. Remedial Field-Oriented Control of Five-Phase Fault-Tolerant Permanent-Magnet Motor by Using Reduced-Order Transformation Matrices. IEEE Trans. Ind. Electron. 2017, 64, 169–178. [Google Scholar] [CrossRef]
- Chen, Y.; Song, J.; Zhang, J.; Huang, Q. Design and analysis of six-phase fault-tolerant PMSM for electric vehicle. In Proceedings of the 2016 Prognostics and System Health Management Conference (PHM-Chengdu), Chengdu, China, 19–21 October 2016; pp. 1–6. [Google Scholar]
- Wang, X.L.; Zhong, Q.C.; Deng, Z.Q.; Yue, S.Z. Fault-tolerant control of multi-phase permanent magnetic bearingless motors. In Proceedings of the XIX International Conference on Electrical Machines (ICEM 2010), Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar]
- Mohammadpour, A.; Parsa, L. A Unified Fault-Tolerant Current Control Approach for Five-Phase PM Motors with Trapezoidal Back EMF Under Different Stator Winding Connections. IEEE Trans. Power Electron. 2013, 28, 3517–3527. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Cheng, M. Fault-Tolerant Control of Dual Three-Phase Permanent-Magnet Synchronous Machine Drives Under Open-Phase Faults. IEEE Trans. Ind. Electron. 2017, 32, 2052–2063. [Google Scholar] [CrossRef]
- Hosseyni, A.; Trabelsi, R.; Iqbal, A. Fault Tolerant Vector Controlled Five-phase Permanent Magnet Synchronous Motor Drive with an Open Phase. In Proceedings of the 2018 15th International Multi-Conference on Systems, Signals & Device (SSD), Hammamet, Tunisia, 19–22 March 2018; pp. 780–784. [Google Scholar]
- Zhu, J.; Niu, X.B. Investigation of short-circuit fault-tolerant brushless permanent magnet AC motor drive with redundancy. In Proceedings of the 2010 5th IEEE Conference on Industrial Electronics and Applications, Taichung, Taiwan, 15–17 June 2010; pp. 1238–1242. [Google Scholar]
- Freire, N.M.A.; Cardoso, A.J.M. A Fault-Tolerant PMSG Drive for Wind Turbine Applications with Minimal Increase of the Hardware Requirements. IEEE Trans. Ind. Appl. 2014, 50, 2039–2049. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Z.; Wang, D.; Li, Y.; Li, M. A Review on Fault-Tolerant Control of PMSM. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 3854–3859. [Google Scholar]
- Wu, F.; Zheng, P.; Jahns, T.M. Six-Phase Fault-Tolerant Permanent Magnet Motors Drives with Reduced Switch Counts: Topology Comparisons and Hardware Demonstration. In Proceedings of the 2015 IEEE Transportation Electricfication Conference and Expo (ITEC), Dearborn, MI, USA, 14–17 June 2015; pp. 1–6. [Google Scholar]
- Changpan, Z.; Wei, T.; Xiangdong, S.; Zhaoji, Z.; Guijie, Y.; Jianyong, S. Control strategy for dual three-phase PMSM based on reduced order mathematical model under fault condition due to open phases. J. Eng. 2018, 2018, 489–494. [Google Scholar] [CrossRef]
- Huang, Q.-L.; Yong, C.; Li, X. Fault-Tolerant Control Strategy for Five-Phase PMSM with Third-Harmonic Current Injection. IEEE Access. 2018, 6, 58501–58509. [Google Scholar] [CrossRef]
- Tani, A.; Mengoni, M.; Zarri, L.; Serra, G.; Casadei, D. Control of multiphase induction motors with an odd number of phases under open circuit phase faults. IEEE Trans. Power Electron. 2012, 27, 565–577. [Google Scholar] [CrossRef]
- Ting, D.; Fenghui, L.; Li, S. Fault-tolerant method for six-phase PMSM by adjusting phase angle. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017; pp. 1–5. [Google Scholar]
- Moon, J.; Lee, W.; Park, S.; Kim, J. Fault tolerant control method of seven-phase BLDC motor in asymmetric fault condition due to open phase. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, South Korea, 1–5 June 2015; pp. 1591–1596. [Google Scholar]
- Yarlagadda, A.K.; Eate, V.K.; Babu, Y.S.K.; Chakraborti, A. A Modified Seven Level Cascaded H Bridge Inverter. In Proceedings of the 2018 5th IEEE Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON), Gorakhpur, India, 2–4 November 2018; pp. 1–6. [Google Scholar]
- Feng, G.; Lai, C.; Li, W.; Tjong, J.; Kar, N. Open-phase Fault Modeling and Optimized Fault Tolerant Control of Dual Three-phase Permanent Magnet Synchronous Machines. IEEE Trans. Power Electron. 2019, 34, 11116–11127. [Google Scholar] [CrossRef]
- Barrero, F.; Prieto, J.; Levi, E.; Gregor, R. An Enhanced Predictive Current Control Method for Asymmetrical Six-Phase Motor Drives. IEEE Trans. Ind. Electron. 2011, 58, 3242–3252. [Google Scholar] [CrossRef]
- Fei, M. Multi-phase synchronous motors: Minimum dissipation fault-tolerant controls. In Proceedings of the International Symposium on Power Electronics Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 20–22 June 2012; pp. 219–224. [Google Scholar]
- Barrero, F.; Arahal, M.R.; Gregor, R.; Toral, S.; Duran, M.J. One–step Modulation Predictive Current Control Method for the Asymmetrical Dual–three phase Induction Machine. IEEE Trans. Ind. Electron. 2009, 56, 974–1983. [Google Scholar] [CrossRef]
- Guzmán, H.; Durán, M.J.; Barrero, F.; Toral, S. Fault-tolerant current predictive control of five-phase induction motor drives with an open phase. In Proceedings of the 2011 37th Annual Conference of the IEEE Industrial Electronics Society (IECON), Melbourne, Australia, 7–11 November 2011; pp. 3680–3685. [Google Scholar]





| Phase Current | iA1, iB1, iC1 | iA2, iB2, iC2 | iA3, iB3, iC3 | iA4, iB4, iC4 | |
|---|---|---|---|---|---|
| Fault Phase | |||||
| iA1 | Amplitude | 0, 0.86, 0.86 | 1.31, 1.18, 1 | 1.26, 1.26, 1 | 1.18, 1.31, 1 |
| Initial angle | 0°, 90°, −90° | 169°, 37°, −70° | 157°, 23°, −90° | 143°, 11°, −110° | |
| iB1 | Amplitude | 0.86, 0, 0.86 | 1, 1.31, 1.18 | 1, 1.26, 1.26 | 1, 1.18, 1.31 |
| Initial angle | 60°, 0°, −120° | 79°, −41°, −173° | −60, −53°, 174° | 40°, −67°, 162° | |
| iC1 | Amplitude | 0.86, 0.86, 0 | 1.18, 1, 1.31 | 1.26, 1, 1.26 | 1.31, 1, 1.18 |
| Initial angle | 120°, −60°, 0° | 67°, −40°, −161° | 53°, −60°, −173° | 41°, −80°, 173° | |
| iA2 | Amplitude | 1.31, 1, 1.18 | 0, 0.86, 0.86 | 1.31, 1.18, 1 | 1.26, 1.26, 1 |
| Initial angle | 87°, −35°, −142° | 0°, −15°, 165° | 64°, −68°, −176° | 52°, −81°, 165° | |
| iB2 | Amplitude | 1.18, 1.31, 1 | 0.86, 0, 0.86 | 1, 1.31, 1.18 | 1, 1.26, 1.26 |
| Initial angle | 98°, −34°, −155° | 45°, 0°, −135° | 65°, −56°, 172° | 45°, −68°, 158° | |
| iC2 | Amplitude | 1, 1.18, 1.31 | 0.86, 0.86, 0 | 1.18, 1, 1.31 | 1.26, 1, 1.26 |
| Initial angle | 86°, −22°, −154° | 105°, −75°, 0° | 52°, −55°, −177° | 38°, −75°, 172° | |
| iA3 | Amplitude | 1.26, 1, 1.26 | 1.31, 1, 1.18 | 0, 0.86, 0.86 | 1.31, 1.18, 1 |
| Initial angle | −83°, 30°, 144° | 71°, −50°, −157° | 0°, −30°, 150° | 49°, −83°, 167° | |
| iB3 | Amplitude | 1.26, 1.26, 1 | 1.18, 1.31, 1 | 0.86, 0, 0.86 | 1, 1.31, 1.18 |
| Initial angle | 97°, −37°, −150° | 83°, −49°, −170° | 30°, 0°, −150° | 50°, −71°, 157° | |
| iC3 | Amplitude | 1, 1.26, 1.26 | 1, 1.18, 1.31 | 0.86, 0.86, 0 | 1.18, 1, 1.31 |
| Initial angle | 90°, −23°, −156° | 70°, −37°, −169° | 90°, −90°, 0° | 37°, −70°, 169° | |
| iA4 | Amplitude | 1.18, 1, 1.31 | 1.26, 1, 1.26 | 1.31, 1, 1.18 | 0, 0.86, 0.86 |
| Initial angle | 82°, −25°, −136° | 68°, −45°, −158° | 56°, −65°, −172° | 0°, −45°, 135° | |
| iB4 | Amplitude | 1.31, 1.18, 1 | 1.26, 1.26, 1 | 1.18, 1.31, 1 | 0.86, 0, 0.86 |
| Initial angle | 94°, −38°, −145° | 81°, −52°, −165° | 68°, −64°, 175° | 15°, 0°, −165° | |
| iC4 | Amplitude | 1, 1.31, 1.18 | 1, 1.26, 1.26 | 1, 1.18, 1.31 | 0.86, 0.86, 0 |
| Initial angle | 94°, −26°, −158° | 75°, −38°, −172° | 55°, −52°, 177° | 75°, −105°, 0° |
| Phase Current | iA1, iB1, iC1 | iA2, iB2, iC2 | iA3, iB3, iC3 | iA4, iB4, iC4 | |
|---|---|---|---|---|---|
| Fault Phase | |||||
| iA1 | Amplitude | 0, 1.24, 1.24 | 1.24, 1.24, 0.91 | 1.24, 1.24, 0.71 | 1.24, 1.24, 0.91 |
| Initial angle | 0°, −90°, 90° | −10°, −147°,102° | −17°, −164°, 90° | −33°, 170°, 78° | |
| iB1 | Amplitude | 1.24, 0, 1.24 | 0.91, 1.24, 1.24 | 0.71, 1.24, 1.24 | 0.91, 1.24, 1.24 |
| Initial angle | −30°, 0°, 150° | −18°, 230°,93° | −30°, 223°, 77° | −42°, 207°, 70° | |
| iC1 | Amplitude | 1.24, 1.24, 0 | 1.24, 0.91, 1.24 | 1.24, 0.71, 1.24 | 1.24, 0.91, 1.24 |
| Initial angle | 30°, −150°, 0° | −27°, −138°,110° | −43°, −150°,103° | −50°, −162°, 87° | |
| iA2 | Amplitude | 1.24, 0.91, 1.24 | 0, 1.24, 1.24 | 1.24, 1.24, 0.91 | 1.24, 1.24, 0.71 |
| Initial angle | −5°, −117°, 132° | 0°, −105°,75° | −25°, −162°, 87° | −32°, −178°, 75° | |
| iB2 | Amplitude | 1.24, 1.24, 0.91 | 1.24, 0, 1.24 | 0.91, 1.24, 1.24 | 0.71, 1.24, 1.24 |
| Initial angle | 12°, 235°, 123° | −45°, 0°, 135° | −33°, −147°, 77° | −45°, 208°, 62° | |
| iC2 | Amplitude | 0.91, 1.24, 1.24 | 1.24, 1.24, 0 | 1.24, 0.91, 1.24 | 1.24, 0.71, 1.24 |
| Initial angle | 3°, −108°, 115° | 15°, −165°,0° | −42°, −153°, 95° | −58°, −165°, 88° | |
| iA3 | Amplitude | 1.24, 0.71, 1.24 | 1.24, 0.91, 1.24 | 0, 1.24, 1.24 | 1.24, 1.24, 0.91 |
| Initial angle | −13°, −120°,133° | −20°, −132°,117° | 0°, −120°, 60° | −40°, −177°, 72° | |
| iB3 | Amplitude | 1.24, 1.24, 0.71 | 1.24, 1.24, 0.91 | 1.24, 0, 1.24 | 0.91, 1.24, 1.24 |
| Initial angle | 13°, 227°, 120° | −3°, −140°,108° | −60°, 0°, 120° | −48°, 200°, 63° | |
| iC3 | Amplitude | 0.71, 1.24, 1.24 | 0.91, 1.24, 1.24 | 1.24, 1.24, 0 | 1.24, 0.91, 1.24 |
| Initial angle | 0°, −106°, 106° | −12°, −122°, 100° | 0°, 180°, 0° | −57°, −168°, 80° | |
| iA4 | Amplitude | 1.24, 0.91, 1.24 | 1.24, 0.91, 1.24 | 1.24, 0.91, 1.24 | 0, 1.24, 1.24 |
| Initial angle | −12°, −124°,125° | −28°, −135°, 118° | −35°, −147° 102° | 0°, −135°, 45° | |
| iB4 | Amplitude | 1.24, 1.24, 0.91 | 1.24, 1.24, 0.71 | 1.24, 1.24, 0.91 | 1.24, 0, 1.24 |
| Initial angle | 94°, −38°, −145° | −2°, −148°, 105° | −18°, −155°, 87° | −75°, 0°, 105° | |
| iC4 | Amplitude | 0.91, 1.24, 1.24 | 0.71, 1.24, 1.24 | 0.91, 1.24, 1.24 | 1.24, 1.24, 0 |
| Initial angle | −3°, −115°, 108° | −15°, −122°, 92° | −27°, −138°, 85° | −15°, 165°, 0° |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Zhang, W.; Wang, Y.; Chen, Z. Fault-Tolerant Control Strategy for 12-Phase Permanent Magnet Synchronous Motor. Energies 2019, 12, 3462. https://doi.org/10.3390/en12183462
Gao H, Zhang W, Wang Y, Chen Z. Fault-Tolerant Control Strategy for 12-Phase Permanent Magnet Synchronous Motor. Energies. 2019; 12(18):3462. https://doi.org/10.3390/en12183462
Chicago/Turabian StyleGao, Hanying, Wen Zhang, Yu Wang, and Zhuo Chen. 2019. "Fault-Tolerant Control Strategy for 12-Phase Permanent Magnet Synchronous Motor" Energies 12, no. 18: 3462. https://doi.org/10.3390/en12183462




