A Converter Based on Independently Inductive Energy Injection and Free Resonance for Wireless Energy Transfer
Abstract
:1. Introduction
- (1)
- Energy injection process is not affected by the resonance network. Therefore, the power flow can be independently controlled by changing the period of the energy injection stage.
- (2)
- There is no energy backflow in the free resonance state, and the reactive power can be eliminated.
- (3)
- Two time margins of the state transition are applied in the proposed control strategy. Therefore, there are soft switching time periods in the switching operation and the switches need not to be switched at zero current crossing point.
2. Basic Structure and System Models
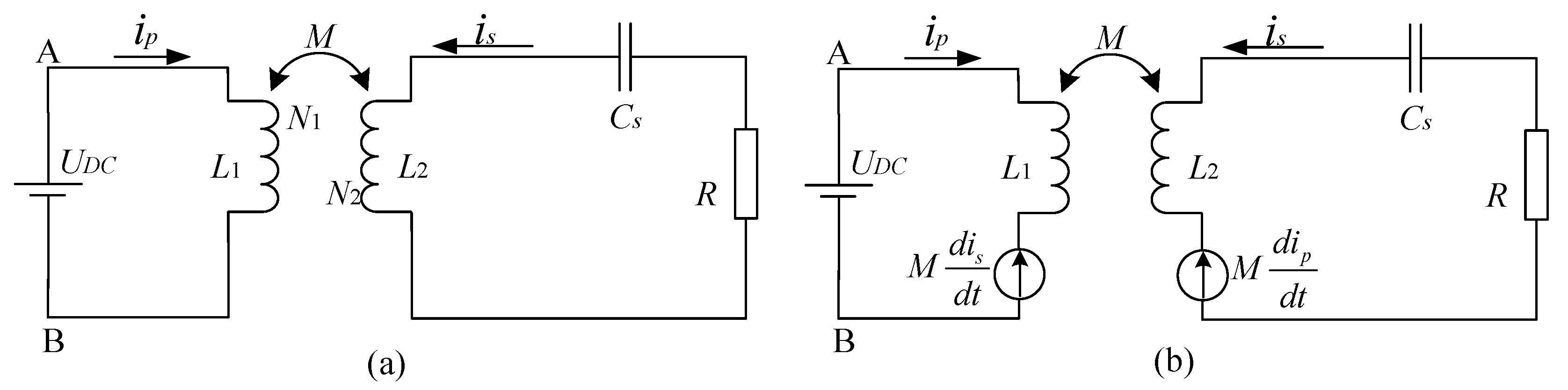
2.1. Structure of the IIEIFR IPT System
- (1)
- Energy injection stage. In this stage, B is connected to B2. UDC is connected to L1 and L1 is isolated from Cp. UDC independently injects energy into the primary coil. In this stage, part of the energy is transferred to the secondary coil, as shown in Figure 2a. In Figure 2, the activated circuit parts were indicated by solid lines and inactive circuit parts were indicated by dashed lines.
- (2)
- Free resonance stage. In this stage, B is connected to B1. UDC is isolated from L1, and Cp is connected to L1 to form a resonant tank and the system begins to resonate, as shown in Figure 2b. The energy continues to be transferred to the secondary coil.
- (3)
- Shutdown stage. B is switched to the center point, not connected to either B1 or B2, where UDC, Cp, and L1 are isolated from each other, as shown in Figure 2c. In this stage, the system stops transferring energy to the secondary part and the remaining energy is stored in the capacitor Cp as electrical energy.
2.2. System Modeling
2.2.1. Energy Injection Stage
2.2.2. Free Resonance Stage
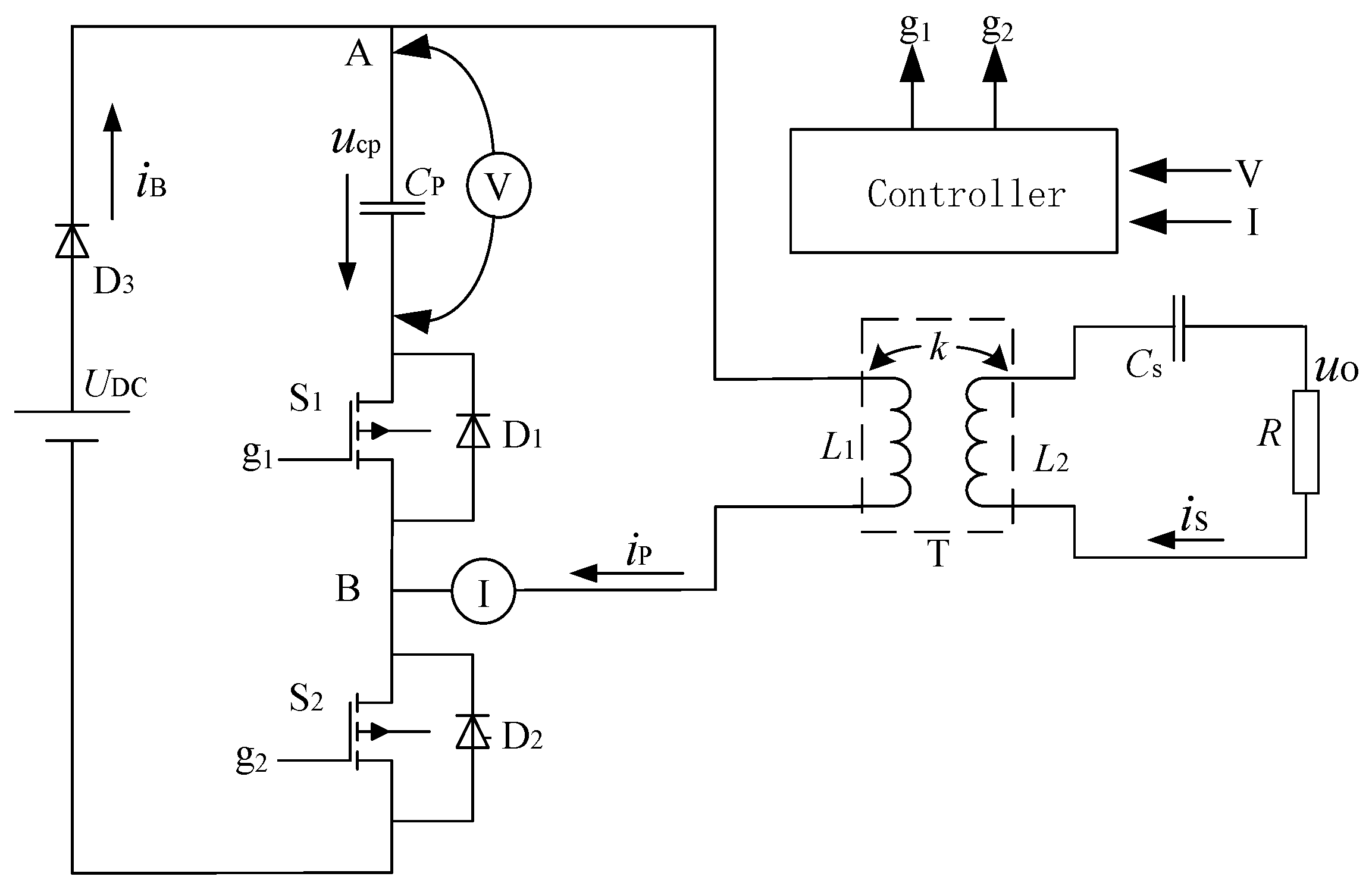
3. IIEIFR Power Converter
3.1. Topology of the IIEIFR IPT System
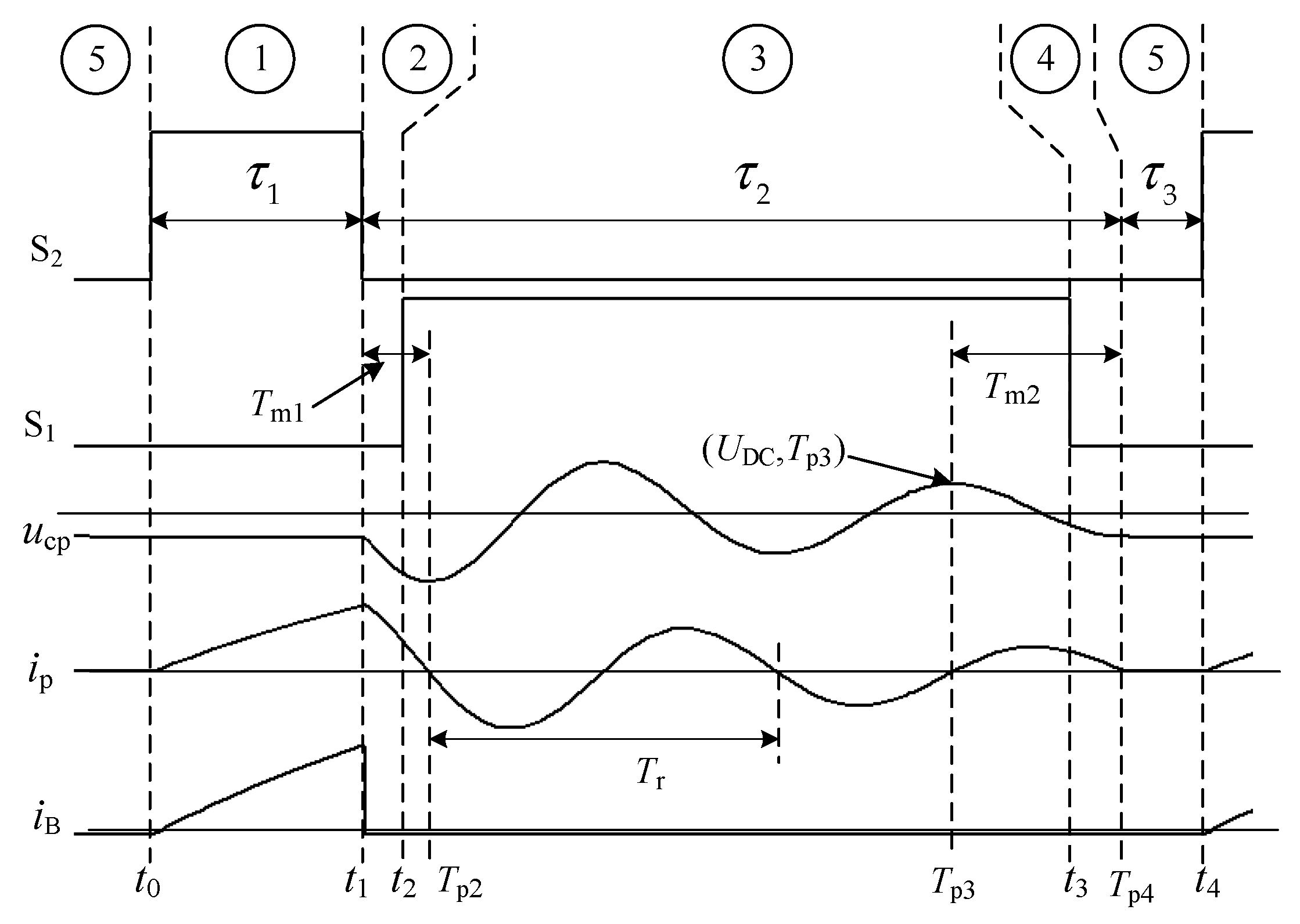
3.2. State Analysis
3.3. Parameter Settings
3.3.1. Time Parameters
3.3.2. Output Power
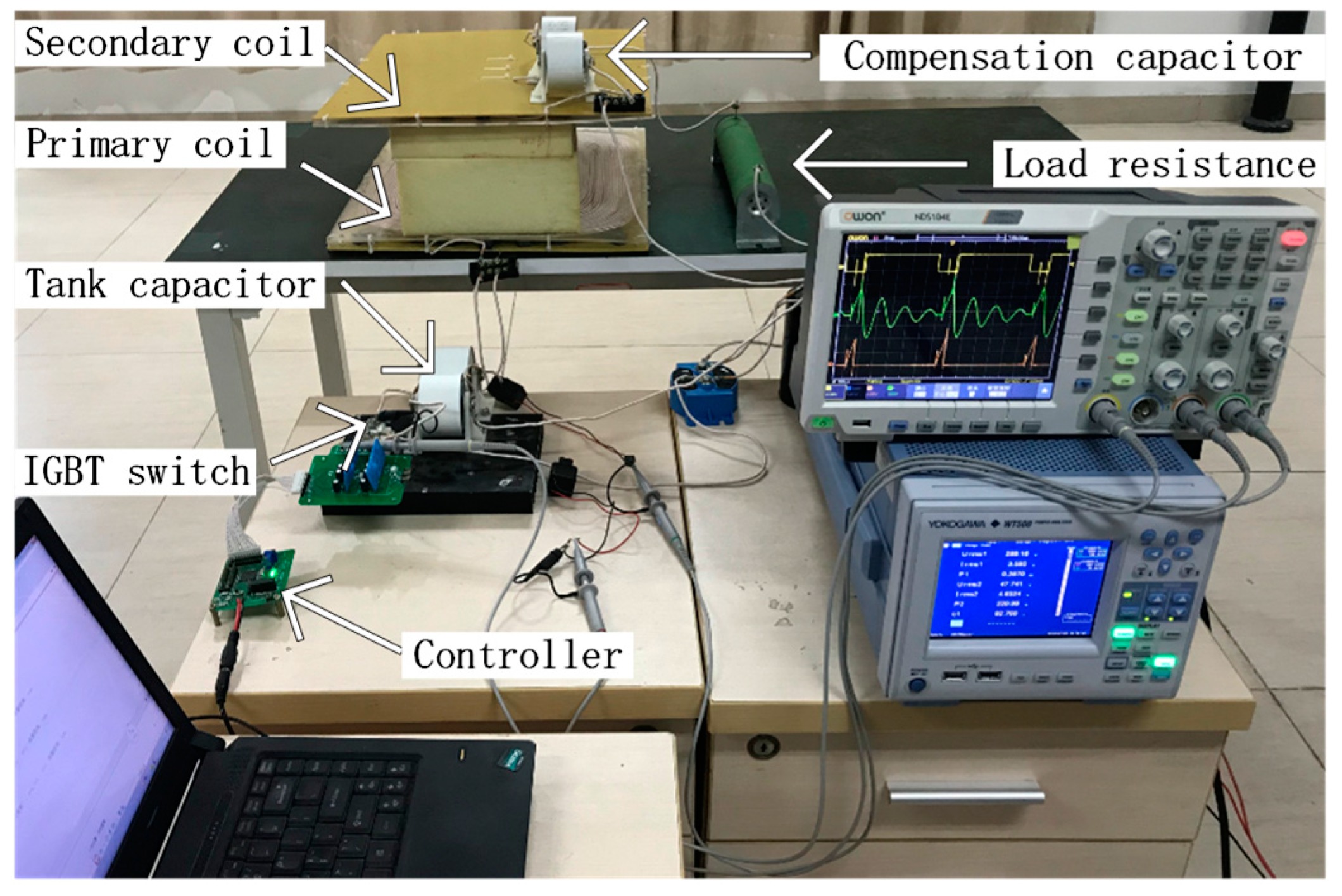
4. Experimental Prototype
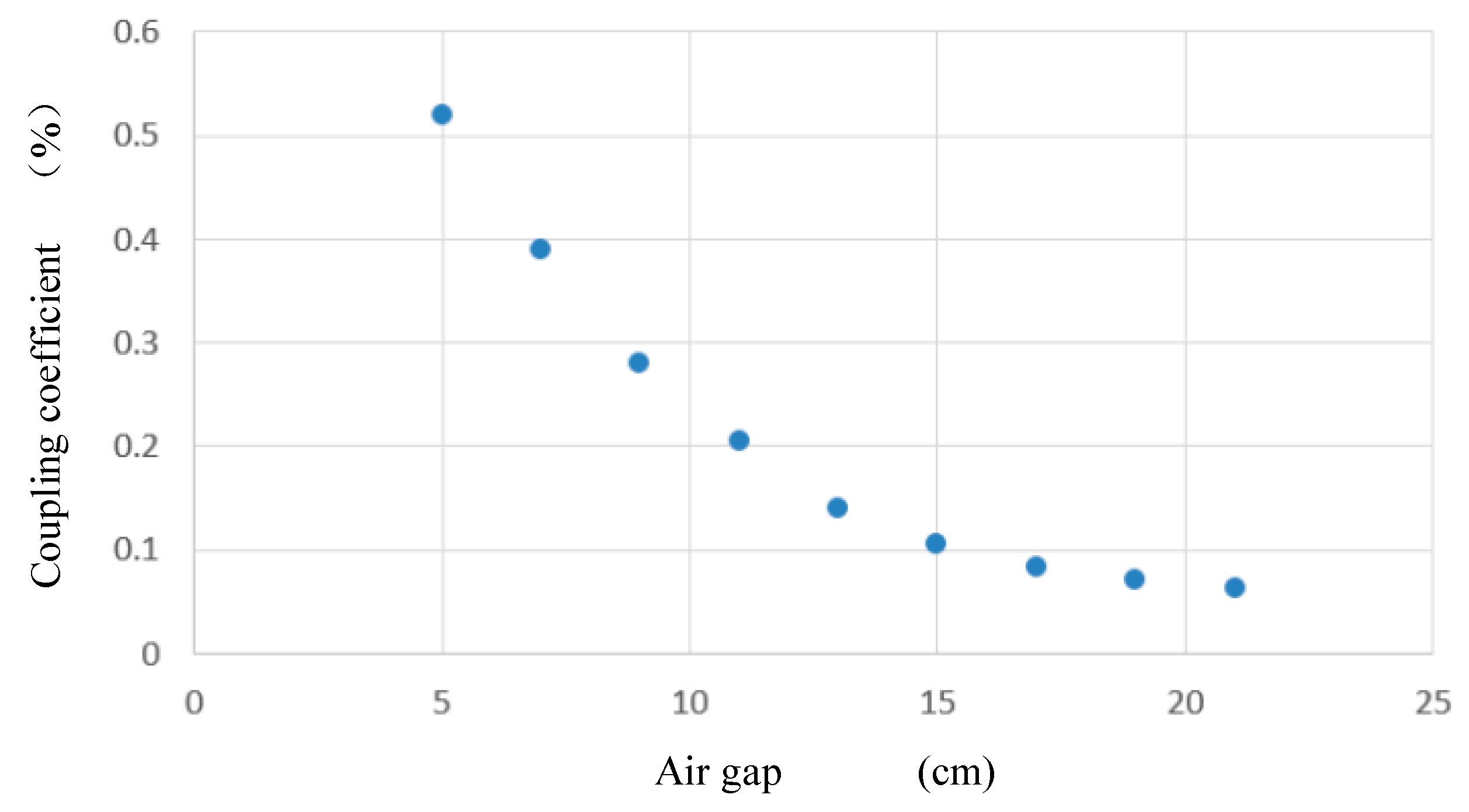
4.1. Magneto-Electric System
4.2. Power Converter
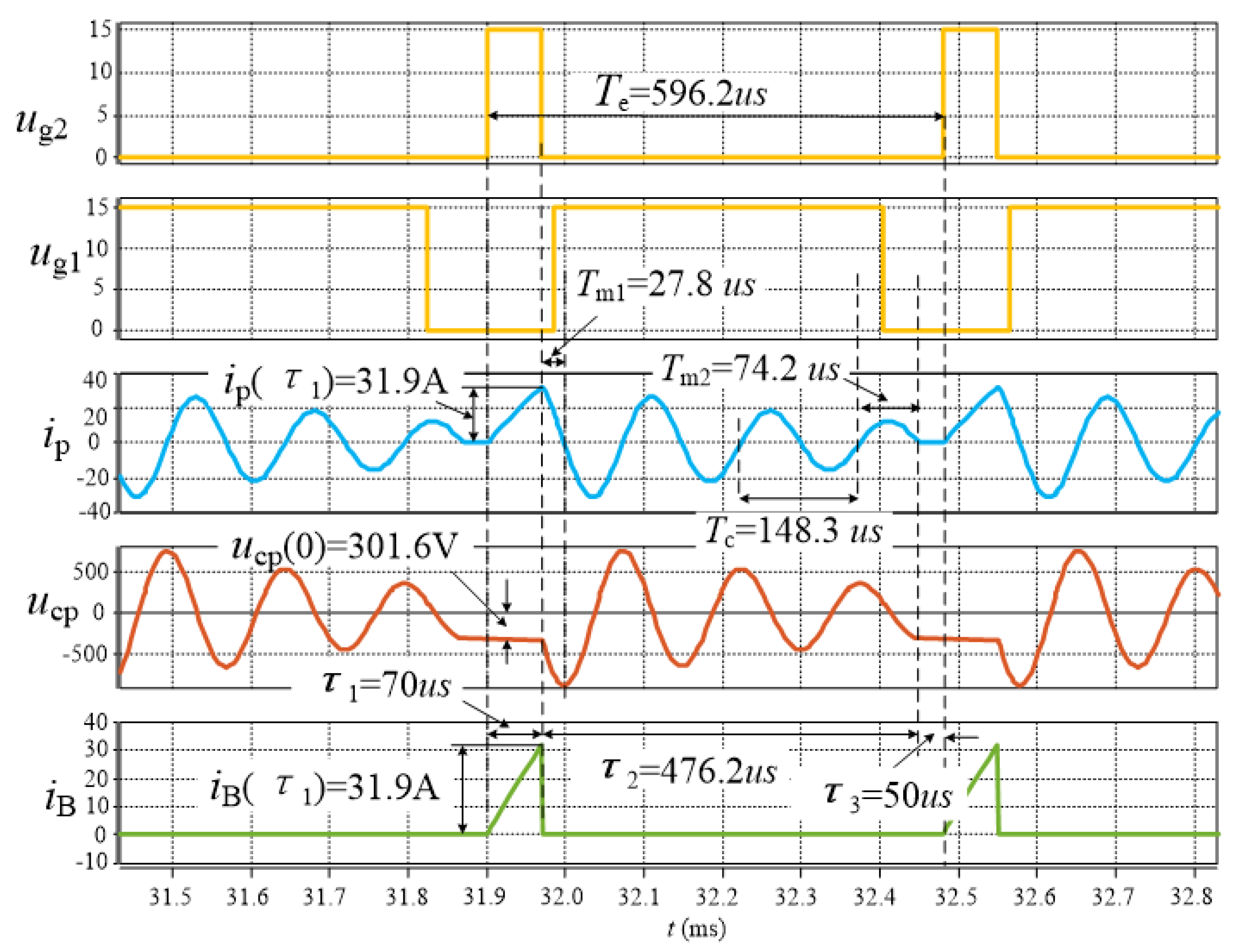
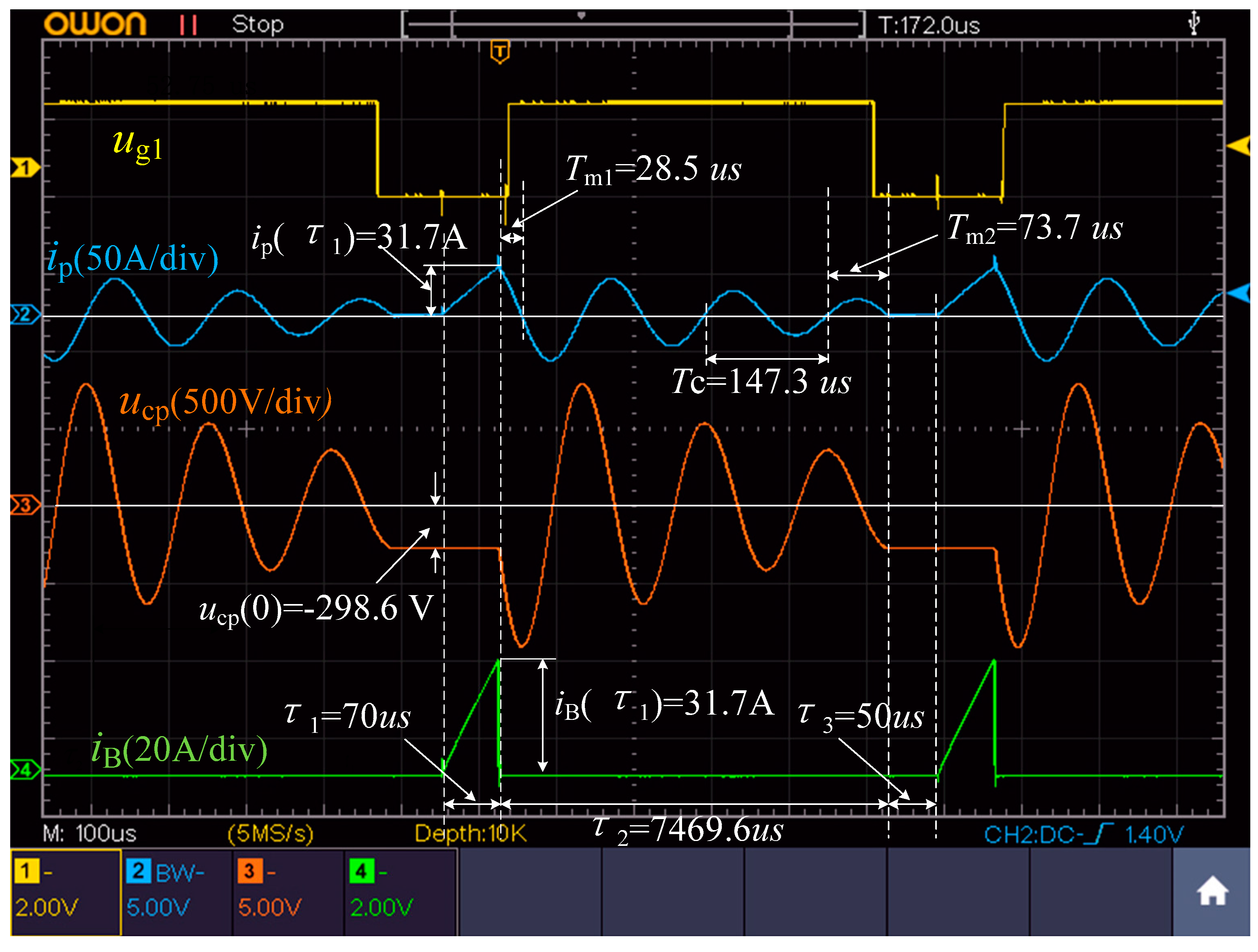
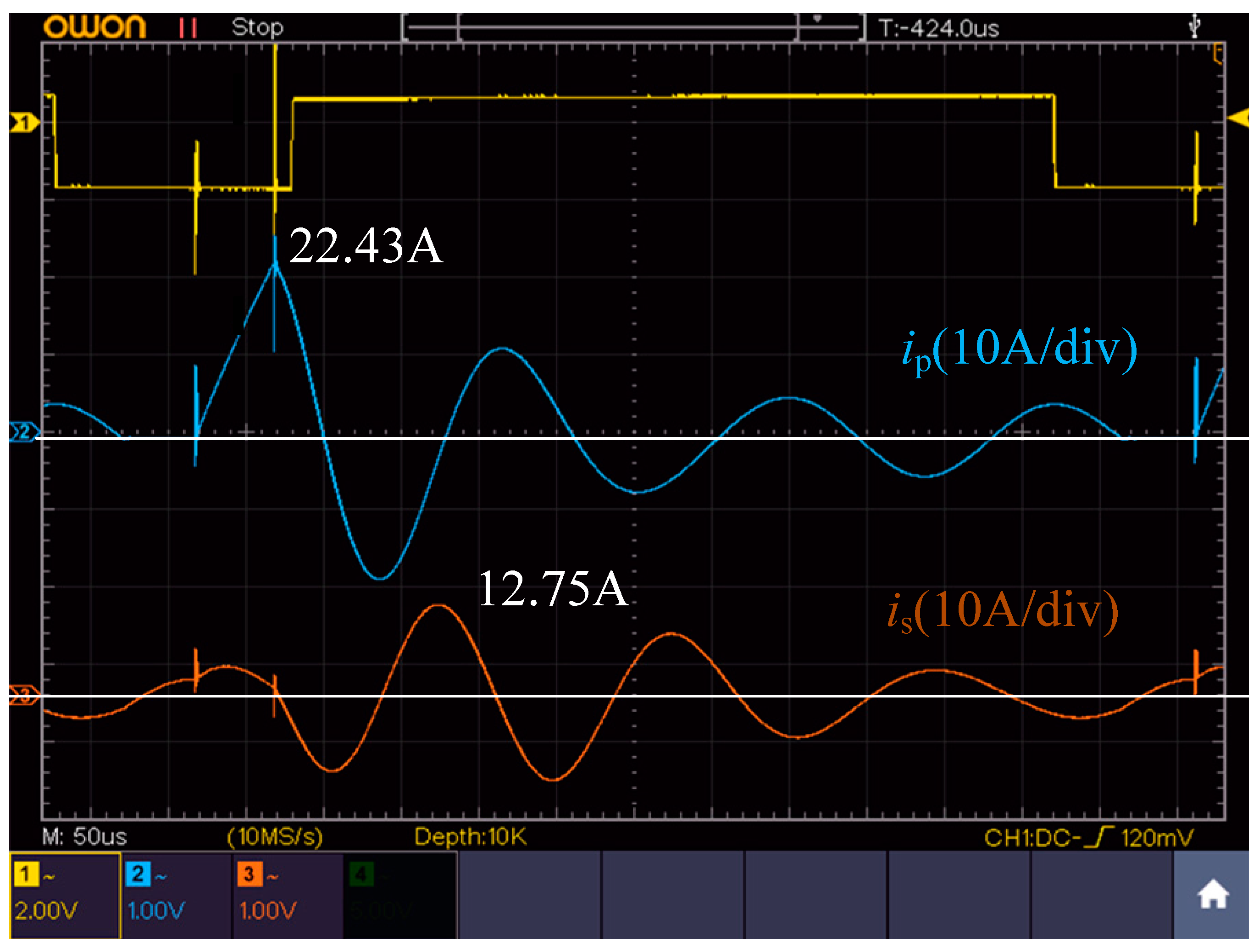
5. Simulation and Experimental Verification
5.1. Features of the IIEIFR ICP System
5.2. Power Control
5.3. Soft Switching
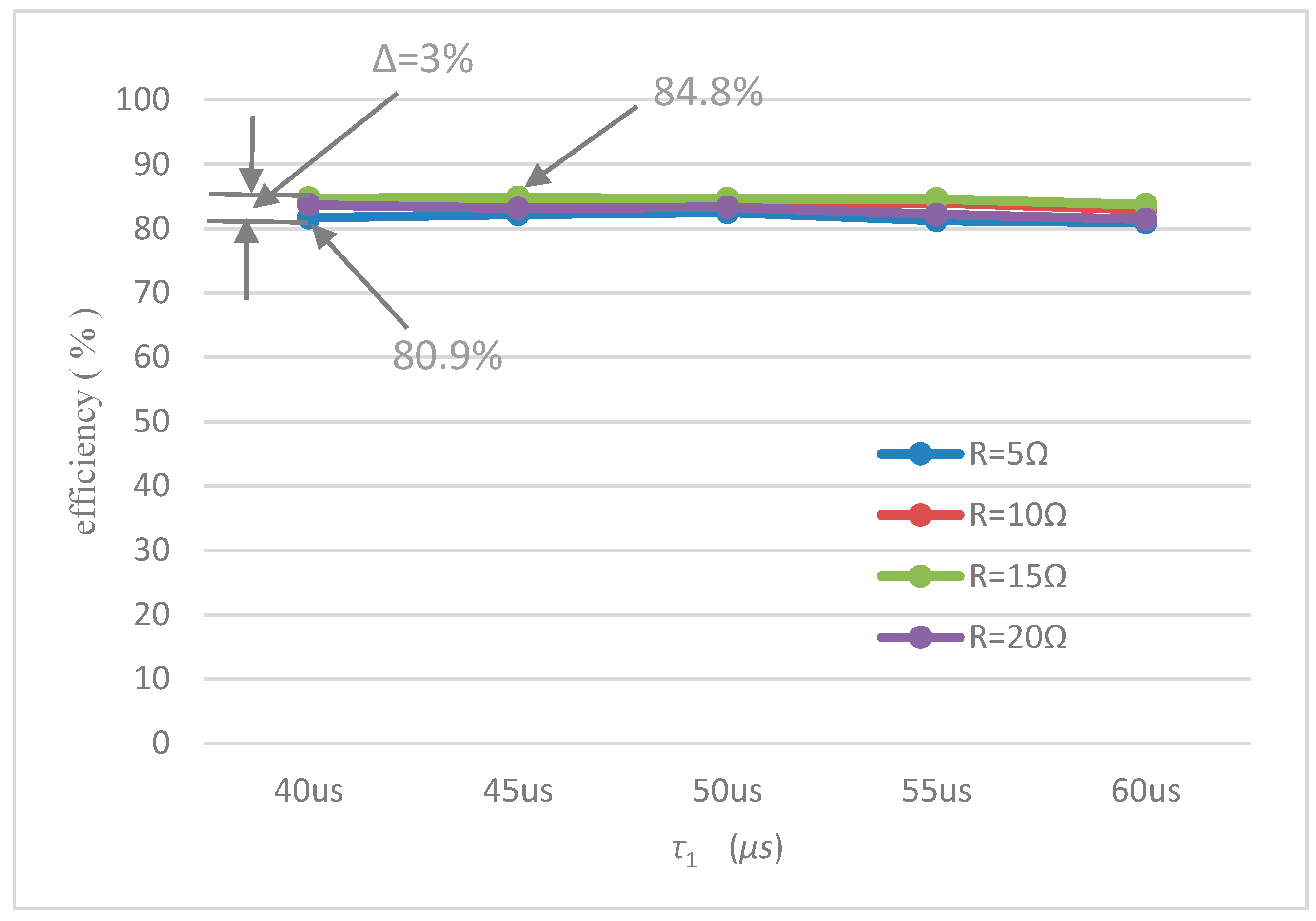
5.4. Power and Efficiency
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, C.G.; Seo, D.H.; You, J.S.; Park, J.H.; Cho, B.H. Design of a Contactless Battery Charger for Cellular Phone. IEEE Trans. Ind. Electron. 2001, 48, 1238–1247. [Google Scholar] [CrossRef]
- Lu, Y.; Ma, D.B. Wireless Power Transfer System Architectures for Portable or Implantable Applications. Energies 2016, 9, 1087. [Google Scholar] [CrossRef]
- Wu, H.H.; Gilchrist, A.; Sealy, K.D.; Bronson, D. A High Efficiency 5 kW Inductive Charger for EVs Using Dual Side Control. IEEE Trans. Ind. Inform. 2012, 8, 585–595. [Google Scholar] [CrossRef] [Green Version]
- García, X.T.; Vázquez, J.; Roncero-Sánchez, P. Design, Implementation Issues and Performance of an Inductive Power Transfer System for Electric Vehicle Chargers with Series–series Compensation. IET Power Electron. 2015, 8, 1920–1930. [Google Scholar] [CrossRef]
- Jiang, C.; Chau, K.T.; Liu, C.; Lee, C.H.T. An Overview of Resonant Circuits for Wireless Power Transfer. Energies 2017, 10, 894. [Google Scholar] [CrossRef]
- Ibrahim, M.; Pichon, L.; Bernard, L.; Razek, A.; Houivet, J.; Cayol, O. Advanced Modeling of a 2-kw Series-series Resonating Inductive Charger for Real Electric Vehicle. IEEE Trans. Veh. Technol. 2015, 64, 421–430. [Google Scholar] [CrossRef]
- Hwang, K.; Cho, J.; Kim, D.; Park, J.; Kwon, J.H.; Kwak, S.I.; Park, H.H.; Ahn, S. An Autonomous Coil Alignment System for the Dynamic Wireless Charging of Electric Vehicles to Minimize Lateral Misalignment. Energies 2017, 10, 315. [Google Scholar] [CrossRef]
- Villa, J.L.; Sallan, J.; Sanz Osorio, J.F.; Llombart, A. High-misalignment tolerant compensation topology for icpt systems. IEEE Trans. Ind. Electron. 2012, 59, 945–951. [Google Scholar] [CrossRef]
- Kan, T.; Nguyen, T.D.; White, J.C.; Malhan, R.K.; Mi, C.C. A new integration method for an electric vehicle wireless charging system using lcc compensation topology: Analysis and design. IEEE Trans. Power Electron. 2017, 32, 1638–1650. [Google Scholar] [CrossRef]
- Sohn, Y.H.; Choi, B.H.; Lee, E.S.; Lim, G.C.; Cho, G.H.; Rim, C.T. General unified analyses of two-capacitor inductive power transfer systems: Equivalence of current-source SS and SP compensations. IEEE Trans. Power Electron. 2015, 30, 6030–6045. [Google Scholar] [CrossRef]
- Moradewicz, A.J.; Kazmierkowski, M.P. Contactless energy transfer system with FPGA-controlled resonant converter. IEEE Trans. Ind. Electron. 2010, 57, 3181–3190. [Google Scholar] [CrossRef]
- Jesús, S.; Villa, J.L.; Andrés, L.; José, F.S. Optimal design of ICPT systems applied to electric vehicle battery charge. IEEE Trans. Ind. Electron. 2009, 56, 2140–2149. [Google Scholar] [CrossRef]
- Keeling, N.A.; Covic, G.A.; Boys, J.T. A unity power factor IPT pick-up for high power applications. IEEE Trans. Ind. Electron. 2010, 57, 744–751. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, I.O.; Moon, G.W. Analysis and design of a hybrid-type converter for optimal conversion efficiency in electric vehicle chargers. IEEE Trans. Ind. Electron. 2017, 64, 2789–2800. [Google Scholar] [CrossRef]
- Choi, S.Y.; Gu, B.W.; Jeong, S.Y.; Rim, C.T. Advances in wireless power transfer systems for roadway-powered electric vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 3, 18–36. [Google Scholar] [CrossRef]
- Zheng, C.; Ma, H.; Lai, J.S.; Zhang, L. Design Considerations to Reduce Gap Variation and Misalignment Effects for the Inductive Power Transfer System. IEEE Trans. Power Electron. 2015, 30, 6108–6119. [Google Scholar] [CrossRef]
- Cirimele, V.; Diana, M.; Freschi, F.; Mitolo, M. Inductive power transfer for automotive applications: State-of-the-art and future trends. IEEE Trans. Ind. Appl. 2018, 54, 4069–4079. [Google Scholar] [CrossRef]
- Mi, C.C.; Buja, G.; Choi, S.Y.; Rim, C.T. Modern advances in wireless power transfer systems for roadway powered electric vehicles. IEEE Trans. Ind. Electron. 2016, 63, 6533–6545. [Google Scholar] [CrossRef]
- Matysik, J.T. The Current and Voltage Phase Shift Regulation in Resonant Converters with Integration Control. IEEE Trans. Ind. Electron. 2007, 54, 1240–1242. [Google Scholar] [CrossRef]
- Gati, E.; Kampitsis, G.; Manias, S. Variable Frequency Controller for Inductive Power Transfer in Dynamic Conditions. IEEE Trans. Power Electron. 2017, 32, 1684–1696. [Google Scholar] [CrossRef]
- Matysik, J.T. A New Method of Integration Control with Instantaneous Current Monitoring for Class D Series-Resonant Converter. IEEE Trans. Ind. Electron. 2006, 53, 1564–1576. [Google Scholar] [CrossRef]
- Moghaddami, M.; Sundararajan, A.; Sarwat, A.I. A Power-Frequency Controller with Resonance Frequency Tracking Capability for Inductive Power Transfer Systems. IEEE Trans. Ind. Appl. 2018, 54, 1773–1783. [Google Scholar] [CrossRef]
- Miller, J.M.; Onar, O.C.; Chinthavali, M. Primary-side power flow control of wireless power transfer for electric vehicle charging. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 147–162. [Google Scholar] [CrossRef]
- Madawala, U.K.; Neath, M.; Thrimawithana, D.J. A power–frequency controller for bidirectional inductive power transfer systems. IEEE Trans. Ind. Electron. 2013, 60, 310–317. [Google Scholar] [CrossRef]
- Berger, A.; Agostinelli, M.; Vesti, S.; Oliver, J.A.; Cobos, J.A.; Huemer, M. A wireless charging system applying phase-shift and amplitude control to maximize efficiency and extractable power. IEEE Trans. Power Electron. 2015, 30, 6338–6348. [Google Scholar] [CrossRef]
- Dede, E.J. Improving the Efficiency of IGBT Series-resonant Inverters using Pulse Density Modulation. IEEE Trans. Ind. Electron. 2011, 58, 979–987. [Google Scholar] [CrossRef]
- Fujita, H.; Akagi, H. Pulse-density-modulated Power Control of a 4 kw, 450 kHz Voltage-source Inverter for Induction Melting Applications. IEEE Trans. Ind. Appl. 1996, 32, 279–286. [Google Scholar] [CrossRef]
- Li, H.L.; Hu, A.P.; Covic, G.A. Development of a Discrete Energy Injection Inverter for Contactless Power Transfer. In Proceedings of the 2008 3rd IEEE Conference on Industrial Electronics and Applications, Singapore, 3–5 June 2008; pp. 1757–1761. [Google Scholar] [CrossRef]
- Li, H.L.; Hu, A.P.; Covic, G.A. A Direct AC–AC Converter for Inductive Power-Transfer Systems. IEEE Trans. Power Electron. 2012, 27, 661–668. [Google Scholar] [CrossRef]
- Chen, L.; Hong, J.; Guan, M.; Wu, W.; Chen, W. A Power Converter Decoupled from the Resonant Network for Wireless Inductive Coupling Power Transfer. Energies 2019, 12, 1192. [Google Scholar] [CrossRef]
- Wang, C.S.; Covic, G.A.; Stielau, O.H. Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems. IEEE Trans. Ind. Electron. 2004, 51, 148–157. [Google Scholar] [CrossRef]
- Kamineni, A.; Covic, G.A.; Boys, J.T. Self-Tuning Power Supply for Inductive Charging. IEEE Trans. Power Electron. 2017, 32, 3467–3479. [Google Scholar] [CrossRef]
- Esteve, V.; Jordan, J.; Sanchis-Kilders, E.; Dede, E.; Maset, E.; Ejea, J. Enhanced pulse-density-modulated power control for high frequency induction heating inverters. IEEE Trans. Ind. Electron. 2015, 62, 6905–6914. [Google Scholar] [CrossRef]
- Lin, F.Y.; Covic, G.A.; Boys, J.T. Evaluation of Magnetic Pad Sizes and Topologies for Electric Vehicle Charging. IEEE Trans. Power Electron. 2015, 30, 6391–6407. [Google Scholar] [CrossRef]








| D1 | D2 | D3 | D4 | D5 | D6 |
| 460 mm | 370 mm | 440 mm | 350 mm | 160 mm | 80 mm |
| H1 | H2 | H3 | H4 | W1 | W2 |
| 5 mm | 10 mm | 5 mm | 3 mm | 20 mm | 150 mm |
| Parameter/Part | Value |
|---|---|
| UDC | 300 V |
| Cp | 0.88 μF |
| L1, L2 | 640 μH |
| R | 10–50 Ω |
| S1, S2 | GD100HFU120C1S |
| ucp (0) (V) | ip (τ1) (A) | Tc (μs) | Tm1 (μs) | Tm2 (μs) | τ2 (μs) |
|---|---|---|---|---|---|
| 300 | 32.8 | 146 | 29 | 73 | 467.1 |
| Air Gap (cm) | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 |
|---|---|---|---|---|---|---|---|---|
| Pin (W) | 350 | 350 | 350 | 350 | 350 | 350 | 350 | 350 |
| Pop (W) | 342.7 | 343.7 | 341.8 | 343.3 | 346.1 | 342.8 | 339.9 | 338.94 |
| Pos (W) | 309.6 | 303.1 | 302.8 | 301.2 | 294.6 | 291.9 | 287.2 | 281.1 |
| ηp (%) | 97.94 | 98.09 | 97.76 | 98.13 | 98.79 | 98.03 | 97.04 | 96.84 |
| ηs (%) | 88.46 | 86.64 | 86.43 | 85.99 | 84.03 | 83.4 | 82.06 | 80.31 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Hong, J.; Guan, M.; Lin, Z.; Chen, W. A Converter Based on Independently Inductive Energy Injection and Free Resonance for Wireless Energy Transfer. Energies 2019, 12, 3467. https://doi.org/10.3390/en12183467
Chen L, Hong J, Guan M, Lin Z, Chen W. A Converter Based on Independently Inductive Energy Injection and Free Resonance for Wireless Energy Transfer. Energies. 2019; 12(18):3467. https://doi.org/10.3390/en12183467
Chicago/Turabian StyleChen, Lin, Jianfeng Hong, Mingjie Guan, Zaifa Lin, and Wenxiang Chen. 2019. "A Converter Based on Independently Inductive Energy Injection and Free Resonance for Wireless Energy Transfer" Energies 12, no. 18: 3467. https://doi.org/10.3390/en12183467




