Online Current Loop Tuning for Permanent Magnet Synchronous Servo Motor Drives with Deadbeat Current Control
Abstract
:1. Introduction
2. Discrete-Time Motor Model
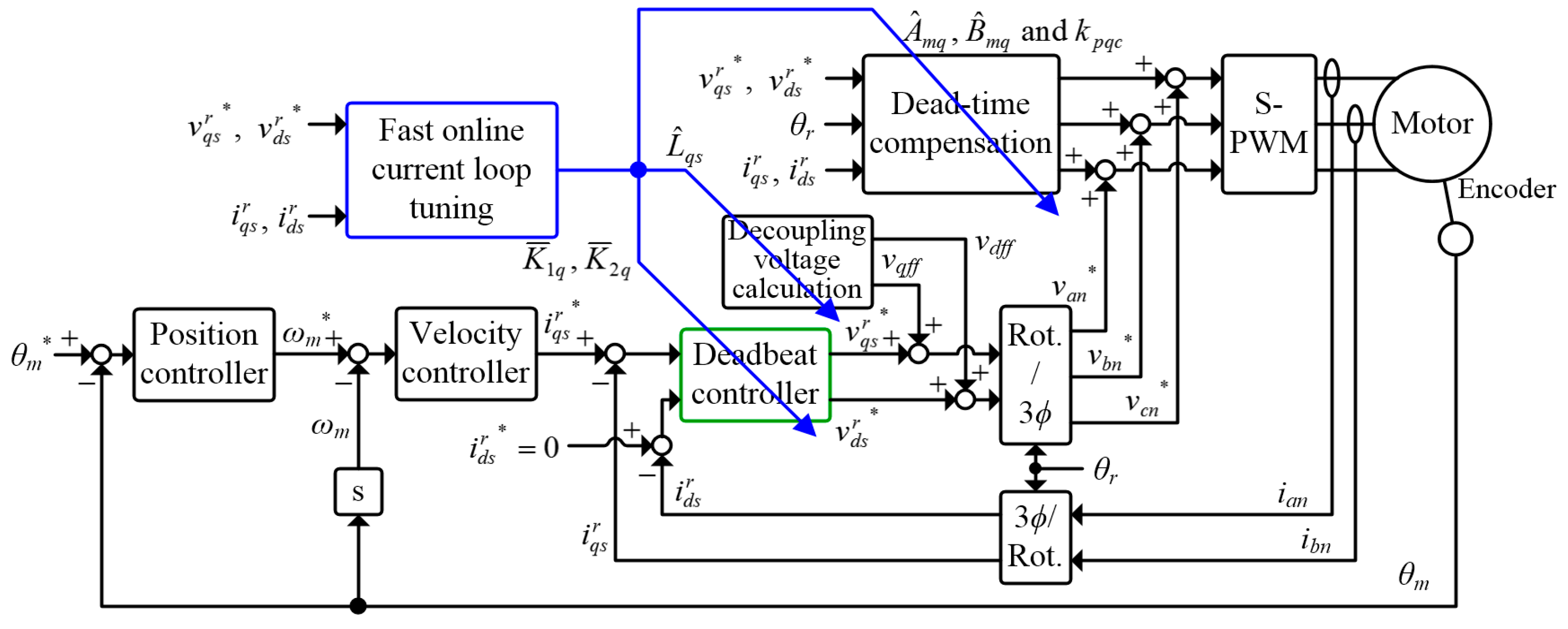
3. Overall Control System
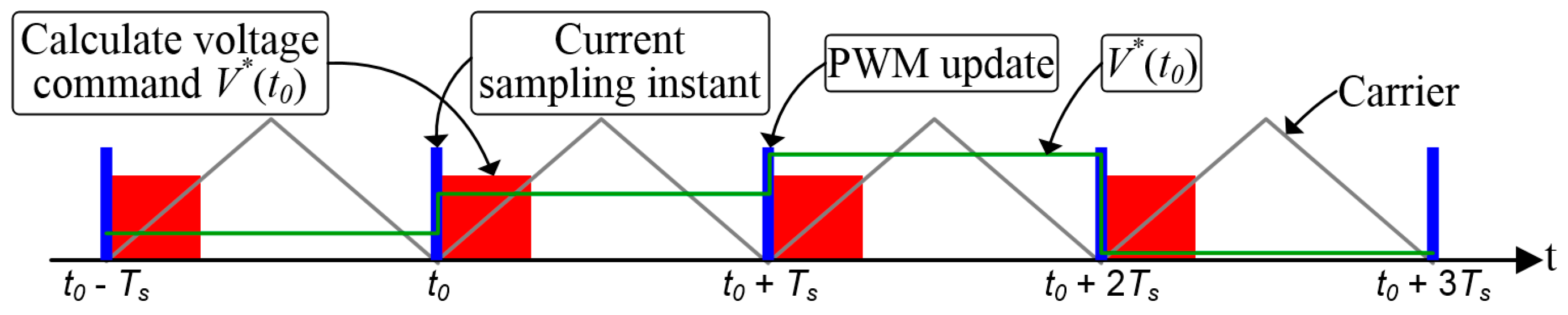
3.1. Servo Control System
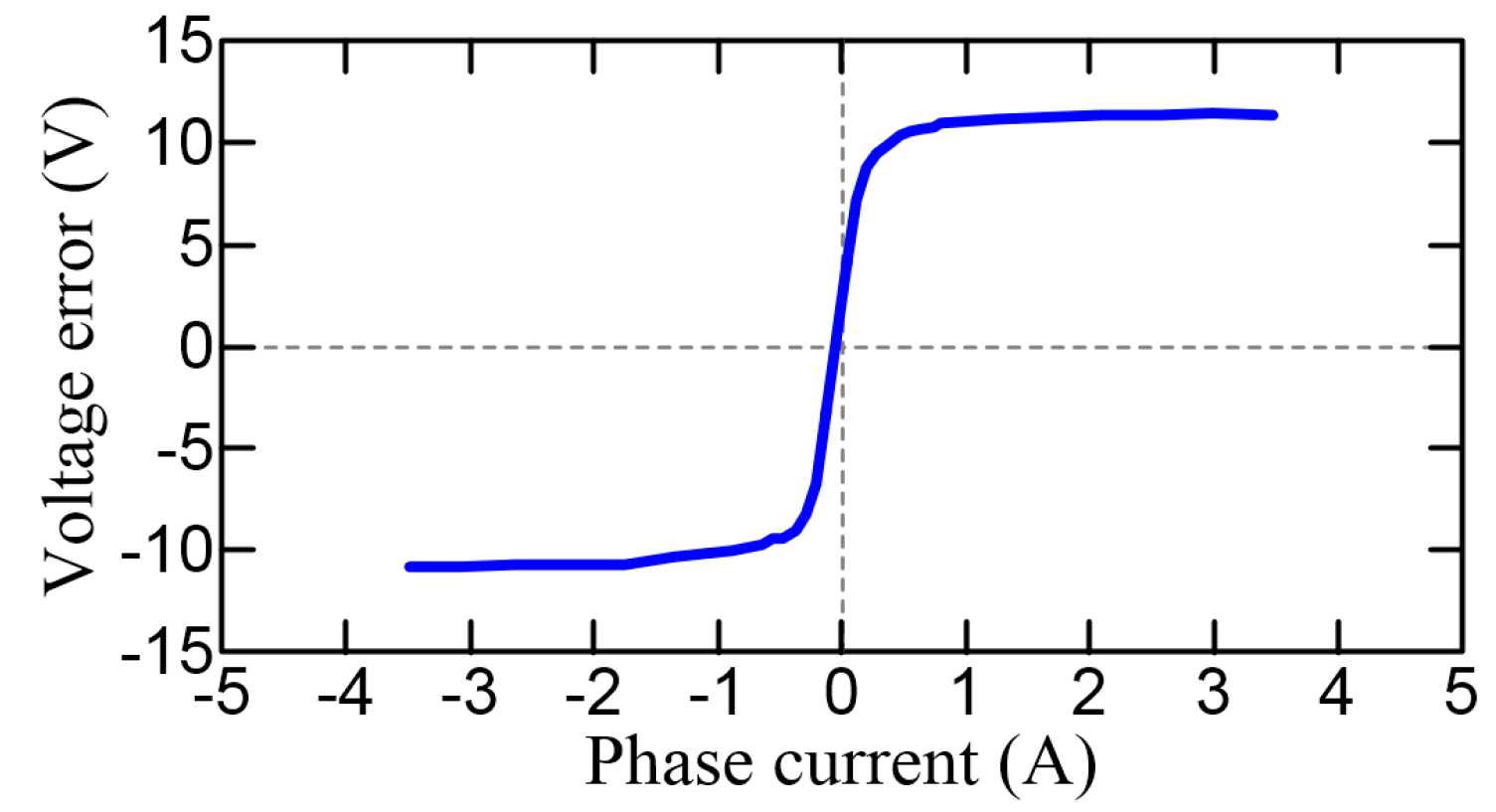
3.2. Dead-Time Compensation
4. Deadbeat Current Controller
Deadbeat Controller Design
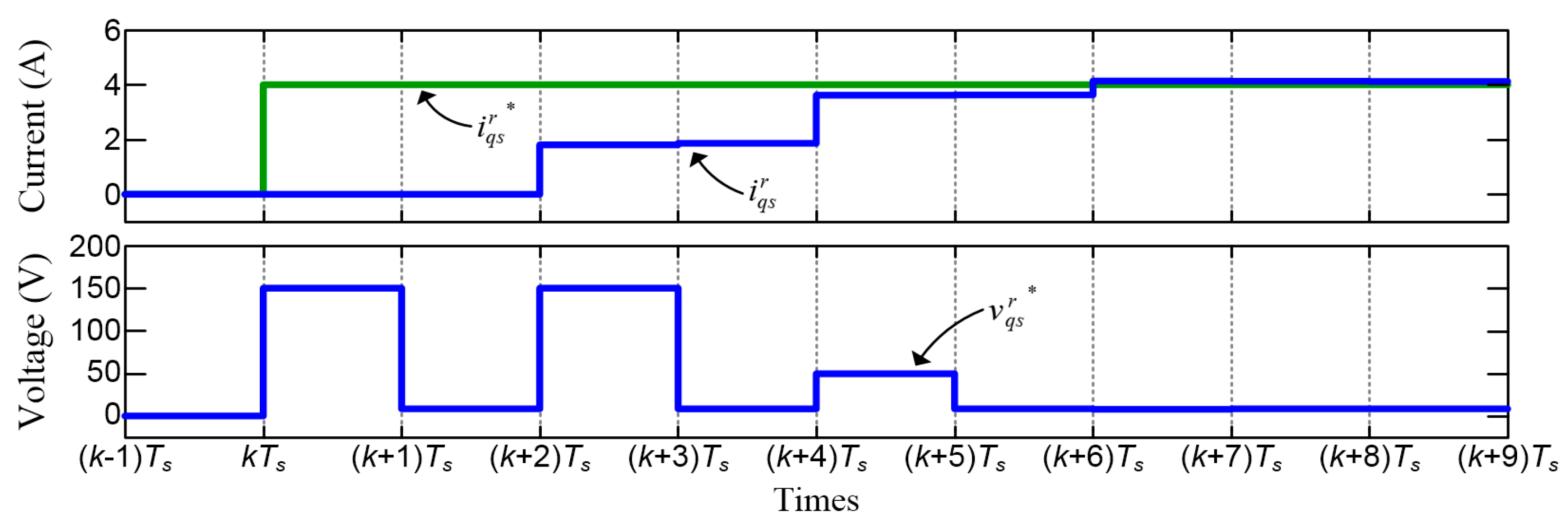
5. Simulation Results
5.1. Results with Correct Motor Parameters
5.2. Results with Parameter Mismatch
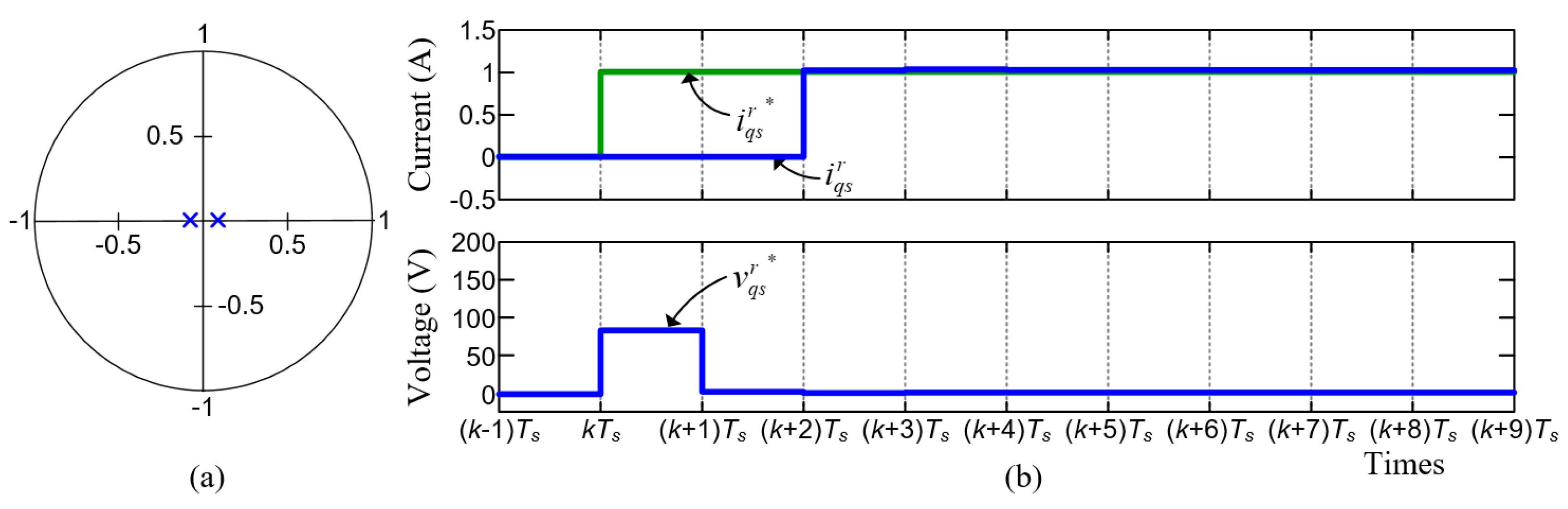
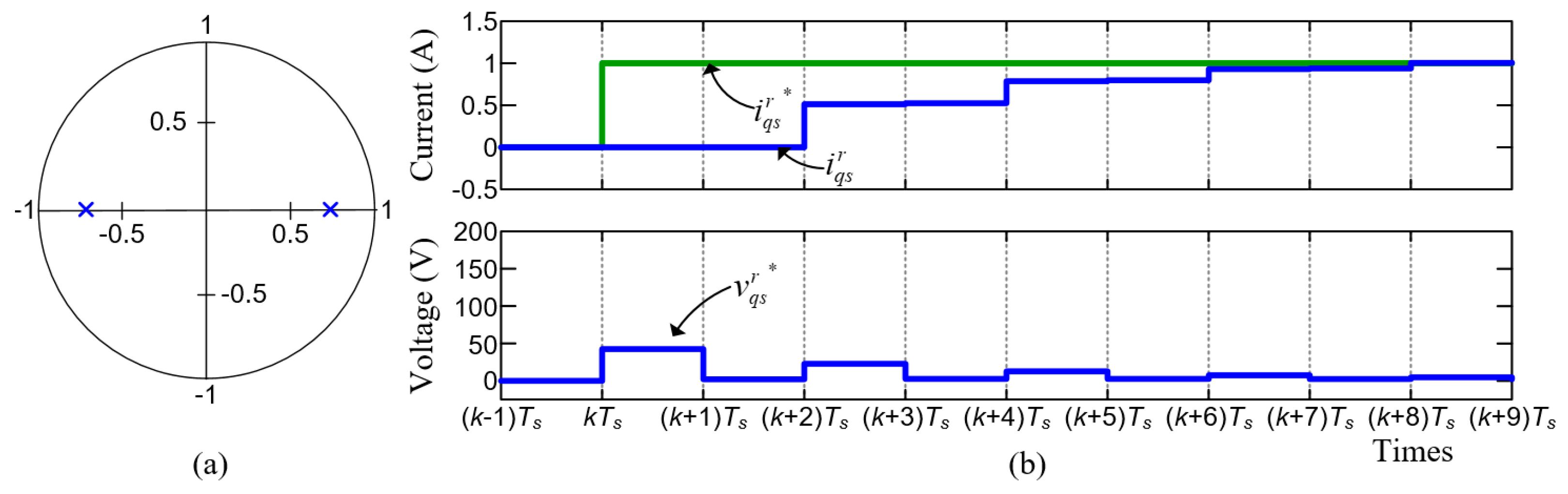
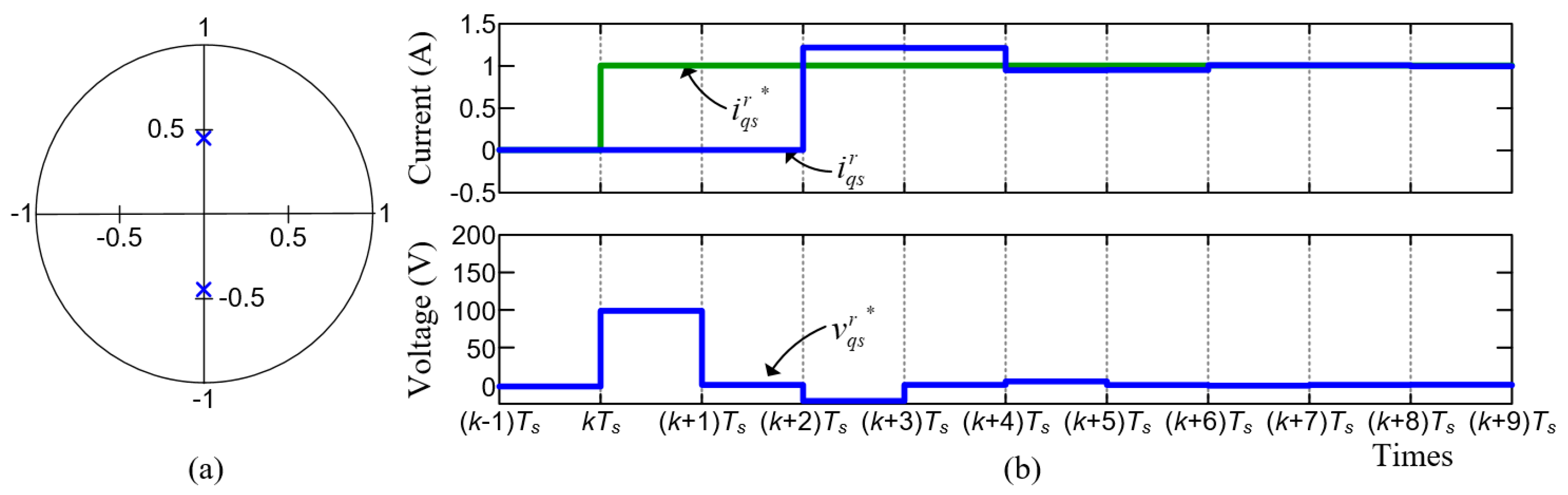
6. Online Current Loop Tuning
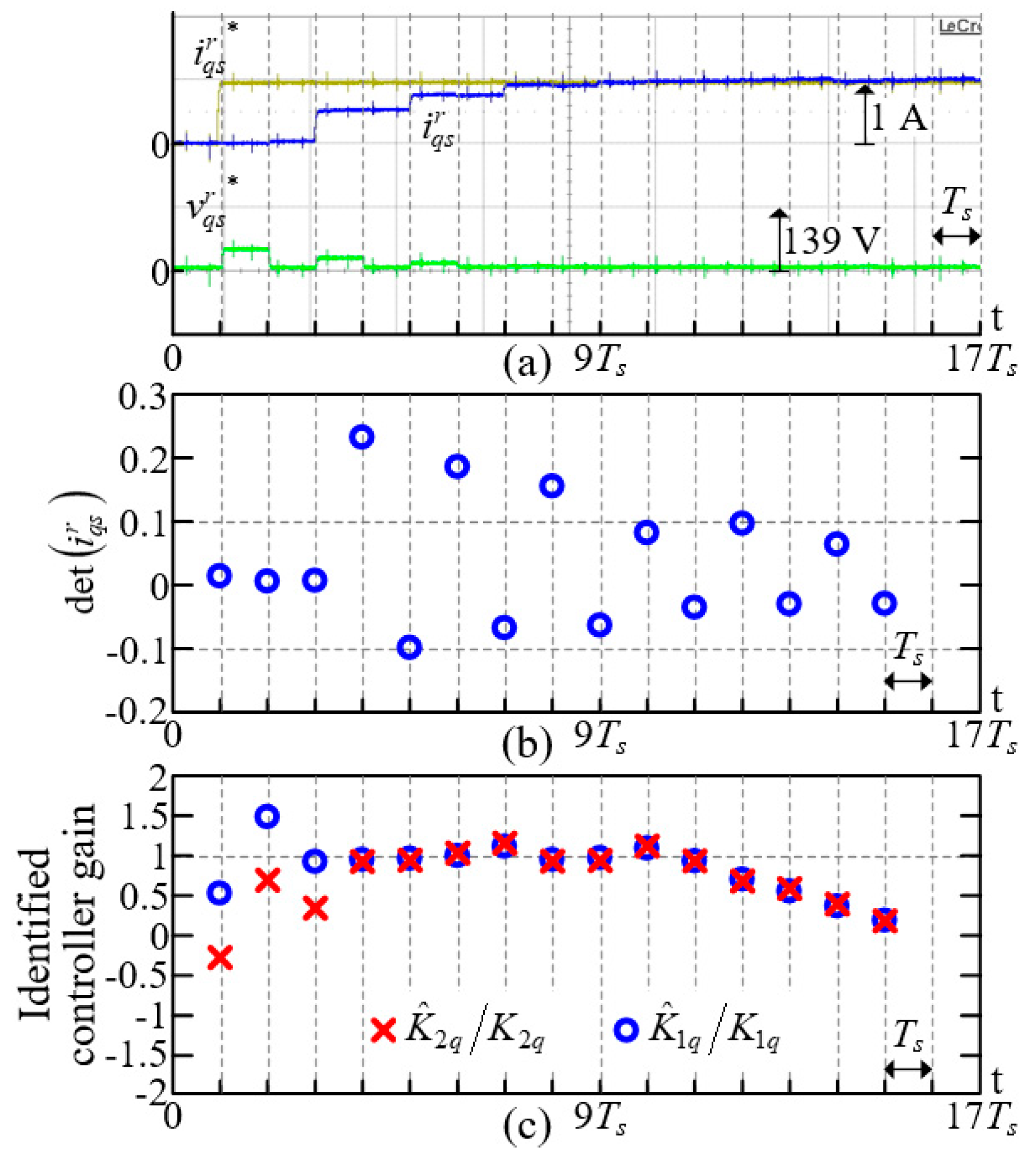
6.1. Controller Gain Identification
6.2. Estimation Accuracy Improvement
6.3. Identification When Voltage Command Is Limited
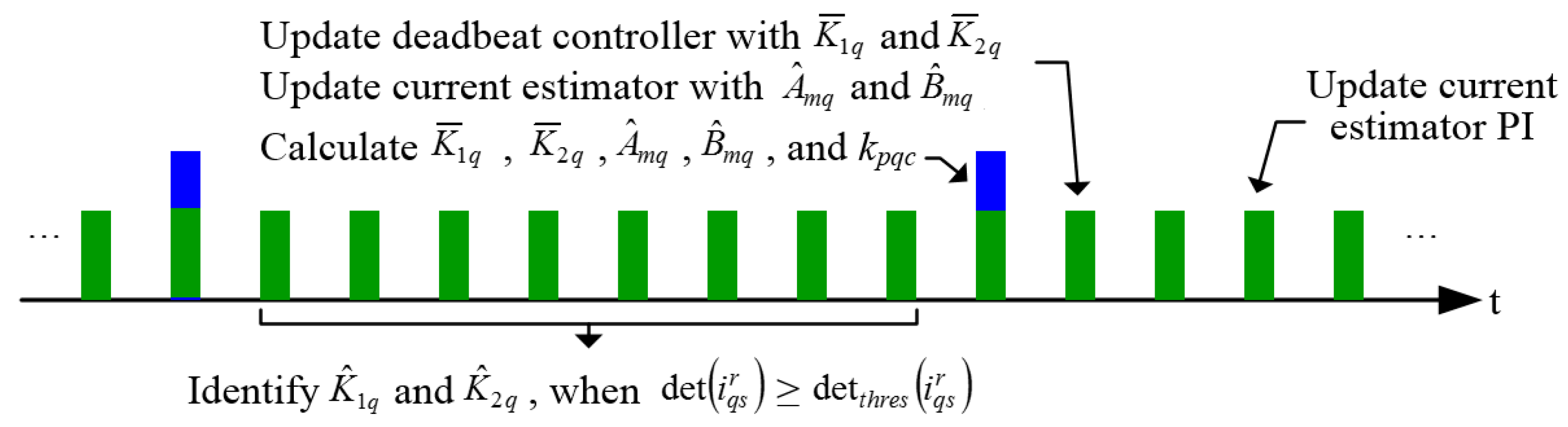
6.4. Gain Update Method
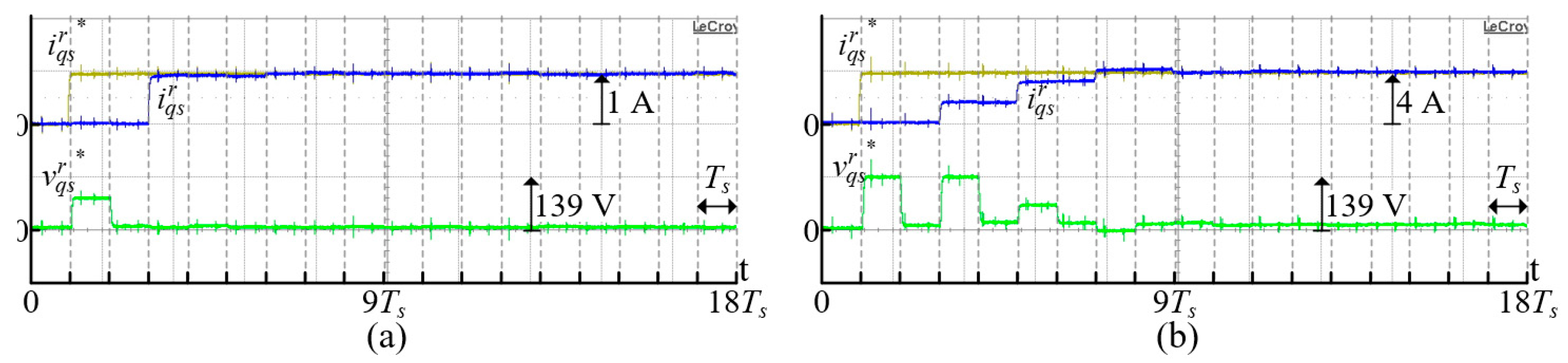
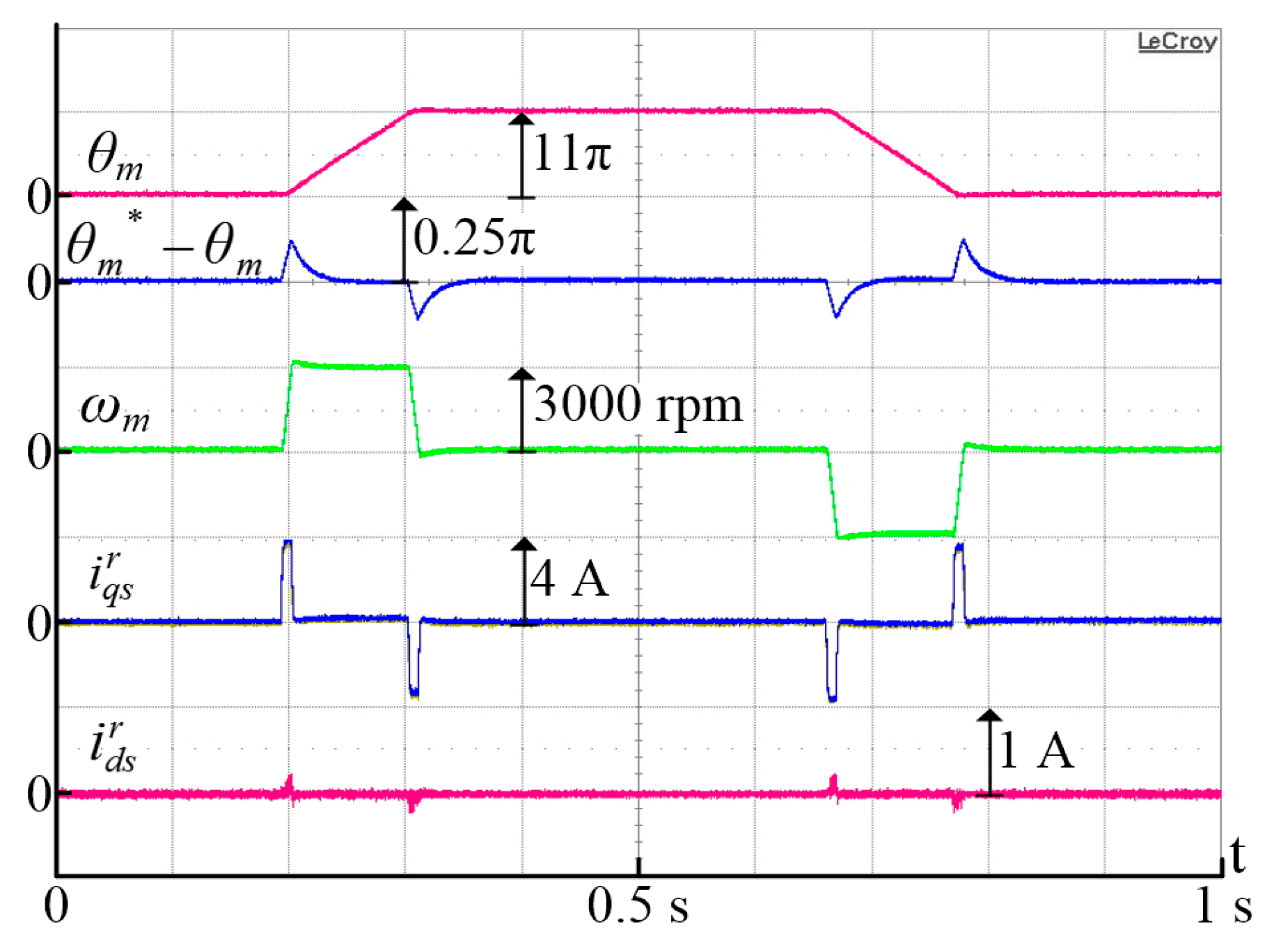
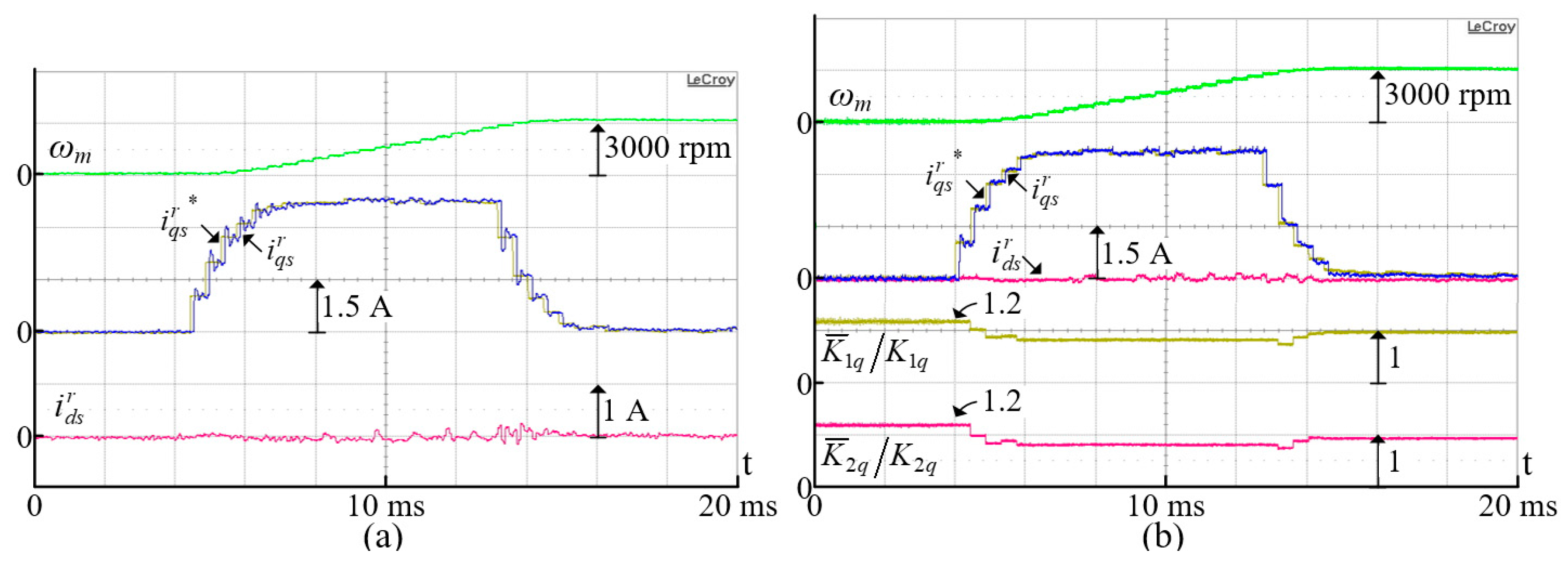
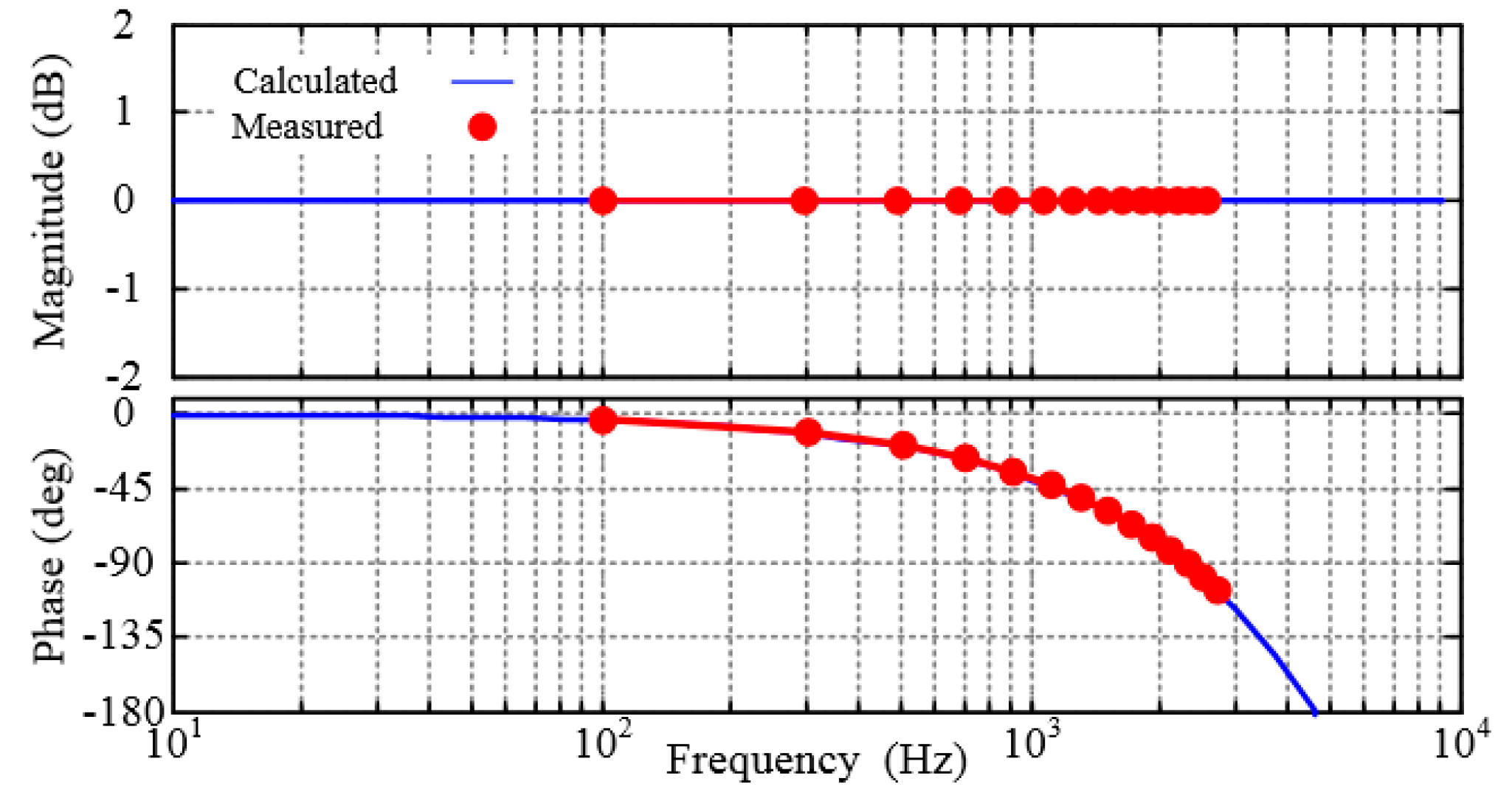
7. Experimental Results
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Value | Unit | |
|---|---|---|
| DC voltage | 300 | V |
| Sampling period for current loop (Ts) | 55 | μs |
| Sampling period for speed and position loop | 440 | μs |
| Dead-time | 2 | μs |
| Value | Unit | |
|---|---|---|
| Rated speed/pole pairs | 3000/5 | rpm |
| Rated current | 4 | A |
| Magnet flux (λm) | 0.042 | Wb-turns |
| Stator resistance (rs) | 1.4 | Ω |
| d-axis inductance (Lds) | 4.46 | mH |
| q-axis inductance (Lqs) | 4.54 | mH |
References
- Bocker, J.; Beineke, S.; Bahr, A. On the Control Bandwidth of Servo Drives. In Proceedings of the 13th European Conference Power Electronics Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
- Huh, K.K.; Lorenz, R.D. Discrete-Time Domain Modeling and Design for AC Machine Current Regulation. In Proceedings of the Conference Record 42th IEEE/IAS Annual Meeting, New Orleans, LA, USA, 23–27 September 2007; pp. 2066–2073. [Google Scholar]
- Kim, H.; Degner, M.W.; Guerrero, J.M.; Briz, F.; Lorenz, R.D. Discrete-Time Current Regulator Design for AC Machine Drives. IEEE Trans. Ind. Appl. 2011, 46, 1425–1435. [Google Scholar]
- Yepes, A.G.; Vidal, A.; Malvar, J.; Lopez, O.; Jesus, D.G. Tuning Method Aimed at Optimized Setting Time and Overshoot for Synchronous Proportional-Integral Current Control in Electric Machines. IEEE Trans. Power Electron. 2014, 29, 3041–3054. [Google Scholar] [CrossRef]
- Andersson, A.; Thiringer, T. Assessment of an Improved Finite Control Set Model Predictive Current Controller for Automotive Propulsion Applications. IEEE Trans. Ind. Electron. 2019, 67, 91–100. [Google Scholar] [CrossRef]
- Cortes, P.; Kazmierkowski, M.P.; Kennel, R.M.; Quevedo, D.E.; Rodriguez, J. Predictive Control in Power Electronics and Drives. IEEE Trans. Ind. Electron. 2008, 55, 4312–4324. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, D.; Liu, J.; Gao, S.; Xu, W. Performance Improvement of Model-Predictive Current Control of Permanent Magnet Synchronous Motor Drives. IEEE Trans. Ind. Appl. 2017, 53, 3683–3695. [Google Scholar] [CrossRef]
- Lin, C.K.; Liu, T.H.; Yu, J.T.; Fu, L.C.; Hsiao, C.F. Model-Free Predictive Current Control for Interior Permanent-Magnet Synchronous Motor Based on Current Difference Detection Technique. IEEE Trans. Ind. Electron. 2014, 61, 667–681. [Google Scholar] [CrossRef]
- Lin, C.K.; Yu, J.T.; Lai, Y.S.; Yu, H.C. Improved Model-Free Predictive Current Control for Synchronous Reluctance Motor Drives. IEEE Trans. Ind. Electron. 2016, 63, 3942–3953. [Google Scholar] [CrossRef]
- Young, H.A.; Perez, M.A.; Rodriguez, J. Analysis of Finite-Control-Set Model Predictive Current Control with Model Parameter Mismatch in a Three-Phase Inverter. IEEE Trans. Ind. Electron. 2016, 63, 3100–3107. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Koh, B.K.; Lee, Y.I. A Comparison of Finite Control Set and Continuous Control Set Model Predictive Control Schemes for Speed Control of Induction Motors. IEEE Trans. Ind. Informat. 2018, 14, 1334–1346. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Liang, J.; Xia, B.; Walker, P.D.; Zhang, N. Deadbeat Control Based on a Multipurpose Disturbance Observer for Permanent Magnet Synchronous Motors. IET Electr. Pwer Appl. 2018, 12, 708–716. [Google Scholar] [CrossRef]
- Isermann, R. Digital Control System; Springer: Berlin, Germany, 1981. [Google Scholar]
- Moon, H.T.; Kim, H.S.; Youn, M.J. A Discrete-Time Predictive Current Control for PMSM. IEEE Trans. Power Electron. 2003, 18, 464–472. [Google Scholar] [CrossRef]
- Walz, S.; Lazar, R.; Buticchi, G.; Liserre, M. Dahlin-Based Fast and Robust Current Control of a PMSM in Case of Low Carrier Ratio. IEEE Access 2019, 7, 102199–102208. [Google Scholar] [CrossRef]
- Yang, S.M.; Lee, C.H. A Deadbeat Current Controller for Field Oriented Induction Motor Drives. IEEE Trans. Power Electron. 2002, 17, 772–778. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, B.; Mei, Y. Deadbeat Predictive Current Control of Permanent-Magnet Synchronous Motors with Stator Current and Disturbance Observer. IEEE Trans. Power Electron. 2017, 32, 3818–3834. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Zhang, Y. Model Predictive Current Control for PMSM Drives with Parameter Robustness Improvement. IEEE Trans. Power Electron. 2019, 34, 1645–1657. [Google Scholar] [CrossRef]
- Boileau, T.; Leboeuf, N.; Babak, N.M.; Farid, M.T. Online Identification of PMSM Parameters: Parameter Identifiability and Estimator Comparative Study. IEEE Trans. Ind. Appl. 2011, 47, 1944–1957. [Google Scholar] [CrossRef]
- Liu, K.; Zhu, Z.Q.; Zhang, Q.; Zhang, J. Influence of Nonideal Voltage Measurement on Parameter Estimation in Permanent-Magnet Synchronous Machine. IEEE Trans. Ind. Electron. 2012, 59, 2438–2447. [Google Scholar] [CrossRef]
- Hamida, M.A.; Leon, J.D.; Glumineau, A.; Boisliveau, R. An Adaptive Interconnected Observer for Sensorless Control of PM Synchronous Motors with Online Parameter Identification. IEEE Trans. Ind. Electron. 2013, 60, 739–748. [Google Scholar] [CrossRef]
- Ichikawa, S.; Timita, M.; Doki, S.; Okuma, S. Sensorless Control of Permanent-Magnet Synchronous Motors Using Online Parameter Identification Based on System Identification Theory. IEEE Trans. Ind. Electron. 2006, 53, 363–372. [Google Scholar] [CrossRef]
- Inoue, Y.; Yamada, K.; Morimoto, S.; Sanada, M. Effectiveness of Voltage Error Compensation and Parameter Identification for Model-Based Sensorless Control. IEEE Trans. Ind. Appl. 2009, 45, 213–221. [Google Scholar] [CrossRef]
- Feng, G.; Lai, C.; Mukherjee, K.; Kar, N.C. Current Injection-Based Online Parameter and VSI Nonlinearity Estimation for PMSM Drives Using Current and Voltage DC Components. IEEE Trans. Transp. Electrific. 2016, 2, 119–128. [Google Scholar] [CrossRef]
- Mohamed, Y.A.I.; Saadany, E.F.E. Robust High Bandwidth Discrete-Time Predictive Current Control with Predictive Internal Model–A Unified Approach for Voltage-Source PWM Converters. IEEE Trans. Power Electron. 2008, 23, 126–136. [Google Scholar] [CrossRef]
- Yang, S.M.; Lin, K.W. Automatic Control Loop Tuning for Permanent-Magnet AC Servo Motor Drives. IEEE Trans. Ind. Electron. 2016, 63, 1499–1506. [Google Scholar] [CrossRef]
- Shen, G.; Yao, W.; Chen, B.; Wang, K.; Lee, K.; Lu, Z. Automeasurement of the Inverter Output Voltage Delay Curve to Compensate for Inverter Nonlinearity in Sensorless Motor Drives. IEEE Trans. Power. Electron. 2014, 29, 5542–5553. [Google Scholar] [CrossRef]


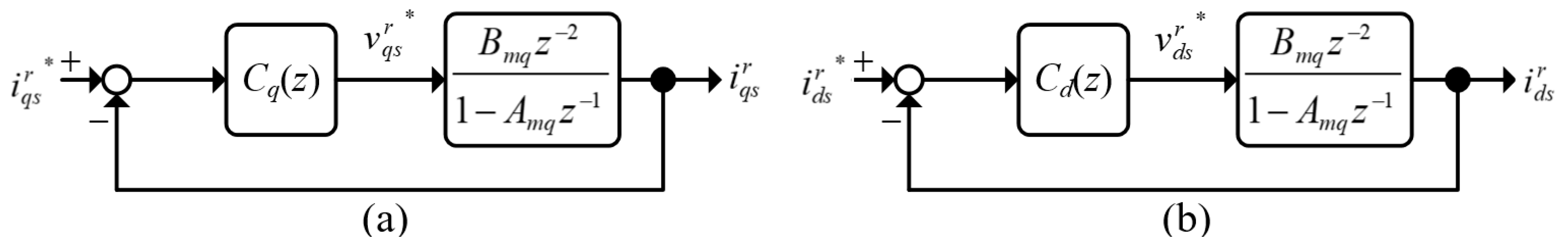










© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, Z.-C.; Huang, C.-H.; Yang, S.-M. Online Current Loop Tuning for Permanent Magnet Synchronous Servo Motor Drives with Deadbeat Current Control. Energies 2019, 12, 3555. https://doi.org/10.3390/en12183555
You Z-C, Huang C-H, Yang S-M. Online Current Loop Tuning for Permanent Magnet Synchronous Servo Motor Drives with Deadbeat Current Control. Energies. 2019; 12(18):3555. https://doi.org/10.3390/en12183555
Chicago/Turabian StyleYou, Zih-Cing, Cheng-Hong Huang, and Sheng-Ming Yang. 2019. "Online Current Loop Tuning for Permanent Magnet Synchronous Servo Motor Drives with Deadbeat Current Control" Energies 12, no. 18: 3555. https://doi.org/10.3390/en12183555
APA StyleYou, Z.-C., Huang, C.-H., & Yang, S.-M. (2019). Online Current Loop Tuning for Permanent Magnet Synchronous Servo Motor Drives with Deadbeat Current Control. Energies, 12(18), 3555. https://doi.org/10.3390/en12183555





